Keywords

1 Introduction

The observed variations of the main magnetic field generated in the Earth’s core have characteristic timescales that exceed several years, since shorter variations are almost completely shielded by the electrically conductive mantle [1,2,3,4]. Exceptions, relatively small in terms of their energy, are short-term phenomena such as torsional oscillations [5,6,7,8,9] with periods of a few years and jerks with durations of about a year [10,11,12,13], subject of active current study.

Changes of the Earth’s internally generated magnetic field spanning the time scales from a few years to a few thousand years are classified as secular variation (SV) [14, 15]. The main characteristic of SV is its period; however, strictly speaking, it is not a period, but rather a characteristic time or timescale, since SV periodicity in the mathematical sense of the word has not been proved. This variation results from the effect of magnetic induction in the fluid outer core and from effects of magnetic diffusion in the core and the mantle [16, 17].

Temporal spectrum of the observed geomagnetic field has a semi-discrete structure described by the following three types of variations [18,19,20,21,22,23].

  1. 1.

    Variations of the first type are characterized by harmonic periods from a few tens up to a hundred years (in particular T = 20, 30 and 60 years). These variations are likely to be of internal origin, potentially being a manifestation of torsional oscillations in the fluid core [24]. The morphology of these variations and the high correlation with changes in the Earth’s diurnal rotation also confirm their classification as torsional [25,26,27,28]. The physical nature of this class of variations as well as the mechanism of torsional waves generation is however still a matter of debate [5,6,7,8,9, 16, 29].

  2. 2.

    The main part of the SV spectrum includes periods of several hundred and several thousand years (in particular, 360, 600, 900, 1200, 1800, 2700, 3600, 5400 and 9000 ± 10% years). These variations occur in the upper part of the core (or at the core-mantle boundary) due to thermal and compositional convection, propagation of magnetohydrodynamic waves and short-scale diffusion processes [17, 30,31,32,33,34,35]. The variation of 9000 ± 1000 years is interpreted as the natural oscillation of the hydromagnetic dynamo [17, 19, 22, 32].

  3. 3.

    Fluctuations with timescales of tens of thousands of years and longer are primarily connected with decay modes, which are not oscillations. They result from magnetic diffusion processes in the entire core [14, 32,33,34]. Here we do not consider the longer variations, because they could hardly be covered by the model used in the present work, restricted by only < 200 years of observations.

Determination of the geomagnetic field frequency/time characteristics has always been an important problem, which has been approached using various mathematical methods: spectral Fourier analysis [28, 36], maximum entropy method [37, 38], autoregressive and correlation methods [39], and wavelet analysis [40, 41]. A detailed review of mathematical approaches used in the search of periodicities in geomagnetic data series is presented in [42, 43] and references therein.

One of the most significant limitations of the above-mentioned essentially harmonic methods [38,39,40,41,42,43] is the fundamental impossibility of studying a period exceeding the length of the time series. For example, according to tests performed by Jackson and Mound [24], the longest meaningful period would not exceed 75% of the time series length. Besides, an assumption about broadband continuous spectrum of field variability becomes more and more popular [17, 42,43,44,45]. Already in 1983 Barton [46] performed spectral analysis of declination and inclination time series, concluding that there was no evidence for discrete periods but, instead, for bands of preferred periods at 60–70, 400–600, 1000–3000 and 5000–8000 years. Still earlier, in 1968, Currie [47] argued that the temporal power spectrum of geomagnetic field observations was governed by a power law, i.e., fk, where f is the frequency. More recently, Olson et al. [17] and Bouligand et al. [48, 49] carried out a detailed study of the frequency spectrum of dipole field variations from numerical geodynamo simulations, and found a broadband variability appropriately described by power laws. Their results agree well with the composite paleomagnetic dipole spectrum [50].

Against this background of numerous attempts of revealing any periodicity or characteristic times, we developed an original statistical approach to determining the long-term characteristics of time series [51,52,53,54]. For our studies, we chose the totally integrated energy E of the observed potential part of the main geomagnetic field [52,53,54]. This energy could be formally derived by means of the well-known work of Lowes [55], but apparently this was made only much later [56, 57]. This total energy seems to be the most adequate global variable for studying global temporal variations of the observed geomagnetic field.

The study of the energy contained in the potential part of the main geomagnetic field was initiated in [58]. Based on this work, Lowes [55, 59] determined the contribution of n-th spherical harmonic degree to the radial energy density normalized by the area of the sphere:

$$ R_n = (n + 1)\left( \frac{a}{r} \right)^{2n + 4} \sum_m^n {\left[ {(g_n^m )^2 + (h_n^m )^2 } \right]} $$
(1)

Here \(g_n^m \,\) and \(h_n^m\) are standard Gauss coefficients, a is the radius of the Earth and r is the radius of a sphere that varies from the core radius rc to infinity. The resulting Rn is expressed in (Tesla)2.

Expression (1) is the so-called “spatial Lowes-Mauersberger power spectrum”. We prefer (perhaps, more physically correct) to name it r-density spectrum of energy renormalizing it to J/m. This density varies with r, while the total energy E is spatially independent, compare with [43]. To derive an expression for energy, we first obtain the contribution of the n-th harmonic degree Rn (in J/m) to the radial energy density of the potential field as

$$ \frac{4\pi r^2 }{{2\mu_0 }}R_n = 2\pi a^2 \frac{n + 1}{{\mu_0 }}\left( \frac{a}{r} \right)^{2(n + 1)} \sum_{m = 0}^n {\left[ {(g_n^m )^2 + (h_n^m )^2 } \right]} $$
(2)

Integrating (2) along the radius from the core-mantle boundary r = rc (where rc is the radius of the Earth’s core) to infinity we obtain the contribution of the n-th harmonic degree to the total energy (in J) as:

$$ \begin{aligned} E_n & = 2\pi a^{2n + 4} \frac{n + 1}{{\mu_0 }}\sum_{m = 0}^n {\left[ {(g_n^m )^2 + (h_n^m )^2 } \right]} \int_{r_c }^{ + \infty } {\frac{dr}{{r^{2n + 2} }}} \\ & = \frac{2\pi a^3 }{{\mu_0 }}\left( {\frac{a}{{r_{\text{c}} }}} \right)^{2n + 1} \frac{n + 1}{{2n + 1}}\sum_{m = 0}^n {\left[ {(g_n^m )^2 + (h_n^m )^2 } \right]} \\ \end{aligned} $$
(3)

There is actually no need to integrate to infinity since even when integrating up to r equal to several times rc, one obtains practically the same result with error less than 0.3%.

The integral energy E used in this study is simply the sum of all En terms from (3).

We use this E to obtain timescales T = E/(dE/dt) which will be defined in detail in the next section. As an analogue to our timescales we consider the instantaneous correlation time of Hulot and Le Mouël [60] involving the ratio of the Gauss coefficients to their time-derivatives as

$$ \tau_n = \left\{ {\frac{{\sum_{m = 0}^n {[(g_n^m )^2 + (h_n^m )^2 ]} }}{{\sum_{m = 0}^n {[(\dot{g}_n^m )^2 + (\dot{h}_n^m )^2 ]} }}} \right\}^{1/2} . $$
(4)

This timescale is usually linked to spectrum (1) by many authors [33, 44, 48, 49] studying the geomagnetic field variation and \(\tau_n\) is one of the most popular characteristic timescale definitions. However, it is not so good for global investigations because it is a function of n. A more significant limitation of the correlation time (4) is that it is defined only on the Earth’s surface. At the same time, the geomagnetic field energy is dominated by contributions from the regions located near the Earth’s core, which is obvious from formulae (2) and (3). The integral energy E proposed here and all its derivatives are free from these disadvantages [52,53,54].

The primary goal of this paper is to explore global characteristic geomagnetic timescales. The detailed definition of these follows in Sect. 2 where we explore the 1840–2020 evolution of E and its timescales T. Section 3 deals with statistical and probability distribution descriptions of the annual energy timescales T. In Sect. 4 we outline the most statistically significant characteristic timescales for the geodynamo correlating them with modern/ancient geomagnetic field, trends, alpha effects, drifts and fluid velocities in the Earth’s core. Final Sect. 5 presents a brief discussion and conclusions of this study.

2 Energy Evolution and Discrete Timescales

The central idea of this paper is to define and explore the characteristic instantaneous geomagnetic timescales T as the ratio of the global energy E, as defined by formula (3), to its time-derivative, referred to thereafter as power P = dE/dt. Thus, by definition

$$ T \equiv E/(dE/dt) $$
(5)

An immediate bonus of this definition is introducing a positive/negative sign of the timescale T. The sign indicates rise/decay of the energy E. Definitions similar to (5), but without taking sign into account and in most cases local, has long been used [22, 33, 49, 60,61,62]. The innovation of our study is however to apply timescale definition (5) to a global evolutional and statistical analysis of geomagnetic energy as defined by (3).

The simplest time-process related to definition (5) is the one with T = const. Viewing (5) as a differential equation, we introduce its solution as an exponential dependence:

$$ E = C\,\exp (t/T) $$
(6)

Therefore, a reasonable initial step would be to model the evolution of E by exponents (6) on some suitable time intervals where the timescale T could be regarded as constant.

We use the open-source (http://www.spacecenter.dk/files/magnetic-models/COV-OBSx1) geomagnetic model COV-OBS.x1 [63, 64]. It spans 1840–2020 and is based on annual initial data. The authors of the model successfully extrapolated it down to the half-year (yr/2) resolution. We used the results of this extrapolation for definition of the annual time-derivative dE/dt. It was calculated for each year as a ratio [E(t − yr/2) − E(t + yr/2)]/yr. Here t is the particular year and yr is 1 year. The corresponding time-values are transformed into seconds for calculating P = dE/dt in Watts.

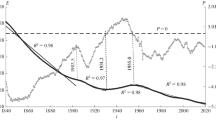
Figure 1 shows the evolution of the energy E and power P = dE/dt. At two instances, marked in Fig. 1, the power becomes zero, which corresponds to the local energy extrema. These naturally divide the plot of E into three monotonous parts that can be approximated by exponential functions (6) with an error less than 2% for two intervals from 1932 to 2020, whereas the first interval 1840–1931.5 was approximated with error about 5%. Dividing this interval into two, we reduce the approximation errors to their minimum values placing the dividing point near the first local maximum of P. We consider important to have an error sufficiently lower than the energy variation 2(Emax − Emin)/(Emax + Emin) = 0.07. Thus, we split the evolution of E for the given time interval into 4 epochs approximated with an error δ less than 3% (t is the time in years) as:

$$ \left\{ \begin{gathered} E = {136} \cdot e^{t/T_a } \cdot 10^{18} \;{\text{J}},\;\;{\text{where}}\;1840 < t < 1903.5\;{\text{and}}\;\delta = {\text{2\% }} \hfill \\ E = \,{28}{\text{.6 }} \cdot e^{t/T_b } \cdot 10^{18} \;{\text{J}},\;\;{\text{where}}\;1904 < t < 1931.5\;{\text{and}}\;\delta = {\text{3\% }} \hfill \\ E = \,{3}{\text{.22}} \cdot e^{t/T_c } \cdot 10^{18} \;{\text{J}},\;\;{\text{where}}\;1932 < t < 1955.5\;{\text{and}}\;\delta = {\text{2\% }} \hfill \\ E = \,{19}{\text{.9}} \cdot e^{t/T_d } \cdot 10^{18} \;{\text{J}},\;\;{\text{where}}\;1956 < t < 2020\;{\text{and}}\;\delta = {\text{2\% }} \hfill \\ \end{gathered} \right. $$
(7)
Fig. 1
figure 1

Evolution of the global energy E (multicolor) and power P (blue) obtained from COV-OBS.x1 model [63, 64]. The left vertical axis is for E (Joules), the right for P (Watts). Exponential functions (7) approximate the energy E with approximation errors δ, indicated as a percentage. The horizontal dashed line corresponds to P = 0. The inset shows the continuous evolution of timescales T in years following (5). The relevant sections of the evolution of the energy and timescales are marked with the same colors. The corresponding discrete timescales (7–8) are displayed by horizontal lines

Full size image

At this level of accuracy those exponential functions are indistinguishable from linear fits. However, we can still extract timescales with errors of the order a few percents in a sense of (5–6). Accordingly, the ratio of energy to power (T = E/P) gives preliminary and rather rough discrete (in spectral sense) timescales for these four epochs (7) in years:

$$ T_a = - 637{;}\;T_{\text{b}} = - 1342;\;T_c = 2564;\;T_d = - 1818. $$
(8)

Now, we apply (5) and calculate the continuous evolution of the timescales for every year from 1840 to 2020. The result is shown in the inset to Fig. 1. The evolution is divided into relatively long, up to several decades, epochs alternating with short hyperbolic T-transitions. Hyperbolic T-transitions can have duration of several years and associated with the extrema of the energy where P = 0 and |T| tends to infinity.

3 Statistics of the Characteristic Timescales

Following Fig. 1, we can reasonably split the energy evolution during 1840–2020 into four statistically different intervals (7). Each interval is described with a single spectral line or constant timescale T, (Eq. (8) and Fig. 1). The longest intervals are characterized with negative timescales indicating energy decrease. We observe three intervals with negative T and only one interval with positive T.

The intervals with negative T allow to estimate roughly the most probable (− 637 years) and median (about − 1500 years) timescales. At the same time, the shortest interval with positive timescales (2564 years) corresponds to a minor mode in a bimodal timescale distribution.

We now explore statistical and spectral features of annual timescales.

We apply formulae (5) and (3) to the Gauss coefficients provided by the COV-OBS.x1 model [64], and calculate 180 annual T values. The obtained timescales are then arranged in increasing order. This is essential for identifying extreme and median values, and for plotting probability distributions of T. The latter will be thereafter referred to as Ti, with i running from 1 to the maximum value I = 180.

Supposing that each Ti appears with the same probability, we plot the cumulative distribution function (thereafter CDF) for them as shown in Fig. 2.

Fig. 2
figure 2

The cumulative distribution function CFD for timescales Ti as defined in Sect. 2. Main statistical parameters of the timescales are shown (see Table 1 for details) with triangles. A confidence interval (75%) centered at MDN is shown in a darker color

Full size image

The statistical parameters of the timescales are presented in a Table 1. All parameters were calculated from their standard definitions [65, 66] except for geometric mean (GM), which is explained at the end of this section.

Table 1 Statistical parameters of the characteristic timescales Ti, years
Full size table

We start our analysis from the general (calculated from all Ti) median timescale MDN = − 1176 years (the first row of MDN column in Table 1). From this MDN we obtain a 75% confidence interval (based on the number of samples) bounded by timescales − 3400 and − 470 years that is visualized in Fig. 3. Therefore, the dominant trend is the decrease of energy with millennial characteristic timescales. This is similar to the timescales of drifts of the largest magnetic heterogeneities, and of the observed global geomagnetic variations [14, 35, 44, 61, 62, 67,68,69,70].

Fig. 3
figure 3

The probability density function f(T) as defined by formula (11). The most probable or mode value is Mo = − 483 years and the secondary positive mode is 2180 years

Full size image

These 156 (87% of all Ti) Ti values with decreasing (T < 0) energy may be viewed as reflecting a major timescale of the order of 103 years (− 1347 years in the MDN column, last line of the Table 1) characterizing the modern geodynamo with diminishing energy of the observed geomagnetic field. This is in agreement with the characteristic timescale for the dipolar component of the geomagnetic field [15, 17, 32, 35, 60, 61].

The remaining 13% or 24 positive Ti values indicate the energy increase of a timescales of about a few thousand years (3127 years in MDN column, second line of Table 1).

General arithmetic mean AM is 1889 years (the first line in the AM column of Table 1). This positive value does not seem appropriate bearing in mind the domination of negative timescales. An explanation to this apparent contradiction is the large standard deviations and RMS values. Indeed, we observe heavy tails which are linked to extreme minimal (−43,800 years) and maximal (592,000 years) timescales and are obviously overpopulated with respect to a Gaussian distribution. Thus, the true timescale distribution is not Gaussian but clearly bimodal. This is shown in Fig. 3 by a probability density function f(T), which we defined as the simplest finite difference of CDF (see Fig. 2)

$$ f_k = (I - 1)^{ - 1} (T_{k + 1} - T_k )^{ - 1} . $$
(9)

Here a density function f(T) = dCDF/dT is a constant fk for Tk+1 < T < Tk, and k runs from 1 to I − 1. Outside the [T1, TI] interval f(T) = 0. The integral of fdT over all T is obviously equal to one. The most probable, or mode, value Mo would then be − 483 years. It is respectively two and four times smaller than the median and mean values considered above. Besides, we observe extremely uneven f variation and very large range of timescales covering more than 9 orders of magnitude from a value lower than − 104 years up to over than 105 years.

In view of the above, a geometric mean should be a more appropriate measure of a characteristic mean timescale. The geometric mean is well-defined for positive-only values (see GM column in the Table 1 for Ti > 0), and can similarly be defined for Ti < 0 as follows:

$$ GM_+ = \left( {\prod_{i = 157}^{180} {T_i } } \right)^{1/24} = {4571}\;{\text{years,}}\;\;GM_- = - \left( {\prod_{i = 1}^{156} {|T_i } |} \right)^{1/156} = - {1380}\;{\text{years}} $$
(10)

Introducing \(S = \sum {{\text{sgn}} (T_i )\lg |T_i |}\) we write \(GM_\pm = {\text{sgn}} (S)10^{|S|/L}\), where L is 24 for positive and 156 for negative Ti. Combining these expressions for positive and negative Ti, we obtain for a general geometric mean (note the minus sign in the exponent to GM+):

$$ GM = - |GM_- |^{156/180} (GM_+ )^{ - 24/180} = - 174\;{\text{years}} $$
(11)

This value reflects a characteristic “rapid” change of the energy E in the modern era. Besides, |GM| is close to the length (180 years) of the field annual means series. The corresponding geomagnetic field timescale is about 2GM = − 348 years, doubled due to the proportionality of the energy to the square of the field.

Let us round up this section by pointing out that there exists an extended gap containing no Ti’s (Fig. 2). The range of missing values extends from the maximum negative T value (column MAX in Table 1) of − 465 years to the minimum positive T value (column MIN) of + 1855 years. A timescale within this gap might occur, but with very low probability, as seen in Fig. 3.

4 Physical Interpretation of Timescales Statistics

In order to make physical interpretation we need to compare our magnetic energy timescales (5) with known timescales of the magnetic field. Generally, such a comparison could be done by magnitude only, because there are rather different definitions of the timescales, e.g., compare expression (4) from Hulot and Le Mouël [60] with our expression (5) based on (3). Taking into consideration that axial dipole component is dominant everywhere, we could establish a rough relationship between our timescales T0 and τ0, similar to Hulot and Le Mouël’s definition:

$$ T_{0} = |(g_1^0 )^2 /[d(g_1^0 )^2 /dt]| = |g_1^0 /[dg_1^0 /dt]|/2 = \tau_0 /2. $$
(12)

We thus assume that our energy timescale is roughly a half of magnetic field timescale defined in a way similar to our definitions (3) and (5). This also follows from the simple consideration that the energy E is proportional to a square of the magnetic field intensity. Carrying out a Fourier transform on both parts of this relationship one sees immediately that an energy frequency is twice the magnetic field frequency.

An absolute value of the median energy timescale |MDN| = 1176 years corresponds to a geomagnetic field timescale of 2352 years. This is about 30% larger than the exponential decay time of the modern axial dipole, which is about 1700–1900 years and characterized by decreasing trend [32, 34, 35, 71]. Therefore, the magnetic field associated with energy E apparently decays slower even in comparison with the slowest decay mode of the axial dipole.

Dividing the radius of the Earth’s core (rc = 3.5 × 106 m) by this characteristic time (2352 years), we obtain α = 0.04 mm/s, which is an order of magnitude less than the known convective velocities [14, 35, 67, 72,73,74,75,76,77]. Therefore, α should roughly be an analogue of the alpha effect of the mean field theory [77,78,79,80,81]. However, it works against generation reducing the magnetic field intensity because all timescales MDN < 0. To consider the generation we use positive timescales (~ 4000 years, the second row of MDN/GM column in Table 1) giving α+ = 0.02 mm/s. The known molecular magnetic diffusion is about 1 m2/s [80], while the plausible turbulent mean field diffusion η could be a few times larger [77,78,79,80,81]. Thus, a mean-field magnetic Reynolds number value Rm is:

$$ {\text{Rm}} = \alpha_+ r_c /\eta \approx 20 - 40. $$
(13)

This value is subcritical for a mean-field geodynamo [81,82,83]. The integral energy E decays due to prevalence of negative timescales over the positive, as shown above.

Let us find a correlation between the theoretically known [14, 35, 67, 72,73,74,75,76,77] convective velocities and corresponding observational drift velocities of magnetic heterogeneities [14, 35, 44, 61, 62, 67,68,69,70]. The convective velocities and drift velocities in the Earth’s core are of the order of 0.3 mm/s. Dividing the radius of the Earth’s core by these velocities, we obtain the values ~ 350 years that are approximately twice the absolute value of the geometric mean timescale |GM|.

This 348 years global magnetic field timescale is comparable with global “single time constant of secular variation” τsec = 535 years defined by Christensen and Tilgner [33], who used a set of numerical dynamo models together with direct observations to derive scaling relations for magnetic energy. A similar value ω−1 = 415 years was obtained by Bouligand et al. [49] where in their abstract they say: “based on dynamo simulations, the authors argue that a prior for the observational geomagnetic field over decennial to millennial periods can be constructed from the statistics of the field during the short satellite era”. Adopting similar approach, we use bicentennial statistics to describe timescales from a half-thousand up to a half-million years.

5 Concluding Remarks

The central idea of this paper is to explore a characteristic timescale T which is defined as a ratio of the total geomagnetic energy E to its time derivative, or power P = dE/dt. The energy is defined as resulting from integrating from the core-mantle boundary to infinity. The major bonus of such definition is a possibility to determine from direct observation a number of timescales sufficiently larger than the length of the studied time series.

Thus, we can explore insufficiently studied millennia-long processes on the base of relatively short, but much better studied and detailed, time series covering less than several centuries. This is especially important for the geomagnetic variations of long, i.e., from 450 years for T in this study, and even much longer, up to half-million years, characteristic times, which could be obtained from rather short periods of direct measurements.

A novel feature we introduce is to consider the sign which appears at these timescales. Negative timescales T < 0 correspond to energy E decrease, while positive ones to energy E rise. The definitions of timescales similar to our have long been used [22, 33, 49, 60,61,62], but these studies did not take a sign into the account.

We investigated evolution of the power P and 180 annual timescales obtained from COV-OBS.x1 model [63, 64]. The evolution of timescales T is naturally divided into relatively long, up to several decades, epochs with almost constant T alternating with short hyperbolic T-transitions. Hyperbolic T-transitions can have duration of several years and are associated with the extrema of the energy where P = 0 and |T| increases infinitely.

For the study period covering 1840–2020, evolution of energy E is approximated by exponents with an error of less than 3% if the period is divided into four intervals. Each interval is described with a single spectral line or constant timescale T. We observe three intervals with negative T and only one interval with positive T. The intervals with negative T allow to estimate roughly the most probable (− 637 years) and median (about − 1500 years) timescales. At the same time, the shortest interval with positive timescales (2564 years) corresponds to the minor mode in a timescale bimodal distribution.

Statistical analysis of the annual T values determines their standard statistical characteristics. 87% of T values are negative and indicate the decreasing T < 0 trend in energy with the major timescale in the order of one thousand years attributable to modern geodynamo. The remaining 13% indicate the energy increase on the minor timescale that is about a few thousand years. The median timescale is − 1180 years, while the arithmetic mean is + 1890 years. Less probable heavy tails associated with the extreme minimal (− 43,800 years) and maximal (592,000 years) timescales are the likely reason for extremely large standard deviation and RMS values of 44,400 and 44,600 years respectively. There is a gap between − 465 and 1855 years with no T. However, any T could appear there with a probability similar to the probability for the revealed heavy tails.

We calculated and plotted the bimodal probability density function with the most probable value, or mode Mo ≈ − 500 years. The absolute value of |Mo| is two-four times smaller than absolute values of median and mean considered above. The minor mode is about 2000 years. Additionally, we observe extremely non-smooth variations in this function and a very wide range of time scales, covering more than 9 orders of magnitude, from below − 104 years to more than 105 years.

A geometric mean appears a more suitable measure to represent averaged timescales. The mean geometric timescale, GM = − 174 years (Sect. 3), is consistent with the known convective velocities ~ 0.3 mm/s, the observable magnetic heterogeneities drifts [14, 35, 68,69,70] and with global geomagnetic timescales of about 500 years found previously [33, 49].

The prevalent timescales are from half a thousand years, where the maximum number of timescales is concentrated, and up to a few thousand years. Corresponding characteristic velocities or the mean field alpha effects ensure subcritical geodynamo. The obtained results are also consistent with periodical and spectral estimates from geodynamo simulations and geomagnetic field models for both the modern era and the ancient geomagnetic field.

To conclude, we consider how timescales T introduced here relate to long-term periods Q, obtained from studies of geomagnetic field spectrum in paleomagnetic and geodynamo models. Timescales T as defined here have physical meaning only on the interval where the change in energy E is monotonous. For the geomagnetic field, this interval is approximately 2T as follows from formula (12). A periodic process can then be subdivided into a minimum of two such intervals, one corresponding to increasing energy (field strength), and another to decreasing. Thus, in this case Q = 4T, but a large gap in the energy derivative dE/dt arises when energy evolution changes from growth to decrease. This gap can be made smaller if the period Q is subdivided into four intervals, approximately corresponding to a sinusoidal dependence monotonously growing from zero to a maximum, decreasing to zero and then to a minimum, and finally growing back to zero, resulting in Q = 8T. Discontinuities can be further reduced by an approximation like one discussed in Sect. 2, Fig. 1 and formulae (7) and (8). This is of course only a rough estimate, and in order to reveal a relationship between Q and T, it would be necessary to compare the behavior of the same data series within the framework of the classical and our statistical spectral approach. However, for now, we restrict ourselves to the simplest relation

$$ Q = AT $$
(14)

We assume an approximate value of A ≈ 6, as an average resulting from the above estimates for Q. Bearing in mind a high uncertainty of this number, it can still be argued that the results of all long-term (covering > 104 years) studies of geomagnetic field evolution known to us [23, 43, 48, 49, 84,85,86,87] agree reasonably well with the results obtained in this work based only on a 200-year long series.