General Solution of the 2D Navier–Stokes Equations and Its Application to Shock Wave Problems

Abstract

We consider a general solution of the 2D Navier–Stokes equations of viscous gas flow in cylindrical coordinate system (r, θ), which is needed especially for problems of viscous gas flow in angular region. It is found that the solution in the form of an r-power expansion can be obtained starting from its exact solution of the basic equations along a line r = 0 in (r, θ)-plane. Among many possible applications, we utilize it here for problems in Mach reflection consisting of three shocks: Determination of its shock angles, which is crucial to the problem of “Neumann paradox” of Mach reflection; and the investigation of the structure of triple point at the intersection of three shocks, which is the problem of “non-Rankine-Hugoniot zone (NRHZ)”. Furthermore, the present solution is expected to be utilized for the problem of jet stream from a black hole in space.

1 Introduction

We are concerned with a general solution of the 2D Navier–Stokes equations of viscous, compressible flow in cylindrical coordinate system (r, θ). Although this kind of solution is needed for the investigation of various flows in angular flow region, not much is known especially of its general solution. Here we consider it in the form of power series expansion in r, whose coefficients are functions of θ only. It is found that these functions can be determined successively starting from its zeroth order solution, which is in fact an exact solution of the basic equations along a line r = 0 in (r, θ)-plane.

We utilize this solution to the investigation of viscous, compressible flow problems. In particular, in this paper, we use it for two problems in connection with the cause-study of the von Neumann paradox [1,2,3] appearing in phenomenon of Mach reflection in shock waves interaction. One is the determination of angles of three shocks, the other is the internal structure of triple point in Mach reflection, which is the problem of the flow in its non-Rankine-Hugoniot zone [4] (NRHZ). It is needed also to see the change in feature of shock wave reflection itself in rarefied gas flow as the zone is widened enough to influence the main flow field [5]. Furthermore, the present solution expressed in (x, y) system includes the fan-like flow which is expected to be utilized for the cause study on the appearance of jet near a black hole in space by adjusting the boundary condition on the surface around the black hole.

In the followings, first we present basic equations of continuity, momentum and energy for viscous, compressible fluid in (r, θ) coordinates system, which appear seldom in literature. Then we transform them to a form convenient for an r-power expansion to derive equations for its coefficient-functions. They are ordinary differential equations and are integrated successively starting from its zeroth order solution which is an exact solution of the basic equations along r = 0. This first order solution is found to include a fan-like source flow from the origin in (x, y)-plane and to be utilized for the problem of determining the shock angles in Mach reflection, which is the subject of Sect. 3. Next in the 4th section we utilize the solution with more terms to see the feature of the flow field in the non-Rankine-Hugoniot zone appearing in Mach reflection and the result is compared with the one obtained numerically on the basis of Boltzmann-BGK equation [6].

2 The 2D Navier–Stokes Equations for Gas in Cylindrical Coordinate System

Let the velocity, the density, the pressure and the temperature be

$${{\varvec{V}}} = \, (V_r ,V_{\theta} ),\rho,p,T$$

(1)

where V_r, V_θ are respectively (r, θ) components of the velocity V.

The 2D Navier–Stokes equations system for gas flow is composed of equations of continuity, momentum and energy. Here we have to express them in cylindrical coordinate and they are complicated because of the curvilinear coordinate system and the terms due to the flow of compressible gas.

First the continuity equation is simply given as,

$$\frac{\partial }{\partial r}(\rho V_r r) + \frac{\partial }{\partial \theta }(\rho V_\theta ) = 0$$

(2)

Equation of momentum for compressible fluid in Cartesian coordinate system is expressed in the familiar vector form:

$$\rho \left( {{{\varvec{v}}} \cdot {\text{grad}}} \right){{\varvec{v}}} = - {\text{grad}}p + \mu \left[ {\Delta {{\varvec{v}}} + \left( {1 / 3} \right){\text{grad}}\left( {{\text{div}}{{\varvec{v}}}} \right)} \right],$$

where μ and v are the coefficient of viscosity (assumed constant) and the flow velocity in Cartesian coordinate system, respectively. Thus

$${{\varvec{v}}} = \, \left( {u,v} \right), u = V_r {\text{cos}}\theta-V_{\theta} {\text{sin}}\theta, v = V_r {\text{sin}}\theta + V_{\theta} {\text{cos}}\theta.$$

With some manipulation, this equation is transformed into cylindrical coordinate system as follows:

$$\begin{aligned} &\rho \left( {V_r \frac{{\partial V_r }}{{\partial r}} + \frac{{V_\theta }}{r}\frac{{\partial V_r }}{{\partial \theta }} - \frac{{V_\theta ^2 }}{r}} \right) \\ &\qquad \qquad = - \frac{{\partial p}}{{\partial r}} + \mu \left[ {\Delta V_r - \frac{{V_r }}{{r^2 }} - \frac{2}{{r^2 }}\frac{{\partial V_\theta }}{{\partial \theta }} + \frac{1}{3}\frac{\partial }{{\partial r}}\frac{1}{r}\left( {\frac{{\partial rV_r }}{{\partial r}} + \frac{{\partial V_\theta }}{{\partial \theta }}} \right)} \right] \hfill \\ \end{aligned}$$

(3)

$$\begin{aligned} &\rho \left( {V_r \frac{\partial V_\theta }{{\partial r}} + \frac{V_\theta }{r}\frac{\partial V_\theta }{{\partial \theta }} + \frac{V_r V_\theta }{r}} \right) \\ &\qquad \qquad = - \frac{\partial p}{{r\partial \theta }} + \mu \left[ {\Delta V_\theta - \frac{V_\theta }{{r^2 }} + \frac{2}{r^2 }\frac{\partial V_r }{{\partial \theta }} + \frac{1}{3}\frac{1}{r}\frac{\partial }{\partial \theta }\frac{1}{r}\left( {\frac{\partial rV_r }{{\partial r}} + \frac{\partial V_\theta }{{\partial \theta }}} \right)} \right], \hfill \\ \end{aligned}$$

(4)

where

$$\Delta \equiv \frac{\partial^2 }{{\partial r^2 }} + \frac{1}{r}\frac{\partial }{\partial r} + \frac{1}{r^2 }\frac{\partial^2 }{{\partial \theta^2 }}.$$

Energy equation for compressible fluid is given by

$$\rho \left[ {\left( {{{\varvec{V}}} \cdot grad} \right)E + p\left( {{{\varvec{V}}} \cdot grad} \right)\left( {1 / \rho } \right)} \right] = \kappa \Delta T + {\Phi ,}$$

where E, Κ, Φ are the internal energy per unit mass, the heat conductivity (assumed constant), and the dissipation function due to viscosity.

This equation is expressed in (r, θ) coordinates as follows,

$$\rho \left[ {\left( {V_r \frac{\partial }{\partial r} + V_\theta \frac{\partial }{r\partial \theta }} \right)E + p\left( {V_r \frac{\partial }{\partial r} + V_\theta \frac{\partial }{r\partial \theta }} \right)\frac{1}{\rho }} \right] = \kappa \Delta T + {\Phi ,}$$

(5)

with

$$\begin{aligned} {\rm{\Phi }} & = \mu \left\{ {2\left[ {\left( {\frac{{\partial V_r }}{{\partial r}}} \right)^2 + \left( {\frac{{\partial V_\theta }}{{r\partial \theta }} + \frac{{V_r }}{r}} \right)^2 } \right] + \left( {\frac{{\partial V_r }}{{r\partial \theta }} + \frac{{\partial V_\theta }}{{\partial r}} - \frac{{V_\theta }}{r}} \right)^2 } \right.\, \\ &\quad \left. { - \frac{2}{3}\left( {\frac{{\partial V_r }}{{\partial r}} + \frac{{\partial V_\theta }}{{r\partial \theta }} + \frac{{V_r }}{r}} \right)^2 } \right\}. \\ \end{aligned}$$

(6)

These equations are supplemented by thermal and caloric equations of state for a perfect gas:

$$p = \rho RT,$$

(7)

$$E = c_v T,$$

(8)

where R is the specific gas constant and c_v is the specific heat at constant volume (assumed constant).

For convenience, Eqs. (5) and (6) are rewritten as follows:

$$\rho r\left[ {\left( {V_r r\frac{\partial }{\partial r} + V_\theta \frac{\partial }{\partial \theta }} \right)E + p\left( {V_r r\frac{\partial }{\partial r} + V_\theta \frac{\partial }{\partial \theta }} \right)\frac{1}{\rho }} \right] = \kappa r^2 \Delta T + {\Psi ,}$$

(5a)

$$\begin{aligned} {\rm{\Psi }} & = \mu \left\{ {2\left[ {\left( {r\frac{{\partial V_r }}{{\partial r}}} \right)^2 + \left( {\frac{{\partial V_\theta }}{{\partial \theta }} + V_r } \right)^2 } \right] + \left( {\frac{{\partial V_r }}{{\partial \theta }} + r\frac{{\partial V_\theta }}{{\partial r}} - V_\theta } \right)^2 } \right.\, \\ &\quad \left. { - \frac{2}{3}\left( {r\frac{{\partial V_r }}{{\partial r}} + \frac{{\partial V_\theta }}{{\partial \theta }} + V_r } \right)^2 } \right\}. \end{aligned}$$

(6a)

We transform these to a form convenient for r-power expansion in non-dimensional expression. Let representative velocity, pressure and density respectively be U, p₀ and ρ₀ and use the temperature T₀ given by the perfect gas relation (7) by p₀ = ρ₀RT₀, the velocity of sound C_0, by $C_0 = \sqrt {\gamma RT_0 }$ (γ: specific heats ratio), Prandtl number σ given by $\sigma = {{c_p \mu } / \kappa }$ and representative length r₀ by r₀ = μ/(ρ₀C₀), where c_p is the specific heat at constant pressure (assumed constant). Making use of these relations, we represent the variables r, V_r, V_Θ, ρ, p, T, E, as well as the dissipation function Ψ and Laplacian Δ in dimensionless form by,

$$\begin{aligned} &{r / {r_0 }} \to r,\,\,\,\,{{V_r } / {C_0 }} \to V_r ,\,\,\,\,{{V_\theta } / {C_0 }}\,\, \to V_\theta ,\,\,{\rho / {\rho _0 }}\,\, \to \rho \,\,,\,{p / {p_0 }} \\ &\to p,\,\,\,{T / {T_0 }} \to T,\,\,\,{E / {c_v T_0 }} \to E,{{\,{{\Psi }}} / {\kappa T_0 }} \to {{\Psi ,}}\,\,\,\,\,\,{\Delta / {r_0^2 }} \to \Delta \hfill \\ \end{aligned}$$

The dimensionless internal energy E turns out to be identical with the dimensionless temperature T (see Eq. 14).

Thus the basic equations and relations Eqs. (2)–(8) are expressed as follows:

From Eq. (2):

$$\frac{\partial }{\partial r}\left( {r\rho V_r } \right) + \frac{\partial }{\partial \theta }\left( {\rho V_\theta } \right) = 0.$$

(9)

From Eq. (3):

$$\begin{aligned} &\frac{4}{3}r^2 \frac{\partial^2 V_r }{{\partial r^2 }} + \frac{1}{3}r\frac{\partial }{\partial r}\left( {\frac{\partial V_\theta }{{\partial \theta }} + 4V_r } \right) + \frac{\partial^2 V_r }{{\partial \theta^2 }} - \frac{4}{3}V_r - \frac{7}{3}\frac{\partial V_\theta }{{\partial \theta }} = rY_1 , \hfill \\ &Y_1 \equiv \rho \left[ {V_r r\frac{\partial V_r }{{\partial r}} + V_\theta \left( {\frac{\partial V_r }{{\partial \theta }} - V_\theta } \right)} \right] + \frac{r}{\gamma }\frac{\partial p}{{\partial r}}. \hfill \\ \end{aligned}$$

(10)

From Eq. (4):

$$\begin{aligned} &r^2 \frac{\partial^2 V_\theta }{{\partial r^2 }} + r\frac{\partial }{\partial r}\left( {\frac{1}{3}\frac{\partial V_r }{{\partial \theta }} + V_\theta } \right) + \frac{4}{3}\frac{\partial^2 V_\theta }{{\partial \theta^2 }} - V_\theta + \frac{7}{3}\frac{\partial V_r }{{\partial \theta }} = rY_2 , \hfill \\ \,&Y_2 \equiv \rho \left[ {V_r r\frac{\partial V_\theta }{{\partial r}} + V_\theta \left( {\frac{\partial V_\theta }{{\partial \theta }} + V_r } \right)} \right] + \frac{1}{\gamma }\frac{\partial p}{{\partial \theta }}. \hfill \\ \end{aligned}$$

(11)

From Eqs. (5a) and (6a), and by redefining ${\Phi } \equiv \sigma \left( {\gamma - 1} \right){\Psi }$,

$$r^2 \Delta T + {\Phi } = rZ,$$

$$\begin{aligned} {{\Phi }} & = \sigma \left( {\gamma - 1} \right)\left\{ {2\left[ {\left( {r\frac{{\partial V_r }}{{\partial r}}} \right)^2 + \left( {\frac{{\partial V_\theta }}{{\partial \theta }} + V_r } \right)^2 } \right] + \left( {\frac{{\partial V_r }}{{\partial \theta }} + r\frac{{\partial V_\theta }}{{\partial r}} - V_\theta } \right)^2 } \right. \\ &\quad \left. { - \frac{2}{3}\left( {r\frac{{\partial V_r }}{{\partial r}} + \frac{{\partial V_\theta }}{{\partial \theta }} + V_r } \right)^2 } \right\}, \\ \end{aligned}$$

(12)

$$\begin{aligned} Z & \equiv \frac{\sigma }{\gamma }\rho \left[ {\left( {V_r r\frac{\partial }{\partial r} + V_\theta \frac{\partial }{\partial \theta }} \right)T + (\gamma - 1)p\left( {V_r r\frac{\partial }{\partial r} + V_\theta \frac{\partial }{\partial \theta }} \right)\frac{1}{\rho }} \right] \\ & = \frac{\sigma }{\gamma }\left[ {\rho \left( {V_r r\frac{\partial }{\partial r} + V_\theta \frac{\partial }{\partial \theta }} \right)T - (\gamma - 1)T\left( {V_r r\frac{\partial }{\partial r} + V_\theta \frac{\partial }{\partial \theta }} \right)\rho } \right]. \\ \end{aligned}$$

From Eqs. (7) and (8):

$$p = \rho T,$$

(13)

$$E = T.$$

(14)

3 The r-power Expansion

We seek a solution of the system of equations consisting of Eqs. (9)–(14) in the form of an r-power expansion:

$$\begin{aligned} &V_r = \sum_{n = 0}^\infty {r^n V_r ^{(n)} \,\,} ,\,V_\theta = \sum_{n = 0}^\infty {r^n V_\theta ^{(n)} } ,\,\rho = \sum_{n = 0}^\infty {r^n \rho ^{(n)} } ,\,p = \sum_{n = 0}^\infty {r^n p^{(n)} } \, \\ &T = \sum_{n = 0}^\infty {r^n T^{(n)} }, \\ \end{aligned}$$

(15)

where $V_r^{(n)}$,$V_\theta^{(n)}$,$\rho^{(n)}$,$p^{(n)}$, $T^{(n)}$(n = 0, 1, 2…) are all assumed to be functions of θ only. Similarly, the functions Y₁, Y₂, and Z are expressed as power series with respect to r:

$$Y_1 = \sum_{n = 0}^\infty {r^n Y_1^{(n)} } ,\,\,Y_2 = \sum_{n = 0}^\infty {r^n Y_2^{(n)} } ,\,\,Z = \sum_{n = 0}^\infty {r^n Z^{(n)} } ,$$

(16)

where $Y_1^{(n)}$, $Y_2^{(n)}$, $Z^{(n)}$ are also assumed to be functions of θ only.

We substitute Eqs. (15), (16) to Eqs. (9)–(13) and comparing the same order terms of r, we have equations to determine $V_r^{(n)} (\theta )$,$V_\theta^{(n)} (\theta )$,$\rho^{(n)} \left( \theta \right)$,$p^{\left( n \right)} (\theta )$, $T^{\left( n \right)} (\theta )$ (n = 0, 1, 2,…). From Eq. (9):

$$\begin{array}{*{20}l} {V_\theta ^{(0)} D\rho ^{(n)} + \rho ^{(n)} [(n + 1)V_r^{(0)} + DV_\theta ^{(0)} ] = X^{(n - 1)} }, \hfill \\ {X^{( - 1)} = 0}, \hfill \\ {X^{(n - 1)} = - \sum_{i = 0}^{n - 1} \{ V_\theta ^{(n - i)} D\rho ^{(i)} + [(n + 1)V_r^{(n - i)} + DV_\theta ^{(n - i)} ]\,\rho ^{(i)} \} }. \hfill \\ \end{array}$$

(17)

where D stands for the differential operator with respect to θ,

$$D \equiv {d / {d\theta }}.$$

From Eq. (10):

$$\begin{aligned} &[3D^2 + 4(n^2 - 1)]V_r^{(n)} + (n - 7)DV_\theta ^{(n)} = 3Y_1^{(n - 1)} , \\& Y_1^{( - 1)} = 0, \\ & Y_1^{(n - 1)} = \sum_{i = 0}^{n - 1} {\sum_{j = 0}^{n - 1 - i} {\rho ^{(n - 1 - i - j)} \left[ {jV_r^{(i)} V_r^{(j)} + V_\theta ^{(i)} \left( {DV_r^{(j)} - V_\theta ^{(j)} } \right)} \right]} } \, \\ &\qquad \qquad + \frac{{n - 1}}{\gamma }p^{(n - 1)} \quad (n \ge 1). \\ \end{aligned}$$

(18)

From Eq. (11):

$$\begin{aligned} & (n + 7)DV_r^{(n)} + [4D^2 + 3(n^2 - 1)]V_\theta^{(n)} = 3Y_2^{(n - 1)}, \\& Y_2^{( - 1)} = 0, \\ & Y_2^{(n - 1)} = \sum_{i = 0}^{n - 1} {\sum_{j = 0}^{n - 1 - i} {\rho^{(n - 1 - i - j)} } } \left[ {jV_r^{(i)} V_\theta^{(j)} + V_\theta^{(i)} \left( {DV_\theta^{(j)} + V_r^{(j)} } \right)} \right] \\ & \qquad \qquad + \frac{1}{\gamma }Dp^{(n - 1)} \,\,\,\left( {n \ge { 1}} \right). \\ \end{aligned}$$

(19)

From Eq. (12):

$$\begin{aligned} &(D^2 + n^2 )T^{(n)} = - {\rm{\Phi }}^{(n)} + Z^{(n - 1)} \\ &{\rm{\Phi }}^{(n)} = \frac{1}{{n{\text{!}}}}\left[ {\frac{{\partial ^n }}{{\partial r^n }}{\rm{\Phi }}} \right]_{r = 0} , \\ & Z^{( - 1)} = 0, \\ & Z^{(n - 1)} = \frac{\sigma }{\gamma }\left[ {\sum_{i = 0}^{n - 1} {\sum_{j = 0}^{n - 1 - i} {\rho ^{(n - 1 - i - j)} \left( {jV_r^{(i)} T^{(j)} + V_\theta ^{(i)} DT^{(j)} } \right)} } } \right. \\ &\qquad \qquad \qquad \left. - \left( {\gamma - 1} \right){\sum_{i = 0}^{n - 1} {\sum_{j = 0}^{n - 1 - i} {T^{(n - 1 - i - j)} } \left( {V_r^{(i)} j\rho ^{(j)} + V_\theta ^{(i)} D\rho ^{(j)} } \right)} } \right]. \\ \end{aligned}$$

(20)

From Eq. (13):

$$p^{(n)} = \sum_{i = 0}^n {\rho^{(i)} T^{(n - i)} } .$$

(21)

4 Solutions of Eqs. (17)–(20)

In close look at Eqs. (17)–(20), we can see that these equations can be integrated successively starting from the zeroth order solution $V_r^{(0)} (\theta )$, $V_\theta^{(0)} (\theta )$ which are exact solution of the momentum equation of Eqs. (10), (11) or Eqs. (3), (4) of the original Navier–Stokes equations system at r = 0. These can be seen in the following.

First, we rearrange Eqs. (18), (19) for $V_r^{(n)} (\theta )$, $V_\theta^{(n)} (\theta )$ as

$$\left[ \begin{gathered} 3D^2 + 4(n^2 - 1)\,\,\,\,\,\,\,\,(n - 7)D \hfill \\ (n + 7)D\,\,\,\,\,\,\,\,4D^2 + 3(n^2 - 1) \hfill \\ \end{gathered} \right]\left[ \begin{gathered} V_r^{(n)} \hfill \\ V_\theta^{(n)} \hfill \\ \end{gathered} \right] = 3\left[ \begin{gathered} Y_1^{(n - 1)} \hfill \\ Y_2^{(n - 1)} \hfill \\ \end{gathered} \right],$$

(22)

which is reduced to,

$$\Delta^{(n)} \left[ \begin{gathered} V_r^{(n)} \hfill \\ V_\theta^{(n)} \hfill \\ \end{gathered} \right] = 3\left[ \begin{gathered} \Delta_1^{(n - 1)} \hfill \\ \Delta_2^{(n - 1)} \hfill \\ \end{gathered} \right],$$

where

$\begin{aligned} \Delta ^{(n)} &= \left| \begin{gathered} 3D^2 + 4(n^2 - 1)\,\,\,\,\,\,\,\,(n - 7)D \hfill \\ (n + 7)D\,\,\,\,\,\,\,\, 4D^2 + 3(n^2 - 1) \hfill \\ \end{gathered} \right| = 12\left[ {D^2 + (n + 1)^2 } \right] \\ &\quad \left[ {D^2 + (n - 1)^2 } \right] \\ \Delta _1^{(n - 1)} &= \left| \begin{gathered} Y_1^{(n - 1)} \,\,\,\,\,\,\,\,(n - 7)D \hfill \\ Y_2^{(n - 1)} \,\,\,\,\,\,\,\,4D^2 + 3(n^2 - 1) \hfill \\ \end{gathered} \right| = \left[ {4D^2 + 3(n^2 - 1)} \right]Y_1^{(n - 1)} \\ &\quad - (n - 7)DY_2^{(n - 1)} \\ \Delta _2^{(n - 1)} &= \left| \begin{gathered} 3D^2 + 4(n^2 - 1)\,\,\,\,\,\,\,\,Y_1^{(n - 1)} \,\,\,\,\,\, \hfill \\ (n + 7)D\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,Y_2^{(n - 1)} \,\,\,\,\, \hfill \\ \end{gathered} \right| = - (n + 7)DY_1^{(n - 1)} \\ &\quad + \left[ {3D^2 + 4(n^2 - 1)} \right]Y_2^{(n - 1)} \\ \end{aligned}$,

from which we can have the solutions $V_r^{(n)}$, $V_\theta^{(n)}$. Since $\Delta^{(0)}$ and $\Delta^{(1)}$ are of singular nature with double roots unlike the case with n > 1, these two cases for n = 0 and 1 are exceptional and we have to deal them separately.

For n = 0, from Eqs. (18), (19),

$$Y_1^{( - 1)} = Y_2^{( - 1)} = 0,$$

and

$$\Delta^{(0)} = 12(D^2 + 1)^2 ,\Delta_1^{( - 1)} = \Delta_2^{( - 1)} = 0,$$

we therefore have

$$\begin{aligned} V_r^{(0)} &= - A^{(0)} \cos \left( {\theta + \alpha^{(0)} } \right) - B^{(0)} \left[ {\left( {1 / 7} \right)\sin \left( {\theta + \beta^{(0)} } \right) + \theta \cos \left( {\theta + \beta^{(0)} } \right)} \right], \\ V_\theta^{(0)} &= A^{(0)} \sin \left( {\theta + \alpha^{(0)} } \right) + B^{(0)} \theta \sin \left( {\theta + \beta^{(0)} } \right), \hfill \\ \end{aligned}$$

(23)

where A⁽⁰⁾, B⁽⁰⁾, α⁽⁰⁾, β⁽⁰⁾ are integration constants.

From Eq. (17), we have the differential equation for ρ⁽⁰⁾,

$$V_\theta^{(0)} D\rho^{(0)} + \rho^{(0)} [V_r^{(0)} + DV_\theta^{(0)} ] = 0.$$

By substituting Eq. (23), we have the simple differential equation for ρ⁽⁰⁾

$$\frac{{\rho ^{(0)^ \prime}}} {{\rho ^{(0)} }} = - \frac{6}{7}\frac{{B^{(0)} \sin \left( {\theta + \beta ^{(0)} } \right)}}{{A^{(0)} \sin \left( {\theta + \alpha ^{(0)} } \right) + B^{(0)} \theta \sin \left( {\theta + \beta ^{(0)} } \right)}},$$

(24)

from which the solution is given by

$$\rho^{(0)} = C^{(0)} \exp \left[ { - \frac{6}{7}\int^\theta {\frac{{B^{(0)} \sin \left( {\theta + \beta^{(0)} } \right)}}{{A^{(0)} \sin \left( {\theta + \alpha^{(0)} } \right) + B^{(0)} \theta \sin \left( {\theta + \beta^{(0)} } \right)}}d\theta } } \right],$$

(25)

where C⁽⁰⁾ is an integration constant. The equation for the temperature T⁽⁰⁾ is derived from Eq. (20) for n = 0.

Since $Z^{( - 1)} = 0$, we have

$$\begin{aligned} T{^{{(0})}}^{{{\prime\prime}}} & = - \Phi^{{(0)}} = - \sigma (\gamma - 1)\left[ {2/3\left( {V{_{\theta }^{{(0)^{\prime}}}} + V{_{r}^{{(0)}}} } \right)^{2} } \right] + \left[ {\left( {V{_{r}^{{(0)^{\prime}}}} + V{_{\theta }^{{(0)}} }} \right)^{2}} \right] \\ & = - \sigma (\gamma - 1)\frac{8}{{49}}B{^{{(0)^{2} }}} \left[ {7 + \cos \;2\left( {\theta + \beta ^{{(0)}} } \right)} \right]. \\ \end{aligned}$$

Thus we easily have the solution for T⁽⁰⁾ as,

$$T^{(0)} = - {\frac{4}{49}} \sigma (\gamma - 1)B^{(0)2} \left[ {7\theta ^2 - \frac{1}{2}\cos 2(\theta + \beta ^{(0)} )} \right] + D^{(0)} \theta + E^{(0)} ,$$

(26)

where D⁽⁰⁾ and E⁽⁰⁾ are integration constants, and from Eq. (21) p⁽⁰⁾ is given by

$$p^{(0)} = \rho^{(0)} T^{(0)} .$$

(27)

For n = 1, the following relations hold.

$$\begin{aligned} Y_1^{(0)} &= \rho ^{(0)} V_\theta ^{(0)} \left( {DV_r^{(0)} - V_\theta ^{(0)} } \right), \hfill \\ Y_2^{(0)} &= \rho ^{(0)} V_\theta ^{(0)} \left( {DV_\theta ^{(0)} + V_r^{(0)} } \right) + \frac{1}{\gamma }Dp^{(0)}, \hfill \\ \Delta ^{(1)} &= 12(D^2 + 4)D^2 ,\Delta _1^{(0)} = 4D^2 Y_1^{(0)} + 6DY_2^{(0)} ,\,\Delta _2^{(0)} = - 8DY_1^{(0)} + 3D^2 Y_2^{(0)}. \hfill \\ \end{aligned}$$

(28)

Then we have $Y_1^{(0)}$ and $Y_2^{(0)}$ as functions of, θ and so $\Delta_1^{(0)}$ and $\Delta_2^{(0)}$ are determined. Thus we have,

$$\begin{aligned} \,V_r^{(1)} &= A^{(1)} \cos 2(\theta + \alpha^{(1)} ) + B_1^{(1)} + 3\Delta_1^{(0)} /\Delta^{(1)} ,\hfill \\ V_\theta^{(1)} &= - A^{(1)} \sin 2(\theta + \alpha^{(1)} ) + B_2^{(1)} + 3\Delta_2^{(0)} /\Delta^{(1)}. \hfill \\ \end{aligned}$$

(29)

For n > 1, we have generally from Eq. (22),

$$\begin{aligned} V_r^{(n)} &= - A^{(n)} \cos (n + 1)(\theta + \alpha^{(n)} ) - \frac{n - 1}{{n + 1}}B^{(n)} \cos (n - 1)(\theta + \beta^{(n)} ) \\&\quad + 3\Delta_1^{(n - 1)} /\Delta^{(n)} , \\ V_\theta^{(n)} &= A^{(n)} \sin (n + 1)(\theta + \alpha^{(n)} ) + B^{(n)} \sin (n - 1)(\theta + \beta^{(n)} ) + 3\Delta_2^{(n - 1)} /\Delta^{(n)} , \\ \end{aligned}$$

(30)

where A⁽ⁿ⁾, B⁽ⁿ⁾, α⁽ⁿ⁾, β⁽ⁿ⁾ (n = 0, 1, 2,…) are integration constants. $3\Delta_1^{(n - 1)} /\Delta^{(n)}$ and $3\Delta_2^{(n - 1)} /\Delta^{(n)}$ are the particular solutions of inhomogeneous equation Eq. (22), formally given as

$$\begin{aligned} 3\frac{{\Delta_1^{(n - 1)} }}{{\Delta^{(n)} }} &= \frac{1}{16n}\int {\left\{ {\left( {n + 7} \right)\left[ {\sin \left( {n + 1} \right)\left( {\theta - \theta^{\prime}} \right) - \left( {n - 7} \right)\sin \left( {n - 1} \right) \left( {\theta - \theta^{\prime}} \right)} \right]Y_1^{(n - 1)} \left( {\theta^{\prime}} \right)} \right.} \\ &\quad+ \left. {\left[ {\left( {n - 7} \right)\cos \left( {n + 1} \right)\left( {\theta - \theta^{\prime}} \right) - \cos \left( {n - 1} \right)\left( {\theta - \theta^{\prime}} \right)} \right]Y_2^{(n - 1)} \left( {\theta^{\prime}} \right)} \right\}d\theta^{\prime}. \\ \end{aligned}$$

$$\begin{aligned} 3\frac{{\Delta_2^{(n - 1)} }}{{\Delta^{(n)} }} &= \frac{1}{16n}\int {\left\{ {\left( {n + 7} \right)\left[ {\cos \left( {n + 1} \right)\left( {\theta - \theta^{\prime}} \right) - \cos \left( {n - 1} \right)\left( {\theta - \theta^{\prime}} \right)} \right]Y_1^{(n - 1)} \left( {\theta^{\prime}} \right)} \right.} \\ &\quad+ \left. {\left[ {\left( {n + 7} \right)\sin \left( {n - 1} \right)\left( {\theta - \theta^{\prime}} \right) - \left( {n - 7} \right)\sin \left( {n + 1} \right)\left( {\theta - \theta^{\prime}} \right)} \right]Y_2^{(n - 1)} \left( {\theta^{\prime}} \right)} \right\}d\theta^{\prime}. \\ \end{aligned}$$

Unlike the velocity components $V_r^{(n)}$ and $V_\theta^{(n)}$, other variables ρ⁽ⁿ⁾, p⁽ⁿ⁾, T⁽ⁿ⁾ are all systematically dealt for n ≥ 1. We have from Eq. (17),

$$V_\theta^{(0)} \rho^{(n)^ \prime} + \rho^{(n)} [(n + 1)V_r^{(0)} + V_\theta^{(0)^ \prime} ] = X^{(n - 1)} .$$

(31)

Since $V_\theta^{(0)}$, $V_r^{(0)}$ are known from Eq. (23) and X ^(n–1) is supposed to be known from preceding functions of the (n–1)-th order terms (X^(–1) = 0), we can solve it to have,

$$\rho^{(n)} = e^{ - W_n } \left[ {\int_\theta {e^{W_n } X^{(n - 1)} /V_\theta^{(0)} d\theta^{\prime}} + C^{(n)} } \right],$$

(32)

where functions W_n (n = 0, 1, 2, …) are integrating factors given by

$$W_n \equiv \int {\frac{{\left( {n + 1} \right)V_r^{(0)} + DV_\theta^{(0)} }}{{V_\theta^{(0)} }}d\theta^{\prime}} ,$$

and C⁽ⁿ⁾ (n = 0, 1, 2, …) are integration constants.

To obtain the temperature, we use Eq. (20) and we have T⁽ⁿ⁾ and p⁽ⁿ⁾ for n ≥ 1:

$$T^{(n)} = F^{(n)} \sin n(\theta + \gamma^{(n)} ) + \frac{1}{D^2 + n^2 }\left( { - {\Phi }^{(n)} + Z^{(n - 1)} } \right)$$

(33)

$$p^{(n)} = \sum_{i = 0}^n {\rho^{(i)} T^{(n - i)} }$$

(34)

where F⁽ⁿ⁾, γ⁽ⁿ⁾ (n = 0, 1, 2, …) are integration constants.

5 The Zeroth-Order Solution and Its Use for the Determination of Shock Angles in Mach Reflection

Here we consider to utilize the zeroth order solution to the problem of determining the shock angles in Mach reflection whose configuration is illustrated in Fig. 1a, b. Incident, reflected, and Mach stem shock waves are respectively represented by I, R and m. The incident shock angle ω is defined by the angle made by the incident shock and the incoming flow direction (the x-axis). The shock anglesλ, ω΄ are respectively those between the direction of the incoming flow and the tangents of reflected shock R and Mach stem m at their intersection point r = 0. Here we express these shock curves in $(r, \theta)$ coordinates:

• $\theta = \theta_{1,2}(r)$ respectively for m and R, and expand these as

• $\theta_{1,2}^{(n)} =\sum_{n=0}^{\infty}{r^{n}\theta_{1,2}^{(n)}}$ where

• $\theta_{1,2}^{(n)} = (\partial^{n}\theta/\partial r^{n})r = 0 {,}$ especially,

• $\theta_{1}^{(0)}= -\lambda {,}$

• $\theta_{2}^{(0)}= \omega$ to which we utilize the above zeroth order solution, while higher terms of $n > 0$ are related with the bending of shock lines determined successively by the higher order solutions.

Fig. 1

a Configuration of Mach reflection. b Three-shock theory model

This problem is related to resolve the ‘von Neumann paradox’ [1], which is explained symbolically in Fig. 2, where the ω΄ versus ω curves plotted in the reproduction of famous diagram by Harrison and Bleakney [6] given in Bleakney and Taub [3] are compared with the theoretical curves resulting from the three-shock theory by von Neumann [2]. Figure 2a is for the strong wave case of its inverse pressure ratio ξ  = 0.2, while Fig. 2b is the weak case of ξ = 0.9. We can see that these curves agree well with experimental data in weak shock cases, whereas very poor agreement in stronger cases, which displays a paradoxical feature.

Fig. 2

ω΄ versus ω curves. a ξ =  0.2 (strong case). b ξ = 0.9 (weak case) compared with Harrison and Bleakney’s data [6]

There have been many contributions to resolve this situation, so many to refer only a few [4, 7,8,9,10,11,12] from its representatives. Most of these propose the postulation of inserting fan-like flow in the frame of original three-shock theory to result the resolution of the paradox. While these are essentially based on the perfect gas flow theory, some [4, 7, 9] consider it in viscous flow or kinetic model to have results consistent with experimental data. In the followings we show that the present zeroth order solution itself is a fan-like flow and its use is in fact the same as the one in viscous flow model. This fact can give a justification to the postulation of inserting fan-like flow proposed in most of these literatures above.

We are concerned here with the flow field between two shock waves R and m shown in Fig. 1, which is supposed to be almost uniform and parallel. So that the velocity component $V_\theta^{(0)}$ in Eq. (23) must vanish at a certain value of θ in between (–λ, ω΄) while the density gradient $\rho^{(0)^{\prime}}$ must remain finite. This means that the numerator and the denominator of right-hand-side of Eq. (24) must vanish for the same value of θ (say, θ₀), thus we have α⁽⁰⁾ =  β⁽⁰⁾. Then we have

$$\begin{aligned} V_r^{(0)} &= - \left( {A^{(0)} + B^{(0)} \theta } \right)\cos \left( {\theta + \alpha^{(0)} } \right) - B^{(0)} \left[ {\left( {1 / 7} \right)\sin \left( {\theta + \alpha^{(0)} } \right)} \right], \hfill \\ V_\theta^{(0)} &= \left( {A^{(0)} + B^{(0)} \theta } \right)\sin \left( {\theta + \alpha^{(0)} } \right). \hfill \\ \end{aligned}$$

(35)

For convenience, here the above relation is expressed in complex form $\,\,{{\varvec{V}}}^{(0)} = V_r^{(0)} + iV_\theta^{(0)}$, then we have

$$\,\,{{\varvec{V}}}^{(0)} = - A^{(0)} (1 + k\theta )e^{ - i(\theta + \alpha^{(0)} )} - B^{(0)} [(1/7)\sin (\theta + \alpha^{(0)} )]$$

(36)

with

$$k = B^{(0)} /A^{(0)} .$$

Equation (25) for the density ρ⁽⁰⁾ can now be integrated to give

$$\rho^{(0)} = c^{(0)} \exp \left[ { - \frac{6}{7}\int^\theta {\frac{{B^{(0)} }}{{A^{(0)} + B^{(0)} \theta }}d\theta } } \right] = c^{(0)} \left( {A^{(0)} + B^{(0)} \theta } \right)^{ - {6 / 7}}$$

(37)

and the temperature T⁽⁰⁾ is given by Eq. (26).

These integration constants: A⁽⁰⁾, B⁽⁰⁾, C⁽⁰⁾, D⁽⁰⁾, E⁽⁰⁾, and so far undetermined angles (ω΄,λ) and $\alpha^{(0)}$ altogether eight unknowns are determined by eight boundary conditions given by the shock wave values at θ = –λ for Mach stem shock m and at θ = ω΄ for reflected shock R:

$${{\varvec{V}}}_{1,2} = (\,\,{{\varvec{V}}}^{(0)} )_{\theta = - \lambda ,\omega^{\prime}} ,\,\,\,\,\rho_{1,2} ,\,p_{1,2} = (\rho^{(0)} ,p^{(0)} )_{\theta = - \lambda ,\omega^{\prime}}$$

(38)

where ${{\varvec{V}}}_{1} = (V_{1r} ,V_{1\theta } )$, ${{\varvec{V}}}_{2} = (V_{2r} ,V_{2\theta } )$ are respectively the velocities behind shock waves m and R with their r and θ components V_1r, V_1θ; V_2r, V_2θ and their density and pressure values ρ₁, ρ₂; p₁, p₂. These shock values are given from the Rankine-Hugoniot conditions at R and m depending on the shock angles (ω΄,λ).

Now original three-shock theory [2] models the flow as illustrated in in Fig. 1b by two uniform flows ${{\varvec{V}}}_{1}$, ${{\varvec{V}}}_{2}$ separated by a slip flow line s in setting,

$$\theta_{2} -\theta_{1} = \, 0,$$

(39)

where θ₁, θ₂ are respectively the direction angles of ${{\varvec{V}}}_{1}$, ${{\varvec{V}}}_{2}$ from the x-axis (the incoming flow direction). Since this simple model caused the paradox, many authors [8, 10,11,12,13] proposed an alternative use of a fan-like flow in place of the slip flow line to resolve the ‘paradox’. Here note that the flow represented by Eq. (35) above is a fan-like source flow from point O in (x, y)-plane and, in fact, we are utilizing it for the condition at the intersection point r = 0. Also it must be noted that the three-shock theory is in fact based on Euler’s equation of perfect gas flow and uniform flow accompanied by the slip-flow is the natural and only solution of the Euler’s equation to the three-shock model. On the other hand, the present fan-like flow setting is based on a solution of the Navier–Stokes equation which is consistent with the use of the viscous flow model for the flow field behind shock waves R and m in providing a foundation for the use of fan-like flow.

Let δ₁, δ₂ be the respective angles made by the velocity vectors ${{\varvec{V}}}_{1}$, ${{\varvec{V}}}_{2}$ with the corresponding shock waves m, R. Then we have

$$\delta_1 + \theta_1 = \lambda ,\,\,\delta_2 + \theta_2 + \omega^{\prime} = \pi ,$$

(40)

so that

$$\begin{aligned} \frac{{V_{1r} }}{{V_{1\theta } }} &= \cot \delta _1 = \cot (\lambda - \theta _1 ) \\ \frac{{V_{2r} }}{{V_{2\theta } }} &= \cot \delta _2 = \cot (\pi - \theta _2 - \omega ^{\prime}) = - \cot (\theta _2 + \omega ^{\prime}) \\ \end{aligned}$$

From Eq. (35),

$$\frac{{V_r^{(0)} }}{{V_\theta^{(0)} }} = - \cot (\theta + \alpha^{(0)} ) - \,\frac{1}{7}\frac{{B^{(0)} }}{{A^{(0)} + B^{(0)} \theta }}\,\,$$

and the boundary conditions:

$$\frac{{V_{1r} }}{{V_{1\theta } }} = \left( {\frac{{V_r^{(0)} }}{{V_\theta^{(0)} }}} \right)_{\theta = - \lambda } ,\,\,\,\frac{{V_{2r} }}{{V_{2\theta } }} = \left( {\frac{{V_r^{(0)} }}{{V_\theta^{(0)} }}} \right)_{\theta = \omega^{\prime}} \,,$$

we have

$$\begin{gathered} \cot (\lambda - \theta_1 ) = - \cot ( - \lambda + \alpha^{(0)} ) - \,\frac{1}{7}\frac{{B^{(0)} }}{{A^{(0)} - B^{(0)} \lambda }}\,\,, \hfill \\ - \cot (\omega^{\prime} + \theta_2 ) = - \cot (\omega^{\prime} + \alpha^{(0)} ) - \,\frac{1}{7}\frac{{B^{(0)} }}{{A^{(0)} + B^{(0)} \omega^{\prime}}}\,\,, \hfill \\ \end{gathered}$$

or

$\begin{gathered} \sin (\alpha^{(0)} - \theta_1 ) = \sin ( - \lambda + \alpha^{(0)} )\sin (\lambda - \theta_1 )\left( { - \,\frac{1}{7}\frac{{B^{(0)} }}{{A^{(0)} - B^{(0)} \lambda }}} \right), \hfill \\ \sin (\theta_2 - \alpha^{(0)} ) = \sin (\omega^{\prime} + \alpha^{(0)} )\sin (\omega^{\prime} + \theta_2 )\left( { - \,\frac{1}{7}\frac{{B^{(0)} }}{{A^{(0)} + B^{(0)} \omega^{\prime}}}} \right). \hfill \\ \end{gathered}$,

From which we have the spread of fan-like flow $\delta \theta \equiv \theta_2 - \theta_1$ as

$$\begin{aligned} \delta \theta & = \left( {\alpha^{(0)} - \theta_1 } \right) + \left( {\theta_2 - \alpha^{(0)} } \right) \\ &= \sin^{ - 1} \left[ {\frac{{ - B^{(0)} }}{7}\frac{{\sin ( - \lambda + \alpha^{(0)} )\sin (\lambda - \theta_1 )}}{{A^{(0)} - B^{(0)} \lambda }}} \right] \\&\quad+ \sin^{ - 1} \left[ {\frac{{ - B^{(0)} }}{7}\frac{{\sin (\omega^{\prime} + \alpha^{(0)} )\sin (\omega^{\prime} + \theta_2 )}}{{A^{(0)} + B^{(0)} \omega^{\prime}}}} \right] \\ \end{aligned}$$

(41)

Here we can see that $B^{(0)} = 0$ provides δθ = 0 which is the slip flow, while non-zero $B^{(0)}$ provides the fan-like flow with divergence angle δθ. For example, when δθ = 8.7 × 10^–3 rad (0.5°) and the incident shock Mach number is 1.10, ω΄ ≈ 85 deg for ω = 63 deg, which is in good agreement with the experiment [14].

Actual procedure to determine ω΄ and λ is found to be the same as the ones appearing in our previous papers [9, 14] and we can utilize the results given in these papers. In Fig. 2, we can see that the present-theory curve agrees well with experimental data in weak shock case, while poor agreement in stronger case, which reflects the sharp bend of the shock curve near the intersection. It is seen that the present approach actually provides a kind of justification for the postulation in using viscous gas flow instead of perfect gas.

6 Internal Structure of Triple Point

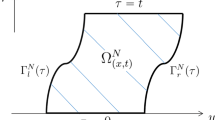
Here we utilize the solution to investigate the flow-field inside the triple point appearing in Mach reflection, which is referred as non-Rankine-Hugoniot zone [4]. This problem is usually studied [13, 15] by computing the entire Mach reflection flow-field, but there is a difficulty: We have to have finer mesh locally near the triple point to see its internal structure but it is not easy to set the area beforehand because the area moves with advancing time step, although there are some contrivances to overcome it [16]. Here our approach is analytical and we can do it in steady flow to have a finite region set locally including the non-Rankine-Hugoniot zone in advance, so the scheme is free from the above difficulty.

In the followings, we first set the boundary for the non-R-H zone by two hyperbolas r_a, r_b as seen in Fig. 3 and investigate the flow field between these boundaries as the one^{17, 18)} for plane shock wave structure problem, which usually considers the problem in studying the solution of the Navier–Stokes equations system of one-dimensional viscous gas flow to satisfy the Rankine-Hugoniot shock condition for up- and down- stream in respective regions. Here we have to deal with a plane flow and no Rankine-Hugoniot relation is expected, so instead we use the 2D Navier–Stokes equations and use the zeroth order solution given in Sect. 5 at the downstream flow boundary r_b, while incoming uniform flow at the in-flow boundary r_a.

Fig. 3

Nomenclatures and boundaries of non-R-H zone

6.1 Setting of Boundaries

Figure 3 shows the nomenclature and the considered flow-field. The symbols I, R, and m designate the incident shock, reflected shock and Mach stem. The uniform flow U ahead of the incident shock flows parallel to the x-axis. The y-axis is defined perpendicular to the x-axis. The origin of (x, y)-coordinate system lies in the triple-point region. Since the shock thickness is finite, there is some yet harmless uncertainty in the location of the origin O. The region is divided by wave fronts into three regions (I), (II), and (III), and the edges of shock zone are approximated by hyperbolas, whose asymptotes meet the origin. Rigorously speaking, the asymptotes described here is a parallel line to the mathematical asymptote. Then we define the polar coordinate (r, θ). The edge of shock zone facing the uniform region (I) is r = r_a(θ), and that facing the region (III) is r = r_b(θ). We approximate these edges by hyperbolas whose asymptotes are parallel to the dashed line in Fig. 3. Let the three asymptotes in Fig. 3 be θ  = π − ω, θ  = ωˊ, and θ = 2π − λ. These equations are expressed in (r, θ)-coordinate as follows:

$$r_b :\,\,\,r = b\left[ {\frac{{ - \sin \omega^{\prime}\sin \lambda }}{{\sin (\theta - \omega^{\prime})\sin (\theta + \lambda )}}} \right]^{1/2}$$

(42)

where a and b are the distances from the origin to the intersection of two hyperbolas with the x-axis (a = r_a(π), b = r_b(0)).

6.2 Solution in Zone (II)

We use the solution given in Sect. 4 in the form of power series in r. In the present circumstances, we impose the condition that the solution must be single valued in the flow region inside the two boundaries, r_a, r_b so that we have B⁽⁰⁾ = 0 in Eq. (23), and thus

$$V_r^{(0)} = - A^{(0)} \cos \left( {\theta + \alpha^{(0)} } \right),\,\,V_\theta^{(0)} = A^{(0)} \sin \left( {\theta + \alpha^{(0)} } \right)$$

(43)

and $\rho^{(0)} = C^{(0)}$ from Eq. (25), $T^{(0)} = E^{(0)}$ from Eq. (26), and $p^{(0)} = \rho^{(0)} T^{(0)} = C^{(0)} E^{(0)}$ from Eq. (27). Making use of these, we can proceed to the second-order approximation. Since $Y_1^{(0)} ,Y_2^{(0)} = 0$ from Eqs. (28), (43), and thus $\Delta_1^{(0)} ,\Delta_2^{(0)} = 0$ from Eq. (28), we have

$$V_r^{(1)} = A^{(1)} \cos 2(\theta + \alpha^{(1)} ) + B_1^{(1)} ,\,\,V_\theta^{(1)} = - A^{(1)} \sin 2(\theta + \alpha^{(1)} ) + B_2^{(1)}$$

from Eq. (29). So that we have the velocity to the first order of r,

$$\begin{aligned} V_r &= V_r^{(0)} + rV_r^{(1)} = - A^{(0)} \cos \left( {\theta + \alpha^{(0)} } \right)\, + r\left[ {A^{(1)} \cos 2(\theta + \alpha^{(1)} ) + B_1^{(1)} } \right], \\ V_\theta &= V_\theta^{(0)} + rV_\theta^{(1)} = A^{(0)} \sin \left( {\theta + \alpha^{(0)} } \right) + r\left[ { - A^{(1)} \sin 2(\theta + \alpha^{(1)} ) + B_2^{(1)} } \right] \\ \end{aligned}$$

(44)

which can be expressed in using complex velocity ${\bf{V}} = \,V_r + i\,\,V_\theta$,

$${\bf{V}} = - {\bf{A}}^{(0)} e^{ - i\theta } + r[{\bf{A}}^{(1)} e^{ - 2i\theta } + {\bf{B}}^{(1)} {\bf{]}}$$

(45)

where we set

$${\bf{A}}^{(0)} = A^{(0)} e^{ - i\alpha^{(0)} } ,\,\,{\bf{A}}^{(1)} = A^{(1)} e^{ - 2i\alpha^{(1)} } ,\,\,{\bf{B}}^{(1)} = B_1^{(1)} + iB_2^{(1)}$$

The expression for ρ⁽¹⁾ can be derived from Eq. (32), where

$$W_1 = - \log \left| {\sin \left( {\theta + \alpha^{(0)} } \right)} \right|,\,\,X^{(0)} = - 2C_0 B_1^{(1)}$$

Thus we have

$$\begin{aligned} \rho^{(1)} & = \sin \left( {\theta + \alpha^{(0)} } \right)\left[ { - \frac{{2C_0 B_1^{(1)} }}{{A^{(0)} }}\int {\frac{d\theta }{{\sin^2 \left( {\theta + \alpha^{(0)} } \right)}} + C^{(1)} } } \right] \\ &= \frac{{2C_0 B_1^{(1)} }}{{A^{(0)} }}\cos \left( {\theta + \alpha^{(0)} } \right) + C^{(1)} \sin \left( {\theta + \alpha^{(0)} } \right) \\ \end{aligned}$$

Equation (33) with Φ⁽¹⁾  = Z⁽⁰⁾ = 0 leads to

$$T^{(1)} = E^{(1)} \sin \left( {\theta + \gamma^{(1)} } \right)$$

where E⁽¹⁾ and γ⁽¹⁾ are the integration constants. Thus the density ρ, the pressure p, and the temperature T are expressed as

$$\begin{aligned} \rho &= \rho^{(0)} + r\rho^{(1)} = C^{(0)} + r[(2B_1^{(1)} C^{(0)} /A^{(0)} )\cos (\theta + \alpha^{(0)} ) + C^{(1)} \sin (\theta + \alpha^{(0)} )]\,, \hfill \\ p &= p^{(0)} + r(C^{(0)} T^{(1)} + \rho^{(1)} T^{(0)} ) = C^{(0)} E^{(0)} + r(C^{(0)} T^{(1)} + \rho^{(1)} T^{(0)} ), \hfill \\ T &= T^{(0)} + rT^{(1)} = E^{(0)} + rE^{(1)} \sin \left( {\theta + \gamma^{(1)} } \right), \hfill \\ \end{aligned}$$

(46)

where $A^{(0)} ,\alpha^{(0)} ;A^{(1)} ,\alpha^{(1)} ;B_1^{(1)} ;C^{(0)} ,C^{(1)} ;E^{(0)} ,E^{(1)} ,\gamma^{(1)}$ are integration constants to be determined by the boundary conditions at r = r_a, and r = r_b. To this, we express the uniform velocity to the zone (I) in a complex form:

$${\bf{V}} = V_r + iV_\theta = Me^{ - i\theta } ,\,\,M \equiv {U / {C_0 }}$$

(47)

so that, along the parabola r = r_a, we have from Eqs. (45) to (47)

$$- {\bf{A}}^{(0)} e^{ - i\theta } + r_a (\theta )[{\bf{A}}^{{\text{(1)}}} e^{ - 2i\theta } + {\bf{B}}^{{\text{(1)}}} {\bf{]}} = Me^{ - i\theta }$$

(48)

For the condition on the parabola r = r_b, we utilize the fan-like flow given by the solution (35) of Sect. 5 with its integration constants and angles λ, ω΄ determined to have, along r = r_b,

(49)

Notice that the boundary value set on the parabola $r = r_b$, which is apart from the shock lines $\theta = - {\bf{ }}\lambda$, ω΄, corresponds to the situation in the plane shock wave structure problem in which boundaries are set apart the shock front.

Now obviously we cannot have any solution to satisfy Eqs. (48), (49) above completely, so we seek an approximate solution. Here we consider it for a small region near the origin of non-R-H zone. So we put, θ =  π + φ in Eq. (48) and $\theta = - \alpha^{(0)} + \tilde{\phi },$ in Eq. (49), and expand these equations respectively in φ and $\tilde{\phi },$ to have from their expansion coefficients for the velocity,

where we put $r_a ^{\prime}\left( \pi \right) = s,\,\,\,\,r_b ( - \alpha^{(0)} ) = \hat{r}_b$. From these above we can determine ${\bf{A}}^{(0)}$, ${\bf{A}}^{(1)}$, ${\bf{B}}^{(1)}$ as,

$${\bf{A}}^{(0)} = - a\frac{{\mathop{z}\limits^{\rightharpoonup} - z}}{\Delta }S - M,\,\,\,{\bf{A}}^{(1)} = - \frac{z}{\Delta }S,\,\,\,{\bf{B}}^{(1)} = \frac{{\overline{z}}}{\Delta }S,\,\,$$

(50)

where

$$z = s + ia;\,\,w = a + \hat{r}_b e^{i\alpha^{(0)} } ;\,\,\Delta = \overline{z}\overline{w} - zw;\,\,S = - M - A^{(0)} (1 - k\alpha^{(0)} )e^{ - i\alpha^{(0)} }$$

In the same manner, we can determine the constants $C^{(0)} ,C^{(1)}$ for ρ, and E⁽⁰⁾, E⁽¹⁾, γ⁽¹⁾ for p, T. For example $C^{(0)} ,C^{(1)}$ for the density $\rho$ are determined from equations given by conditions (48), (49) for $\rho$ at $\phi = \tilde{\phi } = 0$.

6.3 Streamline and Density Distribution Along It

6.3.1 Streamline

Let r = r (θ, θ _a) be a streamline through a point r(θ _a) on r_a, then

$$\frac{1}{r}\frac{dr}{{d\theta }} = \frac{V_r }{{V_\theta }}\,\,{\text{with}}\,\,r = r(\theta_a ,\theta_a ) = r_a (\theta_a )$$

(51)

Here we use $V_r = V_r^{(0)} + rV_r^{(1)} \,\,,\,\,\,\,\,\,\,V_\theta = \,V_\theta^{(0)} + r\,\,\,V_\theta^{(1)} ,$ and expand the right-hand-side term in the power of r to have an approximation and use Eq. (44) to have:

$$\begin{aligned} \frac{1}{r}\frac{{dr}}{{d\theta }}\, & = \,{(\frac{{{V_r}}}{{{V_\theta }}})_{r = 0}} + r{[\frac{\partial }{{\partial r}}(\frac{{{V_r}}}{{{V_\theta }}})]_{r = 0}} = \frac{{V_r^{(0)}}}{{V_\theta ^{(0)}}} + r\frac{{(V_r^{(1)}V_\theta ^{(0)} - V_\theta ^{(1)}V_r^{(0)}}}{{V_\theta ^{{{(0)}^2}}}} \\ & = \, - \cot \varphi + r\frac{{{L_1}\sin \varphi + {L_2}\cos \varphi }}{{{A^{(0)}}{{\sin }^2}\varphi }} \\ \end{aligned} $$

(52)

where

$\phi = \theta + \alpha^{(0)} ,\,\,\,\,L_1 = A^{(1)} \cos 2(\alpha^{(1)} - \alpha^{(0)} ) + B_1^{(1)} ,\,\,\,\,L_2 = A^{(1)} \sin 2(\alpha^{(1)} - \alpha^{(0)} ) + B_2^{(1)}$.

By putting rsinφ = z, Eq. (52) is transformed as

$$\frac{1}{z^2 }\frac{dz}{{d\phi }} = \frac{1}{{A^{(0)} }}\left( {L_1 \frac{1}{\sin^2 \phi } + L_2 \frac{\cos \phi }{{\sin^3 \phi }}} \right)$$

which is integrated to have,

$$- \left[ \frac{1}{z} \right]_{z_a }^z = \frac{1}{{A^{(0)} }}\left[ { - L_1 \cot \phi - \frac{1}{2}\frac{1}{\sin^2 \phi }} \right]_{\phi_a }^\phi$$

where z_a and φ_a correspond to boundary condition r = r_a (θ_a), θ = θ_a. Eventually, the streamline is expressed as the following equation.

$$\frac{1}{{r\sin (\theta + \alpha^{(0)} )}} = \frac{1}{{r_a \sin (\theta_a + \alpha^{(0)} )}} + K(\theta )$$

(53)

with

$$K(\theta ) \equiv \frac{1}{{A^{(0)} }}\left[ {L_1 (\cot \phi - \cot \phi_a ) + \frac{1}{2}L_2 \left( {\frac{1}{\sin^2 \phi } - \frac{1}{\sin^2 \phi_a }} \right)} \right]$$

(54)

where

$\,\,\phi_a = \theta_a + \alpha^{(0)}$.

We can see in Eq. (53) that without the $K(\theta )$ term this represents a straight line $r\sin \left( {\theta + \alpha^{(0)} } \right) = {\text{const}}.$, so that we have a uniform flow in the direction of $\theta = - \alpha^{(0)}$ in this case. Thus non-zero $K(\theta )$ term contributes to make a distortion from the straight line. This feature of the curve in use of ${\bf{A}}^{(0)}$, ${\bf{A}}^{(1)}$, ${\bf{B}}^{(1)}$ values given in Eq. (50) is illustrated in Fig. 4a. Comparison with the result based on the Boltzmann-BGK equation is also shown in Fig. 4b. Note that the present result shows very narrow region around the triple point.

Fig. 4

Results for stream line by a the present analysis, b the numerical calculation on the basis of Boltzmann-BGK equation [7]

6.3.2 Density Distribution

We have the density distribution in Eq. (46)

$$\rho = C^{(0)} + r[(2B_1^{(1)} C^{(0)} /A^{(0)} )\cos (\theta + \alpha ^{(0)} ) + C^{(1)} \sin (\theta + \alpha ^{(0)} )]$$

(46)

This can be expressed simply in (x_γ, y_γ)-coordinate system which is a $\alpha^{(0)}$-rotated system from the original one in Fig. 1, and given as.

$x_\gamma = r\cos \phi ,y_\gamma = r\sin \phi ,\,\,\,\,\phi = \theta + \alpha^{(0)}$.

Thus we have

$$\rho = C^{(0)} \left[ {1 + \left( {2B_1^{(1)} /A^{(0)} } \right)x_\gamma + \left( {{{C^{(1)} } / {C^{(0)} }}} \right)y_\gamma )} \right]$$

(55)

So it represents a straight line in (x_γ, y_γ)-coordinates in the present approximation, while its distribution along a streamline through a point r(θ_a) on r_a, is expressed in using Eqs. (49), (53) as,

$$\rho = C^{(0)} \left[ {1 + r(\theta ,\theta_a )(2B_1^{(1)} /A^{(0)} )(\cos \varphi + C^{\prime}\sin \varphi )} \right],$$

where $C^{\prime} = {{A^{(0)} C^{(1)} } / {\left( {2B_1^{(1)} C^{(0)} } \right)}}$. This expression provides the changing feature of the density along the streamline s in showing that its main change is sinusoidal with a distortion by the factor r(θ, θ_a) as shown schematically [18] in Fig. 5a. It is compared also with the one in Fig. 5b which is given numerically by the Boltzmann-BGK equation [7, 17]. These density lines start from the same density of incoming uniform flow, and become different after passing through shock wave(s) on different streamlines. It looks similar to the one for one-dimensional flow in a finite region.

Fig.5

a Schematic diagram of density distribution along a streamline, b numerical results [18] for number density distribution by the Boltzmann-BGK equation on y = – 1

7 Concluding Remarks

We constructed a general solution of the 2D Navier–Stokes equations in cylindrical coordinates (r, θ)-system in the form of r-power expansion whose coefficients are functions of θ only, and we showed these functions are determined successively starting from the solution of the original equations along the line r = 0 in (r, θ)-plane.

It turned out that this zeroth order solution itself is found to represent a fan-like flow from an origin in ordinary (x, y)-plane and use of this solution for the determination of shock angles of Mach reflection is effectively equivalent to the current widely accepted proposal of replacing the slip flow line in the original three-shock theory by a fan-like flow for the solution of the “von Neumann paradox”. As a result, present approach actually provides a kind of justification for the postulation in using viscous gas instead of perfect gas.

The solution was utilized to study the internal structure of the triple point. It is concerned with the flow in the non-Rankine-Hugoniot zone, to which we set two bounding hyperbola as seen in Fig. 3 and used the solution there in conformity with boundary conditions along bounding hyperbola as the incoming flow along front curve and the fan-like flow given by the zeroth-order solution at the rear. The last condition corresponds to the use of Rankine-Hugoniot condition to the plane shock structure case.

Since we can study the flow directly in the zone which can be set in advance and the present approach has an advantage in that we are free from the difficulty of making ever finer mesh to the zone moving with advancing time steps as the case in the conventional approach of computing entire flow field.

Use of the solution to this problem was found to be effective to have reasonable result even with an approximation of only a few terms of the expansion in comparison with numerical result [7] of the corresponding one by the Boltzmann-BGK equation.