1 Thermodynamic Formulation

1.1 Introduction

Water is important in our daily life, and it has been studied extensively including high-pressure phase diagram [1]. One of the complexities brought to the interpretation of the shock data is the shock Hugoniot compression curve seems tangent or invade into the ice VII phase even at relatively low pressures.

Shock Hugoniot data for water have been measured precisely by several authors, and among them the equation of state of Rice-Walsh type has been proposed [2, 3].

We have measured the shock Hugoniot compression curve for water by using the high-pressure gas gun with the optical sensitive method of detecting the shock front up to around 1 GPa pressure region [4, 5], i.e., the lowest segment of the Hugoniot curve as shown by Rybakov [1]. This is the pressure region Hugoniot seems contact with ice boundary.

We have found that the shock Hugoniot in this region is given by

$$u_s = A + Bu_p ,$$
(1)

where us, and up denote the shock velocity and the particle velocity, respectively [4, 5]. And, A, and B denote the empirical coefficients, whose values are found to be equal to the following.

$$A = 1.45\,[{\text{km/s],}}$$
(2)
$$B=1.99$$
(3)

Shock Hugoniot is given by Eq. (1), then the internal energy or the shock pressure as a function of η is written by

$${\varepsilon }_{H}={\varepsilon }_{0}+\frac{1}{2}\frac{{A}^{2}{\eta }^{2}}{(1-B\eta {)}^{2}},$$
(4)
$$p_H = \frac{\rho_0 A^2 \eta }{{(1 - B\eta )^2 }},$$
(5)

where η is defined as the degree of compression

$$\eta \equiv 1-\frac{v}{{v}_{0}}$$
(6)

where v denotes the specific volume, and 0 is the suffix corresponding to the initial state.

In this report, the equation of state for water has been studied based on the above shock data and shock Hugoniot functions.

1.2 Polynomial Expansion of Thermodynamic Variables

The present theory is formulated by extending the thermodynamic expansion formula published firstly by Bethe [6] and Zel’dovich and Raizer [7]. The expansion itself can be used for any medium with arbitrary equation of state. The increase in the shock pressure and that in the internal energy are thermodynamically expanded in terms of the volume change and the entropy change up to the fourth order of volume change. They are given by the equations,

$$\begin{aligned}\Delta p&=\boldsymbol{ }{\left(\frac{\partial p}{\partial v}\right)}_{{S}_{0}}\Delta v+\frac{1}{2}{\left(\frac{{\partial }^{2}p}{\partial {v}^{2}}\right)}_{{S}_{0}}\Delta {v}^{2}+\frac{1}{6}{\left(\frac{{\partial }^{3}p}{\partial {v}^{3}}\right)}_{{S}_{0}}\Delta {v}^{3}\\ &\quad+\frac{1}{24}{\left(\frac{{\partial }^{4}p}{\partial {v}^{4}}\right)}_{{S}_{0}}\Delta {v}^{4}+{\left(\frac{\partial p}{\partial S}\right)}_{{v}_{0}}\Delta S+{\left(\frac{{\partial }^{2}p}{\partial S\partial v}\right)}_{{S}_{0}}\Delta S\Delta v\end{aligned}$$
(7)
$$\begin{aligned}\Delta \varepsilon &={\left(\frac{\partial \varepsilon }{\partial v}\right)}_{{S}_{0}}\Delta v+\frac{1}{2}{\left(\frac{{\partial }^{2}\varepsilon }{\partial {v}^{2}}\right)}_{{S}_{0}}\Delta {v}^{2}+\frac{1}{6}{\left(\frac{{\partial }^{3}\varepsilon }{\partial {v}^{3}}\right)}_{{S}_{0}}\Delta {v}^{3}\\ &\quad+\frac{1}{24}{\left(\frac{{\partial }^{4}\varepsilon }{\partial {v}^{4}}\right)}_{{S}_{0}}\Delta {v}^{4}+{\left(\frac{\partial \varepsilon }{\partial S}\right)}_{{v}_{0}}\Delta S+{\left(\frac{{\partial }^{2}\varepsilon }{\partial S\partial v}\right)}_{{S}_{0}}\Delta S\Delta v\end{aligned}$$
(8)

Polynomial expansion up to fifth order of volume change is not very difficult, but I decided the expansion up to fourth. One of the reasons of this decision is the difference in the order depends on what you choose for the variables. In the discussion of shock Hugoniot, the difference appears in the pressure and energy expression due to the Rankine-Hugoniot relationship. Advantage of choosing internal energy is that one does not need to define higher order derivatives of the Grüneisen parameter.

Rewriting the last several terms, we obtain

$$\begin{aligned}\Delta p&={\left(\frac{\partial p}{\partial v}\right)}_{{S}_{0}}\Delta v+\frac{{v}_{0}^{2}}{2}{\left(\frac{{\partial }^{2}p}{\partial {v}^{2}}\right)}_{{S}_{0}}{\Delta v}^{2}+\frac{{v}_{0}^{3}}{6}{\left(\frac{{\partial }^{3}p}{\partial {v}^{3}}\right)}_{{S}_{0}}{\Delta v}^{3}\\ &\quad+\frac{{v}_{0}^{4}}{24}{\left(\frac{{\partial }^{4}p}{\partial {v}^{4}}\right)}_{{S}_{0}}{\Delta v}^{4}+\frac{{\gamma }_{0}}{{v}_{0}}{T}_{0}\Delta S+{\left(\frac{\partial }{\partial v}\left[\frac{\gamma }{v}T\right]\right)}_{{S}_{0}}\Delta S\Delta v,\end{aligned}$$
(9)
$$\begin{aligned}\Delta \varepsilon &=-{p}_{0}\Delta v-\frac{1}{2}{\left(\frac{\partial p}{\partial v}\right)}_{{S}_{0}}{\Delta v}^{2}-\frac{1}{6}{\left(\frac{{\partial }^{2}p}{\partial {v}^{2}}\right)}_{{S}_{0}}{\Delta v}^{3}\\ &\quad-\frac{1}{24}{\left(\frac{{\partial }^{3}p}{\partial {v}^{3}}\right)}_{{S}_{0}}{\Delta v}^{4}+{T}_{0}\Delta S-\frac{{\gamma }_{0}}{{v}_{0}}{T}_{0}\Delta S\Delta v,\end{aligned}$$
(10)

where we have used the following formula.

$${\left(\frac{\partial p}{\partial S}\right)}_{{v}_{0}}={\left(\frac{\partial p}{\partial \varepsilon }\right)}_{{v}_{0}}{\left(\frac{\partial \varepsilon }{\partial S}\right)}_{{v}_{0}}=\frac{{\gamma }_{0}}{{v}_{0}}{T}_{0}$$
(11)
$${\left(\frac{{\partial }^{2}p}{\partial S\partial v}\right)}_{{S}_{0}}={\left(\frac{\partial }{\partial v}\left[\frac{\gamma }{v}T\right]\right)}_{{S}_{0}}$$
(12)

We define the decrement in three variables by

$$\begin{array}{c}\Delta p\equiv p-{p}_{0}>0\\ \Delta v\equiv v-{v}_{0}<0\\ \Delta S\equiv S-{S}_{0}>0\end{array}$$
(13)

Since we consider the compression wave, variables have the sign shown in Eq. (13), where we have used the formula in Eq. (10).

$${\left(\frac{\partial \varepsilon }{\partial v}\right)}_{{S}_{0}}=-{p}_{0}$$
(14)

We also show the expansion in terms of the non-dimensional variable η.

$$\begin{aligned}\Delta p &={\left(\frac{\partial p}{\partial \eta }\right)}_{{S}_{0}}\eta +\frac{1}{2}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}{\eta }^{2}+\frac{1}{6}{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}{\eta }^{3}\\ &\quad+\frac{1}{24}{\left(\frac{{\partial }^{4}p}{\partial {\eta }^{4}}\right)}_{{S}_{0}}{\eta }^{4}+\frac{{\gamma }_{0}}{{v}_{0}}{T}_{0}\Delta S-{v}_{0}{\left(\frac{\partial }{\partial v}\left[\frac{\gamma }{v}T\right]\right)}_{{S}_{0}}\eta \Delta S\end{aligned}$$
(15)
$$\begin{aligned}\Delta \varepsilon &=+{v}_{0}{p}_{0}\eta +\frac{{v}_{0}}{2}{\left(\frac{\partial p}{\partial \eta }\right)}_{{S}_{0}}{\eta }^{2}+\frac{{v}_{0}}{6}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}{\eta }^{3}\\ &\quad+\frac{{v}_{0}}{24}{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}{\eta }^{4}+{T}_{0}\Delta S+{\gamma }_{0}{T}_{0}\eta \Delta S\end{aligned}$$
(16)

For later use, we will calculate the term appearing in the last in Eq. (15).

$$\begin{aligned}{\left(\frac{\partial }{\partial v}\left[\frac{\gamma }{v}T\right]\right)}_{S}&=\frac{\gamma }{v}{\left(\frac{\partial T}{\partial v}\right)}_{S}+\frac{T}{v}{\left(\frac{d\gamma }{dv}\right)}_{S}-\frac{\gamma T}{{v}^{2}}\\ &=-\frac{T}{{v}^{2}}\left[\frac{v}{{v}_{0}}\left(\frac{d\gamma }{dv}\right)+{\gamma }^{2}+\gamma \right]\end{aligned}$$
(17)

Applying this to the initial state, we have

$$\begin{array}{cc}{\left(\frac{\partial }{\partial v}\left[\frac{\gamma }{v}T\right]\right)}_{{S}_{0}}& =-\frac{{T}_{0}}{{v}_{0}^{2}}\left[{\left(\frac{d\gamma }{d\eta }\right)}_{0}+{\gamma }_{0}^{2}+{\gamma }_{0}\right]\end{array}$$
(18)

It is noted that this expression contains the derivative of the Grüneisen parameter at the initial state, which is unknown at moment.

This formulation is based on the fact that the entropy change associated with shock compression in any medium is of the order of cube power of the change in volume. If Eq. (18) is inserted to Eq. (15), we have

$$\begin{aligned}\Delta p &={\left(\frac{\partial p}{\partial \eta }\right)}_{{S}_{0}}\eta +\frac{1}{2}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}{\eta }^{2}+\frac{1}{6}{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}{\eta }^{3}\\&\quad+\frac{1}{24}{\left(\frac{{\partial }^{4}p}{\partial {\eta }^{4}}\right)}_{{S}_{0}}{\eta }^{4} +{T}_{0}\Delta S\left[\frac{{\gamma }_{0}}{{v}_{0}}+\frac{1}{{v}_{0}}\left[{\left(\frac{d\gamma }{d\eta }\right)}_{0}+{\gamma }_{0}^{2}+{\gamma }_{0}\right]\eta \right]\end{aligned}$$
(19)

and,

$$\begin{aligned}\Delta \varepsilon &=+{v}_{0}{p}_{0}\eta +\frac{{v}_{0}}{2}{\left(\frac{\partial p}{\partial \eta }\right)}_{{S}_{0}}{\eta }^{2}+\frac{{v}_{0}}{6}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}{\eta }^{3}\\ &\quad+\frac{{v}_{0}}{24}{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}{\eta }^{4}+{T}_{0}\Delta S\left[1+{\gamma }_{0}\eta \right],\end{aligned}$$
(20)

where we assumed that initial pressure p0 is neglected compared with the shock pressure.

1.3 Hugoniot Expression by the Use of the Rankine-Hugoniot Relationship

Now we use the Rankine-Hugoniot relationship in order to apply the general expansion formula, (15) and (16) into shock Hugoniot function.

$$\varepsilon -{\varepsilon }_{0}=\frac{p+{p}_{0}}{2}({v}_{0}-v)$$
(21)

or

$$\Delta \varepsilon =\frac{2{p}_{0}+\Delta p}{2}(-\Delta v)=-{p}_{0}\Delta v-\frac{1}{2}\Delta p\Delta v=+{v}_{0}{p}_{0}\eta +\frac{{v}_{0}}{2}\eta \Delta p$$
(22)

Combining the Rankine-Hugoniot relationship, Eqs. (21) or (22), we will discuss the shock Hugoniot curve.

It is noticeable that maximum power of volume change used in the polynomial expression of shock pressure, Eq. (19) or of internal energy, Eq. (20) is different due to the existence of η in Eq. (22). This is the reason why we will formulate the equation of state in terms of the internal energy and not of pressure, as explained earlier. Thereafter, we will discuss the shock Hugoniot using the internal energy equation, which we could retain terms up to the fourth order of volume change.

If Eq. (19) is inserted to Eq. (22), we obtain

$$\begin{aligned}\Delta {\varepsilon }_{H} &=+{v}_{0}{p}_{0}\eta +\frac{{v}_{0}}{2}\eta \Delta p\\ &={v}_{0}{p}_{0}\eta +\frac{{v}_{0}{\eta }^{2}}{2}\left[{\left(\frac{\partial p}{\partial \eta }\right)}_{{S}_{0}}+\frac{1}{2}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}\eta +\frac{1}{6}{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}{\eta }^{2}\right]+\frac{{\gamma }_{0}\eta }{2}{T}_{0}\Delta S,\end{aligned}$$
(23)

where only the terms of up to the fourth order in η are retained. To do so, the pressure change, Eq. (19) of only up to the third order terms is necessary as explained earlier.

If we compare Eq. (23) with Eq. (20),

$$\begin{aligned}\Delta \varepsilon &=+{v}_{0}{p}_{0}\eta +\frac{{v}_{0}}{2}{\left(\frac{\partial p}{\partial \eta }\right)}_{{S}_{0}}{\eta }^{2}+\frac{{v}_{0}}{6}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}{\eta }^{3}+\frac{{v}_{0}}{24}{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}{\eta }^{4}\\ &+{T}_{0}\Delta S\left[1+{\gamma }_{0}\eta \right]\end{aligned}$$
(24)

Two equations are equal up to the second order of volume change. This fact is called the second order contact between the shock Hugoniot and the isentrope centering the same initial state. In other words, the entropy change by shock compression is a tiny quantity in the order of third order of magnitude of the volume change [2, 3]. Or more specifically, the terms in Eq. (23) of the third order or smaller,

$$\begin{array}{cc}\Delta {\varepsilon }_{III}& =\frac{{v}_{0}\eta }{2}\left[\frac{1}{2}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}{\eta }^{2}+\frac{1}{6}{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}{\eta }^{3}\right]+\frac{{\gamma }_{0}\eta }{2}{T}_{0}\Delta S\end{array}$$
(25)

should be equal to the corresponding terms in Eq. (24), namely,

$$\begin{array}{cc}\Delta {\varepsilon }_{III}& =\frac{{v}_{0}}{6}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}{\eta }^{3}+\frac{{v}_{0}}{24}{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}{\eta }^{4}+{T}_{0}\Delta S\left[1+{\gamma }_{0}\eta \right]\end{array}$$
(26)

In order for the third or higher order quantities in both equations to be equivalent, the assumption that the entropy change should be of the third order quantity. So, we write the entropy change as

$$\rm{\Delta }S = \frac{v_0 }{{12T_0 }}\left( {\frac{\partial^2 p}{{\partial \eta^2 }}} \right)_{S_0 } \eta^3 + \frac{a_0 }{{T_0 }}\eta^4 ,$$
(27)

where the first term in Eq. (27), the third order term is derived by the comparison of Eqs. (26) and (27) in the third order terms. One may determine the parameter a0 to be consistent to both equations. If Eq. (27) is inserted into Eqs. (25), (26), we get

$$\Delta {\varepsilon }_{III}=\frac{{v}_{0}\eta }{2}\left[\frac{1}{2}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}{\eta }^{2}+\frac{1}{6}{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}{\eta }^{3}\right]+\frac{{\gamma }_{0}{v}_{0}}{24}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}{\eta }^{3}$$
(28)
$$\begin{aligned}\Delta {\varepsilon }_{III}&=\frac{{v}_{0}}{6}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}{\eta }^{3}+\frac{{v}_{0}}{24}{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}{\eta }^{4}\\ &\quad+\left[\frac{{v}_{0}}{12}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}{\eta }^{3}+{a}_{0}{\eta }^{4}\right]\left[1+{\gamma }_{0}\eta \right]\end{aligned}$$
(29)

By comparing the above two equations, the third order term is apparently consistent. If we compare the fourth order terms, we obtain

$$\frac{{v}_{0}}{12}{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}+\frac{{\gamma }_{0}{v}_{0}}{24}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}=\frac{{v}_{0}}{24}{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}+{a}_{0}+\frac{{\gamma }_{0}{v}_{0}}{12}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}$$
(30)

then we have

$$\begin{array}{c}{a}_{0}=\frac{{v}_{0}}{24}[{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}-{\gamma }_{0}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}]\end{array}$$
(31)

Finally, it is found that the entropy change by shock compression is given by the following formula.

$$\begin{array}{cc}{T}_{0}\Delta S& =\frac{{v}_{0}}{12}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}{\eta }^{3}+\frac{{v}_{0}}{24}\left[{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}-{\gamma }_{0}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}\right]{\eta }^{4}\end{array}$$
(32)

Then it is possible to insert the entropy change into Eq. (20) and obtain the shock Hugoniot function for the shock energy as a function of volume change.

$$\begin{aligned}\Delta {\varepsilon }_{H}&=+{v}_{0}{p}_{0}\eta +\frac{{v}_{0}}{2}{\left(\frac{\partial p}{\partial \eta }\right)}_{{S}_{0}}{\eta }^{2}+\frac{{v}_{0}}{6}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}{\eta }^{3}+\frac{{v}_{0}}{24}{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}{\eta }^{4}\\ &\quad+\left[1+{\gamma }_{0}\eta \right]\frac{{v}_{0}}{12}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}{\eta }^{3}+\frac{{v}_{0}}{24}\left[{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}-{\gamma }_{0}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}\right]{\eta }^{4}\end{aligned}$$
(33)

Note the third order term in Eq. (33) can be calculated as

$$\frac{{v}_{0}}{4}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}{\eta }^{3}$$
(34)

Then the fourth order terms will be

$$\begin{aligned}&\frac{{v}_{0}}{24}{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}{\eta }^{4}+\frac{{\gamma }_{0}{v}_{0}}{12}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}{\eta }^{4}+\frac{{v}_{0}}{24}\left[{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}-{\gamma }_{0}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}\right]{\eta }^{4}\\ &=\frac{{v}_{0}}{12}\left[{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}+\frac{{\gamma }_{0}}{2}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}\right]{\eta }^{4}\end{aligned}$$
(35)

Finally, Eq. (33) become

$$\begin{aligned}\Delta {\varepsilon }_{H}&=+\,{v}_{0}{p}_{0}\eta +\frac{{v}_{0}}{2}{\left(\frac{\partial p}{\partial \eta }\right)}_{{S}_{0}}{\eta }^{2}+\frac{{v}_{0}}{4}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}{\eta }^{3}\\ &\quad+\frac{{v}_{0}}{12}\left[{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}+\frac{{\gamma }_{0}}{2}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}\right]{\eta }^{4}\end{aligned}$$
(36)

1.4 Application of Linear Relationship Between Shock Velocity and Particle Velocity

Shock Hugoniot function given by Eq. (4) for the internal energy as a function of η can be rewritten by the polynomial expression in terms of the powers of η, then each term of each power can be compared with Eq. (36). The resultant formulas for each derivatives of η are given by

$${\left(\frac{\partial p}{\partial \eta }\right)}_{{S}_{0}}={\rho }_{0}{A}^{2}$$
(37)
$${\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}=4{\rho }_{0}{A}^{2}B$$
(38)
$${\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}=(18B-2{\gamma }_{0}){\rho }_{0}{A}^{2}B$$
(39)

If these equations are inserted into Eq. (36), we have

$$\rm{\Delta }\varepsilon_H = \frac{A^2 }{2}\eta^2 + A^2 B\eta^3 + \frac{3}{2}A^2 B^2 \eta^4 ,$$
(40)

An isentrope centering the same initial state are obtained using Eq. (16) and neglecting the entropy increase terms, then we have

$$\Delta {\varepsilon }_{S}=\frac{{A}^{2}}{2}{\eta }^{2}+\frac{2}{3}{A}^{2}B{\eta }^{3}+\frac{18B-2{\gamma }_{0}}{24}{A}^{2}B{\eta }^{4}$$
(41)

Difference between \(\Delta {\varepsilon }_{H}\) and \(\Delta {\varepsilon }_{S}\) denotes the entropy change due to shock compression, and is equal to the value calculated by Eq. (32).

As you noticed in deriving Eq. (23), pressure formula is used in the energy equation only up to the terms of third order. After that the pressure formulas are derived to the same order of terms. First, Eqs. (15) and (32) are combined.

$$\begin{array}{cc}\Delta {p}_{H}& ={\left(\frac{\partial p}{\partial \eta }\right)}_{{S}_{0}}\eta +\frac{1}{2}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}{\eta }^{2}+\frac{1}{6}{\left(\frac{{\partial }^{3}p}{\partial {\eta }^{3}}\right)}_{{S}_{0}}{\eta }^{3}+\frac{{\gamma }_{0}}{12}{\left(\frac{{\partial }^{2}p}{\partial {\eta }^{2}}\right)}_{{S}_{0}}{\eta }^{3}\end{array}$$
(42)

By the similar power expansion in terms of η, we have from Eqs. (37)–(39),

$$\Delta {p}_{H}={\rho }_{0}{A}^{2}\eta +2{\rho }_{0}{A}^{2}B{\eta }^{2}+3{\rho }_{0}{A}^{2}{B}^{2}{\eta }^{3}$$
(43)

Similarly, an isentrope centering the same initial state is calculated by Eq. (15) as

$$\Delta {p}_{S}={\rho }_{0}{A}^{2}\eta +2{\rho }_{0}{A}^{2}B{\eta }^{2}+\frac{(18B-2{\gamma }_{0}){\rho }_{0}{A}^{2}B}{6}{\eta }^{3}$$
(44)

The entropy increase by shock compression in Eq. (29) can then be calculated by the use of Eqs. (37)–(39) as

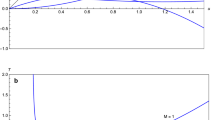
$$\begin{array}{cc}{T}_{0}\Delta S& =\frac{1}{3}{A}^{2}B{\eta }^{3}+\frac{1}{4}\left[(3B-{\gamma }_{0}){A}^{2}B\right]{\eta }^{4}\end{array}$$
(45)

Figure 1 shows the calculated results for the internal energy as a function of the degree of compression. Isentropic energy increase and the entropy increase by shock compression were also calculated and shown in Fig. 1.

Fig. 1
figure 1

Hugoniot energy versus η for water

Full size image

2 Tait Equation as an Isentropic Compression Curve

We will apply the above results to the so-called Tait equation of state in a form of an isentrope [8, 9]

$$p\left( {v,S} \right) = \alpha \left( S \right)\left[ {\left( {\frac{v}{v_0 }} \right)^{ - n} - 1} \right],$$
(46)

where the coefficient, α is assumed to be a function of entropy, whereas the coefficient n is assumed to be a constant.

Integration of Eq. (46) along an isentrope gives an expression of the internal energy as

$$\begin{aligned}\varepsilon \left(v,S\right)&={\varepsilon }_{0}-{\int }_{{v}_{0}}^{v}p\left(v,S\right)dv\\ &={\varepsilon }_{0}-\alpha \left(S\right){v}_{0}{\int }_{1}^{v/{v}_{0}}\left[{\left(\frac{v}{{v}_{0}}\right)}^{-n}-1\right]d\left(\frac{v}{{v}_{0}}\right)\\ &={\varepsilon }_{0}+\alpha (S){v}_{0}\left[\frac{1}{n-1}{\left(\frac{v}{{v}_{0}}\right)}^{-n+1}+\left(\frac{v}{{v}_{0}}\right)-\frac{n}{n-1}\right]\end{aligned}$$
(47)

Expression of the shock Hugoniot using the Tait equation, Eq. (47) should be

$${\varepsilon }_{H}(v)={\varepsilon }_{H}(\eta )={\varepsilon }_{0}+\alpha ({S}_{H}){v}_{0}\left[\frac{1}{n-1}{\left(\frac{v}{{v}_{0}}\right)}^{-n+1}+\left(\frac{v}{{v}_{0}}\right)-\frac{n}{n-1}\right]$$
(48)

It is therefore possible to estimate the increase in the entropy function, α(S) along the shock Hugoniot by comparing the shock energy, εH with the Tait energy calculated by Eq. (47). As expected, weak shock or isentropic approximation of Eq. (48) leads to the expansion starting at the square term of η, and this term compared with Eq. (41) gives the information on the coefficient, α(S0).

$$\alpha ({S}_{0})=\frac{{\rho }_{0}{A}^{2}}{n}$$
(49)

Calculation of Tait isentrope has been made by putting the coefficient n as a parameter to adjust it to the isentropic energy. The result of calculation is shown in Fig. 2. Best fit to the isentrope calculated from the shock Hugoniot, Eq. (41) was obtained by the value of n = 6.4. As you see in Fig. 2, the agreement between two functions is satisfactory.

Fig. 2
figure 2

Tait energy versus η for water

Full size image

Figure 3 shows the result of calculation. As you see in Eq. (48), the increase in the ratio of the Hugoniot energy and the Tait energy should be the entropy function α(S). Figure 3 shows the result of calculation for α(S) along Hugoniot. One may notice that due to the slow increase in entropy along Hugoniot, α(S) along entropy is very steep. It is found in this analysis that the parameter n is somewhat larger than those reported previously.

Fig. 3
figure 3

Entropy function, α(S) in Tait equation versus η or versus SH for water

Full size image

Approximation of the function, α(S) by polynomial expression of η is very easily done and is given by

$$\alpha ({S}_{H})=\alpha (\eta )=\alpha ({S}_{0})\left[1.00+1.14\eta +6.83{\eta }^{2}\right]$$
(50)

Based on these analyses, one may safely use the Tait type equation for flow analysis including shock propagation.

3 Conclusion

It is my honor to present my recent research report on the occasion of 100 years of birth of Prof. Akira Sakurai.

Formulation of the equation of state has been done using polynomial expansion of thermodynamic variables together with shock Hugoniot data for water. Part of the ideas of this formulation stems from the fact that shock Hugoniot has second order contact with an isentrope centering the same initial state with Hugoniot. That means the shock Hugoniot itself contains sufficient information on the isentrope.

Using the available shock Hugoniot data, we will be successfully formulated the equation of state including the shock entropy as a function of shock strength. However, due to the order of expansion of variables limit the applicability of the method of application. Approximately, the pressure limit will be up to 0.5 GPa.

Even so, application of the results to the Tait-type equation of state, and information on an entropy function could be obtained.