Keywords

1 Introduction

Fruit harvesting for the agriculture industry will soon become a major application area for robotic technology. It is desirable for robot actuation to be compliant, to avoid damage arising from collisions that may occur in the working environment, and also to maximize the safety of human co-workers operating in close proximity to robotic platforms. The development of suitable actuators that exhibit compliance is an active field of research [1, 2]. Tendon driven mechanisms provide one approach to build such actuators [3] and the use of agonistic-antagonist elastic tendons with a non-linear extension characteristic enables compliance to be modulated using co-contraction [4, 5].

2 Motors

One major component of robotic arms are their actuators, which often make use of electric motors. Several motor types are currently available. Stepper motors are low cost, robust and can directly generate high output torques without the need for gearing. However, they are relatively heavy for their torque output compared to geared DC motors and require continuous drive current to maintain stationary position. High torque DC brushless motors are becoming increasingly popular in robotics applications, due to their high performance stemming from the availability of powerful magnets, and out-runner designs are capable of directly generating very large torques. However, they also require drive current to maintain a stationary position under load. DC brushed motors are also popular and are straightforward to model [6] and to control [7].

Brushed worm-drive DC motors are another good choice for constructing powerful servo drive system, since they are a mass-produced low-cost item and deliver high-torque [8]. Their non-back-drivability is advantageous in our application since maintenance of static posture then requires no power. In a variable-stiffness design, such an arm can also maintain postures at a fixed level of passive compliance. In mobile applications this is highly advantageous, since it would reduce the drain on limited battery power resources, whilst compliance enables the arm to absorb unforeseen impacts due to its own movement, or that of other agents. Therefore, we consider actuator design that makes use of worm-gear motors.

Fig. 1.
figure 1

Schematic of the two-tendon drive based on the design of the GummiArm.

Full size image

3 Passive Compliance

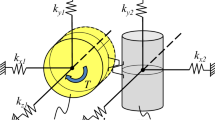
Active compliance in a robot arm can be achieved by means of force sensing and feedback. However, this cannot protect against the shock arising from hard impacts, like a hammer blow, since the bandwidth limitations of a typical controller makes it unable to react fast enough to compensate such impulsive disturbances. In contrast, passive compliance achieved using a series elastic element in the mechanical drive, can protect the arm and actuator mechanism against impacts, since the load is transferred to the actuator via a physical spring. However, high compliance is not always desirable and stiff operation can be advantageous when dealing with unstable loads. Also, in machining operations, stiff industrial robots are ideal. Various methods have been proposed to modulate stiffness [9, 10], which allows the effective spring constant to change to better fit a given task. Here, we follow the approach taken in the GummiArm, which is a soft robotic arm that makes use of the co-contraction of non-linear tendon drive to achieve variable stiffness [11]. We match the dimensions of the drive and link pulleys used in the GummiArm shoulder. In the original design, research-grade Dynamixels were used for actuation. Here we extend the design using low-cost worm-gear motors to drive the tendons. A schematic of the tendons, drive and output pulley mechanisms used here is shown in Fig. 1. The tendons wrap-around the pulleys and are firmly attached and therefore do not just rely of friction to transfer force.

4 Motor Test Rig

A Motor test rig was developed to provide a testbed for experimental investigations of compliant actuation and corresponding control algorithms. In order to support position control of the robotic link driven by compliant tendons, it was necessary to compensate for tendon deformation. The necessitated the measurements of drive and output angles pulleys. This was achieved using incremental encoders mounted on the pulleys. We used GummiArm tendons supplied by Fieldwork Robotics Ltd. which exhibited a non-linear spring constant that increased with extension.

Fig. 2.
figure 2

Test rig and controller. Panel A: Tendon worm-drive link test rig on stand. Panel B: DIN rail Beckhoff EtherCAT panel.

Full size image

The rig was comprised of several 3D printed parts, mounted on 20mm aluminum profile that forms its structural support. The custom components were designed using AutoCAD Fusion 360. Subsequently STL format files were generated and the mechanical parts were manufactured in PLA using a LutzBot TAZ6 3D printer. All parts were attached to the aluminum profile sections with T-nuts, so they could be easily adjusted. The motor tendon-drive test rig is shown in Fig. 2A. The test rig could be mounted in two orientations due to its square cross-section. When the link was orientated in a horizontal orientation. gravity has no effect on its motion. This provides a means to investigate control when movement was only resisted by link moment of inertia and viscous friction. When re-orientated by 90°, the effect gravity on the link could be investigated.

5 Beckhoff EtherCAT Control Panel

To control the 2-tendon link, we designed and built a DIN panel based on the industrial Beckhoff EtherCAT platform (Beckhoff Automation GmbH, Verl, Germany). This is widely used for production line automation and ideally suited to the task. Many Beckhoff EtherCAT system components are available, streamlining the implementation of automation and control systems. We implemented the EtherCAT framework using an embedded PC running the real-time Beckhoff TwinCAT3 software which is integrated into the Microsoft Visual Studio development environment. This supports the development of controllers, and interfaces with all the necessary signal I/O and motor drivers. I/O modules consist of electronic terminal block ‘slices’, which can be slid into the FieldBus system to add functionality in an elegant fashion with no messy wiring. The platform realizes a precise frame rate (typically 1kHz) for signal acquisition and control. In our panel we made use of the following Beckhoff components, although other slices were installed on the FieldBus:

  • CX5130 Embedded PC with Intel Atom® processor

  • EL5152 Incremental encoder interface (24 V HTL, 100 kHz)

  • EL7342 2-channel DC motor terminal (48 V DC, 3.5 A without fan)

The hardware was built into a Rittal GmbH (Herborn, Germany) AE1076.500 Compact AE enclosure (600 × 760 × 210 mm). We used industrial DIN rail assembly technology, so Beckhoff components could be quickly and securely attached, providing an elegant and tidy means of panel construction. The DIN standard supports a wide range of off-the-shelf components, including AD/DC switching power supplies. Panel wiring was routed in cable ducts to maintain a neat layout and connection wires were all terminated appropriately using ferrules. The control panel could be programmed and operated via a single Ethernet cable connection. The panel (Fig. 2B) was mounted on a custom-built stand that also supports the tendon test rig on its rear side. The panel could can easily be expanded to control a multi-joint robotic arm by adding additional I/O slice.

6 Transfer Function and Response of Tendon Mechanism

A full analysis of the worm gear motor actuated tendon system and derivation of the state space model and controller are described in [12]. Here we first note the state space equations for the linearized tendon drive (without motor) is given by the equation:

$$\begin{array}{c}\frac{d}{dt} \left[\begin{array}{c}{\dot{\uptheta}_{o}}\\ {\uptheta}_{o}\end{array}\right]=\left[\begin{array}{cc}-\frac{\mu }{I}& -\left(\frac{mgl}{2I}+\frac{2{\rm{K}}_{r}}{I}\right)\\ 1& 0\end{array}\right]\left[\begin{array}{c}{\dot{\uptheta}_{o}}\\ {\uptheta}_{o}\end{array}\right]+\left[\begin{array}{cc}\frac{2{\rm{K}}_{r}}{I}\frac{{\rm{r}}_{\rm{in}}}{{\rm{r}}_{\rm{o}}}& -\frac{{\rm{K}}_{r}}{I}\frac{{\rm{r}}_{\rm{in}}}{{\rm{r}}_{\rm{o}}}\\ 0& 0\end{array}\right]\left[\begin{array}{c}{\uptheta}_{target}\\ {\uptheta}_{stretch}\end{array}\right]\end{array}$$
(1)

Where \({\uptheta}_{o}\) is the output pulley angle. Although component and model parameters (see Table 1) are sometimes available from datasheets and component measurements, it is also useful to have a means to validate, or even estimate them, though simple observations of system behavior such as the open-loop system step response. To analytically compute the step response of the tendon-link system, we first derive the transfer function for the system for \({\uptheta}_{target}\) given a constant extension \({\uptheta}_{stretch}\) value. Setting the latter to zero, leads to the expression

$$\begin{array}{c}{\ddot{\uptheta }_{o}} = - \frac{\mu }{I} {\dot{\uptheta}_{o}}-\left(\frac{mgl}{2I}+\frac{2{\rm{K}}_{r}}{I}\right){\uptheta}_{o}+\frac{{\rm{K}}_{r}}{I}\frac{{\rm{r}}_{\rm{in}}}{{\rm{r}}_{\rm{o}}}{{2}{\uptheta}}_{target}\end{array}$$
(2)

Taking Laplace transforms with zero initial conditions

$$\begin{array}{c}{{s}^{2}{ \Phi}}_{o}(s) = - \frac{\mu }{I} {s{ \Phi }}_{o}(s)-\left(\frac{mgl}{2I}+\frac{2{\rm{K}}_{r}}{I}\right){ \Phi }_{o}(s)+\frac{{{2}{\rm{K}}}_{r}}{I}\frac{{\rm{r}}_{\rm{in}}}{{\rm{r}}_{\rm{o}}}{ \Phi }_{target}(s)\end{array}$$
(3)

The transfer function of output to input angle is then given by

$$\begin{array}{c}\frac{{ \Phi }_{o}(s)}{{ \Phi }_{target}(s)}=\frac{\frac{{{2}{\rm{K}}}_{r}}{I}\frac{{\rm{r}}_{\rm{in}}}{{\rm{r}}_{\rm{o}}}gl}{\left({s}^{2}+ \frac{\mu }{I} s+\left(\frac{mgl}{2I}+\frac{2{\rm{K}}_{r}}{I}\right)\right)}\end{array}$$
(4)

Equating the transfer function to canonical form

$$\begin{array}{c}\frac{\frac{{{2}{\rm{K}}}_{r}}{I}\frac{{\rm{r}}_{\rm{in}}}{{\rm{r}}_{\rm{o}}}gl}{\left({s}^{2}+ \frac{\mu }{I} s+\left(\frac{mgl}{2I}+\frac{2{\rm{K}}_{r}}{I}\right)\right)} \Leftrightarrow \frac{K}{\left({s}^{2}+2\xi {\omega }_{n}{\rm{s}}+{\omega }_{n}^{2}\right)}\end{array}$$
(5)

Comparing terms yields the natural frequency \({\upomega }_{n}\) and damping ratio \(\xi \) of the system

$$\begin{array}{c}{\omega }_{n}^{2} \Leftrightarrow \left(\frac{mgl}{2I}+\frac{2{\rm{K}}_{r}}{I}\right) { \Rightarrow \omega }_{n}= \sqrt{\left(\frac{mgl}{2I}+\frac{2{\rm{K}}_{r}}{I}\right)}\end{array}$$
(6)
$$\begin{array}{c}2\xi {\omega }_{n} \Leftrightarrow \frac{\mu }{I} \Rightarrow \xi =\frac{\mu }{2I{\omega }_{n}}\end{array}$$
(7)

We note that Eqs. (6) and (7) provides a simple way to estimate system parameters from measurements of natural frequency \({\upomega }_{n}\) and the damping ratio \(\xi \). The latter can be estimated by pulling the link away from equilibrizing, suddenly releasing it, and quantifying the response. This of course changes as a function of tendon co-contraction.

7 State Space Model of System

The A and B matrices of the motor-tendon system, after [12], are given by:

$$\begin{array}{c}A=\left[\begin{array}{cccccccc}-\frac{b}{J}& \frac{Kt}{J}& 0& 0& 0& 0& 0& 0\\ -\frac{Ke}{L}& -\frac{R}{L}& 0& 0& 0& 0& 0& 0\\ {1}& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& -\frac{b}{J}& \frac{Kt}{J}& 0& 0& 0\\ 0& 0& 0& -\frac{Ke}{L}& -\frac{R}{L}& 0& 0& 0\\ 0& 0& 0& {1}& 0& 0& 0& 0\\ 0& 0& \frac{Kr}{{\rm{G}}_{\mathrm{e }}I}\frac{{\rm{r}}_{\rm{in}}}{{\rm{r}}_{\rm{o}}}& 0& 0& -\frac{Kr}{{\rm{G}}_{\mathrm{e }}I}\frac{{\rm{r}}_{\rm{in}}}{{\rm{r}}_{\rm{o}}}& -\frac{\mu }{I}& -\left(\frac{mgl}{2I}+\frac{2Kr}{I}\right)\\ 0& 0& 0& 0& 0& 0& 1& 0\end{array}\right]\end{array}$$
(8)
$$\begin{array}{c}B={\left[\begin{array}{cccccccc}0& -\frac{1}{L}& 0& 0& \frac{1}{L}& 0& 0& 0\\ 0& \frac{1}{2L}& 0& 0& \frac{1}{2L}& 0& 0& 0\end{array}\right]}^{T}\end{array}$$
(9)
Table 1. List of all parameters for agonist-antagonist compliant drive system
Full size table

The C matrix is used by the Luenberger observer. It extracts system output that can be measured from the full state (here only the joint angles) and is used to correct the state estimate.

$$\begin{array}{c}C=\left[\begin{array}{cccccccc}0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right]\end{array}$$
(10)

8 Pseudocode and EtherCAT Implementation

The signal flow graph for the controller is illustrated in Fig. 3. The A, B and C matrices (Eqs. 8, 9, 10) were evaluated in MATLAB. The controller gain vector K and observer gain vector L were designed using the MATLAB lqr command following the derivation described in [12]. Pre-scaling factor nbar was computed in MATLAB as

$$\begin{array}{c}nbar=-inv\left[C\mathrm{inv}(A-BK)B\right]\end{array}$$
(11)

The observed-based state feedback controller design was tested using a Simulink implementation, as illustrated in Fig. 4 and using sub-systems shown in Fig. 5. The target angle and link output from the simulation are shown in Fig. 6. The output followed the input target angle without overshoot or ringing.

We note the mixing matrix M, shown in Eq. (12), is needed in a physical implementation, since the control inputs need to be transformed from target and stretch angles to the corresponding left and right motor inputs:

$$\begin{array}{c}M=\left[\begin{array}{cc}-1& 0.5\\ 1& 0.5\end{array}\right]\end{array}$$
(12)

We implemented open-loop control, P-control (where error is just the scaled difference between target and output) and an observer-based real-time controller on the Beckhoff EtherCAT platform using structured text. To do so, we first linked variables to the hardware slices, providing access to input sensors and connecting output variable to the motor controllers. This framework provided an update function called repetitively at the selected system frame rate of 1 kHz. Within the update frame, we implemented the control of the motors as follows:

  • We accessed the encoder slice variables to read the angular orientation of the two drive and output pulleys.

  • In the case of open-loop and P-control, the motor drive voltage controls were either set directly or as the proportional error respectively.

  • In the case of state feedback control, we estimated the full state of the motor-tendon system using a Luenberger observer. The state estimate was corrected by the prediction error between measured and predicted pulley angles. We calculate the state feedback control signal using the full estimated state and the reference input angle vector scaled by nbar. We used trapezoid integration to update the estimated system state, since it is more robust than Euler integration.

  • The output control signals, (drive voltages to the two worm drive motors) were written to the motor slices, which drove the motors appropriately.

9 Results

We tested the tendons at a single level of co-contraction. A video of open loop operation of the EtherCAT controller driving the 2-tendon arm is shown in this link: https://youtu.be/1L07mjgcbNI. Part1 shows driving the link between target angles as desired, part2 shows tensioning single tendons at a time (which affect joint angle) and part3 shows tensioning followed by moving between targets. A plot of another set of point-to-point angular movements is shown in Fig. 7. It can be seen that despite open-loop operation, there is only a slight overshoot of the link after reaching the target angle.

Fig. 3.
figure 3

State feedback control of motor driven tendon link hardware. The reference input is first weighted by a feedforward compensation gain nbar to achieve unity system DC gain. The input error is linearly transformed by matrix M to generate left and right motor drive. A Luenberger observer is used to estimate the full state of the motor driven tendon link and multiplied with gain K to generate feedback.

Full size image
Fig. 4.
figure 4

Simulink simulation top level schematic. nt. Bus creator and selector blocks are used to appropriately combine and separate signals. Sub-systems, shown in Fig. 5, are used to implement a model of the plant and the Luenberger observer.

Full size image

10 Discussion

We constructed a test rig to examine the operation of variable-stiffness tendon drive with non-back-drivable worm-gear motor actuation. We suggested a simple method of system identification, using step response. We simulated observer-based state feedback control with Simulink and showed our controller design was capably of controlling the link using only measurements of motor and output angles. To control a real link, we built an EtherCAT controller panel. We presented preliminary results of the panel driving the test link making point-to-point movements. Clearly extensive testing of the system is now required, including a rigorous comparison between open-loop. P-control and observer-based state feedback control, which was unfortunately outside the scope of the current work. Finally, we note that from a hardware perspective, our EtherCAT panel design is fully expandable and will support the testing of others joint configurations and full robotic arms, including those which are biologically inspired.

Fig. 5.
figure 5

Simulink sub-systems. Panel A: Motor-tendons controller schematic. State space models for the motors and tendon are shown as sub-systems. Panel B: State space model sub-system schematic. Panel C: Luenberger observer sub-system schematic.

Full size image
Fig. 6.
figure 6

Simulink simulation of the responses of the motor-tendon system under observer-based state feedback control. Dotted line is square-wave input target angle and solid line is output link angle. Note the link follows the target angle and reaches it without overshoot.

Full size image
Fig. 7.
figure 7

Open-loop response of the real physical motor-tendon system during point-to-point movements. Note the slight overshoot of the link after reaching the target angle.

Full size image