Keywords

1 Introduction

Researchers in the field of structural optimization have redirected their focus on the benefits of using different optimization methods to find optimal structures using existing constraint models. This approach has led to marginal improvements in the time needed to achieve results, but the problems being solved still do not represent realistic problem requirements. In order to have optimization results directly applicable in practice the mathematical model must represent all factors which are used in conventional design. Specifically in truss design there are numerous factors which still need to be addressed and implemented in the optimization process in order to make results practically applicable. In recent years authors of have made the transition from using the simpler and less accurate fixed buckling constraints to using Euler buckling dynamic constraints or other dynamic buckling constraints.

Authors in [1, 2] used different optimization methods to achieve minimal weight results using Euler buckling constraints with continuous cross-section variables. In [3, 4] researchers compared the effects on results between mathematical models which don’t use buckling constraints and ones which use dynamic constraints for buckling and continuous cross-section variables. A key factor in defining sizing optimization problems is cross-section variable definition. In practice, continuous cross-sections are not practically applicable, which is why authors in [5, 6] presented a comparison of optimal results for models which use continuous versus discrete cross-section variables. Most recently in [7] a new approach to sizing optimization was presented which limits the number of different cross-sections which can be used in any given solution further increasing the complexity of the problem, but at the same time bringing results closer to practical use.

Shape constraints are generally given as constraints of node coordinates, as is done in papers [8, 9]. The problem with this approach is the possibility of creating overly short elements which are practically inapplicable. Researchers in [10,11,12] all achieved impractical shape optimization results with points converging to create elements shorter than 30 cm, even reaching element lengths shorter than 3 cm. These results point to a need to apply additional minimal element length constraints when using shape optimization. This research presents a use of minimal length constraints for shape optimization. The approach is used on shape and sizing shape truss optimization examples most commonly found in literature.

2 Minimal Weight Truss Optimization

Sizing optimization views cross section parameters as variables and requires an initial model of the truss. These parameters can be cross section geometry (cross-section type) and/or dimensions. Shape optimization considers node positions as variables. The x, y, and z (in space trusses) coordinates can take any value in a previously set range which is also determined by the precision (minimal used units) of the variables. Shape optimization is rarely used as the only optimization type. It is usually part of a sequential optimization process with sizing optimization, or as in this paper it can also be simultaneously used with sizing optimization. The typical weight minimization optimization problem is mathematically defined as follows:

$$ \left\{ {\begin{array}{*{20}l} {minW = \mathop \sum \limits_{i = 1}^{i = n} \rho_{i} A_{i} l_{i} \;{\text{where}}\;A = \left\{ {A_{1} , \ldots ,A_{n} } \right\},} \\ {{\text{subjected to}}\;\left\{ {\begin{array}{*{20}l} {A_{min} \le A_{i} \le A_{max} } & {{\text{for}}\;i = 1, \ldots ,n,} \\ {\sigma_{min} \le \sigma_{i} \le \sigma_{max} } & {{\text{for}}\;i = 1, \ldots ,n,} \\ {u_{min} \le u_{j} \le u_{max} } & {{\text{for}}\;j = 1, \ldots ,k.} \\ \end{array} } \right.} \\ \end{array} } \right. $$
(46.1)

This paper proposes the use of two more constraints in order to achieve optimal results which can be applicable in practice. These constraints are an Euler buckling dynamic constraint and a minimal bar length constraint for shape optimization problems.

2.1 Euler Buckling

Long thin elements subjected to compression are susceptible to buckling therefore they are checked for stresses which exceed critical buckling stress. The existence of even a single element exceeding critical values compromises the structures stability and such solutions are discarded. The use of Euler buckling constraints implies that only compressed bars are tested using the following expressions:

$$ \sigma_{Ai}^{P} \le \sigma_{ki} \;{\text{where}}\;\sigma_{Ai}^{P} = \frac{{F_{Ai}^{P} }}{{A_{i} }}\;{\text{and}}\;\sigma_{ki} = \frac{{F_{ki} }}{{A_{i} }} $$
(46.2)

Stress in compressed elements is given as \(\sigma_{Ai}^{P}\), the critical buckling stress is σki, the cross-section area is Ai, calculated axial compression force is \(F_{Ai}^{P}\) and Fki is Euler’s critical buckling force of the ith element.

$$ F_{ki} = \frac{{\pi^{2} \cdot E_{i} \cdot I_{i} }}{{l_{ki}^{2} }},\quad \left| {F_{Ai}^{P} } \right| \le F_{ki} \;{\text{for}}\;i = 1,...,n $$
(46.3)

Module of elasticity is Ei, Ii is the minimal axial moment of inertia for the cross-section of the ith element and lki is the buckling length of the ith element from the set of 1 to n. Depending on the software used for finite element analysis force or stress constraints can be used. Since sizing constraints vary cross-section areas, and therefore the moments of inertia in each iteration and shape optimization varies both the length (critical length) of bars and in some cases direction of the forces in the bars this constraint is considered as dynamic.

2.2 Minimal Element Length Constraint

The minimal element length constraint value for each example is determined by ex-perience or design guidelines given in literature or corresponding standards. The mathematical formulation of this constraint is given as:

$$ \begin{aligned} l_{i} & \ge l_{\min } \quad for\; i = 1, \ldots ,n \\ l_{i} & = \sqrt {\left( {x_{b}^{i} - x_{a}^{i} } \right)^{2} + \left( {y_{b}^{i} - y_{a}^{i} } \right)^{2} } \\ \end{aligned} $$
(46.4)

The element length li is from the 1 to n range which is between nodes a and b with coordinates (\(x_{a}^{{i}{}}\), \(y_{a}^{i}\)) and (\(x_{b}^{{i}{}}\),\(y_{b}^{i}\)) in that order. Existing node coordinate constraints implicitly define maximal element values therefore they are not necessary, however if there were a need for such a constraint the same method could be used to create it. This could be an interesting constraint for avoiding the use of extensions if bar lengths exceed stock lengths.

3 Optimization Method and Examples

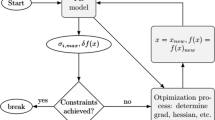
The optimization used for this research is genetic algorithm (GA). The algorithm is comprised of three elementary operators: selection, crossover, and mutation. Selection is the process of conveying genetic information through generations. Crossover denotes the operations (process) between two parents, where an exchange of genetic information is conducted, and new generations are produced. The mutation operator creates a random change in the genetic structure of some of the individuals for overcoming early convergence [2]. Algorithm operation is based on survival of the fittest, through evolution which allows for the exchange genetic material. Selection is used as a process of ranking individuals in the population using values from the fitness function, which defines the quality of the individual.

An original software was created in Rhinoceros 7 using Grasshopper, Galapagos and Karamba plugins, which allow for the choice of optimization type and the choice of used constraints. The Galapagos optimization operator uses GA as its optimization method. Constraints are developed in the form of penalty functions in order to avoid unusable solutions.

3.1 10 Bar Truss

A common example found in literature for truss optimization is the 10 bar truss (Fig. 46.1). This truss has 10 independent sizing variables (full round cross-sections) and 4 shape variables (x and y coordinates for nodes (3) and (4)). Bar elements are made from Aluminum 6063-T5 whose characteristics are: Young modulus 68,947 MPa, and a density of 2.7 g/cm3. The applied loads are F = 444.82 kN, in nodes 2 and 4, as shown in Fig. 46.1. The model is constrained with to a maximal displacement of ±0.0508 m of all nodes in all directions, and axial stress of ±72.3689 MPa for all bars. Discrete variables for cross-section diameters are taken from [5].

Fig. 46.1
figure 1

10 bar truss problem

Full size image

3.2 47 Bar Truss

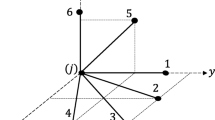
The 47 bar truss problem has 22 nodes placed symmetrically around the y axis, as shown in Fig. 46.2. Cross-section elements are grouped in 27 groups according to the symmetry. This example also uses full round cross-sections, except the material used is construction steel. Material characteristics used are: Young modulus 206,842.719 MPa, and a density of 7.4 g/cm3. The structure is subjected to three independent load cases (LC1, LC2 and LC3). The first load case (LC1) consists of forces F = 26.689 kN in the +x direction and 66.275 kN in the –y direction in nodes 17 and 22. The second load case (LC2) consists of forces F = 26.689 kN in the +x direction and 66.275 kN in the –y direction in node 17. The third load case (LC3) consists of forces F1 = 26.689 kN in the +x direction and force F2 = 66.275 kN in the –y direction of node 22.

Fig. 46.2
figure 2

47 bar truss problem

Full size image

The 47 bar truss problem has stress constraints of 137.895 MPa for tension and 103.421 MPa for compression. This problem, however, does not have a displacement constraint. Discrete variables for cross-section diameters are: 6, 8, 12, 12, 14, 15, 16, 17, 18, 20, 22, 24, 25, 28, 30, 32, 35, 36, 38, 40, 45, 50, 55, 56, 60, 63, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110, 115, 120, 125, 130, 140, 150, 160, 170, 180, 190, 200, 220 and 250, in mm.

Shape optimization variables are grouped according to the symmetry. Node coordinates have the following ranges.

0 m ≤ x(2–8) ≤ 3.05 m, –0.08 m ≤ x(10–14) ≤ 2.29 m, –0.08 m ≤ x(18–20) ≤ 2.29 m, –0.08 m ≤ x(21) ≤ 3.81 m, –1.52 m ≤ y(4) ≤ 4.57 m, 4.57 m ≤ y(6) ≤ 7.62 m, 7.62 m ≤ y() ≤ 10.67 m, 9.14 m ≤ y(10) ≤ 12.19 m, 10.67 m ≤ y(12) ≤ 13.72 m, 12.19 m ≤ y(14) ≤ 15.24 m and 13.72 m ≤ y(20,21) ≤ 16.76 m.

4 Results

Shape optimization results use a 240 mm diameter for the 10 bar truss, and 75 mm for the 47 bar truss, which are the minimal possible diameters of the most stressed bars in the initial configurations respectively. Figure 46.3 shows the layout of the 10 bar truss optimal solutions for shape optimization (9371.591 kg) and sizing and shape optimization (3685.142 kg) where bars 2 and 6 are practically parallel with bar 9.

Fig. 46.3
figure 3

Results of the 10 bar truss optimization of shape (left), and sizing and shape (right)

Full size image
Table 46.1 Node coordinates for shape and sizing shape optimization of the 10 bar truss problem
Full size table
Table 46.2 Node coordinates for shape and sizing shape optimization of the 47 bar truss problem
Full size table

Tables 46.1 and 46.2 show the node coordinates for the 10 bar and 47 bar truss results for both optimization cases respectively.

Figure 46.4 shows the layout of the 47 bar truss optimal solutions for shape optimization (3204.269 kg) and sizing and shape optimization (1687.102 kg).

Fig. 46.4
figure 4

Results of the 47 bar truss optimization of shape (left), and sizing and shape (right)

Full size image

All solutions are the best results of at least 10 repeated optimizations of the same problem with the same initial values repeated for each optimization.

5 Conclusion

The results of examples presented in this paper show that the addition of a minimal length constraint solves the problem of impractically short elements in shape or sizing and shape optimization. The data however also shows the imperfections in the initial configurations. The 10 bar truss when optimized for sizing and shape gives a resulting structure where even though the nodes do not overlap, the bars are in the same plane. This leads to the conclusion that the 10 bar truss can be expected to not need bar (9) in the initial topology if shape is optimized.

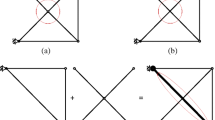
Similarly, compared to results from literature of the 47 bar truss which use sequential optimization of sizing then shape, the solutions presented by this research do not have a convergence of nodes which lead to an impractical solution (Fig. 46.5).

Fig. 46.5
figure 5

Sizing and shape optimization results for 47 bar from [13]

Full size image

These optimal results are, however, useful for presenting the need for elementary changes in the initial topology. The solution presented in [13], similarly to [10] shows that there is possibly no need for bars 15 and 16, and that nodes (19) and (20) should be joined in the initial model.

It can be therefore concluded that topological optimization is a necessary addition to the structural optimization process. Simultaneous optimization of all three factors is the most complex but yields the smallest weight, however this is not always possible. When optimizing any truss it is best to try all possible combinations of optimization types in order to adapt the problem to achieve the best results.