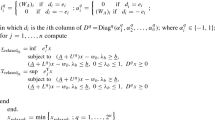Keywords

1 Introduction

Optimization under uncertainty plays a crucial role in modeling and solving real-world problems with inexact input data. In this paper, we consider the approach of interval linear programming [9, 17], which provides a suitable model for problems with uncertain data that can be independently perturbed within the given lower and upper bounds. Throughout the last years, interval programming has been used as an uncertain model for various practical optimization problems, such as transportation problems with interval data [1, 4] or portfolio optimization [2] to mention some.

Several difficult tasks in interval linear programming can be solved by decomposing the problem at hand into an exponential number of classical linear programs. This is also the idea behind the frequently used orthant decomposition method, which exploits the fact that the feasible set of an interval linear program becomes a convex polyhedron when we restrict the solution space to a single orthant [7, 16].

Here, we propose and explore an alternative approach to solving such tasks by utilizing the powerful techniques of integer programming. To illustrate the idea, we derive a (mixed) integer programming reformulation for computing the best optimal value of an interval linear program based on a non-linear absolute-value formulation of the problem [8]. A similar approach can be beneficial in solving other related problems, such as describing the set of all optimal solutions of an interval linear program [5, 12]. We conduct a computational experiment to compare the absolute-value formulation and the derived mixed-integer programming reformulation for the optimal value range problem and show their efficiency against the traditional orthant decomposition [17].

2 Interval Linear Programming

Let us first review some of the notions and notation used throughout the paper. For a comprehensive introduction to interval linear programming see [9, 17] and references therein.

Given a vector \(x \in \mathbb {R}^n\), we denote by diag(x) the diagonal matrix with entries diag(x)ii = x i for i ∈{1, …, n}. The inequality relations on the set of matrices and vectors, as well as the absolute value operator \(\lvert {\cdot }\rvert \), are understood element-wise.

Interval Data

Let the symbol \(\mathbb {I}\mathbb {R}\) denote the set of all closed real intervals. Given two real matrices \( \underline {A},\overline {A} \in \mathbb {R}^{m \times n}\) satisfying \( \underline {A} \le \overline {A}\), we define an interval matrix\(\mathbf {A} \in \mathbb {I}\mathbb {R}^{m \times n}\) as the set

$$\displaystyle \begin{aligned} \mathbf{A} = [\underline{A}, \overline{A}] = \{ A \in \mathbb{R}^{m \times n} : \underline{A} \le A \le \overline{A} \}. \end{aligned}$$

Alternatively, an interval matrix can also be determined by the centerA c and radiusA Δ, where

$$\displaystyle \begin{aligned} A_c = \frac{1}{2}(\overline{A} + \underline{A}), \qquad A_\Delta = \frac{1}{2}(\overline{A} - \underline{A}). \end{aligned} $$
(1)

An interval vector\(\mathbf {a} \in \mathbb {I}\mathbb {R}^n\) can be defined analogously as an n × 1 interval matrix. In the text, we denote all interval matrices and interval vectors by bold letters.

Interval Programming

For an interval matrix \(\mathbf {A} \in \mathbb {I}\mathbb {R}^{m \times n}\) and interval vectors \(\mathbf {b} \in \mathbb {I}\mathbb {R}^m\), \(\mathbf {c} \in \mathbb {I}\mathbb {R}^n\), we define an interval linear program (abbreviated as ILP) as the set of all linear programs in the form

$$\displaystyle \begin{aligned} \min\, c^T x \mbox{ subject to } Ax \le b, \end{aligned} $$
(2)

with A ∈A, b ∈b and c ∈c. For short, we also write an interval linear program determined by the triplet (A, b, c) as

$$\displaystyle \begin{aligned} \min\, {\mathbf{c}}^T x \mbox{ subject to } \mathbf{A}x \le \mathbf{b}. \end{aligned} $$
(3)

A particular linear program (2) is called a scenario of the interval linear program (3).

For the sake of simplicity, the formulation of an interval linear program introduced in (3) is not the most general one. Since the commonly used transformations in linear programming are not always applicable in the interval framework due to the so-called dependency problem (see e.g. [6]), different formulations of interval linear programs may have different properties. However, the approach presented in this paper can also be utilized for other types of interval linear programs in the same manner.

Feasibility and Optimality

Several different concepts of feasible and optimal solutions of interval linear programs have been introduced in the literature. In this paper, we adopt the notion of weak feasibility and optimality.

A vector \(x^* \in \mathbb {R}^n\) is called a weakly feasible solution of ILP (3), if it is a feasible solution of some scenario, i.e. if Ax ∗≤ b holds for some A ∈A and b ∈b. In general, the set of all weakly feasible solutions of an ILP forms a non-convex polyhedron, which is convex in each orthant [16]. By the Gerlach theorem for interval systems of inequalities [7], a vector \(x \in \mathbb {R}^n\) is a weakly feasible solution of ILP (3) if and only if it solves the non-linear system

$$\displaystyle \begin{aligned} {A}_c x \le {A}_\Delta \lvert{x}\rvert + \overline{b}. \end{aligned} $$
(4)

Similarly, we say that a vector \(x^* \in \mathbb {R}^n\) is a weakly optimal solution of the ILP, if it is an optimal solution of some scenario with A ∈A, b ∈b, c ∈c. Unless stated otherwise, we use the term “feasible/optimal solution” in the context of interval programming to refer to weakly feasible and weakly optimal solutions, respectively.

Optimal Values

A common approach to computing optimal values of an interval linear program is to find the best and the worst value, which is optimal for some scenario of the program.

Let f(A, b, c) denote the optimal value of the linear program (2), setting f(A, b, c) = −∞ for unbounded programs and f(A, b, c) = ∞ for infeasible programs. Then, we define optimal value range of interval linear program (3) as the interval \([ \underline {f}, \overline {f}]\), where the best optimal value \( \underline {f}\) and the worst optimal value \(\overline {f}\) are

$$\displaystyle \begin{aligned} \underline{f}(\mathbf{A},\mathbf{b},\mathbf{c}) &= \min\,\{ f(A,b,c) : A \in \mathbf{A}, b \in \mathbf{b}, c \in \mathbf{c}\},\\ \overline{f}(\mathbf{A},\mathbf{b},\mathbf{c}) &= \max\,\{ f(A,b,c) : A \in \mathbf{A}, b \in \mathbf{b}, c \in \mathbf{c}\}. \end{aligned} $$

The worst optimal value \(\overline {f}\) of ILP (3) can be computed in polynomial time by solving a linear program (see [3, 15]). On the other hand, computing the best optimal value \( \underline {f}\) of (3) is an NP-hard problem [17]. Since it might be difficult to compute the value exactly, methods providing a sufficiently tight approximation are also of interest [11, 13].

Orthant Decomposition

As the set of all weakly feasible solutions of an interval linear program becomes a convex polyhedron when we restrict the solution space to a single orthant, we can utilize this property to solve various problems over the feasible set. This idea leads to the often used orthant decomposition method, which solves a given problem in interval programming by decomposing it into a set of linear programming subproblems, one for each orthant of the solution space.

Orthant decomposition can also be used to obtain the best optimal value \( \underline {f}\) of ILP (3). Here, we can formulate a linear program to compute the minimum value of the objective function over the feasible set in a given orthant and then take the smallest of the computed values (see [17] for further details). An orthant of the solution space \(\mathbb {R}^n\) can be described as the set

$$\displaystyle \begin{aligned} \{ x \in \mathbb{R}^n : \mbox{diag}(s)x \ge 0 \} \end{aligned}$$

for a particular sign vector s ∈{±1}n. Therefore, we can compute \( \underline {f}\) by solving the linear program

(5)

for each s ∈{±1}n. For a given vector s, denote by f s(A, b, c) the optimal value of program (5). Then, we obtain the best optimal value as

$$\displaystyle \begin{aligned} \underline{f}(\mathbf{A}, \mathbf{b}, \mathbf{c}) = \min \left\{ f_s(\mathbf{A}, \mathbf{b}, \mathbf{c}) : s \in \{\pm 1 \}^n \right\}. \end{aligned}$$

This amounts to solving (at most) 2n linear programs to compute \( \underline {f}\), with n denoting the number of variables of the ILP. Note that the number of orthants that have to be explored can be lowered, if some of the variables are known to be sign-restricted (non-negative or non-positive).

3 Integer Programming Reformulations

In this section, we build on the absolute-value characterization of the feasible set by Gerlach stated in (4). We derive a mixed-integer linear programming reformulation of the system in order to design an alternative method for computing the best optimal value of an interval linear program.

The aim is to utilize the available techniques and efficient algorithms of integer linear programming to tackle some of the difficult interval problems, such as the problem of computing the optimal value range.

Absolute-Value Formulation

Instead of using the orthant decomposition, we can also restate the method for computing the best optimal value as an absolute-value program [8], which is derived from the Gerlach theorem for describing the weakly feasible set. By this result, we can compute \( \underline {f}\) as the optimal value of the non-linear program

$$\displaystyle \begin{aligned} \begin{array}{ll@{\ }l} \mbox{minimize } &{{c}_c^T x - {c}_\Delta^T \lvert{x}\rvert} \\ \mbox{subject to } & {A}_c x - {A}_\Delta \lvert{x}\rvert \le \overline{b}. \end{array} \end{aligned} $$
(6)

We can now attempt to solve formulation (6) directly as a non-linear program, or we can further linearize the program by modeling \(\lvert {x}\rvert \) via binary variables and additional linear constraints as a mixed-integer linear program.

MIP Reformulation

Now, we can use the absolute-value formulation (6) to derive a mixed-integer linear program for computing the best optimal value \( \underline {f}\). To do this, we apply one of the traditional ways to model absolute values in integer programs using binary variables.

Here, we split the variable x into a positive and negative part as x = x + − x −, using the lower and upper bound on x and auxiliary binary variables y i. Then, we model the absolute value \(\lvert {x}\rvert \) by introducing a new variable z = x + + x −, leading to the formulation

(7)

Note that we can also reduce the number of variables in the model by simply substituting the expressions in terms of x + and x − for the variable x and its absolute value z. Using the definition of the center and the radius of an interval matrix stated in (1), we obtain the simplified mixed-integer linear program

(8)

Further Applications

Apart from computing the optimal value range, integer programming reformulations can also prove useful in solving other difficult problems in interval linear programming. A description of many important characteristics and properties of an interval linear program can be derived from the Gerlach and the Oettli–Prager theorems [7, 16], which describe the weakly feasible set via a system of absolute-value inequalities.

For example, the set of all weakly optimal solutions of ILP (3) can be described by primal feasibility, dual feasibility and strong duality as the set of x-solutions of the system

$$\displaystyle \begin{aligned} \begin{array}{ll@{\ }l} Ax \le b,\\ A^T y = c,\ y \le 0,\\ c^T x = b^T y,\\ A \in \mathbf{A},\ b \in \mathbf{b},\ c \in \mathbf{c}. \end{array} \end{aligned} $$
(9)

Note that this is a parametric system, since there are dependencies between the two occurrences of the interval parameters that cannot be captured by a simple interval linear system (e.g. the two occurrences of the matrix A ∈A should represent the same matrix in any considered scenario). However, we can relax these dependencies to obtain an interval linear system (see also [5, 10] and references therein), which provides an outer approximation of the optimal solution set:

$$\displaystyle \begin{aligned} \begin{array}{ll@{\ }l} \mathbf{A}x \le \mathbf{b},\quad {\mathbf{A}}^T y = \mathbf{c},\ y \le 0,\quad {\mathbf{c}}^T x = {\mathbf{b}}^T y. \end{array} \end{aligned} $$
(10)

Here, we assume that the two occurrences of the interval parameters A, b and c are independent and in a particular scenario of the system, different values from the respective interval matrices and vectors can be chosen for them. System (10) is a classical interval linear system, so we can use the description of the weakly feasible set provided by the Gerlach and the Oettli–Prager theorems, leading to the absolute-value system

$$\displaystyle \begin{aligned} \begin{array}{ll@{\ }l} {A}_c x \le {A}_\Delta \lvert{x}\rvert + \overline{b},\\ \overline{A}^T y \le \overline{c},\ \underline{A}^T y \ge \underline{c},\ y \le 0,\\ \lvert{{c}_c^T x - {b}_c^T y}\rvert \le {c}_\Delta^T \lvert{x}\rvert - {b}_\Delta^T y. \end{array} \end{aligned} $$
(11)

For system (11), we can formulate a mixed-integer linear program in a similar way as in the problem of computing the best optimal value. The program can then be used to compute an interval enclosure of the optimal set by finding the minimal/maximal value of each x i over (11). We can also apply various integer programming relaxations and heuristics to derive more efficient approximation techniques for the optimal set. A tight approximation of the optimal set is also essential in solving the recently proposed outcome range problem [14], which generalizes the optimal value range by introducing an additional linear outcome function to the program.

4 Computational Experiment

We conducted a computational experiment to compare the derived integer programming reformulation with the traditionally used orthant decomposition method and the non-linear absolute-value formulation for the problem of finding the best optimal value \( \underline {f}\) of ILP (3). Since all of these techniques are used to compute the value \( \underline {f}\) exactly, the main criterion for comparison is the elapsed computation time.

Instances

We compared the different programs for computing the best optimal value on a set of (pseudo-)randomly generated feasible instances. Since the best optimal value \( \underline {f}\) can always be achieved for the upper bound \(\overline {b}\) of the interval right-hand-side vector b, we only generated interval data for the constraint matrix and the objective vector. Thus, each instance is described by an interval matrix \(\mathbf {A} \in \mathbb {I}\mathbb {R}^{m \times n}\), a fixed right-hand-side vector \(b \in \mathbb {R}^m\) and an interval objective vector \(\mathbf {c} \in \mathbb {I}\mathbb {R}^{n}\).

All of the instances are in the inequality-constrained form (3) with bounded variables satisfying x ∈ [−106, 106]. With a 0.1 probability a generated interval coefficient includes both positive and negative values (i.e., 0 belongs to the interval), otherwise the coefficient satisfies \({A}_\Delta \in [0, 0.2 \lvert {{A}_c}\rvert ]\) and \({c}_\Delta \in [0, \lvert {{c}_c}\rvert ]\). Due to the exponential nature of the considered problem, the number of variables and the number of constraints in the generated instances was limited. We generated problem instances of 31 sizes with

$$\displaystyle \begin{aligned} n \in \{ 5, 10, 15, 20 \} \mbox{ and } m \in \{10, 20, 50, 100, 200, 500, 1000, 2000, 5000 \}.\end{aligned}$$

For each size, 20 problem instances were generated.

Methods and Implementation

Three formulations of programs for computing the exact best optimal value \( \underline {f}\) were tested and compared in the experiment:

  • the commonly used orthant decomposition method, solving in each orthant of the solution space (determined by a sign vector s ∈{±1}n) the linear program:

  • the non-linear absolute-value formulation based on the Gerlach theorem:

    $$\displaystyle \begin{aligned} \begin{array}{ll@{\ }l} \mbox{minimize } &{{c}_c^T x - {c}_\Delta^T \lvert{x}\rvert} \\ \mbox{subject to } & {A}_c x - {A}_\Delta \lvert{x}\rvert \le \overline{b},\qquad \end{array} \end{aligned}$$

  • and the derived mixed-integer linear programming reformulation:

All of the methods were implemented in Python 3.8 and Gurobi 9.1 solver was used to solve the corresponding models. The non-linear formulation (6) was modeled using the general constraints in Gurobi supporting absolute-value expressions.

Results

We used the three methods to compute the best optimal value \( \underline {f}\) for a total of 500 instances of inequality-constrained interval linear programs. The experiment was carried out on a computer with a 16 GB RAM and an Intel Core i7-8650U processor. The results of the experiment are summarized in Tables 1 and 2, showing the average computation time (in seconds) of each method on a set of instances of a given problem size.

Table 1 The average elapsed running time (in seconds) of the three methods on instances with the best optimal value \( \underline {f}\) attained at the boundary of the bounding box. The fastest running times are indicated by bold values
Full size table
Table 2 The average elapsed running time (in seconds) of the three methods on general instances. The fastest running times are indicated by bold values
Full size table

Table 1 presents the results of the experiment on problems, for which the best optimal value was attained at the boundary of the bounding box. This is a subset of the instances with a lower ratio of the number of constraints to the number of variables. The resulting running times show that this class of problems can be solved very efficiently through integer programming and through the absolute-value formulation. This holds even for problems of larger size, where the orthant decomposition approach may be too time-consuming. These results also indicate that the alternative approaches may prove useful in designing methods for quickly checking (weak) unboundedness of interval linear programs.

The results in Table 2 show the average running times of the three methods on the general problems. While the orthant decomposition is faster for the smallest problems with only 5 variables, we can observe the expected behavior on larger instances, where mixed-integer programming and the absolute-value formulation show their notable advantage in efficiency over exploring all orthants of the solution space. Here, using the mixed-integer programming formulation seems to be the fastest approach, with the absolute-value general constraints being slightly behind. Although the computation becomes more time-consuming with the growing number of variables and constraints, both of these approaches still present a significant improvement over the straight-forward orthant decomposition.

5 Conclusion

We explored the applicability of integer programming methods for solving some of the difficult problems in interval linear programming. Specifically, we considered the NP-hard problem of computing the best value, which is optimal for some scenario of a given interval linear program. Based on an absolute-value formulation of the problem, we derived a mixed-integer linear program to compute the best optimal value. The conducted computational experiments show the significant advantages of utilizing the existing integer programming solvers over the commonly used orthant decomposition method, which explores all orthants of the solution space.

Since many problems in interval optimization are difficult to solve exactly, approximation methods are also of interest. Integer programming reformulations open a new direction for deriving algorithms for tightly approximating the optimal value range of an interval linear program. Other challenging problems may also be considered, such as approximating the set of all optimal solutions or computing the outcome range for a given function over the optimal set. These difficult problems can benefit from utilizing the theoretical foundations, relaxation techniques and efficient heuristics of integer programming.