Computational Aspects of Solving Grid Equations in Heterogeneous Computing Systems

Abstract

The prediction of environmental disasters, both technogenic and natural, is currently based on advances in mathematical modeling. The high cost and costly maintenance of computing clusters actualizes the research in the field of heterogeneous computing. One of the directions of them is to maximize the use of all available hardware resources, including the central processor and the video adapters (GPU). The purpose of the research is to develop an algorithm and a software module that implements it for solving a system of linear algebraic equations (SLAE) by the modified alternating-triangular iterative method (MATM) (self-adjoint and non-self-adjoint cases) for the hydrodynamics problem of shallow water using NVIDIA CUDA technology. The conducted experiment with the flow distribution along the Ox and Oz axes of the computational grid at a fixed value of the grid nodes along the Oy axis allowed reducing the implementation time of one step of the MATM on the GPU. A regression equation was obtained at the experimental data processing in the Statistica program, on the basis of which it was found that the implementation time of one step of the MATM on the GPU is affected only by the number of threads along the axis Oz. The optimal two-dimensional configuration of threads in a computing unit executed on a single thread multiprocessor is determined, in which the calculation time on the GPU for one step of the MATM is minimal.

Supported by Russian Science Foundation, project № 21-71-20050.

1 Introduction

The prediction process of environmental disasters of natural and technogenic nature requires an operational approach in order to reduce the negative consequences on the environment and the population living in the surrounding areas. Hydrophysical processes have a significant impact on the water shoreline, coastal protection structures and coastal constructions. Currently, the research of hydrodynamical processes in waters with complex bathymetry is one of the most important problems. This problem can be effectively solved using mathematical modeling methods.

Mathematical modeling of hydrodynamical processes is based on the Navier-Stokes motion equations, the continuity equations, as well as the heat and salt transfer equations. As a result of numerical implementation, a continuous mathematical model is transformed into a discrete one, the solution of which is reduced to the solution of a system of linear algebraic equations (SLAE).

Many Russian and foreign scientists are engaged in research and forecasting of aquatic ecosystems. Representatives of the scientific school by G.I. Marchuk study the computational aspects of atmospheric and ocean physics. Comprehensive re-searches of the environment and biota in the Azov and Black Seas are performed under the leadership of G.G. Matishov. Bonaduce A., Staneva J. proposed the mathematical models of sea level dynamicss [1]. Marchesiello P., Androsov A., etc. scientists are engaged in improving ocean models [2, 3]. Developed software systems, designed for monitoring and forecasting the state of waters (SALMO, CHARISMA, MARS3D, CHTDM, CARDINAL, PHOENICS, Ecointegrator), have a number of advantages, are easy to use, and allow solving computationally labors problems for a wide range of research areas. The disadvantages include the lack of consideration of the spatially inhomogeneous transport of water environment, the lack of accuracy in modeling the vortex structures of currents, the shore and bottom topography [1,2,3,4].

The team of authors developed the AZOV3D software, which uses the spatial-three-dimensional models of the hydrodynamics of shallow waters (coastal systems). These models include the motion equations in all three coordinate directions and taking into account the wind stress, bottom friction, complex geometry of the shore and bottom of water, Coriolis force, precipitation evaporation, as well as the nonlinear character of microturbulent exchange in the vertical direction [5]. Testing of this software was performed during the reconstruction of the extreme storm surge of water on September 23–24, 2014 in the port area of Taganrog, when the level rise was more than 4 m at the average depth of the bay is about 5 m. The prediction was performed with the error of 3–5%.

The complex geometry of the computational domain requires the use of computational grids with a large number of nodes in spatial coordinates. As a result, it’s necessary to solve the SLAE with dimension from $10^7$, $10^9$ and more [6]. The implementation of such calculations for the time interval from the occurrence of an emergency to the receipt of forecasting results, established by regulatory acts, is very difficult without the use of parallel computing and supercomputer technologies. The high cost and costly maintenance of computing clusters actualizes research in the field of heterogeneous computing, which aims to maximize the use of all available hardware resources, which include video adapters along with the central processor. Modern video adapters have a large amount of VRAM (up to 24 GB) and stream processors, the number of which can achieve the several thousand. There are software interfaces that allow you to implement the computing process on a graphics accelerator, one of which is NVIDIA CUDA. International research teams are actively conducting research in this area [7, 8].

The purpose of the research is to develop algorithms for solving large-dimen-sional SLAE in a limited time, and their software implementation in the environment of heterogeneous computing systems.

2 Grid Equations Solving Method

Let A be is linear, positive definite operator ($A>0$) and in a finite-dimensional Hilbert space H it is necessary to solve the operator equation [9, 10]

$$\begin{aligned} A x = f, A : H \rightarrow H. \end{aligned}$$

(1)

For the grid Eq. (1), iterative methods are used, which in canonical form can be represented by the equation [9, 10]

$$\begin{aligned} B \frac{x^{m+1} - x^m}{\tau _{m+1}} + A x^m = f, B : H \rightarrow H, \end{aligned}$$

(2)

where m is the iteration number, $\tau _{m+1}>0$ is the iteration parameter, B is the preconditioner. Operator B is constructed proceeding from the additive representation of the operator $A_0$ – the symmetric part of the operator A

$$\begin{aligned} A_0 = R_1 + R_2, R_1 = R_2^*, \end{aligned}$$

(3)

where $A = A_0 + A_1$, $A_0 = A_0^*$, $A_1 = - A_1^*$.

The preconditioner is formed as follows

$$\begin{aligned} B = \left( D + \omega R_1 \right) D^{-1} \left( D + \omega R_2 \right) , D = D^*> 0, \omega > 0, \end{aligned}$$

(4)

where D is the diagonal operator, $R_1, R_2$ are the lower- and upper-triangular operators respectively.

The algorithm for calculating the grid equations by the modified alternating-triangular method of the variational type is written in the form:

$$\begin{aligned} r^m = A x^m - f, B(\omega _m)w^m = r^m, \tilde{\omega }_m = \sqrt{\frac{(D w^m, w^m)}{(D^{-1} R_2 w^m, R_2 w^m)}}, \end{aligned}$$

$$\begin{aligned} s_m^2 = 1 - \frac{ \left( A_0 w^m, w^m \right) ^2 }{ \left( B^{-1} A_0 w^m \right) \left( B w^m, w^m \right) }, k_m^2 = \frac{\left( B^{-1} A_1 w^m, A_1 w^m \right) }{\left( B^{-1} A_0 w^m, A_0 w^m \right) }, \end{aligned}$$

(5)

$$\begin{aligned} \theta _m = \frac{ 1 - \sqrt{\frac{s_m^2 k_m^2}{ \left( 1 + k_m^2 \right) }}}{ 1 + k_m^2 \left( 1 - s_m^2 \right) }, \tau _{m+1} = \theta _m \frac{\left( A_0 w^m, w^m \right) }{\left( B^{-1} A_0 w^m, A_0 w^m \right) }, \end{aligned}$$

$$\begin{aligned} x^{m+1} = x^m - \tau _{m+1} w^m, \omega _{m+1} = \tilde{\omega }_m, \end{aligned}$$

where $r^m$ is the residual vector, $w^m$ is the correction vector, the parameter $s_m$ describes the rate of convergence of the method, $k_m$ describes the ratio of the norm of the skew-symmetric part of the operator to the norm of the symmetric part.

The method convergence rate is:

$$\begin{aligned} \rho \le \ \frac{ \nu ^* - 1 }{\nu ^* + 1}, \end{aligned}$$

(6)

where $\nu ^* = \nu \left( \sqrt{1+k^2} + k \right) ^2$, where $\nu$ is the condition number of the matrix $C_0$, $C_0 = B^{-1/2} A_0 B^{-1/2}$.

The value $\omega$ is optimal for

$$\begin{aligned} \omega = \sqrt{\frac{(D w^m, w^m)}{(D^{-1} R_2 w^m, R_2 w^m)}} \end{aligned}$$

(7)

and the condition number of the matrix is estimated $C_0$:

$$\begin{aligned} \nu = \max \limits _{y \ne 0} \left( \frac{1}{2} + \frac{\sqrt{(Dy,y)(D^{-1}R_2y, R_2y)}}{(A_0y,y)} \right) \le \frac{1}{2} \left( 1 + \sqrt{ \frac{\varDelta }{\delta } } \right) = \frac{ 1 + \sqrt{\xi }}{2 \sqrt{\xi }}, \end{aligned}$$

(8)

where $\xi = \frac{\delta }{\varDelta }$, $D \le \frac{1}{\delta } A_0$, $R_1 D^{-1} R_2 \le \frac{\varDelta }{4} A_0$.

3 Software Implementation of the Method for Solving Grid Equations

To solve the hydrodynamics problem, a computational grid is introduced as [11]

$$\begin{aligned} \bar{w}_h&= {t^n=n \tau , x_i = ih_x, y_i=jh_y, z_k=kh_z; n=\overline{0,n_t-1}, i= \overline{0, n_1-1},} \\&\quad \,\, j = \overline{0, n_2-1}, k = \overline{0, n_3-1}, n_t\tau = { T, n_1h_x=l_x, n_2h_y=l_y, n_3h_z=l_z}, \end{aligned}$$

where $\tau$ is the time step; $h_x$, $h_y$, $h_z$ are space steps; $n_t$ is the time layers number; T is the upper bound on the time coordinate; $n_1$, $n_2$, $n_3$ are the nodes number by spatial coordinates; $l_x$, $l_y$, $l_z$ are space boundaries of a rectangular parallelepiped in which the computational domain is inscribed.

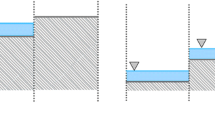
At discretization the hydrodynamics model, we obtained a system of grid equations. Each equation of the system can be represented in a canonical form. We will use a seven-point template (Fig. 1):

$$\begin{aligned} c(m_0)u(m_0) - \sum _{i=1}^{6}c(m_0,m_i)u(m_i)=F(m_0), \end{aligned}$$

$m_0(x_i, y_j, z_k)$ is the template center, $M'(P)=\{m_1(x_{i+1},y_j, z_k)$, $m_2(x_{i-1}, y_j, z_k)$, $m_3(x_i,y_{j+1}, z_k), m_4(x_i,y_{j-1}, z_k), m_5(x_i,y_j, z_{k+1}), m_5(x_i,y_j, z_{k-1})\}$ is the neighborhood of the template center, $c_0\equiv c(m_0)$ is the template center coefficient, $c_i\equiv c(m_0, m_i)$ are coefficients of the neighborhood of the template center, F is the vector of the right parts, u is the calculated vector.

Fig. 1.

Grid template for solving hydrodynamic equations.

The developed software module uses one-dimensional arrays. The transition from a three-dimensional representation of the grid node (i, j, k) to a one-dimensional (node number) is performed using the following formula:

$$\begin{aligned} m_0=i+jn_1+kn_1n_2. \end{aligned}$$

The numbers of nodes in the neighborhood of the template center are calculated by the formulas:

$$\begin{aligned} \begin{array}{c} m_1=m_0+1, m_2=m_0-1, m_3=m_0+n_1,\\ m_4=m_0-n_1, m_5=m_0+n_1n_2, m_6=m_0-n_1n_2. \end{array} \end{aligned}$$

The MATM algorithm consists of four stages:

• calculating the values of the residual vector $r^m$ and its uniform norm;

• calculating the correction vector $w^m$;

• calculating the scalar products and iterative parameters based on them $\tau _{m+1}, \omega _{m+1}$;

• transition to the next iterative layer.

The computational process is performed until the norm of the residual vector reaches the specified accuracy.

The most laborious part of the algorithm is the calculation of the correction vector from the equation:

$$\begin{aligned} (D+\omega R_1)y^m = r^m, (D+\omega R_2)w^m = Dy^m. \end{aligned}$$

The algorithm fragment of solving SLAE with the lower-triangular matrix is given below (Algorithm 1).

The residual vector is calculated in 14N arithmetic operations, where N is a basic arithmetic operation such as adding, multiplying etc. The complexity of calculating the values of the correction vector is 19N arithmetic operations (9N and 10N each for solving SLAE of upper-triangular and lower-non-triangular types, respectively). The transition to the next iteration will require 2N arithmetic operations. In total, the total number of arithmetic operations required to solve the SLAE with a seven-diagonal matrix using MATM in the case of known iterative parameters $\tau _{m+1}, \omega _{m+1}$ is 35N.

We determine the complexity of adaptive optimization of the minimum correction MATM. The calculation of $A_0 w^m, A_1 w^m$ and $R_2 w^m$ vectors requires 13N, 11N and 7N operations each. The multiplication of vectors by diagonal operators $D^{-1}$ and D will require N operations each. The conversion B to determine vectors $B^{-1}A_0w^m$ and $B^{-1}A_1w^m$ will require 19N operations each. It is also necessary to calculate 6 scalar products, each of which will require 2N operations. Thus, each adaptive optimization of the minimum correction MATM requires 83N arithmetic operations in the non-self-adjoint case and 49N in the self-adjoint case. The calculation process of iterative parameters $\tau _{m+1}, \omega _{m+1}$ is laborious, but its establishment is observed quite quickly at solving grid equations in the adaptive case. As a result, these parameters do not need to be calculated at each iteration.

4 Parallel Implementation

Parallel algorithms focused on heterogeneous computing systems were developed for numerical implementation of the proposed hydrodynamics model. Each computing node of the system can contain from 1 to 2 central processing units (CPU) containing from 4 to 32 cores, and from 1 to 4 NVIDIA video accelerators with CUDA technology (GPU), having from 192 (NVIDIA GeForce GT 710) to 5120 (NVIDIA Tesla V100) CUDA cores. Data exchange between nodes is performed using MPI (Message Passing Interface) technology. An algorithm that controls all available CPU and GPU threads performs the organization of calculations on each node. The computational domain is divided into subdomains assigned to the computational nodes. Next, each subdomain is divided into fragments assigned to each CPU core and each GPU computing unit (Fig. 2).

Fig. 2.

Decomposition of the computational domain. Node1, Node2, Node3 are computational nodes; CPU, GPU are fragments of the computational domain, calculated on the CPU and GPU, respectively; blockDim.x, blockDim.z – dimensions of the computing CUDA block.

The solution of mathematical modeling problems using numerical methods, in particular, the finite difference method (FDM) on equal-dimensional grids, leads to the necessary to use with sparse matrices, the elements of which for internal nodes are a repeating sequence. This leads to inefficient memory consumption in the case of high-dimensional problems. Using the CSR (Compressed Sparse Row) matrix storage format avoids the necessary to store null elements. However, all non-zero elements, including many duplicate ones, are stored in the corresponding array. This disadvantage is not critical at using computing systems with shared memory. However, it can negatively affect the performance at data transferring between nodes in heterogeneous and distributed computing systems. A CSR1S modification of the CSR format was developed to improve the efficiency of data storage with a repeating sequence of elements for modeling hydrodynamic processes by the finite difference method. In this case, to change the differential operator, instead of repeatedly searching and replacing values in an array of non-zero elements, it is enough to simply change them in an array that preserves a repeating sequence.

Let’s consider the conversion of a sparse matrix from CSR1S to CSR format. The input data of the algorithm is an object of the matrix class with repeated elements SMatrix1Seq, encapsulating an array of non-zero elements Values; the array of indexes of columns, containing non-zero elements ColIdx; the array of indexes of non-zero elements that are first in the rows (the last element of the array is the total number of non-zero elements) RowIdx; the array for storing a repeating sequence; the array for storing the indexes of columns, containing the first elements of a repeating sequence. In this case, the Values, ColIdxandRowIdx arrays indicate elements that are not part of a repeating sequence. The output data – an object of the MatrixCsr class – a sparse matrix in CSR format containing arrays Values, ColIdxandRowIdx. The data types and array assignments are similar to the corresponding arrays of the SMatrix1Seq class. We present an algorithm for converting a sparse matrix from the CSR1S to CSR format.

• 1. Calculation the size of the MatrixCsr class arrays (output arrays).

• 2. Reserving of RAM for storing output arrays.

• 3. Saving the resultValues array size value.

• 4. Copying the non-repeating elements from the Values input array to the resultValues output array.

• 5. Filling the resultValues array with duplicate elements using CUDA.

• 6. Copying the column indexes of non-repeating elements.

• 7. Copying the column indexes of duplicate elements using CUDA.

• 8. Copying the indexes of rows, containing non-repeating elements.

• 9. Copying the indexes of rows, containing duplicate elements using CUDA.

• 10. Generating an output object of the MatrixCsr class, containing the resultValues array of non-zero elements, an array of column indexes of non-repeating elements, and an array of row indexes, containing non-repeating elements.

• 11. Clearing the resources, returning the result to the calling method.

Let’s estimate the memory capacity in the CSR format:

$$\begin{aligned} P_{csr} = N_{nz} B_{nz} + (N_{nz} + R + 1) B_{idx}, \end{aligned}$$

in the CSR1S format:

$$\begin{aligned} P_{csr1s} = (N_{nz} - N_{seq} (R_{seq} + 1)) B_{nz} + (N_{nz} - R_{seq} (N_{seq} + 1)+ R + 1) B_{idx}, \end{aligned}$$

where R is the number of matrix rows; $R_{seq}$ is the number of matrix rows, containing a repeating sequence of elements; $N_{nz}$ is the number of non-zero matrix elements; $N_{seq}$ is number of elements in a repeating sequence; $B_{nz}$ is the memory capacity to store a single non-zero element; $B_{idx}$ to store a single non-zero element to store a single index.

Let’s introduce the coefficients $k_r = R_{seq}/R$ and $k_i = B_{idx}/B_{nz}$. After arithmetic transformations, we obtained the following:

$$\begin{aligned} P_{csr1s}=B_{nz}[N_{nz}(k_i+1)- N_{seq}(k_ik_rR+k_rR+1)-k_i(k_rR-R-1)]. \end{aligned}$$

Efficient function libraries have been developed to solve the system of grid equations that arise during the sampling process in CSR format on GPUs using CUDA technology. The developed algorithm for solving the problem uses the modified CSR1S data storage format with further conversion to the CSR format to solve the resulting SLAE on a graphics accelerator using NVIDIA CUDA technology. In this case, there is the problem of developing a matrix conversion algorithm the from CSR1S to CSR format in the shortest possible time.

Experimental researches of the dependence of the execution time of the transformation algorithm on the number of elements of the repeated sequence $N_{seq}$ and the ratio of the matrix rows containing the sequence to the total number of rows $k_r$ were performed. According to the obtained results, the algorithm with using NVIDIA CUDA technology is more efficient at $N_{seq}>7$. The point of equal efficiency decreases starting from $k_r=0.7$. The resulting regression equation $k_r = -0.02N_{seq}+0.08329$ with the determination coefficient 0.9276 describes the boundary of equal time consumption of the sequential algorithm and the algorithm using NVIDIA CUDA. Thus, we can calculate the minimum value $k_r$, by substituting a value $N_{seq}$ into it, above which the second algorithm will be more efficient than the first.

The part of the computational load is passed to the graphics accelerator to increase the efficiency of calculations. For this, the corresponding algorithm and its software implementation on the CUDA C language were developed [12].

An algorithm for finding a solution to a system of equations with a lower-triangular matrix (straight line) on CUDA C is given (Algorithm 2).

The input parameters of the algorithm are the vectors of the coefficients of the grid equations $c_0, c_2, c_4, c_6$ and the constant $\omega$. The output parameter is the vector of the water flow velocity r. Before running the algorithm, we must programmatically set the dimensions of the CUDA computing block blockDim.x, blockDim.z in spatial coordinates x, z, respectively. The CUDA framework runs this algorithm for each thread; in this case, the values of the variables threadIdx.x, threadIdx.z, blockIdx.x, blockIdx.z automatically initialized by the indexes of the corresponding threads and blocks. Global thread indexes are calculated in rows 1 and 2. The row index i, the layer index k, which the current thread processes, are calculated in rows 3 and 5. The variable j is initialized in row 4, representing a counter by coordinate y. The calculation pipeline is organized as a loop in line 6. The indexes of the central node of the grid template $m_0$ and surrounding nodes $m_2, m_4, m_6$ are calculated in rows 8, 10–12. The two-dimensional array cache is located in the GPU shared memory and designed to store the calculation results of on the current layer by the coordinate y. This allows us to reduce the number of reads from slow global memory and accelerate the calculation process by up to 30%.

The conducted researches represent a significant dependence of the implementation time of the algorithm for calculating the preconditioner on the ratio of threads in spatial coordinates.

GeForce MX 250 video adapter was used in experimental researches; it specifications: the VRAM capacity is 4 GB, the core clock frequency is 1518–1582 MHz, the memory clock frequency is 7000 MHz, the video memory bus bit rate is 64 bits, and the number of CUDA cores is 384.

The purpose of the experiment is to determine the flow distribution along the Ox and Oz axes of the computational grid at fixed value of grid nodes along the Oy axis, equal to 10000, so that the implementation time on the GPU of one MATM step is minimal.

Two values are taken as factors: X is the number of threads on the axis Ox, Z is the number of threads on the axis Oz. The criterion function $T_{GPU}$ is the implementation time of a single MATM step on GPU, ms.

The composition of the streams X and Z must not exceed 1024. This restriction is imposed by CUDA, since 1024 is the number of threads in a single block. Therefore, the levels of variation of the factors X and Z were chosen as shown in the Table 1.

Table 1. Experiment results.

The regression equation was obtained in the result of experimental data processing:

$$\begin{aligned} T_{GPU} = 119.797 - 9.371 \log _{2}{Z}, \end{aligned}$$

(9)

where $T_{GPU}$ is the implementation time of a single MATM step on GPU, ms; Z is the number of threads on the axis Oz. The coefficient of determination was 0.78.

As a result of the analysis of experimental data, it was found that only the number of threads along the axis Oz affects the implementation time of one MATM step on GPU. The implementation time of one MATM step on GPU is inversely proportional to the number of nodes of the computational grid along the axis Oz. The calculation time decreases according to the logarithmic law at increasing the number of nodes along the axis Oz. Therefore, it is advisable to perform the domain decomposition in the form of parallelepipeds, in which the size on the Oz axis is maximum, and on the Ox axis is minimal.

Due to the conducted experimental researches, we established the optimal values of X and Z, which were equaled to the 16 and 64, respectively.

5 Conclusion

The algorithm and software unit that implements it were developed in the result of the conducted researches to solve the SLAE, which arises during the sampling of the hydrodynamics problem of shallow water, MATM using NVIDIA CUDA technology. The method of domain decomposition, applicable for heterogeneous computing systems, was described. The developed modification of the CSR – CSR1S format made it possible to increase the efficiency of data storage with a repeating sequence of elements. It is determined that the algorithm using the NVIDIA CUDA technology is more effective at $N_{seq}>7$. In this case, the point of equal efficiency decreases, starting from $k_r=0.7$. The optimal two-dimensional configuration of threads in a computing unit, implemented on a single thread multiprocessor, was determined, in which the implementation time on GPU of a single MATM step is minimal and equaled to the 64 ms.