Abstract
In classical modal logic, necessity \({\mathop {\Box } A}\), possibility \({\mathop {\Diamond } A}\), impossibility \({\mathop {\Box } \lnot A}\) and non-necessity \({\mathop {\Diamond } \lnot A}\) form a Square of Oppositions (SO) whose corners are interdefinable using classical negation. The relationship between these modalities in intuitionistic modal logic is a more delicate matter since negation is weaker. Intuitionistic non-necessity \({\mathop {\boxminus }}\) and impossibility  , first investigated by Došen, have received less attention and—together with their positive counterparts \({\mathop {\Box }}\) and \({\mathop {\Diamond }}\)—form a square we call the Došen Square. Unfortunately, the core property of constructive logic, the Disjunction Property (DP), fails when the modalities are combined and, interpreted in birelational Kripke structures à la Došen, the Square partially collapses. We introduce the constructive logic \(\mathsf {CKD}\), whose four semantically independent modalities \({\mathop {\Box }}\), \({\mathop {\Diamond }}\), \({\mathop {\boxminus }}\),
, first investigated by Došen, have received less attention and—together with their positive counterparts \({\mathop {\Box }}\) and \({\mathop {\Diamond }}\)—form a square we call the Došen Square. Unfortunately, the core property of constructive logic, the Disjunction Property (DP), fails when the modalities are combined and, interpreted in birelational Kripke structures à la Došen, the Square partially collapses. We introduce the constructive logic \(\mathsf {CKD}\), whose four semantically independent modalities \({\mathop {\Box }}\), \({\mathop {\Diamond }}\), \({\mathop {\boxminus }}\),  prevent the Došen Square from collapsing under the effect of intuitionistic negation while preserving DP. The model theory of \(\mathsf {CKD}\) involves a constructive Kripke frame interpretation of the modalities. A Hilbert deduction system and an equivalent cut-free sequent calculus are presented. Soundness, completeness and finite model property are proven, implying that \(\mathsf {CKD}\) is decidable. The logics \({\mathsf {HK} {\mathop {\boxminus }}}\), \({\mathsf {HK} {\mathop {\Box }}}\),
prevent the Došen Square from collapsing under the effect of intuitionistic negation while preserving DP. The model theory of \(\mathsf {CKD}\) involves a constructive Kripke frame interpretation of the modalities. A Hilbert deduction system and an equivalent cut-free sequent calculus are presented. Soundness, completeness and finite model property are proven, implying that \(\mathsf {CKD}\) is decidable. The logics \({\mathsf {HK} {\mathop {\boxminus }}}\), \({\mathsf {HK} {\mathop {\Box }}}\),  and
and  of Došen and other known theories of intuitionistic modalities are syntactic fragments or axiomatic extensions of \(\mathsf {CKD}\) .
of Došen and other known theories of intuitionistic modalities are syntactic fragments or axiomatic extensions of \(\mathsf {CKD}\) .
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others

1 Introduction
The reader may recall the classical square of opposition (SO) [38] seen on the left side in Fig. 1, whose four corners express the distinction between contradictory and contrary oppositions, that were traditionally labelled with four letters A, E, I, O designating propositions, and connected by means of six edges. The SO has been applied to concepts in linguistics, mathematics and philosophy and can be generalised in a number of ways. From the vantage point of classical modal logic, the oppositions can be expressed in terms of the modal operators \({\mathop {\Diamond }}\) and \(\Box \), which traditionally express possibility and necessity, and are interdefinable in terms of negation, i.e., \({\mathop {\Diamond } A = \lnot \Box \lnot A}\) and \({\Box A = \lnot \mathop {\Diamond } \lnot A}\). In constructive modal logic this is no longer the case, which results in four independent modal operators, complementing \({\mathop {\Diamond }}\) and \(\Box \) with their opposing counterparts [10], namely impossibility  and non-necessity \({\mathop {\boxminus }}\). In this work we construct the Došen square (DS) seen on the right side in Fig. 1, by investigating the relationships between the modalities
and non-necessity \({\mathop {\boxminus }}\). In this work we construct the Došen square (DS) seen on the right side in Fig. 1, by investigating the relationships between the modalities  in a constructive theory, in which they remain independent under (intuitionistic) negation (\({{\sim }}\)) in the sense that they are not interdefinable anymore, unlike in classical logic. We will shortly discuss the interpretation of the DS.
in a constructive theory, in which they remain independent under (intuitionistic) negation (\({{\sim }}\)) in the sense that they are not interdefinable anymore, unlike in classical logic. We will shortly discuss the interpretation of the DS.
1.1 State of the Art
In classical Kripke semantics, the modal operators \({\mathop {\Diamond }}\) and \(\Box \) are interpreted w.r.t. frames \(\mathfrak {F} = (S, R)\), consisting of a set of states S and a binary accessibility relation R on S. The satisfaction of formulas is defined relative to models \(\mathfrak {M} = (\mathfrak {F}, \, V)\) extending a frame by a valuation  that associates a set \(V(s) \subseteq Var \) of propositional variables satisfied at a state s. Their interpretation is given by quantifying existentially and universally over states in the image of the relation R
that associates a set \(V(s) \subseteq Var \) of propositional variables satisfied at a state s. Their interpretation is given by quantifying existentially and universally over states in the image of the relation R
where \(\mathfrak {M}, s \,\models \, A\) expresses that A is satisfied at state s in \(\mathfrak {M} \). Standardly, in modal extensions of intuitionistic propositional logic (\(\mathsf {IPL}\)), Kripke models are based on a birelational Kripke frame \({\mathfrak {F} = (S, \sqsubseteq , R)}\), where the accessibility relation R and the intuitionistic partial order \({\sqsubseteq }\) are relations on the same domain. Because the classical clauses (1) and (2) fail to ensure intuitionistic heredity:
one common approach is to impose the frame conditions \({( \sqsubseteq \, ; R) \subseteq (R\, ; \sqsupseteq )}\) and \(( \sqsubseteq \, ; R) \subseteq (R\, ; \sqsubseteq )\), where \(R\, ; S =_{\scriptstyle {df}}\{(x,z)\mid \exists y. x\, R\, y\ \text {and}\ y\, S\, z\}\) denotes sequential composition of two binary relations R and S. In the Došen square we enforce heredity without any frame conditions by the following ‘doubly quantified’ (constructive) interpretation:
We can pronounce \({\mathop {\Diamond } A}\) as “hereditarily, there is an R-accessible state at which A holds” and \({\mathop {\Box } A}\) as “hereditarily, for all R-accessible states A holds”, hence the labelling of the Došen square in Fig. 1, in which such sentences have been still further abbreviated. The mainstream approach is to either adopt the ‘singly quantified’ approach (1) and (2) for both \(\Box \) and \(\Diamond \) [35, 40, 41] or to ‘mix and match’, adopting (1) for \({\mathop {\Diamond }}\) and (4) for \({\mathop {\Box }}\) [29, 34]. The ‘doubly quantified’ approach for both modalities, first introduced by [39] and later used in the logic \(\mathsf {CK}\) [3, 20, 25, 33], is far less common, as it leads to non-normal modal logics invalidating the axiom \(\Diamond (A \vee B) \rightarrow \Diamond A \vee \Diamond B\). Computationally, this makes sense (see [24, 33]), and it has the consequence that \(\sqsubseteq \) is not required to be antisymmetric as in standard intuitionistic Kripke frames. In \(\mathsf {CK}\), this gives rise to cyclic structures which are crucial in establishing the Finite Model Property (FMP) [25]. Furthermore, the nullary case \({{\sim } \Diamond \bot }\) is invalidated as well, because frames for \(\mathsf {CK}\) include so-called fallible states which verify all formulas of the language. Fallible states may be accessible from other states via the modal accessibility relation in the clause for \(\Diamond \) and so become ‘visible’ in the form of \(\Diamond \bot \) statements and \({\sqsubseteq }\) is no longer reflexive. Constructive modal logics such as \(\mathsf {CK}\) therefore allow for truth-value ‘gluts’ (i.e., they allow for the truth of formulas of the form \({A \wedge {\sim } A}\)) as well as truth value ‘gaps’ (i.e., formulas of the form \({A \vee {\sim } A}\) fail to be verified at a state).
Consider now the impossibility and non-necessity operators [10]  and \({\mathop {\boxminus }}\) which occupy the right side of the squares in Fig. 1, where
and \({\mathop {\boxminus }}\) which occupy the right side of the squares in Fig. 1, where  (or \({\mathop {\boxminus }}\)) is the negative counterpart of the positive modality \(\Diamond \) (or \(\Box \)) and vice versa:Footnote 1
(or \({\mathop {\boxminus }}\)) is the negative counterpart of the positive modality \(\Diamond \) (or \(\Box \)) and vice versa:Footnote 1

Classically, these modalities can be expressed in terms of \(\Diamond \) and \(\Box \) as \(\lnot \!\Diamond A\) (or \(\Box \lnot A\)) and \(\lnot \! \Box A\) (or \(\Diamond \lnot A\)). Intuitionistically, this is no longer the case, because intuitionistic negation \({{\sim }}\) is weaker than classical negation \(\lnot \) as it fails Excluded Middle (EM).
To our knowledge, Došen was the first to pay extensive attention to the negative modalities in intuitionistic logic. For each  , Došen produced a logic \(HK\otimes \), combining \(\otimes \) with \(\mathsf {IPL}\). In \(HK\Box \), the classical truth conditions for \(\Box \) in (2) are employed together with the frame condition \((\sqsubseteq ; R) \subseteq (R ; \sqsubseteq )\), whilst in \(HK\Diamond \) the classical truth conditions for \(\Diamond \) in (1) are employed together with \({(\sqsupseteq ; R) \subseteq (R ; \sqsupseteq )}\) [6]. In
, Došen produced a logic \(HK\otimes \), combining \(\otimes \) with \(\mathsf {IPL}\). In \(HK\Box \), the classical truth conditions for \(\Box \) in (2) are employed together with the frame condition \((\sqsubseteq ; R) \subseteq (R ; \sqsubseteq )\), whilst in \(HK\Diamond \) the classical truth conditions for \(\Diamond \) in (1) are employed together with \({(\sqsupseteq ; R) \subseteq (R ; \sqsupseteq )}\) [6]. In  , the truth conditions (5) are employed for
, the truth conditions (5) are employed for  and \({(\sqsubseteq ; R) \subseteq (R ; \sqsupseteq )}\) are imposed, and in \({HK\mathop {\boxminus }}\) the truth conditions (6) are employed for \({\mathop {\boxminus }}\) with the frame condition \({(\sqsupseteq ; R ) \subseteq (R ; \sqsubseteq )}\) [9,10,11]. Each \(HK\otimes \) for
and \({(\sqsubseteq ; R) \subseteq (R ; \sqsupseteq )}\) are imposed, and in \({HK\mathop {\boxminus }}\) the truth conditions (6) are employed for \({\mathop {\boxminus }}\) with the frame condition \({(\sqsupseteq ; R ) \subseteq (R ; \sqsubseteq )}\) [9,10,11]. Each \(HK\otimes \) for  is a conservative extension of \(\mathsf {IPL}\) which is sound and complete with respect to birelational frames, subject to the associated frame conditions. The work of Došen was very much out on a limb with respect to the mainstream in intuitionistic logic, which concentrated on the positive modalities almost entirely [42], and only in recent years have the negative modalities been given more attention in the literature on intuitionistic and constructive logic [15, 16, 28]. Curiously, Došen did not produce a logic which combines
is a conservative extension of \(\mathsf {IPL}\) which is sound and complete with respect to birelational frames, subject to the associated frame conditions. The work of Došen was very much out on a limb with respect to the mainstream in intuitionistic logic, which concentrated on the positive modalities almost entirely [42], and only in recent years have the negative modalities been given more attention in the literature on intuitionistic and constructive logic [15, 16, 28]. Curiously, Došen did not produce a logic which combines  , \({\mathop {\boxminus }}\), \(\Diamond \) and \(\Box \) with \(\mathsf {IPL}\) on a single birelational frame \((S, \sqsubseteq , R)\) in which the modalities are interpreted with respect to the same R.
, \({\mathop {\boxminus }}\), \(\Diamond \) and \(\Box \) with \(\mathsf {IPL}\) on a single birelational frame \((S, \sqsubseteq , R)\) in which the modalities are interpreted with respect to the same R.
Some combinations of the modalities  with each other and negation \({{\sim }}\) have been explored. For example, [6] consider a system \(HK\Box \Diamond \), combining \(\Diamond \) and \(\Box \). They give two equivalent axiomatisations of \(HK\Box \Diamond \), yet the theory does not have the DP, nor is it conservative over either \(HK\Diamond \) and \(HK\Box \) (see [6] for discussion). Drobyschevich [15] investigates the properties of the combined modality
with each other and negation \({{\sim }}\) have been explored. For example, [6] consider a system \(HK\Box \Diamond \), combining \(\Diamond \) and \(\Box \). They give two equivalent axiomatisations of \(HK\Box \Diamond \), yet the theory does not have the DP, nor is it conservative over either \(HK\Diamond \) and \(HK\Box \) (see [6] for discussion). Drobyschevich [15] investigates the properties of the combined modality  in an extension \(\mathsf {N}^\star \) of \(\mathsf {IPL}\) he calls HKNR and he studies
in an extension \(\mathsf {N}^\star \) of \(\mathsf {IPL}\) he calls HKNR and he studies  in \({HK\mathop {\boxminus }}\) in an extension he calls \({HKN\mathop {\boxminus }}\). \(\mathsf {N}^\star \) is an extension of
in \({HK\mathop {\boxminus }}\) in an extension he calls \({HKN\mathop {\boxminus }}\). \(\mathsf {N}^\star \) is an extension of  but without \(\bot \), known as \(\mathsf {N}\) [11]. In \(\mathsf {N}^\star \), however, \({\mathop {\boxminus }}\) and
but without \(\bot \), known as \(\mathsf {N}\) [11]. In \(\mathsf {N}^\star \), however, \({\mathop {\boxminus }}\) and  collapse into a single modality, since \(\mathrel {R} \) is a functional accessibility relation, called the ‘Routley star’ operation. Addition of \(\Diamond \) to
collapse into a single modality, since \(\mathrel {R} \) is a functional accessibility relation, called the ‘Routley star’ operation. Addition of \(\Diamond \) to  plus frame conditions imposed to ensure hereditariness, have the result that the modalities
plus frame conditions imposed to ensure hereditariness, have the result that the modalities  and \(\Diamond \) become interdefinable as
and \(\Diamond \) become interdefinable as  and
and  via intuitionistic negation. But, from a constructive point of view, the directions of
via intuitionistic negation. But, from a constructive point of view, the directions of  and
and  are suspicious. If we can prove the absurdity of something being impossible (i.e.,
are suspicious. If we can prove the absurdity of something being impossible (i.e.,  ), this doesn’t mean we have a positive construction which will allow us to show that something is possible (i.e., \(\Diamond A\)). Likewise, if we can prove that a certain possibility is absurd (i.e., \({{\sim } \Diamond A}\)), then we can’t conclude that we have a proof that it is impossible. Similarly, addition of \(\Box \) to \({HK\mathop {\boxminus }}\) plus frame conditions make \({\mathop {\Box }}\) and \({\mathop {\boxminus }}\) interdefinable (\({\mathop {\Box } B \leftrightarrow {\sim } \mathop {\boxminus } B}\) and \({\mathop {\boxminus } B \leftrightarrow {\sim } \mathop {\Box } B}\)) and similar reservations regarding the constructive content of the implications \({{\sim } \mathop {\boxminus } B \rightarrow \mathop {\Box } A}\) and \({{\sim } \mathop {\Box } B \rightarrow \mathop {\boxminus } B}\) can be made. Adding \(\Box \) and its associated heredity frame condition forces axiom \({\mathop {\boxminus } B \vee {\sim } \mathop {\Box } B}\) without \({\mathop {\boxminus } B}\) or \({{\sim } \mathop {\Box } B}\) being provable by itself. This breaks DP and thus constructiveness of non-necessity. This is a general side effect of the frame conditions: Each positive modality \(\oplus \) induces the disjunction \({{\sim } \ominus A \vee \ominus A}\), where \(\ominus \) is the corresponding negative modality, and each negative modality \(\ominus \) induces the disjunction \({{\sim } \oplus A \vee \oplus A}\). Similar effects have been observed for \(\mathsf {N}^\star \) [13], where the scheme
), this doesn’t mean we have a positive construction which will allow us to show that something is possible (i.e., \(\Diamond A\)). Likewise, if we can prove that a certain possibility is absurd (i.e., \({{\sim } \Diamond A}\)), then we can’t conclude that we have a proof that it is impossible. Similarly, addition of \(\Box \) to \({HK\mathop {\boxminus }}\) plus frame conditions make \({\mathop {\Box }}\) and \({\mathop {\boxminus }}\) interdefinable (\({\mathop {\Box } B \leftrightarrow {\sim } \mathop {\boxminus } B}\) and \({\mathop {\boxminus } B \leftrightarrow {\sim } \mathop {\Box } B}\)) and similar reservations regarding the constructive content of the implications \({{\sim } \mathop {\boxminus } B \rightarrow \mathop {\Box } A}\) and \({{\sim } \mathop {\Box } B \rightarrow \mathop {\boxminus } B}\) can be made. Adding \(\Box \) and its associated heredity frame condition forces axiom \({\mathop {\boxminus } B \vee {\sim } \mathop {\Box } B}\) without \({\mathop {\boxminus } B}\) or \({{\sim } \mathop {\Box } B}\) being provable by itself. This breaks DP and thus constructiveness of non-necessity. This is a general side effect of the frame conditions: Each positive modality \(\oplus \) induces the disjunction \({{\sim } \ominus A \vee \ominus A}\), where \(\ominus \) is the corresponding negative modality, and each negative modality \(\ominus \) induces the disjunction \({{\sim } \oplus A \vee \oplus A}\). Similar effects have been observed for \(\mathsf {N}^\star \) [13], where the scheme  is valid and for \({HK\mathop {\Box } \mathop {\Diamond }}\), where \(\Diamond A \vee \Box \lnot A\) is an axiom, both in violation of the DP.
is valid and for \({HK\mathop {\Box } \mathop {\Diamond }}\), where \(\Diamond A \vee \Box \lnot A\) is an axiom, both in violation of the DP.
1.2 Contributions
The combination of the modalities \(\Box \), \({\mathop {\Diamond }}\),  and \({\mathop {\boxminus }}\) so as to ensure a constructive logic is a delicate matter. Can the negative modalities
and \({\mathop {\boxminus }}\) so as to ensure a constructive logic is a delicate matter. Can the negative modalities  and \({\mathop {\boxminus }}\) live happily side-by-side with their ‘positive’ counterparts \(\Diamond \) and \(\Box \), within a constructive setting? According to consolidated tradition, a constructive logic means a logic in which the Disjunction Property (DP) holds: whenever \(A \vee B\) is a theorem then either A is a theorem, or B is a theorem. Constructiveness thus construed is not a property of operators, but of logics. Our question is therefore whether we can combine the modalities whilst retaining the DP. In this paper we show that if we interpret
and \({\mathop {\boxminus }}\) live happily side-by-side with their ‘positive’ counterparts \(\Diamond \) and \(\Box \), within a constructive setting? According to consolidated tradition, a constructive logic means a logic in which the Disjunction Property (DP) holds: whenever \(A \vee B\) is a theorem then either A is a theorem, or B is a theorem. Constructiveness thus construed is not a property of operators, but of logics. Our question is therefore whether we can combine the modalities whilst retaining the DP. In this paper we show that if we interpret  and \({\mathop {\boxminus }}\) constructively like \({\mathop {\Box }}\) and \({\mathop {\Diamond }}\) in (4) and (3),
and \({\mathop {\boxminus }}\) constructively like \({\mathop {\Box }}\) and \({\mathop {\Diamond }}\) in (4) and (3),

then we can avoid the collapse of the modalities  , \({\mathop {\boxminus }}\), \({\mathop {\Diamond }}\) and \(\Box \), abandoning the frame conditions relating \(\sqsubseteq \) and R:Footnote 2 The logic created by thus adding the negative modalities to \(\mathsf {CK}\) [25, 33], we dub \(\mathsf {CKD}\). \(\mathsf {CKD}\) is both conservative over \(\mathsf {CK}\) and constructive in the sense that it satisfies DP.
, \({\mathop {\boxminus }}\), \({\mathop {\Diamond }}\) and \(\Box \), abandoning the frame conditions relating \(\sqsubseteq \) and R:Footnote 2 The logic created by thus adding the negative modalities to \(\mathsf {CK}\) [25, 33], we dub \(\mathsf {CKD}\). \(\mathsf {CKD}\) is both conservative over \(\mathsf {CK}\) and constructive in the sense that it satisfies DP.
The Došen square is not supposed to be analogous to the SO; in fact, only certain features of the square of oppositions hold in \(\mathsf {CKD}\). The logic \(\mathsf {CKD}\) will treat the relationships between the modalities in DS as follows. On the one hand, \({\mathop {\Diamond }}\) and  will be contradictories, i.e.,
will be contradictories, i.e.,  is valid. Similarly, necessity \({\mathop {\Box }}\) and unnecessity \({\mathop {\boxminus }}\) will be incompatible, i.e., \({{\sim } (\Box A \wedge \mathop {\boxminus } A)}\) is valid. Due to the absence of the Excluded Middle and fallibility, the modalities \({\mathop {\Diamond } {\sim } A}\) and \({\mathop {\boxminus } A}\) are independent in \(\mathsf {CKD}\), distinguishing the Došen square from the classical SO. In \(\mathsf {CKD}\) \({\mathop {\Diamond } {\sim } A \rightarrow \mathop {\boxminus } A}\) follows from infallibility, expressed by
is valid. Similarly, necessity \({\mathop {\Box }}\) and unnecessity \({\mathop {\boxminus }}\) will be incompatible, i.e., \({{\sim } (\Box A \wedge \mathop {\boxminus } A)}\) is valid. Due to the absence of the Excluded Middle and fallibility, the modalities \({\mathop {\Diamond } {\sim } A}\) and \({\mathop {\boxminus } A}\) are independent in \(\mathsf {CKD}\), distinguishing the Došen square from the classical SO. In \(\mathsf {CKD}\) \({\mathop {\Diamond } {\sim } A \rightarrow \mathop {\boxminus } A}\) follows from infallibility, expressed by  . Moreover, we have \({\mathop {\boxminus } A \rightarrow \mathop {\Diamond } {\sim } A}\) assuming \({\mathop {\Box } (A \vee {\sim } A)}\), which expresses the necessitation of the Excluded Middle. Similarly, \({\mathop {\Box } {\sim } A}\) and
. Moreover, we have \({\mathop {\boxminus } A \rightarrow \mathop {\Diamond } {\sim } A}\) assuming \({\mathop {\Box } (A \vee {\sim } A)}\), which expresses the necessitation of the Excluded Middle. Similarly, \({\mathop {\Box } {\sim } A}\) and  are independent. Again, the connection hinges on the absence of gluts and gaps: In \(\mathsf {CKD}\) we have that infallibility
are independent. Again, the connection hinges on the absence of gluts and gaps: In \(\mathsf {CKD}\) we have that infallibility  entails
entails  and similarly \({\mathop {\Box } (A \vee {\sim } A)}\) entails
and similarly \({\mathop {\Box } (A \vee {\sim } A)}\) entails  . Unless every state has an \(\mathrel {R} \)-successor (seriality) – expressible by \({\mathop {\Diamond } \top }\) – the modality pairs \({\mathop {\Box }}\), \({\mathop {\Diamond }}\) and
. Unless every state has an \(\mathrel {R} \)-successor (seriality) – expressible by \({\mathop {\Diamond } \top }\) – the modality pairs \({\mathop {\Box }}\), \({\mathop {\Diamond }}\) and  , \({\mathop {\boxminus }}\) are independent. However, like in the classical SO it holds that from seriality \({\mathop {\Diamond } \top }\) follows \({\mathop {\Box } A \rightarrow \mathop {\Diamond } A}\) and
, \({\mathop {\boxminus }}\) are independent. However, like in the classical SO it holds that from seriality \({\mathop {\Diamond } \top }\) follows \({\mathop {\Box } A \rightarrow \mathop {\Diamond } A}\) and  .
.
In Sect. 2 the model theory of \(\mathsf {CKD}\) is introduced and the DP is proven. In Sect. 3.1, an axiomatic Hilbert system, \(H_{\mathsf {CKD}}\), is provided for \(\mathsf {CKD}\), and its conservativity over \(\mathsf {CK}\) and over \(\mathsf {N}\) is sketched. In Sect. 3.2, a sequent calculus, \(G_{\mathsf {CKD}}\), for \(\mathsf {CKD}\) is provided, proving its soundness and completeness with respect to C-frames , and its translation into \(H_{\mathsf {CKD}}\) is obtained. As a corollary of completeness, it follows that the theory of \(\mathsf {CKD}\) has the FMP, is cut-free and decidable. In Sect. 4 we end with Conclusions.
2 The Došen Square \(\mathsf {CKD}\) of Constructive Modalities
We begin by introducing the frames and models we will make use of.
Definition 1
(C-frame). A C-frame \(\mathfrak {F} = (S, \le , F, \mathrel {R})\) consists of a set \({S\ /\!\!\!\!= \emptyset }\) of states, a preordering \(\le \) (reflexive & transitive) on S, a subset \(F \subseteq S\) of fallible states, s.t. \(s_1 \le s_2\) and \(s_1 \in F\) implies \(s_2 \in F\) and a binary relation \(\mathrel {R} \) on S. On a C-frame we define the ordering \( {{\sqsubseteq } =_{\scriptstyle {df}}\{ (s,s') \mid s \le s' \, \& \, s' \not \!\in \, F \}}\) and if \(F = \emptyset \) then \(\mathfrak {F} \) is called infallible.
C-frames are non-standard in three ways. Firstly, we do not require any frame property to constrain the interaction of \(\le \) and \(\mathrel {R} \). In this way, we obtain a minimal logic to fuse the modalities \({\mathop {\Diamond }}\), \({\mathop {\Box }}\),  and \({\mathop {\boxminus }}\) on a single accessibility relation. Secondly, we only require \(\le \) to be a preorder rather than a partial ordering, i.e., omitting antisymmetry allows for the possibility of cyclic structures which are crucial in establishing the FMP. Thirdly, by adding the fallibility set \(F \subseteq S\) we can declare frame states as ‘internally exploded’ and make states \(s \in S\) such that \(s \mathrel {R} s' \in \, F\) border states “one world away from absurdity”. This is instrumental to preserve constructiveness for certain extensions of \(\mathsf {CKD}\) and amounts to working with an intuitionistic accessibility \({\sqsubseteq }\) that is not only not antisymmetric but also not reflexive.
and \({\mathop {\boxminus }}\) on a single accessibility relation. Secondly, we only require \(\le \) to be a preorder rather than a partial ordering, i.e., omitting antisymmetry allows for the possibility of cyclic structures which are crucial in establishing the FMP. Thirdly, by adding the fallibility set \(F \subseteq S\) we can declare frame states as ‘internally exploded’ and make states \(s \in S\) such that \(s \mathrel {R} s' \in \, F\) border states “one world away from absurdity”. This is instrumental to preserve constructiveness for certain extensions of \(\mathsf {CKD}\) and amounts to working with an intuitionistic accessibility \({\sqsubseteq }\) that is not only not antisymmetric but also not reflexive.
Definition 2
(C-model). A C-model \(\mathfrak {M} = (\mathfrak {F}, V)\) consists of a C-frame \(\mathfrak {F} = (S, \le , F, \mathrel {R})\) together with a valuation function  from S to the subset of propositional variables subject to heredity and explosion conditions: if \(s_1 \le s_2\) then (i) \(V(s_1) \subseteq V(s_2)\) and (ii) if \(s \in F\) then \(V(s) = Var \).
from S to the subset of propositional variables subject to heredity and explosion conditions: if \(s_1 \le s_2\) then (i) \(V(s_1) \subseteq V(s_2)\) and (ii) if \(s \in F\) then \(V(s) = Var \).
The language \(\mathcal {L}_{\mathsf {CKD}}\) of \(\mathsf {CKD}\) coincides with that of intuitionistic propositional logic (\(\mathsf {IPL}\)) extended by the four modalities  .
.
Definition 3
(Language \(\mathcal {L}_{\mathsf {CKD}}\) ). The language \(\mathcal {L}_{\mathsf {CKD}}\) is based on a denumerable set of propositional variables \( Var = \{p,q,\ldots \}\). The set of well-formed \(\mathsf {CKD}\)-formulas over \( Var \) is inductively defined by the following grammar:

Note that \({{\sim } A}\) abbreviates intuitionistic negation \(A \rightarrow \bot \), \(A \leftrightarrow B\) is expressed by \((A \rightarrow B) \wedge (B \rightarrow A)\) and implication \(\rightarrow \) is right-associative.
The interpretation of \(\mathcal {L}_{\mathsf {CKD}}\) is by means of the following satisfaction relation:
Definition 4
(Satisfaction in C-models). Let \(\mathfrak {M} = (S, \le , F, \mathrel {R}, V)\) be a C-model. The notion of a formula A being satisfied in a C-model \(\mathfrak {M} \) at a state s is defined inductively, for the modal operators as in (3), (4), (7), (8) and for the other operators as in \(\mathsf {IPL}\).Footnote 3
The semantics of Definition 4 permits us to assume that each fallible state \(f \in F\) is a dead end of the frame, i.e., there is no s with either \(f \mathrel {R} s\) or \({f \sqsubseteq s}\). Moreover, we may assume without loss of generality that every \(f \in F\) is reachable by an \(\mathrel {R} \)-step from a non-fallible state, i.e., there is \(s \not \!\in \, \,F\) with \(s \mathrel {R} f\). We call such frames \(\bot \)-condensed. In \(\bot \)-condensed frames we have  for all \(s \in S\) iff \(\mathfrak {M} \) is infallible, i.e., \({F = \emptyset }\).
for all \(s \in S\) iff \(\mathfrak {M} \) is infallible, i.e., \({F = \emptyset }\).
Definition 5
(Validity). A formula A is valid in a C-model \(\mathfrak {M} \), written \(\mathfrak {M} \,\models \, A\), if \(\mathfrak {M}, s \,\models \, A\) for all \(s \in S\). If \(\mathfrak {M} \) is clear from the context, we will simply write \(s \,\models \, A\). A formula A is valid in a C-frame \(\mathfrak {F} \), written \(\mathfrak {F} \,\models \, A\), if \(\mathfrak {M} \,\models \, A\) for all models \(\mathfrak {M} = (\mathfrak {F}, V)\) over \(\mathfrak {F} \). We lift all the validity relations to sets of formulas \(\varGamma \) in the usual conjunctive way, for a state \(\mathfrak {M}, s \,\models \, \varGamma \), a model \(\mathfrak {M} \,\models \, \varGamma \) and frame \(\mathfrak {F} \,\models \, \varGamma \).
Lemma 1
Satisfaction is hereditary and explosive, i.e., (i) \(s \,\models \, A\) iff \({\forall s' \sqsupseteq s.\, s' \,\models \, A}\) and (ii) \(s \in F\) implies \(s \,\models \, A\).
We define a semantic consequence relation axiomatising the semantic levels of the modal satisfaction relation at the frame, model and state level (global vs. local consequence) [21, 31]. It allows us to map the semantic definition of a logical system to its syntactic axiomatisation in the form a Hilbert calculus, to be used in the discussion of the correspondences between Došen’s logics and \(\mathsf {CKD}\) (see Theorem 3).
Definition 6
(Semantic Entailment). Let \(\varOmega \) (frame hypotheses), \(\varPhi \) (model hypotheses), \(\varGamma \) (state hypotheses) and \(\varPi \) (state assertions) be sets of formulas. We write \(\varOmega ; \varPhi ; \varGamma \,\models \, \varPi \) iff for all C-frames \(\mathfrak {F} =(S, \le , F, \mathrel {R})\) with \(\mathfrak {F} \,\models \, \varOmega \) and all models \(\mathfrak {M} = (\mathfrak {F}, V)\) with \(\mathfrak {M} \,\models \, \varPhi \) and all states \(s \in S\) with \(\mathfrak {M}, s \,\models \, \varGamma \), we have \(\mathfrak {M}, s \,\models \, \varPi \).
Let \(\mathsf {CKD} \) be the set of all universally valid formulas, i.e., \(\mathsf {CKD} = \{ A \mid \emptyset ; \emptyset ; \emptyset \,\models \, A \}\). This set is a logical theory, i.e., closed under Modus Ponens and Substitution. The theory \(\mathsf {CKD}\) does not validate the axiom  of Drobyshevich nor any of the axiom schemes \({\otimes A \vee {\sim } \otimes A}\) for
of Drobyshevich nor any of the axiom schemes \({\otimes A \vee {\sim } \otimes A}\) for  , as can be readily verified.
, as can be readily verified.
One of the hallmarks of constructive logics is the disjunction property (DP), stating that the proof of a disjunction \(A\vee B\) requires positive evidence in the form of a proof of either A or B. The absence of frame conditions in \(\mathsf {CKD}\) admits of a particularly simple model-theoretic argument for the Disjunction Property (Theorem 1) that proceeds completely analogously to \(\mathsf {IPL}\).
Theorem 1
(Disjunction Property). The theory \(\mathsf {CKD} \) has the Disjunction Property.
A striking feature of \(\mathsf {CKD}\) is that the Finite Model Property (Theorem 8) depends on permitting \(\le \)-cycles in C-frames. Consider the cyclic countermodel \(\mathfrak {M} _{c}\) on the right in Fig. 2. The states \(s_0\), \(s_1\) each satisfy \({{\sim } \mathop {\boxminus } A}\), \({{\sim } \mathop {\boxminus } B}\) and \({\mathop {\boxminus } (A \wedge B)}\), being mutual \({\sqsubseteq }\)-successors sharing the same theory. Yet, they cannot be condensed into a single state \(s \,=\, \{s_0, s_1\}\), as s would have both \(s_0'\) and \(s_1'\) as immediate \(\mathrel {R} \)-successors, and satisfy \({s \,\models \, \mathop {\boxminus } A \wedge \mathop {\boxminus } B}\) which is inconsistent with the properties of \(s_0\) and \(s_1\). Observe that \(\mathfrak {M} _{c}\) does not satisfy Došen’s \({\mathsf {HK} {\mathop {\boxminus }}}\) frame condition [10] \({(\sqsupseteq \mathrel {\,;\,} \mathrel {R}) \subseteq (\mathrel {R} \mathrel {\,;\,} \sqsubseteq )}\) that generates the constructively disputable scheme \({{\sim } \mathop {\boxminus } A \rightarrow \mathop {\Box } A}\). Even more, \(\mathfrak {M} _c\) provides a countermodel for the distribution axioms \({\mathop {\boxminus } (A \wedge B) \rightarrow (\mathop {\boxminus } A \vee \mathop {\boxminus } B)}\) and \({\mathop {\Diamond } (A \vee B) \rightarrow (\mathop {\Diamond } A \vee \mathop {\Diamond } B)}\). Their absence is characteristic of \(\mathsf {CKD}\) as a non-normal modal logic, due to the ‘doubly-quantified’ truth conditions in the existential modalities \({\mathop {\boxminus }}\) (8) and \({\mathop {\Diamond }}\) (3).
Proposition 1
The scheme \({({\sim } \mathop {\boxminus } A \wedge {\sim } \mathop {\boxminus } B) \rightarrow {\sim } \mathop {\boxminus } (A \wedge B)}\) is valid in \({\mathsf {HK} {\mathop {\boxminus }}}\) [10] but not a theorem of \(\mathsf {CKD}\). Every \(\mathsf {CKD}\) counter model for it is infinite or cyclic.
3 Proof Systems for \(\mathsf {CKD}\)
We develop the proof theory of \(\mathsf {CKD}\), in the form of the Hilbert calculus \(H_{\mathsf {CKD}}\) and the Gentzen-style sequent calculus \(G_{\mathsf {CKD}}\). The calculus \(H_{\mathsf {CKD}}\) captures semantic entailment \(\varOmega ; \varPhi ; \varGamma \,\models \, \varPi \) where the set of state hypotheses \({\varGamma = \emptyset }\) is empty, which corresponds to the restriction [21] of rule \( Nec \) to apply to theorems only. In contrast, the sequent calculus \(G_{\mathsf {CKD}}\) works entirely at the state level (i.e., \({\varOmega = \emptyset = \varPhi }\)).
3.1 \(\mathsf {CKD}\) Global Reasoning: The Hilbert Calculus \(H_{\mathsf {CKD}}\)
Definition 7
(Hilbert Deduction and \(\mathsf {CKD}\) Axioms). Let \(\varOmega \) and \(\varPhi \) be sets of formulas. We write \(\varOmega ;\varPhi \vdash _{H}A\) if there is a sequence \(A_0, A_1, \ldots A_{n-1}\) of formulas such that \(A_{n-1} = A\) and each \(A_i\) (\(i \in n\)) is either a model hypothesis from \(\varPhi \), a substitution instance of some frame hypothesis or axiom in \(\varOmega \), or arises by the rules of Modus Ponens (\( MP \)) or Necessitation (\( Nec \)) from formulas \(A_j\) (\(j < i\)) appearing earlier. The set of axioms \(\mathsf {CKD} _{ax}\) consist of those for \(\mathsf {IPL}\) (see, e.g., [14]) and the modal axioms as depicted in the following. We write \(\mathsf {CKD}; \varPhi \vdash _{H}A\) for \(\mathsf {CKD} _{ax}; \varPhi \vdash _{H}A\).

Theorem 2
(Hilbert Soundness). If \(\mathsf {CKD}; \varPhi \vdash _{H}A\) then \({\emptyset ; \varPhi ; \emptyset \,\models \, A}\).
The axioms \({\mathop {\Box } K}\), \({\mathop {\Diamond } K}\),  , \({\mathop {\boxminus } K}\) in combination with \( Nec \) ensure that the logic is extensional, i.e., satisfies the Replacement Principle: If \(\mathsf {CKD}; \varPhi \vdash _{H}A \leftrightarrow B\) then \(\mathsf {CKD}; \varPhi \vdash _{H}\phi [A] \leftrightarrow \phi [B]\) where \(\phi [.]\) is an arbitrary formula context. In the axiomatisation by [10] replacement is achieved with the R-Rules
, \({\mathop {\boxminus } K}\) in combination with \( Nec \) ensure that the logic is extensional, i.e., satisfies the Replacement Principle: If \(\mathsf {CKD}; \varPhi \vdash _{H}A \leftrightarrow B\) then \(\mathsf {CKD}; \varPhi \vdash _{H}\phi [A] \leftrightarrow \phi [B]\) where \(\phi [.]\) is an arbitrary formula context. In the axiomatisation by [10] replacement is achieved with the R-Rules

for \({\oplus \in \{\mathop {\Diamond }, \mathop {\Box } \}}\) and  . These are derivable from our axioms \({\mathop {\Box } K}\), \({\mathop {\Diamond } K}\),
. These are derivable from our axioms \({\mathop {\Box } K}\), \({\mathop {\Diamond } K}\),  , \({\mathop {\boxminus } K}\), Modus Ponens \( MP \) and Necessitation \( Nec \).
, \({\mathop {\boxminus } K}\), Modus Ponens \( MP \) and Necessitation \( Nec \).
The axioms \(\otimes K\) (for  ) deal with the consequences of a necessary implication \({\mathop {\Box } (A \rightarrow B)}\) for statements made under modalities. Analogously, the axioms \(\otimes 2\) express the consequences of an impossible property
) deal with the consequences of a necessary implication \({\mathop {\Box } (A \rightarrow B)}\) for statements made under modalities. Analogously, the axioms \(\otimes 2\) express the consequences of an impossible property  for modalised statements. The import of axiom \({{\mathop {\Box }}2}\) is that if a disjunction \(A \vee B\) is necessary and one of the disjuncts is impossible, then the other disjunct is necessary. The axiom \({{\mathop {\Diamond }}2}\) says that if a disjunction \(A \vee B\) is possible and one of the disjuncts is impossible, then the other disjunct is possible. The axiom
for modalised statements. The import of axiom \({{\mathop {\Box }}2}\) is that if a disjunction \(A \vee B\) is necessary and one of the disjuncts is impossible, then the other disjunct is necessary. The axiom \({{\mathop {\Diamond }}2}\) says that if a disjunction \(A \vee B\) is possible and one of the disjuncts is impossible, then the other disjunct is possible. The axiom  states that if two properties are impossible, then their disjunction is impossible, too. The axiom \({{\mathop {\boxminus }}2}\) says that if one property is impossible and another is non-necessary, then its disjunction is non-necessary. \( N 5 \) implies that if a conjunction \(A \wedge B\) is impossible while one of the conjuncts is possible then the other conjunct is non-necessary. \( N 6 \) is the statement that if a disjunction is necessary and one disjunct non-necessary then the other disjunct is possible. The final axiom \( N 7 \) gives a representation of absurdity as non-necessity of truth.
states that if two properties are impossible, then their disjunction is impossible, too. The axiom \({{\mathop {\boxminus }}2}\) says that if one property is impossible and another is non-necessary, then its disjunction is non-necessary. \( N 5 \) implies that if a conjunction \(A \wedge B\) is impossible while one of the conjuncts is possible then the other conjunct is non-necessary. \( N 6 \) is the statement that if a disjunction is necessary and one disjunct non-necessary then the other disjunct is possible. The final axiom \( N 7 \) gives a representation of absurdity as non-necessity of truth.
Let us verify that possibility \({\mathop {\Diamond } A}\) and impossibility  are contradictory, i.e.,
are contradictory, i.e.,  . Since \(\vdash _{H}A \leftrightarrow (A \wedge \top )\) we obtain
. Since \(\vdash _{H}A \leftrightarrow (A \wedge \top )\) we obtain  by the Replacement Principle. Then, instantiating \( N 5\) as
by the Replacement Principle. Then, instantiating \( N 5\) as  , we can derive
, we can derive  by \(\mathsf {IPL}\). Finally chaining up in \(\mathsf {IPL}\) with the implication \( N 7 \) this implies
by \(\mathsf {IPL}\). Finally chaining up in \(\mathsf {IPL}\) with the implication \( N 7 \) this implies  .
.
As explained above, in the standard Kripke model theory, the presence of frame conditions force a collapse of the modalities and the loss of DP. In \(\mathsf {CKD}\) where we maintain their independence we can study existing theories as fragments and extensions. Došen’s model theory of \(\mathsf {HK} \otimes \)-frames [10] in the language \(\mathcal {L} _{\otimes } = \{\bot , \wedge , \vee , \rightarrow , \otimes \}\) for fixed  generates the logic called \(\mathsf {HK} \otimes \). A \(\mathsf {HK} \otimes \)-frame is an infallible C-frame satisfying the \(\text {HK}\otimes \) frame condition (see Sect. 1). On such C-frames our truth conditions for \(\otimes \) collapse to the ones of Došen for \(\Diamond \),
generates the logic called \(\mathsf {HK} \otimes \). A \(\mathsf {HK} \otimes \)-frame is an infallible C-frame satisfying the \(\text {HK}\otimes \) frame condition (see Sect. 1). On such C-frames our truth conditions for \(\otimes \) collapse to the ones of Došen for \(\Diamond \),  , \(\Box \) and \({\mathop {\boxminus }}\). As a result, \(\mathsf {CKD}\) is conservative over \(\mathsf {HK} \otimes \) in the language fragment \(\mathcal {L} _{\otimes }\). However, the modalities
, \(\Box \) and \({\mathop {\boxminus }}\). As a result, \(\mathsf {CKD}\) is conservative over \(\mathsf {HK} \otimes \) in the language fragment \(\mathcal {L} _{\otimes }\). However, the modalities  of \(\mathsf {CKD}\) are weaker than the ones of \(\mathsf {HK} \otimes \). This is not surprising since we want to avoid the collapses arising from a naive fusion in the standard model theory. The properties of \(\otimes \) in \(\mathsf {HK} \otimes \) can be regained in \(\mathsf {CKD}\) by imposing frame conditions. Recall that \(\mathsf {N}\) [11] is
of \(\mathsf {CKD}\) are weaker than the ones of \(\mathsf {HK} \otimes \). This is not surprising since we want to avoid the collapses arising from a naive fusion in the standard model theory. The properties of \(\otimes \) in \(\mathsf {HK} \otimes \) can be regained in \(\mathsf {CKD}\) by imposing frame conditions. Recall that \(\mathsf {N}\) [11] is  in the language
in the language  without \(\bot \). Now consider the axiom schemes:
without \(\bot \). Now consider the axiom schemes:

It can be shown that \(\mathsf {CKD} \) in \({\mathcal {L} _{\mathop {\Box }}}\) corresponds to \({\mathsf {HK} \mathop {\Box }}\) and in \(\mathcal {L} _{\mathsf {N}}\) to \(\mathsf {N} \);  is
is  restricted to
restricted to  ; \({\mathsf {CKD} + {\mathop {\boxminus }}1}\) corresponds to \({\mathsf {HK} \mathop {\boxminus }}\) in \({\mathcal {L} _{\mathop {\boxminus }}}\) and \({\mathsf {CKD} + {\mathop {\Diamond }}1 + {\mathop {\Diamond }}2}\) generates the theory \({\mathsf {HK} \mathop {\Diamond }}\) in \({\mathcal {L} _{\mathop {\Diamond }}}\). Finally, the extension
; \({\mathsf {CKD} + {\mathop {\boxminus }}1}\) corresponds to \({\mathsf {HK} \mathop {\boxminus }}\) in \({\mathcal {L} _{\mathop {\boxminus }}}\) and \({\mathsf {CKD} + {\mathop {\Diamond }}1 + {\mathop {\Diamond }}2}\) generates the theory \({\mathsf {HK} \mathop {\Diamond }}\) in \({\mathcal {L} _{\mathop {\Diamond }}}\). Finally, the extension  coincides with the non-constructive theory \({\mathsf {HK} {\mathop {\Box }}{\mathop {\Diamond }}}\) investigated by Božić & Došen [6] in \({\mathcal {L} _{{\mathop {\Box }}{\mathop {\Diamond }}} =_{\scriptstyle {df}}\{ \bot , \wedge , \vee , \rightarrow , \mathop {\Box }, \mathop {\Diamond } \}}\). In \({\mathcal {L} _{{\mathop {\Box }}{\mathop {\Diamond }}}}\) the logic \(\mathsf {CKD}\) does not lose constructiveness like \({\mathsf {HK} {\mathop {\Box }}{\mathop {\Diamond }}}\) does. In fact, \(\mathsf {CKD}\) is conservative over \(\mathsf {CK}\) [25] that combines the positive modalities \({\mathop {\Box }}\), \({\mathop {\Diamond }}\) by extending \(\mathsf {IPL}\) with the axioms \(\Box K \) and \(\Diamond K \) and the \( Nec \) rule.
coincides with the non-constructive theory \({\mathsf {HK} {\mathop {\Box }}{\mathop {\Diamond }}}\) investigated by Božić & Došen [6] in \({\mathcal {L} _{{\mathop {\Box }}{\mathop {\Diamond }}} =_{\scriptstyle {df}}\{ \bot , \wedge , \vee , \rightarrow , \mathop {\Box }, \mathop {\Diamond } \}}\). In \({\mathcal {L} _{{\mathop {\Box }}{\mathop {\Diamond }}}}\) the logic \(\mathsf {CKD}\) does not lose constructiveness like \({\mathsf {HK} {\mathop {\Box }}{\mathop {\Diamond }}}\) does. In fact, \(\mathsf {CKD}\) is conservative over \(\mathsf {CK}\) [25] that combines the positive modalities \({\mathop {\Box }}\), \({\mathop {\Diamond }}\) by extending \(\mathsf {IPL}\) with the axioms \(\Box K \) and \(\Diamond K \) and the \( Nec \) rule.
Theorem 3
(Conservativity). \(\mathsf {CKD}\) is a conservative extension of \(\mathsf {N}\) and \(\mathsf {CK}\) and \({\mathsf {HK} \mathop {\Box }}\). The theories \(\mathsf {HK} {\otimes }\) for  and \({\mathsf {HK} \mathop {\Box } \mathop {\Diamond }}\) are axiomatic extensions of \(\mathsf {CKD}\):
and \({\mathsf {HK} \mathop {\Box } \mathop {\Diamond }}\) are axiomatic extensions of \(\mathsf {CKD}\):

3.2 Landing at Došen Square: The Sequent Calculus \(G_{\mathsf {CKD}}\)
The proof theory of \(\mathsf {CK}\) has previously been investigated in terms of a Natural Deduction system [3], multisequent calculi [22,23,24], nested sequents [2] and a tableaux-based calculus [33]. Our sequent calculus \(G_{\mathsf {CKD}}\) is a refinement of the multisequent calculus of Dragalin [12] for \(\mathsf {IPL}\), similar to [22], that is enriched by additional scopes to cover local and global properties. This is required for the interpretation of the four modalities, and is consonant with Poggiolesi’s remark that

In relation to the many variants explored in the literature (see [30]) \(G_{\mathsf {CKD}}\) can be considered a higher-arity extension in the sense of Sato [32] and Blamey and Humberstone [5]. Notably, following Dragalin, we consider the logical variant of the Gentzen calculus (in the terminology of [30]) approach to sequents, where all structural rules are built into the axioms and logical rules. This is justified as we are dealing with a logical theory that has not been discussed before and thus are primarily interested in model-theoretic expressiveness, completeness, constructiveness and finite-model property.
A sequent in \(\mathsf {CKD}\) is a structure \(\varGamma \star \varDelta \star \varTheta \vdash \varPi \star \varSigma \star \varPsi \) where the sets \(\varGamma \) and \(\varPi \) express direct truth and falsity at a state, as in a standard sequent. The sets \(\varDelta \), \(\varTheta \), \(\varSigma \) and \(\varPsi \) are finite (possibly empty) sets of signed formulas each of which can be strong \(A^+\) or weak \(A^-\). With this structure, our sequents provide a formalisation of Došen square as visualised in Fig. 3. Note, that in \(\varGamma \) (\(\varPi \)) all formulas have no sign. Specifically, \(\varDelta \) and \(\varTheta \) contain positive existential and universal statements about modally reachable successors, while \(\varSigma \) and \(\varPsi \) are negative existential and universal statements. Depending on the scope set, the sign \(t\in \{+,-\}\) of a polarised formula \(A^t\) distinguishes local or hereditary global properties, where for a set X of signed formulas we write \(X^t =_{\scriptstyle {df}}\{A^t \mid A^t \in X\}\). For instance, \(A^+ \in \varDelta \) expresses the constraint that there exists an immediate \(\mathrel {R} \)-successor satisfying A, while \(A^- \in \varDelta \) is the weaker statement that such a successor is reachable via \({\mathrel {{\sqsubseteq }{;}{\mathrel {R}}}}\), i.e., only after an initial intuitionistic step. Analogously, \(A^- \in \varSigma \) says that A is false along immediate \(\mathrel {R} \)-successors whereas \(A^+ \in \varSigma \) is the stronger statement that A is false along all \({\mathrel {{\sqsubseteq }{;}{\mathrel {R}}}}\). This is captured by the following Definition 8.
Definition 8
(Refutability). A sequent \(\varGamma \star \varDelta \star \varTheta \vdash \varPi \star \varSigma \star \varPsi \) is refuted in a state s of a C-model \(\mathfrak {M} = (S, \le , F, \mathrel {R}, V)\) iff the following holds:

A sequent is called refutable, written \(\varGamma \star \varDelta \star \varTheta \,\not \models \, \varPi \star \varSigma \star \varPsi \) if there exists a C-model \(\mathfrak {M} \) and a state s of \(\mathfrak {M} \) in which it is refuted. A sequent is called valid, written \(\varGamma \star \varDelta \star \varTheta \,\models \, \varPi \star \varSigma \star \varPsi \), if it is not refutable.
\(G_{\mathsf {CKD}}\) Sequent Rules. The sets \(\varGamma \), \(\varPi \) are without sign. In the rules \(cpL^t\) and \(cpR^t\) all signs are dropped in the occurrences of the sets \(\varTheta , \varTheta ^+\) and \(\varSigma , \varSigma ^+\) in the premisses. Tagged rules (\(\dagger \)) require its conclusion to be strict, i.e., \({\mid }\varDelta \cup \varPi \cup \varPsi {\mid } \ge 1\). We treat all scopes as sets with implicit duplication and permutation.
The sequent rules for \(\mathsf {CKD}\) are seen in Fig. 4. In the top part, the rules \( Ax \), \({\bot }L \), \({\top }R \), \({\wedge }L \), \({\wedge }R \), \({\vee }L \), \({\vee }R \), \({\rightarrow }L \) and \({\rightarrow }R \) are the left and right introduction rules for a (multisequent, logical [30]) Gentzen sequent calculus of \(\mathsf {IPL}\). These rules operate in the central \(\varGamma \vdash \varPi \) scopes, leaving the corner scopes of the Došen square untouched. In the bottom part of Fig. 4 we list the left and right introduction rules  ,
,  , \({{\mathop {\Box }}L}\), \({{\mathop {\Box }}R}\),
, \({{\mathop {\Box }}L}\), \({{\mathop {\Box }}R}\),  ,
,  , \({{\mathop {\boxminus }}L}\) and \({{\mathop {\boxminus }}R}\) for the modalities. These modal rules, applied in forward direction, take a signed formula from one of the corners \(\varDelta \), \(\varTheta \), \(\varSigma \) and \(\varPsi \) of the Došen square (Fig. 3) and introduce an associated modal operator in the conclusion sequent, instead. From \(\varPsi ^-\) and \(\varTheta ^+\) we introduce the \({\mathop {\Box }}\) modalities in rules \({{\mathop {\Box }}L}\) and \({{\mathop {\Box }}R}\); From \(\varPsi ^+\) and \(\varTheta ^-\) we introduce \({\mathop {\boxminus }}\) via \({{\mathop {\boxminus }}L}\) and \({{\mathop {\boxminus }}R}\). No other rule depends on the presence of formulas in \(\varPsi \) or \(\varTheta \). From \(\varDelta ^-\) and \(\varSigma ^+\) stem all occurrences of
, \({{\mathop {\boxminus }}L}\) and \({{\mathop {\boxminus }}R}\) for the modalities. These modal rules, applied in forward direction, take a signed formula from one of the corners \(\varDelta \), \(\varTheta \), \(\varSigma \) and \(\varPsi \) of the Došen square (Fig. 3) and introduce an associated modal operator in the conclusion sequent, instead. From \(\varPsi ^-\) and \(\varTheta ^+\) we introduce the \({\mathop {\Box }}\) modalities in rules \({{\mathop {\Box }}L}\) and \({{\mathop {\Box }}R}\); From \(\varPsi ^+\) and \(\varTheta ^-\) we introduce \({\mathop {\boxminus }}\) via \({{\mathop {\boxminus }}L}\) and \({{\mathop {\boxminus }}R}\). No other rule depends on the presence of formulas in \(\varPsi \) or \(\varTheta \). From \(\varDelta ^-\) and \(\varSigma ^+\) stem all occurrences of  through
through  and
and  , while \(\varDelta ^+\) and \(\varSigma ^-\) constitute a reservoir for \({\mathop {\Diamond }}\) introduced via
, while \(\varDelta ^+\) and \(\varSigma ^-\) constitute a reservoir for \({\mathop {\Diamond }}\) introduced via  and
and  . So far, \(G_{\mathsf {CKD}}\) does not present surprises as a Gentzen-style calculus. The speciality of \(G_{\mathsf {CKD}}\) lies in the four rules \({cp}L ^- \), \({cp}L ^+ \), \({cp}R ^- \) and \({cp}R ^+ \) seen in the center of Fig. 4. The sign introduction rules \({cp}L ^t\), \({cp}R ^t\) work in opposite direction to the modal introduction rules \({\otimes }L\), \({\otimes }R\). Together, they orchestrate the ‘Grand Modal Dispatch’ of the DS as suggested in Fig. 3.
. So far, \(G_{\mathsf {CKD}}\) does not present surprises as a Gentzen-style calculus. The speciality of \(G_{\mathsf {CKD}}\) lies in the four rules \({cp}L ^- \), \({cp}L ^+ \), \({cp}R ^- \) and \({cp}R ^+ \) seen in the center of Fig. 4. The sign introduction rules \({cp}L ^t\), \({cp}R ^t\) work in opposite direction to the modal introduction rules \({\otimes }L\), \({\otimes }R\). Together, they orchestrate the ‘Grand Modal Dispatch’ of the DS as suggested in Fig. 3.
Definition 9
(Derivability). A derivation of a sequent \(\varGamma \star \varDelta \star \varTheta \vdash \varPi \star \varSigma \star \varPsi \) is either an axiom (rule \( Ax \)), an instance of \({\bot }L \) or \({\top }R \) or an application of a logical rule to derivations concluding its premises, that is built using the rules in Fig. 4. We say that a sequent is underivable, written \(\varGamma \star \varDelta \star \varTheta \not \vdash \varPi \star \varSigma \star \varPsi \), if no derivation exists for it.
\(G_{\mathsf {CKD}}\) is conceived as a refutation system. Its purpose is to establish that a state specification (based on the six scopes) presented as a sequent is refutable. Refutability (Definition 8) and derivability (Definition 9) are linked in the sense that a sequent is underivable iff it is refutable, as established in the soundness and completeness proofs.
Theorem 4
( \(G_{\mathsf {CKD}}\) Soundness). If \(\varGamma \star \varDelta \star \varTheta \,\not \models \, \varPi \star \varSigma \star \varPsi \) then \(\varGamma \star \varDelta \star \varTheta \not \vdash \varPi \star \varSigma \star \varPsi \).
The proof of Theorem 4 is standard, by showing that for each sequent rule in Fig. 4 that if the conclusion is refutable then at least one of its premises is refutable as well.
As examples consider the \(G_{\mathsf {CKD}}\) derivations in Fig. 5. The left derivation demonstrates the incompatibility of \({\mathop {\Diamond }}\) and  and the right indicates why a proof of the distribution \({\mathop {\boxminus } (A \wedge B) \rightarrow (\mathop {\boxminus } A \vee \mathop {\boxminus } B)}\) is doomed to fail. The application (1) of rule \({{\mathop {\boxminus }}R}\) on the right of Fig. 5, corresponding to an intuitionistic \(\le \)-step in backwards direction, must clear the \(\varPi \)-scope and drop the constraint \({\mathop {\boxminus } B}\). Because of this, the formula B is missing in situation (2) so that the sequent cannot be derived.
and the right indicates why a proof of the distribution \({\mathop {\boxminus } (A \wedge B) \rightarrow (\mathop {\boxminus } A \vee \mathop {\boxminus } B)}\) is doomed to fail. The application (1) of rule \({{\mathop {\boxminus }}R}\) on the right of Fig. 5, corresponding to an intuitionistic \(\le \)-step in backwards direction, must clear the \(\varPi \)-scope and drop the constraint \({\mathop {\boxminus } B}\). Because of this, the formula B is missing in situation (2) so that the sequent cannot be derived.
Theorem 5
For each \(H_{\mathsf {CKD}} \) derivation \({\emptyset ; \emptyset \vdash _{H}D}\) there is a \(G_{\mathsf {CKD}} \) derivation of the sequent \({\emptyset \star \emptyset \star \emptyset \vdash D \star \emptyset \star \emptyset }\) using the rules of Fig. 4 plus the \( cut \) rule: From \(\varGamma \star \varDelta \star \varTheta \vdash D, \varPi \star \varSigma \star \varPsi \) and \(D, \varGamma \star \varDelta \star \varTheta \vdash \varPi \star \varSigma \star \varPsi \) infer \(\varGamma \star \varDelta \star \varTheta \vdash \varPi \star \varSigma \star \varPsi \).
A sequent \( {\varGamma \star \varDelta \star \varTheta \,{\vdash }\, \varPi \star \varSigma \star \varPsi } \) is called strict if \({\mid }\varDelta \cup \varPi \cup \varPsi {\mid } \ge 1\) and polarised if \({\mid }\varTheta ^- \cup \varSigma ^-{\mid } \le 1\). One can show that every derivable sequent is strict and that polarised sequents can be proven only using polarised sequents. For polarised and strict sequents the following ‘hilbertification’ provides a translation of \(G_{\mathsf {CKD}}\) back into \(H_{\mathsf {CKD}}\).
Definition 10
(Hilbertification). Let each sequent \(\varGamma \star \varDelta \star \varTheta \vdash \varPi \star \varSigma \star \varPsi \) be translated into the formula  where
where

and for empty sets we put \({\hat{\varGamma }=_{\scriptstyle {df}}\top \ \text {if}\ \varGamma = \emptyset }\), \({\check{\varPi }=_{\scriptstyle {df}}\bot \ \text {if}\ \varPi = \emptyset }\), and for  and X a set of signed formulas: \(\hat{\otimes }X = \top \) if \({X^+ = \emptyset }\) and \(\check{\otimes }X = \bot \) if \({X^- = \emptyset }\).
and X a set of signed formulas: \(\hat{\otimes }X = \top \) if \({X^+ = \emptyset }\) and \(\check{\otimes }X = \bot \) if \({X^- = \emptyset }\).
Theorem 6
Let \( {\varGamma \star \varDelta \star \varTheta \,{\vdash }\, \varPi \star \varSigma \star \varPsi } \) be a polarised sequent, derivable using the rules of Fig. 4. Then, there exists a Hilbert derivation of

Theorem 5 and 6 give us a back-and-forth translation of deductions in the Hilbert and Gentzen systems for \(\mathsf {CKD}\). However, this involves the \( cut \) rule, so neither calculus gives us a decision procedure. We address this by proving completeness of \(G_{\mathsf {CKD}}\) and thus completeness of \(H_{\mathsf {CKD}}\), leading to our final completeness result that implies cut-elimination. First, let us introduce some technical definitions.
Definition 11
(Saturation). A sequent \(\varGamma \star \varDelta \star \varTheta \vdash \varPi \star \varSigma \star \varPsi \) is called saturated if the following closure conditions hold:

In a saturated sequent the sets \(\varGamma \) and \(\varPi \) are coupled through the constraints (1)–(5). Closure conditions (6)–(9) are lower bounds on the presence of positive signs in \(\varSigma \) and \(\varTheta \) and on the negative signs in \(\varDelta \) and \(\varPsi \). If \( {\varGamma _1 \star \varDelta _1 \star \varTheta _1 \,{\vdash }\, \varPi \star \varSigma _1 \star \varPsi _1} \) is saturated then any sequent \( {\varGamma \star \varDelta _2 \star \varTheta _2 \,{\vdash }\, \varPi \star \varSigma _2 \star \varPsi _2} \) with \(\varTheta _1^+ \subseteq \varTheta _2^+\), \(\varSigma _1^+ \subseteq \varSigma _2^+\), \(\varDelta _1^- \subseteq \varDelta _2^-\) and \(\varPsi _1^- \subseteq \varPsi _2^-\) is saturated, too. In other words, we can add positive signs, or add and remove negative signs from \(\varTheta \), \(\varSigma \) without losing saturation. Analogously, we can add negative signs or add and remove positive signs in \(\varDelta \), \(\varPsi \) and preserve saturation.
Definition 12
A set \( SF \) of formulas is subformula closed if for every subformula A of a formula \(M \in SF \) it holds that \(A \in SF \). Let \( SF ^+ = SF \cup \{ \bot \}\). We say that a sequent \( {\varGamma \star \varDelta \star \varTheta \,{\vdash }\, \varPi \star \varSigma \star \varPsi } \) is called a \( SF \)-sequent if \(\varGamma \cup \varDelta \cup \varTheta \cup \varPi \cup \varSigma \cup \varPsi \subseteq SF ^+\). Moreover, a \( SF \) sequent is called consistent if it cannot be derived in the \( cut \)-free calculus. It is called \( SF \)-complete if for every \(M \in SF ^+\) we have \(M \in \varGamma \) or \(M \in \varPi \).
For saturated, consistent and \( SF \)-complete sequents the essential information lies in \(\varGamma \), in the positive signs \(B^+ \in \varDelta \), \(F^+ \in \varPsi \) and the negative signs \(E^- \in \varSigma \), \(C^- \in \varTheta \). All of these express the existence and properties of immediate \(\mathrel {R} \)-successors (see Definition 8).
Definition 13
(Canonical Interpretation). Let \( SF \) be a subformula closed set. We define a basic canonical C-structure \(\mathfrak {M} ^c = (S^c, \le ^c, F^c, \mathrel {R} ^c, V^c)\) over \( SF \) as follows: The states \(w \in S^c\) are the saturated and consistent \( SF \) sequents \(w = {\langle \varGamma \star \varDelta \star \varTheta \,{\vdash }\, \varPi \star \varSigma \star \varPsi \rangle } \). Relating these canonical states, we define the intuitionistic accessibility relation \(\le ^c\) and the compatibility relation \(\mathrel {R} ^c\) on \(S^c\) as follows:
Let \(w = {\langle \varGamma \star \varDelta \star \varTheta \,{\vdash }\, \varPi \star \varSigma \star \varPsi \rangle } \in S^c\) be an arbitrary state. The valuation of propositional variables p is given by stipulating \(p \in V^c(w)\) iff \(p \in \varGamma \) or \(\bot \in \varGamma \). The state w is fallible \(w \in F^c\) iff \(\bot \in \varGamma \).
Lemma 1
The canonical structure \(\mathfrak {M} ^c =_{\scriptstyle {df}}(S^c, F^c, \le ^c, \mathrel {R} ^c, V^c)\) in Definition 13 is a C-model in the sense of Definition 2 such that for every sequent \(w \in S^c\) the pair \((\mathfrak {M} ^c, w)\) refutes w according to Definition 8.
Theorem 7
(Gentzen Completeness). Every underivable sequent is refutable, i.e., if \(\varGamma \mathrel {\star }\varDelta \mathrel {\star }\varTheta \not \vdash \varPi \mathrel {\star }\varSigma \mathrel {\star }\varPsi \) then \(\varGamma \mathrel {\star }\varDelta \mathrel {\star }\varTheta \,\not \models \, \varPi \mathrel {\star }\varSigma \mathrel {\star }\varPsi \).
The completeness proof proceeds in the standard fashion via canonical models (see Definition 13) constructed by saturation of unprovable end-sequents. Consistent saturation in all scopes \(\varGamma \), \(\varDelta \), \(\varTheta \), \(\varPi \), \(\varSigma \) and \(\varPsi \) only involves subformulas (counting \(\bot \) as a subformula) of the original sequent. The canonical model does not require maximal saturation or depends on the \( cut \) rule to achieve completeness of canonical states. Hence, the \( cut \) rule is admissible in \(\mathsf {CKD}\). Moreover, since all rules of \(\mathsf {CKD} \) (not using \( cut \)) have the subformula property, it follows that \(\mathsf {CKD}\) has the Finite Model Property. The Completeness Theorem 7 for our finite axiomatisation (Gentzen or Hilbert system) implies decidability. Therefore, we have the following theorem.
Theorem 8
The theory \(\mathsf {CKD} \) has the Finite Model Property, is cut-free and decidable.
4 Conclusion
We have introduced a logic \(\mathsf {CKD}\), which combines the modalities  with \(\mathsf {IPL}\). \(\mathsf {CKD}\) is constructive since it has the Disjunction Property, and it is a conservative extension of the logics \(\mathsf {CK}\) [25], \(\mathsf {N}\) [11] and \({\mathsf {HK} \mathop {\Box }}\) [6]. Technically, this is a clear contribution, since many extensions of \(\mathsf {N}\) are not constructive, and combining the modalities
with \(\mathsf {IPL}\). \(\mathsf {CKD}\) is constructive since it has the Disjunction Property, and it is a conservative extension of the logics \(\mathsf {CK}\) [25], \(\mathsf {N}\) [11] and \({\mathsf {HK} \mathop {\Box }}\) [6]. Technically, this is a clear contribution, since many extensions of \(\mathsf {N}\) are not constructive, and combining the modalities  with \(\mathsf {IPL}\) can easily lead to loss of constructivity. But, we would add, this is also a contribution on another front: by combining the modalities
with \(\mathsf {IPL}\) can easily lead to loss of constructivity. But, we would add, this is also a contribution on another front: by combining the modalities  with \(\mathsf {IPL}\) we have constructed a logic in which all parts of the Došen square are included. Moreover, Došen’s logics \(\mathsf {HK} {\otimes }\) for
with \(\mathsf {IPL}\) we have constructed a logic in which all parts of the Došen square are included. Moreover, Došen’s logics \(\mathsf {HK} {\otimes }\) for  are axiomatic extensions of \(\mathsf {CKD}\).
are axiomatic extensions of \(\mathsf {CKD}\).
The proof theory of \(\mathsf {CKD}\) has been given in the form of a Hilbert calculus \(H_{\mathsf {CKD}}\) and a sequent calculus \(G_{\mathsf {CKD}}\), and a constructive (bidirectional) translation between both proof systems is established. The soundness and completeness of \(H_{\mathsf {CKD}}\) and \(G_{\mathsf {CKD}}\) is proven, relative to a semantics based on C-frames and C-models. The structural complexity of \(G_{\mathsf {CKD}}\) sequents arises from the aim to enforce the subformula property (analyticity) and to enable a Gentzen-style separation between left and right introduction rules for each operator (orthogonality). Finally, as a corollary of Gentzen completeness, it follows that the theory of \(\mathsf {CKD}\) has the finite model property, is cut-free and decidable.
\(G_{\mathsf {CKD}}\) is the first sequent calculus that combines all four modalities  preserving the disjunction property of intuitionistic logic. It is instructive to look at special fragments: In the modal-free fragment \(\mathsf {IPL}\), i.e., without the rules \({\otimes }L\), \({\otimes }R\) for
preserving the disjunction property of intuitionistic logic. It is instructive to look at special fragments: In the modal-free fragment \(\mathsf {IPL}\), i.e., without the rules \({\otimes }L\), \({\otimes }R\) for  , all scope sets except \(\varGamma \) and \(\varPi \) may be assumed empty. Hence, the dispatch rules \({cp}L ^t\), \({cp}R ^t\) become obsolete and \(G_{\mathsf {CKD}}\) reduces to the rules \(\{ Ax , {\bot }L, {\top }R, {\wedge }L, {\wedge }R,\) \({\vee }L, {\vee }R, {\rightarrow }L, {\rightarrow }R \}\) corresponding to Dragalin’s sequent calculus for \(\mathsf {IPL}\). In the \({\mathop {\Box }}\)-fragment of \(G_{\mathsf {CKD}}\) (i.e., \(\mathsf {IPL}\) plus \({\mathop {\Box }}\)), the modal rules \({{\mathop {\Box }}L}\), \({{\mathop {\Box }}R}\) generate only the positive signs \(\varTheta ^+\) and negative signs \(\varPsi ^-\) while \({\varDelta = \varSigma = \emptyset }\). Hence, from the modal dispatch only \({cp}R ^- \) remains. The resulting sequents \({\varGamma \star \emptyset \star \varTheta ^+ \vdash \varPi \star \emptyset \star \varPsi ^-}\) correspond to an intuitionistic version of the 4-ary sequents \(\varGamma \Rightarrow _{\varTheta ^+}^{\varPsi ^-} \varPi \) of Blamey and Humberstone’s logicFootnote 4 \(\mathsf {K} ^4\) [5], called \(\mathsf {H{-}ask} \) by [30]. These \(\mathsf {K} ^4\) sequents are translatable as formulas \({(\bigwedge \varGamma \wedge \bigwedge \mathop {\Box } \varTheta ^+) \rightarrow (\bigvee \varPi \vee \bigvee \mathop {\Box } \varPsi ^-)}\) (see [30] and also Definition 10). The constructive nature of \(\mathsf {CKD}\) appears in the fact that the right introduction rules
, all scope sets except \(\varGamma \) and \(\varPi \) may be assumed empty. Hence, the dispatch rules \({cp}L ^t\), \({cp}R ^t\) become obsolete and \(G_{\mathsf {CKD}}\) reduces to the rules \(\{ Ax , {\bot }L, {\top }R, {\wedge }L, {\wedge }R,\) \({\vee }L, {\vee }R, {\rightarrow }L, {\rightarrow }R \}\) corresponding to Dragalin’s sequent calculus for \(\mathsf {IPL}\). In the \({\mathop {\Box }}\)-fragment of \(G_{\mathsf {CKD}}\) (i.e., \(\mathsf {IPL}\) plus \({\mathop {\Box }}\)), the modal rules \({{\mathop {\Box }}L}\), \({{\mathop {\Box }}R}\) generate only the positive signs \(\varTheta ^+\) and negative signs \(\varPsi ^-\) while \({\varDelta = \varSigma = \emptyset }\). Hence, from the modal dispatch only \({cp}R ^- \) remains. The resulting sequents \({\varGamma \star \emptyset \star \varTheta ^+ \vdash \varPi \star \emptyset \star \varPsi ^-}\) correspond to an intuitionistic version of the 4-ary sequents \(\varGamma \Rightarrow _{\varTheta ^+}^{\varPsi ^-} \varPi \) of Blamey and Humberstone’s logicFootnote 4 \(\mathsf {K} ^4\) [5], called \(\mathsf {H{-}ask} \) by [30]. These \(\mathsf {K} ^4\) sequents are translatable as formulas \({(\bigwedge \varGamma \wedge \bigwedge \mathop {\Box } \varTheta ^+) \rightarrow (\bigvee \varPi \vee \bigvee \mathop {\Box } \varPsi ^-)}\) (see [30] and also Definition 10). The constructive nature of \(\mathsf {CKD}\) appears in the fact that the right introduction rules  and \({{\mathop {\boxminus }}R}\) are not obviously (locally) invertible, due to the restriction of the scopes in their premises. In classical logic, where \({\sqsubseteq }\) is the identity relation and there is no difference between positive and negative signs in the sequent’s scope, the rule
and \({{\mathop {\boxminus }}R}\) are not obviously (locally) invertible, due to the restriction of the scopes in their premises. In classical logic, where \({\sqsubseteq }\) is the identity relation and there is no difference between positive and negative signs in the sequent’s scope, the rule  could be replaced by the sound rule \({\varGamma \star \varDelta \star \varTheta \vdash \varPi \star D,\varSigma \star \varPsi \Rightarrow \varGamma \star \varDelta \star \varTheta \vdash \mathop {\Diamond } D, \varPi \star \varSigma \star \varPsi }\), which is invertible. Similarly, the rule \({{\mathop {\boxminus }}R}\) could be relaxed as the invertible rule \({\varGamma \star \varDelta \star D, \varTheta \vdash \varPi \star \varSigma \star \varPsi \Rightarrow \varGamma \star \varDelta \star \varTheta \vdash \mathop {\boxminus } D, \varPi \star \varSigma \star \varPsi }\). In such a classical collapse, \(G_{\mathsf {CKD}}\) might be seen as a 6-ary multi-sequent calculus for the modalities
could be replaced by the sound rule \({\varGamma \star \varDelta \star \varTheta \vdash \varPi \star D,\varSigma \star \varPsi \Rightarrow \varGamma \star \varDelta \star \varTheta \vdash \mathop {\Diamond } D, \varPi \star \varSigma \star \varPsi }\), which is invertible. Similarly, the rule \({{\mathop {\boxminus }}R}\) could be relaxed as the invertible rule \({\varGamma \star \varDelta \star D, \varTheta \vdash \varPi \star \varSigma \star \varPsi \Rightarrow \varGamma \star \varDelta \star \varTheta \vdash \mathop {\boxminus } D, \varPi \star \varSigma \star \varPsi }\). In such a classical collapse, \(G_{\mathsf {CKD}}\) might be seen as a 6-ary multi-sequent calculus for the modalities  in the spirit of Blamey and Humberstone.
in the spirit of Blamey and Humberstone.
Two novel features of the semantics for \(\mathsf {CKD}\) deserve to be highlighted for those unfamiliar with the literature on constructive logic: C-frames admit fallible states, and C-models adopt doubly-quantified truth conditions for modal operators, these latter explaining why \(\Diamond \) does not distribute over disjunction, just like in \(\mathsf {CK}\) [20, 25, 33]. We note that, fallible states appear to be relevant also in \(\mathsf {N} \). Došen [11] (see also [28, 36]) proves completeness of \(\mathsf {N}\) on  -frames in the language \(\mathcal {L} _{\mathsf {N}}\) which does not contain \(\bot \). In the proof, however, canonical states with inconsistent theories must be permitted. As a result, the standard model theory via
-frames in the language \(\mathcal {L} _{\mathsf {N}}\) which does not contain \(\bot \). In the proof, however, canonical states with inconsistent theories must be permitted. As a result, the standard model theory via  -frames is no longer adequate in the extended language \(\mathcal {L} _{\mathsf {N}} \cup \{\bot \}\), since it would force the axiom
-frames is no longer adequate in the extended language \(\mathcal {L} _{\mathsf {N}} \cup \{\bot \}\), since it would force the axiom  , which is not part of \(\mathsf {N} \). This problem does not re-occur in \(\mathsf {CKD}\) since the definition of C-models permits fallible states to reject
, which is not part of \(\mathsf {N} \). This problem does not re-occur in \(\mathsf {CKD}\) since the definition of C-models permits fallible states to reject  . Hence, in \(\mathsf {CKD}\) the fusion of \(\mathsf {N}\) and full \(\mathsf {IPL}\) can be studied.
. Hence, in \(\mathsf {CKD}\) the fusion of \(\mathsf {N}\) and full \(\mathsf {IPL}\) can be studied.
There are various other logics in the vicinity of \(\mathsf {CKD}\) which can be studied, too. For example, the theory of C-frames in which \(\mathrel {R} \) is a transitive subrelation of \(\le \) that is reflexive on infallible states (if \(s \not \!\in \, F\) then \(s \mathrel {R} s\)) generates Propositional Lax Logic \(\mathsf {PLL}\) [20] also known as Computational Logic \(\mathsf {CL}\) [4]. Both negative modalities  and \({\mathop {\boxminus } A}\) collapse in this case, and become semantically equivalent to intuitionistic negation \({{\sim } A}\), whilst \(\Box \) collapses since \(\Box A \leftrightarrow A\). Only \({\mathop {\Diamond }}\) remains independent, yielding the (only) monadic modal operator
and \({\mathop {\boxminus } A}\) collapse in this case, and become semantically equivalent to intuitionistic negation \({{\sim } A}\), whilst \(\Box \) collapses since \(\Box A \leftrightarrow A\). Only \({\mathop {\Diamond }}\) remains independent, yielding the (only) monadic modal operator  of Lax Logic, axiomatised by the single axiom
of Lax Logic, axiomatised by the single axiom  , and the axiom
, and the axiom  if additionally R is a subrelation of \({\sqsubseteq }\).
if additionally R is a subrelation of \({\sqsubseteq }\).
Other logics arise from \(\mathsf {CKD}\) when the combined relation \({\mathrel {{\sqsubseteq }{;}{\mathrel {R}}}}\) is functional. C-frames in which \({\mathrel {{\sqsubseteq }{;}{\mathrel {R}}}}\) is functional collapse  and \({\mathop {\boxminus } A}\) to a form of negation \(\lnot A\), known as Routley negation in the literature on \(\mathsf {FDE}\) [17,18,19]. Routley negation is weaker than intuitionistic negation \({{\sim } A}\) in that it satisfies contraposition and DeMorgan laws while permitting gaps and gluts. In C-frames in which \({\mathrel {{\sqsubseteq }{;}{\mathrel {R}}}}\) is functional the theories \(\mathsf {N}^\star \) and \(\mathsf {N}^\star _i\) of Routley negation [27] can be developed. Specifically, if \({\mathrel {{\sqsubseteq }{;}{\mathrel {R}}}}\) is weakly functionalFootnote 5 then we obtain the theory called \(\mathsf {N} '\) [28] that extends \(\mathsf {IPL}\) by axioms [27]
and \({\mathop {\boxminus } A}\) to a form of negation \(\lnot A\), known as Routley negation in the literature on \(\mathsf {FDE}\) [17,18,19]. Routley negation is weaker than intuitionistic negation \({{\sim } A}\) in that it satisfies contraposition and DeMorgan laws while permitting gaps and gluts. In C-frames in which \({\mathrel {{\sqsubseteq }{;}{\mathrel {R}}}}\) is functional the theories \(\mathsf {N}^\star \) and \(\mathsf {N}^\star _i\) of Routley negation [27] can be developed. Specifically, if \({\mathrel {{\sqsubseteq }{;}{\mathrel {R}}}}\) is weakly functionalFootnote 5 then we obtain the theory called \(\mathsf {N} '\) [28] that extends \(\mathsf {IPL}\) by axioms [27]
with derivation rules of Modus Ponens and Contraposition (“from \(A \rightarrow B\) infer \(\lnot B \rightarrow \lnot A\)”). If we further assume that frames are infallible, the relation \({\mathrel {{\sqsubseteq }{;}{\mathrel {R}}}}\) becomes functional, and we arrive at Heyting-Ockham logic \(\mathsf {N}^\star \) [7, 27, 28] (extended by quantifiers in [36]) that extends \(\mathsf {N} '\) by the axiom \(\lnot \bot \). Note that \(\mathsf {CKD}\) on functional frames also collapses the positive modalities \({\mathop {\Box } A \leftrightarrow \mathop {\Diamond } A}\) into a single modality \(\Box \) that preserves the properties of \({\mathop {\Box }}\). This naturally generates an extension of \(\mathsf {N}^\star \) with modality \(\Box \) in a coherent theory that appears not to have been considered in the literature.
There are a number of open problems which could be considered in the future. The Correspondence Theory for \(\mathsf {CKD}\) could be explored and a sequent calculus provided for extensions of \(\mathsf {CKD}\), such as \(\mathsf {N}^\star \) and \(\mathsf {N}^\star _i\) in language \({\{ \mathop {\Box }, \mathop {\Diamond }, \lnot \}}\) where \(\lnot \) collapses both  and \({\mathop {\boxminus }}\) into a single modality \(\lnot \). Following [36], the addition of quantifiers to \(\mathsf {CKD}\) could be investigated. On the proof-theoretic front, means for termination control (such as invertibility of rules, duplication elimination, blocking conditions) of the sequent calculus \(G_{\mathsf {CKD}}\) could be investigated, and the algorithmic complexity of the theory \(\mathsf {CKD}\) determined. Since \(\mathsf {CKD}\) is constructive, the question naturally arises of what lambda calculus is related to \(\mathsf {CKD}\) via the Curry Howard isomorphism, and if there exists a natural deduction calculus for \(\mathsf {CKD}\). Recent work by [1] provides a novel semantics for proofs in \(\mathsf {CK}\), and could form the basis of constructing a semantics of proofs in \(\mathsf {CKD}\) including negative modalities. Finally, it would be interesting to investigate if the neighbourhood semantics for CK and other non-normal extensions proposed by [8] could be used to interpret the negative modalities of CKD.
and \({\mathop {\boxminus }}\) into a single modality \(\lnot \). Following [36], the addition of quantifiers to \(\mathsf {CKD}\) could be investigated. On the proof-theoretic front, means for termination control (such as invertibility of rules, duplication elimination, blocking conditions) of the sequent calculus \(G_{\mathsf {CKD}}\) could be investigated, and the algorithmic complexity of the theory \(\mathsf {CKD}\) determined. Since \(\mathsf {CKD}\) is constructive, the question naturally arises of what lambda calculus is related to \(\mathsf {CKD}\) via the Curry Howard isomorphism, and if there exists a natural deduction calculus for \(\mathsf {CKD}\). Recent work by [1] provides a novel semantics for proofs in \(\mathsf {CK}\), and could form the basis of constructing a semantics of proofs in \(\mathsf {CKD}\) including negative modalities. Finally, it would be interesting to investigate if the neighbourhood semantics for CK and other non-normal extensions proposed by [8] could be used to interpret the negative modalities of CKD.
Notes
- 1.
Such negative modalities have been considered in the literature on FDE and Routley semantics as ways of capturing forms of negation [17,18,19, 28, 36] often called ‘constructible’ or ‘strong’ negation [26, 37]. We do not suggest that the role of
 and \({\mathop {\boxminus }}\) in the logic \(\mathsf {CKD}\) is to capture forms of negation; rather, we are simply interested in how they behave in a constructive setting (i.e. in which the Disjunction Property holds) as modal operators.
and \({\mathop {\boxminus }}\) in the logic \(\mathsf {CKD}\) is to capture forms of negation; rather, we are simply interested in how they behave in a constructive setting (i.e. in which the Disjunction Property holds) as modal operators. - 2.
Our claim is that the doubly quantified truth conditions are a neat way out of the bind, not that they are necessary in order to provide a logic which combines \(\Box \), \({\mathop {\Diamond }}\),
 and \({\mathop {\boxminus }}\) interpreted with respect to the same relation.
and \({\mathop {\boxminus }}\) interpreted with respect to the same relation. - 3.
As usual, we can take \(\top =_{\scriptstyle {df}}p \rightarrow p\) for a variable \(p \in Var \). Interestingly, also absurdity \(\bot \) is representable, viz. as the non-necessity of truth, i.e., \({\bot =_{\scriptstyle {df}}\mathop {\boxminus } \top }\). First, \(\mathfrak {M}, s \,\models \, \bot \) implies \({\mathfrak {M}, s \,\models \, \mathop {\boxminus } \top }\) since by definition there is no \(s'\) with \({s \sqsubseteq s'}\). Second, if \({\mathfrak {M}, s \,\models \, \mathop {\boxminus } \top }\) and \(s \not \!\in \, F\) we would have \({s \sqsubseteq s}\) and so by the truth condition for \({\mathop {\boxminus }}\) there must be \(s''\) with \(s \mathrel {R} s''\) and
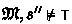 . This is impossible, hence \(s \in F\) and so \(\mathfrak {M}, s \,\models \, \bot \).
. This is impossible, hence \(s \in F\) and so \(\mathfrak {M}, s \,\models \, \bot \). - 4.
- 5.
A frame is weakly functional if \({\forall s \in S \setminus F.\, \exists s'.\ s \mathrel {{\sqsubseteq }{;}{\mathrel {R}}} s'}\) and \( \forall s, s_1', s_2'.\, s \mathrel {{\sqsubseteq }{;}{\mathrel {R}}} s_1' \& s \mathrel {{\sqsubseteq }{;}{\mathrel {R}}} s_2' \Rightarrow s_1' \cong s_2'\), where \(s_1' \cong s_2'\) iff \(s_1' \le s_2'\) and \(s_2' \le s_1'\). The frame is functional if the existence condition holds in the stronger form \({\forall s \in S.\, \exists s'.\, s \mathrel {{\sqsubseteq }{;}{\mathrel {R}}} s'}\).
References
Acclavio, M., Catta, D., Straßburger, L.: Towards a denotational semantics for proofs in constructive modal logic. arXiv preprint arXiv:2104.09115 (2021)
Arisaka, R., Das, A., Straßburger, L.: On nested sequents for constructive modal logics. Logical Methods in Computer Science 11 (2015)
Bellin, G., de Paiva, V., Ritter, E.: Extended Curry-Howard correspondence for a basic constructive modal logic. In: Methods for Modalities II (2001)
Benton, N., Bierman, G., de Paiva, V.: Computational types from a logical perspective. J. Funct. Program. 8(2), 177–193 (1998)
Blamey, S., Humberstone, L.: A perspective on modal sequent logic. Publ. Res. Inst. Math. Sci. 27, 763–782 (1991)
Božić, M., Došen, K.: Models for normal intuitionistic modal logics. Studia Logica 43(3), 217–245 (1984)
Cabalar, P., Odintsov, S.P., Pearce, D.: Logical foundations of well-founded semantics. In: P.D. et al. (ed.) Proceedings of International Conference on Knowledge Representation and Reasoning (2006)
Dalmonte, T., Grellois, C., Olivetti, N.: Intuitionistic non-normal modal logics: a general framework. J. Philos. Logic 49, 833–882 (2020)
Došen, K.: Negation in the light of modal logic. In: Gabbay, D.M., Wansing, H. (eds.) What is Negation?, pp. 77–86. Springer, Heidelberg (1999). https://doi.org/10.1007/978-94-015-9309-0_4
Došen, K.: Negative modal operators in intuitionistic logic. Publications de L’Institut Mathématique 35(49), 3–14 (1984)
Došen, K.: Negation as a modal operator. Rep. Math. Logic 20(1986), 15–27 (1986)
Dragalin, A.G.: Mathematical Intuitionism: Introduction to Proof Theory. American Mathematical Society (1988)
Drobyshevich, S.: Double negation operator in logic \({N}^\star \). J. Math. Sci. 205(3) (2015)
Drobyshevich, S.A., Odintsov, S.P.: Finite model property for negative modalities. Sibirskie Elektronnye Matematicheskie Izvestiia 10 (2013)
Drobyshevich, S.A.: Composition of an intuitionistic negation and negative modalities as a necessity operator. Algebra Logic 52, 1–19 (2013). https://doi.org/10.1007/s10469-013-9235-8
Drobyshevich, S.: On classical behavior of intuitionistic modalities. Logic Log. Philos. 24(1), 79–104 (2015)
Dunn, J.M.: Star and perp: two treatments of negation. Philos. Perspect. 7, 331–357 (1993)
Dunn, J.M.: Negation, a notion in focus, vol. 7, chap. Generalized Ortho Negation, pp. 3–26. Walter de Gruyter Berlin (1996)
Dunn, J.M., Zhou, C.: Negation in the context of gaggle theory. Studia Logica 80(2–3), 235–264 (2005). https://doi.org/10.1007/s11225-005-8470-y
Fairtlough, M., Mendler, M.: Propositional lax logic. Inf. Comput. 137(1), 1–33 (1997)
Fitting, M.: Basic modal logic. In: Gabbay, D.M., Hogger, C.J., Robinson, J.A. (eds.) Handbook of Logic in Artificial Intelligence and Logic Programming, vol. 1, pp. 368–448. Oxford University Press, New York (1993)
Mendler, M., Scheele, S.: Towards constructive DL for abstraction and refinement. J. Autom. Reason. 44(3), 207–243 (2010). https://doi.org/10.1007/s10817-009-9151-8
Mendler, M., Scheele, S.: Cut-free Gentzen calculus for multimodal CK. Inf. Comput. 209(12), 1465–1490 (2011)
Mendler, M., Scheele, S.: On the computational interpretation of CK\(_n\). Fundamenta Informaticae 130, 1–39 (2014)
Mendler, M., de Paiva, V.: Constructive CK for contexts. In: Proceedings of the First Workshop on Context Representation and Reasoning, CONTEXT 2005 (2005)
Nelson, D.: Constructible falsity. J. Symb. Logic 14(1), 16–26 (1949)
Odintsov, S., Wansing, H.: Routley star and hyperintensionality. J. Philos. Logic 50, 33–56 (2020)
Odintsov, S.P.: Combining intuitionistic connectives and Routley negation. In: Siberian Electronic Mathematical Reports (2005)
Plotkin, G., Stirling, C.: A framework for intuitionistic modal logics. In: Halpern, J. (ed.) Theoretical Aspects of Reasoning About Knowledge, pp. 399–406. Monterey (1986)
Poggiolesi, F.: Gentzen Calculi for Modal and Propositional Logic. Springer, Heidelberg (2011). https://doi.org/10.1007/978-90-481-9670-8
Popkorn, S.: First Steps in Modal Logic. Cambridge University Press, Cambridge (1994)
Sato, M.: A study of Kripke-type models for some modal logics by Gentzen’s sequential method. Publ. Res. Inst. Math. Sci. 13, 381–468 (1977)
Scheele, S.: Model and Proof Theory of Constructive ALC, Constructive Description Logics. Ph.D. thesis, University of Bamberg (2015)
Simpson, A.K.: The proof theory and semantics of intuitionistic modal logic. Ph.D. thesis, University of Edinburgh, Scottland (1994)
Sotirov, V.H.: Modal theories with intuitionistic logic. In: Proceedings of the Conference on Mathematical Logic, Sophia, pp. 139–171 (1980)
Speranski, S.O.: Negation as a modality in a quantified setting. J, Logic Comput. (2021)
Wansing, H.: On split negation, strong negation, information, falsification, and verification. In: Bimbó, K. (ed.) J. Michael Dunn on Information Based Logics. OCL, vol. 8, pp. 161–189. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-29300-4_10
Westerståhl, D.: On the Aristotelian square of opposition. Kapten Mnemos Kolumbarium, en festskrift med anledning av Helge Malmgrens (2005)
Wijesekera, D.: Constructive modal logic I. Ann. Pure Appl. Logic 50, 271–301 (1990)
Wolter, F., Zakharyaschev, M.: Intuitionistic modal logics as fragments of classical bimodal logics. Logic at work, pp. 168–186 (1997)
Wolter, F., Zakharyaschev, M.: The relation between intuitionistic and classical modal logics. Algebra Logic 36(2), 73–92 (1997)
Wolter, F., Zakharyaschev, M.: Intuitionistic modal logic. In: Cantini, A., Casari, E., Minari, P. (eds.) Logic and Foundations of Mathematics, pp. 227–238. Springer, Heidelberg (1999). https://doi.org/10.1007/978-94-017-2109-7_17
Acknowledgements
The authors would like to thank the anonymous referees and the PC, who provided useful and detailed comments on the submission version of the paper, and Stanislav Speranski, for sharing thoughts on constructive negation as a modality.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Mendler, M., Scheele, S., Burke, L. (2021). The Došen Square Under Construction: A Tale of Four Modalities. In: Das, A., Negri, S. (eds) Automated Reasoning with Analytic Tableaux and Related Methods. TABLEAUX 2021. Lecture Notes in Computer Science(), vol 12842. Springer, Cham. https://doi.org/10.1007/978-3-030-86059-2_26
Download citation
DOI: https://doi.org/10.1007/978-3-030-86059-2_26
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-86058-5
Online ISBN: 978-3-030-86059-2
eBook Packages: Computer ScienceComputer Science (R0)










 and
and  and
and 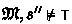 . This is impossible, hence
. This is impossible, hence