Developing a Bi-objective Model to Configure a Scalable Manufacturing Line Considering Energy Consumption

Abstract

Today, due to intense global competition, manufacturing systems need to be highly responsive and adaptive to fulfill market demand fluctuations and personalized production. Reconfigurable manufacturing system (RMS) is one of the main paradigms which has been introduced to overcome the dynamic nature of today’s industry. In addition, RMSs are also a basis to develop new generation of sustainable production systems. This paper addresses the problem of designing a scalable manufacturing line for a part family considering both cost- and energy-effectiveness criteria. Hence, a bi-objective mathematical programming model is proposed. The main decision is to configuration and/or reconfiguration of production line by adding a set of new machines from a list of candidate reconfigurable machine tools (RMTs) and/or transforming them among the stages to fulfill anticipated demands in the periods of a time horizon. A numerical example is solved to illustrate the validation of the model. CPLEX is utilized to implement an augmented epsilon constraint method to extract Pareto front. The results show that different strategies in configuration the production line have significant impact on cost- and energy-effectiveness criteria.

1 Introduction

Nowadays, despite fierce competition, limited opportunities, and frequent changes in products demand, it is necessary to have a manufacturing system that can quickly adjust its functionality and production capacity within a part family. Hence, RMSs have been introduced to build a “live” factory which can cost effectively and quickly respond to the customer requirements [1]. In addition to the cost effectiveness and the ability to easily change production capacity (scalability) of a manufacturing system, the energy efficiency, because of ecological, economic and political reasons, is also an important criterion for industrial enterprises. Designing scalable manufacturing lines which simultaneously consider the cost and energy effectiveness are the challenging and yet interesting problem which motivated us in this paper.

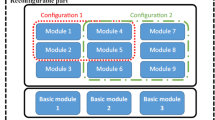
An RMS is a dynamic manufacturing system which its functionality and production capacity can be easily adapted to satisfy changeable requirements. In order to achieve these capabilities, RMTs with modular and adjustable structures are often used as part of RMSs [2]. An RMT can be used as a group of machines that changing of its configuration lead to different functionalities or production rates. An RMT usually compose of modules which can be assembled and disassembled to achieve different configurations of the machine. Development of RMTs can prevent the implementation of multiple machines that share many common and costly modules while being rarely used at the same time [3]. Recently, a comprehensive literature review dedicated to RMTs have been conducted by Gadalla and Xue [4].

To design a scalable manufacturing system, the concept of reconfigurability can be utilized in both system and machine levels. In the system level, configuration of RMSs can include many diverse aspects. Abdi and Labib [5] presented some strategic issues during RMS design. Moreover, the level of responsiveness and scalability for a production system can also be affected by the reconfigurability of its machines. Therefore, selecting appropriate machines to launch a manufacturing system is an attractive subject of study. Moghaddam et al. [6] did one of the first attempts to adjust the capacity of a manufacturing system by transforming one RMT configuration to another. They developed a mathematical model for a case of single product flow line (SPFL). Their research proved that transforming of RMTs can be considered as a significant factor to tackle the problem of RMS capacity scalability. Thereafter, Moghaddam et al. [7] extended their model to be utilized for a part family. However, they implemented their proposed model to minimize the total cost of the manufacturing system while in the RMS design literature usually there are also other objectives which can be considered to improve the performance of the system, e.g. energy consumption, throughput, flexibility, etc.

On each configuration because of utilizing various modules/tools, an RMT can operate with special characteristics, e.g. reliability and rate of energy consumption. Ashraf and Hasan [8] developed a multi-objective model to select an appropriate configuration for a reconfigurable manufacturing line. They considered four objective function including cost, reconfigurability, operation capability, and reliability. Touzout et al. [9] investigated the problem of process planning in an RMS considering sustainability. They proposed a tri-objective model which considered minimizing the energy consumption as a criterion in addition to the traditional two criteria, cost and completion time. He et al. [10] studied an energy-responsive optimization method for machine tool selection and operation sequencing in a shop floor. However, these papers didn’t consider the effect of energy consumption in the designing phase of an RMS. This is while, the environmental impact of utilizing a machine tool is significant that can be reduced if it has already been considered during system designing phase. It is worth noting that the global manufacturing industry sector is responsible for 31% of primary energy consumption and 36% of CO2 emissions [10]. Hence, reducing the energy consumed by machine tool systems can significantly effect on sustainability. Motivated by these facts, the emphasis of this research is on the development of a bi-objective mathematical model to design a scalable manufacturing flow line for a part family considering cost and energy consumption.

The rest of the paper is organized as follows: The problem description and model formulation are presented in Sect. 2. In Sect. 3, a simple test case to evaluate the proposed method is demonstrated, and the related computational results are presented. Finally, the conclusion and areas for future research are presented in Sect. 4.

2 Problem Description and Model Formulation

2.1 Problem Definition

The problem consists of the configuration of a flexible manufacturing flow line to produce several products of a special part family. The demands have already been anticipated for each period of time $t\in T$. The flow line contains a set of stages $s\in S$ in which a special operation can be processed. The schematic layout of shop floor is presented in Fig. 1. The main decision is to determine configuration of production line by selecting a set of machines from a list of candidate RMTs to fulfill the predicted demands. At the beginning of each period of time, the production capacity of each stage should be met by adding some new RMTs, changing the configuration of some prior RMTs in the stage, or transforming some prior RMTs from the other stages to the considered stage. Each RMT $i\in I$ has a set of ${\mathcal{J}}_{i}$ configurations. One or more operations can be processed in each configuration ${j\in \mathcal{J}}_{i}$ with a special rate of production and energy consumption. Hence, designing of the production flow line will be guided by two objectives including the minimization of the total system cost and the minimization of the system energy consumption.

Fig. 1.

Schematic layout of reconfigurable manufacturing flow line (revised from [11])

2.2 Model Formulation

Here, the sets and indices, the parameters, and the decision variables to formulate the problem are described. Thereafter, the mathematical formulation is presented.

Parameters

${D}_{st}$ Demand rate of the operation related to $s$ th stage in time period $t$

${P}_{ijs}$ Production rate of machine configuration $ij$ to perform the operation of stage $s$

${\alpha }_{ijs}$ Binary parameter. If the operation of $s$ th stage can be processed by machine configuration $ij$ , then ${\alpha }_{ijs}=1$ ; otherwise, ${\alpha }_{ijs}=0$

${C}_{i}$ Purchasing cost of the machine $i$

${C}_{ijs}^{^{\prime}}$ Operation cost of machine configuration $ij$ to perform the operation of stage $s$

${E}_{ijs}$ Energy consumption of machine configuration $ij$ to perform the operation of stage $s$

${A}_{ij{j}^{^{\prime}}}$ Number of added auxiliary modules to the $i$ th machine for transforming configuration $j$ to ${j}^{^{\prime}}$

$R_{{ijj^{\prime}}}$ Number of removed auxiliary modules from the $i$ th machine for transforming configuration $j$ to ${j}^{^{\prime}}$

$CA, CR$ Cost of adding/removing an auxiliary module to/from an RMT

Decision Variables

${X}_{ijs}^{t}$ Number of new machines configuration $ij$ which are added to stage $s$ at the beginning of period t

${Z}_{ijs}^{t}$ Total number of existing machines configuration $ij$ in $s$ th stage at period $t$

${Y}_{ijs{j}^{^{\prime}}{s}^{^{\prime}}}^{t}$ Number of machines configuration $ij$ in the $s$ th stage at period $(t-1)$ which are added to stage ${s}^{^{\prime}}$ at the beginning of time period $t$ with configuration ${j}^{^{\prime}}$

Mathematical Formulation

$$ \begin{aligned} {\text{Min}} z_{1} = & \mathop \sum \limits_{t \in T} \mathop \sum \limits_{s \in S} \mathop \sum \limits_{i \in I} \mathop \sum \limits_{{j \in {\mathcal{J}}_{i} }} C_{ij} X_{ijs}^{t} + \mathop \sum \limits_{t \in T} \mathop \sum \limits_{s \in S} \mathop \sum \limits_{i \in I} \mathop \sum \limits_{{j \in {\mathcal{J}}_{i} }} C_{ijs}^{^{\prime}} Z_{ijs}^{t} \\ + & \mathop \sum \limits_{t \in T} \mathop \sum \limits_{i \in I} \mathop \sum \limits_{{j \in {\mathcal{J}}_{i} }} \mathop \sum \limits_{{j^{\prime} \in {\mathcal{J}}_{i} }} \mathop \sum \limits_{s \in S} \mathop \sum \limits_{{s^{\prime} \in {\text{S }}}} \left( {CA \times A_{{ijj^{\prime}}} + CR \times R_{{ijj^{\prime}}} } \right). Y_{{ijsj^{\prime}s^{\prime}}}^{t} \\ \end{aligned} $$

(1)

$$ {\text{Min}} z_{2} = \mathop \sum \limits_{t \in T} \mathop \sum \limits_{s \in S} \mathop \sum \limits_{i \in I} \mathop \sum \limits_{{j \in {\mathcal{J}}_{i} }} E_{ijs} Z_{ijs}^{t} $$

(2)

$$ \begin{gathered} Z_{ijs}^{t} = X_{ijs}^{t} \,\,\,\,\,\forall i \in I,j \in {\mathcal{J}}_{i} ,s,t = 1 \hfill \\ {\text{s}}{.}\,{\text{t}}{.} \hfill \\ \end{gathered} $$

(3)

$$ \begin{aligned} Z_{ijs}^{t} = & Z_{ijs}^{t - 1} + X_{ijs}^{t} + \mathop \sum \limits_{{j^{\prime} \in {\mathcal{J}}_{i} }} \mathop \sum \limits_{{\begin{array}{*{20}c} {s^{\prime} \in S} \\ {s^{\prime} \ne s} \\ \end{array} }} Y_{{ij^{\prime}s^{\prime}js}}^{t} + \mathop \sum \limits_{{\begin{array}{*{20}c} {j^{\prime} \in {\mathcal{J}}_{i} } \\ {j^{\prime} \ne j} \\ \end{array} }} Y_{{ij^{\prime}sjs}}^{t} - \mathop \sum \limits_{{j^{\prime} \in {\mathcal{J}}_{i} }} \mathop \sum \limits_{{\begin{array}{*{20}c} {s^{\prime} \in S} \\ {s^{\prime} \ne s} \\ \end{array} }} Y_{{ijsj^{^{\prime}} s^{\prime}}}^{t} \\ - & \mathop \sum \limits_{{\begin{array}{*{20}c} {j^{\prime} \in {\mathcal{J}}_{i} } \\ {j^{\prime} \ne j} \\ \end{array} }} Y_{{ijsj^{^{\prime}} s}}^{t} \,\,\,\,\,\forall i \in I,j \in {\mathcal{J}}_{i} ,s \in S,\,t > 1 \\ \end{aligned} $$

(4)

$$ \mathop \sum \limits_{{j^{\prime} \in {\mathcal{J}}_{i} }} \mathop \sum \limits_{{s^{\prime} \in S}} Y_{{ijsj^{^{\prime}} s^{\prime}}}^{t} \le Z_{ijs}^{t - 1} \,\,\,\,\,\,\forall i \in I,j \in {\mathcal{J}}_{i} ,s \in S,t > 1 $$

(5)

$$ \mathop \sum \limits_{i \in I} \mathop \sum \limits_{{j \in {\mathcal{J}}_{i} }} P_{ijs} Z_{ijs}^{t} \ge D_{st} \,\,\,\,\,\,\,\forall s \in S, t \in T $$

(6)

$$ X_{ijs}^{t} \le M \times \alpha_{ijs} \,\,\,\,\,\,\,\forall i \in I,j \in {\mathcal{J}}_{i} ,s \in S,t \in T $$

(7)

$$ Y_{{ijsj^{^{\prime}} s^{\prime}}}^{t} \le M \times \alpha_{ijs} \,\,\,\,\,\,\,\forall i \in I,j,j^{\prime} \in {\mathcal{J}}_{i} ,s,s^{\prime} \in S,t \in T $$

(8)

$$ Y_{{ijsj^{\prime}s^{\prime}}}^{t} \le M \times \alpha_{{ij^{\prime}s^{\prime}}} \,\,\,\,\,\,\,\,\forall i \in I,j,j^{\prime} \in {\mathcal{J}}_{i} ,s,s^{\prime} \in S,t \in T $$

(9)

$$ X_{ijs}^{t} ,Z_{ijs}^{t} \in {\mathbb{Z}}^{ + } \,\,\,\,\,\,\,\forall i \in I,j \in {\mathcal{J}}_{i} ,s \in S,t \in T $$

(10)

$$ Y_{{ijsj^{\prime}s^{\prime}}}^{t} \in {\mathbb{Z}}^{ + } \,\,\,\,\,\,\,\forall i \in I,j,j^{\prime} \in {\mathcal{J}}_{i} ,s,s^{\prime} \in S,t \in T $$

(11)

The model has two objective function. The first objective in Eq. (1) minimizes the total cost. The second objective in Eq. (2) minimizes the energy consumption of production line. Equation (3) ensures that the total number of existing machines at the end of the first period should be exactly equal to the new machines. For each period of time $t > 1$, Eq. (4) guarantees that the total number of machines in the current period (t) should be balanced with the prior period ($t - 1$).

Equation (5) ensures that the number of machines which could be reconfigured in each stage at the time period t should at most be equal with the total number of existing machines at the time period ($t -$ 1). Equation (6) indicates that the production rate of existing machines in each stage should be more than demand rate at the period. Constraint sets (7), (8) and (9) guarantee that no machine assigns to unauthorized state. Constraint sets (10) and (11) define the decision variables.

3 Numerical Example

To validate the proposed model, the following example is illustrated. This example is based on the data presented in Table 1. Moreover, it is assumed that the cost of adding an auxiliary module to an RMT is 50, and the cost of removing an auxiliary module is 25 [7].

Table 1. Machine configurations and their production rates, energy consumptions, costs, basic and auxiliary modules used in the instance problem (summarized and revised from [12]).

Fig. 2.

The process plan and anticipated demand rates of each part in each production period

A simple hypothetical part family containing three different parts with special process plans and anticipated demand rates during each production period is shown in Fig. 2. Based on these data, the required production capacity at each stage in each production period can be extracted as shown in Table 2. For example, the required demand rate in the second stage at the first period can be calculated as: $D_{2,1} = 15 + 20 = 35$.

Table 2. Required production capacity at each stage in each production period ($D_{st}$).

In order to solve the bi-objective mathematical model and generate the Pareto optimal solutions, we utilize augmented epsilon-constraint method. The model is implemented in GAMS 24.1.3 and solved using the solver CPLEX on a computer with a 2.8 GHz Intel CPU and with 4 GB of installed memory. The solver could solve the problem less than 1 s. Figure 3 shows the obtained Pareto front for the instance problem.

Fig. 3.

The obtained Pareto front for the instance problem

In the following, two extreme points $\beta_{1} :\left( {Z_{1} = 15855, Z_{2} = 161} \right)$ and $\beta_{2} :\left( {Z_{1} = 14470, Z_{2} = 165} \right)$ of the Pareto front are selected to be illustrated. Actually, $\beta_{1}$ has the best amount of energy consumption, and $\beta_{2}$ has the best amount of system cost among the other points of Pareto front. The machine configurations selected in the points $\beta_{1}$ and $\beta_{2}$ are presented in Fig. 4 and Fig. 5, respectively. At the beginning of each period, the transformed/reconfigured RMTs are shown by yellow boxes while the newly purchased RMTs are shown by blue boxes. A significant observation in the illustrated points is the impact of reconfiguration ability of the RMTs on setting the capacity of the production line. For example, in the point $\beta_{2}$ which is a cost-effective solution, the production line starts with seven RMTs at the first period, and it adjusts the capacity by reconfiguration actions to fulfill the required demands. On the other hand, in the point $\beta_{1}$ which is an energy-effective solution, the production line starts with six RMTs that consume lower amount of energy, then it adjusts the capacity by reconfiguration actions and purchasing new RMTs. However, these are four different strategies that can be considered in the process of decision making.

Fig. 4.

The machine configurations selected in the non-dominated point $\beta_{1}$

Fig. 5.

The machine configurations selected in the non-dominated point $\beta_{2}$

4 Conclusions

In this research, a new mathematical programming model was presented to design a capacity scalable manufacturing line considering cost- and energy-effectiveness criteria. In addition, a numerical example based on a case from the literature was solved to illustrate the validation of the model and to help for better understanding the concepts. Results show that different strategies in implementing the production line can be considered regarding to the level of cost- and energy-effectiveness criteria, and the presented model can help managers to make appropriate decisions in this area.

For future works, developing some effective algorithms are proposed to solve the real-world size problems in an acceptable computational time. Moreover, some other aspects such as limitation in adding new machines and considering the situation of utilizing common/limited modules to perform the reconfiguration actions are proposed.