Anisotropic Permeability of Geomaterials: Lab Test and Borehole Environment Model

Abstract

Theoretical substantiation and lab tests of the method for synthesis of a relationship describing angular anisotropy of the effective permeability in borehole environment based on the inverse coefficient problem solution in terms of the data on percolation tests of regularly non-uniform cylindrical specimens with a central hole are set forth in the paper. With a view to provide the algorithmic support of GIS data inversion in the course of determination of poroperm properties of production intervals the researchers developed and implemented by the hybrid numerical method to realize the multiphysical model of the evolution of geomechanical and electrohydrodynamic fields under filtration of multiphase fluid in the borehole environment with consideration for anisotropy of permeability induced by difference in components of the external stress fields. The numerical experiments enabled to establish that in the overbalanced drilling the configuration of invaded zone depends on the proportion between horizontal stress components outside of the well influence zone.

1 Introduction

To solve the problems on advance degassing of coal seams and coalmine methane utilization design (Seidle 2011), investigation of geothermal systems (Salimzadeh et al. 2018), construction of underground gas storages (Caglayan et al. 2020), inversion of geophysical borehole surveying data with the view to establish production intervals and to assess poroperm properties of rocks (Hsu and Robinson 2019; Ahmed 2019; Yeltsov et al. 2014; Garcia and Heidari 2021) and other actual problems requires the development of multiphysical models and their appropriate verification. Such models comprising the conservation law and state equations also involve empirical relationships between parameters of the physical field arising in borehole environment, such as petrophysical formulas of electroconductivity of a heterogenic medium, relationship of phase permeability versus fluid concentration, the reservoir rock poroperm properties—stress relationship. The last factor as well as probable difference between components of the external stress field and disturbance of rock mass stability caused by boring operations can provoke the permeability anisotropy in the vicinity of a borehole. Subsequently, the borehole environment can not be described in terms of one dimensional models (Yeltsov et al. 2012; Nazarova and Nazarov 2018), so 2D and 3D models should be used, but they imply the proper parametric base resting on respective experiments, where specific features of poroperm properties distribution are considered.

The paper reports the data on percolation tests of regularly heterogeneous cylindrical specimens with central hole. The specimens made of a synthetic geomaterial are used to work out a process for determination of the effective permeability—polar angle relationship based on solution of the inverse coefficient problem. The researchers propose 2D multiphysical model describing evolution of geomechanical and electrohydrodynamic fields in the borehole environment under multiphase filtration.

2 Anisotropic Permeability by Lab Test Data and Inverse Problem Solution

2.1 Experimental Design

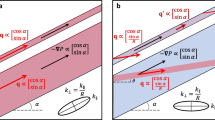
Cylindrical specimens (height $h=$110 mm, external radius $R=$ 75 mm, central channel diameter $2a=$ 8 mm) were assembled of six components of the same shape (Fig. 1a), but different permeability. The components were made of the conditioned cryogel consisted of three calibrated sand fractions (0.5, 1, and 1.5 mm) under the original technological process (Nazarova et al. 2019). Permeability values of specimen components assessed under the standard procedure (RF Standard 26450.2–85 1985), appeared ${k}_{0}=$ 24 mD, ${k}_{1}=$ 29 mD, and ${k}_{2}=$ 35 mD.

Fig. 1

Specimen structure (a) and test bench (b)

Specimen 1 in isolating rubber collar 2 was placed in sealed metal chamber 3 (Fig. 1b), the rest free space stuffed with coarse-grain sand 4 (fraction 5 mm) exhibited high permeability (more than 3 Darcy) and did not notably affect the filtration characteristics of the test system. The air was pumped under constant pressure pm through central hole 5. The air flowrate ${Q}_{mn}$ was recorded at a stationary mode with relative precision of 2% at side surface of the specimen segment (central angle $2\beta =$ 30°, Figs. 1a and 2), which position was determined by angle ${\varphi }_{n}$ (the flowmeter was connected through adapter 6). Measurement results at ${p}_{m}=$ 1.05, 1.10,…,1.25 bar and ${\varphi }_{n}=$ 30°, 45°,…,150° are reported in Table 1.

Fig. 2

Model of the experiment and boundary conditions (a), computational grid (b)

Table 1 Flowrate ${Q}_{mn}$ (ml/min) at different input pressure ${p}_{m}$ and angle ${\varphi }_{n}$

2.2 Model of the Percolation Experiment

Evolution of hydrodynamic fields in the test specimen in polar coordinates $(r,\theta )$ (Fig. 2a) is described by the system including (Kochin et al. 1964):

Continuity equation

$$ \frac{{\partial \left( {\omega \rho } \right)}}{\partial t} + {\text{div}}\left( {\rho \vec{V}} \right) = 0; $$

(1)

Darcy’s law

$$ \vec{V} = - \frac{K}{\eta }{\text{grad}}\,p $$

(2)

and state equation

$$ p = p_{0} \rho /\rho_{0} $$

(3)

where $\omega$—porosity, $p$—pressure, $\rho$ and $\eta$—density and viscosity of gas,${\rho }_{0}$—gas density at atmosheric pressure ${p}_{0}$, $\overrightarrow{V}=({V}_{r},{V}_{\theta })$—seepage velocity, permeability $K$ is the piecewise constant function versus polar angle

$$ K\left( \theta \right) = \left\{ { \begin{array}{*{20}c} {k_{0} } & {0 \le \theta \le \pi /3, \pi \le \theta \le 4\pi /3} \\ {k_{1} } & {\pi /3 \le \theta \le 2\pi /3, 4\pi /3 \le \theta \le 5\pi /3} \\ {k_{2} } & {2\pi /3 \le \theta \le \pi , 5\pi /3 \le \theta \le 2\pi } \\ \end{array} } \right. $$

System (1)—(3) reduces to non-linear parabolic equation

$$ \frac{\partial p}{{\partial t}} = b\,{\text{div}}\left( {Kp\,{\text{grad}}\,p} \right) $$

(4)

$(b={\rho }_{0}/\omega {\eta p}_{0})$ for which the following boundary conditions are formulated (Fig. 2a):

$$\begin{aligned}&p\left( {a,\theta ,t} \right) = p_{m} ; \\\left( {R,\theta ,t} \right) &= p_{0} \qquad {\text{at}}\qquad \left| {\theta - \varphi_{n} } \right| \le \beta ;\\ V_{r} \left( {R,\theta ,t} \right) &= 0\qquad {\text{at}}\qquad \left| {\theta - \varphi_{n} } \right| > \beta . \end{aligned}$$

(5)

The flowrate through the sector at side surface of the specimen determined by angle ${\varphi }_{n}$ (Figs. 1 and 2a) is calculated by formula

$$ Q\left( t \right) = hR\mathop \int \limits_{{\varphi_{n} - \beta }}^{{\varphi_{n} + \beta }} V_{r} \left( {R,\theta ,t} \right)d\theta , $$

(6)

where radial velocity ${V}_{r}$ is found from (2).

System (4), (5) was solved by the finite-difference method of alternating directions (Samarskii 2001) at nonuniform grid (Fig. 2b). It is important to point out that stationary distribution of hydrodynamic field parameters does not depend on $b$ value.

Pressure distribution (Fig. 3) in the specimen at the steady-state filtration mode at ${\varphi }_{n}=$ 60° and ${p}_{m}=$ 1.25 bar indicates the existence of depressed zones of comparatively low gradient far from the sector where the flowrate was measured.

Fig. 3

Contour lines of $p/{p}_{0}$

2.3 Test Data Interpretation

The inverse problem statement runs as follows: using the measurement data on flow rates ${Q}_{mn}$ (Table 1) it is required to find continuous function describing dependence of the effective permeability versus angle $\theta$. Suppose that $K(\theta )=A+(B-A)\theta /\pi$ (0 $\le \theta \le \pi$) and introduce the objective function

$$ {\Psi }\left( {A,B} \right) = \sqrt {45\mathop \sum \limits_{m = 1}^{5} \mathop \sum \limits_{n = 1}^{9} \left[ {Q\left( {A,B,{ }p_{m} ,t} \right) - Q_{mn} } \right]^{2} } \Bigg/\mathop \sum \limits_{m = 1}^{5} \mathop \sum \limits_{n = 1}^{9} Q_{mn} $$

where $Q$—stationary flowrate, computed from (4), (6) at some$A$,$B$,${p}_{m}$, and ${\varphi }_{n}$ values. The minimum of function $\Psi$, which was determined by the modified conjugate-gradient method (Nazarov et al. 2013), provides solution of the inverse problem, viz., values of $A$ and $B$ coefficients.

Figure 4 demonstrates level lines of the objective function, the toned area is equivalency domain $\Psi \le$ 0.05. It is obvious that $\Psi$ is unimodal, so the stated inverse problem is uniquely solvable. Within up to 10% accuracy the target coefficients: $A=$ 22–23 mD and $B=$ 37–38 mD are in good compliance with permeability values ${k}_{0}$, ${k}_{1}$, and ${k}_{2}$ of separate sections of the test specimen.

Fig. 4

Level lines of objective function $\Psi$

3 Mass Transfer in Borehole Environment

Poroperm properties anisotropy is governed by both specific structural features of a seam and non-homogeneous stress state in well environment. Due consideration should be given to this peculiarity in modeling intended to describe mass transfer processes in the vicinity of borehole.

Let at time moment $t=$ 0 a horizontal formation filled with a multiphase fluid and bounded with impermeable interfaces beds is penetrated to its entire thickness $h$ by a vertical borehole of radius $a$. In the overbalanced drilling case when the initial reservoir pressure ${p}_{s}$ is lower than bottom hole pressure ${p}_{b}$, a flashed zone and mud cake tend to come into being. The poroelastic model describing quasistatic deformation of a reservoir under two-phase fluid filtration includes:

Equilibrium equation

$$ \sigma_{ij,j} = 0; $$

(7)

Hooke’s law

$$ \sigma_{ij} = \lambda \varepsilon \,\delta_{ij} + 2\mu \varepsilon_{ij} - p $$

(8)

Cauchy’s relations

$$ \varepsilon_{ij} = 0.5\left( {u_{i,j} + u_{j,i} } \right) $$

(9)

continuity equation for each phase

$$ \frac{{\partial \left( {\omega S_{n} } \right)}}{\partial t} + {\text{div}}\,\vec{V}_{n} = 0 $$

(10)

Darcy’s law

$$ \vec{V}_{n} = - \frac{{Kk_{n} }}{{\eta_{n} }}{\text{grad}}{\mkern 1mu} \,p $$

(11)

salt transfer equation

$$ \frac{{\partial \left( {\omega CS_{1} } \right)}}{\partial t} + {\text{div}}\left( {C\vec{V}_{1} } \right) = 0; $$

(12)

as well as empirical dependences of porosity $\omega$ versus pressure $p$

$$ \omega = \omega_{0} + \beta p; $$

(13)

permeability $K$ versus effective stress (Nazarova and Nazarov 2018; Nazarova et al. 2019)

$$ K = K_{0} \exp \left( { - \gamma \sigma_{f} } \right) $$

(14)

and growth rate of mud cake thickness $D$ versus flow rate $Q$ (Yeltsov et al. 2012)

$$ 2\pi ah\frac{\partial D}{{\partial t}} = \psi Q, $$

(15)

where ${u}_{i}$, ${\varepsilon }_{ij}$, and ${\sigma }_{ij}$—components of displacement vector, strain and stress tensors; $i,j=r,\theta$; $(r,\theta )$—cylindrical coordinates; ${\delta }_{ij}$—Kronecker delta; $\lambda ,\mu$—Lame parameters; ${\sigma }_{f}={\sigma }_{ii}/3-p$; ${S}_{n}$—saturation of phase $n$ (here $n=1$ corresponds to drilling mud filtrate, $n=2$—oil, ${S}_{1}+{S}_{2}=1$); $C$—salinity; ${k}_{n}={S}_{n}^{{\alpha }_{n}}$—relative phase permeability, ${\alpha }_{n}$—empirical parameters; ${\overrightarrow{V}}_{n}$—seepage velocity; ${\eta }_{n}$—viscosity; $\beta$ and $\gamma$—fluid and reservoir rock compressibilities $\psi =\xi /(1-\xi )(1-{\omega }_{m})$; ${\omega }_{m}$—porosity of mud cake; $\xi$—clayey content in drill mud;

$$ Q = ah\mathop \smallint \limits_{0}^{2\pi } \left( {\vec{V}_{1} \left( {a,\theta ,t} \right)} \right)_{r} d\theta . $$

System (7)–(15) is solved in domain $\{a\le r\le R, 0\le \theta \le \pi \}$, with formulation of initial

$$ p\left( {r,\theta ,0} \right) = p_{s} ,\qquad S_{1} \left( {r,\theta ,0} \right) = S_{0} ,\qquad C\left( {r,\theta ,0} \right) = C_{0} , \qquad D\left( 0 \right) = 0 $$

(16)

and boundary

$$\begin{aligned} \sigma_{rr} \left( {a,\theta } \right) = p_{b} ,&\qquad \sigma_{rr} \left( {R,\theta } \right) = (q_{1} \cos^{2} \theta + q_{2} \sin^{2} \theta )\sigma_{V}\\ &\sigma_{r\theta } \left( {a,\theta } \right) = \sigma_{r\theta } \left( {R,\theta } \right) = 0 \end{aligned}$$

(17)

$$\begin{aligned} &p\left( {a,\theta ,t} \right) = p_{b} ,\,\,\,\,p\left( {a,\theta ,t} \right) = p_{b} ,\\&S_{1} \left( {a,\theta ,t} \right) = S_{m} ,\,\,\,\,S_{1} \left( {R,\theta ,t} \right) = S_{0} ,\\ &C\left( {a,\theta ,t} \right) = C_{m} ,\,\,\,\,C\left( {a,\theta ,t} \right) = C_{m}\end{aligned}$$

(18)

conditions (line $\theta =0,\pi$—symmetry axis), where $R$ is size of well influence zone ($a\ll R$), ${S}_{0}$, ${C}_{0}$—water saturation and salinity in an intact reservoir,${S}_{m}$ and ${C}_{m}$ are water saturation and salinity of drill mud, ${q}_{1}$ and ${q}_{2}$ are lateral pressure coefficients corresponding to maximum ${\sigma }_{\mathrm{max}}$ and minimum ${\sigma }_{\mathrm{min}}$ horizontal stresses in the external field; ${\sigma }_{V}={\rho }_{1}gH$ is lithostatic stress at reservoir occurrence depth $H$, ${\rho }_{1}$ is average overlaying rock density.

The stated boundary-value problem, implemented by the hybrid numerical method (Nazarova et al. 2020), enabled to develop the rapid computing algorithm at every time moment in the same grid (similar to grid in Fig. 2b); system (7)–(9) and (17) was solved by the finite element method (original code (Nazarova and Nazarov 2009), while (10)–(16), (18) was solved by the finite-difference method of alternating directions) (Samarskii 2001).

Let exemplify the effect of “induced” anisotropy of permeability on distribution of electrohydrodynamic fields in borehole environment. The computation was based on the following model parameters matching to an actual production interval of an operating well, Kogalym oil deposit, West Siberia (Yeltsov et al. 2014): $H=$ 2518 m, ${\rho }_{1}=$ 2500 kg/m³, $g=$ 9.81 m/s², $\lambda =\mu =$ 20 GPa, $a=$ 0.1 m, $R=$ 2 m, ${K}_{0}=$ 34 mD, ${\eta }_{1}=$ 0.001 ${\text{Pa}} \cdot {\text{s}}$, ${\eta }_{2}=$ 0.004 ${\text{Pa}} \cdot {\text{s}}$, ${\alpha }_{1}=$ 2, ${\alpha }_{2}=$ 3, $\beta ={10}^{-9}$ 1/Pa, $\gamma ={10}^{-10}$ 1/Pa, $\xi =$ 0.45, ${\omega }_{m}=$ 0.2, ${q}_{1}=$ 0.7, ${q}_{2}=$ 0.62, ${p}_{s}=(1+{q}_{1}+{q}_{2}){\sigma }_{V}/3$ (Khristianovich 1989), ${p}_{b}=$ 1.05 ${p}_{s}$, ${C}_{0}=$ 1 g/l, ${C}_{m}=$ 20 g/l, ${S}_{0}=0.3$, ${S}_{m}=0.9$.

Figure 5 demonstrates distribution of water saturation ${S}_{1}$, salinity $C$ and true resistivity $Z$, calculated from Archie formula (Archie 1942) in modification (Yeltsov et al. 2012)

$$ Z = \frac{A}{{\omega^{2} C(S_{0} + S_{1} )^{2} }} , $$

Fig. 5

Distribution of salinity $C$ (a), water saturation ${S}_{1}$ (b) and true resistivity $Z$ (c)

($A$—empiric constant) at time moment $t=2$ days. It is obvious that minor difference between horizontal stress components in the external field leads to qualitative alteration in distribution of information-bearing parameters applicable to inverse logging data. In particular, drill mud penetration values in direction of ${\sigma }_{\mathrm{max}}$ action are 15–20% higher than similar magnitudes in orthogonal direction.

This factor should be taken into account to inverse the evidence obtained by advanced borehole geoelectrical methods (Yeltsov et al. 2014; Garcia et al. 2019; Bennis and Torres-Verdin 2019).