Keywords

1 Introduction

Since its appearance in China in December 2019, the coronavirus disease 2019 (COVID-19) has been subject to intensive activities in the field of mathematical modelling [1,2,3,4,5]. Modelling is done to allow a better understanding of the evolution dynamics of the disease. Several models have been proposed, some to describe the dynamics, other to estimate the parameters, but all aim at allowing decision makers to take appropriate measures in dealing with the epidemic. In fact, mathematical models play a very important role in the understanding of the spread of several diseases. The advent of COVID-19 is so another opportunity for mathematical modelers to translate the results of their modelling into clear terms for decision makers. The majority of Western countries have relied on mathematical models to predict the spread of the disease in their countries [1, 5,6,7,8]. This has allowed them to take measures ranging from hand washing to general containment. Similarly, on the African continent, many leaders rely on mathematical models for the management of epidemic such as COVID-19.

In Burkina Faso, a commitee of experts comprising various competences including mathematicians was set up as soon as the first case of coronavirus disease was reported in the country in March 2020. Since this date, the authorities’ concern was to know the dynamics of the pandemic and to see how to act to eliminate it. In doing so, several exchanges took place with public health doctors. It was at the end of these discussions that it was decided to develop a model which highlights the compartments of infected persons reported and not reported. Also it was a question of putting the accent on the high-risk hospitalized and quarantine or low-risk hospitalized. This explains the adoption of such a model study in this paper. The model concerning this paper make it possible to do projections and especially to see the effects of confinements, quarantines and cover fires in the country. Finally, the parameters used in this model for the simulations are parameters specific to the health context of Burkina Faso.

The difference between the former model (see [2]) and this one is that the new model takes into account some concerns of hospital practitioners and health epidemiologists from the Burkina Faso National Health Commission against COVID-19, people, of people hospitalized with serious health situation and death cases. We consider that dead people can contaminate health care workers or their loved ones when handling the bodies.

The paper is organized along 6 Sections. In the Sect. 2, we show the mathematical model, Sect. 3 is devoted to the basic properties. We present real daily data given by Burkina Faso National Health Commission against Coronavirus Disease 2019 (COVID-19) in Sect. 4 and we make simulations according to these data in Sect. 5. In Sect. 6 we end by a conclusion.

2 Mathematical Model

The model built for the coronavirus disease 2019 (COVID-19) in this paper is a SEIRD model, taking into account Susceptibles cases(S), Exposed persons (E), Infected individual (I), Recovered patients (R) and the Dead patients (D). Based on the epidemiological characteristics of COVID-19, the SEIRD model and its variants are more appropriate to study the dynamics of this disease, which is caused by the SARS-Cov-2. The output of the mathematical model gives the following transfer diagram (Fig. 1):

Fig. 1
figure 1

Transfer diagram for the mathematical model of COVID-19

Full size image

According to Fig. 1, we obtain the following system of ten differential equations describing the dynamics of the disease.

Here, we define the variables as follow:

  • S(t) (Susceptible) represents persons not infected by the disease pathogen.

  • E(t) (Exposed) refers to persons who are in the incubation period after being infected by the disease pathogen, and haves no visible clinical signs. These individuals could infect other people but with a lower probability than people in the infectious compartments. After the incubation period, these persons move to one of the Infectious states. In this model, it can be seen has contact persons

  • I(t) (Infectious) refers the number of persons who are beginning to develop clinical signs, these persons are symptomatic infectious,

  • I d(t) refers to Infectious; that is persons who can infect other people, are developing clinical signs and therefore will be detected and reported by authorities (when arriving in the H R or the H d compartments). After this period, the people in this compartment are taken in charge by sanitary authorities and we classify them as Hospitalized patients. It is the reported infectious cases.

  • I u(t) is the number of unreported symptomatic infectious individuals (i.e., symptomatic infectious with mild symptoms) at time t.

  • Persons hospitalized or quarantined at home (but detected and reported by the authorities) who will recover (denoted by H R): These persons are in hospital (or quarantined at home) and can still infect other people. At the end of this state, these persons move to the Recovered state. It is the low-risk hospitalized cases.

  • Hospitalized people who are going to die (denoted by H d): These persons are hospitalized and can still infect other people. At the end of this state, these persons move to the death state. It is the high-risk hospitalized cases.

  • \(R_{I_u}\) Recovered persons from unreported infectious cases (denoted by \(R_{I_u}\)): These persons have survived the disease, are no longer infectious and have developed a natural immunity to the disease pathogen.

  • \(R_{I_d}\) Recovered persons from reported infectious cases (denoted by \(R_{I_d}\)): These persons have survived the disease, are no longer infectious and have developed a natural immunity to the disease pathogen.

  • D Dead persons (denoted by D): These persons have not survived the disease.

  • N is the number of people within the territory before the start of the pandemic.

The transcription of the transfer diagram gives the following mathematical system:

$$\displaystyle \begin{aligned} \begin{cases} \dot{S}=- \dfrac{S(t)}{N}\bigg( m_E(t) \beta_E E(t)+m_I(t) \beta_I I(t)+\beta_{I_u} m_{I_u}(t) I_u(t) +\beta_{I_d} m_{I_d}(t) I_d(t) \bigg)\\ \ \ \ \ \ \ \ \ \ \ - \dfrac{S(t)}{N}\bigg(\beta_{H_R} m_{H_R}(t) H_R(t) +\beta_{H_d} m_{H_d}(t) H_d(t)\bigg),\\ {} \dot{E}=\dfrac{S(t)}{N}\bigg( m_E(t) \beta_E E(t)+m_I(t) \beta_I I(t)+\beta_{I_u} m_{I_u}(t) I_u(t) +\beta_{I_d} m_{I_d}(t) I_d(t)\bigg)\\ \ \ \ \ \ \ \ \ \ \ +\dfrac{S(t)}{N}\bigg(\beta_{H_R} m_{H_R}(t) H_R(t) +\beta_{H_d} m_{H_d}(t) H_d(t)\bigg)-\alpha E(t),\\ {} \dot{I}=\alpha E(t)-\beta I(t),\\ {} \dot{I_d}=\beta_1 \beta I(t)-\theta I_d(t),\\ {} \dot{I_u}=\beta_2\beta I(t)-\eta I_u(t),\\ {} \dot{H_R}=\omega_1\theta I_d(t)-\rho H_R(t),\\ {} \dot{H_d}=\omega_2\theta I_d(t)+(1-\xi)\rho H_R-\gamma H_d(t)-\nu H_d,\\ {} \dot{R_{I_d}}=\xi\rho H_R(t)+\nu H_d,\\ {} \dot{R_{I_u}}=\eta I_u(t),\\ {} \dot{D}=\gamma H_d(t). \end{cases} \end{aligned} $$
(1)

The initial data of the system is supplemented by

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} S(t_0)=S_0>0,\quad E(t_0)=E_0>0, \quad I(t_0)=I_0>0, \quad I_d(t_0)=0 \quad I_u(t_0)\geq0, \\ \\ H_R(0)=0,\quad H_d(0)=0,\quad R_{I_u}(0)=0, \quad R_{I_d}(0)=0\;\;\;\mathrm{and} \;\;\; D(0)=0. \end{array} \end{aligned} $$
(2)

The time t is in day, the asymptomatic infectious individuals I(t) are infectious for an average time period of 1∕α days. We suppose that the population is constant i.e N = S(t) + E(t) + I(t) + R(t).

We notice that 8th, 9th and 10th equations of system (1) are not coupled with the other equations. So we can solve the first seven equations of the system and compute them after the other three equations. Thus, the system taken into account is the following with seven equations:

$$\displaystyle \begin{aligned} \begin{cases} \dot{S}=- \dfrac{S(t)}{N}\bigg( m_E(t) \beta_E E(t)+m_I(t) \beta_I I(t)+\beta_{I_u} m_{I_u}(t) I_u(t) +\beta_{I_d} m_{I_d}(t) I_d(t) \bigg)\\ \ \ \ \ \ \ \ \ \ \ - \dfrac{S(t)}{N}\bigg(\beta_{H_R} m_{H_R}(t) H_R(t) +\beta_{H_d} m_{H_d}(t) H_d(t)\bigg),\\ {} \dot{E}=\dfrac{S(t)}{N}\bigg( m_E(t) \beta_E E(t)+m_I(t) \beta_I I(t)+\beta_{I_u} m_{I_u}(t) I_u(t) +\beta_{I_d} m_{I_d}(t) I_d(t)\bigg)\\ \ \ \ \ \ \ \ \ \ \ +\dfrac{S(t)}{N}\bigg(\beta_{H_R} m_{H_R}(t) H_R(t) +\beta_{H_d} m_{H_d}(t) H_d(t)\bigg)-\alpha E(t),\\ {} \dot{I}=\alpha E(t)-\beta I(t),\\ {} \dot{I_d}=\beta_1 \beta I(t)-\theta I_d(t),\\ {} \dot{I_u}=\beta_2\beta I(t)-\eta I_u(t),\\ {} \dot{H_R}=\omega_1\theta I_d(t)-\rho H_R(t),\\ {} \dot{H_d}=\omega_2\theta I_d(t)+(1-\xi)\rho H_R-\gamma H_d(t)-\nu H_d. \end{cases} \end{aligned} $$
(3)

3 Basic Properties

In this section, we prove the positivity and the boundedness of the solution of the system (1) with initial conditions defined in (2).

For that, let us state the following lemma.

Lemma 3.1 ([9])

Suppose \(\varOmega \subset {\mathbb {R}}\times \mathbb {C}^n\) is open and \(f_i\in C(\varOmega , \mathbb {R}), \;i=1,\,2\,\cdots ,\, n.\) If \(f_i\vert _{x_i(t)=0,\,X_t\in C_{+0}^n}\geq 0\) , X t = (x 1t, x 2t, ⋯ , x nt), then, \(\phi =(\phi _1,\phi _2,\cdots ,\phi _n)\in C([-\tau , 0],\mathbb {R}_{+0}^n)\) is the invariant domain of the following equations.

$$\displaystyle \begin{aligned} \dfrac{dx_i(t)}{dt}=f_i(t, X_t),\; t\geq \sigma,\; i=1,\,2\,\cdots,\, n; \end{aligned}$$

where \(\mathbb {R}_{+0}^n=\{(x_{1},\,x_{2},\cdots ,\,x_{n}):x_i\geq ,\; i=1,\,2\,\cdots ,\, n.\)

Proposition 3.1

The system (1) is invariant in \(\mathbb {R}_{+}^{10}\).

Proof

Let us write system (1) as

$$\displaystyle \begin{aligned} \dfrac{dX}{dt}=f(X(t)),\;X(0)=X_0\geq0, \end{aligned}$$

so, note that

$$\displaystyle \begin{aligned} \begin{array}{rcl} & &\displaystyle \dfrac{dS}{dt}\vert_{S=0}=0,\\ & &\displaystyle \dfrac{dE}{dt}\vert_{E=0}=\dfrac{S}{N}\bigg( m_I \beta_I I+\beta_{I_u} m_{I_u} I_u+\beta_{I_d} m_{I_d}I_d+\beta_{H_R} m_{H_R} H_R +\beta_{H_d} m_{H_d} H_d\bigg)\geq 0,\\ & &\displaystyle \dfrac{dI}{dt}\vert_{I=0}=\alpha E\geq 0,\quad \dfrac{dI_d}{dt}\vert_{I_d=0}=\beta_1\beta I\geq 0,\\ & &\displaystyle \dfrac{dI_u}{dt}\vert_{I_u=0}=\beta_2\beta I\geq 0,\quad \dfrac{dH_R}{dt}\vert_{H_R=0}=\omega_1\theta I_d\geq 0,\\ & &\displaystyle \dfrac{dH_d}{dt}\vert_{H_d=0}=\omega_2\theta I_d+(1-\xi)\rho H_R\geq 0, \;\mathrm{since}\; \zeta\in]0,1[. \end{array} \end{aligned} $$

From Lemma 3.1, we conclude that system (1) is invariant in \(\mathbb {R}_{+}^{10}\).

Lemma 3.2

The solution of system (1) is bounded in the region

$$\displaystyle \begin{aligned} \varOmega=\{(S, E, I, I_d, I_u, H_R, H_d, R_{I_d}, R_{I_u}, D)\in\mathbb{R}_+^{10}\vert S+E+I+I_d+I_u+H_R+H_d+R_{I_d}+R_{I_u}+D=N\}. \end{aligned}$$

Proof

For system (1), we observe that

\(\dot N=0\), ⇒ N(t) = Cst, ∀t ≥ 0, thus all the solution of system (1) are bounded.

The only equilibrium of the model is the disease free equilibrium (DFE) defined by E DFE = (N, 0, 0, 0, 0, 0, 0, 0, 0, 0) = (S 0, 0, 0, 0, 0, 0, 0, 0, 0, 0).

Proposition 3.2

The basic reproduction number for the model system (1) is defined by

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathcal{R}_{0}& =&\displaystyle \dfrac{1}{\alpha} m_{E}(t)\beta_{E} +\dfrac{1}{\beta}m_{I}(t)\beta_{I}+\dfrac{\beta_{2}}{\eta}m_{I_{u}}(t)\beta_{I_{u}}+\dfrac{\beta_{1}}{\theta} m_{I_{d}}(t)\beta_{I_{d}}+\dfrac{\omega_{1}\beta_{1}}{\rho} m_{H_{R}}(t)\beta_{H_{R}} \\ \end{array} \end{aligned} $$
(4)
$$\displaystyle \begin{aligned} \begin{array}{rcl} & &\displaystyle +\dfrac{\beta_{1}}{\gamma+\nu}(\omega_{2}+\omega_{1}(1-\xi))m_{H_{d}}(t)\beta_{H_{d}} . \end{array} \end{aligned} $$
(5)

Proof

We use the method of next generation matrix in [10] to compute the reproduction number \(\mathcal {R}_{0}\). So we get:

$$\displaystyle \begin{aligned} \mathcal{F}=\left( \begin{array}{c} \mathcal{F}_{1} \\ {} \mathcal{F}_{2} \\ {} \mathcal{F}_{3} \\ {} \mathcal{F}_{4} \\ {} \mathcal{F}_{5} \\ {} \mathcal{F}_{6} \\ \end{array} \right)=\left( \begin{array}{c} \dfrac{S(t)}{N}\left(m_{E}(t)\beta_{E}E(t)+m_{I}(t)\beta_{I}I(t)+m_{I_{u}}(t)\beta_{I_{u}}I_{u}(t)+m_{I_{d}}(t)\beta_{I_{d}}I_{d}(t)\right)\\ +\dfrac{S(t)}{N}\left(m_{H_{R}}(t)\beta_{H_{R}}H_{R}(t)+m_{H_{d}}(t)\beta_{H_{d}}H_{d}(t)\right)\\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array} \right) \end{aligned}$$

and

$$\displaystyle \begin{aligned} \mathcal{V}=\left( \begin{array}{c} \mathcal{V}_{1} \\ {} \mathcal{V}_{2} \\ {} \mathcal{V}_{3} \\ {} \mathcal{V}_{4} \\ {} \mathcal{V}_{5} \\ {} \mathcal{V}_{6} \\ \end{array} \right) =\left( \begin{array}{c} -\alpha E(t)\\ {} \alpha E(t)-\beta I(t)\\ {} \beta_{1}\beta I(t)-\theta I_{d}(t)\\ {} \beta_{2}\beta I(t)-\eta I_{u}(t)\\ {} \omega_{1}\theta I_{d}(t)-\rho H_{R}(t)\\ {} \omega_{2}\theta I_{d}(t)+(1-\xi)\rho H_{R}(t)-\gamma H_{d}(t)-\nu H_{d}(t) \end{array} \right). \end{aligned}$$

We get the Jacobian matrixes of these two functions \(\mathcal {F}\) and \(\mathcal {V}\) as follow.

$$\displaystyle \begin{aligned} F=\mathcal{D}\mathcal{F}_{(E,I)}=\left(\begin{array}{cccccc} \dfrac{\partial \mathcal{F}_{1}}{\partial E} & \dfrac{\partial \mathcal{F}_{1}}{\partial I} & \dfrac{\partial \mathcal{F}_{1}}{\partial I_{u}} & \dfrac{\partial \mathcal{F}_{1}}{\partial I_{d}}& \dfrac{\partial \mathcal{F}_{1}}{\partial H_{R}}& \dfrac{\partial \mathcal{F}_{1}}{\partial H_{d}}\\[0.5cm] \dfrac{\partial \mathcal{F}_{2}}{\partial E}& \dfrac{\partial \mathcal{F}_{2}}{\partial I}& \dfrac{\partial \mathcal{F}_{2}}{\partial I_{u}} & \dfrac{\partial \mathcal{F}_{2}}{\partial I_{d}}& \dfrac{\partial \mathcal{F}_{2}}{\partial H_{R}}& \dfrac{\partial \mathcal{F}_{2}}{\partial H_{d}}\\ {} [0.5cm] \dfrac{\partial \mathcal{F}_{3}}{\partial E}& \dfrac{\partial \mathcal{F}_{3}}{\partial I}& \dfrac{\partial \mathcal{F}_{3}}{\partial I_{u}} & \dfrac{\partial \mathcal{F}_{3}}{\partial I_{d}}& \dfrac{\partial \mathcal{F}_{3}}{\partial H_{R}}& \dfrac{\partial \mathcal{F}_{3}}{\partial H_{d}}\\ {} [0.5cm] \dfrac{\partial \mathcal{F}_{4}}{\partial E}& \dfrac{\partial \mathcal{F}_{4}}{\partial I}& \dfrac{\partial \mathcal{F}_{4}}{\partial I_{u}} & \dfrac{\partial \mathcal{F}_{4}}{\partial I_{d}}& \dfrac{\partial \mathcal{F}_{4}}{\partial H_{R}}& \dfrac{\partial \mathcal{F}_{4}}{\partial H_{d}}\\ {} [0.5cm] \dfrac{\partial \mathcal{F}_{5}}{\partial E}& \dfrac{\partial \mathcal{F}_{5}}{\partial I}& \dfrac{\partial \mathcal{F}_{5}}{\partial I_{u}} & \dfrac{\partial \mathcal{F}_{5}}{\partial I_{d}}& \dfrac{\partial \mathcal{F}_{5}}{\partial H_{R}}& \dfrac{\partial \mathcal{F}_{5}}{\partial H_{d}}\\ {} [0.5cm] \dfrac{\partial \mathcal{F}_{6}}{\partial E}& \dfrac{\partial \mathcal{F}_{6}}{\partial I}& \dfrac{\partial \mathcal{F}_{6}}{\partial I_{u}} & \dfrac{\partial \mathcal{F}_{6}}{\partial I_{d}}& \dfrac{\partial \mathcal{F}_{6}}{\partial H_{R}}& \dfrac{\partial \mathcal{F}_{6}}{\partial H_{d}}\\ \end{array} \right) \end{aligned}$$

and at the point E DFE, we have

$$\displaystyle \begin{aligned} F=\left( \begin{array}{ccccccc} m_{E}(t)\beta_{E} & m_{I}(t)\beta_{I} & m_{I_{u}}(t)\beta_{I_{u}} & m_{I_{d}}(t)\beta_{I_{d}} & m_{H_{R}}(t)\beta_{H_{R}} & m_{H_{d}}(t)\beta_{H_{d}} \\ {} 0 & 0 & 0 & 0 & 0 & 0 \\ {} 0 & 0 & 0 & 0 & 0 & 0 \\ {} 0 & 0 & 0 & 0 & 0 & 0 \\ {} 0 & 0 & 0 & 0 & 0 & 0 \\ {} 0 & 0 & 0 & 0 & 0 & 0 \end{array} \right). \end{aligned}$$
$$\displaystyle \begin{aligned} \mathcal{D}\mathcal{V}_{(E,I)}=\left(\begin{array}{cccccc} \dfrac{\partial \mathcal{V}_{1}}{\partial E} & \dfrac{\partial \mathcal{V}_{1}}{\partial I} & \dfrac{\partial \mathcal{V}_{1}}{\partial I_{u}} & \dfrac{\partial \mathcal{V}_{1}}{\partial I_{d}}& \dfrac{\partial \mathcal{V}_{1}}{\partial H_{R}}& \dfrac{\partial \mathcal{V}_{1}}{\partial H_{d}}\\[0.5cm] \dfrac{\partial \mathcal{V}_{2}}{\partial E}& \dfrac{\partial \mathcal{V}_{2}}{\partial I}& \dfrac{\partial \mathcal{V}_{2}}{\partial I_{u}} & \dfrac{\partial \mathcal{V}_{2}}{\partial I_{d}}& \dfrac{\partial \mathcal{V}_{2}}{\partial H_{R}}& \dfrac{\partial \mathcal{V}_{2}}{\partial H_{d}}\\ {} [0.5cm] \dfrac{\partial \mathcal{V}_{3}}{\partial E}& \dfrac{\partial \mathcal{V}_{3}}{\partial I}& \dfrac{\partial \mathcal{V}_{3}}{\partial I_{u}} & \dfrac{\partial \mathcal{V}_{3}}{\partial I_{d}}& \dfrac{\partial \mathcal{V}_{3}}{\partial H_{R}}& \dfrac{\partial \mathcal{V}_{3}}{\partial H_{d}}\\ {} [0.5cm] \dfrac{\partial \mathcal{V}_{4}}{\partial E}& \dfrac{\partial \mathcal{V}_{4}}{\partial I}& \dfrac{\partial \mathcal{V}_{4}}{\partial I_{u}} & \dfrac{\partial \mathcal{V}_{4}}{\partial I_{d}}& \dfrac{\partial \mathcal{V}_{4}}{\partial H_{R}}& \dfrac{\partial \mathcal{V}_{4}}{\partial H_{d}}\\ {} [0.5cm] \dfrac{\partial \mathcal{V}_{5}}{\partial E}& \dfrac{\partial \mathcal{V}_{5}}{\partial I}& \dfrac{\partial \mathcal{V}_{5}}{\partial I_{u}} & \dfrac{\partial \mathcal{V}_{5}}{\partial I_{d}}& \dfrac{\partial \mathcal{V}_{5}}{\partial H_{R}}& \dfrac{\partial \mathcal{V}_{5}}{\partial H_{d}}\\ {} [0.5cm] \dfrac{\partial \mathcal{V}_{6}}{\partial E}& \dfrac{\partial \mathcal{V}_{6}}{\partial I}& \dfrac{\partial \mathcal{V}_{6}}{\partial I_{u}} & \dfrac{\partial \mathcal{V}_{6}}{\partial I_{d}}& \dfrac{\partial \mathcal{V}_{6}}{\partial H_{R}}& \dfrac{\partial \mathcal{V}_{6}}{\partial H_{d}}\\ \end{array} \right) \end{aligned}$$

and at the point E DFE, we have

$$\displaystyle \begin{aligned} V=\mathcal{D}\mathcal{V}_{(E_{DFE})}=\left( \begin{array}{cccccc} -\alpha & 0 & 0 & 0 & 0 & 0\\ {} \alpha & -\beta & 0 & 0 & 0 & 0 \\ {} 0 & \beta_{1}\beta & 0 & -\theta & 0 & 0 \\ {} 0 & \beta_{2}\beta & -\eta & 0 & 0 & 0 \\ {} 0 & 0 & 0 & -\omega_{1}\theta & -\rho & 0 \\ {} 0 & 0 & 0 & -\omega_{2}\theta & (1-\xi)\rho & -\gamma-\nu \\ \end{array} \right). \end{aligned}$$

Thus, we obtain

$$\displaystyle \begin{aligned} -FV^{-1}= \left( \begin{array}{cc} A & B \\ {} C & D \end{array} \right) \end{aligned}$$

where

$$\displaystyle \begin{aligned} A=-\left(\hspace{-1pt} \begin{array}{c} \dfrac{-1}{\alpha} m_{E}(t)\beta_{E} -\dfrac{1}{\beta}m_{I}(t)\beta_{I}-\dfrac{\beta_{2}}{\eta}m_{I_{u}}(t)\beta_{I_{u}}-\dfrac{\beta_{1}}{\theta} m_{I_{d}}(t)\beta_{I_{d}}-\dfrac{\omega_{1}\beta_{1}}{\rho} m_{H_{R}}(t)\beta_{H_{R}} \\ -\dfrac{\beta_{1}}{\gamma+\nu}(\omega_{2}+\omega_{1}(1-\xi))m_{H_{d}}(t)\beta_{H_{d}} \end{array} \hspace{-1pt}\right) \in \mathcal{M}_{1,1}(\mathbb{R}), \end{aligned}$$
$$\displaystyle \begin{aligned} B=0_{1,6}\in\mathcal{M}_{1,6}(\mathbb{R}),\quad C=0_{5,1}\in\mathcal{M}_{5,1}(\mathbb{R})\quad \mathrm{and}\quad D=0_{5,5}\in\mathcal{M}_{5,5}(\mathbb{R}). \end{aligned}$$

The basic reproduction number is defined as the dominant eigeinvalue of the matrix − FV −1.

Therefore,

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathcal{R}_{0}& =&\displaystyle \dfrac{1}{\alpha} m_{E}(t)\beta_{E} +\dfrac{1}{\beta}m_{I}(t)\beta_{I}+\dfrac{\beta_{2}}{\eta}m_{I_{u}}(t)\beta_{I_{u}}+\dfrac{\beta_{1}}{\theta} m_{I_{d}}(t)\beta_{I_{d}}+\dfrac{\omega_{1}\beta_{1}}{\rho} m_{H_{R}}(t)\beta_{H_{R}} \\ & &\displaystyle +\dfrac{\beta_{1}}{\gamma+\nu}(\omega_{2}+\omega_{1}(1-\xi))m_{H_{d}}(t)\beta_{H_{d}} \end{array} \end{aligned} $$

The basic reproduction number \( \mathcal {R}_{0}\) is defined as the number of cases that one infected person generates on average during his infectious period, within an uninfected population and without any special control measures. This number does not change during the spread of the disease.

The effective reproduction number \( \mathcal {R}_{e}(t)\) is defined as the number of cases that one infected person generates during his infectious period. This effective reproduction number depends on time, therefore, on public policies (it changes during the spread of the disease). Furthermore, \(\mathcal {R}_{e}(t)=\mathcal {R}_{e}-\mathcal {R}_{0}\) at t = 0 and the spread of the disease slows when \( \mathcal {R}_{e}(t)<1\).

Without any public policies,

$$\displaystyle \begin{aligned} m_E(t)=m_I(t)=m_{I_u}(t)=m_{I_d}(t)=m_{H_R}(t)=m_{H_d}(t)=1, \end{aligned}$$

so

$$\displaystyle \begin{aligned} \mathcal{R}_{0}=\dfrac{1}{\alpha}\beta_{E} +\dfrac{1}{\beta}\beta_{I}+\dfrac{\beta_{2}}{\eta}(t)\beta_{I_{u}}+\dfrac{\beta_{1}}{\theta}\beta_{I_{d}}+\dfrac{\omega_{1}\beta_{1}}{\rho}\beta_{H_{R}}+\dfrac{\beta_{1}}{\gamma+\nu}(\omega_{2}+\omega_{1}(1-\xi))\beta_{H_{d}}\end{aligned} $$

and, therefore,

(6)

Using Theorem 2 in [10], the following result is established.

Proposition 3.3

The disease free equilibrium E DFE of he model (3) is locally asymptotically stable if \( \mathcal {R}_{0}<1\) and unstable if \( \mathcal {R}_{0}>1\).

4 Data

In this part, we show real data generated by CORUS, the Burkina Faso National Health Commission against the Coronavirus Disease 2019 (COVID-19). Recall that the first cases were reported in Burkina Faso on March 9, 2020.

In Appendix A, Table 1 represents the daily cumulative number of reported infected cases and Table 2 the daily cumulative reported dead cases.

Table 1 Daily cumulative reported cases data from March 9, 2020 to April 20, 2020 for Burkina Faso by Burkina Faso National Health Commission against the Coronavirus Disease 2019 (COVID-19)
Full size table
Table 2 Daily cumulative reported dead cases data from March 9, 2020 to April 17, 2020 for Burkina Faso by Burkina Faso National Health Commission against the Coronavirus Disease 2019 (COVID-19)
Full size table

5 Numerical Simulations

For the numerical simulations, we focus on the public policies represented in the model (1) by functions \(m_E,\; m_I,\; m_{I_u},\; m_{I_d}, \;m_{H_R}\) and \(m_{H_d}\). From the beginning date of the public policies, we decrease the contact rate, as a result of the various types of measures taken by the public authorities. The effect of these measures can be seen on the spikes of the different types of infectious cases; the spikes decrease according to the degrees of the measures taken. The curve of the contact rate (contact function) is represented in the Fig. 4.

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \gamma(t)& =&\displaystyle m_E(t)=m_I(t)=m_{I_u}(t)=m_{I_d}(t)=m_{H_R}(t)=m_{H_d}(t)\\ {} & =&\displaystyle \begin{cases} 1,\;\; 0\leq t<t_0,\\ {} \gamma_{min0}+(\gamma_0-\gamma_{min0})\exp(-\mu_1(t-t_1)),\;\; t_0\leq t< t_1,\\ {} \cdots \\ {} \gamma_{minq}+(\gamma_q-\gamma_{minq})\exp(-\mu_q(t-t_{q-1})),\;\; t_{q-1}\leq t< \infty, \end{cases} \end{array} \end{aligned} $$
(7)

where γ minq is the minimum contact rate and μ q is the rate at which the contact decreases.

Depending on the public measures taken, μ i increases, so the contact rate γ(t) decreases and it is possible to limit the number of infected persons (see Fig. 4). μ i is chosen in such a way that the simulation for the time interval aligns with the cumulative reported case data. Also, the effective reproduction number \(\mathcal {R}_{e}(t)\) is strongly dependent on the contact function which decreases exponentially by interval as shown in Fig. 5. Thus we are able to predict the future values of the epidemic from the early cumulative reported data. The earlier public policy decisions are made, the better the management of the epidemic. For Burkina Faso, we present the model, first, without any public policy intervention and, secondly with public policies taken by the local government. It is important to observe that the basic reproduction number with the parameters taken for this simulation: \(\mathcal {R}_{0}=\mathcal {R}_{e}(0)=4.5\); this mean that 10 persons infect 45 persons, which is very high. The role of public policies is to reduce this \(\mathcal {R}_{e}\) down to less than one, which will ensure the extinction of the epidemic.

5.1 Situation Without Public Policies

Without any public policies, the situation of the pandemic would be dramatic for the African countries and for Burkina Faso in particular. In fact, as shown in the simulation (see Figs. 2 and 3), 9 millions persons would be infected by the COVID-19 and around 850 thousand would die, that is 9% of infected persons.

Fig. 2
figure 2

Cumulative Infected persons generated by the model

Full size image
Fig. 3
figure 3

Cumulative dead persons generated by the model

Full size image
Fig. 4
figure 4

Contact function

Full size image
Fig. 5
figure 5

Effective reproduction number R e(t) through the time

Full size image

5.2 Situation with Public Policies

Fortunately, in Burkina Faso, as in almost all countries in the world, from the first cases of the disease, a succession of barrier measures were taken, ranging from hand washing, to the closing of schools, and, places of worship and markets, and the establishment of curfews. Consequently, in the following simulations, we have chosen our contact function in such a way that the cumulative number of infected persons (model (1)) fits the data produced by the Burkina Faso National Health Commission against COVID-19.

Figure 5 represents the dynamic of the effective reproduction number and Fig. 4 represents the dynamic of the contact function. These two curves clearly show the effects of three measurements according to their implementation time.

Figure 6 presents the histogram of the daily reported infected cases and the infected and the dead given by the model 1.

Fig. 6
figure 6

Daily evolution of reported cases. The histogram is from real data and the curves from the model

Full size image

6 Conclusion

In this paper, we are proposing a model for the transmission of the coronavirus disease 2019. We calculated the \(\mathcal {R}_{0}\) which is very essential in understanding the disease and we have showed the local stability of the disease free equilibrium DFE. We subsequently adjusted the model to the actual data of the National Health Commission against the coronavirus disease 2019. From this adjustment, we have been able to draw a number of consequences for the further management of the pandemic.

Firstly, from Fig. 5, we can say that the peak of the epidemic was reached in Burkina Faso around April 5, 2020 (Fig. 6).

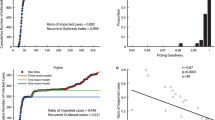
Secondly, the data collected are not sufficiently homogenous, which allow for some reservation on the reliability of the data (Fig. 7). Nevertheless these data constitute a basis to make prescriptions for the dynamics of the disease and especially for removing the barrier measures. We achieved this by fitting the model with the data in Figs. 8, 9 and 10.

Fig. 7
figure 7

Daily evolution of reported cases generated by the model

Full size image
Fig. 8
figure 8

Cumulative reported infected cases, real data (black point) and red curve (from the model)

Full size image
Fig. 9
figure 9

Cumulative reported dead cases. real data (black point) and red curve (from the model)

Full size image
Fig. 10
figure 10

Cumulative reported infected and dead cases. The blacks point are generated by the real data and the curves from the model

Full size image

Finally, we can notice that the effective reproduction number \(\mathcal {R}_{e}\) would be less than 0.5 at April 15, 2020, naturally according to the data fit with the model (1). We therefore think that one week after this date, certain barrier measures could be reviewed, for instance to allow for the opening of markets but maintaining the rule of distance, the opening of schools under conditions which do not allow the spread of the disease, and authorization for many other sectors of active life to be reopen.