Differential-Linear Cryptanalysis from an Algebraic Perspective

Abstract

The differential-linear cryptanalysis is an important cryptanalytic tool in cryptography, and has been extensively researched since its discovery by Langford and Hellman in 1994. There are nevertheless very few methods to study the middle part where the differential and linear trail connect. In this paper, we study differential-linear cryptanalysis from an algebraic perspective. We first introduce a technique called Differential Algebraic Transitional Form (DATF) for differential-linear cryptanalysis, then develop a new theory of estimation of the differential-linear bias and techniques for key recovery in differential-linear cryptanalysis.

The techniques are applied to the CAESAR and LWC finalist Ascon, the AES finalist Serpent, and the eSTREAM finalist Grain v1. The bias of the differential-linear approximation is estimated for Ascon and Serpent. The theoretical estimates of the bias are more accurate than that obtained by the Differential-Linear Connectivity Table (Bar-On et al., EUROCRYPT 2019), and the techniques can be applied with more rounds. Our general techniques can also be used to estimate the bias of Grain v1 in differential cryptanalysis, and have a markedly better performance than the Differential Engine tool tailor-made for the cipher. The improved key recovery attacks on round-reduced variants of these ciphers are then proposed. To the best of our knowledge, they are thus far the best known cryptanalysis of Serpent, as well as the best differential-linear cryptanalysis of Ascon and the best initialization analysis of Grain v1. The results have been fully verified by experiments. Notably, security analysis of Serpent is one of the most important applications of differential-linear cryptanalysis in the last two decades. The results in this paper update the differential-linear cryptanalysis of Serpent-128 and Serpent-256 with one more round after the work of Biham, Dunkelman and Keller in 2003.

This work was supported by the National Natural Science Foundation of China (Grant No. 61672516 and 61872359), the National Key R&D Program of China (Grant No. 2020YFB1805402), and the Youth Innovation Promotion Association of Chinese Academy of Sciences.

1 Introduction

Differential cryptanalysis and linear cryptanalysis are the two best-known techniques for cryptanalysis of block ciphers. Differential-linear attack [LH94, BDK02] is a chosen plaintext two-stage technique of cryptanalysis in which the first stage is covered by differential cryptanalysis, which ensures propagation of useful properties midway through the block cipher. The second stage is then performed from the middle of the cipher to the ciphertext using linear cryptanalysis. The technique was discovered by Langford and Hellman [LH94] and demonstrated on the example of 8-round DES.

Theoretically, the differential-linear attack can be considered as a truncated differential or a multidimensional linear attack, but is an extreme case for both types, which is usually measured by the differential-linear bias. Recently, in 2017, Blondeau, Leander and Nyberg [BLN17] gave an exact expression of the bias under an assumption that the two parts of the cipher are independent, and revisited the previous treatments of differential-linear bias by Biham et al. in 2002–2003 [BDK02, BDK03], Liu et al. in 2009 [LGZL09], and Lu in 2012 [Lu12], and formulated assumptions under which a single differential-linear characteristic gives a close estimate of the bias.

More recently, at EUROCRYPT 2019, Bar-On et al. [BDKW19] showed that in many cases, dependency between two parts of the cipher significantly affects the complexity of the differential-linear attack, and might be exploited to make the attack more efficient. The authors of [BDKW19] presented the Differential-Linear Connectivity Table (DLCT) which allows to take into account the dependency between the two subciphers, and to choose the differential characteristic and the linear approximation in a way that takes advantage of this dependency. They then showed that the DLCT can be constructed efficiently using the Fast Fourier Transform, and demonstrated the strength of the DLCT by using it to improve differential-linear attacks on ICEPOLE and on 8-round DES, and to explain published experimental results on Serpent and on the CAESAR finalist Ascon which did not comply with the standard differential-linear framework.

In this paper, we study differential-linear cryptanalysis from an algebraic point of view. In theory, the bias of a differential-linear approximation can be determined by the algebraic normal forms of the output bits, with input bits as variables. Nevertheless, this is computationally infeasible for a cipher. In Sect. 3, we introduce an algebraic and feasible technique called Differential Algebraic Transitional Form (DATF) for differential-linear cryptanalysis, and then develop a new theory of estimation of the differential-linear bias and techniques for key recovery in differential-linear cryptanalysis. The algebraic transitional form (ATF) is similar to the algebraic normal form (ANF), but an algebraic expression in the ANF can be replaced by a transitional variable in the ATF. This ensures the feasibility of calculating the ATF by iteration. With the DATF technique, the ATF of the difference of output bits can be computed round by round, rather than from the derivative of the output function with respect to the input difference. Based on the DATF algorithm, we describe two feasible frameworks for estimating the differential-linear bias. One is efficient and has a moderate accuracy. The other is less efficient, but more accurate. Further we exploit an algorithm for key recovery. Unlike the convention, it is an organic combination of distinguisher searching and key guessing, and thus has an advantage over the existing techniques. We stress that our techniques are purely algebraic and quite different from the previous methods, including the DLCT [BDKW19] and its subsequent work [CKW19, CKL+19] as well as the techniques proposed for ARX ciphers [Leu16, BLT20].

As illustrations, we apply our theory and techniques to three different types of ciphers, the authenticated cipher Ascon [DEMS16], the block cipher Serpent [ABK98], and the stream cipher Grain v1 [HJMM08], respectively in Sect. 4, Sect. 5 and Sect. 6.

Ascon is a family of authenticated encryption and hashing algorithms designed by Dobraunig et al. [DEMS16, DEMS19] that has been selected as the primary choice for lightweight authenticated encryption in the final portfolio of the CAESAR competition and is currently competing in the NIST Lightweight Cryptography competition. In [DEMS15], Dobraunig et al. presented practical differential-linear attacks on up to 5 rounds of Ascon, including a 4-round differential-linear distinguisher. The authors of [DEMS15] stated that while the overall bias of the approximation is expected to be $2^{-20}$ by the theory of the classical differential-linear framework, experiments show that the bias is $2^{-2}$ which is significantly higher. Bar-On et al. [BDKW19] recomputed the bias of the distinguisher using the DLCT and obtained a theoretical bias of $2^{-5}$.

The theory in this paper shows that the bias of this differential-linear approximation is estimated to be $2^{-2.365}$. This value is extremely close to the experimentally obtained bias of $2^{-2}$, and much higher than the theoretical bias of $2^{-5}$ obtained in [BDKW19] using the DLCT. We also show a 5-round differential-linear approximation with a theoretical bias of $2^{-5.415}$ by imposing 9 conditions. Our experiments show that the bias is $2^{-4.54}$, when these conditions are satisfied.

We further propose in Sect. 4 a key recovery attack on 5-round Ascon-128, which is also applicable to Ascon-128a. The attack benefits from the above differential-linear approximation with an experimental bias of $2^{-5.5}$ using less conditions. The data complexity of the attack is on average $2^{26}$, and the expected time complexity is about $2^{26}$. This attack improves the existing differential-linear attack on 5-round Ascon-128 with complexity $2^{36}$ [DEMS15].

Serpent is a 128-bit block cipher designed by Anderson, Biham and Knudsen. It is a finalist in the Advanced Encryption Standard (AES) competition. In the past 20 years, there have been tremendous efforts devoted to cryptanalysis of Serpent, e.g., [BDK03, DIK08, Lu12, Lu15, BLN17, BDKW19]. In 2003, Biham, Dunkelman and Keller [BDK03] presented the first differential-linear attack on 11-round Serpent, using a 9-round differential-linear distinguisher with bias of $2^{-60}$. An improved attack was presented by Dunkelman et al. in [DIK08]. The authors of [DIK08] performed experiments with 4 rounds of Serpent, obtained the bias $2^{-13.75}$ for the 4-round approximation rather than $2^{-15}$, and concluded that the actual bias of the 9-round approximation is $2^{-57.75}$ and not $2^{-60}$. In [BDKW19], Bar-On et al. recomputed the bias of the 4-round differential-linear distinguisher using the DLCT and obtained the value $2^{-13.68}$.

In Sect. 5, we revisit the analysis of the bias of this distinguisher by our theory, and show an estimate of $2^{-13.736}$. This value is closer to the experimental value even than that of [BDKW19]. We conjecture that the gap between the experimental value and our estimate is a statistical error. We further apply the DATF with one more round, and obtain the bias $2^{-17.736}$ for the 5-round distinguisher.

For an 11-round variant of Serpent from round 4 to round 14, we propose in Sect. 5 a key recovery attack with improved time complexities. The data complexity of the attack is $2^{125.7}$ chosen ciphertexts, the time complexity is $2^{125.7}$ memory accesses, and the memory complexity is $2^{99}$ bytes. The success probability of the attack is expected to be more than 99%. As far as we know, this is the first differential-linear attack on 11-round Serpent-128, through nearly 20 years of community efforts since the publication of its first 10-round attack of the same kind in 2003 [BDK03].

As mentioned in [BDKW19], the differential-linear technique yields the best known attacks on the AES finalist Serpent [DIK08, Lu15]. In Sect. 5.3, we nevertheless find that there is a same flaw in the attacks on 12-round Serpent-256 in [DIK08, Lu15] which leads to underestimated time complexity, up to a factor of $2^{16}$ or $2^{20}$ by our analysis, and the existing 12-round attacks are thus worse than a brute-force attack.

In Sect. 5.3, we extend the chosen ciphertext attack on 11-round Serpent to 12 rounds (starting from round 4 and ending at round 15). The attack on 12-round Serpent-256 has the data complexity of $2^{127}$ chosen ciphertexts, time complexity of $2^{251}$ memory accesses, and memory complexity of $2^{99}$ bytes. The success probability of the attack is expected to be more than 77%. To the best of our knowledge, this is the first correct attack on 12-round Serpent as well as the best known cryptanalysis on Serpent, almost 20 years after Biham, Dunkelman and Keller presented the first 11-round attack of different kind in 2001 [BDK01] and the first 11-round attack of the same kind in 2003 [BDK03].

The stream cipher Grain v1, proposed by Hell et al. [HJMM08], is an eSTREAM finalist in the hardware profile. At ASIACRYPT 2010, Knellwolf et al.  [KMN10] proposed conditional differential attacks on NFSR-based cryptosystems, and applied the attack to Grain v1 with 104 rounds. Since the seminal work of [KMN10], there are a lot of efforts working towards the conditional differential attacks on Grain v1, e.g., [Ban14, Ban16, MTQ17, LG19]. In the literature, the largest number of initialization rounds of Grain v1 that can be attacked is 120, proposed by Li and Guan [LG19] using a conditional differential approximation with an experimental bias $2^{-12.8}$.

In Sect. 6, we apply our theory and techniques to conditional differential attacks on the initialization of Grain v1, and finding an optimized key recovery attack on round-reduced Grain v1. Using the DATF, we revisit the analysis of the bias of the 120-round differential approximation of [LG19], and obtain an estimate of $2^{-13.39}$. This is very close to the experimental value $2^{-12.8}$, and much higher than the estimate of $2^{-18.13}$ obtained by the method called Differential Engine proposed by Banik [Ban14]. Further, a new differential with a theoretical bias $2^{-20.77}$ in the output difference of 125 rounds is found for Grain v1, by an exhaustive search over all the input differences up to 4 bits using the DATF. We have verified by experiments that the bias is $2^{-17.4}$. Our estimate of the bias is smaller than the experimental value, but much higher than the estimate $2^{-24.78}$ by the Differential Engine tool. By imposing 13 equations on the key bits and initial value, where 18 expressions of the key bits need to be guessed, we can mount a chosen IV attack to recover 20 key-bit information on 125-round Grain v1, with time complexity of about $2^{57}$, data complexity of $2^{52}$ and negligible memory. The success probability of the attack is expected to be more than 92.5%. To the best of our knowledge, this is thus far the best key recovery attack in practical complexity as well as the best initialization analysis of Grain v1, in the single key setting.

Table 1. The differential-linear and differential bias

The results on the differential-linear bias of Ascon and Serpent and the differential bias of Grain v1 are summarized in Table 1, with the comparisons of the previous results, where CDL means conditional differential-linear (DL) and CD means conditional differential. Compared with the DLCT tool, the DATF techniques can be applied with more rounds for Ascon and Serpent, and provide more accurate estimation of the DL bias. Besides, our techniques can also be applied to differential cryptanalysis. Compared with the Differential Engine method tailor-made for Grain-like ciphers, our techniques are more general and have a much better performance. Compared with the experimental approach, the algebraic techniques are more formalized and intelligent for conditional attacks and, in particular, much faster when the bias is low. This helps us find better conditional approximations for Ascon and Grain v1.

Table 2. Key recovery attacks on Ascon, Serpent, and Grain v1

Our cryptanalytic results of Ascon, Serpent and Grain v1 are summarized in Table 2, with comparisons of the previous attacks. For Ascon, our attack outperforms the previous differential-linear one but not the cube-like attack [LDW17]. For Serpent, to the best of our knowledge, we provide the first correct attack on its 12-round variant, and the first differential-linear attack on its 11-round variant with 128-bit key. The best known theoretical attack on Grain v1 is the fast correlation attack on its full version proposed in [TIM+18], with time complexity of $2^{76.7}$, data complexity of $2^{75.1}$ and memory¹ of about $2^{69}$. This attack targets at state recovery in the keystream generator, while our attack targets at key recovery in the initialization. Moreover, our attack on Grain v1 has practical complexities and has been fully verified by experiments on the real cipher, compared with the impractical complexities of the fast correlation attack which was verified on a toy cipher in [TIM+18].

Fig. 1.

Differential-linear cryptanalysis

2 Differential-Linear Cryptanalysis

Differential-linear cryptanalysis consists of two stages. The first stage ensures propagation of useful properties in the middle of the cipher, which is covered by differential cryptanalysis. The second stage is performed from the middle of the cipher to the ciphertext using linear cryptanalysis.

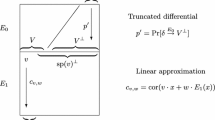
Let E be a cipher which can be described as a cascade of two subciphers $E_0$ and $E_1$, i.e., . Let $\varDelta _{in}$ and $\varDelta _{out}$ be respectively the input and output differences of the differential characteristic for $E_0$, and $\lambda _{in}$ and $\lambda _{out}$ respectively the input and output masks of the linear characteristic for $E_1$, as shown in Fig. 1.

Assume that the differential $\varDelta _{in} \rightarrow \varDelta _{out}$ is satisfied with probability p, and the linear approximation $\lambda _{in} \rightarrow \lambda _{out}$ with probability $1/2 + q$ (or with bias q). In case the differential is not satisfied (probability $1-p$) we assume a random behavior of the parities of the output subset. The probability that a pair with input difference $\varDelta _{in}$ will satisfy $\lambda _{out} \cdot C = \lambda _{out} \cdot C'$ is in that case $p(1/2 + 2q^2) + (1 - p) \cdot 1/2 = 1/2 + 2pq^2$. The data complexity of the differential-linear attack/distinguisher is $O(p^{-2}q^{-4})$.

3 Algebraic Perspective of Differential-Linear Cryptanalysis

In this section, from an algebraic perspective, we discuss the estimation of the differential-linear bias as well as techniques for key recovery in differential-linear cryptanalysis, starting from some basic concepts and facts.

3.1 Basic Concepts and Facts

Let $\mathbb {F}_2$ denote the binary field and $\mathbb {F}_2^n$ the n-dimensional vector space over $\mathbb {F}_2$. An n-variable Boolean polynomial is a mapping from $\mathbb {F}_2^n$ into $\mathbb {F}_2$, which can be uniquely represented as a multivariate polynomial over $\mathbb {F}_2$,

$$ f(x_1,x_2,\cdots ,x_n)=\bigoplus _{c = (c_1, \cdots , c_n)\in \mathbb {F}_2^n}{a_{c}\prod _{i = 1}^{n}{x_i^{c_i}}}, \ a_c \in \mathbb {F}_2, $$

called the algebraic normal form (ANF).

A variable is called isolated if it appears and only appears in the linear part of the ANF of f. For example, $x_1$ is an isolated variable in $x_1\oplus x_2x_3\oplus x_4x_5$.

For a variable $x_i$, the Boolean polynomial $f(x_1,x_2,\cdots ,x_n)$ can uniquely be represented as $f=f'' x_i \oplus f'$ with $f'$ and $f''$ independent of $x_i$, which implies $f'=f|_{x_i=0}$ and $f''=f|_{x_i=1}\oplus f|_{x_i=0}$. The partial derivative of f with respect to the variable $x_i$ is the polynomial $f''$, denoted by $D_{x_i} f$. For example, $D_{x_2} (x_1\oplus x_2x_3\oplus x_4x_5)=x_3$.

For $\varDelta \in \mathbb {F}_2^n$ and an n-variable Boolean polynomial f on X, the derivative of f with respect to $\varDelta$ is the polynomial

$$D_{\varDelta } f(X)=f(X)\oplus f(X \oplus \varDelta ),$$

and the polynomial $f_{\varDelta }$ is defined as

$$f_{\varDelta }(X, x)=f(X\oplus x\varDelta ),$$

where x is a binary variable that we introduce. Note that $f_{\varDelta }$ is a Boolean polynomial on $n+1$ variables. From the above definitions, it is clear that

$$D_x f_{\varDelta } = D_{\varDelta } f.$$

Example 1

Let $f(x_1,x_2,x_3)=x_1 \oplus x_2 x_3 \oplus x_3$ and $\varDelta =(1,1,0)$. On one hand, the derivative of f with respect to $\varDelta$ is

$$\begin{aligned} D_{\varDelta }f&=f(X)\oplus f(X \oplus \varDelta ) =f(x_1,x_2,x_3) \oplus f(x_1\oplus 1,x_2\oplus 1,x_3)\\&=(x_1 \oplus x_2 x_3 \oplus x_3) \oplus ((x_1\oplus 1) \oplus (x_2\oplus 1) x_3 \oplus x_3) =x_3 \oplus 1. \end{aligned}$$

On the other hand, by the definition of $f_{\varDelta }$ we have

$$f_{\varDelta }=f(x_1\oplus x,x_2\oplus x,x_3)=(x_1\oplus x) \oplus (x_2\oplus x) x_3 \oplus x_3=(x_3 \oplus 1) x \oplus x_1 \oplus x_2 x_3 \oplus x_3$$

and the partial derivative of $f_{\varDelta }$ with respect to x is $D_{x}{f_{\varDelta }}=x_3 \oplus 1=D_{\varDelta }f$.

Given a Boolean polynomial f on $X=(x_1,x_2,\cdots ,x_n)$, if the polynomial f can be represented as a polynomial g on $(y_1, y_2, \cdots , y_m)$, where each $y_i$ can be seen as a polynomial on X, to say, $y_i=\phi _i(X)$, then the ANF of g is called in this paper an algebraic transitional form (ATF) of f. The variables $y_1, y_2, \cdots , y_m$ are called transitional variables. Note that the ATF of a Boolean polynomial is not unique. Actually, the polynomial f is a composition of g and $\varPhi =(\phi _1,\phi _2,\cdots ,\phi _m)$, that is, $f(X)=g(\varPhi (X))$, denoted by .

Each polynomial $\phi _i$ can also be represented in terms of the ATF. From this point of view, an iterated cipher can be iteratively represented by the ATF in practical time if it is feasible to compute the ANF of its round function. It can be extended to iteratively computed the ATF of the difference of a cipher. To this end, we further introduce the following notations and basic facts.

For an input difference $\varDelta \in \mathbb {F}_2^n$, $\phi _i(X\oplus x\varDelta )=\phi _i \oplus (D_{\varDelta } \phi _i) x$. By introducing transitional variables $\alpha _i$’s and $\beta _i$’s, we represent $\phi _i(X\oplus x\varDelta )$ as $\alpha _i\oplus x \beta _i$. Denote $\alpha =(\alpha _1,\alpha _2,\cdots ,\alpha _m)$ and $\beta =(\beta _1,\beta _2,\cdots ,\beta _m)$. Then the polynomial $f_\varDelta =f(X\oplus x\varDelta )$ can be represented as

$$g(\alpha \oplus x \beta )=g(\alpha _1\oplus x \beta _1, \alpha _2\oplus x \beta _2,\cdots , \alpha _m\oplus x \beta _m),$$

which is called a differential algebraic transitional form (DATF) of f with respect to $\varDelta$. More exactly, we have

where $\varPsi =(\varPhi ,D_{\varDelta }\varPhi )$. Since $\varPsi$ is independent of x, we obtain

Proposition 1

If an n-variable Boolean polynomial f is a composition of an m-variable Boolean polynomial g and a function $\varPhi$ from $\mathbb {F}_2^n$ into $\mathbb {F}_2^m$, i.e., , then the derivative of f with respect to $\varDelta$ is a composition of the partial derivative of the DATF $g(\alpha \oplus x \beta )$ with respect to x and the function $\varPsi =(\varPhi , D_{\varDelta } \varPhi )$, i.e., , where $\alpha$ and $\beta$ are m-variable vectors and x is a binary variable.

Example 2

Let $\varDelta =(1,1,0,0,0)$ and with $g(y_1,y_2,y_3)=y_1 \oplus y_2 y_3 \oplus y_3$, $\varPhi (x_1,x_2,x_3,x_4,x_5)=(x_1 \oplus x_2 x_3 \oplus x_3, x_2 \oplus x_3 x_4 \oplus x_4, x_3 \oplus x_4 x_5 \oplus x_5)$. The ANF of f is $f(X)=x_1 \oplus x_{{2}}x_{{4}}x_{{5}} \oplus x_{{2}}x_{{5}} \oplus x_4 x_5 \oplus x_5$.

On one hand, the derivative of f with respect to $\varDelta$ is

$$D_{\varDelta }f=f(X) \oplus f(X\oplus \varDelta )=x_{{4}}x_{{5}} \oplus x_{{5}} \oplus 1.$$

On the other hand, we have

$$\begin{aligned} D_{x} g(\alpha \oplus x \beta )&=D_{x} g(\alpha _1\oplus x \beta _1,\alpha _2\oplus x \beta _2,\alpha _3\oplus x \beta _3)\\&=D_{x} ((\alpha _1 \oplus x \beta _1) \oplus (\alpha _2\oplus x\beta _2) (\alpha _3\oplus x\beta _3) \oplus (\alpha _3 \oplus x\beta _3))\\&=D_{x} ((\beta _1 \oplus \beta _2 (\alpha _3\oplus \beta _3)\oplus \alpha _2\beta _3\oplus \beta _3)x \oplus \alpha _1 \oplus \alpha _2\alpha _3 \oplus \alpha _3)\\&=\beta _1 \oplus \beta _2 (\alpha _3\oplus \beta _3)\oplus \alpha _2\beta _3\oplus \beta _3. \end{aligned}$$

Computing $D_{\varDelta } \varPhi = (x_3 \oplus 1,1,0)$ and substituting $(\alpha ,\beta )$ with $\varPsi =(\varPhi , D_{\varDelta } \varPhi )$, e.g., $\beta _1=x_3 \oplus 1,\beta _2=1,\beta _3=0$ and $\alpha _3=x_3 \oplus x_4 x_5 \oplus x_5$, it gives

3.2 Calculation of the Differential-Linear Bias

In theory, the differential-linear bias can be determined by the algebraic normal forms (ANFs) of the output bits, with input bits as variables. Nevertheless, it is computationally infeasible to compute the ANFs of the output bits of a cipher. To make it feasible, we compute their algebraic transitional forms (ATFs) rather than the ANFs. More exactly, we compute the differential algebraic transitional forms (DATFs) of internal bits as well as output bits of a cipher, and then estimate the differential-linear bias.

For a cipher E, we consider it as a function from $\mathbb {F}_2^n$ into $\mathbb {F}_2^m$. The differential-linear bias corresponding to $(\varDelta _{in}$, $\lambda _{out})$ describes the bias of differential-linear approximation $\lambda _{out} \cdot C \oplus \lambda _{out} \cdot C'=0$, that is, $\lambda _{out} \cdot E(P) \oplus \lambda _{out} \cdot E(P\oplus \varDelta _{in})=0$. Denoting $f=\lambda _{out} \cdot E$ gives $f(X)\oplus f(X\oplus \varDelta _{in})=0$. The bias is determined by the Hamming weight of the partial derivative of $f_{\varDelta _{in}}=f(X+x\varDelta _{in})$ with respect to x. By Proposition 1 we know the derivative of f with respect to $\varDelta _{in}$ can be computed from its DATF.

Now we show how to compute the DATF for an iterated cipher. Given the round function $\texttt {R}$ of the cipher and an input difference $\varDelta _{in}$, the procedure for computing the DATF of the output bits is depicted in Algorithm 1. Note that we only concern the nonlinear operation and thus the first (last resp.) linear layer can be omitted in the procedure if it is performed before (after resp.) the nonlinear operation, and that the key and round keys can be taken as a part of the state that is treated as a vector of variables or polynomials.

For an input binary variable vector X, we first initialize $Y^{(0)}=X\oplus x\varDelta _{in}$ where x is a binary variable. Any instance of $(Y^{(0)}|_{x=0}, Y^{(0)}|_{x=1})$ corresponds to a pair with difference $\varDelta _{in}$ in the convention. Next we compute the algebraic normal form of the output of the first rounds, i.e., $Y^{(1)}=\texttt {R}(Y^{(0)})$. We then rewrite $Y^{(i-1)}$ as $Y'^{(i-1)}\oplus xY''^{(i-1)}$ with both $Y'^{(i-1)}$ and $Y''^{(i-1)}$ independent of x, introduce new variable vectors $\alpha ^{(i-1)}$ and $\beta ^{(i-1)}$, and record the expressions $\alpha ^{(i-1)}=Y'^{(i-1)}$ and $\beta ^{(i-1)}=Y''^{(i-1)}$ in an equation set Q. Noting that in this step we use the “Transitional Rule” described below as the rule for introducing transitional variable. That is, $\alpha ^{(i-1)}\oplus x\beta ^{(i-1)}=\texttt {ATF}(Y^{(i-1)}, x)$. After this we compute the ATF of the output of the i-th round $Y^{(i)}=\texttt {R}(\alpha ^{(i-1)}\oplus x\beta ^{(i-1)})$. Finally, we obtain the ATF of the output $Y^{(r)}$ together with an expression set Q. A diagram of the procedure is depicted in Fig. 2.

• Transitional Rule: For a Boolean polynomial $u=u''x\oplus u'$ with $u'$ and $u''$ independent with the variable x, if $u'$ involves two or more variables, then replace $u'$ with a new transitional variable; if $u''$ involves two or more variables, then replace $u''$ with another new transitional variable. The new expression derived from u is denoted by $\texttt {ATF}(u,x)$, or $\texttt {ATF}(u)$ for short. In other words, for any polynomial w not involving the variable x, we have

  $$\begin{aligned} {\texttt {ATF}(w)}={\left\{ \begin{array}{ll} \text {var}_{w}, &{} \text {if }w \text { involves two or more variables}\\ w, &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

  where $\text {var}_{w}$ is a transitional variable identified by w, and thus ${\texttt {ATF}(w)}$ is a constant or a variable up to a constant. By the rule, we know $\texttt {ATF}(u,x)=\texttt {ATF}(u'')x\oplus \texttt {ATF}(u')$ has at most three variables including x. For a polynomial vector, $\texttt {ATF}$ operates on each component of the vector. This rule ensures that $\texttt {ATF}(f,x)$ is an ATF of f in a very simplified way that keeps x unchanged.

Remark 1

Our experiments show that the DATF techniques perform best when the Transitional Rule is applied before the nonlinear operations. Hereinafter, the rule is thus used before the nonlinear operations by default.

Fig. 2.

Differential algebraic transitional form (Algorithm 1)

The polynomial $Y^{(r)}$ is a DATF of $E=\texttt {R}^{r}$ with respect to $\varDelta _{in}$, and thus $\lambda _{out}\cdot Y^{(r)}$ is a DATF of $f=\lambda _{out}\cdot E$. As analyzed previously, $D_{\varDelta _{in}} f$ can be computed from $D_{x} (\lambda _{out}\cdot Y^{(r)})=\lambda _{out}\cdot D_{x} Y^{(r)}$ and Q.

The Complexity of Algorithm 1. Let $t_{\texttt {R}}$ be the complexity of computing the ANF of the round function R, and d the algebraic degree of $\texttt {R}$. The dominant step is Line 9 in the loop. Usually, after a few rounds, all the components of $Y'^{(i)}$ and $Y''^{(i)}$ involve at least two variables due to the propagation of both the value and difference. By the transitional rule, each component of the vectors $\alpha ^{(i)}$ and $\beta ^{(i)}$ is set to a transitional variable. Then the complexity for computing the ATF of $\texttt {R}(\alpha ^{(i)}\oplus x\beta ^{(i)})$ is at most $2^{d} t_{\texttt {R}}$. So the complexity of Algorithm 1 is $\mathcal {O}(2^{d}rt_{\texttt {R}})$ in the worst case. Taking d and r as small constants, the complexity is then $\mathcal {O}(t_{\texttt {R}})$. It is feasible to compute the algebraic expression of $\texttt {R}(\alpha ^{(i)}\oplus x\beta ^{(i)})$ if it is feasible to compute the ANF of the round function $\texttt {R}$ with small degree. This is the case for most iterated ciphers without addition operations.

Next we show how to estimate the differential-linear bias. Given the ATF of the output $Y^{(r)}$ and the expression set Q generated by Algorithm 1, we target at estimating the differential-linear bias of the parity of the output pair with linear mask $\lambda _{out}$. First we compute the ATF of the parity $e=\lambda _{out}\cdot Y''^{(r)}$, where $Y''^{(r)}=D_{x} Y^{(r)}$ is the partial derivative of $Y^{(r)}$ with respect to x. Note that the bias will be 0 if there is an isolated variable in the ATF of e, assuming that all the variables follow uniform distribution and are independent of each other. Therefore, we compute the bias of the polynomial obtained by removing all the isolated variables from the ATF of e. For the sum of the isolated variables, we substitute the expressions Q and obtain a new polynomial. Then we update e with this new polynomial, and deal with this polynomial iteratively until it is zero. By the piling-up lemma, we finally obtain the bias $\varepsilon$. The whole procedure is depicted as Algorithm 2.

In Algorithm 2, we use a procedure $\texttt {Bias}()$ to compute the bias given an algebraic expression in binary variables, in which another procedure Separate() is used to separate the expression as a sum of m polynomials that have no common variables. For a polynomial that could not be separated, if it involves a small number of variables, e.g., 20, we can easily compute the bias from its Hamming weight; otherwise, we guess the values of the variables one by one, and apply $\texttt {Bias}()$ repeatedly until all the polynomials have a small number of variables.

Lemma 2

Given the ATF of f, if the variables are independent and identically distributed, then the output of $\texttt {Bias}(f)$ gives the bias of f.

Proof

Let $\varepsilon _{f}$ be the bias of f, and it needs to prove $\varepsilon _{f}=\texttt {Bias}(f)$. Since $f=\sum _{i=1}^{m} f_i$ after the first step Separate(f) and $f_i$’s are independent (because their variables are disjoint and independent), we have $\varepsilon _{f}=2^{m-1}\varepsilon _{f_1}\varepsilon _{f_2}\cdots \varepsilon _{f_m}$ by the piling-up lemma. This is calculated by $2^{m-1}\texttt {Bias}({f_1})\texttt {Bias}({f_2})\cdots \texttt {Bias}({f_m})$ in Line 17 of the procedure. Therefore, it is sufficient to prove $\varepsilon _{f}=\texttt {Bias}(f)$ for the case $m=1$. This is clearly true when the number n of variables is small. The rest can be proved by induction. Suppose that it is true that $\varepsilon _{f}=\texttt {Bias}(f)$ for any f with at most $n-1$ variables. Let v be a variable of f. Since $\frac{1}{2}+\varepsilon _{f}={\text {Pr}}(v=0)\cdot (\frac{1}{2}+\varepsilon _{f|_{v=0}})+{\text {Pr}}(v=1)\cdot (\frac{1}{2}+\varepsilon _{f|_{v=1}})$, we have

$$\begin{aligned} \varepsilon _{f}&={\text {Pr}}(v=0)\cdot \varepsilon _{f|_{v=0}}+{\text {Pr}}(v=1)\cdot \varepsilon _{f|_{v=1}} \end{aligned}$$

(3.1)

and according the variable distribution and the inductive assumption it implies

$$\varepsilon _{f}=\frac{1}{2}\varepsilon _{f|_{v=0}}+\frac{1}{2}\varepsilon _{f|_{v=1}}=\frac{1}{2}\texttt {Bias}(f|_{v=0})+\frac{1}{2}\texttt {Bias}(f|_{v=1})=\texttt {Bias}(f).$$

Since the ATF of the parity with respect to the output linear mask $\lambda _{out}$ is $e=e^*+e_l$ with $e^*=e-e_l$ and $e_l$ sharing no common variables, where $e_l$ is the sum of the isolated variables of e, the bias of e is twice the product of the biases of $e^*$ and $e_l$. Substituting the expressions in Q into $e_l$ gives a new Boolean polynomial, and its bias can be computed in a similarly way. From this observation, the following statement can be derived.

Theorem 3

Assuming that all the variables of $e^{*}$’s in Algorithm 2 are independent and identically distributed, the output $\varepsilon$ of Algorithm 2 is the bias of the differential-linear approximation $\varDelta _{in}\rightarrow \lambda _{out}$.

Proof

As the previous analysis of Algorithm 1, we know $Y^{(i)}$ is a DATF of $\texttt {R}^{i}$ with respect to $\varDelta _{in}$, and thus $\lambda _{out}\cdot Y^{(r)}$ is a DATF of $f=\lambda _{out}\cdot \texttt {R}^{r}$. By Proposition 1, $D_{x} (\lambda _{out}\cdot Y^{(r)})=\lambda _{out}\cdot D_{x} Y^{(r)}=e$ is an ATF of $D_{\varDelta _{in}} f$. Suppose that Line 5 executes t and only t times in the algorithm. Let $e_l^{(i)}$ be the polynomial $e_l$ after i executions of Line 5, and $e^{(i)}$ the polynomial obtained by substituting the expressions Q into $e_l^{(i)}$. Then $D_{\varDelta _{in}} f$ can be represented as $e^{*}+\sum _{i=1}^{t-1}e^{*(i)}+e^{(t)}$, where $e^{*}=e-e_l^{(1)}$ and $e^{*(i)}=e^{(i)}-e_l^{(i+1)}$. Since Line 5 repeates only t times, we have $e^{(t)}=0$ and thus $D_{\varDelta _{in}} f$ is represented as $e^{*}+\sum _{i=1}^{t-1}e^{*(i)}$, in which the expressions $e^{*}$ and $e^{*(i)}$’s have independent variables under the assumption of the theorem. By the piling-up lemma and Lemma 2, the bias of $D_{\varDelta _{in}} f$ is equal to $2^{t-1}\texttt {Bias}(e^{*})\prod _{i=1}^{t-1}\texttt {Bias}(e^{*(i)})$, which is the output $\varepsilon$ of Algorithm 2.

The Complexity of Algorithm 2. The complexity of Line 5 in the loop dominates the complexity, that is, the computation of $\texttt {Bias}(e^{*})$. The complexity of $\texttt {Bias}(e^{*})$ is at most $2^{m^{*}}$, where $m^{*}$ is the maximum cardinality of the variable sets of the polynomials in $\texttt {Separate}(e^{*})$. So the complexity of Algorithm 2 is $\mathcal {O}(2^{m})$ in the worst case, where m is the maximum of $m^{*}$. In the case for most iterated ciphers without addition operations, especially for lightweight ciphers using small S-boxes, m is small so that the algorithm is practical. In particular, when Line 5 executes only once, m is at most twice the size of S-boxes, since the algorithm treat the output of the last nonlinear operation as the output of the cipher.

In the following we propose a refined method for estimating the differential-linear bias. It follows the main framework of Algorithm 1 and Algorithm 2. The difference is that the assumption of uniform distribution of the transitional variables is removed and replaced by auxiliary computation. The procedure is depicted as Algorithm 3, and the different parts include Line 2, Line 6 and Line 12 (in ). In Line 2, the probability distribution of each input variable is set. In Line 6, the probability distribution of each transitional variable is computed according to the probability distribution of previous variables. In Line 12 of the algorithm, each estimation of bias takes the probability distribution of transitional variables into account. This refined method usually gives a more accurate estimation of the bias, while it requires more computations.

With a probability distribution set $D=\{\Pr (X_i=0)=\frac{1}{2}+\varepsilon _i|X_i \in X, 1\le i\le n\}$, if $X_i$’s are independent, then the probability that f(X) equals zero is

$$\begin{aligned} {\text {Pr}}(f(X)=0)=\sum _{C\in \{X|f(X)=0\}}\prod _{i=1}^{n}(\frac{1}{2}+(-1)^{C_i}\varepsilon _i). \end{aligned}$$

(3.2)

According to (3.2), we execute Step 6 of the algorithm. Adapting the procedure Bias() with (3.2) and (3.1), we execute Step 12. The complexity of the adapted procedure is about n times the complexity of Bias(). Combining Algorithm 1 and Algorithm 2 with these steps, we obtain Algorithm 3.

Similarly as Theorem 3 for Algorithm 2, we conclude the following statement for Algorithm 3. Since the probability distribution of each transitional variable is calculated in the algorithm, the assumption of their distribution is removed.

Theorem 4

Assuming that the variables of the DATF, i.e., $Y^{(i)}$, at each round are independent, the output $\varepsilon$ of Algorithm 3 is the bias of the differential-linear approximation $\varDelta _{in}\rightarrow \lambda _{out}$.

Proof

Since the variables of each round are independent, it can proved by induction on the number i of rounds that all the probability distributions in D are correct according to (3.2). Then under the independence assumption of the variables of the last round, the theorem is proved by the correctness of the modified procedure that adjusts Bias() with (3.2) and (3.1).

The Complexity of Algorithm. Let $T_1$ and $T_2$ respectively be the complexity of Algorithm 1 and Algorithm 2, and n the state size. Then the complexity of Algorithm 3 is at most $T_1+2nT_2$, since the main difference between Algorithm 3 and the combination of Algorithm 1 and Algorithm 2 is generated by (3.2).

3.3 Key Recovery in Differential-Linear Cryptanalysis

To convert a differential-linear distinguisher to a key recovery attack, for a block cipher, we usually guess some key bits, perform partial encryption or decryption, and apply the distinguisher. In the previous work, the distinguisher and the process of key guessing are separately treated. Here we show an algebraic approach to deal with these two processes simultaneously. The approach also applies to iterated ciphers of other types, including stream ciphers and authenticated encryption ciphers.

A crucial stage of this approach is to impose some conditions on the internal bits of the cipher to make uncertain differences determined in the first rounds. Similar techniques were used in conditional differential cryptanalysis [BB93, KMN10] and conditional linear cryptanalysis [BP18], and a similar idea called the partitioning technique was applied to differential-linear cryptanalysis in [Leu16] with an application to Chaskey.

Our precomputation for the key recovery follows the main framework of estimating the differential-linear bias in Algorithm 3. The procedure is depicted as Algorithm 4. For the sake of brevity, here we only explain its differences with Algorithm 3, marked in the procedure. The main difference is that some conditions I are imposed in the first $r_1$ rounds. Note that in each computation of the ANFs and ATFs we reduce the polynomials over the ideal of I, denoted by “$\mod I$”.

After precomputation for the key recovery as shown in Algorithm 4, we obtain a set of expressions $Q_{I}$ and a differential-linear bias $\varepsilon$. Then a system of equations $S=\{f=0|f\in Q_{I}\}$ is derived. Assume that the equations in S are independently and they are always consistent for an arbitrary fixed key. Denote by n the number of equations in S and by m the number of independent expressions of key bits in S. In the key recovery attack, the key is unknown, and thus we need to guess the values of the expressions that involve the key bits. For each guess of these expressions, $O(\frac{1}{\varepsilon ^2})$ pairs of plaintexts with input difference $\varDelta _{in}$ is sufficient to mount a distinguisher. We assume a random behavior of the parities of the output subset for a wrong key. Then the data complexity of the attack is $D=O(\frac{2^{n}}{\varepsilon ^2})$. There are $2^m$ values for the m expressions that need to be guessed in the attack, so the attack time is $T=O(\frac{2^{m}}{\varepsilon ^2})$.

The success probability of the attack is calculated according to analytical results of the success probability of linear attacks (also applicable to differential-linear attacks) in [Sel08, Theorem 2] as below.

Theorem 5

([Sel08]) Denote by $\varPhi$ the cumulative distribution functions of the standard normal distribution. Let $P_S$ be the probability that a linear attack on an m-bit subkey, with a linear approximation of probability p, with N known plaintext blocks, delivers an a-bit or higher advantage. Assuming that the linear approximation’s probability to hold is independent for each key tried and is equal to 1/2 for all wrong keys, we have, for sufficiently large m and N,

$$\begin{aligned} P_S=\varPhi (2\sqrt{N}|p-1/2|-\varPhi ^{-1}(1-2^{-a-1})). \end{aligned}$$

(3.3)

The Complexity of Algorithm 4. Excluding the cost of computing the ATF and bias that is almost the same as Algorithm 3, the running time of Algorithm 4 mainly depends on the cost $t_{I}$ of each computation of $\mod I$. The former is computed as $T_3=T_1+2nT_2$ as previously. Then the complexity of Algorithm 4 is $\mathcal {O}(T_3+nrt_{I})$. Therefore Algorithm 4 is practical when Algorithm 3 is feasible and the size of I is small.

We have implemented Algorithm 4 in SageMath for Ascon, Serpent, and Grain v1. Our experiments show that the algorithm performs well when $r_1$ is small enough (such that the number of independent expressions in I is small), though it is slower than Algorithm 2 and Algorithm 3. It is a good choice to use Algorithm 2 and Algorithm 3 to screen differential-linear approximations. Especially for input difference and output linear mask with small Hamming weights, we can use Algorithm 2 to exhaust all possible differential-linear approximations, and use Algorithm 3 to further screen candidates. In the applications in conditional attacks, we can equip Algorithm 4 with Algorithm 2 for fast computation. As a general method, the algorithm can also be applied with a DL distinguisher obtained by other approaches, in particular when it can not detect a reasonable bias.

4 Applications to Ascon

In this section, we apply our techniques to Ascon for estimating the differential-linear bias, and then propose a key recovery attack to a 5-round variant. Ascon is a family of authenticated encryption and hashing algorithms designed by Dobraunig et al. [DEMS16, DEMS19]. It has been selected as the primary choice for lightweight authenticated encryption in the final portfolio of the CAESAR competition (2014–2019) and is currently competing in the NIST Lightweight Cryptography competition. The analysis in this paper is focused on Ascon-128, and the results are also applicable to Ascon-128a. Note that given the 64 bits of the output, one can invert the last linear layer. Hereinafter we thus consider the cipher without the last linear layer.

4.1 Differential-Linear Bias of Ascon

In [DEMS15], Dobraunig et al. presented practical differential-linear attacks on up to 5 rounds of the Ascon permutation, based on a 4-round differential-linear distinguisher. The authors of [DEMS15] stated that while the overall bias of the approximation is expected to be $2^{-20}$ by the theory of the differential-linear attack, experiments show that the bias is $2^{-2}$ which is significantly higher.

Recently, at EUROCRYPT 2019, Bar-On et al. [BDKW19] recomputed the bias of the distinguisher using the Differential-Linear Connectivity Table (DLCT) and obtained a higher bias of $2^{-5}$. This value is significantly higher than the value $2^{-20}$ which follows from the classical differential-linear framework. On the other hand, it is still much lower than the experimentally obtained bias of $2^{-2}$. The authors of [BDKW19] conjectured that it may be explained by the effect of other differentials and linear approximations.

In the following, we exploit the two algorithms, Algorithm 2 and Algorithm 3, as shown in Sect. 3 to estimate the differential-linear bias for Ascon.

Before applying Algorithm 2, we have to compute the DATF of Ascon by Algorithm 1. We divide the S-box of Ascon into two parts, $p_{S_{L}}$ and $p_{S_{N}}$, and the permutation of Ascon is then divided into two parts, and . The first part of the S-box, $p_{S_{L}}$, is actually a linear transform, as shown below.

In Algorithm 1, we compute the ANF of a half round of p, i.e., $\texttt {R}^{\frac{1}{2}}=p_{A}$, instead of the entire first round. We then set , and for the last round set $\texttt {R}=p_{S_{N}}$. A function of r rounds $p^r$ without the last linear layer is exactly . The 128-bit key and 128-bit nonce are set to 256 binary variables, and the IV is set to a constant defined by the cipher.

For the input difference $\varDelta _{in}$ with differences in bit 63 of $x_3$ and $x_4$, by performing Algorithm 1 with $r=4$, we obtain the ATF of the output $Y^{(4)}$ together with an expression set Q. Note that in Line 3 of Algorithm 1 the number i of rounds ranges from 1 to $r=4$. Applying Algorithm 2 to a single-bit linear mask in bit 9 then gives a differential-linear bias $\varepsilon =2^{-3}$.

Similarly as done in Algorithm 1, in Algorithm 3 we set $\texttt {R}^{\frac{1}{2}}=p_{A}$, , and for the last round $\texttt {R}=p_{S_{N}}$. With the same input difference and output mask, applying Algorithm 3 to 4 rounds of Ascon permutation gives a bias $\varepsilon =2^{-2.365}$. This result slightly improves the estimate of $2^{-3}$ obtained by Algorithm 2, at cost of computations of the probability distribution. It is very close to the experimentally obtained bias of $2^{-2}$, and much higher than the theoretical bias of $2^{-5}$ obtained in [BDKW19] using the DLCT.

4.2 Differential-Linear Cryptanalysis of Ascon

Now we apply the key recovery algorithm, Algorithm 4, to 5-round Ascon-128. By performing Algorithm 4 with $r_1=2$ and $r=5$ over all possible single-bit or two-bit input differences and all possible single-bit output masks, we obtain a differential-linear bias $\varepsilon =2^{-5.415}$ for the input difference $\varDelta _{in}$ with differences in bit 63 of $x_3$ and $x_4$ and the output mask $\lambda _{out}$ in bit 36. The $\texttt {R}$ function is the same as defined previously, and in Line 4 of Algorithm 4 the number i of rounds ranges from 1 to 5. The set of expressions $Q_{I}$ has 9 polynomials, with algebraic degree at most 2. Among these 9 polynomials, 6 of them involve both the key and nonce bits, 2 polynomials involve only a single key bit (bit 63 and 127 respectively), and one involves only two nonce bits (bit 63 XOR bit 127). We impose bit 63 and bit 127 of the nonce to be equal, and run all the possible cases for the other 8 polynomials by experiments on random $2^{28}$ samples for each case. We then derive a bias of $2^{-4.5}$ when all the polynomials equals zero and a reasonable high bias of $2^{-5.5}$ when 5 of them equals zero. The 5 equations are listed as follows, where $k_{i}$ means bit i of the key and $v_{i}$ means bit i of the nonce.

$$\begin{aligned} k_{63}=\,\,&0; \\ k_{127}=\,\,&0; \\ v_{52} =\,\,&k_{12}{}v_{76} + k_{12} + k_{35}{}v_{99} + k_{42}{}v_{106} + k_{45} + k_{52} + k_{99} + k_{109} + k_{116} \\&+ v_{12} + v_{42} + v_{45} + v_{76} + v_{106} + v_{109} + v_{116} + 1; \\ v_{74} =\,\,&k_{10}{}k_{74} + k_{10}{}v_{10} + k_{10} + k_{32}{}k_{96} + k_{32}{}v_{32} + k_{32} + k_{35}{}k_{99} + k_{35}{}v_{35} + k_{35} \\&+ k_{74}{}v_{10} + k_{74} + k_{96}{}v_{32} + k_{96} + k_{99}{}v_{35} + k_{99} \\&+ v_{10} + v_{32} + v_{35} + v_{96} + v_{99} + 1; \\ v_{83} =\,\,&k_{19}{}k_{83} + k_{19}{}v_{19} + k_{19} + k_{41}{}k_{105} + k_{41}{}v_{41} + k_{41} + k_{44}{}k_{108} + k_{44}{}v_{44} + k_{44} \\&+ k_{83}{}v_{19} + k_{83} + k_{105}{}v_{41} + k_{105} + k_{108}{}v_{44} + k_{108} \\&+ v_{19} + v_{41} + v_{44} + v_{105} + v_{108}. \end{aligned}$$

Our experiments show that the differential-linear bias is significantly smaller than $2^{-5.5}$ when one or more equations of the above equations are not satisfied. Fixing the values of $V_{\text {fix}}=\{v_{10}, v_{19}, v_{32}, v_{35}, v_{41}, v_{44}, v_{76}, v_{99}, v_{106}\}$, $2^{15.3+3}$ samples with $v_{52},v_{74},v_{83}$ running over possible values are sufficient to distinguish $k_{63}=k_{127}=0$ from the other cases. For the case $k_{63}=k_{127}=0$, we can also recover 3 extra expressions on key bits. More exactly, in this case, we are able to derive the above 5 equations. We can further set up 9 more equations by flipping the values of $V_{\text {fix}}$ bit by bit. By elimination of nonlinear terms in key bits and after simplification, we obtain 12 linear equations on key bits, that is, $k_{63}=0, k_{127}=0, k_{12}=c_0$, $k_{35}=c_1, k_{42}=c_2, k_{99}=c_3$, $k_{10} + k_{74} = c_{4}, k_{19} + k_{83} = c_{5}, k_{32} + k_{96} = c_{6}$, $k_{41} + k_{105} = c_{7}, k_{44} + k_{108} = c_{8}$, $k_{45} + k_{52} + k_{109} + k_{116} = c_{9}$. Since we know the value $c_4$ of the sum $k_{10} + k_{74}$, we can linearize the quadratic term $k_{10}k_{74}$ to $k_{10}(1+k_{10} + k_{74})=(1+c_4)k_{10}$. By a similar way, the two nonlinear equations can be linearized, and they are linearly independent with the previous equations with a high probability.

Noting that the characteristics of Ascon are rotation-invariant within the 64-bit words, the same method can be used to set up other equations by placing differences in bit i of $x_3, x_4$ and observing the bias at position $(i + 37) \mod 64$. For each i, we can detect whether $k_{i}=k_{i+64}=0$ is satisfied, and then set up 14 linear equations. We can obtain on average 16 i’s with $k_{i}=k_{i+64}=0$, and thus derive $16\times 14=224$ linear equations on key bits, which is sufficient to recover the correct key. We have verified by experiments on thousands of keys that for most cases the linear system has at least 104 linearly independent equations.

The data complexity of the attack is on average $64\times 2^{19.3}+16\times 9\times 2^{17.3}\approx 2^{26}$ bits, and the expected time complexity is about $2^{26}$, for most of the keys. The complexity has been practically verified. This attack significantly improves the existing differential-linear attack on 5-round Ascon-128 with complexity $2^{36}$ [DEMS15]. Our results are summarized in Table 3, with the comparisons of the previous differential-linear attacks.

Table 3. Differential-linear cryptanalysis on Ascon-128

Remark 2

We have made a lot of efforts to apply the method to Ascon for 6 and more rounds, e.g., performing an exhaustive search over all the possible DL approximations with low-weight differences and linear masks, but we did not find any approximation with bias larger than $2^{-64}$. This probably enhances confidence that there does not exist valid DL approximation for 6-round Ascon, at least for low-weight differences and linear masks.

5 Applications to Serpent

In this section, we first give a brief description of the cipher Serpent [ABK98], as well as revisit the estimation of the differential-linear bias in [BDK03] by our techniques, and then propose key recovery attacks to round-reduced Serpent.

5.1 A Brief Description of Serpent

In [ABK98] Anderson, Biham and Knudsen presented the block cipher Serpent. Serpent is an AES finalist. Serpent has a block size of 128 bits and supports a key size of 128, 192 or 256 bits. The cipher is a 32-round SP-network operating on a block of four 32-bit words. Each round is composed of key mixing, a layer of S-boxes and a linear transformation.

In the following, we adopt the notations of [ABK98, BDK03] in the bitsliced version. The intermediate value of the round i is denoted by $\hat{B}_i$ (which is a 128-bit value). The rounds are numbered from 0 to 31. Each $\hat{B}_i$ is composed of four 32-bit words $X_0,X_1,X_2,X_3$. Serpent has 32 rounds, and a set of eight 4-bit to 4-bit S-boxes. Each round function $R_i (i \in \{0, \cdots , 31\})$ uses a single S-box 32 times in parallel. For example, $R_0$ uses $S_0$, 32 copies of which are applied in parallel. Thus, the first copy of $S_0$ takes the least significant bits from $X_0,X_1,X_2,X_3$ and returns the output to the same bits. This can be implemented as a Boolean expression of the 4 words. The set of eight S-boxes is used four times. $S_0$ is used in round 0, $S_1$ is used in round 1, etc. After using $S_7$ in round 7, $S_0$ is used again in round 8, then $S_1$ in round 9, and so on. In the last round (round 31) the linear transformation is omitted and another key is XORed.

5.2 Differential-Linear Bias of Serpent

One of the first applications of the differential-linear cryptanalysis is an attack on the AES finalist Serpent presented by Biham et al. in [BDK03]. The attack is based on a 9-round differential-linear distinguisher with bias of $2^{-60}$ and targets an 11-round variant of the cipher. In [DIK08], Dunkelman et al. performed experiments with reduced round variants of Serpent, and concluded that the actual bias of the approximation is $2^{-57.75}$ and not $2^{-60}$. In [BDKW19], Bar-On et al. recomputed the bias of the distinguisher using the DLCT and obtained the value $2^{-57.68}$.

In this section, we revisit the analysis of the bias of this distinguisher by DATF techniques, and show an estimate of $2^{-57.736}$. This value is extremely close to the experimental value.

Before showing our results, we recall the analysis of [BDK03]. In the following, we adopt the notations of [BDKW19, BDK03], and refer the reader to [BDK03] for the exact difference and mask values. The differential-linear distinguisher of [BDK03] targets a 9-round reduced variant of Serpent that starts with round 2 of the cipher. This variant is denoted by E and decomposed as , where $E_0$ consists of rounds 2–4 and $E_1$ consists of rounds 5–10. For $E_0$, the distinguisher uses a differential characteristic of the form

where $\varDelta _2,\varDelta _3$ are truncated differences. For $E_1$, the distinguisher uses a linear approximation of the form

where all nonzero bits of the mask $\lambda _0$ are included in the bits that are known to be zero in $\varDelta _3$. The authors of [BDK03] found out by experiments that there are other differentials which also predict the difference in the bits of $\lambda _0$. Summing all the differentials, they got that the probability that $\lambda _0\cdot \varDelta _3=0$ is $1/2 + 2^{-7}$, and hence used $p = 2^{-7}$ in their analysis. Using the complexity analysis of the classical differential-linear framework, the authors of [BDK03] concluded that the overall bias of the approximation is $2\times 2^{-7}\times (2^{-27})^2 = 2^{-60}$.

The authors of [DIK08] checked experimentally the first 4 rounds of the differential-linear distinguisher of [BDK03] (that is, a 4-round distinguisher which starts with the difference $\varDelta _0$ and ends with the mask $\lambda _1$) and found that its bias is $2^{-13.75}$, instead of the estimate $2 \cdot 2^{-7} \cdot (2^{-5})^2 = 2^{-16}$. They concluded that the bias of the 9-round distinguisher is $2^{-57.75}$ instead of $2^{-60}$.

The authors of [BDKW19] considered a 3-round variant of Serpent that starts at round 3, denoted it by $E'$, and found that its bias is $2^{-8.68}$. Hence they concluded that the bias of the 4-round distinguisher examined in [DIK08] is $2^{-5}\cdot 2^{-8.68} = 2^{-13.68}$.

We apply Algorithm 3 to the 3-round variant of Serpent $E'$ considered in [BDKW19], with the input difference $\varDelta _{in}=\varDelta _{1}$ and output mask $\lambda _{out}=\lambda _{1}$, and obtain a bias $\varepsilon =2^{-8.736}$. Therefore we conclude that the bias of the 4-round distinguisher examined in [DIK08] is $2^{-5}\cdot 2^{-8.736} = 2^{-13.736}$. This value is extremely close to the experimental value, and slightly more accurate than that of [BDKW19]. Note that the gap is $2^{-20.4}$ while the standard deviation of the bias was $2^{-18.87}$ in the experiment of [DIK08]. We conjecture that the gap between the experimental value and our estimate is a statistical error.

We further apply Algorithm 3 to a 4-round variant of Serpent that starts at round 3, with the input difference $\varDelta _{in}=\varDelta _{1}$ and output mask $\lambda _{out}=\lambda _{2}$, and obtain a bias $\varepsilon =2^{-12.736}$. We thus conclude that the bias of the 5-round distinguisher is $2^{-5}\cdot 2^{-12.736} = 2^{-17.736}$.

5.3 Differential-Linear Cryptanalysis of 11-Round and 12-Round Serpent

In this section, we first point out the flaws in the previous attacks on 12-round Serpent, and then show our improved attack by applying Algorithm 4.

Comments on the Attacks on 12-round Serpent in [DIK08, Lu15]. The authors of [DIK08] found that the S-boxes 2, 3, 19, and 23 do not affect the active bits of $LT^{-1}(\varDelta _0)$, and used this property to extend the 11-round attack to 12 rounds by partially encrypting plaintexts for one more round. Nevertheless, in Step 3(b) of the 11-round attack, the bits input to the 5 active S-boxes in round 1 are partially encrypted, and thus not only the differences but also the values of these bits must be taken into account. Our experiment shows that the S-boxes 2, 3, 19, and 23 affect their values, though they do not affect their differences. This implies that the attack on 12-round Serpent in [DIK08] has an underestimated time complexity, up to a factor of $2^{16}$. The same issue exists in the 12-round attack on Serpent in [Lu15] with time complexity of $2^{244.9}$ encryptions. Instead, they used the property that the S-boxes 1, 8, 10, 30, and 14 of Round 0 do not affect the difference corresponding to the S-boxes 18, 22, 24 and 25 of Round 1, but our experiment shows that all the S-boxes of Round 0 affect their values. This means that the complexity was underestimated by a factor of $2^{20}$. We therefore conclude that these attacks are thus worse than a brute-force attack.²

The Improved Attacks on 11-round Serpent . First, we consider a 6-round variant of Serpent that starts at round 1, using Algorithm 4. The input difference is set to $\varDelta _{in}=\{11, 14, 18, 31, 46, 49, 50, 75, 78, 81, 82, 95, 107, 114, 127\}$, and the output mask $\lambda _{out}=\lambda _{2}$. With $r_1=2$, performing Algorithm 4, we obtain a bias $\varepsilon =2^{-12.736}$. The set of expressions $Q_{I}$ has 16 independent polynomials, 11 of which are generated in round 1. The remaining 5 polynomials are produced in round 2, and the probability that all of these 5 polynomials equal zeros is $2^{-5}$. If we impose the 11 polynomials in round 1 to be zeros, which are all linear, then we obtain a differential-linear distinguisher with a bias of $2^{-5}\cdot 2^{-12.736}=2^{-17.736}$, for 6-round Serpent. By assuming the piling-up lemma to hold for the linear approximation from round 7 to round 10 ($\lambda _2 \xrightarrow [R^4]{q_1=2^{-21}} \lambda _6$), we can obtain a 10-round differential-linear distinguisher with a bias $4\cdot 2^{-17.736} \cdot 2^{-21} \cdot 2^{-21}=2^{-57.736}$, by imposing 11 linear equations on the input bits and key bits in round 1. This is because imposing these equations makes the differential characteristic hold with probability one. Nevertheless, the technique of Sect. 3.3 can not be adopted directly, since the required data exceeds $2^{128}$. As a trade off, the data complexity can be cut down by imposing less equations, at cost of increasing the attack time.

Based on the above observation, we improve the differential-linear attack on 11-round Serpent as follows.

In the attack, we use an input difference with 3 active S-boxes 11, 14, 18:

$$\varDelta _{in}=\{11, 14, 18, 46, 50, 75, 78, 82, 107, 114\},$$

and impose the following 6 equations:

$$\begin{aligned} \begin{aligned} v_{11}&=k_{11};\\ v_{14}&=k_{14} \oplus k_{78} \oplus v_{78} \oplus 1;\\ v_{18}&=k_{18} \oplus k_{50} \oplus v_{50};\\ v_{43}&=k_{43} \oplus k_{107} \oplus v_{107} \oplus 1;\\ v_{46}&=k_{46} \oplus k_{78} \oplus v_{78} \oplus 1;\\ v_{82}&=v_{50} \oplus k_{50} \oplus k_{82} \oplus 1, \end{aligned} \end{aligned}$$

(5.1)

where $v_{i}$ and $k_{i}$ respectively denote bit i of plain-text input to round 1 and the 128-bit subkey $K_1$ of round 1.

The attack is described by the following procedure.

• 1. Select $N = 2^{125.6}$ pairs of plaintexts with difference $\varDelta _{in}$, consisting of $2^{111.6}$ structures, each is chosen by selecting:

• (a) Any pairs of plaintexts $(P_0, P_0\oplus \varDelta _{in})$.

• (b) The pairs of plaintexts $(P_i, P_i\oplus \varDelta _{in})$ for $1\le i\le 2^{14}-1$, where $P_1, \cdots ,P_{2^{14}-1}$ differ from $P_0$ by all the ${2^{14}-1}$ possible (non-empty) subsets of the 6 bits $\{11,14,18,43,46,82\}$, S-box 17 (bits $\{17, 49, 81, 113\}$) and S-box 31 (bits $\{31, 63, 95, 127\}$) in round 1.

• 2. Request the ciphertexts of these plaintext structures (encrypted under the unknown key K).

• 3. For each value of the 6 expressions of $K_1$, choose the $2^{119.6}$ pairs of plaintexts $(P, P\oplus \varDelta _{in})$ with P satisfying (5.1), and perform the following steps for each value of the 8 bits of $K_1$ entering S-box 17 and S-box 31:

• (a) Initialize an array of $2^{56}$ counters to zeros.

• (b) Partially encrypt for each plaintext the S-boxes 17 and 31 in round 1, and find the pairs which satisfy the difference $\varDelta _{0}$ before round 2.

• (c) Given those $2^{119.6}$ pairs, perform for each ciphertext pair: count over all pairs how many times each of the $2^{56}$ possibilities of the 56 bits entering the 7 active S-boxes in round 11 occurs.

• (d) For each guess of the subkey entering these S-boxes, find how many pairs agree on the output subset parity, and how many disagree.

• (e) The highest entry in the array should correspond to the 28 bits of $K_{12}$ entering the 7 active S-boxes in round 11.

• 4. Each trial of the key gives us 42 bits of the subkeys (14 bits in round 1 and 28 bits in round 11), along with a measure for correctness. The correct value of the 40 bits is expected to be the most frequently suggested value.

• 5. The rest of the key bits are then recovered by auxiliary techniques.

The data complexity of the attack is $2^{126.6}$ chosen plaintexts, the time complexity of the attack is $2^{120.6} \cdot 2^{14} \cdot \frac{2}{352} = 2^{127.1}$ encryptions, and the memory complexity is $2^{60}$ bytes for the 11-round attack. Using the formula (3.3), the success probability of the attack is expected to be about 85%. As far as we know, this is the first differential-linear cryptanalysis on 11-round Serpent-128.

Further Improvements on the Attacks on Serpent . In [DIK08], Dunkelman et al. presented a 9-round differential-linear approximation in the inverse direction with a bias of $2^{-54}$, starting from round 13 and ending at round 5, and showed an attack on 11-round Serpent with data complexity of $2^{113.7}$ chosen ciphertexts, time complexity of $2^{137.7}$ memory accesses, and memory complexity of $2^{99}$ bytes.

With the help of Algorithm 4, we can improve the attack on 11-round Serpent in the setting of chosen ciphertext attack, using the techniques as discussed previously. By imposing 12 linear equations on the ciphertext and the bits of subkey $K_{15}$ that are XORed with the 6 active S-boxes in round 14, the 9-round differential-linear approximation in the inverse direction can be extended to 10 rounds with the same bias $2^{-54}$, starting from round 14 and ending at round 5. Then the time complexity can be cut down by a factor of about $2^{-12}$. The improved attack on 11-round Serpent has the data complexity of $2^{125.7}$ chosen ciphertexts, time complexity of $2^{125.7}$ memory accesses, and memory complexity of $2^{99}$ bytes. Using the Formula (3.3), the success probability of the attack is expected to be more than 99%.

Our experiment shows that there is one S-box in round 15 that does not affect either the differences or the values of the 6 active S-boxes in round 14. Based on this observation, we can extend the chosen ciphertext attack on 11-round Serpent to 12 rounds (starting from round 15 and ending at round 4), by guessing the bits of the subkey $K_{16}$ that are XORed with the other 31 S-boxes. The attack on 12-round Serpent-256 has the data complexity of $2^{127}$ chosen ciphertexts, time complexity of $2^{127}\cdot 2^{124}=2^{251}$ memory accesses, and memory complexity of $2^{99}$ bytes. The success probability of the attack is expected to be more than 77%. To the best of our knowledge, this is the first correct attack on 12-round Serpent.

The cryptanalytic results are summarized in Table 4, with the comparisons of the previous differential-linear attacks.

Table 4. Differential-linear cryptanalysis on Serpent

6 Applications to Grain v1

As mentioned earlier, an extreme case of the differential-linear attack can be theoretically considered as a truncated differential attack, see also [BLN17]. The techniques we propose for differential-linear attack can also be used in a (truncated) differential attack. In this section, we apply the previous techniques to differential cryptanalysis of the stream cipher Grain v1, propose key recovery attacks to a round-reduced variant of the cipher, and also revisit the previous differential attacks.

Grain v1 is an NFSR-based stream cipher proposed by Hell et al. [HJMM08]. The cipher is one of the finalists which has been selected in the eSTREAM hardware profile. Grain v1 uses an 80-bit secret key $K=(k_0, k_1, \dots , k_{79})$ and a 64-bit initial value $V=(v_0, v_1, \dots , v_{63})$. It consists of three main building blocks: an 80-bit LFSR, an 80-bit NFSR and a non-linear output function. In this paper, round-reduced variants of Grain v1 with r initialization rounds means the cipher outputs keystream after r rounds and the first keystream bit is $z_r$.

At ASIACRYPT 2010, Knellwolf et al. [KMN10] proposed conditional differential attacks on NFSR-based cryptosystems, with applications to 104-round Grain v1. The framework of this attack is as follows: First, in a chosen plaintext attack scenario, the authors choose a suitable difference that controls difference propagation as many rounds as possible. Second, they impose conditions to prevent the propagation of the difference to the newly generated state bits at first few rounds. Since the bias of the keystream is wanted to be tested, there is an important trade-off between the number of imposed conditions and the number of inputs that can be derived. Finally, depending on whether the conditions involve the initial value only, or also key variables, they obtain distinguishing and partial key recovering attacks. In the literature, the largest number of initialization rounds of Grain v1 that can be attacked is 120, proposed by Li and Guan [LG19] using a conditional differential approximation with an experimental bias $2^{-12.8}$.

6.1 Searching the Differences of Round-Reduced Grain v1

In this section, we exploit the two algorithms, Algorithm 1 and Algorithm 2, as shown in Sect. 3 to estimate the differential-linear bias as well as search for good differences for Grain v1. We use Algorithm 2 rather than Algorithm 3 because of its efficiency. By an exhaustive search over all the differences in at most 4 bits of the initial value, the algorithms find a differential approximation with a theoretical bias $2^{-20.77}$ for 125-round Grain v1. For purposes of comparison, we have applied the existing method called Differential Engine proposed by Banik in [Ban14] to analyzing the bias of the same approximation, and detect a bias of $2^{-24.78}$, which is much smaller. The found input difference is a 2-bit difference, with differences in bit 21 and 46 of the initial value. The output linear mask is located in the first bit of the keystream. Note here that we use modified Algorithm 1 and Algorithm 2 which partially adopt the key recovery techniques of Algorithm 4 with $r_1=50$. From the algorithms we obtain 6 equations represented by the ATFs of the internal bits of Grain v1. The ANFs of the internal bits on the key and initial value are very complicated. Instead of directly converting the ATF into the ANF, we analyze these equations specifically one by one manually.

Using the same method, we revisit the analysis of the conditional differential bias of 120 rounds in [LG19], and obtain a theoretical estimate of $2^{-13.39}$. This is very close to the experimental value $2^{-12.8}$, and much higher than the estimate of $2^{-18.13}$ obtained by the Differential Engine method.

6.2 Analysis of 125-Round Grain v1

Imposing the appropriate conditions is the crucial part of conditional differential attack. It has a trade-off between the two aims: one is to prevent a maximum number of propagation, the other is to find enough IVs that satisfy the conditions. A condition that we assign a certain IV bit to fixed value 0 or 1 is called Type 0 condition, and a condition which is a function of IV bits and key bits is called Type 1 condition.

We now introduce the strategy of our conditions analysis. Since the updated symbolic expressions of Grain v1 are rather complicated after few rounds, it is not easy to analyze conditions. A new variable is used to compute the updated expression and we store the original complex one and factor the condition expression as $f+\sum \limits _{i=1}^nf_ig_i$. Thus it is easier to analyze expressions and impose simple conditions. To obtain enough IVs that satisfy the conditions, we allow Type 1 conditions to have the term $\sum \limits _{i,j}k_iv_j$ and we guess the value of each $k_i$ when we attack 125-round Grain v1. We finally impose 10 Type 0 conditions and 13 Type 1 conditions.

We have performed for 8 random keys each with $2^{40}$ pairs of initial values that satisfy the above equations, and observed a bias of $2^{-17.4}$ with standard deviation of $2^{-20.5}$. Hence we use the bias $2^{-17.4}$ in our attack.

In the above equations, there are in total 20 independent expressions of key bits that need to be guessed in the attack. A primary analysis of the attack gives a data complexity of $2\cdot 2^{13}\cdot 2^{38}=2^{52}$ chosen IVs and a time complexity of $2^{20}\cdot 2^{39}=2^{59}$. Since 20 expressions of key bits are recovered, the full key recovery attack runs in time $2^{60}$. Using the Formula (3.3), the success probability of the attack is expected to be more than 87.7%.

By imposing two extra bits of IV to be zeros, e.g., $v_{47}=v_{50}=0$, two less expressions of the key need to be guessed, and the time complexity of the attack can be cut down to $2^{18}\cdot 2^{39}=2^{57}$, keeping the data complexity unchanged. After recovering the 18 expressions of the key, we can recover the other two key expressions, at cost of additional but negligible time and data. The success probability of the attack is expected to be more than 92.5%. To the best of our knowledge, this is the best known initialization analysis of Grain v1 in the single key setting. The results are summarized in Table 5, with the comparisons of the previous differential attacks. Note here that this table does not include the distinguishing, related key or weak-key attacks.

Table 5. Differential cryptanalysis on Grain v1 in the single key setting

7 Discussions and Open Problems

Here we would like to discuss why our theoretical value is more accurate than that of the DLCT tool [BDKW19] and why the gap behaves different for Ascon, Serpent and Grain v1. As a general case, it has been proven in Theorem 4 that the theoretical value given by Algorithm 3 is accurate, under the assumption that the variables of each round are independent. The number of transitional variables in each round is at most twice the number of updated bits. Thus the assumption is competitive with the traditional assumption of differential-linear cryptanalysis, i.e., round independence within $E_0$ and $E_1$ (see also [BLN17, BDKW19]). For a concrete case, especially in the case of low-weight differences and linear masks, a much weaker assumption might be required in the DATF techniques. Compared with round independence assumption, our assumption for Ascon and Serpent is weaker, which leads to more accurate estimation.

When applying Algorithm 3 to 3- and 4-round Serpent, we have two observations: (1) there are no isolated variables in the ATF of the parity e, that is, Line 12 of Algorithm 3 runs only once; (2) the number of transitional variables is small. The property (1) avoids using the piling-up lemma in Line 12 of Algorithm 3 and makes the assumption become a weaker one. The property (2) makes the assumption easy to be satisfied. They are the reasons that our value is extremely close to the experimental value and why we conjecture that the gap between the experimental value and our estimate is generated by the statistical error.

For the approximation of 4-round Ascon, Line 12 of Algorithm 3 runs twice, and the number of transitional variables is relatively small. This makes the assumption more valid, because a transitional variable in $e-e_l$ relies on the transitional variables of the expression obtained by substituting Q into $e_l$. This may produce an inaccurate estimation when using the piling-up lemma in Line 12. We conjecture this is the reason why there is still a gap in the case of Ascon.

For the application to Grain v1, it is much more complicated. Algorithm 2 rather than Algorithm 3 is applied in the key-dependent setting. For 120 rounds, Line 5 of Algorithm 2 runs twice, that is, the piling-up lemma in Line 5 is used once. For 125 rounds, Line 5 of Algorithm 2 runs three times, that is, the piling-up lemma in Line 5 is used twice. These produce a bigger gap between the assumption and the truth. Moreover, a significant difference between the theoretical analysis and experimental evaluation of the 125-round bias is the number of conditional equations, i.e., 6 equations on the internal bits for the former and 23 conditions in the key and IV bits for the latter.

To conclude, the less the frequency of using the piling-up lemma and the smaller the number of transitional variables related to the approximation, the more accurate the theoretical estimation of its bias would be.

Usage and Limitation. The underlying idea of the DATF techniques is simple and easy implemented in symbolic computation software, e.g., SageMath. All the algorithms are practical for almost iterated cipher without using addition operations reduced to a moderate number of rounds, e.g., Ascon reduced to 4–5 out of 12 rounds, Serpent reduced to 4–6 out of 32 rounds, and Grain v1 reduced to 125 out of 160 rounds. The running time ranges from a few seconds to dozens of minutes, for calculating the bias of one differential-linear or differential trail in SageMath. The techniques are superior to the DLCT in both the accuracy and the length of the trail, which has at least been illustrated in the above instances, and the new techniques proposed in this paper thus can be seen, at least, as a complementary analytical tool to the existing theory of differential-linear cryptanalysis as well as differential cryptanalysis. It seems that the DATF techniques are suitable for analysis of low-weight differential-linear or differential trails and not suitable for linear trails. Thus using the DATF together with the classical differential-linear cryptanalytic methods might be a good choice.

Open Problems and Future Work. In the future, it is worthy of working on the applications of the DATF techniques to more cryptographic primitives. The techniques can be applied to most iterated ciphers but not to ARX ciphers that use addition operations. A natural question is how to adjust the techniques applicable to a cipher using additions. It is also worthy of comparative study between the DLCT and DATF techniques. A main question raised is whether the DATF techniques are more efficient and more accurate than the DLCT tool in the general case. Though our estimates of the bias in the differential-linear approximation are close to the experimental values, there are still some gaps in some cases. These cases happen when the assumption is not satisfied. It is worthy of further study of the DATF techniques as well as exploration of new methods, for analysis of the differential-linear bias under weaker assumptions or without assumptions.

8 Conclusion

In this paper, we have shown a new theory of differential-linear cryptanalysis from an algebraic perspective, including the estimation of the differential-linear bias and techniques for key recovery. As illustrations, we applied it to the CAESAR finalist Ascon, the AES finalist Serpent, and the eSTREAM finalist Grain v1, and gained the most accurate estimation of the bias as well as the best known differential-linear or differential attacks. In particular, the results in this paper update the cryptanalysis of Serpent with one more round. Our technique for key recovery is an organic combination of distinguisher searching and key guessing, and thus outperforms the previous key recovery in differential-linear cryptanalysis. We believe that this new cryptanalytic tool is useful in both cryptanalysis and design of symmetric cryptosystems.