Abstract
In a recent seminal work, Bitansky and Shmueli (STOC ’20) gave the first construction of a constant round zero-knowledge argument for \(\mathbf {NP}\) secure against quantum attacks. However, their construction has several drawbacks compared to the classical counterparts. Specifically, their construction only achieves computational soundness, requires strong assumptions of quantum hardness of learning with errors (QLWE assumption) and the existence of quantum fully homomorphic encryption (QFHE), and relies on non-black-box simulation.
In this paper, we resolve these issues at the cost of weakening the notion of zero-knowledge to what is called \(\epsilon \)-zero-knowledge. Concretely, we construct the following protocols:
– We construct a constant round interactive proof for \(\mathbf {NP}\) that satisfies statistical soundness and black-box \(\epsilon \)-zero-knowledge against quantum attacks assuming the existence of collapsing hash functions, which is a quantum counterpart of collision-resistant hash functions. Interestingly, this construction is just an adapted version of the classical protocol by Goldreich and Kahan (JoC ’96) though the proof of \(\epsilon \)-zero-knowledge property against quantum adversaries requires novel ideas.
– We construct a constant round interactive argument for \(\mathbf {NP}\) that satisfies computational soundness and black-box \(\epsilon \)-zero-knowledge against quantum attacks only assuming the existence of post-quantum one-way functions.
At the heart of our results is a new quantum rewinding technique that enables a simulator to extract a committed message of a malicious verifier while simulating verifier’s internal state in an appropriate sense.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Zero-Knowledge Proof. Zero-knowledge (ZK) proof [GMR89] is a fundamental cryptographic primitive, which enables a prover to convince a verifier of a statement without giving any additional “knowledge” beyond that the statement is true. In the classical setting, there have been many feasibility results on ZK proofs for specific languages including quadratic residuosity [GMR89], graph isomorphism [GMW91], statistical difference problem [SV03] etc., and for all \(\mathbf {NP}\) languages assuming the existence of one-way functions (OWFs) [GMW91, Blu86]. On the other hand, van de Graaf [Gra97] pointed out that there is a technical difficulty to prove security of these protocols against quantum attacks. Roughly, the difficulty comes from the fact that security proofs of these results are based on a technique called rewinding, which cannot be done when an adversary is quantum due to the no-cloning theorem. Watrous [Wat09] considered post-quantum ZK proof, which means a classical interactive proof that satisfies (computational) zero-knowledge property against quantum malicious verifiers, and showed that some of the classical constructions above are also post-quantum ZK. Especially, he introduced a new quantum rewinding technique which is also applicable to quantum adversaries and proved that 3-coloring protocol of Goldreich, Micali, and Wigderson [GMW91] is secure against quantum attacks assuming that the underlying OWF is post-quantum secure, i.e., uninvertible in quantum polynomial-time (QPT).Footnote 1 Since the 3-coloring problem is \(\mathbf {NP}\)-complete, this means that there exists a post-quantum ZK proof for all \(\mathbf {NP}\) languages assuming the existence of post-quantum OWFs.
Round Complexity. An important complexity measure of ZK proofs is round complexity, which is the number of interactions between a prover and verifier. In this aspect, the 3-coloring protocol [GMW91] (and its quantumly secure version [Wat09]) is not satisfactory since that requires super-constant number of rounds.Footnote 2 Goldreich and Kahan [GK96] gave the first construction of a constant round ZK proof for \(\mathbf {NP}\) assuming the existence of collision-resistant hash function in the classical setting. However, Watrous’ rewinding technique does not seem to work for this construction (as explained in Sect. 1.2), and it has been unknown if their protocol is secure against quantum attacks.
Recently, Bitansky and Shmueli [BS20] gave the first construction of post-quantum ZK argument [BC90] for \(\mathbf {NP}\), which is a weakened version of post-quantum ZK proof where soundness holds only against computationally bounded adversaries. In addition to weakening soundness to computational one, there are several drawbacks compared to classical counterparts. First, they assume strong assumptions of quantum hardness of learning with erros (QLWE assumption) [Reg09] and the existence of quantum fully homomorphic encryption (QFHE) [Mah18a, Bra18]. Though the QLWE assumption is considered fairly standard due to reductions to worst-case lattice problems [Reg09, Pei09, BLP13], a construction of QFHE requires circular security of an QLWE-based encryption scheme, which has no theoretical evidence. In contrast, a constant round classical ZK argument for \(\mathbf {NP}\) is known to exist under the minimal assumption of the existence of OWFs [FS90, PW09]. Second, their security proof of quantum ZK property relies on a novel non-black-box simulation technique, which makes use of the actual description of malicious verifier instead of using it as a black-box. In contrast, classical counterparts can be obtained by black-box simulation [FS90, GK96, PW09]. Therefore, it is of theoretical interest to ask if we can achieve constant round quantum ZK by black-box simulation. Third, somewhat related to the second issue, their construction also uses building blocks in a non-black-box manner, which makes the actual efficiency of the protocol far from practical. Again, classical counterparts are known based on black-box constructions [GK96, PW09].
Given the state of affairs, it is natural to ask the following questions:
-
1.
Are there constant round post-quantum ZK proofs for \(\mathbf {NP}\) instead of arguments?
-
2.
Are there constant round post-quantum ZK proofs/arguments for \(\mathbf {NP}\) from weaker assumptions than those in [BS20]?
-
3.
Are there constant round post-quantum ZK proofs/arguments for \(\mathbf {NP}\) based on black-box simulation and/or black-box construction?
-
4.
Are known constructions of constant round classical ZK proofs/arguments for \(\mathbf {NP}\) (e.g., [FS90, GK96, PW09]) secure against quantum attacks if we instantiate them with post-quantum building blocks?
1.1 Our Results
In this work, we partially answer the above questions affirmatively at the cost of weakening the quantum ZK property to quantum \(\epsilon \)-ZK, which is the quantum version of \(\epsilon \)-ZK introduced in [DNS04].Footnote 3
Quantum \(\epsilon \)-Zero-Knowledge. The standard quantum ZK property roughly requires that for any QPT \(V^*\), there exists a QPT simulator \(\mathcal {S}\) that simulates the interaction between \(V^*\) and an honest prover so that the simulation is indistinguishable from the real execution against any QPT distinguishers. On the other hand, in quantum \(\epsilon \)-ZK, a simulator is allowed to depend on a “accuracy parameter” \(\epsilon \). That is, it requires that for any QPT malicious verifier \(V^*\) and a noticeable accuracy parameter \(\epsilon \), there exists a QPT simulator \(\mathcal {S}\) whose running time polynomially depends on \(\epsilon ^{-1}\) that simulates the interaction between \(V^*\) and an honest prover so that no QPT distinguisher can distinguish it from real execution with advantage larger than \(\epsilon \). Though this is a significant relaxation of quantum ZK, this still captures meaningful security. For example, we can see that quantum \(\epsilon \)-ZK implies both quantum versions of witness indistinguishability and witness hiding similarly to the analogous claims in the classical setting [BKP19].Footnote 4 Moreover, by extending the observation in [DNS04] to the quantum setting, we can see the following: Suppose that a QPT malicious verifier solves some puzzle whose solution is efficiently checkable (e.g., finding a witness of an \(\mathbf {NP}\) statement) after an interaction between an honest prover. Then, quantum \(\epsilon \)-ZK implies that if the verifier succeeds in solving the puzzle with noticeable probability p after the interaction, then there is a QPT algorithm (whose running time polynomially depends on \(p^{-1}\)) that solves the same puzzle with noticeable probability (say, p/2) without interacting with the honest prover. This captures the naive intuition of the ZK property that “anything that can be done after the execution can be done without execution” in some sense, and this would be sufficient in many cryptographic applications. Thus we believe that quantum \(\epsilon \)-ZK is conceptually a similar notion to the standard quantum ZK. More discussion on (quantum) \(\epsilon \)-ZK and other related notions of ZK can be found in Sect. 1.3.
Our Constructions. We give two constructions of constant round quantum \(\epsilon \)-ZK protocols.
-
We construct a constant round quantum \(\epsilon \)-ZK proof for \(\mathbf {NP}\) assuming the existence of collapsing hash functions [Unr16b, Unr16a], which is considered as a counterpart of collision-resistant hash functions in the quantum setting. Especially, we can instantiate the construction based on the QLWE assumption. Our construction is fully black-box in the sense that both simulation and construction rely on black-box usage of building blocks and a malicious verifier. Interestingly, this construction is just an adapted version of the classical protocol of [GK96] though the proof of quantum \(\epsilon \)-zero-knowledge property requires novel ideas.
-
We construct a constant round quantum \(\epsilon \)-ZK argument for \(\mathbf {NP}\) assuming the minimal assumption of the existence of post-quantum OWFs. This construction relies on black-box simulation, but the construction itself is non-black-box.
At the heart of our results is a new quantum rewinding technique that enables a simulator to extract a committed message of a malicious verifier while simulating verifier’s internal state in some sense. We formalize this technique as an extraction lemma, which we believe is of independent interest.
1.2 Technical Overview
Though we prove a general lemma which we call extraction lemma (Lemma 3.1) and then prove quantum \(\epsilon \)-ZK of our constructions based on that in the main body, we directly explain the proof of quantum \(\epsilon \)-ZK without going through such an abstraction in this overview.
Known Classical Technique and Difficulty in Quantum Setting. First, we review a classical constant round ZK proof by Goldreich and Kahan [GK96] (referred to as GK protocol in the following), and explain why it is difficult to prove quantum ZK for this protocol by known techniques. GK protocol is based on a special type of 3-round proof system called \(\varSigma \)-protocol.Footnote 5 In a \(\varSigma \)-protocol, a prover sends the first message a, a verifier sends the second message e referred to as a challenge, which is just a public randomness, and the prover sends the third message z. A \(\varSigma \)-protocol satisfies a special type of honest-verifier ZK, which ensures that if a challenge e is fixed, then one can simulate the transcript (a, e, z) without using a witness. Though this may sound like almost the standard ZK property, a difficulty when proving ZK is that a malicious verifier may adaptively choose e depending on a, and thus we cannot fix e at the beginning. To resolve this issue, the idea of GK protocol is to let the verifier commit to a challenge e at the beginning of the protocol. That is, GK protocol roughly proceeds as follows:Footnote 6
-
1.
A verifier sends a commitment \(\mathsf {com}\) to a challenge e of a \(\varSigma \)-protocol.
-
2.
The prover sends the first message a of the \(\varSigma \)-protocol.
-
3.
The verifier opens \(\mathsf {com}\) to open a challenge e and its opening information r (i.e., the randomness used for the commitment).
-
4.
The prover aborts if the verifier’s opening is invalid. Otherwise it sends the third message z of the \(\varSigma \)-protocol.
When proving the ZK property of GK protocol, they rely on a rewinding argument. That is, a simulator first runs the protocol with a malicious verifier until Step 3 to extract a committed message e inside \(\mathsf {com}\), and then rewind the verifier’s state back to just after Step 1, and then simulates the transcript by using the extracted knowledge of e.
On the other hand, this strategy does not work if we consider a quantum malicious verifier since a quantum malicious verifier may perform measurements in Step 3, which is in general not reversible. In other words, since we cannot copy the verifier’s internal state after Step 1 due to the no-cloning theorem, we cannot recover that state after running the protocol until Step 3.
Watrous [Wat09] proved that we can apply a rewinding argument for quantum verifiers under a certain condition. Roughly speaking, the condition is that there is a simulator that succeeds in simulation for quantum verifiers with a fixed (verifier-independent) and noticeable probability. For example, if the challenge space is polynomial size, then a simulator that simply guesses a challenge e suffices. However, for achieving negligible soundness error, the challenge space should be super-polynomial size, in which case it seems difficult to construct such a simulator. Also, relaxing quantum ZK to quantum \(\epsilon \)-ZK does not seem to resolve the issue in any obvious way.
Quantum Analysis of GK Protocol. In spite of the above mentioned difficulty, we succeed in proving quantum \(\epsilon \)-ZK for a slight variant of GK protocol. In the following, we explain the idea for our results.
Simplified Goal: Simulation of Non-Aborting Case. First, we apply a general trick introduced in [BS20], which simplifies the task of proving quantum ZK. In GK protocol, we say that a verifier aborts if it fails to provide a valid opening to \(\mathsf {com}\) in Step 3. Then, for proving quantum ZK of the protocol, it suffices to construct two simulators \(\mathsf {Sim}_{\mathsf {a}}\) and \(\mathsf {Sim}_{\mathsf {na}}\) that work only when the verifier aborts and does not abort and they do not change the probability that the verifier aborts too much, respectively. The reason is that if we randomly choose either of these two simulators and just run the chosen one, then the simulation succeeds with probability 1/2 since the guess of if the verifier aborts is correct with probability 1/2. Then, we can apply Watrous’ rewinding technique to convert it to a full-fledged simulator. Essentially the same trick also works for quantum \(\epsilon \)-ZK.
Moreover, it is easy to construct \(\mathsf {Sim}_{\mathsf {a}}\) because the first message of a \(\varSigma \)-protocol can be simulated without witness, and one need not provide the third message to the verifier when it aborts. Therefore, the problem boils down to constructing a simulator \(\mathsf {Sim}_{\mathsf {na}}\) that works only when the verifier does not abort.
Initial Observations. For explaining how to construct \(\mathsf {Sim}_{\mathsf {na}}\), we start by considering the simplest case where a verifier never aborts. Moreover, suppose that the commitment scheme used for committing to a challenge e satisfies the strict-binding property [Unr12], i.e., for any commitment \(\mathsf {com}\), there is at most one valid message and randomness. Then, a rewinding strategy similar to the classical case works since, in this case, the verifier’s message in Step 3 is information-theoretically determined, and such a deterministic computation does not collapse a quantum state in general.Footnote 7 However, for ensuring statistical soundness, we have to use a statistically hiding commitment, which cannot be strict-binding. Fortunately, this problem can be resolved by using collapse-binding commitments [Unr16b], which roughly behave similarly to strict-binding commitments for any computationally bounded adversaries.Footnote 8 Since this is rather a standard technique, in the rest of this overview, we treat the commitment as if it satisfies the strict-binding property.
Next, we consider another toy example where a verifier sometimes aborts. Suppose that a malicious verifier \(V^*\) is given an initial state  in its internal register \(\mathbf {V}\) where
in its internal register \(\mathbf {V}\) where  and
and  are orthogonal, and runs as follows:
are orthogonal, and runs as follows:
-
1.
\(V^*\) randomly picks e, honestly generates a commitment \(\mathsf {com}\) to e, and sends it to the prover (just ignoring the initial state).
-
2.
After receiving a, \(V^*\) performs a projective measurement
 on \(\mathbf {V}\), and immediately aborts if
on \(\mathbf {V}\), and immediately aborts if  is applied, and otherwise honestly opens (e, r).
is applied, and otherwise honestly opens (e, r). -
3.
After completing the protocol, \(V^*\) outputs its internal state in \(\mathbf {V}\).
It is trivial to construct a simulator for this particular \(V^*\) since it just ignores prover’s messages. But for explaining our main idea, we examine what happens if we apply the same rewinding strategy as the classical case to the above verifier. After getting a commitment \(\mathsf {com}\) from \(V^*\), a simulator sends a random a to \(V^*\) to extract e. Since we are interested in constructing a simulator that works in the non-aborting case, suppose that \(V^*\) does not abort, i.e., sends back a valid opening (e, r). At this point, \(V^*\)’s internal state collapses to  . Then the simulator cannot “rewind” this state to the original verifier’s state
. Then the simulator cannot “rewind” this state to the original verifier’s state  in general, and thus the simulation seems to get stuck. However, our key observation is that, conditioned on that \(V^*\) does not abort, \(V^*\)’s state always collapses to
in general, and thus the simulation seems to get stuck. However, our key observation is that, conditioned on that \(V^*\) does not abort, \(V^*\)’s state always collapses to  even in the real execution. Since our goal is to construct \(\mathsf {Sim}_\mathsf {na}\) that is only required to work for the non-aborting case, it does not matter if \(V^*\)’s state collapses to
even in the real execution. Since our goal is to construct \(\mathsf {Sim}_\mathsf {na}\) that is only required to work for the non-aborting case, it does not matter if \(V^*\)’s state collapses to  when the simulator runs extraction. More generally, extraction procedure may collapse verifier’s internal state if a similar collapsing happens even in the real execution conditioned on that the verifier does not abort.
when the simulator runs extraction. More generally, extraction procedure may collapse verifier’s internal state if a similar collapsing happens even in the real execution conditioned on that the verifier does not abort.
Our Idea: Decompose Verifier’s Space. To generalize the above idea, we want to decompose verifier’s internal state after Step 1 into aborting part and non-aborting part. However, the definition of such a decomposition is non-trivial since a verifier may determine if it aborts depending on the prover’s message a in addition to its internal state. Therefore, instead of decomposing it into always-aborting part and always-non-aborting part as in the example of the previous paragraph, we set a noticeable threshold t and decompose it into “not-abort-with-probability \(<\!t\) part” and “not-abort-with-probability \(\ge \!t\) part” over the randomness of a.
For implementing this idea, we rely on Jordan’s lemma (e.g., see a lecture note by Regev [AR06]) in a similar way to the work by Nagaj, Wocjan, and Zhang [NWZ09] on the amplification theorem for \(\mathbf {QMA}\). Let \(\varPi \) be a projection that corresponds to “Step 2 + Step 3 + Check if the verifier does not abort” in GK protocol. A little bit more formally, let \(\mathbf {V}\) be a register for verifier’s internal state and \(\mathbf {Aux}\) be an auxiliary register. Then \(\varPi \) is a projection over \(\mathbf {V}\otimes \mathbf {Aux}\) that works as follows:
-
1.
Apply a unitary \(U_{\mathsf {aux}}\) over \(\mathbf {Aux}\) that maps
 to
to  where \(\mathcal {R}\) is the randomness space to generate the first message of the \(\varSigma \)-protocol and \(a_{\mathsf {rand}}\) is the first message derived from the randomness \(\mathsf {rand}\).Footnote 9
where \(\mathcal {R}\) is the randomness space to generate the first message of the \(\varSigma \)-protocol and \(a_{\mathsf {rand}}\) is the first message derived from the randomness \(\mathsf {rand}\).Footnote 9
-
2.
Apply a unitary \(U_V\) that corresponds to Step 3 for prover’s message \(a_{\mathsf {rand}}\) in \(\mathbf {Aux}\) except for measurement,
-
3.
Apply a projection to the subspace spanned by states that contain valid opening (e, r) for \(\mathsf {com}\) in designated output registers,
-
4.
Apply \((U_V U_{\mathsf {aux}})^\dagger \).
One can see that the probability that the verifier does not abort (i.e., sends a valid opening) is  where
where  is verifier’s internal state after Step 1. Then Jordan’s lemma gives an orthogonal decomposition of the Hilbert space of \(\mathbf {V}\otimes \mathbf {Aux}\) into many one- or two-dimensional subspaces \(S_1,...,S_N\) that are invariant under \(\varPi \) and
is verifier’s internal state after Step 1. Then Jordan’s lemma gives an orthogonal decomposition of the Hilbert space of \(\mathbf {V}\otimes \mathbf {Aux}\) into many one- or two-dimensional subspaces \(S_1,...,S_N\) that are invariant under \(\varPi \) and  such that we have the following:
such that we have the following:
-
1.
For any \(j\in [N]\) and
 , the projection \(\varPi \) succeeds with probability \(p_j\), i.e.,
, the projection \(\varPi \) succeeds with probability \(p_j\), i.e.,  .
. -
2.
A success probability of projection \(\varPi \) is “amplifiable” in each subspace. That is, there is an “amplification procedure” \(\mathsf {Amp}\) that maps any
 to
to  with overwhelming probability within \(\mathsf {poly}(\lambda ,p_j^{-1})\) times iteration of the same procedure (that does not depend on j) for any \(j\in [N]\). Moreover, this procedure does not cause any interference between different subspaces.
with overwhelming probability within \(\mathsf {poly}(\lambda ,p_j^{-1})\) times iteration of the same procedure (that does not depend on j) for any \(j\in [N]\). Moreover, this procedure does not cause any interference between different subspaces.
Then we define two subspaces
Then for any  , we can decompose it as
, we can decompose it as

by using (sub-normalized) states  and
and  such that
such that  and
and  . In this way, we can formally define a decomposition of verifier’s internal state into “not-abort-with-probability \(<\!t\) part” and “not-abort-with-probability \(\ge \!t\) part”.
. In this way, we can formally define a decomposition of verifier’s internal state into “not-abort-with-probability \(<\!t\) part” and “not-abort-with-probability \(\ge \!t\) part”.
Extraction and Simulation. Then we explain how we can use the above decomposition to implement extraction of e for simulation of non-aborting case. First, we consider an easier case where the verifier’s state after Step 1 only has \(S_{\ge t}\) component  . In this case, we can use \(\mathsf {Amp}\) to map
. In this case, we can use \(\mathsf {Amp}\) to map  onto the span of \(\varPi \) within \(\mathsf {poly}(\lambda ,t^{-1})\) times iteration. After mapped to \(\varPi \), we can extract (e, r) without collapsing the state by the definition of \(\varPi \) and our assumption that the commitment is strict-binding. This means that given
onto the span of \(\varPi \) within \(\mathsf {poly}(\lambda ,t^{-1})\) times iteration. After mapped to \(\varPi \), we can extract (e, r) without collapsing the state by the definition of \(\varPi \) and our assumption that the commitment is strict-binding. This means that given  , we can extract (e, r), which is information theoretically determined by \(\mathsf {com}\), with overwhelming probability. In general, such a deterministic computation can be implemented in a reversible manner, and thus we can extract (e, r) from
, we can extract (e, r), which is information theoretically determined by \(\mathsf {com}\), with overwhelming probability. In general, such a deterministic computation can be implemented in a reversible manner, and thus we can extract (e, r) from  almost without damaging the state.
almost without damaging the state.
On the other hand, the same procedure does not work for  since \(\mathsf {poly}(\lambda ,t^{-1})\) times iteration is not sufficient for amplifying the success probability of \(\varPi \) to overwhelming in this subspace. Our idea is to let a simulator run the above extraction procedure in superposition even though \(S_{<t}\) component may be damaged.
since \(\mathsf {poly}(\lambda ,t^{-1})\) times iteration is not sufficient for amplifying the success probability of \(\varPi \) to overwhelming in this subspace. Our idea is to let a simulator run the above extraction procedure in superposition even though \(S_{<t}\) component may be damaged.
Specifically, our extraction procedure \(\mathsf {Ext}\) works as follows:
-
1.
Given a verifier’s internal state
 after Step 1, initialize \(\mathbf {Aux}\) to
after Step 1, initialize \(\mathbf {Aux}\) to  and runs \(\mathsf {Amp}\) for \(\mathsf {poly}(\lambda ,t^{-1})\) times iteration. Abort if a mapping onto \(\varPi \) does not succeed. Otherwise, proceed to the next step.
and runs \(\mathsf {Amp}\) for \(\mathsf {poly}(\lambda ,t^{-1})\) times iteration. Abort if a mapping onto \(\varPi \) does not succeed. Otherwise, proceed to the next step. -
2.
Apply \(U_V U_{\mathsf {aux}}\), measure designated output registers to obtain \((e_\mathsf {Ext},r_\mathsf {Ext})\), and apply \((U_V U_{\mathsf {aux}})^\dagger \). We note that \((e_\mathsf {Ext},r_\mathsf {Ext})\) is always a valid opening of \(\mathsf {com}\) since \(\mathsf {Ext}\) runs this step only if it succeeds in mapping the state onto \(\varPi \) in the previous step. We also note that this step does not collapse the state at all by the strict-binding property of the commitment.
-
3.
Uncompute Step 1 and measure \(\mathbf {Aux}\). Abort if the measurement outcome is not 0. Otherwise, proceed to the next step.
-
4.
Output the extracted opening \((e_\mathsf {Ext},r_\mathsf {Ext})\) along with a “post-extraction state”
 in register \(\mathbf {V}\). For convenience, we express
in register \(\mathbf {V}\). For convenience, we express  as a sub-normalized state whose norm is the probability that \(\mathsf {Ext}\) does not abort and the post-extraction state conditioned on that the extraction succeeds is
as a sub-normalized state whose norm is the probability that \(\mathsf {Ext}\) does not abort and the post-extraction state conditioned on that the extraction succeeds is  .
.
In the following, we analyze \(\mathsf {Ext}\). We consider the decomposition of  as defined in the previous paragraph:
as defined in the previous paragraph:

Suppose that \(\mathsf {Ext}\) does not abort, i.e., it outputs a valid opening \((e_\mathsf {Ext},r_\mathsf {Ext})\) along with a post-extraction state  . Then,
. Then,  can be expressed as
can be expressed as

for some  and
and  such that
such that  ,
,  , and
, and  since there is no interference between \(S_{<t}\) and \(S_{\ge t}\) when running \(\mathsf {Amp}\) and \(S_{\ge t}\) component hardly changes as observed above. This is not even a close state to the original state
since there is no interference between \(S_{<t}\) and \(S_{\ge t}\) when running \(\mathsf {Amp}\) and \(S_{\ge t}\) component hardly changes as observed above. This is not even a close state to the original state  in general since the \(S_{<t}\) component may be completely different. However, our key observation is that, conditioned on that the verifier does not abort, at most “t-fraction” of \(S_{<t}\) component survives even in the real execution by the definition of the subspace \(S_{<t}\). That is, in the verifier’s final output state conditioned on that it does not abort, the average squared norm of a portion that comes from \(S_{<t}\) component is at most t. Thus, even if a simulator fails to simulate this portion, this only impacts the accuracy of the simulation by a certain function of t, which is shown to be \(O(t^{1/3})\) in the main body.
in general since the \(S_{<t}\) component may be completely different. However, our key observation is that, conditioned on that the verifier does not abort, at most “t-fraction” of \(S_{<t}\) component survives even in the real execution by the definition of the subspace \(S_{<t}\). That is, in the verifier’s final output state conditioned on that it does not abort, the average squared norm of a portion that comes from \(S_{<t}\) component is at most t. Thus, even if a simulator fails to simulate this portion, this only impacts the accuracy of the simulation by a certain function of t, which is shown to be \(O(t^{1/3})\) in the main body.
With this observation in mind, the non-aborting case simulator \(\mathsf {Sim}_{\mathsf {na}}\) works as follows.
-
1.
Run Step 1 of the verifier to obtain \(\mathsf {com}\) and let
 be verifier’s internal state at this point.
be verifier’s internal state at this point. -
2.
Run \(\mathsf {Ext}\) on input
 . Abort if \(\mathsf {Ext}\) aborts. Otherwise, obtain an extracted opening \((e_\mathsf {Ext},r_\mathsf {Ext})\) and a post-extraction state
. Abort if \(\mathsf {Ext}\) aborts. Otherwise, obtain an extracted opening \((e_\mathsf {Ext},r_\mathsf {Ext})\) and a post-extraction state  , and proceed to the next step.
, and proceed to the next step. -
3.
Simulate a transcript \((a,e_\mathsf {Ext},z)\) by the honest-verifier ZK property of the \(\varSigma \)-protocol.
-
4.
Send a to the verifier whose internal state is replaced with
 . Let (e, r) be the verifier’s response. Abort if (e, r) is not a valid opening to \(\mathsf {com}\). Otherwise send z to the verifier.
. Let (e, r) be the verifier’s response. Abort if (e, r) is not a valid opening to \(\mathsf {com}\). Otherwise send z to the verifier. -
5.
Output the verifier’s final output.
By the above analysis, we can see that \(\mathsf {Sim}_\mathsf {na}\)’s output distribution is close to the real verifier’s output distribution with an approximation error \(O(t^{1/3})\) conditioned on that the verifier does not abort. Furthermore, the probability that the verifier does not abort can only be changed by at most \(O(t^{1/3})\). If we could set t to be a negligible function, then we would be able to achieve quantum ZK rather than quantum \(\epsilon \)-ZK. However, since we have to ensure that \(\mathsf {Amp}\)’s running time \(\mathsf {poly}(\lambda ,t^{-1})\) is polynomial in \(\lambda \), we can only set t to be noticeable. Since we can set t to be an arbitrarily small noticeable function, we can make the approximation error \(O(t^{1/3})\) be an arbitrarily small noticeable function. This means that the protocol satisfies quantum \(\epsilon \)-ZK.
Black-Box Simulation. So far, we did not pay attention to the black-box property of simulation. We briefly explain the definition of black-box quantum ZK and that our simulator satisfies it. First, we define black-box quantum ZK by borrowing the definition of quantum oracle machine by Unruh [Unr12]. Roughly, we say that a simulator is black-box if it only accesses unitary part of a verifier and its inverse in a black-box manner, and does not directly act on the verifier’s internal registers. With this definition, one part where it is unclear if our simulator is black-box is the amplification procedure \(\mathsf {Amp}\). However, by a close inspection, we can see that \(\mathsf {Amp}\) actually just performs sequential measurements \(\{\varPi ,I_{\mathbf {V},\mathbf {Aux}}-\varPi \}\) and  , which can be done by black-box access to the verifier as seen from the definition of \(\varPi \). Therefore, we can see that our simulator is black-box.
, which can be done by black-box access to the verifier as seen from the definition of \(\varPi \). Therefore, we can see that our simulator is black-box.
A Remark on Underlying \(\varSigma \)-Protocol. In the original GK protocol, any \(\varSigma \)-Protocol can be used as a building block. However, in our technique, we need to use delayed-witness \(\varSigma \)-protocol where the first message a can be generated without knowledge of a witness due to a technical reason. An example of delayed-witness \(\varSigma \)-protocol is Blum’s Graph Hamiltonicity protocol [Blu86]. Roughly, the reason to require this additional property is for ensuring that a simulator can perfectly simulate the first message a of the \(\varSigma \)-protocol when running the extraction procedure. In the classical setting, a computationally indistinguishable simulation of a works, but we could not prove an analogous claim in our setting.
OWF-Based Construction. Next, we briefly explain our OWF-based quantum \(\epsilon \)-ZK argument. The reason why we need a stronger assumption in our first construction is that we need to implement the commitment for the challenge by a constant round statistically hiding commitment, which is not known to exist from OWF. Then, a natural idea is to relax it to computationally hiding one if we only need computational soundness. We can show that the extraction technique as explained above also works for statistically binding commitments with a small tweak. However, we cannot prove soundness of the protocol without any modification due to a malleability issue. For explaining this, we recall that the first message a of a \(\varSigma \)-protocol itself is also implemented as a commitment. Then, the computational hiding of commitment does not prevent a computationally bounded prover, which is given a commitment \(\mathsf {com}\) to e, from generating a “commitment” a whose committed message depends on e. Such a dependence leads to an attack against soundness. To prevent this, an extractable commitment scheme is used to generate a in the classical setting [PW09]. However, since it is unclear if the extractable commitment scheme used in [PW09] is secure against quantum adversaries, we take an alternative approach that we let a prover prove that it knows a committed message inside a by using a proof of knowledge before a verifier opens a challenge as is done in [Gol01, Sec.4.9], [Gol04, App.C.3]. A naive approach to implement this idea would be to use ZK proof of knowledge, but this does not work since a constant round ZK argument is what we are trying to construct. Fortunately, we can instead use witness indistinguishable proof of knowledge (WIPoK) with a simple OR proof trick. Specifically, we let a prover prove that “I know committed message in a” OR “I know witness w for x” where x is the statement being proven in the protocol. In the proof of soundness, since we assume x is a false statement, a witness for the latter statement does not exist. Then we can extract a committed message inside a to break the hiding property of the commitment scheme used by the verifier if the committed message depends on e. On the other hand, in the proof of \(\epsilon \)-ZK property, we can use the real witness w in an intermediate hybrid to simulate WIPoK without using knowledge of a committed message. In such a hybrid, we can rely on honest-verifier ZK of the \(\varSigma \)-protocol to change a to a simulated one for an extracted challenge e.
Finally, we remark that though we are not aware of any work that explicitly claims the existence of a constant round WIPoK that works for quantum provers from OWFs, we observe that a combination of known works easily yields such a construction. (See the full version for more details.) As a result, we obtain constant round quantum \(\epsilon \)-ZK argument from OWFs.
1.3 Related Work
\(\epsilon \)-Zero-Knowledge and Related Notions. Though we are the first to consider \(\epsilon \)-ZK in the quantum setting, there are several works that consider \(\epsilon \)-ZK in the classical setting. We briefly review them. We note that all of these results are in the classical setting, and it is unknown if similar results hold in the quantum setting. The notion of \(\epsilon \)-ZK (originally called \(\epsilon \)-knowledge) was introduced by Dwork, Naor, and Sahai [DNS04] in the context of concurrent ZK proofs. Bitansky, Kalai, and Paneth [BKP18] gave a construction of 4-round \(\epsilon \)-ZK proof for \(\mathbf {NP}\) assuming the existence of key-less multi-collision resistant hash function.Footnote 10 Barak and Lindell [BL02] showed the impossibility of constant round black-box ZK proof with strict-polynomial time simulation, and observed that strict-polynomial time simulation is possible if we relax ZK to \(\epsilon \)-ZK. This can be understood as a theoretical separation between ZK and \(\epsilon \)-ZK. On the other hand, Fleischhacker, Goyal, and Jain [FGJ18] showed that there does not exist 3-round \(\epsilon \)-ZK proof for \(\mathbf {NP}\) even with non-black-box simulation under some computational assumptions, which is the same lower bound as that for ZK proofs if we allow non-black-box simulation.
Another relaxation of ZK is super-polynomial simulation (SPS)-ZK [Pas03], where a simulator is allowed to run in super-polynomial time. One may find a similarity between \(\epsilon \)-ZK and SPS-ZK in the sense that the latter can be seen as a variant of \(\epsilon \)-ZK where we set the accuracy parameter \(\epsilon \) to be negligible. On the other hand, it has been considered that \(\epsilon \)-ZK is much more difficult to achieve than SPS-ZK. For example, the work of Bitansky, Khurana, and Paneth [BKP19] gave a construction of a 2-round argument for \(\mathbf {NP}\) that achieves a weaker notion of ZK than \(\epsilon \)-ZK, and the result is considered a significant breakthrough in the area even though there is a simple construction of 2-round SPS-ZK argument for \(\mathbf {NP}\) [Pas03].
Several works considered other weakened notions of ZK [DNRS03, BP12, CLP15, JKKR17, BKP19]. Some of them are weaker than \(\epsilon \)-ZK, and others are incomparable. For example, “weak ZK” in [BP12, CLP15] is incomparable to \(\epsilon \)-ZK whereas “weak ZK” in [BKP19] is weaker than \(\epsilon \)-ZK.
Post-Quantum Zero-Knowledge with Classical Computational Soundness. Ananth and La Placa [AL20] gave a construction of post-quantum ZK argument for \(\mathbf {NP}\) with classical computational soundness assuming the QLWE assumption. Though such a protocol would be easy to obtain if we assume average-case classical hardness of certain problems in \(\mathbf {BQP}\) (e.g., factoring) in addition to the QLWE assumption, what is interesting in [AL20] is that they only assume the QLWE assumption.
Post-Quantum Zero-Knowledge with Trusted Setup. Several works studied (non-interactive) post-quantum ZK proofs for \(\mathbf {NP}\) in the common random/reference string model [Kob03, DFS04, PS19]. Among them, Peikert and Shiehian [PS19] proved that there exists non-interactive post-quantum ZK proof for \(\mathbf {NP}\) in the common reference string model assuming the QLWE assumption.Footnote 11
Zero-Knowledge for \(\mathbf {QMA}\). The complexity class \(\mathbf {QMA}\) is a quantum analogue of \(\mathbf {NP}\). Broadbent, Ji, Song, and Watrous [BJSW20] gave a construction of a ZK proof for \(\mathbf {QMA}\). Recently, Broadbent and Grilo [BG20] gave an alternative simpler construction of a ZK proof for \(\mathbf {QMA}\). Bitansky and Shmueli [BS20] gave a constant round ZK argument for \(\mathbf {QMA}\) by combining the construction of [BG20] and their post-quantum ZK argument for \(\mathbf {NP}\). We believe that our technique can be used to construct a constant round \(\epsilon \)-ZK proof for \(\mathbf {QMA}\) by replacing the delayed-witness \(\varSigma \)-protocol for \(\mathbf {NP}\) with the delayed-witness quantum \(\varSigma \)-protocol for \(\mathbf {QMA}\) recently proposed by Brakerski and Yuen [BY20].Footnote 12 This is beyond the scope of this paper, and we leave a formal proof as a future work.
Several works studied non-interactive ZK proofs/arguments for \(\mathbf {QMA}\) in preprocessing models [CVZ20, BG20, Shm20, ACGH20].
Collapsing Hash Functions. The notion of collapsing hash functions was introduced by Unruh [Unr16b] for a replacement of collision-resistant hash functions in post-quantum setting. Unruh [Unr16a] gave a construction of a collapsing hash function under the QLWE assumption. Actually, the construction is generic based on any lossy function with sufficiently large “lossy rate”.Footnote 13 Currently, we are not aware of any other construction of collapsing hash function based on standard assumptions, but any new construction of collapsing hash function yields a new instantiation of our first construction.
Zhandry [Zha19] proved that any collision-resistant hash function that is not collapsing yields a stronger variant of public-key quantum money (with infinitely often security). Given the difficulty of constructing public key quantum money, he suggested that most natural post-quantum collision-resistant hash functions are likely already collapsing.
Relation to [CCY20]. Our idea of decomposing a verifier’s internal space into “aborting space” and “non-aborting space” is inspired by a recent work of Chia, Chung, and Yamakawa [CCY20]. In [CCY20], the authors consider a decomposition of a prover’s internal space into “know-answer space” and “not-know-answer space” to prove soundness of parallel repetition version of Mahadev’s classical verification of quantum computation protocol [Mah18b]. Though the conceptual idea and some technical tools are similar, the ways of applying them to actual problems are quite different. For example, in our case, we need a careful analysis to make sure that a post-extraction state is close to the original one in some sense while such an argument does not appear in their work since their goal is proving soundness rather than ZK. On the other hand, their technical core is a approximated projection to each subspace, which is not needed in this paper.
Subsequent work. Subsequently to this work, Chia, Chung, Liu, and Yamakawa [CCLY21] proved that there does not exist a constant round post-quantum ZK argument for \(\mathbf {NP}\) unless \(\mathbf {NP}\in \mathbf {BQP}\), which is highly unlikely. This justifies the relaxation to \(\epsilon \)-ZK in our constructions.
2 Preliminaries
Basic Notations. We use \(\lambda \) to denote the security parameter throughout the paper. For a positive integer \(n\in \mathbb {N}\), [n] denotes a set \(\{1,2,...,n\}\). For a finite set \(\mathcal {X}\), \(x \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \mathcal {X}\) means that x is uniformly chosen from \(\mathcal {X}\). A function \(f:\mathbb {N}\rightarrow [0,1]\) is said to be negligible if for all polynomial p and sufficiently large \(\lambda \in \mathbb {N}\), we have \(f(\lambda )< 1/p(\lambda )\), said to be overwhelming if \(1-f\) is negligible, and said to be noticeable if there is a polynomial p such that we have \(f(\lambda )\ge 1/p(\lambda )\) for sufficiently large \(\lambda \in \mathbb {N}\). We denote by \(\mathsf {poly}\) an unspecified polynomial and by \(\mathsf {negl}\) an unspecified negligible function. We use PPT and QPT to mean (classical) probabilistic polynomial time and quantum polynomial time, respectively. For a classical probabilistic or quantum algorithm \(\mathcal {A}\), \(y \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \mathcal {A}(x)\) means that \(\mathcal {A}\) is run on input x and outputs y. When \(\mathcal {A}\) is classical probabilistic algorithm, we denote by \(\mathcal {A}(x;r)\) to mean the execution of \(\mathcal {A}\) on input x and a randomness r. When \(\mathcal {A}\) is a quantum algorithm that takes a quantum advice, we denote by \(\mathcal {A}(x;\rho )\) to mean the execution of \(\mathcal {A}\) on input x and an advice \(\rho \). For a quantum algorithm \(\mathcal {A}\), a unitary part of \(\mathcal {A}\) means the unitary obtained by deferring all measurements by \(\mathcal {A}\) and omitting these measurements. We use the bold font (like \(\mathbf {X}\)) to denote quantum registers, and \(\mathcal {H}_\mathbf {X}\) to mean the Hilbert space corresponding to the register \(\mathbf {X}\). For a quantum state \(\rho \), \(M_{\mathbf {X}}\circ \rho \) means a measurement in the computational basis on the register \(\mathbf {X}\) of \(\rho \). For quantum states \(\rho \) and \(\rho '\), \(\mathsf {TD}(\rho ,\rho ')\) denotes trace distance between them. When we consider a sequence \(\{X_\lambda \}_{\lambda \in \mathbb {N}}\) of some objects (e.g., bit strings, quantum states, sets, Hilbert spaces etc.) indexed by the security parameter \(\lambda \), we often simply write X to mean \(X_\lambda \) or \(\{X_\lambda \}_{\lambda \in \mathbb {N}}\), which will be clear from the context. Similarly, for a function f in the security parameter \(\lambda \), we often simply write f to mean \(f(\lambda )\).
Standard Computational Models
-
A PPT algorithm is a probabilistic polynomial time (classical) Turing machine. A PPT algorithm is also often seen as a sequence of uniform polynomial-size circuits.
-
A QPT algorithm is a polynomial time quantum Turing machine. A QPT algorithm is also often seen as a sequence of uniform polynomial-size quantum circuits.
-
An adversary (or malicious party) is modeled as a non-uniform QPT algorithm \(\mathcal {A}\) (with quantum advice) that is specified by sequences of polynomial-size quantum circuits \(\{\mathcal {A}_\lambda \}_{\lambda \in \mathbb {N}}\) and polynomial-size quantum advice \(\{\rho _\lambda \}_{\lambda \in \mathbb {N}}\). When \(\mathcal {A}\) takes an input of \(\lambda \)-bit, \(\mathcal {A}\) runs \(\mathcal {A}_{\lambda }\) taking \(\rho _\lambda \) as an advice.
Interactive Quantum Machine and Oracle-Aided Quantum Machine. We rely on the definition of an interactive quantum machine and oracle-aided quantum machine that is given oracle access to an interactive quantum machine following [Unr12]. Roughly, an interactive quantum machine \(\mathcal {A}\) is formalized by a unitary over registers \(\mathbf {M}\) for receiving and sending messages and \(\mathbf {A}\) for maintaining \(\mathcal {A}\)’s internal state. For two interactive quantum machines \(\mathcal {A}\) and \(\mathcal {B}\) that share the same message register \(\mathbf {M}\), an interaction between \(\mathcal {A}\) and \(\mathcal {B}\) proceeds by alternating invocations of \(\mathcal {A}\) and \(\mathcal {B}\) while exchanging messages over \(\mathbf {M}\).
An oracle-aided quantum machine \(\mathcal {S}\) given oracle access to an interactive quantum machine \(\mathcal {A}\) with an initial internal state \(\rho \) (denoted by \(\mathcal {S}^{\mathcal {A}(\rho )}\)) is allowed to apply unitary part of \(\mathcal {A}\) and its inverse in a black-box manner where \(\mathcal {S}\) can act on \(\mathcal {A}\)’s internal register \(\mathbf {A}\) only through oracle access. We refer to [Unr12] for more formal definitions of interactive quantum machines and black-box access to them.
Indistinguishability of Quantum States. We define computational and statistical indistinguishability of quantum states similarly to [BS20].
We may consider random variables over bit strings or over quantum states. This will be clear from the context. For ensembles of random variables \(\mathcal {X}=\{X_i\}_{\lambda \in \mathbb {N},i\in I_\lambda }\) and \(\mathcal {Y}=\{Y_i\}_{\lambda \in \mathbb {N},i\in I_\lambda }\) over the same set of indices \(I=\bigcup _{\lambda \in \mathbb {N}}I_\lambda \) and a function \(\delta \), we write \(\mathcal {X}{\mathop {\approx }\limits ^{comp}}_{\delta }\mathcal {Y}\) to mean that for any non-uniform QPT algorithm \(\mathcal {A}=\{\mathcal {A}_\lambda ,\rho _\lambda \}\), there exists a negligible function \(\mathsf {negl}\) such that for all \(\lambda \in \mathbb {N}\), \(i\in I_\lambda \), we have
Especially, when we have the above for \(\delta =0\), we say that \(\mathcal {X}\) and \(\mathcal {Y}\) are computationally indistinguishable, and simply write \(\mathcal {X}{\mathop {\approx }\limits ^{comp}}\mathcal {Y}\).
Similarly, we write \(\mathcal {X}{\mathop {\approx }\limits ^{stat}}_{\delta }\mathcal {Y}\) to mean that for any unbounded time algorithm \(\mathcal {A}\), there exists a negligible function \(\mathsf {negl}\) such that for all \(\lambda \in \mathbb {N}\), \(i\in I_\lambda \), we have
Especially, when we have the above for \(\delta =0\), we say that \(\mathcal {X}\) and \(\mathcal {Y}\) are statistically indistinguishable, and simply write \(\mathcal {X}{\mathop {\approx }\limits ^{stat}}\mathcal {Y}\). Moreover, we write \(\mathcal {X}\equiv \mathcal {Y}\) to mean that \(X_i\) and \(Y_i\) are distributed identically for all \(i\in I\)Footnote 14.
2.1 Post-Quantum One-Way Functions and Collapsing Hash Functions
A post-quantum one-way function (OWF) is a classically computable function that is hard to invert in QPT. A collapsing hash function is a quantum counterpart of collision-resistant hash function introduced by Unruh [Unr16b]. Unruh [Unr16a] gave a construction of collapsing hash functions based on the QLWE assumption. We give formal definitions in the full version since they are only used for constructing other cryptographic primitives and not directly used in our constructions.
2.2 Commitment
We use commitments in our constructions. Though they are mostly standard, we need one new security notion which we call strong collapse-binding, which is a stronger variant of collapse-biding introduced by Unruh [Unr16b]. Roughly speaking, this security requires that for any superposition of messages and randomness corresponding the same commitment generated by an adversary, the adversary cannot distinguish if the message and randomness registers are measured or not. The difference from the original collapse-binding property is that both message and randomness registers are measured rather than only the message register. We observe that the collapse-binding commitment based on collapsing hash functions in [Unr16b] also satisfies the strong collapse-binding property. Especially, there exists a strong collapse-binding commitment under the QLWE assumption. See the full version for details of the definition and construction of strong collapse-binding commitments.
2.3 Interactive Proof and Argument
We define interactive proofs and arguments similarly to [BS20].
Notations. For an \(\mathbf {NP}\) language \(L\) and \(x\in L\), \(R_{L}(x)\) is the set that consists of all (classical) witnesses w such that the verification machine for L accepts (x, w).
A (classical) interactive protocol is modeled as an interaction between interactive quantum machines \(P\) referred to as a prover and \(V\) referred to as a verifier that can be implemented by PPT algorithms. We denote by \(\langle P(x_{P}), V(x_{V}) \rangle (x)\) an execution of the protocol where x is a common input, \(x_P\) is \(P\)’s private input, and \(x_V\) is \(V\)’s private input. We denote by \(\mathsf {OUT}_V\langle P(x_{P}), V(x_{V}) \rangle (x)\) the final output of \(V\) in the execution. An honest verifier’s output is \(\top \) indicating acceptance or \(\bot \) indicating rejection, and a quantum malicious verifier’s output may be an arbitrary quantum state.
Definition 2.1
(Interactive Proof and Argument for \(\mathbf {NP}\) ). An interactive proof or argument for an \(\mathbf {NP}\) language \(L\) is an interactive protocol between a PPT prover \(P\) and a PPT verifier \(V\) that satisfies the following:
Perfect Completeness. For any \(x\in L\), and \(w\in R_L(x)\), we have
Statistical/Computational Soundness. We say that an interactive protocol is statistically (resp. computationally) sound if for any unbounded-time (resp. non-uniform QPT) cheating prover \(P^*\), there exists a negligible function \(\mathsf {negl}\) such that for any \(\lambda \in \mathbb {N}\) and any \(x\in \{0,1\}^\lambda \setminus L\), we have
We call an interactive protocol with statistical (resp. computational) soundness an interactive proof (resp. argument).
Delayed-Witness \(\varSigma \)-Protocol. We introduce a special type of \(\varSigma \)-protocol which we call delayed-witness \(\varSigma \)-protocol where the first message can be generated without witness.
Definition 2.2
(Delayed-Witness \(\varSigma \)-Protocol). A (post-quantum) delayed-witness \(\varSigma \)-protocol for an \(\mathbf {NP}\) language L is a 3-round interactive proof for \(\mathbf {NP}\) with the following syntax.
Common Input: An instance \(x\in L\cap \{0,1\}^{\lambda }\) for security parameter \(\lambda \in \mathbb {N}\).
\(P\)’s Private Input: A classical witness \(w\in R_L(x)\) for x.
-
1.
\(P\) generates a “commitment” a and a state \(\mathsf {st}\). For this part, \(P\) only uses the statement x and does not use any witness w. We denote this procedure by \((a,\mathsf {st}) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \varSigma .P_1(x)\). Then it sends a to the verifier, and keeps \(\mathsf {st}\) as its internal state.
-
2.
\(V\) chooses a“challenge” \(e \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \{0,1\}^\lambda \) and sends e to \(P\).
-
3.
\(P\) generates a “response” z from \(\mathsf {st}\), witness w, and e. We denote this procedure by \(z \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \varSigma .P_3(\mathsf {st},w,e)\). Then it sends z to \(V\).
-
4.
\(V\) verifies the transcript (a, e, z) and outputs \(\top \) indicating acceptance or \(\bot \) indicating rejection. We denote this procedure by \(\top /\bot \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \varSigma .V(x,a,e,z)\).
We require a delayed-witness \(\varSigma \)-protocol to satisfy the following property in addition to perfect completeness and statistical soundness.Footnote 15
Special Honest-Verifier Zero-Knowledge. There exists a PPT simulator \(\mathsf {Sim}_{\varSigma }\) such that we have
where \(x\in L\cap \{0,1\}^\lambda \), \(w\in R_L(x)\), and \(e\in \{0,1\}^\lambda \).
Instantiations. An example of a delayed-witness \(\varSigma \)-protocol is a parallel repetition version of Blum’s Graph Hamiltonicity protocol [Blu86]. In the protocol, we need a computationally hiding and perfectly binding non-interactive commitment scheme, which exists under the QLWE assumption as noted in Sect. 2.2. In summary, a delayed-input \(\varSigma \)-protocol for all \(\mathbf {NP}\) languages exists under the QLWE assumption.
Quantum \(\epsilon \)-Zero-Knowledge Proof and Argument. Here, we define quantum black-box \(\epsilon \)-zero-knowledge proofs and arguments. The difference from the definition of quantum zero-knowledge in [BS20] are:
-
1.
(\(\epsilon \)-Zero-Knowledge) We allow the simulator to depend on a noticeable “accuracy parameter” \(\epsilon \), and allows its running time to polynomially depend on \(\epsilon ^{-1}\), and
-
2.
(Black-Box Simulation) the simulator is only given black-box access to a malicious verifier.
Definition 2.3
(Post-Quantum Black-Box \(\epsilon \)-Zero-Knowledge Proof and Argument). A post-quantum black-box \(\epsilon \)-zero-knowledge proof (resp. argument) for an \(\mathbf {NP}\) language \(L\) is an interactive proof (resp. argument) for \(L\) that satisfies the following property in addition to perfect completeness and statistical (resp. computational) soundness:
Quantum Black-Box \(\epsilon \)-Zero-Knowledge. There exists an oracle-aided QPT simulator \(\mathsf {Sim}\) such that for any non-uniform QPT malicious verifier \(V^*=\{V^*_\lambda ,\rho _\lambda \}_{\lambda \in \mathbb {N}}\) and any noticeable function \(\epsilon (\lambda )\), we have
where \(\lambda \in \mathbb {N}\), \(x\in L\cap \{0,1\}^\lambda \), \(w\in R_L(\lambda )\), and \(\mathsf {OUT}_{V^*_\lambda }(\mathsf {Sim}^{V^*_\lambda (\rho _\lambda )}(x))\) is the state in the output register of \(V^*_\lambda \) after the simulated execution of \(V^*_\lambda \) by \(\mathsf {Sim}\).
Remark 2.1
In the above definition of quantum black-box \(\epsilon \)-zero-knowledge, we do not consider an entanglement between auxiliary input of a malicious verifier and distinguisher unlike the original definition of quantum zero-knowledge by Watrous [Wat09]. However, in the full version we show that the above definition implies indistinguishability against a distinguisher that may get an entangled state to verifier’s auxiliary input by taking advantage of black-box simulation.
Witness Indistinguishable Proof of Knowledge. The definition of witness indistinguishable proof of knowledge is given in the full version.
2.4 Quantum Rewinding Lemma
Watrous [Wat09] proved a lemma that enables us to amplify the success probability of a quantum algorithm under certain conditions. The following form of the lemma is based on that in [BS20, Lemma 2.1].
Lemma 2.1
([Wat09, BS20]). There is an oracle-aided quantum algorithm \(\mathsf {R}\) that gets as input the following:
-
A quantum circuit \(\mathsf {Q}\) that takes n-input qubits in register \(\mathsf {Inp}\) and outputs a classical bit b (in a register outside \(\mathsf {Inp}\)) and an m output qubits.
-
An n-qubit state \(\rho \) in register \(\mathsf {Inp}\).
-
A number \(T\in \mathbb {N}\) in unary.
\(\mathsf {R}(1^T,\mathsf {Q},\rho )\) executes in time \(T\cdot |\mathsf {Q}|\) and outputs a distribution over m-qubit states \(D_{\rho }:=\mathsf {R}(1^T,\mathsf {Q},\rho )\) with the following guarantees.
For an n-qubit state \(\rho \), denote by \(\mathsf {Q}_{\rho }\) the conditional distribution of the output distribution \(\mathsf {Q}(\rho )\), conditioned on \(b = 0\), and denote by \(p(\rho )\) the probability that \(b = 0\). If there exist \(p_0, q \in (0,1)\), \(\gamma \in (0,\frac{1}{2})\) such that:
-
Amplification executes for enough time: \(T\ge \frac{\log (1/\gamma )}{4p_0(1-p_0)}\),
-
There is some minimal probability that \(b = 0\): For every n-qubit state \(\rho \), \(p_0\le p(\rho )\),
-
\(p(\rho )\) is input-independent, up to \(\gamma \) distance: For every n-qubit state \(\rho \), \(|p(\rho )-q|<\gamma \), and
-
q is closer to \(\frac{1}{2}\): \(p_0(1-p_0)\le q(1-q)\),
then for every n-qubit state \(\rho \),
Moreover, \(\mathsf {R}(1^T,\mathsf {Q},\rho )\) works in the following manner: It uses \(\mathsf {Q}\) for only implementing oracles that perform the unitary part of \(\mathsf {Q}\) and its inverse, acts on \(\mathsf {Inp}\) only through these oracles, and the output of \(\mathsf {R}\) is the state in the output register of \(\mathsf {Q}\) after the simulated execution. We note that \(\mathsf {R}\) may directly act on \(\mathsf {Q}\)’s internal registers other than \(\mathsf {Inp}\).
Remark 2.2
The final claim of the lemma (“Moreover...”) is not explicitly stated in previous works. In the description of \(\mathsf {R}\) in [Wat09], the first qubit of \(\mathsf {Inp}\) is designated to output b, and thus the above requirement is not satisfied. However, this can be easily avoided by just letting \(\mathsf {Q}\) output b in a register outside \(\mathsf {Inp}\) as required above. Then one can see that \(\mathsf {R}\) acts on the input register only through \(\mathsf {Q}\) as seen from the description of \(\mathsf {R}\) in [Wat09] (with the above modification in mind). Looking ahead, this is needed to show our \(\epsilon \)-zero-knowledge simulators are black-box.
3 Extraction Lemma
In this section, we prove our main technical lemma, which we call the extraction lemma. Before giving a formal statement, we give an intuitive explanation. Suppose that we have a two-stage quantum algorithm \(\mathcal {A}=(\mathcal {A}_\mathtt {com},\mathcal {A}_\mathtt {open})\) that works as follows. \(\mathcal {A}_\mathtt {com}\) is given \(\mathsf {pp}\) of a commitment scheme and generates a commitment \(\mathsf {com}\), and passes a quantum state \(\rho _\mathsf {st}\) in its internal register to \(\mathcal {A}_\mathtt {open}\). \(\mathcal {A}_\mathtt {open}\) is given the internal state \(\rho _\mathsf {st}\), and outputs a message-randomness pair (m, r) (which is not necessarily a valid opening to \(\mathsf {com}\)) along with a classical output \(\mathsf {out}\), and let \(\rho '_\mathsf {st}\) be its internal state after the execution. We call a successive execution of \(\mathcal {A}_\mathtt {com}\) and \(\mathcal {A}_\mathtt {open}\) a real experiment. On the other hand, we consider an extraction experiment where an “extractor” \(\mathsf {Ext}\) runs on input \(\rho _\mathsf {st}\) in between \(\mathcal {A}_\mathtt {com}\) and \(\mathcal {A}_\mathtt {open}\) to “extract” a committed message \(m_\mathsf {Ext}\) while generating a simulated \(\mathcal {A}\)’s internal state \(\rho _\mathsf {Ext}\). Then we run \(\mathcal {A}_\mathtt {open}\) with the internal state \(\rho _\mathsf {Ext}\) instead of \(\rho _\mathsf {st}\) to complete the extraction experiment. Roughly, the extraction lemma claims that if the commitment scheme is strong collapse-binding (resp. statistically binding), then there exists an extractor \(\mathsf {Ext}\) such that we have \(m=m_\mathsf {Ext}\) with high probability and distributions of \((m,r,\mathsf {out},\rho '_\mathsf {st})\) in real and extraction experiments are computationally (resp. statistically) indistinguishable conditioned on that (m, r) is a valid opening to \(\mathsf {com}\).
The formal statement is given below.
Definition 3.1
(Extraction Experiments). Let \(\mathsf {Com}=(\mathsf {Setup},\mathsf {Commit})\) be a commitment scheme with message space \(\mathcal {M}\), randomness space \(\mathcal {R}\), commitment space \(\mathcal {C}\mathcal {O}\mathcal {M}\), and a public parameter space \(\mathcal {PP}\). Let \(\mathcal {A}=\{\mathcal {A}_{\mathtt {com},\lambda },\mathcal {A}_{\mathtt {open},\lambda },\rho _{\lambda }\}_{\lambda \in \mathbb {N}}\) be a sequence of two-stage non-uniform QPT algorithms with the following syntax:
-
\(\mathcal {A}_{\mathtt {com},\lambda }(\mathsf {pp};\rho _\lambda )\rightarrow (\mathsf {com},\rho _\mathsf {st})\): It takes as input \(\mathsf {pp}\in \mathcal {PP}\) and an advice \(\rho _\lambda \), and outputs \(\mathsf {com}\in \mathcal {C}\mathcal {O}\mathcal {M}\) and a quantum state \(\rho _\mathsf {st}\) in register \(\mathbf {ST}\).
-
\(\mathcal {A}_{\mathtt {open},\lambda }(\rho _\mathsf {st})\rightarrow (m,r,\mathsf {out},\rho '_\mathsf {st})\): It takes as input a quantum state \(\rho _\mathsf {st}\) in register \(\mathbf {ST}\), and outputs \(m\in \mathcal {M}\), \(r\in \mathcal {R}\), a classical string \(\mathsf {out}\), and a quantum state \(\rho '_\mathsf {st}\) in register \(\mathbf {ST}\).
Let \(\mathsf {Ext}\) be a QPT algorithm and \(\delta \) be a function in \(\lambda \). Then we define following experiments:

Lemma 3.1
(Extraction Lemma). For any strong collapse-binding commitment scheme \(\mathsf {Com}=(\mathsf {Setup},\mathsf {Commit})\), there exists a QPT algorithm \(\mathsf {Ext}\) such that for any noticeable function \(\delta (\lambda )\) and \(\mathcal {A}=\{\mathcal {A}_{\mathtt {com},\lambda },\mathcal {A}_{\mathtt {open},\lambda },\rho _{\lambda }\}_{\lambda \in \mathbb {N}}\) as in Definition 3.1, we have
If \(\mathsf {Com}\) is statistically binding instead of strong collapse-binding, we have
Moreover, \(\mathsf {Ext}(1^\lambda ,1^{\delta ^{-1}},\mathsf {pp},\mathsf {com},\mathcal {A}_{\mathtt {open},\lambda },\rho _\mathsf {st})\) works in the following manner: It uses \(\mathcal {A}_{\mathtt {open},\lambda }\) for only implementing oracles that perform unitary part of \(\mathcal {A}_{\mathtt {open},\lambda }\) and its inverse, and acts on \(\mathbf {ST}\) only through black-box access to the oracles. The second output \(\rho _\mathsf {Ext}\) of \(\mathsf {Ext}\) is the state in \(\mathbf {ST}\) after the execution. We note that \(\mathsf {Ext}\) may directly act on internal registers of \(\mathcal {A}_{\mathtt {open},\lambda }\) other than \(\mathbf {ST}\).
The above lemma abstracts our technical core, which is extraction of the verifier’s committed challenge without collapsing verifier’s internal state too much. (One can think of \(\mathcal {A}\) in the above lemma as the verifier and \(\rho _{\mathsf {st}}\) and \(\rho '_{\mathsf {st}}\) as verifier’s internal states before and after opening the commitment, respectively, in our constant round \(\epsilon \)-zero-knowledge proofs/arguments.) Since the intuition of the proof is already explained in Sect. 1.2, we defer the proof to the full version.
4 Post-quantum \(\epsilon \)-Zero-Knowledge Proof and Argument
In this section, we prove the following theorems.
Theorem 4.1
If the QLWE assumption holds, then there exists a 5-round post-quantum black-box \(\epsilon \)-zero-knowledge proof for all \(\mathbf {NP}\) languages.
Theorem 4.2
If a collapsing hash function exists, then there exists a 5-round post-quantum black-box \(\epsilon \)-zero-knowledge proof for all \(\mathbf {NP}\) languages.
Theorem 4.3
If post-quantunm OWF exists, then there exists a 9-round post-quantum black-box \(\epsilon \)-zero-knowledge argument for all \(\mathbf {NP}\) languages.
In the rest of this section, we prove Theorem 4.1 and 4.2. The proof of Theorem 4.3 is given in the full version.
4.1 Construction
Our construction is the same as the Golderich-Kahan protocol [GK96] except that we instantiate the verifier’s commitment with a strong collapse-binding commitment and we rely on a post-quantum delayed-witness \(\varSigma \)-protocol. Specifically, our construction is built on the following ingredients:
-
A commitment scheme \((\mathsf {CBCom}.\mathsf {Setup},\mathsf {CBCom}.\mathsf {Commit})\) that is statistical hiding and strong collapse-binding with message space \(\{0,1\}^\lambda \) and randomness space \(\mathcal {R}\). As noted in Sect. 2.2, such a commitment scheme exists under the QLWE assumption.
-
A delayed-witness \(\varSigma \)-protocol \((\varSigma .P_1,\varSigma .P_3,\varSigma .V)\) for an \(\mathbf {NP}\) language \(L\) as defined in Definition 2.2. As noted in Sect. 2.3, such a protocol exists under the QLWE assumption.
Then our construction of post-quantum black-box \(\epsilon \)-zero-knowledge proof is given in Fig. 1.
The completeness of the protocol clearly follows from that of the underlying \(\varSigma \)-protocol. In Sect. 4.2 and 4.3, we prove that this protocol satisfies statistical soundness and quantum black-box \(\epsilon \)-zero-knowledge. Then we obtain Theorem 4.1.
4.2 Statistical Soundness
This is essentially the same as the proof in [GK96], but we give a proof for completeness.
For \(x\notin L\) an unbounded-time cheating prover \(P^*\), we consider the following sequence of hybrids. We denote by \(\mathsf {win}_i\) the event that \(P^*\) wins in \(\mathsf {Hyb}_i\).
-
\(\mathsf {Hyb}_1\): This is the original game. That is,
-
1.
\(P^*\) sends \(\mathsf {pp}\) to \(V\).
-
2.
\(V\) chooses \(e \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \{0,1\}^\lambda \) and \(r \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \mathcal {R}\), computes \(\mathsf {com} \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \mathsf {CBCom}.\mathsf {Commit}(\mathsf {pp},e;r)\), and sends \(\mathsf {com}\) to \(P^*\).
-
3.
\(P^*\) sends a to \(V\).
-
4.
\(V\) sends (e, r) to \(P^*\)
-
5.
\(P^*\) sends z to \(V\).
We say that \(P^*\) wins if we have \(\varSigma .V(x,a,e,z)=\top \).
-
1.
-
\(\mathsf {Hyb}_2\): This hybrid is identical to the previous one except that in Step 4, \(V\) uniformly chooses \(r'\) such that \(\mathsf {com}=\mathsf {CBCom}.\mathsf {Commit}(\mathsf {pp},e;r')\) and sends \((e,r')\) to \(P^*\) instead of (e, r). We note that this procedure may be inefficient. This is just a conceptual change and thus we have \(\Pr [\mathsf {win}_1]=\Pr [\mathsf {win}_2]\).
-
\(\mathsf {Hyb}_3\): This hybrid is identical to the previous one except that in Step 2, \(V\) sends \(\mathsf {com} \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \mathsf {CBCom}.\mathsf {Commit}(\mathsf {pp},0^\ell ;r)\) and the generation of e is delayed to Step 4. Since no information of r is given to \(P^*\) due to the modification made in \(\mathsf {Hyb}_2\), by the statistical hiding property of \(\mathsf {CBCom}\), we have \(|\Pr [\mathsf {win}_3]-\Pr [\mathsf {win}_2]|=\mathsf {negl}(\lambda )\). Now, it is easy to prove \(\Pr [\mathsf {win}_3]=\mathsf {negl}(\lambda )\) by reducing it to the statistical soundness of the \(\varSigma \)-protocol. Namely, we consider a cheating prover \(\varSigma .P^*\) against the \(\varSigma \)-protocol that works as follows.
-
1.
\(\varSigma .P^*\) runs \(P^*\) to get the first message \(\mathsf {pp}\).
-
2.
\(\varSigma .P^*\) computes \(\mathsf {com} \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \mathsf {CBCom}.\mathsf {Commit}(\mathsf {pp},0^\ell ;r)\), sends \(\mathsf {com}\) to \(P^*\), and gets the third message a. Then \(\varSigma .P^*\) sends a to its own external challenger as the first message of the \(\varSigma \)-protocol.
-
3.
Upon receiving a challenge e from the external challenger, \(\varSigma .P^*\) uniformly chooses \(r'\) such that \(\mathsf {com}=\mathsf {CBCom}.\mathsf {Commit}(\mathsf {pp},e;r')\), sends \((e,r')\) to \(P^*\), and gets the \(P^*\)’s final message z. Then \(\varSigma .P^*\) sends z to the external challenger.
It is easy to see that \(\varSigma .P^*\) perfectly simulates the environment in \(\mathsf {Hyb}_3\) for \(P^*\). Therefore, \(\varSigma .P^*\)’s winning probability is equal to \(\Pr [\mathsf {win}_3]\). On the other hand, by soundness of the \(\varSigma \)-protocol, \(\varSigma .P^*\)’s winning probability is \(\mathsf {negl}(\lambda )\). Therefore we have \(\Pr [\mathsf {win}_3]=\mathsf {negl}(\lambda )\).
-
1.
Combining the above, we have \(\Pr [\mathsf {win}_1]=\mathsf {negl}(\lambda )\), which means that the protocol satisfies the statistical soundness.
4.3 Quantum Black-Box \(\epsilon \)-Zero-Knowledge
Structure of the Proof. A high-level structure of our proof is similar to that of [BS20]. Specifically, we first construct simulators \(\mathsf {Sim}_\mathsf {a}\) and \(\mathsf {Sim}_\mathsf {na}\) that simulate the “aborting case” and “non-aborting case”, respectively. More precisely, \(\mathsf {Sim}_\mathsf {a}\) correctly simulates the verifier’s view if the verifier aborts and otherwise returns a failure symbol \(\mathsf {Fail}\) and \(\mathsf {Sim}_\mathsf {na}\) correctly simulates the verifier’s view if the verifier does not abort and otherwise returns a failure symbol \(\mathsf {Fail}\). Then we consider a combined simulator \(\mathsf {Sim}_\mathsf {comb}\) that runs either of \(\mathsf {Sim}_\mathsf {a}\) or \(\mathsf {Sim}_\mathsf {na}\) with equal probability. Then \(\mathsf {Sim}_\mathsf {comb}\) correctly simulates the verifier’s view conditioned on that the output is not \(\mathsf {Fail}\), and it returns \(\mathsf {Fail}\) with probability almost 1/2. By applying the Watrous’ quantum rewinding lemma (Lemma 2.1) to \(\mathsf {Sim}_\mathsf {comb}\), we can convert it to a full-fledged simulator.
Though the above high-level structure is similar to [BS20], the analyses of simulators \(\mathsf {Sim}_\mathsf {a}\) and \(\mathsf {Sim}_\mathsf {na}\) are completely different from [BS20] since we consider different protocols. While the analysis of \(\mathsf {Sim}_\mathsf {a}\) is easy, the analysis of \(\mathsf {Sim}_\mathsf {na}\) is a little more complicated as it requires the extraction lemma (Lemma 3.1), which was developed in Sect. 3.
Proof of Quantum Black-Box \(\epsilon \)-Zero-Knowledge. For clarity of exposition, we first show the quantum \(\epsilon \)-zero-knowledge property ignoring that the simulator should be black-box. That is, we give the full description of the malicious verifier and its quantum advice as part of the simulator’s input instead of only the oracle access to the verifier. At the end of the proof, we explain that the simulator is indeed black-box.
In quantum \(\epsilon \)-zero-knowledge, we need to show a simulator \(\mathsf {Sim}\) that takes an accuracy parameter \(1^{\epsilon ^{-1}}\) as part of its input. We assume \(\epsilon (\lambda )= o(1)\) without loss of generality since the other case trivially follows from this case. Without loss of generality, we can assume that a malicious verifier \(V^*\) does not terminate the protocol before the prover aborts since it does not gain anything by declaring the termination. We say that \(V^*\) aborts if it fails to provide a valid opening (e, r) to \(\mathsf {com}\) in Step 2b (i.e., the prover aborts in Step 2c).
First, we construct a simulator \(\mathsf {Sim}_\mathsf {comb}\), which returns a special symbol \(\mathsf {Fail}\) with probability roughly 1/2 but almost correctly simulates the output of \(V^*_\lambda \) conditioned on that it does not return \(\mathsf {Fail}\). The simulator \(\mathsf {Sim}_\mathsf {comb}\) uses simulators \(\mathsf {Sim}_\mathsf {a}\) and \(\mathsf {Sim}_\mathsf {na}\) as sub-protocols:
-
\(\mathsf {Sim}_\mathsf {comb}(x,1^{\epsilon ^{-1}},V^*_\lambda ,\rho _\lambda )\):
-
1.
Choose \(\mathsf {mode} \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \{\mathsf {a},\mathsf {na}\}\).
-
2.
Run \(\mathsf {Sim}_{\mathsf {mode}}(x,1^{\epsilon ^{-1}},V^*_\lambda ,\rho _\lambda )\).
-
3.
Output what \(\mathsf {Sim}_{\mathsf {mode}}\) outputs.
-
1.
-
\(\mathsf {Sim}_\mathsf {a}(x,1^{\epsilon ^{-1}},V^*_\lambda ,\rho _\lambda )\):Footnote 16
-
1.
Set \(V^*_\lambda \)’s internal state to \(\rho _\lambda \).
-
2.
Compute \(\mathsf {pp} \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \mathsf {CBCom}.\mathsf {Setup}(1^\lambda )\) and send \(\mathsf {pp}\) to \(V^*_\lambda \).
-
3.
\(V^*_\lambda \) returns \(\mathsf {com}\).
-
4.
Compute \((a,\mathsf {st}) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \varSigma .P_1(x)\) and send a to \(V^*_\lambda \).
-
5.
\(V^*_\lambda \) returns (e, r).
-
6.
Return \(\mathsf {Fail}\) and abort if \(\mathsf {CBCom}.\mathsf {Commit}(\mathsf {pp},e;r)= \mathsf {com}\). Otherwise, let \(V^*_\lambda \) output the final output notifying that the prover aborts.
-
7.
The final output of \(V^*_\lambda \) is treated as the output \(\mathsf {Sim}_\mathsf {a}\).
-
1.
-
\(\mathsf {Sim}_\mathsf {na}(x,1^{\epsilon ^{-1}},V^*_\lambda , \rho _\lambda )\):
-
1.
Set \(V^*_\lambda \)’s internal state to \(\rho _\lambda \).
-
2.
Compute \(\mathsf {pp} \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \mathsf {CBCom}.\mathsf {Setup}(1^\lambda )\) and send \(\mathsf {pp}\) to \(V^*_\lambda \).
-
3.
\(V^*_\lambda \) returns \(\mathsf {com}\). Let \(\rho _\mathsf {st}\) be the internal state of \(V^*_\lambda \) at this point.
-
4.
Compute \((e_\mathsf {Ext},\rho _\mathsf {Ext}) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \mathsf {Ext}(1^\lambda ,1^{\delta ^{-1}},\mathsf {pp},\mathsf {com},\mathcal {A}_{\mathtt {open},\lambda },\rho _{\mathsf {st}})\) where \(\mathsf {Ext}\) is as in Lemma 3.1 for the commitment scheme \(\mathsf {CBCom}\), \(\delta :=\frac{\epsilon ^2}{3600\log ^4(\lambda )}\), and \(\mathcal {A}=(\mathcal {A}_{\mathtt {com},\lambda },\mathcal {A}_{\mathtt {open},\lambda })\) as defined below:
-
\(\mathcal {A}_{\mathtt {com},\lambda }(\mathsf {pp};\rho _\lambda )\): It sets \(V^*_\lambda \)’s internal state to \(\rho _\lambda \) and sends \(\mathsf {pp}\) to \(V^*_\lambda \). Let \(\mathsf {com}\) be the response by \(V^*_\lambda \) and \(\rho _\mathsf {st}\) be the internal state of \(V^*_\lambda \) at this point. It outputs \((\mathsf {com},\rho _\mathsf {st})\).
-
\(\mathcal {A}_{\mathtt {open},\lambda }(\rho _\mathsf {st})\): It generates \((a,\mathsf {st}) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \varSigma .P_1(x)\),Footnote 17 sets \(V^*_\lambda \)’s internal state to \(\rho _\mathsf {st}\), and sends a to \(V^*_\lambda \). Let (e, r) be the response by \(V^*_\lambda \) and let \(\rho '_{\mathsf {st}}\) be the internal state of \(V^*_\lambda \) at this point. It outputs \((e,r,\mathsf {out}:=(a,\mathsf {st}),\rho '_{\mathsf {st}})\).
Here, we remark that \(V^*_\lambda \)’s internal register corresponds to \(\mathbf {ST}\) and e corresponds to m in the notation of Lemma 3.1.
-
-
5.
Set the verifier’s internal state to \(\rho _\mathsf {Ext}\).
-
6.
Compute \((a,z) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \mathsf {Sim}_{\varSigma }(x,e_{\mathsf {Ext}})\) and send a to \(V^*_\lambda \).
-
7.
\(V^*_\lambda \) returns (e, r).
-
8.
Return \(\mathsf {Fail}\) and abort if \(e\ne e_\mathsf {Ext}\) or \(\mathsf {CBCom}.\mathsf {Commit}(\mathsf {pp},e;r)\ne \mathsf {com}\). Otherwise, send z to \(V^*_\lambda \).
-
9.
The final output of \(V^*_\lambda \) is treated as the output \(\mathsf {Sim}_\mathsf {na}\).
-
1.
Intuitively, \(\mathsf {Sim}_\mathsf {a}\) (resp. \(\mathsf {Sim}_\mathsf {na}\)) is a simulator that simulates the verifier’s view in the case that verifier aborts (resp. does not abort).
More formally, we prove the following lemmas.
Lemma 4.1
(\(\mathsf {Sim}_\mathsf {a}\) simulates the aborting case). For any non-uniform QPT malicious verifier \(V^*=\{V^*_\lambda ,\rho _\lambda \}_{\lambda \in \mathbb {N}}\), let \(\mathsf {OUT}_{V^*_{\mathsf {a}}}\langle P(w), V^*_\lambda (\rho _\lambda ) \rangle (x)\) be the \(V^*_\lambda \)’s final output that is replaced with \(\mathsf {Fail}\) if \(V^*_\lambda \) does not abort. Then we have
where \(\lambda \in \mathbb {N}\), \(x\in L\cap \{0,1\}^\lambda \), and \(w\in R_L(x)\).
Proof
Since \(\mathsf {Sim}_\mathsf {a}\) perfectly simulates the real execution for \(V^*_\lambda \) when it aborts, Lemma 4.1 immediately follows.
Lemma 4.2
(\(\mathsf {Sim}_\mathsf {na}\) simulates the non-aborting case). For any non-uniform QPT malicious verifier \(V^*=\{V^*_\lambda ,\rho _\lambda \}_{\lambda \in \mathbb {N}}\), let \(\mathsf {OUT}_{V^*_{\mathsf {na}}}\langle P(w), V^*_\lambda (\rho _\lambda ) \rangle (x)\) be the \(V^*_\lambda \)’s final output that is replaced with \(\mathsf {Fail}\) if \(V^*_\lambda \) aborts. Then we have
where \(\lambda \in \mathbb {N}\), \(x\in L\cap \{0,1\}^{\lambda }\), and \(w\in R_L(x)\).
Proof
Here, we analyze \(\mathsf {Sim}_\mathsf {na}(x,1^{\epsilon ^{-1}},V^*_\lambda , \rho _\lambda )\). In the following, we consider hybrid simulators \(\mathsf {Sim}_{\mathsf {na},i}(x,w,1^{\epsilon ^{-1}},V^*_\lambda ,\rho _\lambda )\) for \(i=1,2,3\). We remark that they also take the witness w as input unlike \(\mathsf {Sim}_\mathsf {na}\).
-
\(\mathsf {Sim}_{\mathsf {na},1}(x,w,1^{\epsilon ^{-1}},V^*_\lambda ,\rho _\lambda )\): This simulator works similarly to \(\mathsf {Sim}_\mathsf {na}(x,1^{\epsilon ^{-1}},V^*_\lambda , \rho _\lambda )\) except that it generates \((a,\mathsf {st}) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \varSigma .P_1(x)\) and \(z \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \varSigma .P_3(\mathsf {st},w,e_{\mathsf {Ext}})\) instead of \((a,z) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \mathsf {Sim}_{\varSigma }(x,e_\mathsf {Ext})\) in Step 6. By the special honest-verifier zero-knowledge property of the \(\varSigma \)-protocol, we have
$$\begin{aligned} \{\mathsf {Sim}_\mathsf {na}(x,1^{\epsilon ^{-1}},V^*_\lambda , \rho _\lambda )\}_{\lambda ,x,w} {\mathop {\approx }\limits ^{comp}}\{\{\mathsf {Sim}_{\mathsf {na},1}(x,w,1^{\epsilon ^{-1}},V^*_\lambda ,\rho _\lambda )\}_{\lambda ,x,w}\}_{\lambda ,x,w} \end{aligned}$$where \(\lambda \in \mathbb {N}\), \(x\in L\cap \{0,1\}^{\lambda }\), and \(w\in R_L(x)\).
-
\(\mathsf {Sim}_{\mathsf {na},2}(x,w,1^{\epsilon ^{-1}},V^*_\lambda ,\rho _\lambda )\): This simulator works similarly to \(\mathsf {Sim}_{\mathsf {na},1}(x,w,1^{\epsilon ^{-1}},\)\(V^*_\lambda ,\rho _\lambda )\) except that the generation of z is delayed until Step 8 and it is generated as \(z \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \varSigma .P_3(\mathsf {st},w,e)\) instead of \(z \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \varSigma .P_3(\mathsf {st},w,e_{\mathsf {Ext}})\). The modification does not affect the output distribution since it outputs \(\mathsf {Fail}\) if \(e\ne e_\mathsf {Ext}\) and if \(e=e_\mathsf {Ext}\), then this simulator works in exactly the same way as the previous one. Therefore we have
$$\begin{aligned} \{\mathsf {Sim}_{\mathsf {na},1}(x,w,1^{\epsilon ^{-1}},V^*_\lambda ,\rho _\lambda )\}_{\lambda ,x,w} \equiv \{\mathsf {Sim}_{\mathsf {na},2}(x,w,1^{\epsilon ^{-1}},V^*_\lambda ,\rho _\lambda )\}_{\lambda ,x,w} \end{aligned}$$where \(\lambda \in \mathbb {N}\), \(x\in L\cap \{0,1\}^{\lambda }\), and \(w\in R_L(x)\).
-
\(\mathsf {Sim}_{\mathsf {na},3}(x,w,1^{\epsilon ^{-1}},V^*_\lambda ,\rho _\lambda )\): This simulator works similarly to \(\mathsf {Sim}_{\mathsf {na},2}(x,w,1^{\epsilon ^{-1}},V^*_\lambda ,\rho _\lambda )\) except that Step 4 and 5 are deleted and the check of \(e\ne e_\mathsf {Ext}\) in Step 8 is omitted. That is, it outputs \(\mathsf {Fail}\) in Step 8 if and only if we have \(\mathsf {CBCom}.\mathsf {Commit}(\mathsf {pp},e;r)\ne \mathsf {com}\). We note that \(e_\mathsf {Ext}\) and \(\rho _\mathsf {Ext}\) are no longer used at all and thus need not be generated. We can see that Step 3 is exactly the same as executing \((\mathsf {com},\rho _\mathsf {st}) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \mathcal {A}_{\mathtt {com},\lambda }(\mathsf {pp};\rho _\lambda )\) and Step 6 and 7 of previous and this experiments are exactly the same as executing \((e,r,\mathsf {out}=(a,\mathsf {st}),\rho '_\mathsf {st}) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \mathcal {A}_{\mathtt {open},\lambda }(\rho _\mathsf {Ext})\) and \((e,r,\mathsf {out}=(a,\mathsf {st}),\rho '_\mathsf {st}) \overset{\mathsf {\scriptscriptstyle \$}}{\leftarrow } \mathcal {A}_{\mathtt {open},\lambda }(\rho _\mathsf {st})\), respectively where we define \(\rho '_\mathsf {st}\) in simulated experiments as \(V^*_\lambda \)’s internal state after Step 7. Moreover, the rest of execution of the simulators can be done given \((\mathsf {pp},\mathsf {com},e,r,\mathsf {out}=(a,\mathsf {st}),\rho '_\mathsf {st})\). Therefore, by a straightforward reduction to Lemma 3.1, we have
$$\begin{aligned} \{\mathsf {Sim}_{\mathsf {na},2}(x,w,1^{\epsilon ^{-1}},V^*_\lambda ,\rho _\lambda )\}_{\lambda ,x,w} {\mathop {\approx }\limits ^{comp}}_\delta \{\mathsf {Sim}_{\mathsf {na},3}(x,w,1^{\epsilon ^{-1}},V^*_\lambda ,\rho _\lambda )\}_{\lambda ,x,w} \end{aligned}$$where \(\lambda \in \mathbb {N}\), \(x\in L\cap \{0,1\}^{\lambda }\), and \(w\in R_L(x)\).
We can see that \(\mathsf {Sim}_{\mathsf {na},3}(x,w,1^{\epsilon ^{-1}},V^*_\lambda ,\rho _\lambda )\) perfectly simulates the real execution for \(V^*_\lambda \) and outputs \(V^*_\lambda \)’s output conditioned on that \(V^*_\lambda \) does not abort, and just outputs \(\mathsf {Fail}\) otherwise. Therefore, we have
where \(\lambda \in \mathbb {N}\), \(x\in L\cap \{0,1\}^{\lambda }\), and \(w\in R_L(x)\). Combining the above, Lemma 4.2 is proven.
By combining Lemmas 4.1 and 4.2, we can prove the following lemma.
Lemma 4.3
(\(\mathsf {Sim}_\mathsf {comb}\) simulates \(V^*_\lambda \)’s output with probability almost 1/2). For any non-uniform QPT malicious verifier \(V^*=\{V^*_\lambda ,\rho _\lambda \}_{\lambda \in \mathbb {N}}\), let \(p_{\mathsf {comb}}^{\mathsf {suc}}(x,1^{\epsilon ^{-1}},V^*_\lambda ,\rho _\lambda )\) be the probability that \(\mathsf {Sim}_\mathsf {comb}(x,1^{\epsilon ^{-1}},V^*_\lambda , \rho _\lambda )\) does not return \(\mathsf {Fail}\) and \(D_{\mathsf {sim},\mathsf {comb}}( x,1^{\epsilon ^{-1}},V^*_\lambda ,\rho _\lambda )\) be a conditional distribution of \(\mathsf {Sim}_\mathsf {comb}(x,1^{\epsilon ^{-1}},V^*_\lambda , \rho _\lambda )\), conditioned on that it does not return \(\mathsf {Fail}\). There exists a negligible function \(\mathsf {negl}\) such that for any \(x=\{x_\lambda \in L\cap \{0,1\}^\lambda \}_{\lambda \in \mathbb {N}}\), we have
Moreover, we have
where \(\lambda \in \mathbb {N}\), \(x\in L\cap \{0,1\}^{\lambda }\), and \(w\in R_L(x)\).
Proof
(sketch.) Intuition of the proof is very easy: By Lemma 4.1 and 4.2, \(\mathsf {Sim}_\mathsf {a}\) and \(\mathsf {Sim}_\mathsf {na}\) almost simulate the real output distribution of \(V^*_\lambda \) conditioned on that \(V^*_\lambda \) aborts and does not abort, respectively. Therefore, if we randomly guess if \(V^*_\lambda \) aborts and runs either of \(\mathsf {Sim}_\mathsf {a}\) and \(\mathsf {Sim}_\mathsf {na}\) that successfully works for the guessed case, the output distribution is close to the real output distribution of \(V^*_\lambda \) conditioned on that the guess is correct, which happens with probability almost 1/2.
Indeed, the actual proof is based on the above idea, but for obtaining concrete bounds as in Eq. 1 and 2, we need some tedious calculations. We give a full proof in the full version since the proof is easy and very similar to that in [BS20] (once we obtain Lemma 4.1 and 4.2).
Then, we convert \(\mathsf {Sim}_\mathsf {comb}\) to a full-fledged simulator that does not return \(\mathsf {Fail}\) by using the quantum rewinding lemma (Lemma 2.1). Namely, we let \(\mathsf {Q}\) be a quantum algorithm that takes \(\rho _\lambda \) as input and outputs \(\mathsf {Sim}_\mathsf {comb}(x,1^{\epsilon ^{-1}},V^*_\lambda , \rho _\lambda )\) where \(b:=0\) if and only if it does not return \(\mathsf {Fail}\), \(p_0:=\frac{1}{4}\), \(q:=\frac{1}{2}\), \(\gamma :=\delta \), and \(T:=2\log (1/\delta )\). Then it is easy to check that the conditions for Lemma 2.1 is satisfied by Eq. 1 in Lemma 4.3 (for sufficiently large \(\lambda \)). Then by using Lemma 2.1, we can see that \(\mathsf {R}(1^T,\mathsf {Q},\rho _\lambda )\) runs in time \(T\cdot |\mathsf {Q}|=\mathsf {poly}(\lambda )\) and its output (seen as a mixed state) has a trace distance bounded by \(4\sqrt{\gamma }\frac{\log (1/\gamma )}{p_0(1-p_0)}\) from \(D_{\mathsf {sim},\mathsf {comb}}(x,1^{\epsilon ^{-1}},V^*_\lambda ,\rho _\lambda )\). Since we have \(\gamma =\delta =\frac{\epsilon ^2}{3600\log ^4(\lambda )}=1/\mathsf {poly}(\lambda )\), we have \(4\sqrt{\gamma }\frac{\log (1/\gamma )}{p_0(1-p_0)}< 30\sqrt{\gamma } \log ^2 (\lambda )=\frac{\epsilon }{2}\) for sufficiently large \(\lambda \) where we used \(\log (1/\gamma )=\log (\mathsf {poly}(\lambda ))=o(\log ^2(\lambda ))\). Thus, by combining the above and Eq. 2 in Lemma 4.3, if we define \(\mathsf {Sim}(x,1^{\epsilon ^{-1}},V^*_\lambda ,\rho _\lambda ):=\mathsf {R}(1^T,\mathsf {Q},\rho _\lambda )\), then we have
We can conclude the proof of quantum \(\epsilon \)-zero-knowledge by noting that we have \(\frac{\epsilon }{2}+4\delta < \epsilon \) since we have \(\delta = \frac{\epsilon ^2}{3600\log ^4(\lambda )} < \frac{\epsilon }{8}\).
Black-Box Simulation. Here, we explain that the simulator \(\mathsf {Sim}\) constructed as above only needs black-box access to the verifier. What we need to show are that \(\mathsf {Sim}\) applies the unitary part \(U_{V^*_\lambda }\) of \(V^*_\lambda \) and its inverse \(U_{V^*_\lambda }^\dagger \) only as oracles and \(\mathsf {Sim}\) does not directly act on \(V^*_\lambda \)’s internal register. There are two parts of the construction of \(\mathsf {Sim}\) that are not obviously black-box. The first is Step 4 and 5 of \(\mathsf {Sim}_\mathsf {na}\) where it runs the extraction algorithm \(\mathsf {Ext}\) of Lemma 3.1, and the second is the conversion from \(\mathsf {Sim}_\mathsf {comb}\) to \(\mathsf {Sim}\) using \(\mathsf {R}\) in Lemma 2.1. In the following, we explain that both steps can be implemented by black-box access to the verifier.
-
1.
By Lemma 3.1, \(\mathsf {Ext}\) uses the unitary part of \(\mathcal {A}_{\mathtt {open},\lambda }\) and its inverse only in a black-box manner, and they can be implemented by black-box access to \(U_{V^*_\lambda }\) and \(U_{V^*_\lambda }^\dagger \). Moreover, since register \(\mathbf {ST}\) in the notation of Lemma 3.1 corresponds to the internal register of \(V^*_\lambda \) in our context, the lemma ensures that \(\mathsf {Ext}\) does not directly act on it. Also, \(\mathsf {Sim}_{\mathsf {na}}\) need not explicitly set \(V^*_\lambda \)’s internal register to \(\rho _\mathsf {Ext}\) in Step 5 if we do the above black-box simulation since a state in the register automatically becomes \(\rho _\mathsf {Ext}\) after the execution as stated in Lemma 3.1. Therefore, this step can be implemented by black-box access to \(V^*_\lambda \).
-
2.
Given the above observation, we now know that both \(\mathsf {Sim}_\mathsf {a}\) and \(\mathsf {Sim}_\mathsf {na}\) only need black-box access to \(V^*_\lambda \). This means that \(\mathsf {Q}\) only needs black-box access to \(V^*_\lambda \). Since \(\mathsf {R}\) only uses \(\mathsf {Q}\) as oracles that perform the unitary part of \(\mathsf {Q}\) and its inverse as stated in Lemma 2.1 and they can be implemented by black-box access to \(V^*_\lambda \), \(\mathsf {R}\) uses \(U_{V^*_\lambda }\) and \(U_{V^*_\lambda }^\dagger \) only as oracles. Moreover, since the register \(\mathsf {Inp}\) in Lemma 2.1 corresponds to the internal register of \(V^*_\lambda \) in our context, \(\mathsf {R}\) does not directly act on it.
By the above observations, we can see that the simulator \(\mathsf {Sim}\) only needs black-box access to \(V^*_\lambda \).
4.4 Instantiation from Collapsing Hash Function
Our construction in Fig. 1 is based on two building blocks: a statistically hiding and strong collapse-binding commitment scheme and a delayed-witness \(\varSigma \)-protocol. Though the former can be instantiated by a collapsing hash function, we do not know how to instantiate the latter by a collapsing hash function since it needs non-interactive commitment that is not known to be implied by collapsing hash functions. However, we can just use a 4-round version of a delayed-witness \(\varSigma \)-protocol where the first message “commitment” in the \(\varSigma \)-protocol is instantiated based on Naor’s commitments [Nao91] instead of a non-interactive one. Since Naor’s commitments can be instantiated under any OWF and collapsing hash function is trivially also one-way, we can instantiate the 4-round version of a delayed-witness \(\varSigma \)-protocol based on a collapsing hash function. We can prove security of the construction based on 4-round version of a delayed-witness \(\varSigma \)-protocol in essentially the same manner as the security proofs in Sect. 4.2 and 4.3. We also note that this does not increase the number of rounds of our construction. Based on these observations, we obtain Theorem 4.2.
Notes
- 1.
Strictly speaking, Watrous’ assumption is a statistically binding and post-quantum computationally hiding commitment scheme, and he did not claim that this can be constructed under the existence of post-quantum OWFs. However, we can see that such a commitment scheme can be obtained by instantiating the construction of [Nao91, HILL99] with a post-quantum OWF.
- 2.
3-round suffices for achieving a constant soundness error, but super-constant times sequential repetitions are needed for achieving negligible soundness error (i.e., a cheating prover can let a verifier accept on a false statement only with a negligible probability). Negligible soundness error is a default requirement in this paper.
- 3.
- 4.
- 5.
In this paper, we use \(\varSigma \)-protocol to mean a parallel repetition version where soundness error is reduced to negligible.
- 6.
We note that this construction is based on an earlier work of [BCY91].
- 7.
This is also observed in [BS20].
- 8.
Strictly speaking, we need to use a slightly stronger variant of collapse-binding commitments which we call strong collapse-binding commitments. Such commitments can be constructed under the QLWE assumption or the existence of collapsing hash functions in more general. See Sect. 2.2 for more details.
- 9.
\(\mathbf {Aux}\) stores multiple qubits, but we denote by
 to mean
to mean 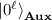 for the appropriate length \(\ell \) for notational simplicity.
for the appropriate length \(\ell \) for notational simplicity. - 10.
The protocol achieves full-fledged ZK if we allow the simulator to take non-uniform advice or assume a super-polynomial assumption.
- 11.
In [PS19], they do not explicitly claim ZK against quantum adversaries. However, since their security proof does not rely on rewinding, it immediately extends to post-quantum security if we assume the underlying assumption against quantum adversaries.
- 12.
Actually, their protocol is delayed-input, i.e., the first message generation does not use the statement either.
- 13.
A lossy function is defined similarly to a lossy trapdoor function [PW08] except that we do not require the existence of trapdoor.
- 14.
In other words, \(\mathcal {X}{\mathop {\approx }\limits ^{stat}}_{\delta }\mathcal {Y}\) means that there exists a negligible function \(\mathsf {negl}\) such that the trace distance between \(\rho _{X_i}\) and \(\rho _{Y_i}\) is at most \(\delta (\lambda ) + \mathsf {negl}(\lambda )\) for all \(\lambda \in \mathbb {N}\) and \(i\in I_\lambda \) where \(\rho _{X_i}\) and \(\rho _{Y_i}\) denote density matrices corresponding to \(X_{i}\) and \(Y_{i}\).
- 15.
We do not require special soundness, which is often a default requirement of \(\varSigma \)-protocol.
- 16.
Though \(\mathsf {Sim}_\mathsf {a}\) does not depend on \(\epsilon \), we include \(1^{\epsilon ^{-1}}\) in the input for notational uniformity.
- 17.
We note that we consider x to be hardwired into \(\mathcal {A}_{\mathtt {open},\lambda }\). We also note that though \(\mathcal {A}_{\mathtt {open},\lambda }\) does not take explicit randomness, it can generate randomness by say, applying Hadamard on its working register and then measuring it.
References
Alagic, G., Childs, A.M., Grilo, A.B., Hung, S.-H.: Non-interactive classical verification of quantum computation. In: Pass, R., Pietrzak, K. (eds.) TCC 2020, Part III. LNCS, vol. 12552, pp. 153–180. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64381-2_6
Ananth, P., La Placa, R.L.: Secure quantum extraction protocols. In: Pass, R., Pietrzak, K. (eds.) TCC 2020, Part III. LNCS, vol. 12552, pp. 123–152. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64381-2_5
Aharon, N., Regev, O.: Witness-preserving Amplification of QMA (lecture note) (2006). https://cims.nyu.edu/regev/teaching/quantum_fall_2005/ln/qma.pdf
Brassard, G., Crepeau, C.: Sorting out zero-knowledge. In: Quisquater, J.-J., Vandewalle, J. (eds.) EUROCRYPT 1989. LNCS, vol. 434, pp. 181–191. Springer, Heidelberg (1990). https://doi.org/10.1007/3-540-46885-4_20
Brassard, G., Crépeau, C., Yung, M.: Constant-round perfect zero-knowledge computationally convincing protocols. Theor. Comput. Sci. 84(1), 23–52 (1991)
Broadbent, A., Grilo, A.B.: QMA-hardness of consistency of local density matrices with applications to quantum zero-knowledge. In: 61st FOCS, pp. 196–205 (2020)
Broadbent, A., Ji, Z., Song, F., Watrous, J.: Zero-knowledge proof systems for QMA. SIAM J. Comput. 49(2), 245–283 (2020)
Bitansky, N., Kalai, Y.T., Paneth, O.: Multi-collision resistance: a paradigm for keyless hash functions. In: 50th ACM STOC, pp. 671–684 (2018)
Bitansky, N., Khurana, D., Paneth, O.: Weak zero-knowledge beyond the black-box barrier. In: 51st ACM STOC, pp. 1091–1102 (2019)
Barak, B., Lindell, Y.: Strict polynomial-time in simulation and extraction. In: 34th ACM STOC, pp. 484–493 (2002)
Brakerski, Z., Langlois, A., Peikert, C., Regev, O., Stehlé, D.: Classical hardness of learning with errors. In: 45th ACM STOC, pp. 575–584 (2013)
Blum, M.: How to prove a theorem so no one else can claim it. In: Proceedings of the International Congress of Mathematicians, pp. 1444–1451 (1986)
Bitansky, N., Paneth, O.: Point obfuscation and 3-round zero-knowledge. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 190–208. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_11
Brakerski, Z.: Quantum FHE (almost) as secure as classical. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part III. LNCS, vol. 10993, pp. 67–95. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_3
Bitansky, N., Shmueli, O.: Post-quantum zero knowledge in constant rounds. In: 52nd ACM STOC, pp. 269–279 (2020)
Brakerski, Z., Yuen, H.: Quantum Garbled Circuits. arXiv:2006.01085 (2020)
Chia, N.-H., Chung, K.-M., Liu, Q., Yamakawa, T.: On the Impossibility of Post-Quantum Black-Box Zero-Knowledge in Constant Rounds. arXiv:2103.11244 (2021)
Chia, N.-H., Chung, K.-M., Yamakawa, T.: Classical verification of quantum computations with efficient verifier. In: Pass, R., Pietrzak, K. (eds.) TCC 2020, Part III. LNCS, vol. 12552, pp. 181–206. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64381-2_7
Chung, K.-M., Lui, E., Pass, R.: From weak to strong zero-knowledge and applications. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part I. LNCS, vol. 9014, pp. 66–92. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46494-6_4
Coladangelo, A., Vidick, T., Zhang, T.: Non-interactive zero-knowledge arguments for QMA, with preprocessing. In: Micciancio, D., Ristenpart, T. (eds.) CRYPTO 2020, Part III. LNCS, vol. 12172, pp. 799–828. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-56877-1_28
Damgård, I., Fehr, S., Salvail, L.: Zero-knowledge proofs and string commitments withstanding quantum attacks. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 254–272. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_16
Dwork, C., Naor, M., Reingold, O., Stockmeyer, L.J.: Magic functions. J. ACM 50(6), 852–921 (2003)
Dwork, C., Naor, M., Sahai, A.: Concurrent zero-knowledge. J. ACM 51(6), 851–898 (2004)
Fleischhacker, N., Goyal, V., Jain, A.: On the existence of three round zero-knowledge proofs. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part III. LNCS, vol. 10822, pp. 3–33. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_1
Feige, U., Shamir, A.: Zero knowledge proofs of knowledge in two rounds. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 526–544. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_46
Goldreich, O., Kahan, A.: How to construct constant-round zero-knowledge proof systems for NP. J. Cryptol. 9(3), 167–190 (1996)
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof systems. SIAM J. Comput. 18(1), 186–208 (1989)
Goldreich, O., Micali, S., Wigderson, A.: Proofs that yield nothing but their validity for all languages in NP have zero-knowledge proof systems. J. ACM 38(3), 691–729 (1991)
Goldreich, O.: The Foundations of Cryptography - Volume 1: Basic Techniques. Cambridge University Press, Cambridge (2001)
Goldreich, O.: The Foundations of Cryptography - Volume 2: Basic Applications. Cambridge University Press, Cambridge (2004)
Graaf, J.V.D.: Towards a formal definition of security for quantum protocols. PhD thesis, University of Montreal, Montreal, Canada (1997)
Håstad, J., Impagliazzo, R., Levin, L.A., Luby, M.: A pseudorandom generator from any one-way function. SIAM J. Comput. 28(4), 1364–1396 (1999)
Jain, A., Kalai, Y.T., Khurana, D., Rothblum, R.: Distinguisher-dependent simulation in two rounds and its applications. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part II. LNCS, vol. 10402, pp. 158–189. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_6
Kobayashi, H.: Non-interactive quantum perfect and statistical zero-knowledge. In: Ibaraki, T., Katoh, N., Ono, H. (eds.) ISAAC 2003. LNCS, vol. 2906, pp. 178–188. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-24587-2_20
Mahadev, U.: Classical homomorphic encryption for quantum circuits. In: 59th FOCS, pp. 332–338 (2018)
Mahadev, U.: Classical verification of quantum computations. In: 59th FOCS, pp. 259–267 (2018)
Naor, M.: Bit commitment using pseudorandomness. J. Cryptol. 4(2), 151–158 (1991)
Nagaj, D., Wocjan, P., Zhang, Y.: Fast Amplification of QMA. arXiv:0904.1549 (2009)
Pass, R.: Simulation in quasi-polynomial time, and its application to protocol composition. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 160–176. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_10
Peikert, C.: Public-key cryptosystems from the worst-case shortest vector problem: extended abstract. In: 41st ACM STOC, pp. 333–342 (2009)
Peikert, C., Shiehian, S.: Noninteractive zero knowledge for NP from (plain) learning with errors. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part I. LNCS, vol. 11692, pp. 89–114. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26948-7_4
Peikert, C., Waters, B.: Lossy trapdoor functions and their applications. In: 40th ACM STOC, pp. 187–196 (2008)
Pass, R., Wee, H.: Black-box constructions of two-party protocols from one-way functions. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 403–418. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_24
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. J. ACM 56(6), 34:1-34:40 (2009)
Shmueli, O.: Multi-theorem (Malicious) Designated-Verifier NIZK for QMA. arXiv:2007.12923 (2020)
Sahai, A., Vadhan, S.P.: A complete problem for statistical zero knowledge. J. ACM 50(2), 196–249 (2003)
Unruh, D.: Quantum proofs of knowledge. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 135–152. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_10
Unruh, D.: Collapse-binding quantum commitments without random oracles. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016, Part II. LNCS, vol. 10032, pp. 166–195. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_6
Unruh, D.: Computationally binding quantum commitments. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part II. LNCS, vol. 9666, pp. 497–527. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_18
Watrous, J.: Zero-knowledge against quantum attacks. SIAM J. Comput. 39(1), 25–58 (2009)
Zhandry, M.: Quantum lightning never strikes the same state twice. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part III. LNCS, vol. 11478, pp. 408–438. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17659-4_14
Acknowledgement
NHC’s research is support by the U.S. Department of Defense and NIST through the Hartree Postdoctoral Fellowship at QuICS and by NSF through IUCRC Planning Grant Indiana University: Center for Quantum Technologies (CQT) under award number 2052730. KMC’s research is partially supported by MOST, Taiwan, under Grant no. MOST 109-2223-E-001-001-MY3 and Executive Yuan Data Safety and Talent Cultivation Project (ASKPQ-109-DSTCP).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 International Association for Cryptologic Research
About this paper
Cite this paper
Chia, NH., Chung, KM., Yamakawa, T. (2021). A Black-Box Approach to Post-Quantum Zero-Knowledge in Constant Rounds. In: Malkin, T., Peikert, C. (eds) Advances in Cryptology – CRYPTO 2021. CRYPTO 2021. Lecture Notes in Computer Science(), vol 12825. Springer, Cham. https://doi.org/10.1007/978-3-030-84242-0_12
Download citation
DOI: https://doi.org/10.1007/978-3-030-84242-0_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-84241-3
Online ISBN: 978-3-030-84242-0
eBook Packages: Computer ScienceComputer Science (R0)




 on
on  is applied, and otherwise honestly opens (e, r).
is applied, and otherwise honestly opens (e, r). to
to  where
where  , the projection
, the projection  .
. to
to  with overwhelming probability within
with overwhelming probability within  after Step
after Step  and runs
and runs  in register
in register  as a sub-normalized state whose norm is the probability that
as a sub-normalized state whose norm is the probability that  .
. be verifier’s internal state at this point.
be verifier’s internal state at this point. . Abort if
. Abort if  , and proceed to the next step.
, and proceed to the next step. . Let (e, r) be the verifier’s response. Abort if (e, r) is not a valid opening to
. Let (e, r) be the verifier’s response. Abort if (e, r) is not a valid opening to 
 to mean
to mean 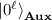 for the appropriate length
for the appropriate length 