Abstract
Among the large class of modified gravity theories, teleparallel gravity theories are distinguished by the fact that they express gravity by the torsion of a flat (curvature-free), metric-compatible connection. This approach, which offers both an alternative formulation of general relativity itself, as well as modifications thereof, is appealing under several aspects. Teleparallel gravity theories can be understood as gauge theories of the translation group, whose Lagrangian is of first derivative order in the fundamental fields, and thus has more in common with the Yang-Mills Lagrangian known from particle physics. Further, they offer a rich phenomenology, giving rise to numerous viable candidate theories addressing the open questions in cosmology. This chapter gives an introduction to the foundations of teleparallel gravity, an overview of modified teleparallel theories, and a summary of the phenomenology of various such theories in cosmology and beyond.
The original version of this chapter was revised. The affiliations of authors, Sebastian Bahamonde, Konstantinos F. Dialektopoulos, Manuel Hohmann, Jackson Levi Said have been updated. The correction to this chapter is available at https://doi.org/10.1007/978-3-030-83715-0_39
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
1 Foundations of Teleparallel Gravity
Teleparallel Gravity theories have received growing attention during the last decade. Their most distinguishing feature is the use of a different geometric setting compared to General Relativity, which features a flat (curvature-free) connection, and torsion instead of curvature. This section gives a brief introduction to the mathematical background and foundations of Teleparallel Gravity. Section 14.1.1 gives an overview of the geometric setting and dynamical field content. Its relation to a gauge theory of translations is explained in Sect. 14.1.2. Local Lorentz invariance is discussed in Sect. 14.1.3. Section 14.1.4 briefly elucidates how matter couples to the teleparallel geometry. Finally, Sect. 14.1.5 gives an account of the most simple Teleparallel Gravity theory, which is equivalent to General Relativity at the level of its field equations. The notation used here and in the following sections on Teleparallel Gravity is summarized in the Convention Table in the beginning of the book.
1.1 Teleparallel Geometry
The most important, distinguishing feature of Teleparallel Gravity [1] is its use of an affine connection, whose connection coefficients will be denoted by  , and which is different from the Levi-Civita connection of the metric \(g_{\mu \nu }\). This connection is chosen to be flat, in the sense that has vanishing curvature
, and which is different from the Levi-Civita connection of the metric \(g_{\mu \nu }\). This connection is chosen to be flat, in the sense that has vanishing curvature

where we denote quantities related to the teleparallel connection with a bullet  to distinguish them from their Levi-Civita counterparts. For instance,
to distinguish them from their Levi-Civita counterparts. For instance,  denotes the teleparallel covariant derivative, while \(\nabla _{\mu }\) denotes the Levi-Civita covariant derivative. The flatness of the connection allows a path-independent parallel transport, hence maintaining a notion of being parallel at a distance, which is the reason for calling it “teleparallel” [2]. Further, the teleparallel connection is metric compatible, so that its non-metricity tensor vanishes,
denotes the teleparallel covariant derivative, while \(\nabla _{\mu }\) denotes the Levi-Civita covariant derivative. The flatness of the connection allows a path-independent parallel transport, hence maintaining a notion of being parallel at a distance, which is the reason for calling it “teleparallel” [2]. Further, the teleparallel connection is metric compatible, so that its non-metricity tensor vanishes,

while its torsion

is allowed to be non-vanishing. In Teleparallel Gravity, the torsion takes the role of the gravitational field strength, in contrast to General Relativity, where this role is attributed to the Levi-Civita curvature.
There are different, equivalent possibilities to implement the teleparallel connection as a dynamical field. In the original formulation by Einstein [2], the only fundamental dynamical field is a tetrad (or vielbein) field \(e^A = e^A{}_{\mu }\mathrm{d}x^{\mu }\). Here and in the remainder of this section, capital Latin letters \(A, B = 0, \ldots , 3\) denote Lorentz indices. The tetrad defines both the metric
and the coefficients

of the teleparallel affine connection, where \(\eta _{AB} = \mathrm {diag}(-1, 1, 1, 1)\) is the Minkowski metric and \(e_A = e_A{}^{\mu }\partial _{\mu }\) is the inverse tetrad satisfying \(e^A{}_{\mu }e_A{}^{\nu } = \delta _{\mu }^{\nu }\) and \(e^A{}_{\mu }e_B{}^{\mu } = \delta ^A_B\). This particular choice of the connection is known as the Weitzenböck connection, and it belongs to a family of flat, metric compatible connections. The constituents of this family can be expressed in terms of the connection one-forms  of a flat Lorentz spin connection via the relation
of a flat Lorentz spin connection via the relation

Here, flatness corresponds to vanishing curvature of the spin connection,

while metric compatibility follows from the antisymmetry  . In the covariant formulation of teleparallel gravity theories [3], the spin connection is promoted to a dynamical field, and its flatness must be imposed either through Lagrange multipliers in the gravitational action or by explicitly allowing only for flat connections and accordingly restricting the variation with respect to the spin connection in the derivation of the Euler-Lagrange equations [4]. Yet another possibility to ensure the flatness of the spin connection is to consider it as a dependent quantity
. In the covariant formulation of teleparallel gravity theories [3], the spin connection is promoted to a dynamical field, and its flatness must be imposed either through Lagrange multipliers in the gravitational action or by explicitly allowing only for flat connections and accordingly restricting the variation with respect to the spin connection in the derivation of the Euler-Lagrange equations [4]. Yet another possibility to ensure the flatness of the spin connection is to consider it as a dependent quantity  derived from a local Lorentz transformation \(\Lambda ^A{}_B\), and to promote the latter to a fundamental dynamical field next to the tetrad [5, 6].
derived from a local Lorentz transformation \(\Lambda ^A{}_B\), and to promote the latter to a fundamental dynamical field next to the tetrad [5, 6].
Another implementation of teleparallel geometry is the Palatini approach, which considers as fundamental fields the metric \(g_{\mu \nu }\) and the affine connection coefficients  , and enforces metric compatibility and flatness of the connection via Lagrange multipliers [7].
, and enforces metric compatibility and flatness of the connection via Lagrange multipliers [7].
1.2 Translation Gauge Theory
One argument that is commonly mentioned in favour of Teleparallel Gravity is its possible interpretation as a gauge theory of translations. Various approaches and realisations of this gauge theory have been studied [8]. It was first found in the non-covariant formulation of Teleparallel Gravity that the tetrad allows for a gauge symmetry, which can be related to infinitesimal translations, and that imposing this symmetry leads to an action equivalent to the Einstein-Hilbert action [9, 10]. Relaxing the condition of local Lorentz invariance yields a more general class of theories [11]. A more sophisticated approach relates Teleparallel Gravity to higher gauge theory, and generalisations of Cartan geometry [12]. Cartan geometry has also been suggested as a possible interpretation of the non-standard nature of translational gauge transformations, which act not only on an internal space, is usual in gauge theory, but also on the underlying spacetime manifold [13]. This interpretation has been contrasted with a formulation making use of a principal bundle of translations [14]. Despite their differences, the aforementioned approaches have in common that the tetrad field is related to a gauge potential of translations, while the spin connection is related to an external Lorentz gauge symmetry. However, for a more fundamental understanding of how the tetrad and spin connection in the covariant formulation of Teleparallel Gravity arise, it is helpful to take a step backwards and view Teleparallel Gravity in the more general context of Poincaré gauge theory, and even more generally in the context of metric-affine gravity [15, 16]. We therefore briefly review their description in terms of gauge connections.
We denote by \(FM\) the general linear frame bundle of the spacetime manifold \(M\). The fiber \(F_xM\) at a point \(x \in M\) is the set of all frames, i.e., ordered bases of the tangent space \(T_xM\). Any frame can be expressed by a bijective linear map \(f: \mathbb {R}^4 \rightarrow T_xM\). Given coordinates \((x^{\mu })\) on \(M\), we can introduce coordinates \((x^{\mu }, f_A{}^{\mu })\) on \(FM\), where the frame \(f\) maps an element \(v \in \mathbb {R}^4\) with components \(v^A\) to \(v^Af_A{}^{\mu }\partial _{\mu } \in T_xM\). Note that \(FM\) is a principal bundle: the group \(H_0 = \mathrm {GL}(4, \mathbb {R})\) acts from the right on the fibres of \(FM\). Writing the matrix components of an element \(\Lambda \in H_0\) as \(\Lambda ^A{}_B\), the action reads
in the coordinates we used.
A frame allows expressing tensor fields in a basis that is different from the coordinate basis. Changing the frame changes the basis, while keeping the point fixed at which the tensor field is evaluated. In order to incorporate translations as well, one considers a larger bundle, which may be constructed as follows. Let \(G_0 = \mathrm {GA}(4, \mathbb {R}) = \mathbb {R}^4 \rtimes \mathrm {GL}(4, \mathbb {R})\) be the general affine group. The group \(H_0\), being a subgroup of \(G_0\), acts on \(G_0\) by left multiplication: given \(\tilde{\Lambda } \in H_0\) and \((\Lambda , v) \in G_0\), one has
This action gives rise to an associated bundle \(AM = FM \times _{H_0} G_0\), which we call the affine frame bundle. To understand the geometry of \(AM\), recall that for each \(x \in M\) the elements of the fiber \(A_xM\) are given by equivalence classes
where \(\tilde{f} \in F_xM\) is a frame at \(x\) and \((\Lambda , v) \in G_0\), and equivalence is given by the simultaneous action of \(\tilde{\Lambda } \in H_0\) on both of these objects, following the equation above. One can see that every such equivalence class is defined by a frame \(f = \tilde{f} \cdot \Lambda \), as well as a tangent vector \(y = \tilde{f}v\), or in components
since these combinations are invariant under the application of \(\tilde{\Lambda }\). Hence, the affine frame bundle has the structure
or in other words, every element of \(AM\) consists of a base point \(x \in M\), a vector \(y \in T_xM\) and a frame \(f \in F_xM\). Coordinates on \(AM\) thus take the form \((x^{\mu }, y^{\mu }, f_A{}^{\mu })\). One finds that \(AM\) is a principal \(G_0\)-bundle, where the right action is given by
for \((\Lambda , v) \in G_0\).
The bundle \(AM\) is the arena for the gauge theory we model. The gauge connection is given by a one-form \(\hat{\mathbf {A} }\in \Omega ^1(AM, \mathfrak {g}_0)\) on \(AM\), taking values in the Lie algebra \(\mathfrak {g}_0\) of \(G_0\). Since this Lie algebra splits as \(\mathfrak {g}_0 = \mathfrak {h}_0 \oplus \mathfrak {z}\) into the homogeneous part \(\mathfrak {h}_0\) and translations \(\mathfrak {z} \cong \mathbb {R}^4\), the same holds for the gauge connection \(\hat{\mathbf {A}} = \hat{\boldsymbol{\omega }} + \mathbf {e}\). Using the canonical matrix and vector representations of these Lie algebras, it turns out that the most general one-form connection can be written in the form
in our chosen coordinates, where \(E^{\mu }{}_{\nu }\) and \(\hat{\Omega }^{\mu }{}_{\nu \rho }\) are functions of \(x\) only. This form is a consequence of the demand that \(\hat{\mathbf {A}}\) is a principal connection.
Finally, to obtain the gauge fields on the spacetime manifold \(M\), we need to choose a gauge; this corresponds to choosing a section \(\sigma : M \rightarrow AM\). In our coordinates this section can be expressed as
The section allows us to take the pullbacks
Here we have already suggestively identified these pullbacks with the tetrad \(e^A{}_{\mu }\) and teleparallel spin connection \(\hat{\omega }^A{}_{B\mu }\). To justify this identification and to resort to more familiar notation, we introduce new coordinates
and accordingly replace \(\sigma ^{\mu } = \sigma ^A\sigma _A{}^{\mu }\). Then the tetrad (14.16b) becomes
where \(B^A{}_{\rho } = \sigma ^{-1\,A}{}_{\mu }E^{\mu }{}_{\rho }\). This is the form most commonly encountered in the literature [1]. Note that changing the section \(\sigma ^A{}_{\mu }\) simply corresponds to a change of the Lorentz frame, while a change of \(\sigma ^A\) can be interpreted as a translation gauge transformation. Finally, calculating the torsion yields
In the teleparallel geometry the spin connection has vanishing curvature (14.7), and so the two terms involving \(\sigma ^B\) vanish. The torsion then becomes the field strength of the translation gauge potential \(B^A{}_{\mu }\).
1.3 Local Lorentz Invariance
When the concept of teleparallelism was introduced, the only dynamical field was the tetrad \(e^A{}_{\mu }\), which has 16 components. It was believed that gravity is described by the 10 components of the metric, while the additional six components could be attributed to the electromagnetic field strength [2]. However, this turned out not to be the case, and it was realised that these additional components are related to local Lorentz transformations \(e^A{}_{\mu } \mapsto \Lambda ^A{}_Be^B{}_{\mu }\) instead. Further, it was found that in general Teleparallel gravity theories are not invariant under such local Lorentz transformations, due to the presence of the Weitzenböck connection  : in order to solve the field equations of such theories, one cannot choose an arbitrary tetrad corresponding to a particular metric, but only specific tetrads are allowed [17,18,19,20,21]. This means that the extra components present in the tetrad cannot be regarded as pure gauge degrees of freedom. This fact raised a debate regarding the nature of the additional degrees of freedom, whether they might be acausal or even superluminal, or whether some of them can be absorbed by a remnant gauge symmetry that is still present despite the otherwise broken Lorentz symmetry [22,23,24,25,26,27,28,29,30].
: in order to solve the field equations of such theories, one cannot choose an arbitrary tetrad corresponding to a particular metric, but only specific tetrads are allowed [17,18,19,20,21]. This means that the extra components present in the tetrad cannot be regarded as pure gauge degrees of freedom. This fact raised a debate regarding the nature of the additional degrees of freedom, whether they might be acausal or even superluminal, or whether some of them can be absorbed by a remnant gauge symmetry that is still present despite the otherwise broken Lorentz symmetry [22,23,24,25,26,27,28,29,30].
In order to resolve the aforementioned issues, a covariant formulation of Teleparallel Gravity theories was developed, which features the flat Lorentz spin connection  as an additional dynamical field [3, 4, 31, 32]. In the covariant formulation, local Lorentz transformations take the form
as an additional dynamical field [3, 4, 31, 32]. In the covariant formulation, local Lorentz transformations take the form

and thus act on both the tetrad and the spin connection. The teleparallel connection (14.6), and hence also its torsion (14.3), are invariant under this combined transformation. It thus follows that any action constructed from the (in any case invariant) metric, the torsion and their derivatives are locally Lorentz invariant.
Note that the spin connection (14.16a) also naturally arises in the gauge theory approach shown in Sect. 14.1.2. In this picture, local Lorentz transformations are simply transformations of the Lorentz part \(\sigma ^A{}_{\mu }\) of the section defining the gauge.
1.4 Matter Coupling
An important issue in Teleparallel Gravity is the question about how to couple matter to the teleparallel geometry. The most commonly considered procedure is given by the minimal coupling prescription, according to which the metric \(g_{\mu \nu }\) in the matter action is chosen to be the metric (14.4) obtained from the tetrad. This prescription is sufficient for bosonic fields, which couple to the metric only, without direct coupling to a spin connection. This differs from the case of fermions, where a spin connection must be specified. The question about a consistent coupling of fermions and the proper choice of the spin connection is a highly topic [16, 33,34,35,36,37]. We will not enter this debate here, and assume that fermions couple to the metric geometry through the spin connection associated with the Levi-Civita connection only. Following this assumption, the matter action does not depend on the teleparallel spin connection, but only on the tetrad. For the variation with respect to the tetrad we may write
The quantity \(T_A{}^{\mu }\) introduced here is the matter energy-momentum tensor, which we also write in the form \(T_{\mu \nu } = e^A{}_{\mu }g_{\mu \nu }T_A{}^{\rho }\).Footnote 1 Demanding that the matter action is invariant under local Lorentz transformations, which is equivalent to demanding that it depends only on the metric obtained from the tetrad, then implies that the energy-momentum tensor is symmetric, \(T_{[\mu \nu ]} = 0\) [38].
1.5 Teleparallel Equivalent of General Relativity (TEGR)
An interesting feature of Teleparallel Gravity is that it allows for an alternative formulation of General Relativity, in which gravity is mediated by torsion instead of curvature [39]. One possibility to derive the action for the Teleparallel Equivalent of General Relativity (TEGR) is by starting from the Einstein-Hilbert action
where \(\kappa ^2=8\pi G\), and by rewriting the Ricci scalar in terms of the torsion of the teleparallel connection. For this purpose, we introduce the contortion tensor

as the difference between the teleparallel and Levi-Civita connection coefficients. By making use of this relation, one can write the Riemann curvature tensor of the Levi-Civita connection in the form

keeping in mind that the curvature of the teleparallel connection vanishes,  , while the curvature of the Levi-Civita connection does not vanish in general. Taking the appropriate contractions, and using the antisymmetry
, while the curvature of the Levi-Civita connection does not vanish in general. Taking the appropriate contractions, and using the antisymmetry  , the Ricci scalar reads
, the Ricci scalar reads

Here we introduced the torsion scalar \(\mathbb {T}\), which can be written in the form

where we used the superpotential

Finally, the last term in the expression (14.25) is a total divergence, and thus appears as a boundary term in the action, which does not contribute to the field equations. Omitting this term and using the fact that the determinants of the metric and the tetrad are related by
the TEGR action finally reads
Variation of this action, together with a matter action, with respect to the tetrad, and transforming the resulting Lorentz index into a spacetime index, yields the field equations

The right-hand side is given by the energy-momentum tensor (14.21). The left-hand side of these field equations is most easily understood by realising the geometric identity

and so it turns out that the field equations indeed agree with those of General Relativity, as one would expect. An interesting property of the action (14.29) is the fact that the teleparallel spin connection  enters only in the form of a boundary term [40]. This can be seen from the relation (14.25) between the Ricci scalar of the Levi-Civita connection and the torsion scalar. The left-hand side is independent of the teleparallel spin connection, and so its variation \(\delta _{\omega }R\) vanishes. This implies
enters only in the form of a boundary term [40]. This can be seen from the relation (14.25) between the Ricci scalar of the Levi-Civita connection and the torsion scalar. The left-hand side is independent of the teleparallel spin connection, and so its variation \(\delta _{\omega }R\) vanishes. This implies

so that variation of the TEGR action with respect to the teleparallel spin connection yields a boundary term only. One consequence is that the teleparallel spin connection drops out of the field equations, as can be seen from the identity (14.25). From this, further follows that the theory is invariant not only under the local Lorentz transformations (14.20), but also under the pure tetrad transformations \(e^A{}_{\mu } \mapsto \Lambda ^A{}_Be^B{}_{\mu }\). This invariance, which does not hold for general teleparallel theories, as discussed in the following section, is one reason why Teleparallel Gravity was originally developed without appealing to a non-trivial spin connection, and the viability of the covariant formulation of TEGR has been challenged [41].
2 Teleparallel Gravity Extensions
Even if \(\Lambda \)CDM has passed most of the observational tests with flying colours, General Relativity (GR), and thus the Teleparallel Equivalent of GR (TEGR) as well, contain some shortcomings. Motivated mostly by the accelerated expansion of the Universe, many people initiated the hunt for a modification of gravity. In the same way as in the curvature case, the literature abounds different theories of Teleparallel Gravity, that introduce new degrees of freedom to describe several phenomena.
Either by introducing scalar fields to the TEGR Lagrangian, or by generalising it to an arbitrary function of the torsion scalar, i.e. \(f(\mathbb {T})\), by introducing non-localities, non-linear boundary terms and other topological invariants, there has been a great plethora of models studied. In this section we will give a brief review on the most well-known modifications.
2.1 \(f(\mathbb {T})\) Gravity
In the curvature case, the most straightforward modification, and maybe the simplest one, is the so-called f(R) gravity. As the name witnesses, it is a generalisation of the Einstein-Hilbert action to an arbitrary function of the Ricci scalar that offers richer phenomenology [42,43,44,45] by introducing a new scalar degree of freedom [46,47,48]. In the same spirit, \(f(\mathbb {T})\) theory was proposed almost a decade ago [19, 49,50,51] and its action reads
It is worth mentioning that even though at the level of field equations GR and TEGR are totally equivalent theories, the same does not happen for f(R) and \(f(\mathbb {T})\) theories. As already discussed in the previous section, \(R = - \mathbb {T} + B\) (14.25), where  is a boundary term, that in TEGR does not contribute to the field equations. However, the arbitrary function \(f(\mathbb {T})\) is non-linear and thus the two theories are no longer equivalent.
is a boundary term, that in TEGR does not contribute to the field equations. However, the arbitrary function \(f(\mathbb {T})\) is non-linear and thus the two theories are no longer equivalent.
Varying the action (14.33) with respect to the tetrad \(e^A{}_{\mu }\) we get its field equations that read

with \(f_\mathbb {T}\) and \(f_{\mathbb {T}\mathbb {T}}\) being respectively the first, and second-order derivatives of f with respect to \(\mathbb {T}\) and \(T_{\mu }{}^{\nu } = e^A{}_{\mu }T_A{}^{\nu }\) is the energy-momentum tensor of the matter fields. As one can immediately notice, the equations for the tetrad are of second order, in contrast with those in f(R) gravity. For the unimodular formulation of \(f(\mathbb {T})\) gravity, where the determinant of the tetrad is kept constant, one can check [52].
Variation of (14.33) with respect to the spin connection [4, 53, 54] gives the antisymmetric part of the tetrad equations (14.34), meaning

There was a period when it was believed that \(f(\mathbb {T})\) gravity violates local Lorentz invariance [17, 18]. Indeed, if one considers the theory with the tetrad being the only variable, the discussion is constrained on a very specific class of frames where the spin connection vanishes. That is why the existence of good and bad tetrads was proposed [20], referring to tetrads in the same equivalence class that solve and do not solve respectively the field equations. An illuminating example is that the diagonal tetrad in spherical symmetry
corresponding to the metric \(g_{\mu \nu } = \mathrm{diag}\left[ A^2(r).B^2(r),r^2,r^2\sin ^2\theta \right] \), is a bad tetrad, not satisfying the field equations (14.34) with a vanishing spin connection for \(f_{\mathbb {T}\mathbb {T}}\ne 0\), while the non-diagonal tetrad associated to the same metric
is a good tetrad. The problem was resolved when the covariant formulation of \(f(\mathbb {T})\) gravity was proposed [3], where both the tetrad \(e^A{}_{\mu }\) and the spin connection  are determined by the field equations (14.34). For a more detailed study about tetrads in spherical symmetry in Teleparallel theories, see [55].
are determined by the field equations (14.34). For a more detailed study about tetrads in spherical symmetry in Teleparallel theories, see [55].
2.2 New General Relativity and Extensions
This modification of TEGR is the first one, and it was proposed by Hayashi and Shirafuji in [11]. The torsion tensor can be decomposed into its three irreducible parts as

where 
 and
and 
Contracting these components, one can construct the following scalars up to quadratic order

The torsion scalar \(\mathbb {T}\) is equal to
and an immediate generalisation of this, with arbitrary coefficients, is the action of the New General Relavitiy, i.e.
For completeness we should mention that there are two more quadratic scalars that one can construct from the torsion tensor,

However, both of them are parity violating and we do not consider them here. For more details one can check Ref. [56], where the authors argue that the parity violating sector could play a crucial role for the well-posedness of the Cauchy problem. It is not clear whether these parity violating scalars can play a fully consistent role in gravitational theories.
The theory (14.41) has been studied and constrained since its proposal in Refs. [23, 57, 58]. In greater detail, Solar System tests were studied [11], singularities of Schwarzschild-like spacetimes in [59], axially symmetric solutions in [60] and its weak-field limit in [61]. More recently, in [62] the propagation of gravitational waves was studied, as well as its Hamiltonian analysis was considered in [5, 63, 64]. Finally, the linearized theory was studied in [65], were the author shows that in order for the theory to be viable, the 2-form field has to feature a gauge symmetry so that it describes a massless Kalb-Ramond field. However, cubic order interactions show [66] that the above gauge symmetry of the 2-form is not preserved at higher orders.
Beyond the NGR theory, extensions of different kinds were considered as well. In [67] it was found that is it possible to construct a conformally invariant theory considering a quadratic Lagrangian based on the tensorial and axial part of torsion, which has the following form,
Note that the vectorial part of the torsion tensor does not appear in this theory. Specifically, in [68] a generalisation of NGR by nine functions of the d’Alembertian operator was considered and the authors show that it can accommodate the ghost- and singularity-free structure that was realised in the metric theories [69,70,71]. In addition, in the same spirit with \(f(\mathbb {T})\), a straightforward generalisation of NGR is the \(f(T_\mathrm{ax},T_\mathrm{vec},T_\mathrm{ten})\) theory proposed in [72]. Apart from richer phenomenology compared to \(f(\mathbb {T})\) gravity, this theory provides us with the ability to study conformal transformations of teleparallel theories in a simple way. In particular, the quadratic scalars constructed by the irreducible parts of the torsion tensor (14.39) transform under the conformal transformation of the tetrad \(\tilde{e}^A{}_{\mu } = \Omega e^A{}_{\mu }\) (or of the metric \(\tilde{g}_{\mu \nu } = \Omega ^2 g_{\mu \nu }\)), with \(\Omega \) being the conformal factor, as
Obviously, unlike the f(R) case [42], in modified teleparallel theories there cannot be an Einstein frame because of the way \(T_\mathrm{vec}\) transforms. More studies on conformal transformations in the teleparallel framework can be found in Refs. [73, 74].
2.3 Higher-Order Derivatives, \(f(\mathbb {T},B,T_{\mathcal {G}},B_{\mathcal {G}})\)
In the \(f(\mathbb {T})\) theory only the torsion scalar takes part in the action, and since it contains only first derivatives of the tetrads, the resulting equations are of second order. This is not a necessity though (if you can ignore or screen out ghosts), and thus the field equations can be of higher order as well; as is in f(R).
One of the most well-studied theories include, in addition to the torsion scalar, the boundary term  . The action of this theory [75,76,77] reads
. The action of this theory [75,76,77] reads
and varying this with respect to the tetrad we take the field equations

It is interesting to notice that such theories are much more general than the f(R) theories, since the last ones are just a subclass when \(f(\mathbb {T},B) = f(-\mathbb {T}+B) = f(R).\) In addition to these, theories with higher derivative terms of the torsion scalar, e.g. \(\nabla ^2 \mathbb {T}, \square \mathbb {T},\) etc., where also proposed [78].
Last but not least, theories with higher-order invariants were also considered in the literature. An interesting example is the inclusion of the Gauss-Bonnet invariant,
Its teleparallel version reads, as with the Ricci scalar,
where \(T_{\mathcal {G}}\) is the teleparallel Gauss-Bonnet term and \(B_{\mathcal {G}}\) its boundary term. Such theories have an action of the form
or even more complicated functions like \(f(\mathbb {T},B,T_{\mathcal {G}}.B_\mathcal {G})\). Such theories present some interesting features in cosmology [79,80,81,82]. Other theories considering non-minimal couplings between matter and gravity have also been considered in Teleparallel Gravity. One example for this is the so-called \(f(\mathbb {T},T)\) gravity, where T is the trace of the energy-momentum tensor [83]. This theory is analogous to the famous f(R, T) gravity considered in the GR framework [84]. Other theories based on Lagrangian like \(f_1(\mathbb {T})+f_2(\mathbb {T})(1+\lambda \mathcal {L}_\mathrm{m})\), where \(\mathcal {L}_\mathrm{m}\) is the matter Lagrangian density and \(\lambda \) is a constant, have been studied in [85]. Furthermore, a more general theory concerning \(f(\mathbb {T},B,\mathcal {L}_\mathrm{m})\) gravity has also been studied in order to connect and generalise these kind of theories [86].
2.4 Teleparallel Non-local Theories
Apart from adding new degrees of freedom, modifications can be done in the foundations of a theory, like violating general covariance, locality, abandoning the equivalence principle, etc. In the Riemaniann geometry, the first non-local proposal came a bit more than a decade ago, with the introduction of a distortion function \(f(\square ^{-1}R)\) of the inverse d’Alembertian operator acting on the Ricci scalar. The action of that theory reads
The argument of f can be expressed using the retarded Green’s function \(G(x,x')\) as
The motivation came clearly from high energies, since such terms arise in quantum loop corrections and they are also considered as possible solution to the black hole information paradox [87, 88]. It was seen however, that even at larger scales, such non-local terms can unify the inflation with the late-time acceleration era and they have been proven ghost-free and stable.
Based on that, it was natural to study what the effect of such terms would be in the teleparallel framework. That is why the teleparallel non-local (TNL) theory
was proposed in [89]. The authors show that the theory is consistent with cosmological data from SNe Ia + BAO + CC + \(H_0\) observations. A generalisation of (14.52) was proposed in [90], where they also introduced the effect of the d’Alembertian operator on the boundary term B. The action of that theory is
A localised version of this has been studied, introducing scalar fields. In addition, using symmetries, a classification of the distortion function has been done.
2.5 Horndeski Analog and Subclasses
Horndeski theory is the most general scalar tensor theory (with a single scalar field) that leads to second-order field equations in four dimensions [91, 92]. Most of the modified theories of gravity can be mapped onto its action; from Brans-Dicke [93], extended quintessence [94, 95], kinetic gravity braiding [96] to f(R) [42]. However, there is no physical requirement that forces us to use the Levi-Civita connection as the fundamental connection to formulate the theory, and thus we have the freedom to build the theory in any affine geometry. For this reason, in [97] S. Bahamonde, K. F. Dialektopoulos and J. Levi Said formulated the BDLS theory, that is the teleparallel analog of the Horndeski gravity.
In greater detail, they wanted to build a theory which has the properties: i. leads to second order field equations; ii. the scalar invariants are not parity violating; and iii. only quadratic contractions of the torsion tensor are included. In that way, BDLS action reads
where
and
where comma denotes the partial derivative, semi-colon the covariant derivative with respect to the Levi-Civita connection, and \(\square \) the associated d’Alembertian operator. The scalars that appear in the (14.55) are


all the rest they are either parity violating or can be obtained combining these [97,98,99].
Obviously, because of the existence of \(G_\mathrm{Tele}\) in the action, this theory contains much more phenomenology compared to its curvature analog. Specifically, it contains the curvature analog as a subclass when \(G_\mathrm{Tele} = 0\). Its relation with various known theories is depicted in Fig. 14.1.
The curvature case of Horndeski was severely constrained [100, 101] after the observation of GW170817 and its companion GW170817A [102], since the speed of the gravitational waves is constrained to the value of the speed of light
That is another reason the BDLS theory is worth studying. In [98] the authors study the tensor mode perturbations on a flat FLRW background and they show that the models that survive the above constraint (14.62) are given by
meaning that many models that were eliminated in the curvature case, like quartic and quintic Galileons, the Fab-Four and more, will survive in the teleparallel framework because of the appearance of the \(J_5\) scalar.
2.6 Teleparallel Dark Energy Models
All the scalar torsion theories in four dimensions with a single scalar field are subclasses of the BDLS theory [103,104,105,106,107,108,109,110,111]. The first one with a non-minimal coupling between the scalar field and the torsion scalar was proposed in [103] under the name teleparallel dark energy, and its action reads
Such models present interesting cosmological behaviour, not necessarily the same compared to \(f(\mathbb {T})\) models [112, 113]. There are similar to the \(\xi R \phi ^2 \) models in the Riemannian geometry and such models will be discussed in detail in Sect. 14.3. Moreover, in [114], a generalisation of the above theory with an extra term \(\chi B\phi ^2\) was considered. This theory contains the theory with the coupling \(\xi R \phi ^2 \) as a special case for the case \(\chi =-\xi \). Apart from these ones, in a recent series of papers [31, 115,116,117] the most general scalar-torsion theories have been presented in their covariant formulation, as well as theories involving kinetic and derivative couplings of the scalar field with torsion.
3 Phenomenology of Teleparallel Gravity
After formulating a possible well-motivated gravitational theory, it is then important to see its viability in terms of its confrontations with observations. It is well-known that GR works very well at Solar System scales, therefore, any meaningful theory must not deviate too much from these predictions at this scale of phenomenology. The easiest way to verify if a modified theory passes these constraints is by computing the so-called post-Newtonian parameters (PPN). Basically, these parameters measure the weak-field approximation of a theory with the corresponding post-Newtonian terms. For a detailed review about this method, see Ref. [118]. Usually, this method is constructed for theories concerning the metric but since Teleparallel Gravity uses tetrads, a different approach is needed as discussed in [119]. These parameters already put some constraints on different modified gravity models. In the context of Teleparallel Gravity, it was found that the PPN parameters of both \(f(\mathbb {T})\) gravity and teleparallel dark energy (see Sect. 14.2) are exactly the same as GR, therefore, these theories automatically pass all the Solar System observations [120,121,122], as confirmed in [123,124,125]. If one further generalises \(f(\mathbb {T})\) to \(f(T_\mathrm{ax},T_\mathrm{vec},T_\mathrm{ten})\) or teleparallel dark energy with an extra coupling between the boundary term and the scalar field as \(\chi B\phi ^2\), the PPN parameters \(\gamma \) and \(\beta \) deviate from GR, constraining these models [122, 126, 127]. These studies were further generalised to more general teleparallel scalar tensor theories such as \(f(\mathbb {T},X,Y,\phi )\) and Teleparallel Horndeski in [128, 129], finding again that only \(\alpha \) and \(\beta \) can differ from GR. For the general \(f(\mathbb {T},B)\) gravity scenario, the precise form of this deviation is investigated in [130, 131], where the solar system tests and gravitomagnetic effects are probed against current observations. Moreover, in [132] the stability of theory and its thermodynamics are probed. One of the strongest bounds coming from these PPN parameters are the observations from Cassini, which is \(|\gamma -1|\lesssim 2\cdot 10^{-5}\) and also, using the lunar laser ranging experiments, \(|\beta -1|\lesssim 2\cdot 10^{-4}\) [118].
There are other new observational bounds that one needs to take into account for constructing a coherent theory. For example, in Ref. [133], it was found that the speed of the propagation of gravitational waves \(c_g\) is very close to the speed of light \(|c/c_g-1|\lesssim 3\cdot 10^{-15}\). The theories \(f(\mathbb {T}), f(\mathbb {T},T_{\mathcal {G}})\) and \(f(\mathbb {T},B)\) predict that \(c_g=c\) [134, 135], so that they are not observationally constrained through this test. Furthermore, there are only two propagating modes in both \(f(\mathbb {T})\) and \( f(\mathbb {T},T_{\mathcal {G}})\) gravity [135, 136], exactly like GR. On the other hand, as in f(R) gravity, \(f(\mathbb {T},B)\) exhibits an extra polarisation mode (longitudinal or breathing mode) [135]. Further generalisations such as Teleparallel Horndeski predicts a different speed of the gravitational waves, and hence, the theory needs to be constrained for a certain type of them. However, one notices that the number of theories respecting \(c_g=c\) is larger than in standard Horndeski gravity. Furthermore, the coupling functions \(G_4(\phi ,X)\) and \(G_5(\phi )\) that were highly constrained in the standard version of Horndeski, can now be restored in its teleparallel analogue [98].
The majority of the work produced in modified Teleparallel Gravity has been done in the context of cosmology. There are several works regarding this for different kinds of theories. Some important results in these theories are:
-
The possibility of explaining the acceleration of the Universe without evoking a cosmological constant (see, for example, Sects. 14.3.6 and 14.3.7).
-
The possibility of roughly describing the evolution of the observed Universe eras (see, for example, Sect. 14.3.6) and crossing of the phantom divide line [114].
-
The possibility of reducing the tension for the value of the \(H_0\) parameter and the growing \(f\sigma _8\) tension (see Sect. 14.3.4).
-
The existence of cosmological bouncing solutions (see Sect. 14.3.8).
-
The possibility of avoiding dark matter for describing the galactic rotation curves [137].
In the following sections, we will briefly describe some of these results, and also some techniques used for studying cosmology in these theories.
3.1 \(f(\mathbb {T})\) Cosmology and the Power-Law Model
The framework that Teleparallel Gravity offers in the form of its \(f(\mathbb {T})\) gravity formulation can be investigated against cosmological observations, where tensions appear to be growing with \(\Lambda \) CDM [138,139,140]. The analysis takes the good tetrad \(e^{a}_{\mu } = \left( 1,a(t),a(t),a(t)\right) \) for a homogeneous and isotropic universe (this reproduces the standard FLRW metric in its Cartesian coordinates form). By choosing the Lagrangian density to take the form \(-\mathbb {T}+F(\mathbb {T})\), the resulting field equations turn out to be [3, 49, 141]
where \(\kappa ^2:=8\pi G\), and the effect of the extension to the TEGR Lagrangian is to act as an exotic fluid with components
Together, these fluid properties satisfy the continuity equation
as well as make up the effective EoS
which returns a constant \(w_{\text {DE}} = -1\) for the appearance of a cosmological constant through the condition \(F_{\mathbb {T}}=0\). Here, we assume that \(F(\mathbb {T}) \ne 0\), so that gravity is indeed modified by \(f(\mathbb {T})\) gravity.
Finally, using the EoS in Eq. (14.70), it follows that \(F/\mathbb {T} - F_\mathbb {T} + 2\mathbb {T}f_{\mathbb {T}\mathbb {T}}=0\) has solutions \(F(\mathbb {T})=c_1\sqrt{\mathbb {T}} + c_2\), where the first part plays no role in the cosmic dynamics in four dimensions, while the second part plays the role of the cosmological constant [142,143,144]. Thus, this case is neglected since it reduces to \(\Lambda \)CDM.
3.2 Cosmography in \(f(\mathbb {T})\) Gravity
Cosmography offers a model independent way in which to determine viable models of gravity through standard candle data (such as SNeIa) [145]. That is, by using the Hubble diagram, gravitational Lagrangians can be constrained in their parameter space by using expansion data. In Refs. [146,147,148], this is considered for the following parameters: Hubble (\(H=\dot{a}/a\)), deceleration (\(q=-\frac{1}{a}\frac{\mathrm{d}^2a}{\mathrm{d}t^2}H^{-2}\)), jerk (\(j=\frac{1}{a}\frac{\mathrm{d}^3a}{\mathrm{d}t^3}H^{-3}\)), and snap (\(s=\frac{1}{a}\frac{\mathrm{d}^4a}{\mathrm{d}t^4}H^{-4}\)). These cosmographic parameters can then be correlated with the Hubble diagram by considering the Taylor expansion of the scale factor about present time, \(a_0=1\), together with the luminosity distance relation
and redshift relation \(a=\left( 1+z\right) ^{-1}\), which result in the Hubble cosmographic relations
where
with \((H,q,j,s)=(H_0,q_0,j_0,s_0)\) are all determined at current times. This expansion is considered up to fourth-order derivatives, due to the lack of accuracy of the cosmological data beyond that point [149, 150]. Fitting each of these parameters, using the Hubble diagram, it is then straightforward to infer an \(F(\mathbb {T})\) model by using the modified Friedmann equations in Eqs. (14.65)–(14.66). To do this, consider \(f(\mathbb {T})=-\mathbb {T}+F(\mathbb {T})\), so that we can impose the following constraints: (i) the effective gravitational constant must be equal to Newton’s constant at present times [148]
which emerges by considering again the Friedmann equation in Eq. (14.65) as \(H^2 = \kappa ^2 (\rho - 2F/(3\kappa ^2))/(6F_{\mathbb {T}})\) and recognising the effective coupling parameter, \(G_{\text {eff}}=G/f_{\mathbb {T}}\) (\(f_{\mathbb {T}}=\mathrm{d}f/\mathrm{d}\mathbb {T}\)). The requirement can then be written as \(G_{\text {eff}}\vert _{z=0} = G \Rightarrow f_{\mathbb {T}}\vert _{z=0} = 1\). This means that at current time we recover TEGR. (ii) The second constraint is an evaluation of the Friedmann equation in Eq. (14.65) at current times, such that the present value of the Lagrange density must be
where \(\Omega _{M0}\) is the present value of the matter density parameter.
In Refs. [146,147,148], various \(f(\mathbb {T})\) models were considered, but we focus on the power-law model here. This can be represented by [151]
where \(\alpha ,\beta ,n\) are arbitrary constants, and the constraints on the Lagrangian density result in the relations
While the parameter \(\beta \) is used, it can be made dimensionless by taking the transformation \(\beta \rightarrow \beta _0/\mathbb {T}_0^n\). To preserve TEGR for Solar System scale physics and the astrophysics regime, the \(\alpha \) parameter can be set to \(-1\) so that this is recovered as a first approximation. The best-fit cosmographic parameters then give \(n=-0.011\) [147]. The result is an expansion rate very close to \(\Lambda \)CDM but not exactly equal. Along a similar vein, in [152] cosmography was used to reconstruct various \(f(\mathbb {T})\) gravity Lagrangians by imposing conditions in the jerk parameter.
This analysis relies heavily on the assumption that higher-order contributions, which have much less accurate observational data, are sub-dominant, which may not always hold. Also, this analysis has only been applied to the popular \(F(\mathbb {T})\) extension to TEGR. It would be interesting to explore other avenues of Teleparallel Gravity such as, for example, the ones presented in Sect. 14.2.
Along a similar rationale, in [153, 154] the \(f(\mathbb {T})\) Lagrangian is reconstructed against phenomenological data, achieving very interesting constraints on viable models.
3.3 The Growth Factor
The inflationary epoch rendered an early Universe that was nearly uniform. It was small quantum fluctuations that then resulted in the seeds of structure formation. Over the cosmic timescale, these seeds then grew into the structure we can observe today. This effect was amplified during the early matter-dominated phase of the Universe, where density perturbations were intensified by gravity. The growth factor can propagate how this growth changes between different theories of gravity.
To explore this aspect of cosmology, the evolution of linear scalar perturbations must be considered, which at the level of the metric appear as
where the spatial metric is chosen to be the Cartesian coordinate system. The problem then becomes, what perturbed tetrad to consider? One approach is given in Ref. [155], but the resulting field equations turn out to restrict the \(f(\mathbb {T})\) Lagrangian to its TEGR value which is not allowable with a good tetrad. It was later in Refs. [142, 156,157,158,159] that the correct good tetrad was studied. In perturbation theory, a good tetrad must adhere to the already discussed conditions for being a good tetrad up to perturbative order (see Sect. 14.2.1 for further details). This is ultimately represented by
where \(\bar{e}^{b}_{0} = \delta ^a_0\) and \(\bar{e}^{b}_{i} = a\delta ^a_i\), and the scalar perturbations are given by
where w and \(\tilde{w}\) are 2 scalar degrees of freedom (DoFs) of mass dimension and h and \(\tilde{h}\) are parity-violating terms. To obtain the correct scalar perturbations in the Newtonian gauge, the setting \(w=-\tilde{w}\) and \(h=0\) [142] needs to be taken, while \(\tilde{h}\) vanishes naturally at the level of the metric. Using this tetrad setting, the correct scalar perturbations at the level of the metric are obtained, as in Eq. (14.78) (in cosmic time rather than conformal time). We consider only the scalar perturbations in this work, but interesting results have also been obtained for tensor perturbations in Refs. [134, 156, 158,159,160,161,162,163]. The end result indeed appears in the linear perturbations of the torsion scalar as
which means that the scalar perturbations have an effect in the \(F(\mathbb {T})\) gravity section, while, the matter perturbations are taken by considering only dust (\(p=0=\delta p\)). The density perturbations, \(\delta \rho \), can then be encapsulated in the so-called gauge invariant fractional matter perturbation given by
where v is the magnitude of the velocity of the fluid, \(v^i=u^i/u^0\) [164]. This regime is best studied by going into the Fourier domain and considering subhorizon modes where \(\phi \sim \psi \). By combining the \(f(\mathbb {T})\) field equations, the following linear matter evolution equation is obtained in Ref. [142]
where \(G_{\text {eff}}= G/(-1+F_{\mathbb {T}})\) is the effective gravitational constant. This is generalised in Ref. [157] to include the Lagrangians formed with arbitrary combinations of the contraction of the stress-energy tensor, \(T=T^{\mu }_{\mu }\).
To probe the growth of matter density perturbations, Ref. [142] defines the variable
which is defined this way to avoid scale factor dependence during matter-dominated eras, and where the reasonable initial conditions \(g(a_i)=1,\,\left( dg/d\ln a\right) \vert _{a=a_i} = 0\) are chosen. Here, \(D(a) := \delta _m(a) / \delta _m(a_i)\) (for some reference scale factor \(a_i\)) is the growth factor.
Considering again the power-law model with \(F(\mathbb {T}) = \beta \mathbb {T}^n\), the growth factor as a function of redshift can be solved numerically and turns out to give the evolution depicted in Fig. 14.2. Given that \(F_{\mathbb {T}}>0\) for the power-law, it follows that the growth factor will be dampened due to the effective gravitational constant relation. The main result of this is that over-dense perturbations grow slower when compared with GR. In Ref. [159], it was also found that the vector perturbations are well-behaved for sub-horizon modes. These results are confirmed in Refs. [156, 158], where it is also noted that the cause of the lack of extra propagating DoFs could be the symmetric nature of the background cosmology.
Matter perturbation evolution for \(\Lambda \)CDM (solid red line), power-law \(F(\mathbb {T})\) (dashed blue line), and constant dark energy EoS in GR (dotted black line) [142]
3.4 The \(H_0\) Tension Problem
The discrepancy between model-independent measurements of the current value of the Hubble parameter [139, 140] and those inferred from the CMB using flat \(\Lambda \)CDM [138, 165] is now corroborated by an overwhelming wealth of evidence. The \(H_0\) tension problem then points to the necessity of new physics beyond flat \(\Lambda \)CDM, such as modified gravity within the Teleparallel Gravity regime [166].
To explore this possibility in Teleparallel Gravity, we need to consider again the perturbations in Eq. (14.79). However, in this scenario the contributions of matter and radiative pressures are not neglected even at perturbative level [167, 168]. Also, the gravitational potentials \(\phi \) and \(\psi \) are no longer equal. As already discussed in Refs. [158, 162], the following modified Poisson equation is derived
where we have transformed to Fourier space. By keeping to the power-law model, Ref. [162] explores this possibility in terms of the \(H_0\) problem as well as the growing \(f\sigma _8\) tension. In this work, the authors show that the \(H_0\) tension can be reduced in conjunction with reducing the \(f\sigma _8\) tension. As they show in Fig. 14.3, a consistent cosmological setup can be constructed for a small value of index n.
One of the principal motivations for exploring modified gravity in cosmology is to better explain the appearance of dark energy without modifying the matter content of the Universe. This entails reinterpreting the Friedmann equation as an effective equation in which the modified gravity component acts as a separate contribution to cosmic evolution beyond GR. This can easily be done by writing [167]
where \(\Omega _{F0} = 1 - \Omega _{m0} - \Omega _{r0}\) is the \(F(\mathbb {T})\) density parameter at current times, and
represent the background evolution of the \(F(\mathbb {T})\) model. In the right panel of Fig. 14.3, the \(n-\Omega _{F0}\) plane is shown, where Ref. [162] reports promising results for small values of n.
The comparison of \(\Lambda \)CDM with the \(f(\mathbb {T})\) gravity power-law model as reported in Ref. [162]. Left panel: Plot of the \(\sigma _8 - H_0\) parameter space comparing the \(\Lambda \)CDM model in red (blue) for CMB+BAO (CMB+BAO+\(H_0\)) data respectively. Additionally, we present the results for the power-law \(f(\mathbb {T})\) model in black (green) for the same data, where the vertical gray band corresponds to \(H_0=73.24\pm 1.74\,\text {km}\,\text {s}^{-1}\) [169]. The extended model has best fit index parameter \(n=0.0043^{+0.0033}_{0.0039}\) (\(0.0054^{0.0020}_{0.0020}\)) [161] (more details here about the data used). Right panel: 68% and 95% confidence levels for CMB+BAO (CMB+BAO+\(H_0\)) data in black (green) [161]
Along a similar vein, the authors of Ref. [170] confront the growth of structure in the Universe by using several cosmological probes. The study involves three \(F(\mathbb {T})\) models, but we highlight the results for the power-law model here. In their analysis, they use growth rate data for \(f\sigma _8\) that has been verified for internal robustness [171], which differs from some other approaches where inconsistencies can arise due to overlaps between separate studies. The second data set used in this study is the updated Hubble expansion through the cosmic chronometric method [172], while the third is the latest standard candle data in Ref. [173]. These three data sets are used in a joint analysis for the power-law \(F(\mathbb {T})\) model resulting in the likelihood plots shown in Fig. 14.4.
The \(1\sigma \), \(2\sigma \) and \(3\sigma \) likelihood contours for the \(F(\mathbb {T})\) power-law model (with \(F(\mathbb {T})=\alpha (\mathbb {T})^b\)) [170]
In this work, the authors use the Akaike Information Criterion (AIC) [174], Bayesian Information Criterion (BIC) [175] and Deviance Information Criterion (DIC) [176] to compare the different models. The power-law is favoured using the AIC and BIC comparisons when compared to \(\Lambda \)CDM. While not performing best using the DIC to compare the models, it still fares relatively well compared to other prominent models in the literature.
Another important contribution to the reduction of the \(H_0\) tension are Refs. [177,178,179], where Hubble data is interpreted as a stochastic process such that the various model ansatz choices must reproduce. By taking this approach, the authors determine a region for acceptable Lagrangian forms for the \(F(\mathbb {T})\) model. While this region is model-independent and goes up to \(z=2.4\), various models can be constrained against cosmic data. In Ref. [179], Gaussian processes are used on Hubble data which is interpreted as being sourced by stochastic processes. Here, the authors reconstruct values of the arbitrary Lagrangian through the Friedmann equation and then use Gaussian processes to determine the best fit for this function. The result is a model independent reconstruction of the Lagrangian \(\mathbb {F}(T)\) (except for the assumption that \(\Lambda \)CDM dominates at current times, which resonates with the results from cosmography in Sect. 14.3.2). These values, together with their 1 and 2 \(\sigma \) errors are shown in Fig. 14.5, which depicts the allowable regions in which all cosmological models must predict values for the arbitrary Lagrangian.
There has also been a growing body of work of confronting observations within other extensions of Teleparallel Gravity, such as [180], where Pantheon data is used in \(f(\mathbb {T},B)\) gravity. In this work, the \(H_0\) tension problem is also confronted with new constraints on literature models within this framework of gravity.
The regions are produced by a model-independent reconstruction from Hubble data with 1 and 2 \(\sigma \) error regions coming from the Gaussian process method (the present matter density parameter is imposed to be \(\Omega _{m0}=0.302\)). The blues regions represent cosmic chronometer data, green includes also supernova data, while orange represents the inclusion of baryonic acoustic data [179]
3.5 Inflation in Teleparallel Theories of Gravity
The first modification of Teleparallel Gravity was introduced in [51], with the aim of studying inflation. In this paper, the authors found that for a Born-Infield \(f(\mathbb {T})\) gravity model, it is possible to cure the horizon problem without an inflation field, and describe a de-Sitter expansion. This paper was the crucial starting point for investigating cosmology in the context of Teleparallel Gravity. So far, the majority of the inflationary models in modified teleparallel theories have been carried out in \(f(\mathbb {T})\) gravity. By performing a 3+1 decomposition for the tetrad, the cosmic inflationary perturbations for \(f(\mathbb {T})\) were computed in [112]. Similar to the Starobinsky inflationary model \(R+\alpha R^2\), in [181] it was found that the case \(-\mathbb {T}+\alpha \mathbb {T}^2\) behaves differently since in this case, a de-Sitter solution occurs (not a quasi de-Sitter). This means that in the teleparallel version of the Starobinsky model, only eternal de Sitter inflation is possible. In [182] it was further found that these models can have good agreements with a hot big bang nucleosynthesis, and also that the system evolves towards a flat FLRW universe naturally, even if we start with a non-flat one. Later in [183], it was found that power-law and intermediate inflationary models in \(f(\mathbb {T})\) gravity are compatible with Planck measurements, and that a self-interacting quartic potential \(V(\phi )\propto \phi ^4\), which has an interesting reheating process is viable in \(f(\mathbb {T})\) inflation. Further, the standard inflationary model is not observationally compatible with this kind of potential. After introducing a suitable scale factor, it was found that depending on a parameter, \(f(\mathbb {T})\) gravity can have a graceful exit inflation or can have a bounce [184]. In that study it was obtained that the problem of a large tensor-to-scalar ratio is not present in the bouncing models. The standard logamediate inflation is not compatible with observations but in [185] it was concluded that in \(f(\mathbb {T})\) gravity, this model can be compatible with Planck observations. Finally, in [186] it was found that a super inflation scenario can be achieved in \(f(\mathbb {T})\) gravity. Concerning extensions to \(f(\mathbb {T})\) gravity, in [187], the authors introduced a coupling between a Maxwell field and the torsion scalar, \(I(\mathbb {T})F_{\mu \nu }F^{\mu \nu }\), finding the possibility of generating large-scale magnetic fields from inflation. In \(f(\mathbb {T},T_{\mathcal {G}})\) gravity, there was obtained a model that unifies inflation with dark energy with a super inflation mechanism [188]. A unimodular \(f(\mathbb {T})\) gravity model was also analysed in the context of inflation, finding another alternative inflationary models with, graceful inflationary exit [189].
The first study related to inflation in the context of teleparallel scalar tensor theories was done in [190], where an extended \(f(\mathbb {T})\) plus an inflation field with a kinetic, a potential term and an interaction term was introduced. In this work, it was found that a possible warm-inflation model is compatible with the Planck data. Later in [191], a similar model was studied, finding a reheating process, with the scalar field being responsible to reheat the Universe after the inflationary era. In [192], another scalar tensor model concerning two non-minimally couplings with the scalar field, one with the torsion scalar \(F(\phi )\mathbb {T}\) and the other with a vector field \(G(\phi )F_{\mu \nu }F^{\mu \nu }\), was considered in the context of anisotropic inflation, obtaining that in the strong coupling regime, the anisotropy shear to expansion ratio has a different value than its standard form. The constant-roll inflation in \(f(\mathbb {T})\), minimally coupled with a scalar field, was analysed in [193], allowing the theory to have a wide range of viability in terms of observations. In [194] the authors studied slow-roll inflation in a more general teleparallel scalar-tensor theory, with a canonical scalar field non-minimally coupled to torsion with a Galileon-type field \(G(\phi ,X)\Box \phi \) and a monomial scalar field potential \(V\propto \phi ^n/n\). This theory is a particular case of the BDLS theory (see Sect. 14.2.5). Based on Planck 2018 data for both the spectral index \(n_s\) and the tensor-to-scalar ratio r, standard inflation with monomial scalar field potential with \(n\ge 2\) is ruled out. However, in this teleparallel version, \(n=2\) (chaotic quadratic inflation) is in agreement with data and \(n=1\) and \(n=2/3\) are even more favoured than previous models. In a model with non-minimally couplings between a scalar field and both the boundary term and the torsion scalar, it was shown that the scalar field does not source linear scalar perturbations, unless the coupling functions satisfy certain conditions [195]. Only in these situations, can one have successful Higgs inflationary models. Finally, considering more exotic models, a tachyonic teleparallel one explaining inflation and agreeing with the current observational Planck limits was studied in [196]. Further, it was also found in [197] that by extending the study with a boundary term non-minimally coupled with the scalar field, accelerated expansion and scaling solutions are attained.
3.6 Dynamical System in Cosmology for Teleparallel Theories Of Gravity
When one starts modifying or extending the Einstein field equations, the cosmological equations become more involved to solve. The FLRW equations can be written as an autonomous system of differential equations, and for this, they can be recast as a dynamical system. Mathematicians have studied these systems for a long time, giving an easy way to understand the dynamics of a model and how the stability of their critical points behave. Hence, this is a powerful mathematical technique, which is very useful for studying cosmology in modified theories of gravity. For a detailed review about dynamical systems, both mathematically and in terms of cosmology, see [198,199,200,201].
There are several works in modified Teleparallel Gravity that use dynamical systems in the context of cosmology. The first work for \(f(\mathbb {T})\) cosmology was presented in [202], where the authors studied a power-law \(f(\mathbb {T})\) finding one critical point behaving as a late-time attractor and another two describing matter and radiation eras as saddle points. Later, in [203], a logarithmic \(f(\mathbb {T})\) cosmology was studied, finding a de-Sitter late-time attractor. In [204,205,206], it was also found that by introducing an interaction between the dark fluids and considering a power law \(f(\mathbb {T})\), it is possible to get tracker cosmological solutions. Other dynamical system studies concerning more general approaches for \(f(\mathbb {T})\) cosmology have been done. For example, in [207] the authors used the nullcline method to study the bifurcation phenomenon to study the global dynamical properties of the dynamical system. In [208], it was found that there are three conditions which ensure that \(f(\mathbb {T})\) cosmology could roughly describe the cosmological history of the evolution of the Universe. Using non-standard dimensionless variables, Hohmann et al. [209] found de-Sitter fixed points, accelerated expansion, crossing the phantom divide, and finite time singularities in \(f(\mathbb {T})\) cosmology. They also found some bounce solutions in this model. Finally, in [210], the authors were able to rewrite the \(f(\mathbb {T})\) dynamical system as a one dimensional one by using the fact that \(\mathbb {T}\) depends only on the Hubble parameter as \(\mathbb {T}=6H^2\) in flat FLRW. Doing this, they found that it is possible to reconstruct the whole history of the Universe starting from a big bang singularity and finalising in an accelerating expansion. In addition, they also found some other exotic solutions, such as cosmological bounce and turnaround, the phantom-divide crossing, the Big Brake and the Big Crunch, and also they found that it may exhibit various singularities.
Let us now briefly review the dynamical system of \(-\mathbb {T}+F(\mathbb {T})\) (TEGR plus \(F(\mathbb {T})\)) cosmology described by the modified flat FLRW equations (14.65) and (14.66). For a universe composed of two fluids with effective energy density described by \(\rho =\rho _\mathrm{rad}+\rho _\mathrm{m}\), where the first fluid represents a radiation fluid and the second one a pressureless fluid, one can introduce the following dimensionless variables
to then rewrite the first FLRW equation (14.65) as follows
which gives a constraint and reduces the dynamical system to be a 3 dimensional one. By introducing \(N=\log (a)\), the dynamical system for this model becomes
where we have introduced the quantity
In order to close the dynamical system, one needs to assume a form for \(F(\mathbb {T})\). The easiest case is to assume that \(m=\text {constant}\), which closes the dynamical system and includes two kind of \(F(\mathbb {T})\), one behaving as a power-law \(F(\mathbb {T})=C_1 \mathbb {T}^{m+1}/(m+1)+C_2\) when \(m\ne -1\) and also including a logarithmic case \(F(\mathbb {T})=C_1 \log (\mathbb {T})+C_2\) for \(m=-1\). We will assume this case for simplicity. For other kinds of \(F(\mathbb {T})\), see the papers mentioned before. The dark energy state parameter (14.70) in the dimensionless variables reads
For \(m=\text {constant}\), one finds that the dynamical system (14.90)–(14.92) has three critical points. The first critical point is \(P_1=(x,y,z)=(0,0,0)\) which is the origin of the phase space and represents a matter-dominated era, since \(\Omega _\mathrm{m}=1\). This critical point has three eigenvalues with different signs, \(\{3,-1,-3m\}\), so that, this point is always a saddle point. This behaviour is expected for describing the standard matter-dominated era, since it is known that this point needs to be represented by a point which attracts trajectories in some directions but repels them along others. The second critical point is \(P_2=(x,y,z)=(0,0,1)\), representing a universe dominated by radiation, \(\Omega _\mathrm{rad}=1\). This point has also three eigenvalues \(\{4,1,-4 m\}\) but now depending if \(m>0\), the point is saddle, and if \(m<0\) the point is unstable. This again has the correct cosmological behaviour, since it is known that there was a radiated-dominated era at some point of the history of the Universe but after this era, this era changed to be a matter-dominated era. This is then achieved by having either an unstable or a saddle point for \(P_2\) (neglecting inflation). The final point is represented by the critical line \(P_3=(x,1-x,0)\) whose cosmological behaviour is representing an accelerating universe with an effective state parameter of \(-1\), which denotes a de-Sitter accelerating expansion. This critical line has three eigenvalues \(\{0,-4,-3\}\). Since one of them is zero, one cannot study its stability property with the standard linear stability theory since it is a non-hyperbolic point, and this method fails for analysing such points. Other stability methods can then be used, such as Lyapunov functions or centre manifold theory. See [198] for a detailed description about these methods. If one uses the second mentioned method, one needs to first shift the critical point to the origin, then introduce new variables in such a way that one can diagonalise the Jacobian matrix associated with the dynamical system. After doing this, the centre manifold can then be constructed according to the theorem described in Sect. 2.4 in [198]. By doing this for our dynamical system, we find that the leading term in the dynamical system is reduced to the centre manifold \(\dot{z}=-4 z+\mathcal {O}(z^2)\), which tells us that the point \(P_3\) is always stable. Thus, the critical line \(P_3\) represents a late-time accelerating attractor behaving as a de-Sitter. Then, \(-\mathbb {T}+F(\mathbb {T})\) cosmology can describe a transition from radiation- to matter-dominated eras, finalising in a dark energy era with a de-Sitter accelerating expansion of the Universe. This analysis would be valid for both logarithmic and power-law kinds of \(F(\mathbb {T})\). As an example, Fig. 14.6 shows the evolution of the relative energy density of matter \(\Omega _\mathrm{m}\), radiation \(\Omega _\mathrm{rad}\) and dark energy \(\Omega _\mathrm{DE}\) related to the modifications coming from \(F(\mathbb {T})\) for the case where \(m=0.1\), which represents a power-law type of \(F(\mathbb {T})\). One can notice that the evolution of the Universe is roughly described as one expected from our Universe, starting from a radiation-dominated era, then passing to a matter dominated era and finalising in a dark energy dominated era.
Other different modified Teleparallel Gravity cosmological models extending \(f(\mathbb {T})\) gravity have also been analysed using dynamical systems techniques. In the papers [211,212,213] , a \(f(\mathbb {T},B)\) gravity model including the boundary term B, which connects the Ricci scalar computed with the Levi-Civita connection and the torsion scalar, was analysed, finding scaling solutions, a matter epoch of the Universe, and that two accelerated phases can be recovered describing de-Sitter universes. Later, using non-minimally torsion-matter theories like \(f_1(\mathbb {T})+f_2(\mathbb {T})\mathcal {L}_\mathrm{m}\), with \(\mathcal {L}_\mathrm{m}\) being the matter density Lagrangian, some scaling decelerated solutions, dark-matter dominated, or dark-energy dominated accelerated solutions were found. Further generalisations such as \(f(\mathbb {T},B,\mathcal {L}_\mathrm{m})\) also found similar results [86]. Other models with higher-order torsion invariants such as \(f(\mathbb {T},T_{\mathcal {G}})\) found scaling solutions and found past, present and future singularities, depending on the parameters of the theory [82]. In two recent papers [214, 215], the authors studied the dynamical system of a teleparallel Lovelock gravity theory and string-inspired theories finding a rich phenomenology that can also describe a late-time acceleration of the Universe. Further higher-order derivative torsion theories such as \(f(\mathbb {T},(\nabla \mathbb {T})^2,\Box \mathbb {T})\) or non-local theories \(\mathbb {T}f(\Box ^{-1}\mathbb {T})\) found vacuum de-Sitter solutions and phantom divide line crossing in agreement with observations [78, 216]. Regarding higher dimensional models, in [217] the authors used dynamical systems to find that \(f(\mathbb {T})\) gravity in eleven dimensions can give rise to an early inflationary epoch driven by the presence of extra dimensions without other matter sources.
In [113], the authors analysed the first teleparallel scalar-tensor theory using dynamical system techniques. He analysed a model called teleparallel dark energy (see Sect. 14.2), which is constructed by a non-minimally coupling between the torsion scalar \(\mathbb {T}\) and a scalar field \(\phi \) as \((1+\xi \phi ^2)\mathbb {T}\), with \(\xi \) being a constant, finding that these models contain certain similarities to Elko spinor dark energy models. In a non-minimally coupled model between the Ricci scalar and a scalar field, it is possible to find scaling solutions but in teleparallel dark energy, this cannot be achieved [113]. However, if the coupling is changed to \(F(\phi )\mathbb {T}\) scaling solutions can be obtained [218]. Further, in [219] the authors analysed the phase space of this model, finding similar results as standard quintessence models but having an additional late-time solution behaving as de-Sitter without any fine-tuning. They also found that the crossing of the phantom divide line is possible for this model. In a series of two papers, Skugoreva et al. [220, 221] also studied this model, giving a detailed comparison between it with the standard non-minimally coupled case constructed from the Ricci scalar, finding that in teleparallel dark energy the presence of oscillatory behaviors is more frequent [220, 221]. If one uses the teleparallel dark energy model and adds an additional coupling between dark matter and dark energy, is a deceleration to acceleration phase transition via a \(Z_2\) symmetry breaking results [222]. Another proposed teleparallel model was introduced in [114] by adding a new coupling \(\chi B \phi ^2\), where \(\chi \) is a constant and B is the boundary term. Clearly, the standard Ricci case non-minimally coupled with the scalar field is recovered by setting \(\chi =-\xi \). The authors studied the case where only a boundary term coupling exists, and they found that the evolution of the model evolves towards a late-time accelerating attractor without any fine-tuning. They also found the possibility of the crossing of the phantom divide line in this model. Later, in [223], it was found that using this coupling, one can also get scaling solutions. Other more exotic models have been also proposed, such as tachyonic teleparallel models [197, 218, 224,225,226,227] finding scaling solutions, alleviating the coincidence problem without fine-tuning, obtaining a late-time accelerating attractor and also finding a field-matter-dominated era. Moreover, quintom models concerning two scalar fields (one phantom and the other canonical), non-minimally coupled two both the torsion scalar and the boundary term, have also been studied using the dynamical system, finding similar results to the other models obtaining the correct picture of the history of the Universe [107].
As discussed in this section, the correct use of recasting the FLRW equations into a dynamical system form helps in understanding the main behaviour of the system without the need for analytically solving the equations directly. In the next section, a different approach that is related to obtain analytical cosmological solutions will be presented.
3.7 Noether Symmetry Approach in Teleparallel Theories of Gravity
The Einstein field equations are a system of ten partial differential equations and certain symmetries need to be assumed (such as spherical or cylindrical symmetries) in order to find analytical solutions. When they are modified, usually, the equations become even more involved, and for this reason, it is not so easy to find analytical solutions in those models (even for the maximally symmetric cases). One useful tool to obtain analytical solutions for a certain Lagrangian is Noether’s symmetry approach, which allows us to reduce dynamics for a certain model by using their symmetries and conserved quantities from the Noether theorem. This allows us to get an exact integration of a system because their symmetries are first integrals.
The procedure to get analytical solutions using Noether’s theorem is quite simple, but in practice it sometimes becomes a hard task. First, the point-like canonical Lagrangian associated with the studied action in the examined geometry needs to be written down. After this, Noether’s theorem is used which can be stated in two parts [228,229,230]:
Theorem 1
(Noether’s theorem part one) Let \(q^i\) be some generalised coordinates in the configured space \(\mathcal {Q}=\{q^{i}\}\) of a non-higher derivative order Lagrangian \(L=L(t,q^i,\dot{q}^i)\) whose tangent space is \(\mathcal {T}\mathcal {Q}=\{q^{i},\dot{q}^i\}\) with dots representing differentiation with respect to the time coordinate. The existence of a Noether symmetry that leaves the Euler Lagrange equations \(E_i(L)=0\) associated with the Lagrangian invariant under the transformations \(\bar{t}=t+\epsilon \xi (t,q^i)\) and \(\bar{q}^i=q^i+\epsilon \eta ^i(t,q^k)\), with \(\epsilon \) being a parameter, implies the existence of a function \(g(t,q^k)\) which satisfies the condition
where \(\mathbf{X}^{[1]}\) is the first prolongation of the generator vector field given by
and \(\mathbf{X}\) is the Noether symmetry vector.
Theorem 2
(Noether’s theorem part two) For any Noether symmetry vector \(\mathbf {X}\) associated with the Lagrangian \(L=L(t,q^i,\dot{q}^i)\), there corresponds a function called the Noether integral of the Euler Lagrange equations, which is given by
and is the first integral of the equations of motion \(\mathrm{d}I/\mathrm{d}t=0\).
Using this theorem, one can get the conserved quantities related to the symmetries of a certain theory. This method has been used in TG in the context of cosmology and also in the case of spherically symmetric spacetimes. It is important to mention that different authors have used an incomplete version of Noether’s theorem just by considering the uncompleted Noether’s condition \(\mathbf{X} L=0\) instead of the complete Noether’s condition (14.95). This method is also correct but it does not give all the possible symmetries of a model. The first work related to this method in teleparallel theories was done in [231] for vacuum \(f(\mathbb {T})\) cosmology, finding power-law \(f(\mathbb {T})=c_1 \mathbb {T}^n\) solutions using the incomplete Noether’s condition and then finding power-law analytical cosmological solutions \(a(t)\propto t^{2n-3}\). Some days later, independently, other authors found the same results in [232]. Using the complete Noether’s condition, a more detailed analysis was carried out in [233] and [234] in \(f(\mathbb {T})\) cosmology, obtaining similar cosmological solutions to the first work. In [235] the authors added a minimally coupled scalar field, obtaining \(f(\mathbb {T})\propto \mathbb {T}^{3/4}\) with a potential \(V(\phi )\propto \phi ^2\). One of the first non-trivial spherically symmetric solutions in \(f(\mathbb {T})\) theories was found using Noether’s symmetry approach in [236]. Among these solutions, one of them behaves similarly to the Schwarzschild solution. For \(f(\mathbb {T},B)\) gravity, in [77], several types of power-law cosmological solutions were obtained, along with a new logarithmic boundary term solution \(f(\mathbb {T},B)=-\mathbb {T}+(1/3) B\log B\), which admits a new cosmological solution \(a(t)=(c_2 e^{C_1t}+3 C_{3}(t +c_4))^{1/3}\). The authors also made a comparison between the symmetries found in \(f(\mathbb {T})\), f(R) and \(-\mathbb {T}+f(B)\) gravity. Further, in [237], new spherically symmetric exact solutions were found in \(f(\mathbb {T},B)\) gravity. The modified teleparallel Gauss-Bonnet theory \(f(\mathbb {T},T_{\mathcal {G}})\) [79] and then the extended case with the boundary terms \(f(\mathbb {T},B,T_{\mathcal {G}},B_{\mathcal {G}})\) [238] also found different kinds of analytical power-law types of gravity solutions for f, with some non-trivial scale factors behaving as a combination of exponential with power-laws or hyperbolic functions.
Later, using Noether’s symmetry approach for a generalised non-local teleparallel theory \((\xi \mathbb {T}+\chi B)f(\Box ^{-1}\mathbb {T},\Box ^{-1}B)\) and without assuming any condition, the authors found that the non-local coupling functions are constrained from the symmetries to be either linear combination or exponential [90]. It is interesting to remark that some non-local theories were using exponential non-local coupling functions by hand to get renormalisable theories, but in [90], this result appears directly from the symmetries of the theory. Regarding teleparallel scalar tensor theories, there have been a large amount of papers on different theories, such as teleparallel dark energy or its extended version to non-minimally coupling \(F(\phi )\mathbb {T}\) [239, 240], adding non-minimal couplings with the boundary term and the scalar field [241, 242], or adding vector fields [243, 244], or with a fermionic field [245], or even adding an unusual coupling \(F(\phi ,\partial _\mu \phi \partial ^\mu \phi )\mathbb {T}\) [246]. In these works, new wormhole spherically symmetric solutions and also non-trivial cosmological solutions were found in flat FLRW and in Bianchi models concerning different non-trivial scale factors, along with different types of coupling functions \(F(\phi )\) between both the torsion scalar and the boundary term B. Therefore, the teleparallel community has used Noether’s symmetry approach in many different works in order to get cosmological and spherically symmetric solutions.
As an example, following [234], let us here briefly review the simplest non-trivial modified TG case, which is vacuum \(f(\mathbb {T})\) gravity in flat FLRW cosmology. The canonical point-like Lagrangian for \(f(\mathbb {T})\) gravity in the minisuperspace of flat FLRW can be found by considering the canonical variables \(a,\mathbb {T}\) in the action (14.33) and then using \(\mathbb {T}=6H^2\) in flat FLRW cosmology. This lets us rewrite the action using Lagrange multipliers to then finally obtain the following point-like Lagrangian
Now, we replace the above point-like Lagrangian into Noether’s condition (14.95), finding a set of partial differential equations for Noether’s vector, and also depending on the function \(f(\mathbb {T})\). For this model, there are seven differential equations
where \(\eta ^i \partial q_i=\eta _1(t,a,\mathbb {T})\partial _a+\eta _2(t,a,\mathbb {T})\partial _\mathbb {T}\). We now need to solve the above system of partial differential equations to get the symmetries of the model. It is easy to see from (14.100) that Noether’s vector is constrained to \(\xi =\xi (t), \eta _1=\eta _1(a)\) and \(g=g(t)\). If one uses these conditions into (14.101), one gets \(\eta _2=f_\mathbb {T} S(a,\mathbb {T})/f_{\mathbb {T}\mathbb {T}}\) with \(S(a,\mathbb {T})\) being an arbitrary function that must be of the form \(S(a,\mathbb {T})=M(a)+N(\mathbb {T})\) due to (14.99). Considering all of these equations, one finds that \(g=\text {constant}\), and then the above system for \(f(\mathbb {T})\ne e^{C_1\mathbb {T}}\) is reduced to be
where m, n and c are constants. This yields the power-law solution \(f\left( \mathbb {T}\right) =f_{0}\mathbb {T}^{n}\) with Noether’s vector and Noether’s integral for \(n\ne 3/2\) and \(n\ne 1/2\) being equal to
with \(\mathcal H\) being the Hamiltonian and \(c_i\) some integration constants. The other cases \(n=3/2\) and \(n=1/2\) have different Noether’s symmetries. Finally, if one assumes the power-law \(f(\mathbb {T})=f_{0}\mathbb {T}^{n}\) obtained by the symmetries, it is easy to find from the modified FLRW equations (14.65)–(14.66) with \(\rho =p=0\), that \(a(t)\propto t^{2n-3}\) is an analytical solution of the system. Thus, even in vacuum, \(f(\mathbb {T})\) power-law admits power-law a(t) solutions. In this way, one is not putting the function \(f(\mathbb {T})\) by hand, instead, the symmetries of the model based on Noether’s theorem are choosing the form of the function. One can follow the other branch of Noether’s equation and find that exponential \(f(\mathbb {T})=f_0 e^{C_1\mathbb {T}}\) are also part of the symmetries of the model. For this case, one can obtain de-Sitter cosmological solutions from the modified FLRW equations.
3.8 Bounce Solutions in Modified Teleparallel Cosmology
One key problem in General Relativity is the existence of both cosmological and black hole singularities. The \(\Lambda \)CDM model, which is based on GR, states that the Universe started from an unnatural initial big bang cosmological singularity and this cannot be alleviated without evoking new physics. This means that the cosmological equations break down at \(t=0\) and some divergences in the curvature appears. In other words, there exists a singularity due to the incompleteness of the geodesic deviation equation . Possible solutions for this in cosmology are the so-called bouncing cosmological solutions, which essentially are solutions describing a contraction of the Universe until a minimum non-zero radius to then describing an expanded Universe passing through a bounce. This means that generically, there needs to be a model starting with a contracting universe whose Hubble parameter is \(H<0\), then passing to a continuous bounce with \(H=0\), to then finalising in an expansion with \(H>0\). There are several types of bounce solutions. Some of them have a different evolution, for example, exhibiting a discontinuity in the Hubble parameter. These solutions do not appear in GR, but it is possible to achieve them if either exotic matter or modified gravity are introduced. The simplest way to achieve this in GR is by introducing a quintom scalar field model with two scalar fields. The first scalar field behaves as a standard canonical scalar field and the other one has an incorrect sign in the kinetic term, and then behaves as a ghost scalar field. It is unclear how physical it is to introduce these kind of exotic scalar fields, due to the possible existence of instabilities. If one modifies GR, on the other hand, it is possible to obtain bouncing solutions without introducing such exotic elements. Basically, the method is very simple, a form of the scale factor (or the Hubble parameter) is assumed, which can describe bounces. Then, a reconstruction technique can be used to get a model (or a theory) that has these kind of solutions. For a more detailed description about bouncing cosmological solutions, see [247].
In the context of TG, the first study that found bouncing cosmological solutions was conducted in \(f(\mathbb {T})\) gravity [248]. To achieve this scenario, it is necessary to first check the existence of bounce solutions at the background level and then study the evolution of perturbations through the bounce. Let us here briefly review what happens at the background level. For the perturbation study, see more details in [248]. One type of bouncing cosmological solution can be described by having the following scale factor
where \(\sigma >0\) and \(a_0\) are constants. The first parameter determines how fast the bounce is, whereas \(a_0\) is the scale factor evaluated at the bouncing point. The Hubble parameter then behaves as
with the time varying from \(-\infty \) to \(+\infty \). Figure 14.7 shows the behaviour of the above Hubble parameter achieving the expected bounce scenario, starting from a matter contraction, then following with a bounce (static) and finalising in an expansion. If we assume a pressureless matter, from the conservation equation the energy density becomes \(\rho =C_1/(3 \sigma t^2+2)\). Since \(\mathbb {T}=6H^2\), we can then find that \(t=t(\mathbb {T})\), and we can then use this expression for the first flat FLRW equation (14.65), to then solve this differential equation for \(f(\mathbb {T})\), yielding
Hubble parameter versus time for the model (14.107) with \(\sigma =70\), in units where \(\kappa ^2=1\), describing a bounce behaviour
The scale factor (14.106) that gives the Hubble parameter (14.107) describing a bouncing cosmological solution is a solution of the above form of \(f(\mathbb {T})\) gravity, which is a GR term plus some correction terms, depending on the scalar torsion. There are other works finding other kinds of bounce solutions in the context of modified TG. In [249], different types of non-singular bounce solutions were found in \(f(\mathbb {T})\), such as \(\Lambda \)CDM with a bounce in the past, with the scale factor behaving as \(a(t)\propto \sinh [\sqrt{t^2+\tau ^2}/t_0]\) or future bounces with Quasi-rip and Little-rip behaviours. In [250] some superbounce solutions in \(f(\mathbb {T})\) gravity that have a ekpyrotic contracting phase preventing large anisotropies are found. The authors also made some comparisons between other modified models starting from GR, such as f(R) and \(f(\mathcal {G})\) gravity. Later, it was found that in \(f(\mathbb {T})\) gravity it is possible to have a bounce inflation model with a graceful decelerated exit [184]. Using dynamical systems techniques, in [209], the authors also found the possibility of bounces and turnaround solutions in \(f(\mathbb {T})\) gravity but the impossibility of cyclic and oscillating universes. In [251], the authors studied a model with \(f(\mathbb {T})\) and a scalar field to then perform perturbations for the bounce inflationary models, finding that it is difficult to obtain a stable bounce inflation solution, since there are many conditions that the models need to satisfy in order to have this property, though, they were able to show that a combination of power-law types of \(f(\mathbb {T})\) can achieve these stable bounce inflation solutions. If one understands the cosmological singularities as a break down of GR at very high energies, then some studies have argued that Loop quantum cosmology could alleviate them. Some works like [252,253,254] have also found bounces in a toy model in \(f(\mathbb {T})\) gravity, assuming Loop quantum cosmological considerations. Further generalisations to \(f(\mathbb {T})\) gravity, such as considering the teleparallel Gauss-Bonnet invariant \(T_{\mathcal {G}}\) in the so-called \(f(\mathbb {T},T_{\mathcal {G}})\) gravity, have also been used to analyse possible bounce solutions, finding five types of them [255, 256]. In [257] the case of Born-Infeld gravity was studied. These kind of theories are achieved from \(f(\mathbb {T})\) gravity with \(f(\mathbb {T})=\frac{\lambda }{2\kappa ^2}((1+\frac{\mathbb {T}}{2\lambda })^{1/2} -1)\), with \(\lambda \) being a parameter of the theory that becomes important at high energies. In this paper, the author found that at high energy regimes, the big bang singularity is absent, and either a de-Sitter inflationary stage of geometrical character or a bounce is present. Later, in [258], they showed that this behaviour is only valid for a certain region of the parameter space, and other singularities such as Big Rip, Big Bang, Big Freeze, and Sudden singularities can emerge. It is interesting to mention that recently, in [259], a regular Schwarzschild black hole solution was found in this theory. In this context, the central Schwarzschild curvature singularity is replaced by an infinitely long cosmic string related to the parameter \(\lambda \).
As was seen in the previous example and also in the papers mentioned here, it is not so complicated to get bouncing cosmological solutions in modified TG. It is important to emphasise that in standard GR, this cannot be achieved without introducing matter that violates the energy conditions.
4 What Can Teleparallel Theories Have to Offer? What Are the Open Problems in Teleparallel Theories?
Teleparallel theories give an alternative starting point for understanding gravity compared with the standard curvature-based approach to gravity used in GR. Some interesting features about them compared to GR are:
-
Modified teleparallel theories are broader than standard modified theories starting from GR:
We have seen that theories equivalent to GR, scalar-tensor gravity, Horndeski theory, f(R) and Gauss-Bonnet gravity based on the teleparallel geometry exist are subclasses of more general families of Teleparallel Gravity theories. In this spirit, Teleparallel Gravity may be used to formulate broader classes of theories than could be constructed by using only the metric and its Levi-Civita connection. This should not be too surprising, since any theory of the latter type can be rewritten into teleparallel language by using the relations (14.4), (14.23) and (14.24) to replace the metric, its Levi-Civita connection and the corresponding curvature by the tetrad and the contortion, and hence the torsion. This teleparallel formulation then gives rise to further extensions and generalisations by splitting off boundary terms or including additional terms that have no equivalent expression in terms of the metric geometry only. An easy example would be to take the case of f(R) and \(f(\mathbb {T})\) gravity. If we start by formulating a theory from GR, then torsion is zero and it is not possible to derive a similar theory to \(f(\mathbb {T})\). On the other hand, if we start from TG, we can generalise \(f(\mathbb {T})\) to \(f(\mathbb {T},B)\) and then we can formulate a teleparallel equivalent version of f(R) by considering \(f(\mathbb {T},B)=f(-\mathbb {T}+B)=f(R)\).
-
It is easy to get second-order field equations, since torsion contains only first-order derivatives:
Since most physical phenomena are described by up to second-order field equations, it is expected that gravity will not have a behaviour different to this. Moreover, higher-order field equations often lead to ghost instabilities. In Teleparallel Gravity it is easy to get second order field equations because the torsion tensor contains only first-order derivatives of the tetrad, in contrast with the Riemann tensor that contains second-order derivatives in the metric. This means that in modifications like \(f(\mathbb {T})\) or even more complicated ones like \(f(T_\mathrm{ax}, T_\mathrm{vec}, T_\mathrm{ten})\), BDLS, etc., the field equations will be of second order, unlike in, e.g., f(R) theory where they are fourth-order in all cases beyond GR. In principle, one could construct a theory with infinite contractions of the torsion tensor and still get second-order field equations.
-
Similarity to Yang-Mills theory—possible connections to gauge theory and particle physics:
The TEGR action in Eq. (14.29) has an obvious similarity with a Yang-Mills type action, since it is quadratic in the first-order derivatives of the tetrad, the latter being the fundamental dynamical field of the theory. This means that has more in common with actions encountered in particle physics than it is the case for the Einstein-Hilbert action. Furthermore, the potential interpretation as a gauge theory of translations makes it more similar to theories describing the other fundamental interactions in Nature, hence paving a potential road map towards a unification of gravity and other forces. While still being non-renormalisable, it may provide an alternative and possibly more promising starting point for constructing a UV complete theory.
-
The possibility of formulating the theory without the equivalence principle: In GR, gravitation is characterised by curvature through the Ricci scalar, which then acts on particles through the geodesic equation. TG is wholly different in that the geometric torsion that is produced to expressed gravity, acts through a Lorentz force-type equation. In this way, we recover the original concept of gravitation as a force similar to the other fundamental forces of Nature. While the equations turn out to be equivalent for TEGR, they differ for modifications to this model. Coupled with the potential of being described as a gauge theory of translations, TG does not rely on the weak equivalence principle in that it would survive a violation [1, 260]. However, in these settings, the Newtonian limits remain intact resulting in a more natural weak-field limit compared with GR.
-
Defining a gravitational energy-momentum tensor:
TG offers the possibility of describing gravitation as a gauge current [1, 5, 6]. Then, by separating inertial and gravitation, it may become possible to define an energy-momentum tensor for gravitation. However, this feature of the theory may require selection of a Lorentz frame, which would limit the applicability of this result [261, 262].
-
The regularity of the TEGR action. One does not need to introduce a Gibbons-Hawking-York boundary term:
One may argue that the TEGR action in Eq. (14.29) is a more natural formulation of the dynamics of GR than the Einstein-Hilbert action, since the latter also contains second order derivatives of the metric. The latter mandates the inclusion of a Gibbons-Hawking-York boundary term in order to possess a well-defined variational problem and Hamiltonian formulation, which is not the case for TEGR. While this does not affect the classical equations of motion, it may affect the quantum behavior and thermodynamics of black holes. Further, it was found in [263] that the black hole entropy is more naturally expressed as a volume integral in TEGR than in GR.
-
Torsional or Curvature-based Gravity:
TEGR is dynamically equivalent to GR in that the identical field equations emerge due to the respective Lagrangian densities being equal up to a boundary term. However, the action may contain further information, such as the renormalisability of the theory, as well as the symmetries of the theory. Moreover, modifications to TEGR offer a much richer avenue to construct new theories, due to the second-order nature of the torsion scalar [264].
Although teleparallel theories have attained a lot of attention in the past ten years, the community effort is still not comparable to that in GR. For this reason, there are several open problems/questions that have not been addressed properly in the literature. Some of these open problems are:
-
Confrontation with cosmological data: Teleparallel theories have shown great promise for consistently describing observations at cosmic scales while also satisfying Solar System and astrophysical-scale physics [105, 134, 160,161,162,163, 167, 170, 265,266,267,268]. Further work needs to be done in this direction to better understand the explaining power of the theory in its various manifestations.
-
Gravitational Waves: A strong effort has been made in regards to understanding the cosmological consequences of gravitational waves in \(f(\mathbb {T})\) gravity [134, 162, 163, 269]. However, there remains many other contexts in which TG has shown promise, and more than this, further work is needed in the astrophysical context. In Refs. [62, 135, 136, 270], it is shown that \(f(\mathbb {T})\) gravity contains only two propagating modes, while other variants of TG can provide more. It would be interesting to investigate further the waveform for astrophysical events, which would entail obtaining further information about the \(3+1\) formalism of the theory and performing simulations of astrophysical events. Ultimately, it is crucial to understand how current and future observatories can be exploited to test TG.
-
The Galactic Rotation Curve Problem: \(f(\mathbb {T})\) gravity has shown positive results for describing the rotation curves without the requirement of adding dark matter [137]. Weak lensing tests have also contributed to constraints on one of the potential models of the theory [271]. However, further analysis needs to be done on considering more cosmologically inspired models, as well as increasing the breadth of the analysis. One possibility is to use the SPARC (Spitzer Photometry and Accurate Rotation Curves) obtained in Ref. [272].
-
Teleparallel quantum gravity: The majority of quantum gravity approaches have been attempted with GR as the starting point, but not so many have been initiated from TG. For example, the loop quantum corrections of the TEGR action (14.29) are not so well-known. One of the first attempts was done in [273]. In GR, this has been studied with a lot of effort, even obtaining corrections of an action with \(\sum _{i=1}^{70}R^i\) [274]. This has been studied within the asymptotic safety approach to quantum gravity [275] that has not also been applied to Teleparallel Gravity. Another interesting route would be to formulate a teleparallel version of loop quantum gravity, since both formulations use a similar mathematical language.
-
What are singularities in Teleparallel Gravity?: Hawking and Penrose proposed a way to define singularities in GR, which is based on the incompleteness of the geodesic equation. Then, a simple way to quantify these singularities is by defining some invariants such as the Kretschmann scalar \(K\equiv R^{\mu \nu \alpha \sigma }R_{\mu \nu \alpha \sigma }\). In TG, it is not clear whether the Hawking-Penrose theorem would be the same, or if one would need to define different invariants to check if there are singularities. Then, it is still open as to how a singularity in the context of TG can be defined.
Notes
- 1.
While \(T_{\mu \nu }\) refers to the energy-momentum tensor,
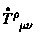 refers to the torsion tensor which is not related.
refers to the torsion tensor which is not related.
References
R. Aldrovandi, J.G. Pereira, Teleparallel Gravity, vol. 173 (Springer, Dordrecht, 2013)
A. Einstein, Riemann-Geometrie mit Aufrechterhaltung des Begriffes des Fernparallelismus. Sitzber. Preuss. Akad. Wiss. 17, 217–221 (1928)
M. Krššák, E.N. Saridakis, The covariant formulation of f(T) gravity. Class. Quant. Grav. 33(11), 115009 (2016). arXiv:1412.8383
A. Golovnev, T. Koivisto, M. Sandstad, On the covariance of teleparallel gravity theories. Class. Quant. Grav. 34(14), 145013 (2017). arXiv:1701.06271
D. Blixt, M. Hohmann, C. Pfeifer, Hamiltonian and primary constraints of new general relativity. Phys. Rev. D 99(8), 084025 (2019). arXiv:1811.11137
D. Blixt, M. Hohmann, C. Pfeifer, On the gauge fixing in the Hamiltonian analysis of general teleparallel theories. Universe 5(6), 143 (2019). arXiv:1905.01048
J. Beltrán Jiménez, L. Heisenberg, T.S. Koivisto, Teleparallel Palatini theories. JCAP 1808, 039 (2018). arXiv:1803.10185
M. Blagojević, F.W. Hehl (eds.), Gauge Theories of Gravitation (World Scientific, Singapore, 2013)
K. Hayashi, T. Nakano, Extended translation invariance and associated gauge fields. Prog. Theor. Phys. 38, 491–507 (1967). ([354(1967)])
Y.M. Cho, Einstein Lagrangian as the Translational Yang-Mills Lagrangian. Phys. Rev. D 14, 2521 (1976). ([393(1975)])
K. Hayashi, T. Shirafuji, New general relativity. Phys. Rev. D 19, 3524–3553 (1979). ([409(1979)])
J.C. Baez, D.K. Wise, Teleparallel gravity as a higher gauge theory. Commun. Math. Phys. 333(1), 153–186 (2015). arXiv:1204.4339
M. Fontanini, E. Huguet, M. Le Delliou, Teleparallel gravity equivalent of general relativity as a gauge theory: translation or Cartan connection? Phys. Rev. D 99(6), 064006 (2019). arXiv:1811.03810
J.G. Pereira, Y.N. Obukhov, Gauge structure of teleparallel gravity. Universe 5(6), 139 (2019). arXiv:1906.06287
M. Blagojevic, Gravitation and Gauge Symmetries. Series in High Energy Physics, Cosmology and Gravitation (CRC Press, 2001)
Yu.N. Obukhov, J.G. Pereira, Metric affine approach to teleparallel gravity. Phys. Rev. D 67, 044016 (2003). arXiv:gr-qc/0212080
B. Li, T.P. Sotiriou, J.D. Barrow, \(f(T)\) gravity and local Lorentz invariance. Phys. Rev. D 83, 064035 (2011). arXiv:1010.1041
T.P. Sotiriou, B. Li, J.D. Barrow, Generalizations of teleparallel gravity and local Lorentz symmetry. Phys. Rev. D 83, 104030 (2011). arXiv:1012.4039
R. Ferraro, F. Fiorini, Non trivial frames for f(T) theories of gravity and beyond. Phys. Lett. B 702, 75–80 (2011). arXiv:1103.0824
N. Tamanini, C.G. Boehmer, Good and bad tetrads in f(T) gravity. Phys. Rev. D 86, 044009 (2012). arXiv:1204.4593
N. Tamanini, C.G. Böhmer, Definition of Good Tetrads for f(T) Gravity, in Proceedings, 13th Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity, Astrophysics, Relativistic Field Theories (MG13): Stockholm, Sweden, July 1-7, 2012, pp. 1282–1284 (2015). arXiv:1304.0672
W. Kopczynski, Problems with metric-teleparallel theories of gravitation. J. Phys. A: Math. General 15, 493–506 (1982)
W.-H. Cheng, D.-C. Chern, J.M. Nester, Canonical analysis of the one parameter teleparallel theory. Phys. Rev. D 38, 2656–2658 (1988)
J.M. Nester, Is there really a problem with the teleparallel theory? Class. Q. Gravity 5, 1003–1010 (1988)
H. Chen, J.M. Nester, H.-J. Yo, Acausal PGT modes and the nonlinear constraint effect. Acta Phys. Polon. B 29, 961–970 (1998)
Y.C. Ong, K. Izumi, J.M. Nester, P. Chen, Problems with propagation and time evolution in f(T) gravity. Phys. Rev. D 88, 024019 (2013). arXiv:1303.0993
R. Ferraro, F. Fiorini, Remnant group of local Lorentz transformations in \(mathcal f (T)\) theories. Phys. Rev. D 91(6), 064019 (2015). arXiv:1412.3424
P. Chen, K. Izumi, J.M. Nester, Y.C. Ong, Remnant symmetry, propagation and evolution in \(f\) (T) gravity. Phys. Rev. D 91(6), 064003 (2015)
C. Bejarano, R. Ferraro, F. Fiorini, M.J. Guzmán, Reflections on the covariance of modified teleparallel theories of gravity. Universe 5, 158 (2019). arXiv:1905.09913
R. Ferraro, M.J. Guzmán, Pseudoinvariance and the extra degree of freedom in \(f(T)\) gravity. Phys. Rev. D 101(8), 084017 (2020). arXiv:2001.08137
M. Hohmann, L. Järv, U. Ualikhanova, Covariant formulation of scalar-torsion gravity. Phys. Rev. D 97(10), 104011 (2018). arXiv:1801.05786
M. Krssak, R.J. van den Hoogen, J.G. Pereira, C.G. Böhmer, A.A. Coley, Teleparallel theories of gravity: illuminating a fully invariant approach. Class. Quant. Grav. 36(18), 183001 (2019). arXiv:1810.12932
J.W. Maluf, Dirac spinor fields in the teleparallel gravity: comment on ‘Metric affine approach to teleparallel gravity’. Phys. Rev. D 67, 108501 (2003). arXiv:gr-qc/0304005
E.W. Mielke, Consistent coupling to Dirac fields in teleparallelism: comment on ‘Metric-affine approach to teleparallel gravity’. Phys. Rev. D 69, 128501 (2004)
Yu.N. Obukhov, J.G. Pereira, Lessons of spin and torsion: reply to ‘Consistent coupling to Dirac fields in teleparallelism’. Phys. Rev. D 69, 128502 (2004). arXiv:gr-qc/0406015
J.B. Formiga, Comment on “Metric-affine approach to teleparallel gravity.” Phys. Rev. D 88(6), 068501 (2013). arXiv:1306.4964
J. Beltran Jimenez, L. Heisenberg, T. Koivisto, The coupling of matter and spacetime geometry. arXiv:2004.04606
Y.N. Obukhov, G.F. Rubilar, Invariant conserved currents in gravity theories with local Lorentz and diffeomorphism symmetry. Phys. Rev. D 74, 064002 (2006). arXiv:gr-qc/0608064
J.W. Maluf, The teleparallel equivalent of general relativity. Ann. Phys. 525, 339–357 (2013). arXiv:1303.3897
M. Krššák, Holographic renormalization in teleparallel gravity. Eur. Phys. J. C 77(1), 44 (2017). arXiv:1510.06676
J.W. Maluf, S.C. Ulhoa, J.F. da Rocha-Neto, Difficulties of Teleparallel Theories of Gravity with Local Lorentz Symmetry. arXiv:1811.06876
T.P. Sotiriou, V. Faraoni, f(R) theories of gravity. Rev. Mod. Phys. 82, 451–497 (2010). arXiv:0805.1726
S. Nojiri, S.D. Odintsov, Introduction to modified gravity and gravitational alternative for dark energy. eConf C0602061, 06 (2006). arXiv:hep-th/0601213. [Int. J. Geom. Meth. Mod. Phys.4,115(2007)]
A. De Felice, S. Tsujikawa, f(R) theories. Living Rev. Rel. 13, 3 (2010). arXiv:1002.4928
S. Nojiri, S.D. Odintsov, Unified cosmic history in modified gravity: from F(R) theory to Lorentz non-invariant models. Phys. Rept. 505, 59–144 (2011). arXiv:1011.0544
Y.S. Myung, Propagating degrees of freedom in \(f(R)\) gravity. Adv. High Energy Phys. 2016, 3901734 (2016). arXiv:1608.01764
C.P.L. Berry, J.R. Gair, Linearized f(R) gravity: gravitational radiation and solar system tests. Phys. Rev. D 83, 104022 (2011). arXiv:hep-th/0601213. [Int. J. Geom. Meth. Mod. Phys.4,115(2007)]
S. Capozziello, C. Corda, M.F. De Laurentis, Massive gravitational waves from f(R) theories of gravity: potential detection with LISA. Phys. Lett. B 669, 255–259 (2008). arXiv:0812.2272
G.R. Bengochea, R. Ferraro, Dark torsion as the cosmic speed-up. Phys. Rev. D 79, 124019 (2009). arXiv:0812.1205
R. Ferraro, F. Fiorini, On born-infeld gravity in Weitzenbock spacetime. Phys. Rev. D 78, 124019 (2008). arXiv:0812.1981
R. Ferraro, F. Fiorini, Modified teleparallel gravity: inflation without inflation. Phys. Rev. D 75, 084031 (2007). arXiv:gr-qc/0610067
S.B. Nassur, C. Ainamon, M.J.S. Houndjo, J. Tossa, Unimodular f(T) gravity. Eur. Phys. J. Plus 131(12), 420 (2016). arXiv:1602.03172
M. Krssak, Variational Problem and Bigravity Nature of Modified Teleparallel Theories. arXiv:1705.01072
M. Hohmann, L. Järv, M. Krššák, C. Pfeifer, Teleparallel theories of gravity as analogue of nonlinear electrodynamics. Phys. Rev. D 97(10), 104042 (2018). arXiv:1711.09930
M. Hohmann, L. Järv, M. Krššák, C. Pfeifer, Modified teleparallel theories of gravity in symmetric spacetimes. Phys. Rev. D 100(8), 084002 (2019). arXiv:1901.05472
F. Mueller-Hoissen, J. Nitsch, Teleparallelism - a viable theory of gravity? Phys. Rev. D 28, 718–728 (1983)
W. Kopczynski, Problems with metric-teleparallel theories of gravitation. J. Phys. Math. General 15, 493–506 (1982)
J.M. Nester, Is there really a problem with the teleparallel theory? Class Quant. Gravity 5, 1003–1010 (1988)
T. Kawai, N. Toma, Singularities of “Schwarzschild Like’’ space-time in new general relativity. Prog. Theor. Phys. 83, 1 (1990)
M. Fukui, K. Hayashi, Axially symmetric solutions of new general relativity. Prog. Theor. Phys. 66, 1500 (1981)
M. Fukui, J. Masukawa, Weak field approximation of new general relativity. Prog. Theor. Phys. 73, 973 (1985)
M. Hohmann, M. Krššák, C. Pfeifer, U. Ualikhanova, Propagation of gravitational waves in teleparallel gravity theories. Phys. Rev. D 98(12), 124004 (2018). arXiv:1807.04580
A. Okolow, J. Swiezewski, Hamiltonian formulation of a simple theory of the teleparallel geometry. Class. Quant. Grav. 29, 045008 (2012). arXiv:1111.5490
Y.C. Ong, J.M. Nester, Counting components in the Lagrange multiplier formulation of teleparallel theories. Eur. Phys. J. C 78(7), 568 (2018). arXiv:1709.00068
T. Ortín, Gravity and Strings Cambridge Monographs on Mathematical Physics (Cambridge University Press, Cambridge, 2004)
J.B. Jiménez, K.F. Dialektopoulos, Non-Linear Obstructions for Consistent New General Relativity. arXiv:1907.10038
J.W. Maluf, F.F. Faria, Conformally invariant teleparallel theories of gravity. Phys. Rev. D 85, 027502 (2012). arXiv:1110.3095
T. Koivisto, G. Tsimperis, The spectrum of teleparallel gravity. arXiv:1810.11847
A. Conroy, T. Koivisto, The spectrum of symmetric teleparallel gravity. Eur. Phys. J. C 78(11), 923 (2018). arXiv:1710.05708
L. Heisenberg, A systematic approach to generalisations of general relativity and their cosmological implications. Phys. Rep. 796, 1–113 (2019). arXiv:1807.01725
T. Biswas, E. Gerwick, T. Koivisto, A. Mazumdar, Towards singularity and ghost free theories of gravity. Phys. Rev. Lett. 108, 031101 (2012). arXiv:1110.5249
S. Bahamonde, C.G. Böhmer, M. Krššák, New classes of modified teleparallel gravity models. Phys. Lett. B 775, 37–43 (2017). arXiv:1706.04920
K. Bamba, S.D. Odintsov, D. Sáez-Gómez, Conformal symmetry and accelerating cosmology in teleparallel gravity. Phys. Rev. D 88, 084042 (2013). arXiv:1308.5789
R.-J. Yang, Conformal transformation in \(f(T)\) theories. EPL 93(6), 60001 (2011). arXiv:1010.1376
S. Bahamonde, C.G. Böhmer, M. Wright, Modified teleparallel theories of gravity. Phys. Rev. D 92(10), 104042 (2015). arXiv:1508.05120
S. Bahamonde, M. Zubair, G. Abbas, Thermodynamics and cosmological reconstruction in \(f(T, B)\) gravity. Phys. Dark Univ. 19, 78–90 (2018). arXiv:1609.08373
S. Bahamonde, S. Capozziello, Noether symmetry approach in \(f(T, B)\) teleparallel cosmology. Eur. Phys. J. C 77(2), 107 (2017). arXiv:1612.01299
G. Otalora, E.N. Saridakis, Modified teleparallel gravity with higher-derivative torsion terms. Phys. Rev. D 94(8), 084021 (2016). arXiv:1605.04599
S. Capozziello, M. De Laurentis, K.F. Dialektopoulos, Noether symmetries in Gauss-Bonnet-teleparallel cosmology. Eur. Phys. J. C 76(11), 629 (2016). arXiv:1609.09289
S. Bahamonde, C.G. Böhmer, Modified teleparallel theories of gravity: Gauss-Bonnet and trace extensions. Eur. Phys. J. C 76(10), 578 (2016). arXiv:1606.05557
G. Kofinas, E.N. Saridakis, Teleparallel equivalent of Gauss-Bonnet gravity and its modifications. Phys. Rev. D 90, 084044 (2014). arXiv:1404.2249
G. Kofinas, G. Leon, E.N. Saridakis, Dynamical behavior in \(f(t, t_g)\) cosmology. Class. Quant. Gravity 31(17), 175011 (2014). arXiv:1404.7100
T. Harko, F.S.N. Lobo, G. Otalora, E.N. Saridakis, \(f(T, mathcal T )\) gravity and cosmology. JCAP 1412, 021 (2014). arXiv:1405.0519
T. Harko, F.S.N. Lobo, S. Nojiri, S.D. Odintsov, \(f(R, T)\) gravity. Phys. Rev. D 84, 024020 (2011). arXiv:1104.2669
T. Harko, F.S.N. Lobo, G. Otalora, E.N. Saridakis, Nonminimal torsion-matter coupling extension of f(T) gravity. Phys. Rev. D 89, 124036 (2014). arXiv:1404.6212
S. Bahamonde, Generalised nonminimally gravity-matter coupled theory. Eur. Phys. J. C 78(4), 326 (2018). arXiv:1709.05319
J.F. Donoghue, General relativity as an effective field theory: the leading quantum corrections. Phys. Rev. D 50, 3874–3888 (1994). arXiv:gr-qc/9405057
S.B. Giddings, Black hole information, unitarity, nonlocality. Phys. Rev. D 74, 106005 (2006). arXiv:hep-th/0605196
S. Bahamonde, S. Capozziello, M. Faizal, R.C. Nunes, Nonlocal teleparallel cosmology. Eur. Phys. J. C 77(9), 628 (2017). arXiv:1709.02692
S. Bahamonde, S. Capozziello, K.F. Dialektopoulos, Constraining generalized non-local cosmology from noether symmetries. Eur. Phys. J. C 77(11), 722 (2017). arXiv:1708.06310
G.W. Horndeski, Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 10, 363–384 (1974)
T. Kobayashi, M. Yamaguchi, J. Yokoyama, Generalized G-inflation: inflation with the most general second-order field equations. Prog. Theor. Phys. 126, 511–529 (2011). arXiv:1105.5723
C. Brans, R.H. Dicke, Mach’s principle and a relativistic theory of gravitation. Phys. Rev. 124, 925–935 (1961). ([142(1961)])
F. Perrotta, C. Baccigalupi, S. Matarrese, Extended quintessence. Phys. Rev. D 61, 023507 (1999). arXiv:astro-ph/9906066
E.J. Copeland, M. Sami, S. Tsujikawa, Dynamics of dark energy. Int. J. Mod. Phys. D 15, 1753–1936 (2006). arXiv:hep-th/0603057
C. Deffayet, O. Pujolas, I. Sawicki, A. Vikman, Imperfect dark energy from kinetic gravity braiding. JCAP 1010, 026 (2010). arXiv:1008.0048
S. Bahamonde, K.F. Dialektopoulos, J.L. Said, Can Horndeski Theory be recast using Teleparallel Gravity?. arXiv:1904.10791
S. Bahamonde, K.F. Dialektopoulos, V. Gakis, J.L. Said, Reviving Horndeski Theory using Teleparallel Gravity after GW170817. arXiv:1907.10057
M. Hohmann, Disformal transformations in scalar-torsion gravity. Universe 5(7), 167 (2019). arXiv:1905.00451
C.D. Kreisch, E. Komatsu, Cosmological constraints on Horndeski gravity in light of GW170817. JCAP 1812(12), 030 (2018). arXiv:1712.02710
Y. Gong, E. Papantonopoulos, Z. Yi, Constraints on scalar-tensor theory of gravity by the recent observational results on gravitational waves. Eur. Phys. J. C 78(9), 738 (2018). arXiv:1711.04102
LIGO Scientific, Virgo Collaboration, B.P. Abbott et al., GW170817: observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett 119(16), 161101 (2017). arXiv:1710.05832
C.-Q. Geng, C.-C. Lee, E.N. Saridakis, Y.-P. Wu, “Teleparallel’’ dark energy. Phys. Lett. B 704, 384–387 (2011). arXiv:1109.1092
G. Kofinas, E. Papantonopoulos, E.N. Saridakis, Self-gravitating spherically symmetric solutions in scalar-torsion theories. Phys. Rev. D 91(10), 104034 (2015). arXiv:1501.00365
C.-Q. Geng, C.-C. Lee, E.N. Saridakis, Observational constraints on teleparallel dark energy. JCAP 1201, 002 (2012). arXiv:1110.0913
M. Zubair, S. Bahamonde, M. Jamil, Generalized second law of thermodynamic in modified teleparallel theory. Eur. Phys. J. C 77(7), 472 (2017). arXiv:1604.02996
S. Bahamonde, M. Marciu, P. Rudra, Generalised teleparallel quintom dark energy non-minimally coupled with the scalar torsion and a boundary term. JCAP 1804(04), 056 (2018). arXiv:1802.09155
L. Jarv, A. Toporensky, General relativity as an attractor for scalar-torsion cosmology. Phys. Rev. D 93(2), 024051 (2016). arXiv:1511.03933
G. Kofinas, Hyperscaling violating black holes in scalar-torsion theories. Phys. Rev. D 92(8), 084022 (2015). arXiv:1507.07434
D. Horvat, S. Ilijić, A. Kirin, Z. Narančić, Nonminimally coupled scalar field in teleparallel gravity: Boson stars. Class. Quant. Grav. 32(3), 035023 (2015). arXiv:1407.2067
M. Jamil, D. Momeni, R. Myrzakulov, Stability of a non-minimally conformally coupled scalar field in F(T) cosmology. Eur. Phys. J. C 72, 2075 (2012). arXiv:1208.0025
Y.-P. Wu, C.-Q. Geng, Primordial fluctuations within teleparallelism. Phys. Rev. D 86, 104058 (2012). arXiv:1110.3099
H. Wei, Dynamics of teleparallel dark energy. Phys. Lett. B 712, 430–436 (2012). arXiv:1109.6107
S. Bahamonde, M. Wright, Teleparallel quintessence with a nonminimal coupling to a boundary term. Phys. Rev. D 92(8), 084034 (2015). arXiv:1508.06580. [Erratum: Phys. Rev.D93,no.10,109901(2016)]
M. Hohmann, Scalar-torsion theories of gravity I: general formalism and conformal transformations. Phys. Rev. D 98(6), 064002 (2018). arXiv:1801.06528
M. Hohmann, C. Pfeifer, Scalar-torsion theories of gravity II: \(L(T, X, Y, \phi )\) theory. Phys. Rev. D 98(6), 064003 (2018). arXiv:1801.06536
M. Hohmann, Scalar-torsion theories of gravity III: analogue of scalar-tensor gravity and conformal invariants. Phys. Rev. D 98(6), 064004 (2018). arXiv:1801.06531
C.M. Will, The confrontation between general relativity and experiment. Living Rev. Rel. 17, 4 (2014). arXiv:1403.7377
J. Hayward, Scalar tetrad theories of gravity. Gen. Rel. Grav. 13, 43–55 (1981)
Z.-C. Chen, Y. Wu, H. Wei, Post-Newtonian approximation of teleparallel gravity coupled with a scalar field. Nucl. Phys. B 894, 422–438 (2015). arXiv:1410.7715
J.-T. Li, Y.-P. Wu, C.-Q. Geng, Parametrized post-Newtonian limit of the teleparallel dark energy model. Phys. Rev. D 89(4), 044040 (2014). arXiv:1312.4332
U. Ualikhanova, M. Hohmann, Parameterized post-Newtonian limit of general teleparallel gravity theories. arXiv:1907.08178
L. Iorio, N. Radicella, M.L. Ruggiero, Constraining f(T) gravity in the Solar System. JCAP 1508(08), 021 (2015). arXiv:1505.06996
L. Iorio, E.N. Saridakis, Solar system constraints on f(T) gravity. Mon. Not. Roy. Astron. Soc. 427, 1555 (2012). arXiv:1203.5781
G. Farrugia, J.L. Said, M.L. Ruggiero, Solar system tests in f(T) gravity. Phys. Rev. D 93(10), 104034 (2016). arXiv:1605.07614
H. Mohseni Sadjadi, Parameterized post-Newtonian approximation in a teleparallel model of dark energy with a boundary term. Eur. Phys. J. C 77(3), 191 (2017)
E.D. Emtsova, M. Hohmann, Post-Newtonian limit of scalar-torsion theories of gravity as analogue to scalar-curvature theories. Phys. Rev. D 101(2), 024017 (2020). arXiv:1909.09355
K. Flathmann, M. Hohmann, Post-Newtonian limit of generalized scalar-torsion theories of gravity. Phys. Rev. D 101(2), 024005 (2020). arXiv:1910.01023
S. Bahamonde, K.F. Dialektopoulos, M. Hohmann, J. Levi Said, Post-Newtonian limit of Teleparallel Horndeski gravity. arXiv:2003.11554
G. Farrugia, J. Levi Said, A. Finch, Gravitoelectromagnetism, solar system test and weak-field solutions in \(f(T,B)\) gravity with observational constraints. Universe 6(2), 34 (2020). arXiv:2002.08183
S. Capozziello, M. Capriolo, L. Caso, Weak field limit and gravitational waves in \(f(T, B)\) teleparallel gravity. Eur. Phys. J. C 80(2), 156 (2020). arXiv:1912.12469
A. Pourbagher, A. Amani, Thermodynamics and stability of \(f(T, B)\) gravity with viscous fluid by observational constraints. Astrophys. Space Sci. 364(8), 140 (2019). arXiv:1908.11595
LIGO Scientific, Virgo, Fermi-GBM, INTEGRAL Collaboration, B.P. Abbott et al., Gravitational waves and gamma-rays from a binary neutron star merger: GW170817 and GRB 170817A. Astrophys. J. 848(2), L13 (2017). arXiv:1710.05834
Y.-F. Cai, C. Li, E.N. Saridakis, L. Xue, \(f(T)\) gravity after GW170817 and GRB170817A. arXiv:1801.05827
G. Farrugia, J.L. Said, V. Gakis, E.N. Saridakis, Gravitational waves in modified teleparallel theories. Phys. Rev. D 97(12), 124064 (2018). arXiv:1804.07365
K. Bamba, S. Capozziello, M. De Laurentis, S. Nojiri, D. Sáez-Gómez, No further gravitational wave modes in \(F(T)\) gravity. Phys. Lett. B 727, 194–198 (2013). arXiv:1309.2698
A. Finch, J.L. Said, Galactic rotation dynamics in f(T) gravity. Eur. Phys. J. C 78(7), 560 (2018). arXiv:1806.09677
Planck Collaboration, N. Aghanim et al., Planck 2018 results. VI. Cosmological parameters. arXiv:1807.06209
A.G. Riess, S. Casertano, W. Yuan, L.M. Macri, D. Scolnic, Large magellanic cloud cepheid standards provide a 1% foundation for the determination of the hubble constant and stronger evidence for physics beyond \(\Lambda \) CDM. Astrophys. J. 876(1), 85 (2019). arXiv:1903.07603
K.C. Wong et al., H0LiCOW XIII. A 2.4% measurement of \(H_{0}\) from lensed quasars: \(5.3\sigma \) tension between early and late-Universe probes. arXiv:1907.04869
Y.-F. Cai, S. Capozziello, M. De Laurentis, E.N. Saridakis, f(T) teleparallel gravity and cosmology. Rept. Prog. Phys. 79(10), 106901 (2016). arXiv:1511.07586
R. Zheng, Q.-G. Huang, Growth factor in \(f(T)\) gravity. JCAP 1103, 002 (2011). arXiv:1010.3512
E.V. Linder, Einstein’s other gravity and the acceleration of the Universe. Phys. Rev. D 81, 127031 (2010). arXiv:1005.3039. [Erratum: Phys. Rev. D82,109902(2010)]
G. Farrugia, J.L. Said, Stability of the flat FLRW metric in \(f(T)\) gravity. Phys. Rev. D 94(12), 124054 (2016). arXiv:1701.00134
Á. de la Cruz Dombriz, Towards new constraints in extended theories of gravity: cosmography and gravitational-wave signals from neutron stars. Galaxies 6(1), 28 (2018)
A. Aviles, A. Bravetti, S. Capozziello, O. Luongo, Cosmographic reconstruction of \(f(mathcal T )\) cosmology. Phys. Rev. D 87(6), 064025 (2013). arXiv:1302.4871
S. Capozziello, V.F. Cardone, H. Farajollahi, A. Ravanpak, Cosmography in f(T)-gravity. Phys. Rev. D 84, 043527 (2011). arXiv:1108.2789
S. Capozziello, R. D’Agostino, O. Luongo, Extended Gravity Cosmography. arXiv:1904.01427
N. Suzuki, D. Rubin, C. Lidman, G. Aldering, R. Amanullah et al., The hubble space telescope cluster supernova survey: v. improving the dark energy constraints \(z>1\) and building an early-type-hosted supernova sample. Astrophys. J 746, 85 (2012). arXiv:1105.3470
A.G. Riess et al., Cepheid calibrations of modern type Ia supernovae: implications for the hubble constant. Astrophys. J. Suppl. 183, 109–141 (2009). arXiv:0905.0697
R. Myrzakulov, Accelerating universe from f(t) gravity. Eur. Phys. J. C 71, 1752 (2011)
S. Chakrabarti, J.L. Said, K. Bamba, On reconstruction of extended teleparallel gravity from the cosmological jerk parameter. Eur. Phys. J. C 79(6), 454 (2019). arXiv:1905.09711
W. El Hanafy, G. Nashed, Phenomenological reconstruction of \(f(T)\) teleparallel gravity. Phys. Rev. D 100(8), 083535 (2019). arXiv:1910.04160
W. El Hanafy, E.N. Saridakis, \(f(T)\) cosmology: From Pseudo-Bang to Pseudo-Rip. arXiv:2011.15070
S.-H. Chen, J.B. Dent, S. Dutta, E.N. Saridakis, Cosmological perturbations in f(T) gravity. Phys. Rev. D 83, 023508 (2011). arXiv:1008.1250
K. Izumi, Y.C. Ong, Cosmological perturbation in f(T) gravity revisited. JCAP 1306, 029 (2013). arXiv:1212.5774
G. Farrugia, J.L. Said, Growth factor in \(f(T,mathcal T )\) gravity. Phys. Rev. D 94(12), 124004 (2016). arXiv:1612.00974
A. Golovnev, T. Koivisto, Cosmological perturbations in modified teleparallel gravity models. JCAP 1811(11), 012 (2018). arXiv:1808.05565
Y.-P. Wu, C.-Q. Geng, Matter density perturbations in modified teleparallel theories. JHEP 11, 142 (2012). arXiv:1211.1778
R.C. Nunes, S. Pan, E.N. Saridakis, New observational constraints on f(T) gravity from cosmic chronometers. JCAP 1608(08), 011 (2016). arXiv:1606.04359
R.C. Nunes, Structure formation in \(f(T)\) gravity and a solution for \(H_0\) tension. arXiv:1802.02281
R.C. Nunes, S. Pan, E.N. Saridakis, New observational constraints on \(f(T)\) gravity through gravitational-wave astronomy. Phys. Rev. D 98(10), 104055 (2018). arXiv:1810.03942
R.C. Nunes, M.E.S. Alves, J.C.N. de Araujo, Forecast constraints on \(f(T)\) gravity with gravitational waves from compact binary coalescences. arXiv:1905.03237
S. Dodelson, Modern Cosmology (Academic, 2003)
B.O.S.S. Collaboration, S. Alam et al., The clustering of galaxies in the completed SDSS-III Baryon oscillation spectroscopic survey: cosmological analysis of the DR12 galaxy sample. Mon. Not. Roy. Astron. Soc. 470(3), 2617–2652 (2017). arXiv:1607.03155
D. Wang, D. Mota, Can \(f(T)\) gravity resolve the \(H_0\) tension?. arXiv:2003.10095
S. Nesseris, S. Basilakos, E.N. Saridakis, L. Perivolaropoulos, Viable \(f(T)\) models are practically indistinguishable from \(\Lambda \) CDM. Phys. Rev. D 88, 103010 (2013). arXiv:1308.6142
A. El-Zant, W. El Hanafy, S. Elgammal, \(H_0\) tension and the phantom regime: a case study in terms of an infrared \(f(t)\) gravity. Astrophys. J. 871(2), 210 (2019). arXiv:1809.09390
A.G. Riess, S. Casertano, W. Yuan, L. Macri, J. Anderson, J.W. MacKenty, J.B. Bowers, K.I. Clubb, A.V. Filippenko, D.O. Jones, B.E. Tucker, New parallaxes of galactic cepheids from spatially scanning the hubble space telescope: implications for the hubble constant. Astrophys. J. 855, 136 (2018). arXiv:1801.01120
F.K. Anagnostopoulos, S. Basilakos, E.N. Saridakis, Bayesian analysis of \(f(T)\) gravity using \(f\sigma _8\) data. arXiv:1907.07533
B. Sagredo, S. Nesseris, D. Sapone, Internal robustness of growth rate data. Phys. Rev. D 98(8), 083543 (2018). arXiv:1806.10822
H. Yu, B. Ratra, F.-Y. Wang, Hubble parameter and baryon acoustic oscillation measurement constraints on the hubble constant, the deviation from the spatially flat LCDM model, the deceleration-acceleration transition redshift. Spatial Curvature. Astrophys. J. 856(1), 3 (2018). arXiv:1711.03437
D.M. Scolnic et al., The complete light-curve sample of spectroscopically confirmed SNe Ia from Pan-STARRS1 and cosmological constraints from the combined pantheon sample. Astrophys. J. 859(2), 101 (2018). arXiv:1710.00845
H. Akaike, A new look at the statistical model identification. IEEE Trans. Autom. Control 19, 716–723 (1974)
G. Schwarz, Estimating the dimension of a model. Ann. Stat. 6, 461–464 (1978)
K.P. Burnham, D.R. Anderson, Multimodel inference: understanding aic and bic in model selection. Sociolog. Methods Res. 33(2), 261–304 (2004)
Y.-F. Cai, M. Khurshudyan, E.N. Saridakis, Model-independent reconstruction of \(f(T)\) gravity from Gaussian Processes. Astrophys. J. 888, 62 (2020). arXiv:1907.10813
S.-F. Yan, P. Zhang, J.-W. Chen, X.-Z. Zhang, Y.-F. Cai, E.N. Saridakis, Interpreting cosmological tensions from the effective field theory of torsional gravity. Phys. Rev. D 101(12), 121301 (2020). arXiv:1909.06388
R. Briffa, S. Capozziello, J. Levi Said, J. Mifsud, E.N. Saridakis, Constraining Teleparallel Gravity through Gaussian Processes. arXiv:2009.14582
C. Escamilla-Rivera, J. Levi Said, Cosmological viable models in f(T,B) gravity as solutions to the \(H_0\) tension. arXiv:1909.10328
K. Bamba, S. Nojiri, S.D. Odintsov, Trace-anomaly driven inflation in \(f(T)\) gravity and in minimal massive bigravity. Phys. Lett. B 731, 257–264 (2014). arXiv:1401.7378
G.G.L. Nashed, W. El Hanafy, A built-in inflation in the \(f(T)\) -cosmology. Eur. Phys. J. C 74, 3099 (2014). arXiv:1403.0913
K. Rezazadeh, A. Abdolmaleki, K. Karami, Power-law and intermediate inflationary models in f(T)-gravity. JHEP 01, 131 (2016). arXiv:1509.08769
K. Bamba, G.G.L. Nashed, W. El Hanafy, S.K. Ibraheem, Bounce inflation in \(f(T)\) cosmology: a unified inflaton-quintessence field. Phys. Rev. D 94(8), 083513 (2016). arXiv:1604.07604
K. Rezazadeh, A. Abdolmaleki, K. Karami, Logamediate inflation in f(T) teleparallel gravity. Astrophys. J. 836(2), 228 (2017). arXiv:1702.07877
A.I. Keskin, Viable super inflation scenario from F(T) modified teleparallel gravity. Eur. Phys. J. C 78(9), 705 (2018)
K. Bamba, C.-Q. Geng, L.-W. Luo, Generation of large-scale magnetic fields from inflation in teleparallelism. JCAP 1210, 058 (2012). arXiv:1208.0665
A.I. Keskin, Super inflation mechanism and dark energy in \(F(T, T_{G})\) gravity. Astrophys. Space Sci. 362(3), 50 (2017)
K. Bamba, S.D. Odintsov, E.N. Saridakis, Inflationary cosmology in unimodular \(F(T)\) gravity. Mod. Phys. Lett. A 32(21), 1750114 (2017). arXiv:1605.02461
M. Jamil, D. Momeni, R. Myrzakulov, Warm intermediate inflation in \(F(T)\) gravity. Int. J. Theor. Phys. 54(4), 1098–1112 (2015). arXiv:1309.3269
P. Goodarzi, H. Mohseni Sadjadi, Reheating in a modified teleparallel model of inflation. Eur. Phys. J. C 79(3), 193 (2019). arXiv:1808.01225
H. Abedi, M. Wright, A.M. Abbassi, Nonminimal coupling in anisotropic teleparallel inflation. Phys. Rev. D 95(6), 064020 (2017)
A. Awad, W. El Hanafy, G.G.L. Nashed, S.D. Odintsov, V.K. Oikonomou, Constant-roll Inflation in \(f(T)\) Teleparallel Gravity. arXiv:1710.00682
M. Gonzalez-Espinoza, G. Otalora, N. Videla, J. Saavedra, Slow-roll inflation in generalized scalar-torsion gravity. arXiv:1904.08068
S. Raatikainen, S. Rasanen, Higgs inflation and teleparallel gravity. JCAP 12(12), 021 (2019). arXiv:1910.03488
A. Rezaei Akbarieh, Y. Izadi, Tachyon inflation in teleparallel gravity. Eur. Phys. J. C 79(4), 366 (2019). arXiv:1812.06649
S. Bahamonde, M. Marciu, J.L. Said, Generalized tachyonic teleparallel cosmology. Eur. Phys. J. C 79(4), 324 (2019). arXiv:1901.04973
S. Bahamonde, C.G. Böhmer, S. Carloni, E.J. Copeland, W. Fang, N. Tamanini, Dynamical systems applied to cosmology: dark energy and modified gravity. Phys. Rep. 775–777, 1–122 (2018). arXiv:1712.03107
D.K. Arrowsmith, C.M. Place, An Introduction to Dynamical Systems (Cambridge University Press, 1990)
A.A. Coley, Dynamical Systems and Cosmology (Kluwer Academic Publishers, Dordrecht, Boston, London, 2003)
J. Wainwright, G.F.R. Ellis, Dynamical Systems in Cosmology (Cambridge University Press, 1997)
P. Wu, H.W. Yu, The dynamical behavior of \(f(T)\) theory. Phys. Lett. B 692, 176–179 (2010). arXiv:1007.2348
Y. Zhang, H. Li, Y. Gong, Z.-H. Zhu, Notes on \(f(T)\) theories. JCAP 1107, 015 (2011). arXiv:1103.0719
M. Jamil, D. Momeni, R. Myrzakulov, Attractor solutions in \(f(T)\) cosmology. Eur. Phys. J. C 72, 1959 (2012). arXiv:1202.4926
M. Jamil, K. Yesmakhanova, D. Momeni, R. Myrzakulov, Phase space analysis of interacting dark energy in f(T) cosmology. Central Eur. J. Phys. 10, 1065–1071 (2012). arXiv:1207.2735
S..K. Biswas, S. Chakraborty, Interacting dark energy in \(f(T)\) cosmology : a dynamical system analysis. Int. J. Mod. Phys. D 24(7), 155004 (2015). arXiv:1504.02431
C..-J.. Feng, X..-Z. Li, L..-Y. Liu, Bifurcation and global dynamical behavior of the \(f(T)\) theory. Mod. Phys. Lett. A 29(7), 1550046, 1450033 (2014). arXiv:1403.4328
B. Mirza, F. Oboudiat, Constraining f(T) gravity by dynamical system analysis. JCAP 1711(11), 011 (2017). arXiv:1704.02593
M. Hohmann, L. Jarv, U. Ualikhanova, Dynamical systems approach and generic properties of \(f(T)\) cosmology. Phys. Rev. D 96(4), 043508 (2017). arXiv:1706.02376
A. Awad, W. El Hanafy, G.G.L. Nashed, E.N. Saridakis, Phase portraits of general \(f(T)\) cosmology. JCAP 1802(02), 052 (2018). arXiv:1710.10194
L. Karpathopoulos, S. Basilakos, G. Leon, A. Paliathanasis, M. Tsamparlis, Cartan symmetries and global dynamical systems analysis in a higher-order modified teleparallel theory. Gen. Rel. Grav. 50(7), 79 (2018). arXiv:1709.02197
A. Paliathanasis, de Sitter and Scaling solutions in a higher-order modified teleparallel theory. JCAP 1708(08), 027 (2017). arXiv:1706.02662
A. Paliathanasis, Cosmological evolution and exact solutions in a fourth-order theory of gravity. Phys. Rev. D 95(6), 064062 (2017). arXiv:1701.04360
P. A. González, S. Reyes, Y. Vásquez, Teleparallel Equivalent of Lovelock Gravity, Generalizations and Cosmological Applications. arXiv:1905.07633
S. Bahamonde, M. Marciu, S.D. Odintsov, P. Rudra, String-inspired Teleparallel Cosmology. arXiv:2003.13434
K. Bamba, D. Momeni, M.A. Ajmi, Phase space description of nonlocal teleparallel gravity. Eur. Phys. J. C 78(9), 771 (2018). arXiv:1711.10475
C.G. Böhmer, F. Fiorini, P. González, Y. Vásquez, \(D=11\) cosmologies with teleparallel structure. Phys. Rev. D 100(8), 084007 (2019). arXiv:1908.03680
G. Otalora, Scaling attractors in interacting teleparallel dark energy. JCAP 1307, 044 (2013). arXiv:1305.0474
C. Xu, E.N. Saridakis, G. Leon, Phase-space analysis of teleparallel dark energy. JCAP 1207, 005 (2012). arXiv:1202.3781
M.A. Skugoreva, E.N. Saridakis, A.V. Toporensky, Dynamical features of scalar-torsion theories. Phys. Rev. D 91, 044023 (2015). arXiv:1412.1502
M.A. Skugoreva, A.V. Toporensky, S.Y. Vernov, Global stability analysis for cosmological models with nonminimally coupled scalar fields. Phys. Rev. D 90, 064044 (2014). arXiv:1404.6226
H. Mohseni Sadjadi, Onset of acceleration in a universe initially filled by dark and baryonic matters in a nonminimally coupled teleparallel model. Phys. Rev. D 92(12), 123538 (2015). arXiv:1510.02085
M. Marciu, Dynamical properties of scaling solutions in teleparallel dark energy cosmologies with nonminimal coupling. Int. J. Mod. Phys. D 26(09), 1750103 (2017)
G. Otalora, Cosmological dynamics of tachyonic teleparallel dark energy. Phys. Rev. D 88, 063505 (2013). arXiv:1305.5896
A. Banijamali, E. Ghasemi, Dynamical characteristics of a non-canonical scalar-torsion model of dark energy. Int. J. Theor. Phys. 55(8), 3752–3760 (2016)
B. Fazlpour, A. Banijamali, Dynamics of generalized tachyon field in teleparallel gravity. Adv. High Energy Phys. 2015, 283273 (2015). arXiv:1408.0203
B. Fazlpour, A. Banijamali, Non-minimally coupled tachyon field in teleparallel gravity. JCAP 1504(04), 030 (2015). arXiv:1410.4446
E. Noether, Invariant variation problems. Gott. Nachr. 1918, 235–257 (1918). arXiv:physics/0503066. [Transp. Theory Statist. Phys.1,186(1971)]
K.F. Dialektopoulos, S. Capozziello, Noether Symmetries as a geometric criterion to select theories of gravity. Int. J. Geom. Meth. Mod. Phys. 15(supp01), 1840007 (2018). arXiv:1808.03484
A. Paliathanasis, Symmetries of Differential equations and Applications in Relativistic Physics. Ph.D. thesis, Athens U. (2014). arXiv:1501.05129
H. Wei, X.-J. Guo, L.-F. Wang, Noether symmetry in \(f(t)\) theory. Phys. Lett. B 707, 298–304 (2012). arXiv:1112.2270
K. Atazadeh, F. Darabi, \(f(T)\) cosmology via Noether symmetry. Eur. Phys. J. C 72, 2016 (2012). arXiv:1112.2824
H. Mohseni Sadjadi, Generalized Noether symmetry in f(T) gravity. Phys. Lett. B 718, 270–275 (2012). arXiv:1210.0937
S. Basilakos, S. Capozziello, M. De Laurentis, A. Paliathanasis, M. Tsamparlis, Noether symmetries and analytical solutions in f(T)-cosmology: a complete study. Phys. Rev. D 88, 103526 (2013). arXiv:1311.2173
M. Jamil, D. Momeni, R. Myrzakulov, Noether symmetry of F(T) cosmology with quintessence and phantom scalar fields. Eur. Phys. J. C 72, 2137 (2012). arXiv:1210.0001
A. Paliathanasis, S. Basilakos, E.N. Saridakis, S. Capozziello, K. Atazadeh, F. Darabi, M. Tsamparlis, New Schwarzschild-like solutions in f(T) gravity through Noether symmetries. Phys. Rev. D 89, 104042 (2014). arXiv:1402.5935
S. Bahamonde, U. Camci, Exact spherically symmetric solutions in modified teleparallel gravity. Symmetry 11(12), 1462 (2019). arXiv:1911.03965
S. Bahamonde, U. Camci, S. Capozziello, Noether symmetries and boundary terms in extended Teleparallel gravity cosmology. Class. Quant. Grav. 36(6), 065013 (2019). arXiv:1807.02891
M. Sharif, I. Shafique, Noether symmetries in a modified scalar-tensor gravity. Phys. Rev. D 90(8), 084033 (2014)
Y. Kucukakca, Scalar tensor teleparallel dark gravity via Noether symmetry. Eur. Phys. J. C 73(2), 2327 (2013). arXiv:1404.7315
G. Gecim, Y. Kucukakca, Scalar-tensor teleparallel gravity with boundary term by Noether symmetries. Int. J. Geom. Meth. Mod. Phys. 15(09), 1850151 (2018). arXiv:1708.07430
S. Bahamonde, U. Camci, S. Capozziello, M. Jamil, Scalar-tensor teleparallel wormholes by noether symmetries. Phys. Rev. D 94(8), 084042 (2016). arXiv:1608.03918
H. Motavalli, A. Rezaei Akbarieh, Teleparallel gravity with scalar and vector fields. Astrophys. Space Sci. 363(10), 200 (2018)
B. Tajahmad, Noether symmetries of a modified model in teleparallel gravity and a new approach for exact solutions. Eur. Phys. J. C 77(4), 211 (2017). arXiv:1610.08099
Y. Kucukakca, Teleparallel dark energy model with a fermionic field via Noether symmetry. Eur. Phys. J. C 74(10), 3086 (2014). arXiv:1407.1188
B. Tajahmad, Studying the intervention of an unusual term in \(f(T)\) gravity via the Noether symmetry approach. Eur. Phys. J. C 77(8), 510 (2017). arXiv:1701.01620
R. Brandenberger, P. Peter, Bouncing cosmologies: progress and problems. Found. Phys. 47(6), 797–850 (2017). arXiv:1603.05834
Y.-F. Cai, S.-H. Chen, J.B. Dent, S. Dutta, E.N. Saridakis, Matter bounce cosmology with the f(T) gravity. Class. Quant. Grav. 28, 215011 (2011). arXiv:1104.4349
A.V. Astashenok, Effective dark energy models and dark energy models with bounce in frames of \(F(T)\) gravity. Astrophys. Space Sci. 351, 377–383 (2014). arXiv:1308.0581
S.D. Odintsov, V.K. Oikonomou, E.N. Saridakis, Superbounce and loop quantum ekpyrotic cosmologies from modified gravity: \(F(R)\), \(F(G)\) and \(F(T)\) theories. Ann. Phys. 363, 141–163 (2015). arXiv:1501.06591
T. Qiu, K. Tian, S. Bu, Perturbations of bounce inflation scenario from \(f(T)\) modified gravity revisited. Eur. Phys. J. C 79(3), 261 (2019). arXiv:1810.04436
J. Haro, J. Amoros, Viability of the matter bounce scenario in \(F(T)\) gravity and Loop Quantum Cosmology for general potentials. JCAP 1412(12), 031 (2014). arXiv:1406.0369
J. Amorós, J. de Haro, S.D. Odintsov, Bouncing loop quantum cosmology from \(F(T)\) gravity. Phys. Rev. D 87, 104037 (2013). arXiv:1305.2344
J. De Haro, J. Amorós, Bouncing cosmologies via modified gravity in the ADM formalism: application to Loop Quantum Cosmology. Phys. Rev. D 97(6), 064014 (2018). arXiv:1712.08399
A. de la Cruz-Dombriz, G. Farrugia, J..L. Said, D. Sáez-Chillón Gómez, Cosmological bouncing solutions in extended teleparallel gravity theories. Phys. Rev. D 97(10), 104040 (2018). arXiv:1801.10085
A. de la Cruz-Dombriz, G. Farrugia, J.L. Said, D. Saez-Gomez, Cosmological reconstructed solutions in extended teleparallel gravity theories with a teleparallel Gauss-Bonnet term. Class. Quant. Grav. 34(23), 235011 (2017). arXiv:1705.03867
F. Fiorini, Nonsingular Promises from born-infeld gravity. Phys. Rev. Lett. 111, 041104 (2013). arXiv:1306.4392
M. Bouhmadi-Lopez, C.-Y. Chen, P. Chen, Cosmological singularities in Born-Infeld determinantal gravity. Phys. Rev. D 90, 123518 (2014). arXiv:1407.5114
C.G. Boehmer, F. Fiorini, The regular black hole in four dimensional Born-Infeld gravity. Class. Quant. Grav. 36, 12 (2019). arXiv:1901.02965
E. Knox, Newton-Cartan theory and teleparallel gravity: the force of a formulation. Stud. Hist. Philos. Mod. Phys. 42, 264–275 (2011)
J.B. Jiménez, L. Heisenberg, T.S. Koivisto, The canonical frame of purified gravity. arXiv:1903.12072
T. Koivisto, M. Hohmann, T. Zlosnik, The general linear Cartan Khronon. Universe 5(6), 153 (2019). arXiv:1905.02967
F. Hammad, D. Dijamco, A. Torres-Rivas, D. Bérubé, Noether charge and black hole entropy in teleparallel gravity. Phys. Rev. D 100(12), 124040 (2019). arXiv:1912.08811
R. Ferraro, f(R) and f(T) theories of modified gravity. AIP Conf. Proc. 1471, 103–110 (2012). arXiv:1204.6273
R.C. Nunes, A. Bonilla, S. Pan, E.N. Saridakis, Observational Constraints on \(f(T)\) gravity from varying fundamental constants. Eur. Phys. J. C 77(4), 230 (2017). arXiv:1608.01960
V.K. Oikonomou, E.N. Saridakis, \(f(T)\) gravitational baryogenesis. Phys. Rev. D 94(12), 124005 (2016). arXiv:1607.08561
S. Capozziello, G. Lambiase, E.N. Saridakis, Constraining f(T) teleparallel gravity by Big Bang Nucleosynthesis. Eur. Phys. J. C 77(9), 576 (2017). arXiv:1702.07952
S. Basilakos, S. Nesseris, F. Anagnostopoulos, E. Saridakis, Updated constraints on \(f(T)\) models using direct and indirect measurements of the Hubble parameter. JCAP 08, 008 (2018). arXiv:1803.09278
C. Li, Y. Cai, Y.-F. Cai, E.N. Saridakis, The effective field theory approach of teleparallel gravity, \(f(T)\) gravity and beyond. JCAP 10, 001 (2018). arXiv:1803.09818
H. Abedi, S. Capozziello, Gravitational waves in modified teleparallel theories of gravity. arXiv:1712.05933
Z. Chen, W. Luo, Y.-F. Cai, E.N. Saridakis, New test on general relativity and \(f(T)\) torsional gravity from galaxy-galaxy weak lensing surveys. Phys. Rev. D 102(10), 104044 (2020). arXiv:1907.12225
F. Lelli, S.S. McGaugh, J.M. Schombert, M.S. Pawlowski, One law to rule them all: the radial acceleration relation of galaxies. Astrophys. J. 836, 152 (2017). arXiv:1610.08981
M. Dupuis, F. Girelli, A. Osumanu, W. Wieland, First-order formulation of teleparallel gravity and dual loop gravity. Class. Quant. Grav. 37(8), 085023 (2020). arXiv:1906.02801
K.G. Falls, D.F. Litim, J. Schröder, Aspects of asymptotic safety for quantum gravity. Phys. Rev. D 99(12), 126015 (2019). arXiv:1810.08550
M. Niedermaier, M. Reuter, The asymptotic safety scenario in quantum gravity. Living Rev. Rel. 9, 5–173 (2006)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Bahamonde, S., Dialektopoulos, K.F., Hohmann, M., Said, J.L. (2021). Teleparallel Gravity: Foundations and Cosmology. In: Saridakis, E.N., et al. Modified Gravity and Cosmology. Springer, Cham. https://doi.org/10.1007/978-3-030-83715-0_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-83715-0_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-83714-3
Online ISBN: 978-3-030-83715-0
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)



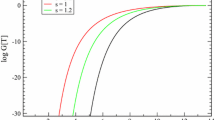
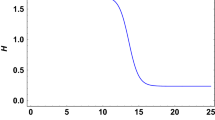







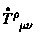 refers to the torsion tensor which is not related.
refers to the torsion tensor which is not related.