1 Introduction

In the historical expansion of the universe there are two accelerated phase cases that are supported by cosmological observations. The first is inflationary stage (old inflation) which describes the evolution of the early universe after the beginning singularity, which was proposed by Guth (1981) in attempt to solving some cosmologic problems (such as the horizon, flatness, etc.). According to the model, the universe expands exponentially (de Sitter type) in a supercooled false vacuum after the Big Bang. However in the new inflationary scenario, the inflation field is characterized by a scalar field \(\emptyset\) (the scalar fields are generally used into inflation mechanisms), which behaves as a source of inflation. This inflation scenario is explained by a slow-roll mechanism which tells that the inflation drives from a false vacuum rolling slowly to a true vacuum, where the scalar field decays at end of the inflation era (Hawking 1982; Bardeen et al. 1983; Linde 1982a, 1982b, 2007). Consequently, the temperature of universe increases (reheating phase). However in the warm inflation scenario (Berera 1995, 1996, 1997, 2000, 2006), the reheating phase region does not appear at the end of the inflation because the decay of the inflation field into radiation energy occurs via dissipation coefficient (is of a crucial importance in this scenario) during the slow-roll accelerating epoch. Here, the universe has a high temperature and its temperature increases with time due to strong interactions between fields. Thus, without reheating the universe smoothly enters the radiation region. Besides these, there is also the chaotic inflation scenario proposed by Linde (1983) in inflationary sectors. This inflation is described by polynomial potential or a quadratic large scalar field description which is its simple form as \(V\sim\emptyset^{n}\). If this field is initially large enough, the inflation starts, and then it slowly rolls down towards the value of potential minimum where the inflation ends. Consequently, the field oscillates at this point where the particles are created. However the inflation continues with an exponential form of the scale factor. For the initial conditions of this inflation, a thermal equilibrium or a supercooled false vacuum is not required. However the inflation occurs away from false vacuum. Therefore, the inflation starts in a chaotic era. This point for chaotic inflation gets a difference when comparing to other inflationary scenarios. Also, it is possible to see that there are power-law form of the scale factor, i.e., \(a ( t ) \sim t^{h}\), with \(h>1\) (Lucchin and Matarrese 1985), hybrid inflation (Linde 1994), Quintessential Inflation (Peebles and Vilenkin 1999), etc., which are described the inflationary era of the universe. On the other hand, the early inflationary universe can be also described by higher order correction terms in Hilbert-Einstein action, and this approach gets a good explanation at high curvature. For instance, the first modified gravity inflationary model, which is also compatible with the observations (Ade et al. 2014b), is proposed by Starobinsky (1980), in which the model \(R + R^{2}\) is a modification of \(R\)-term. This model describes the early inflation of the universe at high energy regime where the quadratic curvature term dominates. In this regards, next, quadratic invariant terms in modified gravity theories have been taken into account by researches (Maeda and Ohta 2004; Rinaldi et al. 2014, 2015; Gorbunov and Tokareva 2014; Myrzakulov et al. 2015; De Laurentis et al. 2015).

On the other side, the second accelerated expansion phase in the universe is the current (or late time) cosmic acceleration. It has been considered that the concept of the dark energy causes this acceleration. As made in the early inflationary universe, the scalar fields bring a good approach to explain the late time acceleration of the universe. For instance, by using a canonical scalar field, in order to have large negative pressure, the equation of the state parameter (EOS) is characterized in the range of \(-1< w< \frac{-1}{3}\) (Caldwell et al. 1998) which describes the quintessence phase. When \(w<-1\) (Caldwell 2002; Nojiri and Odintsov 2003; Cline et al. 2004) this case gives the phantom phase where the scalar field has a negative sign. As for the case \(w=-1\) directly describes de Sitter universe. In this regard, the recent cosmological observations show that the EOS parameter of the universe is closed to the \(w=-1\) border (Ade et al. 2014a, 2015). However to explain both the inflationary scenario and the late time cosmic acceleration, modified gravity theories give an alternative approach with respect to the scalar fields. One of these is the \(f(R)\)-gravity, in which the Einstein term replaces its functional form. In this gravity the late time cosmic acceleration can be shown by using \(f ( R ) = R+ \frac{1}{R}\) model (Carroll et al. 2004). There are also study on inflationary universe in the theory (Sebastiani and Myrzakulov 2015; Odintsov and Oikonomou 2015) Besides the late time cosmic acceleration, the studies on unification of the early time inflation and the late time acceleration of the universe have been made by researchers. When the lagrangian function is taken a general proper form, i.e. \(f ( R ) =R+\alpha R^{n}\), one can show the early time inflation, with \(n>1\) and the late time cosmic acceleration, with \(n<0\) (Nojiri and Odintsov 2003, 2011). By considering the realistic \(f ( R ) \) models it could be shown the early time inflation with large curvature and the late time acceleration with small curvature (Cognola et al. 2008). Another approach is the modified Gauss-Bonnet gravity theory, i.e. \(R+f(G)\), where \(G\) is the Gauss-Bonnet invariant, which some solutions of its field equations show the late time acceleration of the universe (Nojiri and Odintsov 2005, 2011; Nojiri et al. 2006). In this gravity theory, passage from the deceleration phase to the acceleration phase of the universe could be shown in a unifying picture (Goheer et al. 2009), and also the exact scale factor power-law solutions could be seen in the following study (Rastkar et al. 2012). Besides, a more general form of the modified Gauss-Bonnet gravity is \(f(R,G)\) gravity theory (Cognola et al. 2006). Some cosmological studies on this gravity were done by Alimohammadi and Ghalee (2009), Makarenko et al. (2013), de la Cruz-Dombriz and Saez-Gomez (2012). It is possible, the unification of stages of the universe with helping of some realistic \(f ( R ) \), \(f ( G ) \) and \(f(R,G)\) models verified by the solar system test and cosmologic bounds could be seen in the literature (Nojiri and Odintsov 2007a, 2007b). More recently (Keskin and Açıkgöz 2016), we have realized the unified solutions of \(f(R,G)\) gravity theory, where the three evolutionary stages (inflation, deceleration and late time acceleration) of the universe have been discussed in a unified form, in which the inflationary scenario is composed of the two regions. But in the present study we show that there are the three regions in inflation stage with the super inflation mechanism. Apart from these, there is also modified teleparallel (torsion) gravity which generates interesting results. For example, the early time inflation models could be explained in the context of \(f(T)\) gravity (Ferraro and Fiorini 2007; Nashed et al. 2014; Ganiou et al. 2016). An unified inflation and quintessence field can be shown by this gravity (Bamba et al. 2015). Also, study on warm inflation in \(f ( G ) \) gravity can be observed in the literature (Sharif and Ikram 2016b), in which the warm inflation is explored with helping of scalar fields in the FRW universe. The spectral index parameter and the scalar tensor ratio, which are compatible with observational Planck data, are constructed in background of this gravity theory. However, Sharif and Nawazish (2016a) studied the chaotic inflation in \(f ( R ) \) gravity, in which observational parameters was evaluated by using the different chaotic potential models, i.e., quadratic, quadric and fractional potentials. It was discussed consistency of this parameters with Planck constraints. But the current study, we have the realistic observational parameters to explore the super inflation mechanism without using chaotic potentials or any scalar fields which describe inflation. Also, the current acceleration case could be explained by some \(f(T)\) models (Wu and Yu 2010) without using dark energy. Recently, Kofinas and Saridakis (2014a, 2014b) and Kofinas et al. (2014c) have been proposed an extended version of the teleparallel gravity, namely \(F ( T, T_{G} )\) gravity where \(T\) is the torsion scalar and \(T_{G}\) teleparallel equivalent of the Gauss-Bonnet term. This gravity theory is different from both the \(f(T)\) and the \(f(R,G)\) gravity theories (Kofinas and Saridakis 2014a, 2014b) and also the different cosmological applications have been made according to the particular \(F ( T, T_{G} )\) models (Kofinas and Saridakis 2014a, 2014b). Also, generalized second law of thermodynamics aspect of this novel gravity theory has been studied by Zubair and Jawad (2015).

Physical importance of this work is based on modification Einstein gravity (namely \(F ( T, T_{G} )\) gravity theory) without using any scalar field to explain the super inflation mechanism with other stages of the universe in a unified form. For instance, modified Gauss-Bonnet gravity (\(R+f(G)\)) shows the current acceleration of the universe with \(f(G)\). Also, \(R^{2}\) (Starobinsky term) indicates the early time acceleration of the universe. The both cases can be unified in a general form (i.e., \(f ( R,G ) =R+f ( G ) + R^{2}\)). Since \(G\) includes quadratic curvatures, this term is equivalent to the term \(R^{2}\) in terms of cosmic time (i.e., \(\sim t^{-4}\)), when one uses the power-law form of the scale factor. The unified solutions of this form is realized by Keskin and Açıkgöz (2016). Generally speaking, for the functions written in a unified form such as \(f ( R,G ) \), \(f ( R,T ) \), \(f ( R,\emptyset ) \) and \(f ( T,G ) \) gravity theories, etc., where \(T\) is the trace of energy momentum tensor and \(\emptyset\) is the scalar field, respectively, one can realize the similar solutions and unify the stages of the universe with some particular models related to the gravity theories. Based on these motivations, in this study \(F ( T, T _{G} ) \) gravity is considered where \(T_{G}\) includes fourth order of time (i.e., \(\sim t^{-4}\)), and similarly, the quadratic torsion scalar, which shows acceleration, also includes \(\sim t^{- 4}\). Therefore, in this study, by using a proper model given as \(F ( T, T_{G} ) = f ( T ) +f( T_{G} )\), where \(f ( T ) = - T+ \alpha T^{2}\) is clear, the quadratic torsion scalar is mathematically embedded into \(f( T_{G} )\) function via the solutions of the differential equation (this is a unified solution). Herein, Einstein term, \(- T\), does not directly appear in the real value of \(f( T_{G} )\). Hence, apart from deceleration regions the super inflation mechanism and dark energy have been explained by the pure dynamic equations of \(F ( T, T_{G} ) \) gravity in a unified way. By means of these solutions, the matter components inside of the universe exhibit a dynamic picture in the gravity theory. However, the super inflationary mechanism is verified by using realistic inflationary parameters, i.e. \(n_{s}\), \(r\). In one respect, the rate of created matter from a part of quintessence fluid is calculated. Furthermore, a phantom solution of the model has been realized. This solution show that the accelerated expansion of the universe is in the two regions which congruent with the recent observations. The paper has been organized as the following: in Sect. 2, we have briefly given the field equations of the \(F ( T, T_{G} ) \) gravity, in Sect. 3, we have obtained unified solutions of the field equation corresponding to the gravity theory which describe the evolution of the universe. In Sect. 4, it has been realized the phantom solutions of the model, and eventually the Sect. 5 gives a sum of our findings.

2 The field equations of extended teleparallel gravity

The action of this gravity theory for the four-dimension is given by (Kofinas and Saridakis 2014a, 2014b)

$$ S = \frac{1}{2 k^{2}} \int d^{4} x e F ( T, T_{G} )+ S_{m}, $$
(1)

where \(k^{2} =8 \pi\tilde{G}\), \(\tilde{G}\) is the Newton constant, \(S_{m} = \int d^{4} x \sqrt{- g} L_{m}\) corresponds to the energy-momentum tensor of perfect fluid \(T_{\nu}^{\mu} = \mathrm{diag} ( - \rho, p, p, p )\), and \(e= \det(e_{\mu}^{\alpha}) = \sqrt{\vert g \vert }\) is dynamical vielbein fields \(e_{\alpha} ( x^{\mu} )\) in the teleparallel gravity theory. The \(T\) and \(T_{G}\) are also represent the torsion scalar and the Gauss-Bonnet equivalent term, respectively. In the study, we use the FRW metric given as

$$ d s^{2} = - d t^{2} + a^{2} ( t ) \bigl[ d x^{2} + d y^{2} + d z^{2} \bigr] . $$
(2)

The vielbein field for this geometry is diagonally \(e_{\mu}^{\alpha } =(1,a ( t ) ,a ( t ) ,a ( t ) )\). Varying the action (1) with respect to the vielbein, the Friedmann equations corresponding to the gravity theory are obtained as follows (Kofinas and Saridakis 2014a, 2014b)

$$\begin{aligned} &{-}12 H^{2} F_{T} - T_{G} F_{T_{G}} + F ( T, T_{G} )+24 H^{3} \dot{F} _{T_{G}} =2 k^{2} \rho, \end{aligned}$$
(3)
$$\begin{aligned} &F ( T, T_{G} ) - 4H \dot{F}_{T} - T_{G} F_{T_{G}} + \frac{2}{3H} T_{G} \dot{F}_{T_{G}} +8 H^{2} \ddot{F}_{T_{G}} \\ &\quad {}- 4 \bigl( \dot{H} +3 H^{2}\bigr) F_{T} = - 2 k^{2} p, \end{aligned}$$
(4)

where \(F_{T_{G}} = \frac{\partial F ( T, T_{G} ) }{\partial T_{G}}\), \(F_{T} = \frac{\partial F ( T, T_{G} ) }{\partial T}\) and \(H = \frac{\dot{a}}{a}\) is the Hubble parameter. The over dot denotes derivative with respect to time that gives as follows

$$\begin{aligned} &\dot{F}_{T} = F_{TT} \dot{T} + F_{T T_{G}}\dot{T}_{G}, \end{aligned}$$
(5)
$$\begin{aligned} &\dot{F}_{T_{G}} = F_{T T_{G}} \dot{T} + F_{T_{G} T_{G}}\dot{T}_{G}, \end{aligned}$$
(6)
$$\begin{aligned} &\ddot{F}_{T_{G}} = F_{TT T_{G}} \dot{T}^{2} +2 F_{T T_{G} T_{G}} \dot{T} \dot{T}_{G} + F_{T_{G} T_{G} T_{G}}\dot{T}_{G}^{2} + F_{T T_{G}} \ddot{T} \\ &\phantom{\ddot{F}_{T_{G}} =} + F_{T_{G} T_{G}} \ddot{T}_{G}. \end{aligned}$$
(7)

Here, \(T\) and \(T_{G}\) are given as

$$\begin{aligned} &T =6 H^{2}, \end{aligned}$$
(8)
$$\begin{aligned} &T_{G} =24 H^{2} \bigl( \dot{H} + H^{2} \bigr). \end{aligned}$$
(9)

One can write Eqs. (3) and (4) in the standard Einstein equations form:

$$\begin{aligned} &H^{2} = \frac{k^{2}}{3} ( \rho+ \rho_{e} ), \end{aligned}$$
(10)
$$\begin{aligned} &\dot{H} = \frac{- k^{2}}{2} ( \rho+ p + \rho_{e} + p_{e}), \end{aligned}$$
(11)

where the effective energy density and the pressure are defined as follows (Kofinas and Saridakis 2014a, 2014b)

$$\begin{aligned} \rho_{e} =& \frac{1}{2 k^{2}} \bigl(6 H^{2} + T_{G} F_{T_{G}} - F ( T, T_{G} ) +12 H^{2}F_{T} \\ &{}- 24 H^{3} \dot{F}_{T_{G}} \bigr), \end{aligned}$$
(12)
$$\begin{aligned} p_{e} =& \frac{1}{2 k^{2}} \biggl( - 2 \bigl( 2 \dot{H} +3 H^{2} \bigr) +F ( T, T_{G} ) - 4\bigl( \dot{H} +3 H^{2} \bigr) F_{T} \\ &{}- 4H \dot{F} _{T} - T_{G} F_{T_{G}} + \frac{2}{3H} T_{G}\dot{F}_{T_{G}} +8 H^{2} \ddot{F}_{T_{G}} \biggr), \end{aligned}$$
(13)

respectively. Both the \(\rho\) and \(\rho_{e}\) satisfy energy conservation law in the FRW universe

$$ \dot{\rho} +3 H ( \rho+ p ) =0, \qquad \dot{\rho}_{e} +3 H ( \rho_{e} + p_{e} ) =0. $$
(14)

3 Unified solutions of the field equations

Now, we try to find the solutions of the field equations according to the model. This solutions successfully describe all the eras of the universe in a unified way and especially include the super inflation mechanism. Accordingly, when combining Eqs. (3) and (4) the following equation is obtained:

$$\begin{aligned} &4 H^{2} \ddot{F}_{T_{G}} +8 \dot{H} H \dot{F}_{T_{G}} +4 H^{3} \dot{F}_{T_{G}} ( 2+3w ) \\ &\quad {}- 12 \bigl( \dot{H} H^{2} + H^{4} \bigr) ( 1+ w ) F_{T_{G}} + \frac{F ( T, T_{G} ) }{2} ( 1+ w ) \\ &\quad {} - 6 H^{2} F _{T} ( 1+w ) - 2H \dot{F}_{T} - 2 \dot{H} F_{T} =0, \end{aligned}$$
(15)

where \(w= \frac{p}{\rho}\) is the equation of the state (EOS) parameter of ordinary matter. This equation can be used to describe cosmic evolution of the universe because it includes that \(H\), \(F_{T_{G}}\), \(F_{T}\) and derivatives of them. Therefore the left side of Eq. (15) is a dynamic form, namely this equation can describe the dynamical expansion of the universe. On the other hand, to obtain a general expression of the equation above we can define \(M = k^{2} ( p _{e} - w \rho_{e} ) +2 \dot{H} +3 H^{2} ( 1+w ) \) relationship. In this case the right side of the equation has been observed to be equal to \(M\):

$$\begin{aligned} &4 H^{2} \ddot{F}_{T_{G}} +8 \dot{H} H \dot{F}_{T_{G}} +4 H^{3} \dot{F}_{T_{G}} ( 2+3w ) \\ &\quad {} - 12 \bigl( \dot{H} H^{2} + H^{4} \bigr) ( 1+ w ) F_{T_{G}} + \frac{F ( T, T_{G} ) }{2} ( 1+ w ) \\ &\quad {} - 6 H^{2} F _{T} ( 1+w ) - 2H\dot{F}_{T} - 2 \dot{H} F_{T} =M, \end{aligned}$$
(16)

where it is assumed that \(w = w_{e} = - 1 - \frac{2 \dot{H}}{3 H^{2}}\), which is also definition of EOS parameter, that provides \(M=0\). Hence, with \(w = w_{e} = - 1 - \frac{2 \dot{H}}{3 H^{2}}\), it is appearing that both the sides of Eq. (16) are in dynamic form anymore, because the evolution of \(w\) is governed by the left side of Eq. (16). In a word, \(w\) behaves as dark energy in the early or the late time of the universe, in which the parameter exhibits a dynamical picture.

When taking the model

$$ F ( T, T_{G} ) = f_{1} ( T_{G} ) + f_{2} ( T ) , $$
(17)

where \(f_{2} ( T ) = - T + \alpha T^{2}\), Eq. (16) is the following as

$$\begin{aligned} &4 H^{2} \ddot{f}_{1T_{G}} +8 \dot{H} H \dot{f}_{1T_{G}} +4 H^{3} \dot{f}_{1T_{G}} ( 2+3w ) \\ &\quad {} - 12 \bigl( \dot{H} H^{2} + H ^{4} \bigr) ( 1+ w ) f_{1 T_{G}} \\ &\quad {} +\biggl(\frac{f_{1} ( T_{G} ) }{2} + \frac{f_{2} ( T ) }{2} \biggr) ( 1+ w ) - 6 H^{2} f_{2 T} ( 1+w ) \\ &\quad {} - 2H \dot{f}_{2T} - 2 \dot{H} f_{2 T} = 0. \end{aligned}$$
(18)

This equation can be split into two equations (Makarenko et al. 2013; Sharif and Zubair 2014; Keskin and Açıkgöz 2016):

$$\begin{aligned} &4 H^{2} \ddot{f}_{1T_{G}} +8 \dot{H} H \dot{f}_{1T_{G}} +4 H^{3} \dot{f}_{1T_{G}} ( 2+3w ) \\ &\quad {} - 12 \bigl( \dot{H} H^{2} + H ^{4} \bigr) ( 1+ w ) f_{1 T_{G}} + \frac{f_{1} ( T _{G} ) }{2} ( 1+ w ) =0, \end{aligned}$$
(19)
$$\begin{aligned} &- 2H \dot{f}_{2T} - 2 \dot{H} f_{2 T} - 6 H^{2} f_{2 T} ( 1+w ) + \frac{f_{2} ( T ) }{2} ( 1+w ) \\ &\quad {} = 0, \end{aligned}$$
(20)

To find the solution of Eq. (19) we focus on the scale factor power-law solutions that given as

$$\begin{aligned} &a ( t ) = a_{0} t^{h} \rightarrow H = \frac{h}{t}, \\ &\dot{H} = \frac{- h}{t^{2}} \rightarrow\rho= \rho_{0} a^{- 3} \rightarrow T_{G} = \gamma t^{- 4} =24 h^{3} ( h - 1) t^{- 4} \end{aligned}$$
(21)

Using (6), (7), (9), (14) and (21) one can write Eq. (19) in terms of \(T_{G}\):

$$\begin{aligned} &4 T_{G} F_{1T_{G} T_{G} T_{G}} +(7+ h ) F_{1T_{G} T_{G}} \\ &\quad {} = \frac{- k^{2}\rho_{0} ( 1+ w ) ( \gamma ) ^{\frac{- 3 h ( 1+w ) }{4}}}{16 h^{2}} T_{G}^{\frac{3 h ( 1+w )-8}{4}} \\ &\qquad {} + \frac{3 ( 1+w ) }{16} \gamma^{\frac{1}{2}} T_{G} ^{\frac{- 3}{2}} - \frac{54\alpha(1+w) h^{2}}{16}T_{G}^{- 1}. \end{aligned}$$
(22)

From the solution of this differential equation we have

$$\begin{aligned} f_{1} ( T_{G} ) =& A \biggl( \frac{T_{G}}{\gamma} \biggr)^{\frac{3 h (1+ w )}{4}} + B ( T_{G} )^{\frac{1}{2}} + D T_{G} (\ln T_{G} - 1 ) \\ &{}+C T_{G}^{\frac{- h +1}{4}} + c_{2}T_{G}, \end{aligned}$$
(23)

where \(A = \frac{- k^{2} \rho(1+ w ) \gamma}{h^{2} ( - 3 h ( 1+ w ) - h +1 ) ( - 3 h ( 1+ w ) +4 ) (3 h ( 1+ w ) )}\), \(B = - \frac{3(1+ w ) \gamma^{\frac{1}{2}}}{4( h +1)}\), \(D = - \frac{54 h^{2} (1+ w ) \alpha}{16( h +3)}\), \(C= \frac{4 \gamma^{\frac{h +3}{4}} c_{1}}{ ( h +3 ) ( h -1 )}\) and \(c_{1}\), \(c_{2}\) are integration constants, and also we chose \(c_{2} =0\). Note that

$$ T_{G} = \gamma t^{- 4} =24 h^{3} ( h - 1) t^{- 4}, $$
(24)

which satisfies acceleration \(\ddot{a} >0\) when \(\gamma>0\), where \(T_{G}\) is the positive. When \(0<\gamma<1\) it describes the deceleration case \(\ddot{a} < 0\), with negative \(T_{G}\). On the other hand, by using Eqs. (5), (8) and (20) the following equality is obtained:

$$ 6 \alpha h^{3} \bigl[ 4 - 3 h (1+ w ) \bigr] t^{- 4} - h \bigl[ 2 - 3 h (1+ w ) \bigr] t^{- 2} =0. $$
(25)

This equation only holds with the super accelerated and the FRW solutions (Elizalde and Saez-Gomez 2009; Keskin and Açıkgöz 2016), i.e., \(h = \frac{4}{3(1+ w )}\), \(h = \frac{2}{3(1+ w )}\), due to \(t>0\). Generally, in a FRW universe the real valued of the lagrangian function characterizes as follows

$$ F ( T, T_{G} ) = D T_{G} ( \ln T_{G} - 1 ) +C T _{G}^{n} - T + \alpha T^{2}, $$
(26)

where \(n = \frac{3 w+ 1}{12(1+ w )}\). Under the condition \(\gamma>0\) there is a physical meaning of the first and the second terms in (26). Therefore, these are the acceleration terms. However, one can show the Einstein approach in this gravity theory by using the FRW solution and \(k^{2} \rho_{0} =3 h^{2}\), with \(\alpha=0\), and then obtains \(F ( T, T_{G} ) =C T_{G}^{\frac{-h +1}{4}} -T\), which requirement that \(c_{1} =0\). This solution is similar to the solution made by Keskin and Açıkgöz (2016) for extended Gauss-Bonnet gravity. But here, the solution (26) gives a modification on unification of stages of the universe comparing with Keskin and Açıkgöz (2016). Because, it includes both a vacuum state for the early universe and de Sitter expansion for the late time universe besides the other stages of the universe. Now, we will try to show this general picture, in detail.

3.1 The super inflation mechanism

The solution (26) produces the two inflationary scenario. The first is an eternal inflationary scenario (Nashed et al. 2014), where the expansion of the universe is exponentially. When the \(n\) is the large enough the EOS parameter goes to −1, which shows a vacuum state (or cosmological constant). Namely the beginning expansion of the universe should be started from the vacuum state because we chose the value of \(\alpha\) is a very small (i.e., \(\alpha< 10^{-2}\)), where the role of \(\alpha\) will be discussed later. In this case the lagrangian (26) takes the form \(F ( T, T_{G} ) = -T + \alpha T^{2}\), and Eq. (18) will be as follows

$$ \dot{H} \bigl(12 H^{2} F_{TT} + F_{T} \bigr)=0. $$
(27)

Here, the two solutions can be found. The first is the solution \(\dot{H} =0\) providing \(w=-1\) (as expected) when writing into the EOS parameter obtained from Eq. (16). The other is the following as

$$ H= \frac{1}{6 \sqrt{\alpha}}, $$
(28)

where \(\alpha\) must be greater than zero for disappearing of the anti-gravity (Nojiri and Odintsov 2009, 2011) (ghost fields) in the early universe. Also, one can obtain a de Sitter universe when \(\alpha= \frac{1}{12\varLambda}\), where \(\varLambda\) is the cosmological constant. It is clear that the value of this constant is the very large due to \(\alpha< 10^{-2}\), which produces a rapid expansion. This type of the expansion corresponds to the inflation. The density of the vacuum is \(\rho_{v} = \rho_{e} +\rho= \frac{\varLambda}{k^{2}}\), where \(\rho_{e} =\rho\). When the \(H\) value in (28) is written into \(F ( T, T_{G} ) = - T + \alpha T^{2}\), the lagrangian is obtained as \(F ( T, T_{G} ) \sim- T \sim\varLambda\). Here, besides the first and the second terms in the lagrangian (26), the quadratic the term \(\alpha T^{2}\) is also omitted by the vacuum, that may be sourcing from a small value of \(\alpha\) (Nashed et al. 2014). This is \(an\) eternal inflationary scenario which drives in the vacuum state.

The second is the super accelerated inflation scenario which occurs in a super accelerated phase (Keskin and Açıkgöz 2016), which is composed of the two regions. This is described by the \(D T_{G} ( \ln T_{G} - 1 ) \) term in (26), where the EOS parameter of the normal matter in \(D\)-term is in the range \(-1< w\), with \(\alpha>0\). When fixing the values of \(n\) as \(n<0\) after de Sitter type expansion the this term dominates to the other terms, in which there should be a phase transition from de Sitter expansion to a new phase. Otherwise, the universe does not arrive at the present state. When this term is written into Eq. (18) the following result is found:

$$ \frac{27 h^{4} ( 1+w ) \alpha(3 h ( 1+w ) -4)}{2} t^{-4} =0 $$
(29)

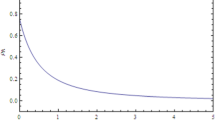
This equation gives the super accelerated solution. Taking the initial time as \(t= 10^{-3}\) the lagrangian function has a singularity as \(F ( T, T_{G} ) \rightarrow-\infty\), if \(\alpha>0\). Therefore, the function is an increasing function with the following cosmic time, which corresponds to the inflation (see Fig. 1). It should be noted that, for the beginning time of the first region in this scenario the both at \(t=0\) and \(t\leq10^{-3}\) the Fig. 1 exhibits a same picture or shows a beginning singularity where there is a pure vacuum state, and expansion of the universe is the exponentially. Therefore, \(10^{- 3}\) will be a border value for beginning time of the super accelerated inflation. However in the super-inflation mechanism the evolution of energy is as following: all vacuum fluid evolves to the type of quintessence fluid, and then the universe crosses to the first region of the super accelerated scenario in this point. Next, from a part of quintessence fluid it is created the normal matter form in the process (this occurs in the second region where interactions between fields occur). Because, for \(h>2\) and \(1< h< 2\) the EOS parameter is the range of \(-1< w< \frac{-1}{3}\) and \(\frac{-1}{3} < w< \frac{1}{3}\), respectively, with super accelerated solution. While the first range, in which \(w\) behaves as the effective EOS parameter, indicates the super acceleration region, the second one shows the matter creation region.

Fig. 1
figure 1

The evolution of the first term in the lagrangian versus cosmic time, where \(h=3\). The function is increasing with the time (\(10^{-3} \leq t\leq10^{0}\)), which shows the inflation where we chose \(\alpha= 10^{-2}\). For \(\alpha< 10^{-2}\) there is the vacuum state where this is described by a singularity due to the power law solutions

Full size image

We can verify this inflation scenario by calculating the spectral index parameter \(n_{s}\) and the scalar tensor ratio \(r\), which are observational inflation parameters. For this we use the slow-roll parameters \(\epsilon\) and \(\eta\) given as \(\epsilon=- \frac{ \dot{H}}{H^{2}}\), \(\eta= - \frac{\ddot{H}}{H \dot{H}}\), which satisfy the slow-roll condition (i.e., \(\epsilon\ll1\) and \(\eta\ll1\)) during inflation (Bamba et al. 2014). Using relationship \(M\) and the first term in lagrangian (26) we obtain slow-roll parameter \(\epsilon\)

$$\begin{aligned} \epsilon =& \frac{3(1+w)}{2} + \frac{81 h^{4} (1+w)\alpha[-3 h (1+w) +4 ] t^{-4}}{2 k^{2} \rho_{e} +81 h^{5} \alpha(1+w)t^{-4}} \\ &{}+ \frac{k^{2} \rho_{e} ( w_{e} -w)}{2 H^{2}}, \end{aligned}$$
(30)

where we identify two slow-roll parameters \(\epsilon_{1}\) and \(\epsilon_{2}\) corresponding to the first \(h>2\) and the second \(1< h< 2\) regions, respectively. When the slow-roll parameter is evolved from \(\epsilon_{1}\) into \(\epsilon_{2}\) we can expect a part of the dark energy (quintessence) evolves to the normal matter, i.e., \(w_{e} \sim w\). For the first region we have \(\epsilon= \epsilon_{1} = \frac{3(1+ w_{e} )}{2}\), with the super accelerated solution. One can write \(\epsilon_{1} = \frac{2}{h}\), which describes a quintessence type expansion under the slow-roll approximation, i.e., \(-1< w_{e} < \frac{-1}{3}\). On the other hand, for the second region when \(\epsilon\sim\epsilon_{2}\) we have \(\epsilon_{2} = \frac{3(1+w)}{2}\) and consequently \(\epsilon_{2} = \frac{1}{h}\), with the FRW value because of the matter creation. The range \(1< h< 2\) satisfies the inflation condition \(\epsilon_{2} <1\). Next, when \(h=1\) the inflation stops (Bamba et al. 2014). On the other side, the spectral index parameter and the scalar-tensor ratio are given by \(n_{s} - 1\sim- 6 \epsilon+2\eta\), \(r=16 \epsilon\) (Bamba et al. 2014), respectively. Also, the number of e-folds \(N\) is given by \(N(t)= \int_{t _{i}}^{t_{e}} H dt\), where \(t_{i}\) and \(t_{e}\) denote the time at the beginning and ending of the inflation, respectively. Using Hubble parameter the number of e-folds is found as \(N ( t ) = \ln( \frac{t_{e}}{t_{i}} )^{h}\), where we define \(t_{e} = 10^{-m}\), \(t_{i} = 10^{-n}\). For \(h>2\), the condition \(r<0.11\) (Ade et al. 2014a, 2015) shows that \(n-m<0.0901\) when \(N\cong60\). The spectral index \(n_{s}\) is approximately equal to 0.98 when \(n-m=0.09\), where the initial time is \(10^{-3}\). As a result, the inflation in this region is driven by the both parameters (this case may be sourcing from the pure-quintessence field), which are in a good agreement with the observation values (i.e., \(n_{s} =0.9603 \pm0.0073\) (\(68\%\) CL) and \(r<0.11\) (\(95\%\) CL)) (Ade et al. 2014a, 2015). For \(1< h <2\), using \(\epsilon_{2}\) we obtain \(n_{s} \sim0.74\) and \(r=2.14\) when \(N\cong50\), and also the slow-roll parameters \(\epsilon_{2} \sim0.13\), \(\eta\sim0.26\). Here, the process starts at \(t= 10^{-2.91}\) and ends at \(t= 10^{0}\). As a result, the inflation in the second region, where the matter is created, is driven by \(n_{s}\) only, due to \(r > 1\) (Bamba et al. 2014). The parameter \(n_{s}\) in this region is also in good agreement with the observational data in a reliable level. However it is appeared that the scalar-tensor ratio parameter, which is related to gravitational waves, is eliminated during the matter creation in the our inflationary scenario. This means that the short-time fluctuations of the quintessence field in the inflation cause both the matter creation and producing of gravitational waves. The results obtained for the super accelerated regions coincide exactly with Keskin and Açıkgöz (2016).

On the other hand, we will try to find that how much a rate of the vacuum energy (or quintessence type dark energy) is converted into the radiation energy during the super accelerated inflation process. For this, using Eqs. (3), (12) and inflationary terms in (26) the following equation can be written

$$ \underbrace{-18\alpha H^{2} +1}_{\varLambda_{1}} + \underbrace{4HD \frac{ \dot{T}_{G}}{T_{G}} - \frac{D T_{G}}{6 H^{2}}}_{\varLambda_{2}} = \varGamma , $$
(31)

where we define \(\varGamma= \frac{\rho}{\rho_{v}}\) that is the ratio of the density of the normal matter emergent in the total energy density and \(\varLambda_{1}\), \(\varLambda_{2}\) are arbitrary functions. This equation can be reduced to the vacuum state given by (28) when \(\rho_{e} = \rho\). After the vacuum state the solution (21) is valid, so Eq. (31) is as \(\varGamma=1- \frac{9\alpha}{4}\), with \(w= \frac{1}{3}\) and \(t=1\), which shows the end point of the inflation according to our scenario. \(\varGamma\) is found as \(\varGamma\sim0.98\), with \(\alpha= 10^{- 2}\). Here, the \(\alpha\) parameter indicates in which phase the inflation will start. Namely, it directly does not determines the time of inflation. The value of \(\alpha\) has been chosen properly, because of some causes. For instance, for the super accelerated phase regions, the following equation can be written

$$ \frac{9 \alpha h^{2}}{2 t^{2}} \bigl( 3 h ( 1+ w ) - 4 \bigr) = \varGamma- 1. $$
(32)

For the solution \(h = \frac{4}{3(1+ w_{e} )}\), the case of \(\alpha\) is not clear. But for the matter creation region, with the FRW solution \(h = \frac{2}{3(1+ w )}\), this equation can be written as

$$ H_{1} = \frac{h}{t} = \frac{1}{3} \sqrt{ \frac{1- \varGamma}{\alpha _{1}}}, $$
(33)

where \(\alpha_{1} = 10^{- 2}\) is the constant value for the super accelerated expansion regions. In Eq. (33) \(\varGamma\neq1\) tells that all the quintessence type energy does not convert into the normal matter. Since \(\alpha_{1} >0\), due to anti-gravity, \(\varGamma\) is smaller than one. However Eq. (33) implies that \(\varGamma\) increases while the Hubble parameter \(H_{1}\) decreases over time. Whereas in the vacuum process, the value of the Hubble parameter (\(H_{2} = \frac{1}{6 \sqrt{ \alpha_{2}}}\)) approximately remains constant. Therefore, it is clear that \(H_{2} > H_{1}\). This condition implies that \(4 \alpha_{2} (1- \varGamma)< \alpha_{1}\). For \(\varGamma\gtrsim0.5\), which is also the vacuum state, the condition approximately becomes \(2 \alpha_{2} < \alpha_{1}\). Namely, at \(\alpha_{1} < 10^{-2}\) the vacuum state is observed. Hence it is clarified that the inflation of the universe starts from a vacuum state. Also, it can be seen that the inflation ends when \(\alpha_{1} < 0\).

On the other side, it is clear that the case \(\varGamma=1\) in Eq. (32), which is not possible, remarks that the universe always remains in the first region of the super accelerated inflation, because Eq. (32) only holds with \(h = \frac{4}{3(1+ w_{e} )}\). The case \(\varGamma=0\), which produces an inconsistency in Eq. (32), shows that the expansion of the universe stops suddenly. Therefore, the creation of the matter in the certain rate was a chance to survive of the universe. Also, if \(\rho_{v}\) is the critic density of the stage \(\varGamma\) is the density parameter of the stage. When the universe is in the vacuum state the value of \(\varGamma\) is 0.5, which implies negatively curvature. After that, \(\varGamma\) is very closed to one, which removes the problems of the flatness and the homogeneity. As a result, \(\sim 98\%\) of dark energy evolves into the radiation energy. The large amount of this energy dominates in the universe. However, \(\sim2\%\) of the quintessence type dark energy remains in the structure of the universe latently. As long as the universe continues to expand, the normal matter energy density (\(\sim 98\%\)) is diluted by this expansion, and we consider that this energy (\(2\%\)) should be created after the inflation. This creation may be in the dust region because the universe arrives at a thermal equilibrium in the radiation region due to interactions between particles. Hence, when \(w< \frac{-1}{3}\) the quintessence type of dark energy dominates, and so the universe accelerates. Note that after the inflation stage we will take \(\alpha<0\) to cut the effect of the first term, due to anti-gravity (Nojiri and Odintsov 2009, 2011).

3.2 Deceleration regions

After the inflation there is only the Einstein term, \(-T\), which describes decelerated case due to \(\gamma<0\), \(\alpha<0\), \(n<0\). When inserting this term into Eq. (18) the Eq. (25) is obtained without the first term. Therefore the radiation \(h= \frac{1}{2}\) and dust \(h= \frac{2}{3}\) regions are observed. Furthermore, at the point \(w = \frac{- 1}{3}\) the universe continues to expand only with the Einstein term, but, there is not the acceleration phase case yet due to \(h =1\).

3.3 Dark energy

An inflation-like expansion is observed with the term \(C T_{G}^{n}\) given by (26) because we fixed \(n <0\) (i.e., \(-1< w< \frac{-1}{3}\)) after the vacuum state. Namely, the late time acceleration of the universe is described by the real value of \(C T_{G}^{n}\). On the other hand, when the universe asymptotically reaches the \(w=-1\) border the model is directly reduced to \(F ( T, T_{G} ) = - T + \alpha T^{2}\) so that it occurs the de Sitter type expansion.

4 Phantom solution of the field equations

In this section, we will show that there is a phantom solution of our model when the universe crosses the \(w=-1\) border. The phantom type scale factor and the Hubble parameter are given as follows (Nojiri and Odintsov 2005; Nojiri et al. 2005, 2006)

$$ a = a_{0} ( t_{s} - t ) ^{- h}, \qquad H = \frac{h}{t_{s} - t} \quad (h> 0) $$
(34)

where \(t_{s}\) indicates the Rip singularity when \(t_{s} =t\). The teleparallel equivalently term, the torsion scalar and the energy density are the following as

$$\begin{aligned} &T_{G} = \frac{24( h +1) h^{3}}{ ( t_{s} - t ) ^{4}}, \qquad T= \frac{6 h^{2}}{ ( t_{s} - t ) ^{2}}, \\ &\rho= \rho_{0} a_{0}^{- 3(1+ w )} ( t_{s} - t )^{3 h (1+ w)}. \end{aligned}$$
(35)

Eq. (19) can be written, as we did previous section, as follows

$$\begin{aligned} &4 \frac{\partial}{\partial T_{G}} S^{(\mathrm{TG})} + \frac{ ( 3- h ) }{T_{G}} S^{(\mathrm{TG})} \\ &\quad = \frac{- k^{2} \rho_{0} ( 1+w ) \beta^{\frac{3 h ( 1+w ) +4}{4}}}{16 h^{2}} T _{G}^{\frac{- 3 h ( 1+w ) -8}{4}} \\ &\qquad {}+ \frac{3 ( 1+w ) }{16} \beta^{\frac{1}{2}} T_{G}^{\frac{- 3}{2}} - \frac{54 \alpha(1+w) h^{2}}{16} T_{G}^{- 1}, \end{aligned}$$
(36)

where \(S^{(\mathrm{TG})} = T_{G} F_{1T_{G} T_{G}}\) and \(\beta= 24( h +1) h^{3}\). By changing \(h\rightarrow-h\), \(f_{1} ( T_{G} ) \) function is found as

$$\begin{aligned} f_{1} ( T_{G} ) =& L \biggl( \frac{T_{G}}{\beta} \biggr)^{\frac{-3 h (1+ w )}{4}} + F ( T_{G} )^{\frac{1}{2}} + K T_{G} ( \ln T_{G} - 1 ) \\ &{}+N T_{G}^{\frac{h +1}{4}} + c_{2}T_{G}, \end{aligned}$$
(37)

where \(L = \frac{k^{2} \rho(1+ w ) \beta}{h^{2}(3 h(1+w)+h+1)(3h(1+w)+4) (3h(1+w))}\), \(F = - \frac{3(1+ w ) \beta^{\frac{1}{2}}}{4( 1- h )}\), \(K = \frac{54 h^{2} (1+ w ) \alpha}{16( h - 3)}\), integration constants \(c_{1}\), \(c_{2}\). On the other hand, from Eq. (20), one obtains

$$\begin{aligned} &{-}18 \alpha h^{3} \bigl[ 4+3 h (1+ w ) \bigr] ( t_{s} - t ) ^{-4} \\ &\quad {}+ h \bigl[ 2 + 3 h (1+ w ) \bigr] ( t_{s} - t ) ^{- 2} =0. \end{aligned}$$
(38)

The super acceleration \(h_{1} = \frac{- 4}{3(1+ w )}\) and the FRW \(h_{2} = \frac{-2}{3(1+ w )}\) values are obtained from (38). The real valued of the lagrangian can be written as

$$ F ( T, T_{G} ) = K T_{G} ( \ln T_{G} - 1 ) +N T _{G}^{\sigma} - T + \alpha T^{2}, $$
(39)

where \(\sigma= \frac{3w+1}{12(1+w)}\), with the FRW value. It is appearing that the expansion of the universe is described by the first and the second terms in (39) (other terms produce \(h_{1}\), \(h_{2}\)). When \(\frac{1}{4} <\sigma<1\) the first term dominates, and the universe accelerates in the range of \(w<-1.22\). In the case \(\sigma>1\) the second term dominates, and the acceleration occurs with \(-1.22< w<-1\). In the both cases the expansion of the phantom phase is shown by positive \(\sigma\). Also, the Big Rip singularity can be occurred at \(t_{s} =t\), where \(a \rightarrow\infty\), \(\rho\rightarrow\infty\) and \(p \rightarrow\infty\) (Bamba et al. 2010). Hence we show that there is a phantom solution of our model which satisfies the two regions.

5 Concluding remarks

In this study, we have discussed the unified solutions of \(F ( T, T_{G} ) \) gravity theory according to the model (17). We have constructed its field equation with helping of the \(M\) relationship which gives the definition of the EOS parameter (in (16)), when \(M=0\). We have obtained a graceful solution (26) which produces both the exponential and the power-law forms of the scale factor, so it successfully describes all the evolutionary stages of the universe and transitions among of them in the unified way. Especially, we present the super inflation mechanism which is composed of the three phase regions:

1. When the limit \(n\rightarrow\infty\) an exponential expansion realizes at \(\alpha< 10^{-2}\), in which the lagrangian (26) acts as the cosmological constant or the vacuum state. This is an eternal inflationary scenario which is composed of one region.

2. After the vacuum state (\(\alpha= 10^{-2}\)) when fixing \(n<0\), the inflation is described by the \(D T_{G} ( \ln T_{G} - 1 ) \) term with the power-law form of the scale factor till the radiation region. This is the super accelerated inflation scenario which is composed of the two regions. The first region is driven by a pure quintessential field in a short-time. The second is a region which the normal matter is created at the rate of 98%, which is of a critical importance to continue to expansion of the universe. However, this inflation scenario has been clarified by using the observational parameters in which the first region is driven by \(n_{s}\) and \(r\), whereas the second region is driven by \(n_{s}\) only. The authors showed the two regions for the inflation of the early universe by using the field equations of extended Gauss-Bonnet gravity without including the vacuum state (Keskin and Açıkgöz 2016). But in the present study, we present the super inflation mechanism which includes the three phase regions by using the \(F ( T, T_{G} ) \) gravity theory, that completes the inflationary mechanism. It should point out that the super inflation mechanism is a new concept in the inflationary sectors. There are some reasons that distinguish this mechanism from the other some inflationary scenarios, as given below:

1. The universe expands either exponential or power-law form of the scale factor in all inflationary scenarios. The super inflation mechanism provides a unification of an eternal (exponential) inflation and quintessential (power-law) inflation cases. The first is described by \(F ( T, T_{G} ) = - T+ \alpha T^{2}\), where \(\alpha T ^{2}\) is omitted by vacuum due to \(\alpha< 10^{-2}\). The second is described by \(D T_{G} ( \ln T_{G} - 1 ) \), where this term is a version of \(\alpha T^{2}\), which is embed into the lagrangian (26) by the solution of differential equation \(M\). Therefore, both the quadratic torsion scalar and its version coming from dynamical Eq. (16) (i.e., \(D T_{G} ( \ln T_{G} - 1 ) \)) behave as a source of acceleration in the super inflation mechanism. Whereas the acceleration in late time of the universe is described by the real value of equivalent term \(T_{G}^{n}\), with \(n<0\). On the other hand, other inflationary scenarios, for example, the chaotic inflation is driven by exponential form of the scale factor only. However the chaotic inflation can be divided into two regions, i.e., an eternal inflation and matter creation regions where creation of the matter occurs at the end of the inflation, whereas in super inflation mechanism the matter creation occurs during inflation, as in warm inflation. The matter creation in chaotic inflation occurs with the oscillations of the simple harmonic equation of scalar field. As for in the super inflation mechanism occurs this case via the evolution of the EOS parameter in the relationship \(M\).

2. While the source of acceleration in chaotic inflation is any polynomial potential, in addition to the Einstein term, \(-T\), as a source of super inflation, extra terms (dark energy terms) are appeared in the gravity theory (i.e., \(\alpha T^{2}\) and \(D T_{G} (\ln T_{G} - 1 )\)).

3. In the warm inflation scenario all vacuum energy is converted into the radiation (Berera 1995, 1996, 1997, 2000, 2006) whereas in super inflationary scenario all the vacuum energy directly does not convert into the radiation. After the vacuum it evolves into the quintessence type dark energy rapidly, in which all asymmetries produced by the vacuum are vanished by this way. It is possible to say that the vacuum energy may have become a visible case or a suitable case to the creation of the normal matter. Also, on the contrary the warm inflation scenario the quintessence field or the other fields do not interact with the radiation energy initially. After the first region of the super accelerated phase the interactions occur, where the temperature of the universe increases. Next, the universe smoothly enters the radiation region where it may be initial of the hot big-bang.

It should note that the super inflation mechanism with scalar fields can be investigated in another separate study, that may produce interesting results.

After the inflation the universe is in the radiation region and then in the dust region, where these are described by the Einstein term, and the beginning of the acceleration, as well.

The quintessence phase region in the late time universe is described by the real value of the term \(T_{G}^{n}\), with \(n <0\), in which the cosmic acceleration of the universe is the inflation-like. Moreover, when the universe enters the case \(w=-1\) the model directly is reduced to the \(F ( T, T_{G} ) = -T + \alpha T^{2}\) form so that de Sitter expansion realizes. Finally, we have shown the phantom solution of our model which satisfies the acceleration of the universe is in the two regions: \(w<-1.22\) and \(-1.22< w<-1\). These ranges coincide with the recent cosmological observations (Ade et al. 2014a, 2015).

On the other hand, it is necessary to emphasize that we can also show all the expansion history of the universe under the constraint \(M=0\) which can be observed from the energy conservation law given by Eq. (14). For instance, the conservation equation for the normal matter satisfies that \(\dot{\rho} +3 H ( \rho+ p ) = \frac{3H}{k ^{2}} ( M - 2 \dot{H} f_{T} ) =0\), and from this equation the equality \(M=2 \dot{H} f_{T}\) is obtained. For the first region of the super inflation mechanism (i.e., the vacuum state), since \(\dot{H} =0\) or \(f(T)\) is constant, \(M\) becomes zero. However in the other regions of the mechanism the term \(D T_{G} ( \ln T_{G} - 1 ) \) dominates, which also provides \(M=0\). Also, the expansion of the universe in the quintessence, de Sitter and the phantom regions are described by the terms \(C T_{G}^{n}\), \(-T + \alpha T^{2}\) (i.e., \(\dot{H} =0\)) and \(K T_{G} ( \ln T_{G} - 1 ) \) or \(N T_{G}^{\sigma}\), respectively. Therefore, all the cases provide that \(M=0\). But, for the deceleration regions the conservation equation shows that \(M= - 2 \dot{H}\), where \(F ( T, T_{G} ) = - T\). Namely, the case \(M=0\) is not protected. Therefore, when the universe is considered as a thermodynamics system surrounded by an apparent horizon the dark energy component must be taken into account in such a system (i.e., as we previously mentioned that \(\sim 2\%\) of the quintessence type dark energy remains in the structure of the universe latently). Accordingly, from Eq. (14), \(\dot{\rho}_{e} +3 H ( \rho_{e} + p_{e} ) = \frac{- 3H}{k^{2}} ( M_{e} - 2 \dot{H} f_{T} - 2 \dot{H} - 3 H^{2} (1+ w_{e} ) ) =0\) can be written, where \(M_{e}\) is an effective version of \(M\). From the sum of the fluids the equality \(\dot{\rho} + \dot{\rho}_{e} +3H ( \rho+ p+ \rho_{e} + p_{e} ) = \frac{3H}{k^{2}} ( ( M - M _{e} ) ( w_{e} - w ) +2 \dot{H} +3 H^{2} (1+ w_{e} )\))

is obtained. The conservation law always satisfies that \(\dot{\rho} + \dot{\rho}_{e} +3H ( \rho+ p+ \rho_{e} + p_{e} ) =0\), which provides \(M=0\) for all the cases anymore, with \(w_{e} =w= - 1 - \frac{2 \dot{H}}{3 H^{2}}\). In other words, it is required the constraint \(M=0\) to hold the conservation law. As a result, the relationship \(M\) can be observed from the background of the energy conservation law given by Eq. (14).

Hence in this novel gravity theory we present the super inflation mechanism and show all the expansion history of the universe in a unified form, besides transitions among of them.

  • Three processes (eternal, quintessential, matter creation regions) in the super inflation mechanism.

  • Two processes (the radiation and the dust) in the deceleration stage.

  • Three processes (quintessence, de Sitter and the phantom) in the late time universe.

In a sense, it is observed that the beginning evolution of the universe is similar to the late time acceleration phases. Note that one can research a phantom-like inflation when \(n>1\) before the limit \(n\rightarrow+\infty\) for the very early time of the universe.