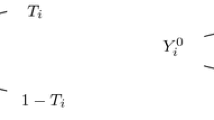A Review of Rigorous Randomized Response Methods for Protecting Respondent’s Privacy and Data Confidentiality

Abstract

Randomized response (RR) methods for protecting respondent’s privacy when collecting data on sensitive characteristics have been proposed and discussed for over fifty years. The basic ideas of RR have also been used to develop the post-randomization method (PRAM) for protecting data confidentiality. Both RR and PRAM randomize true responses using specified probabilities and the choice of those probabilities is central to designing RR methods and PRAM. However, most papers do not give clear guidance on how to choose the transition probabilities. Some rigorous approaches have appeared only recently. This paper reviews the essential elements of RR and PRAM, some important differences between the two, and designing RR methods and PRAM for achieving certain precise privacy and confidentiality protection goals. In particular, we discuss (i) designing an RR survey to guarantee that a randomized response would not reveal much information about the respondent, in a precise sense, and (ii) devising PRAM to strictly control identification risks when releasing microdata.

The views expressed in this article are those of the author and not those of the U.S. Census Bureau.

1 Introduction

The primary objective of randomized response (RR) methods is to protect respondent’s privacy and thereby reduce false responses when collecting data on sensitive or stigmatizing characteristics, such as tax evasion, drug use, gambling, and abortion. The first RR method, introduced by Warner (1965), concerns interview surveys of a binary characteristic, where the population consists of a sensitive group A (e.g., drug users) and its complement $A^c$ (e.g., not drug users). In Warner’s method, a respondent answers one of the two questions: $Q_1$: Do you belong to A? and $Q_2$: Do you belong to $A^c$? Each respondent selects a question by performing a specified random experiment, unobserved by the interviewer, with a given device, e.g., a spinner or a shuffled deck of cards bearing the two questions. The respondent answers the selected question. Thus, the interviewer does not know the question that a respondent answers. The experiment imposes specific and known probabilities, say p and $1-p$, of selecting $Q_1$ and $Q_2$. The value of p determines both the degree of privacy protection and the amount of statistical information loss due to randomization. Thus, to design Warner’s method, one should first select p and then construct an experiment for implementing it.

Following the pioneering work of Warner (1965), numerous other RR methods with different mechanisms for randomizing the true responses have been proposed for both categorical and quantitative variables. We refer interested readers to the books Chaudhuri and Mukerjee (1988), Chaudhuri (2010) and Chaudhuri et al. (2016) for discussion of various methods and further references. In this article, we consider RR methods only for categorical variables. An RR method transforms the true responses probabilistically. For a true response, the RR output is generated from a predetermined probability distribution on an output space. In Sect. 2, we briefly review a general framework and some key theoretical results that are needed for later sections. RR methods for quantitative variables are structurally quite different and can generally be viewed as (additive or multiplicative) random noise infusion to the true values.

For many years, research on RR methods was done primarily by statisticians and for use in face-to-face interview surveys, which requires experiments that are easy to understand and perform correctly and randomization devices that are simple and portable. Various randomization devices and mechanisms have been proposed as different RR methods. Recently, Blair et al. (2015) stated that “our extensive search yields only a handful of published studies that use the randomized response method to answer substantive questions.” Evidently, the theoretical advances in RR methods have not been used much in real surveys. Perhaps, one reason for that gap is the increasing adoption of mail, telephone and online surveys, replacing interview surveys, in the past several decades. Notably, Holbrook and Krosnick (2010) tested RR methods in one telephone and eight Internet surveys of American adults and found that respondents were either unable or unwilling to implement the RR mechanisms properly.

Interestingly, starting around the beginning of this century, interest in RR methods has grown tremendously among computer scientists and in new dimensions. The explosive growth of automated data capture by companies from business transactions, online searches, postings and other activities have raised much public awareness and concerns about privacy. Computer scientists have taken substantial interest in developing theory and methods for privacy-preserving data mining and data publishing; see, e.g., Aggarwal and Yu (2008), Chen et al. (2009) and Fung et al. (2019). New privacy concepts and measures have been developed and RR methods have been implemented by leading companies such as Google, Apple and Microsoft; see Erlingsson et al. (2014), Ding et al. (2017) and Cormode et al. (2018). Perhaps, one impetus for this resurgence and expansion of interest in RR techniques is that in online data capturing, the actual randomization can be carried out easily and accurately by computer programs. Consequently, recent research on RR theory and methods has focused appropriately on the choice of the randomization probabilities, leaving aside ancillary features of possible physical mechanisms for implementing them.

Gouweleeuw et al. (1998) used the basic ideas of RR to introduce the post-randomization method (PRAM) for perturbing categorical data to protect data confidentiality. It also randomizes the true responses, similar to RR. But, the data agency performs randomization after data collection and so, the randomization probabilities may be chosen based on the data set. We discuss some important differences between RR and PRAM in Sect. 2. For both methods, the choice of the transition probabilities is critical. Intuitively, one should try to choose those to minimize data utility (or statistical information) loss while meeting privacy and confidentiality protection goals. Some precise and practical privacy and confidentiality protection goals have been proposed and investigated only recently. One primary objective of this article is to review some rigorous approaches to privacy and confidentiality protection via RR and PRAM. We also attempt to cover some important works that appeared in computer science literature.

In Sect. 2, we describe the essential elements of RR and PRAM and some basic mathematical results. We do not aim to give a comprehensive review of RR and PRAM, but attempt to highlight some important points that we think have not been appreciated well. In Sect. 3, we discuss a rigorous notion of privacy protection. The basic idea is that an RR procedure should guarantee that an output would not reveal much new information about the respondent’s true value. A formal development of this idea compares prior and posterior probabilities. This criterion is closely connected to local differential privacy, which has received considerable attention in recent years. We also discuss a necessary and sufficient condition that an RR method must satisfy in order to guarantee such privacy. In Sect. 4, we discuss optimal RR methods for providing specified privacy. In particular, we describe an admissibility result under a very general view of data utility, and optimal methods under certain criteria. Section 5 relates to data confidentiality protection. Specifically, we consider identity disclosure control in microdata release and review a procedure that uses PRAM to guarantee an upper bound for the probability of correctly identifying any unit in perturbed microdata. Section 6 is devoted some concluding remarks.

2 Basic Elements of RR and PRAM

In this section, we describe the mathematical structures of RR and PRAM. Applying RR to multiple variables is equivalent to applying it to the cross-classification of those variables. Let X denote a categorical variable or cross-classification of several variables that we want to subject to RR. Let ${\mathcal S}_X = \{c_1, \dots , c_k\}$ denote the set of possible categories of X. Let $\pi _i =P(X=c_i), i=1, \dots , k,$ and $\pi = (\pi _1, \dots , \pi _k)^\prime$, which is unknown. The goal of an RR survey is to obtain information about $\pi$ while protecting respondent’s privacy. The basic idea of RR is to collect a stochastic transformation of each respondent’s true category. Let Z denote the output variable with output space ${\mathcal S}_Z = \{d_1, \dots , d_m\}$. A special case is ${\mathcal S}_Z = {\mathcal S}_X$. In general, ${\mathcal S}_Z$ may be different from ${\mathcal S}_X$, with possibly $m\ne k$. For each input, the output is selected according to some probabilities specified by the RR method. Let $p_{ij}=P(Z=d_i|X=c_j), i=1, \dots , m, j=1, \dots , k,$ denote the transition probabilities of an RR method. Obviously, $\sum _i p_{ij} = 1$ for $j=1,\dots , k$. The transition probability matrix (TPM), $P=((p_{ij}))$, is chosen during the planning of an RR method.

For any given P, one can devise multiple physical experiments to implement it (see Nayak et al. 2016). Under the common assumption of truthful respondent participation, all statistical properties of an RR method depend solely on its TPM. The choice of the experiment for implementing a given P does not affect the mathematical properties of the method. Thus, formal assessments and comparisons of RR methods should be made via their TPMs, ignoring the randomization experiments. However, as Leysieffer and Warner (1976), Fligner et al. (1977), Nayak (1994) and others have noted, when comparing different RR methods some papers have incorrectly matched disparate features of the experiments and drawn false conclusions. We consider P as the design of an RR method and discuss the planning and analysis of an RR method in terms of P.

A common assumption for analyzing RR data is multinomial sampling, i.e., random sampling from an infinite population or simple random sampling with replacement if the population is finite. Let $\lambda _{i}=P(Z=d_i), i=1, \dots , m$, and $\lambda = (\lambda _1, \dots \lambda _m)^\prime$. Also, let $S_i$ denote the frequency of $Z=d_i$ and ${\mathbf{S}}=(S_1, \dots , S_k)^\prime$. Then, ${\mathbf{S}}$ is multinomially distributed, ${\mathbf{S}}\sim Mult (n, \lambda )$, where

$$\begin{aligned} {\mathbf {\lambda }}=P{{\pi }} \end{aligned}$$

(1)

and n is the sample size. We can use ${\mathbf{S}}$ to make inferences about $\lambda$. If $m=k$ and P is nonsingular, from an estimator of $\lambda$ one can obtain an estimator of $\pi$ via (1). In particular, $\hat{\lambda }= {\mathbf{S}}/n$, which is the MLE (and UMVUE) of $\lambda$, yields $\hat{\pi }= P^{-1}\hat{\lambda }= P^{-1}({\mathbf{S}}/n).$ It can be seen that $\hat{\pi }$ is an unbiased estimator of $\pi$ and

$$\begin{aligned} Var(\hat{\pi }) = \frac{1}{n}(D_\pi -\pi \pi ^\prime ) + \frac{1}{n}[P^{-1}D_\lambda (P^{-1})^\prime - D_\pi ], \end{aligned}$$

(2)

where $D_\pi$ is a diagonal matrix with diagonal elements $\pi _1, \dots , \pi _k$ and $D_\lambda$ is defined similarly (see Chaudhuri and Mukerjee 1988, p. 43). The first term on the right side of (2) is the sampling variance and the last term is the additional variance due to randomization.

If $m<k$ or rank$(P)<k$, then the model for ${\mathbf{S}}$ is not identifiable with respect to $\pi$ and hence $\pi$ is not estimable from RR data. Thus, for estimability of $\pi$, one should only consider $m\ge k$ and rank$(P)=k$. While $m=k$ is quite common, several methods with $m>k$ have also been proposed, e.g., Leysieffer and Warner (1976), Kuk (1990) and Christofides (2003). Also, we shall see in Sect. 4.2 that $m>k$ in some optimal designs. We should mention that while most authors discussed estimation of $\pi$ under multinomial sampling, Padmawar and Vijayan (2000), Chaudhuri (2001, 2004) and Nayak and Adeshiyan (2009) derived estimators of $\pi$ under general sampling designs.

Now we turn our attention to PRAM. Like RR, it randomizes the true responses with known probabilities. However, that is done after data collection and by data agencies. These two practical matters yield some important differences between RR and PRAM. Here, we state some special and helpful features of PRAM, which we believe have not been well recognized. First, in PRAM, the transition probabilities may be chosen based on the entire data set, containing all true responses (which is not possible in RR surveys as the responses are randomized during data collection). Indeed, unbiased PRAM, discussed below, requires the TPM to depend on the data. When the TPM is data dependent, it is a random matrix and mathematical results in RR for fixed P, e.g., (2), may not hold true. Second, randomization may be applied selectively only to the responses with high disclosure risks. Note that agencies remove all direct identifiers, such as name and address, before releasing data. So, a respondent’s values (true or randomized) are not revealed directly. In contrast, in RR surveys, a respondent’s identity is known to the data collector. Third, related to the previous point, one may partition the data into homogeneous sets and then apply PRAM separately within the partition sets with possibly different TPMs. One method that utilizes data partitioning and unbiased PRAM is described in Sect. 5. Fourth, the randomization is carried out by a computer program, without needing a physical experiment. Fifth, in PRAM ${\mathcal S}_Z = {\mathcal S}_X$ and thus $m=k$ and the original and perturbed data appear in the same format. Sixth, the transition probabilities may not be known publicly. In particular, the transition probabilities cannot be published conveniently or helpfully when those are chosen diversely using the observed data, as in Sect. 5. There, the data agency should use a carefully designed unbiased PRAM to well preserve data utility, so that the released data may practically be treated as original data for making inferences.

Next, to describe unbiased PRAM, let $T_i$ and $S_i$ denote the frequency of $c_i$ in the original and perturbed data, respectively, and let ${\mathbf{T}} =(T_1, \dots , T_k)^\prime$ and ${\mathbf{S}} =(S_1, \dots , S_k)^\prime$. When the data are collected by multinomial sampling, a PRAM with TPM P is said to be unbiased (Gouweleeuw et al. 1998 called this invariant) if

$$\begin{aligned} P{\mathbf{T}} ={\mathbf{T}}. \end{aligned}$$

(3)

It can be easily verified that the solution space of (3) is a convex set and a trivial solution is $P=I$. Gouweleeuw et al. (1998) gave two methods for finding nontrivial solutions.

Unbiased PRAM was motivated by the fact that (3) implies $E[{\mathbf{S}}|{\mathbf{T}}]=P{\mathbf{T}}$ and hence $\hat{\pi }_* = {\mathbf{S}}/n$ is an unbiased estimator of $\pi$. Also, $\hat{\pi }_*$ is always a probability vector and it can be calculated without using P or its inverse. Thus, $\pi$ can be estimated easily from perturbed data. Nayak et al. (2016) derived and explored the exact variance of $\hat{\pi }_*$. In particular, they gave a decomposition of the variance into sampling variance and added variance due to PRAM, similar to (2). They also discussed estimation of $\pi$ under a general sampling plan and unbiased PRAM. There, P is called unbiased if $P\hat{\pi }=\hat{\pi }$, where $\hat{\pi }$ is an appropriately weighted (and usually unbiased) estimator of $\pi$ based on the original data.

We refer interested readers to Gouweleeuw et al. (1998), Willenborg and De Waal (2001), Van den Hout and Van der Heijden (2002), Van den Hout and Elamir (2006) and Shlomo and Skinner (2010) for additional discussion and applications of PRAM. The main task of designing RR and PRAM is choosing the transition probabilities. Naturally, suitable choices should depend on privacy and confidentiality protection goals. In the following sections, we discuss some recently developed precise privacy and confidentiality protection goals and methods for achieving those goals.

3 Privacy Protection by RR

Most privacy measures in statistics literature were developed for the situation where the survey variable is binary with one sensitive category and the response is also binary, see, e.g., Leysieffer and Warner (1976), Lanke (1976), Fligner et al. (1977), Nayak (1994), and Zhimin and Zaizai (2012). Using common terminology, let A and $A^c$ denote the two categories of X, of which A is sensitive, and let Y (for yes) and N (for no) denote the two response categories. The privacy measures in the binary case are mostly functions of the two posterior probabilities P(A|Y) and P(A|N), where the prior probabilities of A and $A^c$ are their population proportions, say $\pi _A$ and $1-\pi _A$. For example, Lanke (1976) measure of the degree of privacy protection is max$\{ P(A|Y), P(A|N) \}$. This and most other measures for the binary case depend also on $\pi _A$, which is unknown. A common suggestion is choose the RR design parameters P(Y|A) and $P(Y|A^c)$ such that a chosen privacy measure does not exceed a threshold at some $\pi _A$. Here, the designer of the survey selects the privacy measure, the threshold and $\pi _A$. For many privacy measures, this is equivalent to requiring

$$\begin{aligned} \max \Big \{\frac{P(Y|A)}{P(Y|A^c)}, \frac{P(Y|A^c)}{P(Y|A)}\Big \}\le \gamma , \end{aligned}$$

(4)

where $\gamma$ is determined by the privacy measure, privacy threshold and $\pi _A$.

3.1 Strict Privacy Criteria

The preceding approaches do not consider an intruder’s personal knowledge about respondents. The following approach, recently initiated by computer scientists, focuses on the basic goal of privacy protection, which is limiting the amount of information an intruder might gain about a respondent from his/her randomized response. Informally, the main idea, due to Evfimievski et al. (2003), is that we should view a privacy breach as an intruder gaining much new information about a respondent and an RR design should guarantee that no such privacy breaches would occur. Furthermore, an intruder’s information (or opinion) should be expressed precisely using subjective probability.

Formally, let $\alpha =(\alpha _1,\alpha _2,\dots ,\alpha _k)$ denote an intruder’s (subjective) prior distribution for a respondent’s true value of X, and for any $Q\subseteq {\mathcal S}_X$, let $P_\alpha (Q)$ and $P_\alpha (Q|d_{i})$ denote, respectively, the intruder’s prior and posterior probabilities of $\{X\in Q\}$, given $Z=d_i$. Here, Q represents a “property” of the respondent. Clearly,

$$ P_\alpha (Q)=\sum _{j:c_{j}\in Q} \alpha _{j}\quad \hbox {and }\quad P_\alpha (Q|d_{i})=\sum _{j:c_{j}\in Q} P_\alpha (X=c_{j}|Z=d_{i}), $$

where

$$P_\alpha (X=c_{j}|Z=d_{i})= \frac{P_\alpha (X=c_{j}, Z=d_{i})}{P_\alpha (Z=d_{i})} =\frac{\alpha _{j} p_{ij}}{\sum _{l=1}^k \alpha _{l}p_{il}}.$$

One idea is that to protect respondent’s privacy, we should guarantee that $P_\alpha (Q|d_i)$ would never be much higher or lower than $P_\alpha (Q)$, i.e., $P_\alpha (Q|d_i)$ would always be “close” to $P_\alpha (Q)$. This idea yields different privacy criteria for different specifications of desired closeness between prior and posterior probabilities.

Evfimievski et al. (2003) used a specific “closeness” criterion and introduced $\rho _1$-to-$\rho _2$ privacy as follows.

Definition 1

Let $0<\rho _1<\rho _2<1$ be two numbers. (a) An RR procedure is said to permit an upward $\rho _1$-to-$\rho _2$ privacy breach with respect to $Q\subseteq {\mathcal S}_X$ and a prior distribution $\alpha$ if

$$P_\alpha (Q) < \rho _1 \quad \hbox {and } \quad P_\alpha (Q|d_{i}) > \rho _2$$

for some $1\le i\le m$ with $P_\alpha (Z=d_i)>0$. Similarly, a procedure permits a downward $\rho _2$-to-$\rho _1$ privacy breach with respect to Q and $\alpha$ if $P_\alpha (Q) > \rho _2$ and $P_\alpha (Q|d_{i}) < \rho _1$ for some $d_i$ with $P_\alpha (Z=d_i)>0$.

(b) An RR procedure provides $\rho _1$-to-$\rho _2$ privacy protection if it does not permit an upward $\rho _1$-to-$\rho _2$ or a downward $\rho _2$-to-$\rho _1$ privacy breach with respect to any Q and $\alpha$.

Using the ratio of posterior to prior probabilities as a measure of closeness between the two, Nayak et al. (2015) defined the following.

Definition 2

For a given $\beta > 1$, an RR procedure admits a $\beta$-factor privacy breach, with respect to $Q\subseteq {\mathcal S}_X$ and a prior $\alpha$ if $P_\alpha (Q)>0$ and

$$\frac{P_\alpha (Q|d_{i})}{P_\alpha (Q)}> \beta \quad \hbox {or} \quad \frac{P_\alpha (Q|d_{i})}{P_\alpha (Q)}<\frac{1}{\beta }$$

for some $d_i$ such that $P_\alpha (Z=d_i)>0$. An RR procedure provides $\beta$-factor privacy if it does not allow a $\beta$-factor breach with respect to any Q and $\alpha$.

Chai and Nayak (2018) developed and explored the preceding ideas generally and we review their main results below. A general criterion for considering two probabilities as sufficiently “close” gives (explicitly or implicitly) for each $0<p<1$, an interval $[l_p, u_p]$ that consists of all values that are considered sufficiently close to p (taking a closed interval for simplicity). So, if a prior probability is p, a privacy breach occurs if and only if a corresponding posterior probability falls outside the interval $[l_p, u_p]$. This yields two functions $h_l(p)\equiv l_p$ and $h_u(p)\equiv u_p$, which specify the lower and upper breach boundaries. Thus, a general criterion may be viewed as a pair of given functions $h_l(p)$ and $h_u(p)$. Considering this, Chai and Nayak (2018) introduced the following.

Definition 3

Let $h_{l}$ and $h_{u}$ be two functions from [0, 1] to [0, 1] such that $0\le h_l(a)\le a\le h_u(a)\le 1$ for all $0\le a\le 1$. An RR procedure is said to satisfy privacy with respect to $h_{l}$ and $h_{u}$ if

$$\begin{aligned} h_l(P_\alpha (Q))\le P_\alpha (Q|d_{i}) \le h_u(P_\alpha (Q)) \end{aligned}$$

(5)

for all $\alpha , Q\subseteq {\mathcal S}_X$ and $i=1, \dots , m$.

This definition says that a posterior probability $p_*$ is sufficiently close to the corresponding prior p if $h_l(p)\le p_*\le h_u(p)$. Geometrically, a (prior, posterior) pair $(p, p_*)$ is a point in the unit square, of which the regions below $h_l$ and above $h_u$ constitute the privacy breach region (PBR) of the criterion in Definition 3. A privacy satisfying RR method must not yield any prior-posterior pair that falls in the PBR. Conversely, the PBR of an RR procedure P is the collection of all non-attainable (prior, posterior) pairs under P. The privacy holding region of P or the complement of the PBR (with respect to the unit square) is $\{(p, p_*), 0\le p, p_*\le 1: P_\alpha (Q) = p$ and $P_\alpha (Q|d_{i}) =p_*$ for some $d_i, \alpha$ and $Q\subseteq {\mathcal S}_X\}$.

3.2 Privacy Characterization

A natural question is for given $h_l$ and $h_u$, how to find a TPM that satisfies (5)? The first $\le$ in (5) is equivalent to $P_\alpha (Q^c |d_i)) \le 1- h_l(1-P_\alpha (Q^c))$. Considering this for all $Q\subseteq {\mathcal S}_X$, and defining $h(a) =\min \{h_u(a), 1-h_l(1-a)\}$, for $0\le a\le 1$, it follows that an RR procedure P satisfies (5) if and only if

$$\begin{aligned} P_\alpha (Q|d_{i}) \le h(P_\alpha (Q)) \end{aligned}$$

(6)

for all $i=1, \dots , m$ and all $\alpha$ and $Q\subseteq {\mathcal S}_X$ such that $0< P_\alpha (Q) < 1$. Chai and Nayak (2018) gave a necessary and sufficient condition for satisfying (6) using the following concept.

Definition 4

(Nayak et al. 2015) The ith row parity of P is defined as

$$ \eta _{i}(P)= \max \Big \{\frac{p_{ij}}{p_{il}} \ \ | \ \ j, l = 1, \dots , k\Big \} =\dfrac{\max _{j}\{p_{ij}\}}{\min _{j}\{p_{ij}\}}, $$

with the convention $0/0= 1$ and $a/0 = \infty$ for any $a>0$. The parity of P is defined as $\eta (P)=\max _i\{\eta _i(P)\}$.

Theorem 1

For a given h, an RR procedure P satisfies (6) if and only if $\eta (P)\le B(h)$, where

$$ B(h) = \inf _{0<p<1}\Big (\dfrac{1-p}{p}\Big )\Big (\dfrac{h(p)}{1-h(p)}\Big ) $$

and $h(p)/[1-h(p)] = \infty$ when $h(p)=1$.

The necessary and sufficient condition in Theorem 1 depends on h only through B(h) and on P only through its parity $\eta (P)$. Thus, B(h) quantifies the privacy demand of h and $\eta (P)$ quantifies the privacy level of P. These two measures are useful for comparing privacy demands of different PBRs and privacy levels of various RR procedures, respectively. Chai and Nayak (2018) also showed that an RR procedure P with $\eta (P)= \gamma >1$ guarantees (6) for all h such that

$$\begin{aligned} h(p)\ge h_{(\gamma )}(p) \equiv \dfrac{\gamma p}{1+(\gamma -1)p}, \quad 0<p<1. \end{aligned}$$

(7)

Thus, $h_{(\gamma )} (.)$ in (7) is the precise upper breach boundary of any P with parity $\gamma$. Choosing $h_l$ and $h_u$ in practical applications may appear a difficult task. But, the preceding discussions give helpful guidance. Specifically, we only need to consider the functions in ${\mathcal H} = \{h_{(\gamma )}(.); \gamma >1\}$ and choose one of those for the upper breach boundary. The precise lower breach boundary corresponding to $h_{(\gamma )}(.)$ is $\tilde{h}_{(\gamma )}(p) = 1-h_{(\gamma )}(1-p)$. In practice, the plots of the precise PBRs for various $\gamma$ might be helpful in selecting an appropriate PBR.

Theorem 1 says that in order to satisfy the criterion in Definition 3, each row parity of P must not exceed an upper bound, determined by $h_l$ and $h_u$. The privacy condition (4) in the binary case with one sensitive category is similar. It gives an upper bound for the parity of just one row, corresponding to the response Y. We should mention that under (4), Nayak (1994) showed that the transition probabilities of an optimal design are $P(Y|A)=1, P(Y|A^c) =1/\gamma$ and hence $P(N|A)=0$ and $P(N|A^c) = 1-1/\gamma$. However, this optimal design asks all respondents in the sensitive group to answer “Yes,” which might be uncomfortable for some respondents. It also implies $P(A|N)=0$, which might encourage some respondents to give the innocuous answer “No.” Thus, the (mathematically) optimal design may not be suitable in real surveys. This indicates that (4) is inadequate and we should impose additional restrictions on the transition probabilities.

We also want to mention the following criterion that has received considerable attention in recent years, especially from computer scientists; see, e.g., Kairouz et al. (2016), Wang et al. (2016), Duchi et al. (2018), and Ye and Barg (2018).

Definition 5

An RR design provides $\epsilon$-local differential privacy ($\epsilon$-LDP), for $\epsilon >0$, if

$$\begin{aligned} \sup _{Q \subseteq \mathcal S_Z}\sup _{c_i, c_j \in \mathcal S_X}\dfrac{P(Z \in Q|X=c_i)}{P(Z \in Q|X=c_j)}\le e^\epsilon . \nonumber \end{aligned}$$

Chai and Nayak (2018) proved that an RR procedure provides $\epsilon$-LDP if and only if

$$ \frac{P_\alpha (Q)}{1+(\gamma -1)(1-P_\alpha (Q))} \le P_\alpha (Q|d_i)\le \frac{\gamma P_\alpha (Q)}{1+(\gamma -1)P_\alpha (Q)} $$

for all $\alpha , Q$ and $d_i$, where $\gamma = e^\epsilon$. This shows that $\epsilon$-LDP coincides with Definition 3, with $h_l(a) = a/[1+(\gamma -1)(1-a)]$ and $h_u(a) = \gamma a/[1+(\gamma -1)a]$. This describes the PBR of $\epsilon$-LPD, which may be used to communicate its privacy promises in terms of bounds on an intruder’s possible information gain. It also follows that an RR design P provides $\epsilon$-LDP if and only if $\eta (P)\le \gamma =e^\epsilon$.

4 Comparison of RR Designs

We have seen that to satisfy the privacy requirement of either $\epsilon$-LDP or Definition 3 we must use a design with $\eta (P)\le \gamma$, for a given value of $\gamma$. For any given $\gamma >1$, let ${\mathcal C}_\gamma =\{P_{m\times k}: \eta (P)\le \gamma \},$ which is the class of all privacy-preserving designs at level $\gamma$. Typically, ${\mathcal C}_\gamma$ is large and a natural question is how should we choose a design from ${\mathcal C}_\gamma$ for practical application? As we noted earlier, for estimability of $\pi$, we should choose $P_{m\times k}$ with $m\ge k$ and full rank. Also, as Chai and Nayak (2018) discussed, P should not have any proportional rows, to be concise. Two designs are statistically equivalent if one can be obtained by merging the proportional rows of the other one. Intuitively, we should choose a P from ${\mathcal C}_\gamma$ that satisfies the preceding two conditions and maximizes data utility. However, data utility is a complex matter and it may be assessed in different ways. In the following, we first review an admissibility result under a broad view of data utility and then discuss design selection under certain optimality criteria.

4.1 Admissible Designs

Blackwell (1951, 1953) introduced a general criterion for comparing experiments, which in our context says the following.

Definition 6

An RR design $P_{m\times k}$ is said to be sufficient for (or at least as informative as) another RR design $A_{r\times k}$, to be denoted $P \succeq A$, if there exists a transition probability matrix $C_{r\times m}$ such that $A=CP$.

If $P \succeq A$ and also $A \succeq P$, then A and P are equivalent, and P is better than A if $P \succeq A$ but $A \not \succeq P$. Furthermore, P is said to be admissible if there does not exist another design that is better than P.

If $P \succeq A$, then applying A is equivalent to randomizing the true responses first using P and then randomizing the outputs of P using C. Intuitively, P should be more informative than A because the second randomization with C inflicts additional loss of statistical information. Formally, $P\succeq A$ implies that given any loss function and any inference rule $\delta$ based on the data from A, there exists a rule $\delta _*$ based on P whose risk function is no larger than the risk function of $\delta$. In this sense, if $P\succeq A$, then P is universally at least as good as A. Chai and Nayak (2018) proved that two designs $P_{m\times k}$ and $A_{r\times k}$ in ${\mathcal C}_\gamma$ are equivalent if and only if $m=r$ and $A=CP$, where C is a permutation matrix, i.e., A can be obtained by permuting the rows of P, or just reordering the elements of the output space. Logically, we should use only admissible designs. Here, an important question is how do we know if a given design P is admissible or not? The following result of Chai and Nayak (2018) answers this question.

Theorem 2

For any given $\gamma$, an RR design $P \in {\mathcal C}_\gamma$ is admissible if and only if (i) $\eta _i(P)=\gamma$ for all i (i.e., each row parity is $\gamma$) and (ii) each row of P contains exactly two distinct values.

Now, we discuss an important RR method, viz., the RAPPOR algorithm, proposed recently by Erlingsson et al. (2014). Google, Apple, Microsoft, and other companies have been using it for online data capture; see, Ding et al. (2017) and Cormode et al. (2018). The basic method applies $\epsilon$-LDP and works as follows. It represents all true responses with indicator vectors $X=(X_1, \dots , X_k)$. Specifically, if the true response is $c_i$, then the ith component of X is 1 and all other components are 0. RAPPOR’s randomization changes each component of $(X_1, \dots , X_k)$ independently with probability $p=1/(\sqrt{\gamma }+1)$ and produces an output vector $Z =(Z_1, \dots , Z_k)$.

The output space of RAPPOR is ${\mathcal S}_Z = \{z = (z_1, \dots , z_k): z_i = 0 \text{ or } 1 \text{ for } i=1, \dots , k\}$, which contains $2^k$ elements. So, RAPPOR’s TPM is of order $2^k\times k$. The transition probabilities can be calculated easily. Let $x^{(i)}$ denote the indicator vector for true response $c_i$, i.e., $x^{(i)} = (x_1, \dots , x_k)$, where $x_i=1$ and $x_j=0$ for all $j\ne i$. For any $z\in {\mathcal S}_z$, let $t_z = \sum _j z_j$. Then, it can be seen that

$$\begin{aligned} P((z_1, \dots , z_k)| x^{(i)}) = \left\{ \begin{array}{ll} p^{t_z-1}(1-p)^{k-t_z+1}, &{} \text { if } z_i=1 \\ p^{t_z+1}(1-p)^{k-t_z-1}, &{} \text { if } z_i =0. \end{array} \right. \end{aligned}$$

(8)

Let $\mathbf {1} = (1, \dots , 1)$ and $\mathbf {0} = (0, \dots , 0)$. From (8), we see that $P(\mathbf {1}| x^{(i)}) = p^{k-1}(1-p)$ and $P(\mathbf {0}| x^{(i)}) = p(1-p)^{k-1}$ for all i. So, the two rows of the RAPPOR’s TPM, corresponding to $z= \mathbf {0}$ and $z= \mathbf {1}$, have parity 1 (not $\gamma$). This shows, in view of Theorem 2, the RAPPOR’s design is not admissible.

We should mention that all other rows of RAPPOR’s TPM satisfy the conditions of Theorem 2. So, the RAPPOR algorithm can be modified to make it admissible. Specifically, removing the two rows corresponding to $\mathbf {0}$ and $\mathbf {1}$ and normalizing the remaining matrix gives an admissible design. RAPPOR also gives a method for estimating $\pi$ from perturbed data. The RAPPOR estimator is unbiased but not efficient. Chai and Nayak (2019) derived a better unbiased estimator that is also minimax under certain conditions.

4.2 Comparison of RR Designs

For $k=2$, i.e., binary X, it follows from Theorem 2 that essentially only one design, given below, is admissible and hence it is the best design.

Theorem 3

For binary X, an optimal RR design in ${\mathcal C}_\gamma$ is $P_{2\times 2}$ with $p_{11} =p_{22}= \gamma (\gamma +1)^{-1}$ and $p_{12} = p_{21} =(\gamma +1)^{-1}$.

The optimal design in Theorem 3 is a Warner’s design. For $k\ge 3$, many designs are admissible and choosing an optimal design requires additional criteria. In the following, we review some recent results.

Agrawal et al. (2009) presented the following optimality result in a special case. They required $\rho _1$-to-$\rho _2$ privacy. An RR design P satisfies $\rho _1$-to-$\rho _2$ privacy if and only if $\eta (P) \le \gamma$, with $\gamma = [\rho _2(1-\rho _1)]/[\rho _1(1-\rho _2)]$. They considered the special case of ${\mathcal S}_Z = {\mathcal S}_X$. This implies that $m=k$. Additionally, they considered only symmetric P. Under these conditions, they proposed to take any P with the minimum condition number as an optimal design. The condition number of a symmetric positive definite matrix is defined as the ratio of its largest and smallest eigenvalues. To justify the criterion, they stated that the stability of numerical calculations with a matrix decreases as its condition number increases. They were mainly concerned with computing the inverse of P, which is often used for calculating an estimate of $\pi$ and its variance. They proved that among all $P\in {\mathcal C}_\gamma$ that are also symmetric, the matrix $P_0$ with elements $p_{ii} = \gamma /(\gamma +k-1), i=1, \dots , k$, and $p_{ij} = 1/(\gamma +k-1)$ for $i\ne j$ has the minimum condition number. Thus, $P_0$ is the best design by their criterion.

Chai and Nayak (2018) also considered the special case of ${\mathcal S}_Z = {\mathcal S}_X$. Thus, the true values are randomized within the categories X. Here, the diagonal elements of P are the probabilities of keeping the true responses unchanged. Intuitively, we should change the true responses as little as possible to minimize data utility loss. This suggests to use a design $P\in {\mathcal C}_\gamma$ that has large diagonal values. One measure of “largeness” of the diagonal values of P is $\sum _i p_{ii}$, the trace of P. With this, a design $P\in {\mathcal C}_\gamma$ with the largest trace may be considered a best design at privacy level $\gamma$. Chai and Nayak (2018) proved that the optimal design $P_0$ of Agrawal et al. (2009), given above, is also the best design under the maximum trace criterion. Note that unlike Agrawal et al. (2009), this approach does not require P to be symmetric, although the optimal design $P_0$ is so.

Next, we review a minimax approach, recently investigated by Chai and Nayak (2019). Assuming multinomial sampling and squared error loss, they considered optimum determination of an RR strategy, which consists of a design P and an estimator $\hat{\pi }=(\hat{\pi }_1, \dots , \hat{\pi }_k)$ of $\pi$. Under squared error loss, the risk function of an RR strategy $(P, \hat{\pi })$ is

$$\begin{aligned} R(P, \hat{\pi }; \pi ) = E_{P,\pi }\Big [\Vert \hat{\pi }-\pi \Vert ^2\Big ] = E_{P,\pi }\Big [\sum _{i=1}^k (\hat{\pi }_i -\pi _i)^2\Big ] , \end{aligned}$$

(9)

where the expectation is with respect to both sampling and randomization. They considered unbiased estimators of $\pi$ that are also linear in ${\mathbf{S}}$, i.e., $\hat{\pi }= L{\mathbf{S}}/n$ for some matrix L, where ${\mathbf{S}}$ is the frequency vector of $d_1, \dots , d_m$ and the divisor n is used for mathematical simplicity. As, $E({\mathbf{S}}) = nP\pi$, $\hat{\pi }= L{\mathbf{S}}/n$ is unbiased if and only if $LP=I$. Recall that privacy protection requires that $P\in {\mathcal C}_\gamma$, for specified $\gamma$. Then, an RR strategy $(P_*, \tilde{\pi }= L_*S/n)$ is minimax among all privacy satisfying strategies if $P_*\in {\mathcal C}_\gamma , P_*L_*=I$ and

$$\begin{aligned} \sup _{\pi } E_{P_*,\pi }\Big [\Vert \frac{L_*S}{n} -\pi \Vert ^2\Big ] = \inf _{P \in {\mathcal C}_\gamma }\inf _{L: LP=I}\sup _{\pi } E_{P,\pi }\Big [\Vert \frac{LS}{n} -\pi \Vert ^2\Big ]. \nonumber \end{aligned}$$

The RR design $P_*$ is a minimax design.

To describe the minimax strategy, derived in Chai and Nayak (2019), for given $\gamma >1$ and $k\ge 2$, define

$$\begin{aligned} f(x)=\dfrac{k^2(x\gamma ^2+k-x)}{(x\gamma +k-x)^2},\quad x\ge 0, \end{aligned}$$

(10)

and

$$\begin{aligned} q = \left\{ \begin{array}{ll} \lfloor \dfrac{k}{1+\gamma }\rfloor , &{} \text { if } f(\lfloor \dfrac{k}{1+\gamma }\rfloor ) \ge f(\lceil \dfrac{k}{1+\gamma }\rceil ) \text { and }\lfloor \dfrac{k}{1+\gamma }\rfloor \ge 1\\ \lceil \dfrac{k}{1+\gamma }\rceil , &{} \text { otherwise}. \end{array} \right. \end{aligned}$$

(11)

Essentially, q is a maximizer of f(.) over positive integers.

To describe how $P_*$ randomizes the true categories, we represent the true responses with indicator vectors $X =(X_1, \dots , X_k)$, as in RAPPOR. Then, for a true response $(x_1, \dots , x_k)$, $P_*$ generates an output $(z_1, \dots , z_k)$ as follows. Suppose the true category is $c_i$, which implies $x_i=1$ and $x_j=0$ for $j\ne i$. Then, $P_*$ assigns $z_i=1$ with probability $p =(q\gamma )/(q\gamma +k-q)$ and $z_i=0$ with probability $1-p$. Next, if $z_i=1$, $P_*$ randomly selects $(q-1)$ of the remaining $(k-1)$ components of z and sets those to 1. If $z_i=0$, $P_*$ assigns 1 to q of the remaining components of z, selected at random. In both cases, all other components of z are 0. Thus, exactly q components of each output vector are 1 and the rest are 0. So, the output space of $P_*$ is ${\mathcal S}_Z^* = \{(z_1, \dots , z_k): z_i \text{ is } \text{0 } \text{ or } \text{1, } i=1, \dots , k, \text{ and } \sum z_i =q\}$ and it contains $m={k\atopwithdelims ()q}$ elements. As before, let $x^{(i)}$ denote the indicator vector for true response $c_i$. Then, it can be seen that the transition probabilities of the minimax design are

$$ P((z_1, \dots , z_k)| x^{(i)}) = \left\{ \begin{array}{ll} \gamma p_0, &{} \text { if } z_i=1 \\ p_0, &{} \text { if } z_i\ne 1 \end{array} \right. $$

for $i=1, \dots , k$ and $(z_1, \dots , z_k)\in {\mathcal S}_Z^*$, where $p_0 = k/[{k\atopwithdelims ()q}(q\gamma +k-q)]$. So, each row of the TPM has two distinct values and parity $\gamma$, satisfying the conditions of Theorem 2.

As we describe next, the minimax estimator $\tilde{\pi }$ of $\pi$ under $P_*$ has a simple form and can be calculated easily. With vector representation, both the original and perturbed data under $P_*$ appear as $n\times k$ matrices, with each row showing one respondent’s data. Let ${\mathbf{V}}^\prime =(V_1, \dots , V_k)$ denote the vector of column sums of the perturbed data matrix. Then, the minimax estimator, derived in Chai and Nayak (2019), is

$$\begin{aligned} \tilde{\pi }=\dfrac{(k-1)(q\gamma +k-q)}{q(\gamma -1)(k-q)} \Big (\frac{\mathbf{V}}{n}\Big ) + \frac{1}{k}\Big [\frac{(1-k)(q\gamma +k-q)}{(\gamma -1)(k-q)}+1\Big ]. \end{aligned}$$

(12)

The minimax estimator is also a method of moments estimator based on ${\mathbf{V}}$. Here, we want to mention that the estimator in RAPPOR is similar to (12). It is based on method of moments and a linear function of the column sums of their perturbed data matrix. Naturally, $\tilde{\pi }$ in (12) is an unbiased estimator and it also follows that the risk function, as defined in (9), of the minimax strategy $(P_*, \tilde{\pi })$ is

$$\begin{aligned} R(P_*, \tilde{\pi }; \pi ) = \frac{1}{n}\Big [\frac{(k-1)^2}{f(q)-k} +\frac{1}{k} - 1\Big ] + \frac{1}{n}\sum _{i=1}^k \pi _i (1-\pi _i), \end{aligned}$$

(13)

where the function f and the quantity q are as defined in (10) and (11). Due to unbiasedness (13) also gives the trace of the variance-covariance matrix of $\tilde{\pi }$, i.e., $R(P_*, \tilde{\pi }; \pi ) = \text{ tr }[V(\tilde{\pi })] = \sum V(\tilde{\pi }_i)$. The last term of (13) is the risk of the MLE of $\pi$ under no randomization. So, it reflects only the sampling variation. The first term in (13) is the added variance due to RR, which interestingly is independent of $\pi$, unlike the sampling variation.

We want to mention that Duchi et al. (2018) also investigated minimaxity of RR strategies and in a much broader setting. They considered a wider class of problems and loss functions. They derived bounds on minimax values and their convergence rates under $\epsilon$-LDP. In particular, they obtained rate optimal methods for certain estimation problems. Naturally, those asymptotic results may not be useful in small samples. Also, rate optimality ignores the multipliers of convergence rates. So, a rate optimal procedure need not be asymptotically efficient because the minimax risks of two methods may converge to zero at the same (and optimal) rate, but with different multipliers. In contrast, the results of Chai and Nayak (2019) are exact, but for a specific problem.

5 Identification Risk Control by Post-randomization

Protecting data confidentiality is a difficult task because disclosure of personal information about survey participants may occur in various forms depending on the context, nature of released data and sensitivity of survey variables. Various types of disclosure and methods for their control are discussed in the books: Willenborg and De Waal (2001), Duncan et al. (2011) and Hundepool et al. (2012). In this article, we shall consider only identity disclosure in microdata release. Consider a complete data set containing values of multiple variables for each of n sampled units. Data agencies commonly publish summaries of the data. But, researchers often want the full data set to explore different models and hypotheses. However, the original data may disclose the values of some sensitive variables for some of the survey participants or units, even if name, social security number and other direct identifiers are removed. In particular, one might be able to correctly identify the records of a target unit by matching gender, race, occupation, and other characteristics that can be obtained easily from other sources. Then, one can learn the identified unit’s values for all other variables. This is called identity disclosure, which is also regarded as one of the most serious violations of data confidentiality.

5.1 Identification Risk Measures

The variables that an intruder might use for matching are called key (or pseudo-identifying) variables, which are usually categorical. For reducing identification risks, agencies perturb the true values of the key variables and then release the perturbed data. For choosing a suitable perturbation method, the agency should first determine its disclosure control goals. For that, the agency needs to select and specify the key variables. Thus, we assume that the key variables are given and all are categorical. As before, let X denote the cross-classification of all key variables and suppose X takes values in ${\mathcal S}_X = \{c_1, \dots , c_k\}$. In this setting, Bethlehem et al. (1990), Skinner and Elliot (2002), Shlomo and De Waal (2008), Shlomo and Skinner (2010) and others have proposed and investigated different measures of identification risk.

Early works focused mainly on the units that are unique in the sample with respect to X. As agencies do not reveal which population units are in the sample, it is reasonable to assume that an intruder would not know if his target is in the sample or not. Such an intruder would correctly match a sample unique unit if it is also population unique with respect to X. Motivated by this, Bethlehem et al. (1990) defined identification risk as the probability that a unit is population unique, given that it is sample unique, both with respect to X. Obviously, this concerns only the sample unique units. Also, it ignores the effects of data perturbation. So, this measure is not useful for determining a suitable perturbation mechanism. Essentially, it aims to assess how much protection the sample unique units get from sampling. We refer to Skinner and Elliot (2002) for a discussion of similar measures and related references.

Shlomo and Skinner (2010) took a more relevant approach that focuses on correct matches in perturbed (and released) data. Naturally, they take data perturbation into account. However, they were concerned only with the unique matches in released data, presuming those to be the worst cases. Consequently, they defined a unit’s identification risk as the probability that the unit is correctly identified given that it has a unique match in released data. This (conditional) probability is with respect to both sampling and data perturbation. This identification risk is unit specific and it varies over the sampled units.

There are some practical difficulties in using the preceding risk measure in finding a suitable perturbation mechanism. First, the risks of the sampled units involve the unknown population frequencies and hence those cannot be calculated from available information. Methods for estimating those have been proposed, but they require assumptions about the population distribution and data modeling. So, the estimates depend on the model assumptions. Second, the effectiveness of data perturbation is assessed using the average of the risks of all sampled units. That may not be appropriate because a small average risk does not imply that disclosure risks of all units are desirably small. Third, the search for a suitable perturbation procedure requires an iterative approach. One would need to assess the effectiveness of several procedures to select a procedure. For example, to apply data swapping, as described in Shlomo and Skinner (2010), one would need to evaluate the average risk measure for various swap rates to choose a suitable value for actual application.

Recently, Nayak et al. (2018), henceforth NZY, refined Shlomo and Skinner (2010) approach and introduced a strict identification risk control goal. They also developed a method for achieving that goal. To describe the NZY approach, consider an intruder J who wants to identify the records of a target unit B in the released perturbed data. Let $X_{(B)}$ denote B’s value of X, and suppose $X_{(B)} = c_j$. NZY assumed that (a) J knows $X_{(B)}$, (b) J knows that B is in the sample and (c) J randomly selects one of the records in the released data that match $X_{(B)}$, and identifies those as B’s data. If no records in released data match $X_{(B)}$, the intruder stops his search for B’s data. While assumptions (a) and (c) are realistic, (b) is overly stringent because agencies do not disclose which population units are included in the sample.

Let $T_j$ and $S_j$ denote the frequencies of $c_j$ in the original and perturbed data, respectively, and let $\mathbf {T}=(T_1, ..., T_k)'$ and $\mathbf {S}=(S_1, ..., S_k)'$. Note that if $X_{(B)} = c_j$, then $S_j$ records in the released data match B on key variables. Intuitively, J’s confidence in a declared match depends on $S_j$. Observing this, NZY considered the following to propose a strict disclosure control goal:

$$ R_j(a) = P(CM|X_{(B)}=c_j, S_j=a), \quad j=1, \dots , k, a \ge 1 $$

where CM denotes the event that B is correctly matched in the preceding setup. NZY proposed that the agency should select a suitable value $\xi$ and guarantee, with appropriate data perturbation, that

$$\begin{aligned} R_j(a) \le \xi \quad \hbox { for all } j=1, \dots , k, \hbox { and all integers } a \ge 1. \end{aligned}$$

(14)

Then, no unit’s correct match probability would exceed $\xi$. This gives a clear and strong identification risk control goal.

Like all past identification risk measures, $R_j(a)$ also depends on the unknown population frequencies. So, we cannot calculate $R_j(a)$’s and thereby verify whether a data perturbation mechanism guarantees (14) or not. To avoid this difficulty, NZY considered

$$ R_j(a, \mathbf {t} ) = P(CM|X_{(B)}=c_j, S_j=a,\mathbf {T}= \mathbf {t} ), $$

further conditioning on ${\mathbf{t}}$. Quite importantly, $R_j(a, {\mathbf{t}} )$’s do not involve unknown parameters under PRAM and so, those can be assessed and controlled without estimating any parameter. Note that $R_j(a, {\mathbf{t}})$’s involve the original frequency vector ${\mathbf{t}}$, but that is available to the data agency. NZY suggested to satisfy (14) by using a data perturbation mechanism such that

$$\begin{aligned} R_j(a, \mathbf {t} ) \le \xi \quad \hbox { for } j=1, \dots , k, \hbox { all } a>0 \hbox { and all } \mathbf {t}. \end{aligned}$$

(15)

Effectively, (15) is their disclosure control goal, which readily implies (14).

5.2 A Post-randomization Method

Taking the preceding approach, NZY developed a class of unbiased PRAMs that can be used to satisfy (15) for $\xi >1/3$. They give two reasons for choosing a $\xi >1/3$ in practical situations. First, intruders should have strong evidence for declaring matches. To be credible, the correct match probability for a declared match should be substantial, perhaps larger than 0.5. Second, as noted earlier, assumption (b) is overly stringent. Usually, an intruder would not know if a target is in the sample or not. For such an intruder, a correct match probability is much smaller than $R_j(a)$, approximately $R_j(a)$ times the target’s sample inclusion probability, which is usually quite small.

For any given $\xi >1/3$, NZY developed an unbiased PRAM to satisfy (15) as follows. First, we should mention that any unbiased PRAM does not affect the empty categories. In other words, an unbiased PRAM does not change a true category to a category that was originally empty. Truly, ${\mathcal S}_Z$ consists of only the categories in ${\mathcal S}_X$ that have positive frequencies in the original data set, i.e., ${\mathcal S}_Z = {\mathcal S}_X^* = \{c_i: c_i\in {\mathcal S}_X \text{ and } t_i>0\}$, which may be a proper subset of ${\mathcal S}_X$. Actually, ${\mathcal S}_X^*$ is also the input space as all observed values are in this set. For notational simplicity, we assume that all categories are nonempty and thus ${\mathcal S}_X^*={\mathcal S}_X$.

The NZY method uses one specific class of unbiased PRAMs. Specifically, they use the transition probabilities

$$\begin{aligned} p_{ij} = P( Z = c_i | X= c_j ) = {\left\{ \begin{array}{ll} 1- \frac{\theta }{t_j}, \quad \text{ if } i=j; \\ \frac{\theta }{(k-1)t_j}, \quad \text{ if } i\ne j, \end{array}\right. } \end{aligned}$$

(16)

where $t_j$ is the original frequency of $c_j$ and $\theta$ is a design parameter, chosen suitably to satisfy (15). Clearly, the TPM $P=((p_{ij}))$ given by (16) is adaptive, viz., it depends on the observed data via the category frequencies. Also, P has a simple structure. It changes a true category $c_j$ with probability $\theta /t_j$, which is inversely proportional to the frequency of the unit’s true category. If a true category is $c_j$, then it is kept unchanged with probability $1-\theta /t_j$. When a true category is changed, the replacement is selected at random from the remaining categories. One helpful feature of this P is that it is determined fully by a single parameter $\theta$. So the effects of P on identification risks and statistical inferences can be studied in terms of $\theta$ only.

One key result of NZY is that for given $1/3<\xi <1$, the above P satisfies (15) if $\theta$ is chosen as the solution of $h(\theta )=\xi$, where

$$ h(\theta ) = {\left\{ \begin{array}{ll} \frac{1-\theta }{1-\theta +\theta ^2}, &{} \text{ if } \theta \le \frac{2}{3}, \\ \frac{2-\theta }{4-2\theta +\theta ^2}, &{} \text{ if } \theta > \frac{2}{3}, \end{array}\right. } $$

and $k\ge (1-\theta )^{-1}$. They also showed that $h(\theta )$ is a strictly decreasing function of $\theta$, with $h(0) = 1$ and $h(1) = 1/3$ and thus for any $1/3<\xi <1$, $h(\theta ) =\xi$ admits a unique solution for $\theta$ in (0, 1). This result gives a theoretical basis for designing a post-randomization method for guaranteeing (15). Also, a suitable PRAM can be designed directly, without iterative calculations or adjustments, unlike previous approaches.

Actually, the method proposed by NZY applies the preceding result separately to subsets of the data set, which are formed by partitioning the data into homogeneous groups and then taking only the sensitive records in each group. That is done to better preserve data utility. While category and cell are synonymous, in the rest of this section we shall use cell for a cross-classified variable and category for individual variables, for additional clarity. So, we shall use cell for X, as it is the cross-classification of all key variables. For given $0<\xi <1$, a cell is considered sensitive if its frequency is less than $1/\xi$. A cell $c_j$ is nonsensitive if $t_j\ge 1/\xi$ because in the original data, the probability of correctly identifying a unit falling in that cell is $1/t_j\le \xi$. The identification risks of all units in the nonsensitive cells are already sufficiently small. So, we only need to post-randomize X for all units in the sensitive cells. All sensitive cells in a partition set form a post-randomization block (PRB). The NZY method applies PRAM to the PRB’s separately. More details of the method and some parts of an illustrative example are given below.

The main purpose of data partitioning is to control the nature and magnitude of possible changes due to PRAM, and even preserve selected parts and summaries of the data set. NZY gave several ideas for data partitioning. One simple approach is to partition the data by broader or generalized categories of the key variables. As an illustrative example, NZY applied the method to a data set publicly released by the U.S. Census Bureau. It contains values of several demographic and economic variables for 59,033 individuals. For illustration, NZY took gender (2), age (92), race (9), marital status (5), and public use microdata area (PUMA) (44) as the key variables, where the values in parentheses show the number of categories of the variables. The cross-classification of these key variables yields 364,320 cells.

In the example, NZY partitioned the data by gender, seven age intervals, viz., 0–17, 18–24, 25–34, 35–44, 45–54, 55–64, and 65 and above, and the three race categories: white, black, and “other races.” That divided the data into 42 partition sets, corresponding to all possible combinations of gender, 7 age intervals, and 3 race classes. For example, all females of “other races” with age between 25 and 34 constitute one partition set. Similarly, all white males in the age interval 55–64 form another partition set. Note, for example, that all individuals in a partition set are either male or female. As the method applies PRAM within each partition set, it will not alter the gender of any individual. Similarly, it will preserve race if the original category is white or black, which are the two major categories. Race may change only among the other races. Age will remain in the partitioning intervals. For example, if the true value is 38, the perturbed value will be between 35 and 44. It will preserve the counts of voting age (18 or above) and senior (65 and above) people, which are important in policy research. Also note that since marital status and PUMA were not used in data partitioning, those may change freely. This partition in one extreme fully preserves gender and on the other extreme permits unlimited changes of marital status and PUMA.

In the example, NZY took $\xi = 0.395$, for which only singleton and doubleton cells (with frequency 1 and 2, respectively) are sensitive. So, all singleton and doubleton cells of X in a partition set formed one PRB. In each of the 42 PRB’s, the true X cells are post-randomized using the transition probabilities given by (16). For $\xi =0.395$, it turns out that $\theta =0.8$ and $(1-\theta )^{-1} = 5$. Earlier, we discussed (16) for one data set and assuming that all cells are nonempty. For applying post-randomization, we need to specialize (16) for each PRB. Specifically, we need to interpret k as the number of cells in the PRB, which changes from PRB to PRB. Also, $c_1, \dots , c_k$ should represent the cells within a PRB. The theoretical results for guaranteeing (15) also require at least $(1-\theta )^{-1} (= 5$ for $\xi =0.395$) cells in each PRB. This was satisfied in the example. Actually, the number of cells in the 42 PRB’s ranged between 124 and 1480. One should not partition the data overly finely into too many sets so that the condition $k\ge (1-\theta )^{-1}$ is satisfied.

We mention some other facts from the NZY example. The five key variables defined 364,320 cells. The data set, with sample size 59,033, showed only 25,406 nonempty cells, of which 13,662 are singleton and 4,777 are doubleton. As $\theta =0.8$, the method changed the true cell of each singleton unit with probability 0.8 and each doubleton unit with probability 0.4. When a true cell was changed, the new cell was picked at random from the remaining cells within the PRB. The method kept the true values of all nonsensitive units unchanged.

Deriving methods for analyzing perturbed data, making appropriate adjustments for data perturbation, is burdensome to data users. Also, data users usually do not get full information about the perturbation mechanism that is needed for modeling the perturbation effects. So, it is important to perturb the data in such a way that standard inferential methods for the original data remain valid for the released data, at least approximately. Generally, we want perturbation methods that add a small (or negligible) variance and no bias. The NZY methods does quite well in that respect, largely due to data partitioning and using unbiased PRAM. The relative frequencies based on perturbed data are unbiased estimators of corresponding population probabilities. NZY examined the variance of these estimators and proved that the additional variance due to data perturbation is of order $1/n^2$, where n is sample size. That is negligible in comparison to sampling variance, which is of order 1/n.

Consistent with the theoretical results, the NZY method exhibited very small effects on data distributions in their example. We reproduce the distributions of marital status and race based on the original and perturbed data in Tables 1 and 2. There, columns 2 and 3 give the original and perturbed frequencies and the numbers in parentheses are relative frequencies. The last column gives the difference between the original and perturbed frequencies. Recall that marital status was allowed to change freely. Even then, the original and perturbed frequencies are very close. The differences between original and perturbed frequencies of race categories are also quite small. Note that the difference is 0 for white and black. That is not by coincidence, but due to the particular data partitioning, which forced to preserve race for those two groups. We refer interested readers to the NZY paper for more details about the method and the example.

Table 1 Frequency distributions of marital status

Table 2 Frequency distribution of race

6 Discussion

The idea of randomizing true responses for protecting respondent’s privacy and data confidentiality has been around for a long time. But, it has not been used much in real surveys, perhaps due to lack of practical privacy measures and adequate guidance on choosing the transition probabilities. In recent years, RR methods have received significant attention from companies and computer scientists in a new context, viz., for protecting privacy when recording data from various online activities. Recent research has yielded precise privacy concepts and measures and rigorous methods for determining the transition probabilities. We have reviewed some of those developments. In particular, we covered one approach to strict privacy protection (in Sects. 3 and 4) and one rigorous method for identification risk control in releasing microdata (in Sect. 5).

RR surveys and PRAM are similar in that both randomize true responses with predetermined probabilities and the transition probabilities govern their mathematical properties. But, one important difference is that in PRAM, the original data (containing true responses of all units) may be used to choose the transition probabilities, whereas in RR surveys, those must be determined before data collection. This implies that in PRAM, randomization may be applied after data partitioning and only to some selected units. The NZY method displays and utilizes these special features of PRAM.

Privacy and data confidentially are difficult but important topics and have been investigated for a long time. Also, research in these areas has increased significantly in recent years. New theories and methods are being developed by researchers in statistics, computer science, public policy, and other fields. Other concepts and methods such as grouping, data swapping, synthetic data, l-diversity, and differential privacy have been developed to mitigate disclosure risks. We consider response randomization as one of the most basic and promising tools for protecting privacy and data confidentiality. In particular, we believe that there is substantial scope for developing post-randomization methods, like the NZY method, for protecting data confidentiality.