Keywords

1 Introduction

Nowadays, computer systems, to control real-time functions, are considered among the most challenging systems. As a consequence, real-time systems have become the focus of much study [4,5,6]. A real-time system is any system which has to respond to externally generated input stimuli within a finite and specified delay. The development of real-time systems is not a trivial task because a failure can be critical for the safety of human beings [1,2,3]. Such system must react to events from the controlled environment while executing specific tasks that can be periodic, aperiodic or sporadic. A periodic task is activated on a regular cycle and must adhere to its hard deadline. It is characterized by its arrival time, worst-case execution time (WCET), period, relative deadline, and a degree of criticality that defines its applicative importance. The degree of criticality is defined as the functional and operational importance of a task. A sporadic task can arrive to the system at arbitrary points in time, but with defined minimum inter-arrival time between two consecutive invocations. It is characterized by its worst-case execution time, minimum inter-arrival time, relative deadline, and a degree of criticality that defines its applicative importance. These attributes are known before system execution. Additional information available on-line, is its arrival time and its absolute deadline. An aperiodic task is activated at random time to cope with external interruptions, and it is based upon soft deadline. Its arrival time is unknown at design time. It is characterized by its worst-case execution time, relative deadline, and a degree of criticality that defines its applicative importance.

Real-time scheduling has been extensively studied in the last three decades. These studies propose several Feasibility Conditions for the dimensioning of realtime systems. These conditions are defined to enable a designer to grant that timeliness constraints associated with an application are always met for all possible configurations. In this paper, Two main classical scheduling are generally used in real-time embedded systems: RM and EDF. EDF is a dynamic scheduling algorithm used in real-time operating systems [8]. EDF is an optimal scheduling algorithm on preemptive uniprocessors, in the following sense: if a collection of independent jobs (each one characterized by an arrival time, an execution requirement, and a deadline) can be scheduled (by any algorithm) such that all the jobs complete by their deadlines, then the EDF will schedule this collection of jobs such that all of them complete by their deadlines. On the other hand, if a set of tasks is not schedulable under EDF, then no other scheduling algorithm can feasibly schedule this task set. Rate Monotonic (RM) for fixed priorities and Earliest, it was defined by Liu and Layland [7] where the priority of tasks is inversely proportional to their periods.

Enforcing timeliness constraints is necessary to maintain correctness of a real-time system. In order to ensure a required real-time performance, the designer should predict the behavior of a real-time system by ensuring that all tasks meet their hard deadlines. Furthermore, scheduling both periodic, sporadic and aperiodic tasks in real-time systems is much more difficult than scheduling a single type of tasks. Thus, the development of real-time systems is not a trivial task because a failure can be critical for the safety of human beings [19]. In this context, the considered problem is how to calculate the effective deadlines (hard and soft) of the different mixed tasks to guarantee that all tasks will always meet their deadlines while improving response times for aperiodic tasks.

The major contribution of this work is a methodology defined in the context of dynamic priority preemptive uniprocessor scheduling to achieve real-time feasibility of a software system. Differently from earlier work [22], which is based on maximum deadlines, the deadline calculation in the current work is based on the degree of criticality of tasks and on their periods. In fact, as the degree of criticality is defined as the functional and operational importance of a task, we consider that an important task must be executed ahead, i.e., that its relative deadline must be well defined to reinforce its execution while using the EDF scheduling algorithm. The calculation of deadlines is done off-line on the hyper-period which is the lowest common multiple (LCM) of the periodic tasks’ periods [20]. We suppose that the maximum number of occurrences of aperiodic tasks in a given interval of time is a random variable with a Poisson distribution which is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time. This proposed approach consists of two phases. The first one defines the NPS server which serves periodically aperiodic tasks. In fact, the server can be accounted for in periodic task schedulability analysis, it has (i) a period which is calculated in such a way that the periodic execution of the server is repeated as many times as the maximum number of aperiodic tasks occurrences in the hyper-period, and (ii) a capacity which is the allowed computing time in each period and it is calculated based on unused processing time by a given set of periodic and sporadic tasks in the hyper-period in a such way aperiodic task execution should not jeopardize schedulability of periodic and sporadic tasks. Then, this approach calculates aperiodic tasks soft deadlines while supposing that an aperiodic task, with highest degree of criticality, gets the highest priority to be executed. The second one calculates hard deadlines of periodic and sporadic tasks ensuring real-time system feasibility while considering the invocation of aperiodic task execution, i.e., while considering the maximum cumulative execution time requested by aperiodic tasks that may occur before periodic and sporadic jobs on the hyper-period. Thus, at runtime, even if an aperiodic task occurs, the periodic and sporadic tasks will certainly respect their deadlines and the response time of aperiodic task is improved. For each periodic or sporadic task, the maximum among its calculated jobs deadlines will be its relative deadline. Thus, at runtime, even if an aperiodic task occurs, the periodic and sporadic tasks will certainly respect their deadlines and the response time of aperiodic task is improved as the invocation of aperiodic task execution is considered when calculating hard deadlines.

The remainder of the paper is organized as follows. Section 2 discusses the related studies. Section 3 presents a computational model, assumptions, and problem formulation. Section 4 gives the proposed scheduling method. Section 5 presents a case study for evaluating our method. Finally, Sect. 6 summarizes this paper with our future work.

2 Related Studies

In this section, we present the related works that deal with real-time systems and scheduling policies.

Several works deal with the synthesis problem of real-time systems. The correctness of such systems depends both on the logical result of the computation and the time when the results are produced. Thus enforcing timeliness constraints is necessary to maintain correctness of a real-time system. In this context, many approaches have been carried out in the area of schedulability analysis for meeting real-time requirement [9,10,11,12,13,14, 26]. Some of them [11,12,13] work on real-time schedulability without considering the deadlines analysis. Some other [9, 10] seek to schedule tasks to respect energy constraints and consider that deadlines are given beforehand. Pillai and Shin [26] propose an optimal algorithm for computing the minimal speed that can make a task set schedulable. Furthermore, these researches does not consider mixed tasks set. Moreover, techniques to calculate tasks’ deadlines are seldom presented. For this reason, the studies that address this problem are few. The work reported in [15] presents a method that minimizes deadlines of periodic tasks only. The research in [18] calculates new deadlines for control tasks in order to guarantee close loop stability of real-time control systems. On the other hand, several related works, such as in [16, 17] have chosen to manage the tasks of a real-time system by modifying either their periods or worst-case execution times (WCET). This orientation affects the performance of the system, since increasing the periods degrades the quality of the offered services, and decreasing the WCET increases the energy consumption.

Furthermore, the research works reported in [23,24,25] take into account the energy requirements without considering the deadlines analysis, as long as they are given beforehand. Indeed, in these researches, the authors seek to schedule tasks to respect energy constraints. In addition, it is done online, which can be heavy and expensive.

We note that most of existing studies working on real-time schedulability, address separately periodic, sporadic or aperiodic tasks but not together. Thus, the originality of this work compared with related studies is that it

  • deals with real-time tasks of various types and constraints simultaneously,

  • parameterizes periodic server to execute aperiodic tasks,

  • calculates soft deadlines of aperiodic tasks,

  • calculates periodic and sporadic tasks hard deadlines which will be certainly respected online,

  • improves response times of aperiodic tasks which can lead to a significant improvement of the system performance.

3 Assumptions and System Formalization

3.1 System Model

It is assumed in this work that a real-time system \(\varPi \) deals with a combination of mixed sets of tasks and constraints: periodic and sporadic tasks with hard constraints, and soft aperiodic tasks. Thus, \(\varPi \) is defined as having three task sets as presented in Fig. 1.

Fig. 1.
figure 1

\(\varPi \)’s tasks sets.

Full size image

We assume that all periodic tasks are simultaneously activated at time \(t=0\);

3.2 Periodic Task Model

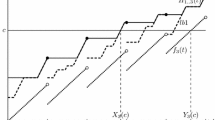
Each periodic task \(\tau _{i}^0\), \( i \in [1,..., n]\), in \(\mathcal {P}\) is characterized by: (i) a release time \(R_i^0 \) which is the time at which a task becomes ready for execution [27], (ii) a worst-case execution time (WCET) \(C_i^0\), (iii) a period \(P_i^0\), (iv) a relative deadline \(D_i^0\) to be calculated, and (v) a degree of criticality \(phi_i^0\). Figure 2 depicts the task parameters:

Fig. 2.
figure 2

Periodic task parameters.

Full size image

Each periodic task \(\tau _{i}^0\) produces an infinite sequence of identical activities called jobs \(\tau _{ij}^0\) [27], where j is a positive integer. Each job \(\tau _{ij}^0\) is described by: (i) a release time \(r_{ij}^0\), (ii) a relative deadline \(d_{ij}^0\), and (iii) an end execution time \(E_{ij}^{0}\). We note that

$$\begin{aligned} D_{i}^0 = max\{ d_{ij}^0\} \end{aligned}$$
(1)

where \(i \in [1,...,n]\).

Finally, we denote by HP the hyper-period which is the lowest common multiple (LCM) of the periodic tasks’ periods.

$$\begin{aligned} HP = LCM\{ P_i^0\} \end{aligned}$$
(2)

where \(i \in [1,...,n]\).

3.3 Sporadic Task Model

Each sporadic task \(\tau _{e}^1\), \( e \in [1,..., m]\), is defined by: (i) a release time \(R_e^1 \), (ii) a worst-case execution time \(C_{e}^1\), (iii) a relative deadline \(D_{e}^1\), (iv) a period \(P_{e}^1\) which measures the minimum interval between the arrival of two successive instances of a task \(\tau _{e}^1\), and (v) a degree of criticality \(phi_e^1\)

Each sporadic task \(\tau _{e}^1\) produces an infinite sequence of jobs \(\tau _{ef}^1\), where f is a positive integer. Each job \(\tau _{ef}^1\) is described by: (i) a release time \(r_{ef}^1\), (ii) a relative deadline \(d_{ef}^1\), and (iii) end execution time \(E_{ef}^{1}\). Figure 3 depicts the sporadic task’s jobs parameters:

$$\begin{aligned} D_{e}^1= max\{ d_{ef}^1\} \end{aligned}$$
(3)

where \(e \in [1,...,m]\).

Fig. 3.
figure 3

Sporadic task parameters.

Full size image

3.4 Aperiodic Task Model

Each aperiodic task \(\tau _{o}^2\), \( o \in [1,..., k]\), is defined by: (i) a worst-case execution time \(C_{o}^2\), (ii) a relative soft deadline \(D_{o}^2\), and (iii) a degree of criticality \(phi_o^2\). An aperiodic task can arrive in a completely random way. Thus, we model this number by the Poisson distribution with a parameter \(\lambda \). We note by OC the maximum number of aperiodic tasks’ occurrences estimated on the hyper-period.

Let NPS be a periodic server that behaves much like a periodic task, but created to execute aperiodic tasks. It is defined by: (i) a period \(P^{s}\), and (ii) a capacity \(C^{s}\). These parameters will be calculated to meet time requirements of aperiodic tasks.

3.5 Problem: Feasible Scheduling of Real-Time Tasks with Various Types

We undertake a real-time system which is composed of mixed tasks sets with various constraints. Thus, the considered problem is how to configure feasible scheduling of software tasks of various types (periodic, sporadic and aperiodic) and constraints (hard and soft) in the context of dynamic priority, preemptive, uniprocessor scheduling. To ensure that this system runs correctly, it is necessary to check whether it respects the following constraints:

  • the execution of aperiodic tasks must occur during the unused processing time by a given set of periodic and sporadic tasks in the hyper-period in such way aperiodic task execution should not jeopardize schedulability of periodic and sporadic tasks. This constraint is given by

    $$ C^{s} \le HP - Q $$

    where, \(C^{s}\) is the capacity of the NPS server and Q is the maximum cumulative execution time requested by periodic and sporadic jobs on the hyper-period HP.

  • During each hyper-period, each periodic or sporadic job has to be completed before the absolute deadline using the EDF scheduling algorithm even if an aperiodic task is executed. In fact, the cumulative execution time requested by aperiodic tasks must be token into consideration when calculating the tasks’ deadlines. Thus, s an aperiodic task will be executed as soon as possible of its activation, and periodic and sporadic tasks will meet their deadlines. This constraint is given by

    • For periodic jobs:

      $$\begin{aligned} \forall i \in \{1, ..., n\} \text {, and } j \in \{1, ..., \frac{HP}{P_i^{0}}] \text {, } E_{ij}^{0} \le r_{ij}^{0} + D_i^{0} \end{aligned}$$
      (4)

    • For sporadic jobs:

      $$\begin{aligned} \forall e \in \{1, ..., m\} \text {, and } f \in \{1, ..., \left\lceil \frac{HP}{P_e^{1}}\right\rceil ] \text {, } E_{ef}^{1} \le r_{ef}^{1} + D_e^{1} \end{aligned}$$
      (5)

In what follows, it is always considered that \( \textit{i} \in [1 ... n] \), \( e \in [1 ... m] \), \( o \in [1 ... k] \), \( \textit{j} \in [1 ... \dfrac{HP}{P_i^0}] \), where \(\dfrac{HP}{P_i^0}\) denotes the number of jobs produced by task \(\tau _{i}\) on hyper-period HP and \( f \in [1 ... \lceil \dfrac{HP}{P_i^0}\rceil ] \). In addition, we suppose that a ztask lower its value, higher the criticality.

4 Contribution: New Solution for Deadlines Calculation

4.1 Motivation

The proposed methodology deals with real-time tasks of various types and constraints simultaneously. This approach is divided into two phases as presented in Fig. 4:

  • First Phase: consists on parameterizing the NPS server which is a service task, with a period \(P^{s}\) and a capacity \(C^{s}\), invoked periodically to execute aperiodic tasks. Then, this approach calculates soft deadlines of aperiodic tasks while supposing that an aperiodic task, with highest degree of criticality, gets the highest priority. The NPS can provide a substantial reduction in the average response time of the aperiodic tasks.

  • Second Phase: starts by calculating jobs’deadlines. In fact, for each periodic/sporadic task, it calculates the deadlines of its jobs that occur on the hyper-period based on the maximum cumulative execution time requested by i) other periodic/sporadic jobs that will occur before the considered periodic/sporadic job on the hyperperiod based on the degree of criticality, and ii) aperiodic tasks that may occur before periodic/sporadic job on the hyper-period. Then, for each periodic/sporadic task, its deadline will be equal to the maximum of its jobs’ deadlines. Thus, at runtime, even if an aperiodic task occurs, this methodology ensures certainly real-time system feasibility of periodic and sporadic tasks.

Fig. 4.
figure 4

New methodology of deadlines calculation.

Full size image

4.2 Proposed Approach

In this section, we present the solution that we propose to extend. This solution is mainly based on the calculation of effective deadlines of mixed tasks set in order to ensure that the system will run correctly and to satisfy the real-time feasibility.

Parameterizing Aperiodic Tasks: As mentioned previously, aperiodic tasks will be run periodically by the periodic server NPS (\(P^{s}, C^{s}\)). As, OC is the maximum number of aperiodic tasks’ occurrences estimated on the hyper-period, then, NPS must be activated OC times to serve all possible activations of aperiodic tasks that may occur. Thus, its period is calculated as below

$$\begin{aligned} P^{s}= \lfloor \dfrac{HP}{OC}\rfloor \end{aligned}$$
(6)

Moreover, aperiodic tasks are scheduled by utilizing unused processing time by a given set of periodic and spordic tasks in the hyper-period. Thus, the capacity of server is calculated as follows: first, we calculate the unused time by subtracting the maximum cumulative execution time requested by periodic and sporadic jobs from HP, and second we divide the obtained result by OC, i.e., the possible activation number, to affirm that in each period the same amount of execution time will be executed, hence the server capacity value.

$$\begin{aligned} C^{s}= \lceil \dfrac{HP - Q}{OC}\rceil \end{aligned}$$
(7)

where, Q is the maximum cumulative execution time requested by periodic and sporadic jobs on the hyper-period HP.

$$\begin{aligned} Q=(\sum _{\tau _{i}^0 \in \mathcal {P}}(C_i^0 \times \dfrac{HP}{P_i^0}))+(\sum _{\tau _{e}^1 \in \mathcal {S}}(C_{e}^1 \times \lceil \dfrac{HP}{P_{e}^1} \rceil )) \end{aligned}$$
(8)

By assuming that the aperiodic task with the highest degree of criticality,i.e., the smallest value of \(\phi _{o}^2\), gets the highest priority, we calculate the deadlines \(D_{o}^2\) as following

$$\begin{aligned} D_{o}^2= \sum _{x=1}^{x=k} C_{x}^2 \times \alpha _x \end{aligned}$$
(9)

where,

$$\begin{aligned} \alpha _x = \left\{ \begin{array}{ll} 1 \text{ if } ( \phi _{o}^2 \ge \phi _{x}^2 ), \\ 0 \text{ else. } \end{array} \right. \end{aligned}$$
(10)

Parameterizing Periodic and Sporadic Tasks: At the peak of activity, a sporadic task \(\tau _{e}\) runs at each \(P_{e}^1\). In this case, we can estimate the value \(r_{ef}^1\) of each job \(\tau _{ef}^1\). Therefore, to calculate the deadline of a sporadic task, we follow the same procedure of a periodic task deadline calculation. For that, we unify the notation of periodic and sporadic tasks by \( \tau _{i_1} (R_{i_1}, C_{i_1}, P_{i_1}, D_{i_1}, \phi _{i_1})\), where \( i_1 \ in [1, ..., n + m] \), also for these parameters. For example, let’s consider a system with two tasks: a periodic task \( \tau _{1}^0 (R_1^0, C_1^0, P_1^0, D_1^0, \phi _1^0) \) and a sporadic task \( \tau _ {1}^1 (R_1^1, C_1^1, P_1^1, D_1^1, \phi _1^1) \), then they becomes \( \tau _ 1 (R_1, C_1, P_1, D_1,\phi _1) \) and \( \tau _2 (R_2, C_2, P_2, D_2, \phi _2) \).

This solution allows the calculation of deadlines of a task \(\tau _{i_1}\). We denote by \(\varDelta _{i_1j_1}\) the job quantity, coming from periodic and sporadic jobs, to be executed before the job \(\tau _{i_1j_1}\). In other words, \(\varDelta _{i_1j_1}\) is the maximum cumulative execution time requested by jobs that have to be executed before each job \(\tau _{i_1j_1}\).

\( \varDelta _{i_1j_1}\) is given by

$$\begin{aligned} \varDelta _{i_1j_1} = (j_1 -1) \times C_{i_1} + \sum _{\tau _l^ \in \mathcal {P}\cup \mathcal {S} and l \ne i} (\lfloor \frac{j_1 \times P_{i_1}}{P_l}\rfloor - \beta _{l}^{i_1j_1}) \times C_l \end{aligned}$$
(11)

where \((j_1 -1) \times C_{i_1}\) represents the cumulative execution time requested by the previous instances of \(\tau _{i_1}\), i.e., if we are working on the \(j_1\)th instance, then we are sure that there are \((j_1-1)\) instances that have already been executed, and \(\sum _{\tau _l^ \in \in \mathcal {P}\cup \mathcal {S} and l \ne i} (\lfloor \frac{j_1 \times P_{i_1}}{P_l}\rfloor - \beta _{l}^{i_1j_1}) \times C_l\) represents the cumulative execution time requested by the other tasks’ jobs, where \(\beta _{l}^{i_1j_1}\) is an integer given by

$$\begin{aligned} \beta _{l}^{i_1j_1} = \left\{ \begin{array}{ll} 0 \text{ if } (\lfloor \frac{j_1 \times P_{i_1}}{P_l}\rfloor \times P_l< j_1 \times P_{i_1}) \text{ or } (\lfloor \frac{j_1 \times P_{i_1}}{P_l}\rfloor \times P_l = j_1 \times P_{i_1} \text{ and } \phi _{i_1}> \phi _{l})\\ 1 \text{ if } (\lfloor \frac{j_1 \times P_{i_1}}{P_l}\rfloor \times P_l > j_1 \times P_{i_1}) \text{ or } (\lfloor \frac{j_1 \times P_{i_1}}{P_l}\rfloor \times P_l = j_1 \times P_{i_1} \text{ and } \phi _{i_1} < \phi _{l}) \end{array} \right. \end{aligned}$$
(12)

The value \(d_{i_1j_1}\) that guarantees the feasibility of this job takes the form

$$\begin{aligned} d_{i_1j_1} = \left\{ \begin{array}{ll} \sum _{\tau _{l}^2 \in \mathcal {A}}(C_l^2 \times \lceil \frac{P{i_1}}{P^{s}}\rceil ) + C_{i_1} + \varDelta _{i_1j_1} - r_{i_1j_1} \\ \text{ if } \varDelta _{i_1j_1} > r_{i_1j_1}, \\ \sum _{\tau _{l}^2 \in \mathcal {A}}(C_l^2 \times \lceil \frac{P{i_1}}{P^{s}}\rceil ) + C_{i_1} \text{ else. } \end{array} \right. \end{aligned}$$
(13)

The deadline \(D_{i_1}\) of task \(\tau _{i_1}\) is expressed by

$$\begin{aligned} D_{i_1} = max\{d_{i_1j_1}\} \end{aligned}$$
(14)

Finally, \(D_{i_1}\) is the fixed deadline for \(\tau _{i_1}\).

New Solution for Deadline Calculation of Periodic, Sporadic and Aperiodic Real-Time Tasks: We can implement our approach by the algorithm below with complexity O(n).

We use the following functions: \(NPS\_Parameters(HP,OC)\) which is a function that returns the NPS server parameters, and \(H\_Dead\_Calc(\mathcal {P},\mathcal {S})\) which a function that returns the periodic and sporadic hard deadlines. This function starts by computing jobs deadlines and then for each periodic/sporadic task, it calculates its fixed deadline to be equal to the maximum of its jobs’ deadlines.

figure a

5 Implementation

5.1 Case Study

We present in this section a simple example of an electric oven whose temperature we want to keep constant after in interruption that may disturb the temperature stability. For example, we want to keep it at 180 °C after a sudden opening of the oven’s door as presented in Fig. 5. The oven is heated by an electrical resistance, the intensity of which can vary. Inside the oven there is also a temperature probe, which allows to measure and monitor the temperature in the oven.

Fig. 5.
figure 5

Electric oven modelisation.

Full size image

This system is implemented by three sets: \(\mathcal {P} = \{\tau _1^0, \tau _2^0\}\), \(\mathcal {S} = \{\tau _1^1\}\) and \(\mathcal {A} = \{\tau _1^2 \}\). The tasks are presented in Table 1:

Table 1. System tasks.
Full size table

We have, \(HP= LCM\{ 8, 16\}= 16s\).

Let’s suppose that the parameter \(\lambda \) of the Poisson distribution is equal to 0.5 occurrences in 10 s. Thus, in the hyper-period we have \(\frac{HP}{10} \times \lambda = \frac{16}{10} \times 0.5=1.6\), i.e., \(OC= 2\) occurrences.

The first step is to configure the periodic server.

The periodic server parameters \(P^{s}\) and \(C^{s}\) are computed respectively as following:

According to Eq. (6), \(P^{s} = \lfloor \dfrac{16}{2}\rfloor = 8 \)

According to Eq. (8), \(Q= 2 \times 2 + 2 \times 1 = 6 \)

According to Eq. (7), \(C^{s} = \lfloor \dfrac{16 - 6 }{2}\rfloor = 5\)

After that, we calculate the soft deadline of the aperiodic task \(\tau _1^2\). According to Eq. (9)

$$\begin{aligned} D_1^2 = C_{1}^2 \times \alpha _1 = 2 \times 1 =2 \end{aligned}$$

Second step is the calculation of periodic and sporadic tasks’ deadlines. As mentioned previously, we unify the notation of periodic and sporadic tasks as following: \(\tau _1^0\) becomes \(\tau _1\), \(\tau _2^0\) becomes \(\tau _2\), and \(\tau _1^1\) becomes \(\tau _3\).

As an example, we take the calculation of deadline \(D_1^0\) for task \(\tau _1^0\), i.e., \(D_1\) for the task \(\tau _1\). The number of jobs of task \(\tau _1\) in the hyper-period HP is \( \frac{HP}{P_3}=\frac{16}{8}= 2\) jobs.

 

First of all, we calculate the job quantity \(\varDelta _{11}\). According to Eq. (11), we have to calculate \(\beta _2^{11}\) and \(\beta _3^{11}\) as indicated Eq. (12).

We have \( \lfloor \frac{1 \times 8}{16}\rfloor \times 16 < 1 \times 8 \), i.e., \(0 < 8 \), then we conclude that \( \beta _2^{11}=0\). In the same way, we have \(\beta _3^{11} = 0\)

According to Eq. (11), \(\varDelta _{11}\) is calculated as following

$$\begin{aligned} \varDelta _{11}&= (1 -1) \times 2 + \lfloor \frac{1 \times 8}{16}\rfloor - 0) \times 2 + \lfloor \frac{1 \times 8}{16}\rfloor - 0) \times 2 \\&= 0 \times 2 + 0 \times 2 + 0 \times 2 = 0 \end{aligned}$$

We have \(r_{11}=0\), so \(\varDelta _{11} = r_{11}\). Thus, according to Eq. (13),

$$\begin{aligned} d_{11}&= \sum _{\tau _{l}^2 \in \mathcal {A}}(C_l^2 \times \lceil \frac{P{i_1}}{P^{s}}\rceil ) + C_1 \\&= 2 + 2 = 4 \end{aligned}$$

 

First of all, we calculate the job quantity \(\varDelta _{12}\). According to Eq. (11), we have to calculate \(\beta _2^{12}\), and \(\beta _3^{12}\) as indicated in Eq. (12). We have \( \lfloor \frac{2 \times 8}{16}\rfloor \times 16 < 2 \times 8\), i.e., \(16 = 16 \), and \(\phi _1 < \phi _2 \) then we conclude that \( \beta _2^{12}=1\). In the same way, wa have \(\beta _3^{11} = 1\)

According to Eq. (11), \(\varDelta _{12}\) is calculated as following

$$\begin{aligned} \varDelta _{12}&= (2 -1) \times 2 + \lfloor \frac{2 \times 8}{16}\rfloor - 1) \times 2 + \lfloor \frac{2 \times 8}{16}\rfloor - 1) \times 2 \\&= 1 \times 2 + 0 \times 2 + 0 \times 2 = 2 \end{aligned}$$

We have \(r_{12}=8\), then \(\varDelta _{12} < r_{12}\) and we have

$$\sum _{\tau _{l}^2 \in \mathcal {A}}(C_l^2 \times \lceil \frac{P{i_1}}{P^{s}}\rceil )=2$$

Thus, according to Eq. (13),

$$ d_{12} = \sum _{\tau _{l}^2 \in \mathcal {A}}(C_l^2 \times \lceil \frac{P{i_1}}{P^{s}}\rceil ) + C_1 = 2 + 2 = 4 $$

Finally, we calculate the deadline \(D_{1}\) of the task \(\tau _{1}\) as bellow

$$D_1 = max \{d_{11}, d_{12}\} =max \{4 ,4 \} = 4 $$

After completing the execution of the proposed approach, the calculated effective deadlines of the different tasks are given in Table 2.

Table 2. Tasks’ calculated deadlines.
Full size table

Figure 6 shows the scheduling of tasks after the execution of the proposed approach. We note that the real-time constraints are respected by the proposed methodology, and the response time of each aperiodic task is equal to its execution time, i.e., they are executed with the best response time.

Fig. 6.
figure 6

Scheduling of tasks after the execution of the proposed approach.

Full size image
Fig. 7.
figure 7

Rates of deadlines reduction in the case of the proposed approach and in the case of GSF algorithm.

Full size image

5.2 Performance Evaluation

We have randomly generated instances with 10 to 50 periodic and sporadic tasks. We compare the proposed approach with the work reported in [15], where the critical scaling factor (CSF) algorithm is developed.

Figure 7 visualizes simulation that compares the proposed approach with the work reported in [15], where the critical scaling factor (CSF) algorithm is developed. We obtain better results in terms of decrease rate of deadlines in the proposed approach. In fact, the reduction rates of deadlines by using [15] are smaller than those by using the proposed work. The gain is more significant when increasing the number of tasks. If 10 tasks are considered, then the gain is equal to \((0.31-0.2) = 0.11\), and if 50 tasks are considered, then the gain is equal to \((0.7-0.52) = 0.18\).

As it was presented in [22], Fig. 8 shows that the NPS algorithm serves to improve the aperiodic response time compared to background service (BK), deferrable server (DS) and total bandwidth server (TBS).

Fig. 8.
figure 8

The improvement of aperiodic tasks response times [22].

Full size image
Table 3. Comparative study.
Full size table

5.3 Comparative Study

Table 3 describes the comparison of the developed approach in this paper with some studies. The originality is manifested by treating different and independent problems together, i.e., periodic, sporadic and aperiodic tasks and hard and soft real-time constraints tasks simultaneously.

We note that the proposed approach allows to reduce the response time, to reduce the calculation time for the reason that there is no need to waste time at doing schedulability tests, to guarantee the meeting of aperiodic tasks deadlines without jeopardizing schedulability of periodic and sporadic tasks and thus improves the overall performance of the real-time system.

6 Conclusion

This paper is interested in real-time systems executing periodic, sporadic and aperiodic tasks. Our study concerns specifically the computing off effective tasks’ deadlines. We propose a new approach that consists on creating the NPS server, it is a service task invoked periodically to execute aperiodic tasks after having calculated aperiodic tasks’ soft deadlines. Then, this approach calculates the periodic and sporadic tasks deadlines based on the degree of criticality of tasks and while considering the invocation of aperiodic task execution. An application to a case study and performance evaluation show the effectiveness of the proposed approach and that the NPS can provide a substantial reduction in the average response time of the aperiodic tasks. In our future works, we will be interested in the implementation of the paper’s contribution that will be evaluated by assuming real case studies.