About Phenomenology and Modeling of Dropwise Condensation

Abstract

The modeling of dropwise condensation remains, at the present time, difficult. Indeed, in order to predict the heat transfers in this regime, it is necessary to know the heat flux which crosses each drop according to its size as well as the drop-size distribution on the surface considering radii that can vary from a few nanometers to several centimeters. As this distribution is a function of the life cycle of each drop, an overview of a drop’s lifecycle has been first done in order to better understand the phenomena underlying dropwise condensation. Particular attention has been paid on the drop growth rate modeling. Secondly, a description of the drop-size distribution models has been done. Due to the very large number of drops, very fast dynamics and the difference in drop-sizes, only two types of modeling are available. The first approach is based on a semi-empirical law to model the distribution of the largest drops (i.e., those with a radius greater than a few microns) together with a population balance for the size distribution of the smallest drops. The second approach consists in the following of all the drops along time in order to determine the stationary drop-size distribution. This approach already succeed to predict the size distribution of the big drops many times. Based of these overviews, an individual-based modeling has been developed and computed, focusing on the behavior of the smallest droplets. A comparison of the results obtained with this model with the ones obtained with classical population-balanced approach has then be realized. Discrepancies of several orders of magnitude have been found on drop-size distribution. This important difference is attributed to one of the hypothesis of population balance modeling, i.e., the hypothesis of constant renewal rate whatever the drop radius. The impact of such deviations in the drop-size distribution on global heat transfer has then be quantified. In most of the configurations studied, the population balance approach predicts global heat fluxes about 30% higher compared to the individual-based model’s ones. Finally, a parametric study has been done considering three parameters that can be potentially controlled in experimental works: advancing contact angle, nucleation sites density, and departure radius.

4.1 Dropwise Condensation: An Effective Way to Transfer Heat

Two regimes of condensation can exist according to the experimental configuration. The first one, commonly encountered in heat exchangers, is filmwise condensation. In that regime, the condensates form a continuous film that cover the cold substrate. In the second regime, i.e., dropwise regime, the condensates form small droplets separated from each other. The latter regime can appear in some portions of space and/or time, but is often reported in literature as difficult to maintain on an extended surface during long time.

About 90 years ago, Schmidt et al. [41] were the first ones to demonstrate experimentally that dropwise condensation leads to very high heat transfer coefficient values, up to one order of magnitude higher than the heat transfer coefficient in filmwise condensation.

This observation has then been experimentally confirmed several times during the last half century [34, 39]. For instance, very recently, heat transfer coefficient up to 250  kW m$^{-2}$ K$^{-1}$ have been measured by Parin [35] on hydrophobic aluminum substrate with 0.2 $\upmu$m silica layer thickness.

The main reasons generally given by authors in literature to explain such a high value of the heat transfer coefficient is the very small dimension of the drops that appear on the cooled substrate, as well as their big number.

Thus, the transport mechanisms (heat transfer, fluid flow, phase change) should be identified and understood at both the drop scale and the macroscale (i.e., the scale of whole the population of drops). So, individual drop’s lifecycle as well as resulting population distribution must be analyzed and modeled.

4.1.1 The Drop’s Lifecycle

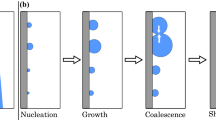
The lifecycle of a single drop can be divided into four main stages: the drop is born, then grows due to condensation, interacts with other drops and disappears. A phenomenology overview of each of these four stages is proposed in the following paragraphs along with summary of some geometrical characteristics of drops and a literature brief about associated heat transfer models.

4.1.1.1 The Drop’s Birth

Following the work of Schmidt et al. in 1930 [41], a first mechanism was proposed for the drops birth: it form from a very thin liquid film (usually not visible) adsorbed on the surface. Jacob in 1936 [20] postulated the rupture of such a liquid film due to hydrodynamic instabilities, leading to the appearance of droplets with a spherical cap shape to minimize the surface energy.

A second mechanism was also proposed nearly at the same time: Von Euken [16], using considerations about the heat transfer rate and the thermal resistance due to an adsorbed film, attributed the formation of drops to a mechanism of nucleation, i.e., the formation of droplets at atomic scale followed by their growth at continuum level. Almost 30 years later, Umur and Griffith [50] showed experimentally that no film exists between the drops and confirmed the nucleation mechanism model.

Classical theory of nucleation considers the Gibbs free energy variation to determine the equilibrium radius $r_{eq}$ of a drop that can appear in an isothermal subcooled vapor (see for example [9]):

$$\begin{aligned} r_{\min } \approx r_{eq}=\frac{2\sigma _{lv}}{\Delta T} \frac{T_{sat}}{\rho _v \mathrm {L}_{lv}} \end{aligned}$$

(4.1)

This equilibrium is unstable: a drop forming with a radius less than $r_{eq}$ will quasi-instantaneously disappear while a drop forming with a radius greater than $r_{eq}$ will grow by vapor condensation process. So, the minimum radius $r_{\min }$ of liquid nuclei forming in the subcooled vapor is expected to be close to $r_{eq}$.

In the presence of a solid substrate, the probability to form a cluster of molecules having a liquid–vapor interface with a curvature radius greater than the equilibrium radius $r_{eq}$ is higher in the case of a spherical cap rather than in the case of a sphere, due to the reduction of the number of molecules involved. In the case of a “real” surface, i.e., a surface with roughnesses, small amount of liquid can be trapped in the pits, forming pre-existing embryos. The minimum radius of nuclei is then governed by the characteristic size of those pits. The correlation with the subcooling of the solid wall can thus be evaluated using Eq. 4.1, in which $\Delta T$ is the temperature difference between the saturation temperature and the wall temperature (“wall subcooling”). In case of heterogeneous nucleation, the initial nuclei of radius $r > r_{eq}$ that formed on specific locations grow and form spherical caps whose volume is a function of the wettability of the liquid on the solid substrate:

$$\begin{aligned} V= \frac{4}{3} \pi r_{eq}^3 \times \left( \frac{2-3\,\cos \theta + \cos ^3 \theta }{4}\right) \end{aligned}$$

(4.2)

It can be noticed that the expression of the radius $r_{eq}$ in Eq. 4.1 is derived assuming an isothermal vapor phase. Several studies have been conducted to take into account temperature gradients in the continuous vapor phase close to the solid wall [19] or within the liquid droplet [24]. As the value of $r_{\min }$ is generally very small (in the order of few nanometers to few tens of nanometers) the effect of temperature gradients on the thermodynamic equilibrium’s change is often negligible, at least for configurations other than superhydrophobics. For instance, Liu and Cheng [24] found that the minimum radius $r_{\min }$ is affected by temperature gradients only for case with simultaneously high values of the contact angle ($\theta = 150$ $^\circ$) and low wall subcooling (less than 1.5 $^\circ$C).

Mc Cormick and Westwater [29] have shown experimentally that the nuclei appear on specific locations on a substrate. These authors repeated condensation experiments on two copper disks covered by an adsorbed monolayer of benzyl mercaptan, leading to advancing contact angle of 92$^\circ$. They observed that 21 previously identified nucleation sites were systematically activated again during each of the 8 following condensation experiments. So, nucleation occurs on very specific places on the surface, indicating that nucleation sites are located on surface accidents, such as cavities or pits. This conclusion was confirmed by doing specific condensation experiments on a substrate on which artificial nucleation sites were made by a spark erosion technique. Observations were then focused on the artificially produced pits during five successive condensations, clearly showing that each of these artificially produced pits were active sites for the formation of drops.

As droplets appear on specific nucleation sites, the number of nuclei can vary greatly depending on the substrate nature or microstructures (inclusions, pits, cracks, etc.). A first evaluation of the nucleation sites density was proposed by Rose [37] in 1976. Considering the drop-size distribution proposed several years earlier [22] and making some assumptions on the mean radius of droplets at the first coalescence event, he found

$$\begin{aligned} N_s = \frac{0.037}{r_{\min }^2} \end{aligned}$$

(4.3)

where $r_{\min }$ is the radius of the nuclei estimated using Eq. 4.1.

It can be highlighted that this law was determined considering drop-size distribution’s law established for droplet radii typically greater than few microns. The minimum radius of liquid embryos according to Eq. 4.1 is about two orders of magnitude less. So, evaluating $N_s$ with Eq. 4.3 may lead to significant discrepancies with real values, as pointed out for instance by Liu and Cheng [24].

From a study to another, the reported nucleation sites density values are spread on 6 orders of magnitude, i.e., from $10^9$ to $10^{15}\,$ m$^{-2}$ [2]. This huge difference in the reported nucleation sites density highlights the difficulty to predict its value accurately, as well as the strong influence of the surface microscale geometry. Moreover, several other parameters may also affect the density of active sites $N_s$ such as surface subcooling, substrate history, etc., or the detection threshold linked to the magnification of the diagnostic tool used to detect the smallest droplets. Consequently, the accurate determination of the nucleation sites density remains, nowadays, a very challenging problem and this parameter will receive a special attention in the following.

4.1.1.2 The Growth of Drop by Condensation Process

Following the nuclei appearance and, due to the temperature difference between the vapor phase and the subcooled substrate, the vapor condenses at the liquid–vapor interfaces inducing the drops growing. Fatica and Katz [18] were the first to propose a heat transfer model through a single droplet. They proposed that drop growth occurs by condensation on drop interface with the latent heat conducted through the drop to the solid surface. They developed a stationary heat transfer model based on axisymmetric heat flux configuration and derived a semi-analytic expression of drop thermal resistance. They already remarked that, due to the low thermal conductivity of the liquid and spherical cap shape, the heat flux is low except close to the triple line. Based on this work, several theoretical studies have been conducted in which the following assumptions are considered:

• The drop-sizes considered being much smaller than the capillary length $l_c=\sqrt{\frac{\sigma _{lv}}{\rho _l g}}$, the drops are supposed to have a spherical cap shape;

• The substrate’s wall is isothermal;

• The gas phase is constituted by pure vapor (without non-condensable gas);

• The only heat transfer mechanism into the drop is thermal conduction (without taking into account thermal inertia);

• The liquid phase is immobile inside the drop (no convection nor Marangoni effect).

In 1966, Le Fevre Rose [22] extended this 1D quasi-static heat transfer model through a single drop by adding several terms. Their model is then constituted by four thermal resistances placed in series between the vapor phase and the substrate’s wall, which involve four temperature jumps:

$$\begin{aligned} \Delta T =T_{sat}-T_s =\Delta T^{i}+\Delta T_{curv}+\Delta T_{l}+\Delta T_{coat} \end{aligned}$$

(4.4)

These temperature jumps are respectively linked to:

• For $\Delta T^{i}$: the vapor–liquid interfacial thermal resistance,

• For $\Delta T_{curv}$: the modification of the saturation conditions induced by the curvature of the interface,

• For $\Delta T_{l}$: the thermal conduction in the liquid within the droplet,

• For $\Delta T_{coat}$: the thermal conduction in the coating of the substrate.

It can be noticed that the model of Le Fevre and Rose considered only hemispherical drops (and thus a contact angle of 90$^\circ$), and was expressed using 2 constants that gather both shape and thermophysical parameters.

This model was used by Wen and Jer [52] in theoretical developments aimed to determine the drop-size distribution of the small droplets, and the macroscopic heat transfer coefficient. In their model, the effect of the coating thermal resistance was not taken into account. This latter was then reintroduced by Abu-Orabi [1]. About 10 years ago, Kim and Kim [21] modified the expression of the drop conductive thermal resistance in order to calculate it for an arbitrary contact angle on a hydrophobic surface. Starting from a constant interface temperature hypothesis they imposed that isotherms are spherical caps passing by triple line and whose curvature radii increase from interface to solid surface. They considered that the average distance between two consecutive isotherms is half of their max distance and calculated the drop temperature difference considering that the mean heat flux through the drop is proportional to this average distance. This liquid thermal resistance expression combined with Eq. 4.4 is currently the most widely used model in the literature, even in the case of hydrophilic surface. The most commonly used expressions of the four temperature jumps are nowadays expressed as

$$\begin{aligned} \Delta T_{l}=\frac{Q_d \theta _{adv}}{4 \pi r \mathrm {k}_l \sin \theta _{adv}} \end{aligned}$$

(4.5)

$$\begin{aligned} \Delta T^{i}=\frac{Q_d}{2 \pi r^2\,h^i(1-\cos \theta _{adv})} \end{aligned}$$

(4.6)

with $h^i$ the heat transfer coefficient at the liquid–vapor interface, calculated from the kinetic model of Schrage [42]:

$$\begin{aligned} h^i=\frac{2f}{2-f}\frac{1}{\sqrt{2\pi R_g T_{sat}}}\frac{\rho _v {\mathrm {L}}_{lv}^{2}}{ T_{sat}} \end{aligned}$$

(4.7)

where f is the condensation coefficient corresponding to the ratio between the rate of molecules that cross the liquid–vapor interface by the total rate of molecules that hit the interface. Its value is generally set to 1 for pure water vapor close to the atmospheric pressure but could vary over several decades depending on conditions or fluid nature. For water, Tanasawa [46] reported values for $h^i$ of 0.383, 2.57, and 15.7 MW m$^{-2}$ K$^{-1}$ for vapor pressure of 0.01, 0.1, and 1 bar, respectively.

From thermodynamic equilibrium considerations, the modification of the saturation conditions due to the curvature of the interface can be expressed as

$$\begin{aligned} \Delta T_{curv}=\frac{2 T_{sat} \sigma _{lv}}{\mathrm {L}_{lv} \rho _v \Delta T}=\frac{r_{\min }}{r}\Delta T \end{aligned}$$

(4.8)

Finally, the temperature jump due to the thermal conduction through the coating is simply

$$\begin{aligned} \Delta T_{coat}=\frac{Q_d \delta _{coat}}{\mathrm {k}_{coat} \pi r^2 \sin ^2 \theta _{adv}} \end{aligned}$$

(4.9)

Fig. 4.1

Variation of the dimensionless temperature jumps according to the curvature drop radius in the case of pure water for f $= 1$ ($\theta _{adv}=85^\circ$, $\Delta T=1$ K, $T_{sat}=373$ K, $\delta _{coat}=100$ nm, $\mathrm {k}_{coat}=2$ W m$^{-1}$ K$^{-1}$, and $h^i=15.7$ MW m$^{-2}$ K$^{-1}$ (f $= 1$))

Fig. 4.2

Variation of the dimensionless temperature jumps according to the curvature drop radius in the case of pure water for f $= 0.01$ ($\theta _{adv}=85^\circ$, $\Delta T=1$ K, $T_{sat}=373$ K, $\delta _{coat}=100$ nm, $\mathrm {k}_{coat}=2$ W m$^{-1}$ K$^{-1}$, and $h^i=78.9$ kW m$^{-2}$ K$^{-1}$ (f $= 0.01$))

For illustration, a comparison of the relative contribution of these four terms to the global temperature jump is shown on Fig. 4.1 in the case of pure water at atmospheric pressure (f $= 1$), considering an advancing contact angle of 85$^\circ$, a wall subcooling of 1 $^\circ$C and with typical values of the thickness and the thermal conductivity of a coating. As expected, the curvature effect is significant for the very small drops whereas the thermal conduction effect is predominant for the biggest drops. The temperature jump due to the interfacial resistance is very low for the selected conditions, as f has been set to one. Obviously, for smaller values of f this resistance may becomes dominant as discussed in the following. Due to a simple geometrical effect (drop is a spherical cap while coating is considered as a wall limited by 2 isothermal surfaces), the temperature jump created by the coating resistance presents an asymmetric bell shape with respect to drop radius. Here, the coating thermal resistance is rather important due to the low conductivity of this layer. For the selected conditions, it has a marked effect for drops radius around 100 nanometers.

In the case of a small value of f (i.e., for low-pressure conditions) the distribution of the temperature jumps is very different (Fig. 4.2). For f $=0.01$, the temperature jump at the interface represents up to 70% of the total temperature jump for $r\approx$ 0.2 $\upmu$m and remains non-negligible for radii up to about 10 $\upmu$m.

Using Eqs. 4.4–4.9 and rearranging the expressions of the temperature jumps, the heat transfer rate $Q_d$ through a single drop is commonly expressed as

$$\begin{aligned} Q_d=\frac{ \Delta T \pi r^2 (1- \frac{r_{\min }}{r})}{\frac{\delta _{coat}}{\mathrm {k}_{coat}\sin ^2\theta _{adv}}+\frac{r \theta _{adv}}{4 \mathrm {k}_l \sin \theta _{adv}}+\frac{1}{2\,h^i (1-cos \theta _{adv})}} \end{aligned}$$

(4.10)

The growth rate $G= \frac{dr}{dt}$ of any given drop is usually deduced from a simplified quasi-static energy balance using Eq. 4.2 for the expression of the volume of the drop:

$$\begin{aligned} Q_d=\frac{d}{dt} \left( \rho _l \frac{4}{3} \pi r^3 \left( \frac{2-3\cos \theta _{adv} +\cos ^3\theta _{adv}}{4} \right) \right) \mathrm {L}_{lv} =\rho _l \mathrm {L}_{lv} \pi r^2(2-3\cos \theta _{adv} +\cos ^3 \theta _{adv}) G \end{aligned}$$

(4.11)

As already pointed out by Miljkovic et al. [31], this model is valid for both hydrophobic and hydrophilic cases as the volume of the drop is calculated exactly for a spherical cap of any contact angle. On the other hand, the expression used by Kim and Kim [21], based on an approximate rate of volume variation, is valid only for hydrophobic configurations.

The growth rate of a drop can then be deduced from Eqs. 4.10 and 4.11:

$$\begin{aligned} G=\frac{dr}{dt}=\frac{A_1 (1-\frac{r_{\min }}{r})}{A_2\, r +A_3} \end{aligned}$$

(4.12)

with:

$$\begin{aligned} A_1= & {} \frac{\Delta T}{\rho \mathrm {L}_{lv} (2-3\cos \theta _{adv}+\cos ^3\theta _{adv})} \end{aligned}$$

(4.13)

$$\begin{aligned} A_2= & {} \frac{\theta }{4 \mathrm {k}_l \sin \theta _{adv}} \end{aligned}$$

(4.14)

$$\begin{aligned} A_3= & {} \frac{\delta _{coat} }{\mathrm {k}_{coat} \sin ^2 \theta _{adv}}+\frac{1}{2h^i (1-\cos \theta _{adv})} \end{aligned}$$

(4.15)

Fig. 4.3

Evolution of drop curvature radius according to time for different advancing contact angles ($\Delta T=1$ K, $T_{sat}=373$ K, $\delta _{coat}=100$ nm, $\mathrm {k}_{coat}=2$ W m$^{-1}$ K$^{-1}$, and $h^i=15.7$ MW m$^{-2}$ K$^{-1}$ (f $= 1$))

An example of the growth dynamic of a single drop is reported on Fig. 4.3 for different advancing contact angles and the same other parameters than the ones considered in Fig. 4.1. For all cases, after a small delay, the drop starts to grow in a slightly S-shaped manner that tends to a linear asymptote (in log–log representation). The asymptotes are roughly parallel (for high drop radii the conduction effect within the drops is prevalent) and the curves are translated to the right according to the contact angle. The growth delay at small radius increases with the contact angle as the curvature effect (in particular) reduces the growth rate at low radii. More the surface is hydrophilic, smaller is the time necessary to reach a given radius. For example, it will take about $10^{-3}$ s for a nucleus to grow up to 10 $\upmu$m for an advancing contact angle of $20$ $^\circ$, while this time rises to more than 10 s for an advancing contact angle of $160$ $^\circ$. This difference is mainly due to the thermal conduction resistance through the drop, that is more important for high contact angle. For a given curvature radius, drops on a hydrophobic substrate present bigger liquid volumes than on a hydrophilic one. As the total volume needed to increase the drop radius is higher in hydrophobic configuration, a more long time is necessary to condense.

So, in order to maximize the heat transfer, it appears at first that it is more interesting to use hydrophilic surface. However, in that case, a major issue will be the evacuation of the biggest drops. This evacuation is mandatory in order to renew the nucleation sites (see Sect. 4.1.1.4) and to avoid the formation of a continuous liquid film.

The second main parameter which may have a strong effect on the growth dynamic is the condensation coefficient f, especially in the case it has a small value (Fig. 4.4). Indeed, in the case of pure water (i.e., without non-condensable gas) it is usually set to one at atmospheric pressure but it can be less at lower pressure [4, 28] (it can be noticed that even a small amount of non-condensable gas can change significantly the value of the interfacial heat transfer coefficient $h^i$). So, the precise determination of f remains mandatory to well predict the heat transfer rate through small droplets. For instance, according to Fig. 4.4, the time necessary to reach a radius of 1 $\upmu$m is more than one order of magnitude higher for f $= 0.01$ than for f $= 1$.

Fig. 4.4

Evolution of drop radius according to time for different condensation coefficients ($\theta _{adv} =85^\circ$, $\Delta T=1$ K, $T_{sat}=373$ K, $\delta _{coat}=100$ nm, $\mathrm {k}_{coat}=2$ W m$^{-1}$ K$^{-1}$ and $h^i=15.7$ MW m$^{-2}$ K$^{-1}$ (f $=1$))

Experimentally, this individual growth rate model is difficult to validate, because when a drop becomes observable (i.e., typically when it reaches a radius of about a few microns) it has already coalesced a great number of times with other non-observable drops; the growth rate is no more governed only by condensation process. So, in order to obtain reference data of the growth rate of a single droplet, some authors have conducted numerical works.

By order of complexity increases, the available approaches include:

• Neumann boundary condition on drop liquid–vapor interface (in replacement of classic imposed temperature one), along with simple quasi-static conduction and Dirichlet condition on the liquid–solid interface,

• Thermocapillary convection considering the flow inside the drop in quasi-static regime,

• The dynamic of the growth (i.e., the deformation of the liquid drop with time) with transient convection and diffusion phenomena.

For example, Phadnis and Rykaczewski [36] analyzed more particularly the effect of stationary Marangoni convection on heat transfer in a single droplet using finite elements method. They compared 2 numerical situations for static drops (the condensation dynamic process was not considered). In the first one, they computed a pure conduction case with a convective boundary condition at the liquid–vapor interface and in the second one, they took into consideration the Marangoni effect. They obtained in this latter case an increase in the heat transfer rate by a factor up to 6 (compared to the case without Marangoni effect) in the case of a single drop of radius 1 mm. Nevertheless, as the increase is far more limited for the smaller drops and—see below—the big drops are rare, the global heat transfer rate increase is found to be limited: they reported an increase of less than $30\%$ in this global heat transfer coefficient compared to the pure conduction case.

The transient resolution of the drop growth dynamic was only recently achieved due mostly to the important computational resources involved in such shape evolving coupled non linear problem. Xu and et al. [55] solved the heat transfer problem in the liquid phase coupled to the flow problem in both vapor and liquid phases, taking into account interfacial mass transfer and drop deformation (prediction of interface motion along with liquid domain deformation). This comprehensive model was used to study the impact of fluid motion inside the drop on heat transfer. The authors shown that flow pattern in growing drop differs strongly from the quasi-static ones for pure vapor condensation. An increase up to a factor 4 in individual drop heat transfer compared to pure conduction case was obtained for large drops. They also showed that the mass flow through the liquid–vapor interface is the dominant factor responsible of the strong convection. The critical radius where convection starts to have a significant influence on droplet growth was then determined for different subcooling temperatures and contact angles. The criterion chosen to define this critical radius was a difference in the heat transfer rate greater than $5\%$ compared to the pure conduction hypothesis. For contact angles from $\theta _{adv} =90^\circ$ to $\theta _{adv} =140^\circ$ and sub-cooling between 1 and $7 ^\circ$ C, the critical radius ranges from 0.5 to 20 $\upmu$m. Droplets have smaller critical radii under larger subcooling temperature or larger contact angle.

Moreover, no model are yet available taking into account the thermal conduction into the substrate and the direct heat transfers between the vapor and the substrate. However, taking them into account could lead to non-negligible modifications of both the temperature field near the droplet and the heat flux at/near the triple line. This point remains to be analyzed more deeply in future works.

It is now clear that simple models that lead to explicit and tractable expressions of drop growth rates are probably oversimplified and may present bias or give unrealistic growth rate values. On the other hand, comprehensive models, even if they are convenient for the detailed study of a single drop, have not yet allow to generate simple expressions of heat and mass transfers at drop scale.

4.1.1.3 The Interactions with Other Drops

As they grow or if they move, the drops interact with many other drops and merge with them. The coalescence of two drops begins when they come into contact, the point of contact being located on the substrate, in the triple line region, for hydrophilic cases, while it is at a given height for hydrophobic configurations. Calling $d_{ij}$ the minimum distance between liquid–vapor interfaces of drop i and drop j, the contact criterion can be written as follows for hydrophilic and hydrophobic surfaces, respectively:

$$\begin{aligned} d_{ij} - (r_i+r_j)\sin \theta _{adv} \le 0 \end{aligned}$$

(4.16)

$$\begin{aligned} d_{ij}-\sqrt{(r_i+r_j)^{2}-(r_i-r_j)^2\cos ^2\theta _{adv}} \le 0 \end{aligned}$$

(4.17)

Generally, the drop-size distribution covers about 7 orders of magnitude, namely from a few nanometers to several centimeters. So, coalescence events imply mostly drops of very different radii and thus, huge differences in volume (volume distribution can be spread on more than 20 orders of magnitude). For sake of simplicity, let us consider first the coalescence of two identical drops. The two drop surfaces touch each other at the contact point and a liquid bridge forms. The surface enclosing this bridge is curved differently than the remaining of the drops surface: in the liquid bridge zone, the surface tension force differs and the liquid starts to move toward the contact zone resulting in the growth of the liquid bridge and leading eventually to an elongated ellipsoidal shape of the resulting drop. This latter will then progressively return to a spherical cap shape in absence of external forces or for small enough drops. Three main forces drive the liquid behavior and thus the coalescence duration:

• The interfacial tension force that induces liquid pressure gradients and thus liquid movement such as minimizing the interfacial area, regularizing the curvature and accommodating static or dynamic contact angle constraints;

• The viscous force that impedes fluid flow;

• Inertia force that limits fluid accelerations.

The two latter effects act as damping factor and thus limit the fluid displacement. As the main driving force acts on drop interface, it is thus expected, as it has been experimentally observed [5, 10], that the center of mass of the resulting drop will be located at the center of mass of the parent droplets.

In the case of an asymmetric coalescence event between two droplets of different radii, an additional effect takes place. Indeed, the internal pressure in the two drops are different. As the liquid pressure varies like the inverse of the radius, it is higher when the drop is small. The more the drop-size ratio is significant, the more the movement of the fluid could be qualitatively described as the liquid contained in the smallest drop is “injected” into the largest one. In other words, momentum conservation associated with the surface tension force leads the smallest drop to move toward the mass center of the big one.

Most of the existing dropwise condensation models consider instantaneous coalescence events although coalescence is a temporal phenomenon whose duration depends on the size of both the parent drops, the coalescence time being longer when the drops are large and close in size. Recently, numerical simulations of coalescence events by a VOF method were carried out by Adhikari [3] in order to analyze the validity of the quasi-instantaneous coalescence hypothesis, with particular attention on the impact of this hypothesis on heat transfers. The author identified two mechanisms that impact heat transfers: a direct mechanism linked to the stabilization time of the drop following coalescence and an indirect mechanism linked to the oscillation of the foot of the resulting drop on the surface, causing cleaning of the area close to the drop (and thus modifying the heat transfers). Taking these two mechanisms into account leads to a 15–20% increase in heat transfer compared to the instantaneous coalescence model in the most unfavorable case tested (i.e., coalescence between two large drops). Thus, it could be necessary to take into account the effect of the transient phase of the coalescence on the heat transfers if the number of coalescence events between large drops is high.

4.1.1.4 The Drop’s Departure

The critical radius $r_{\max }$ beyond which drops start to move on the surface is an essential parameter, which drives the global heat transfers during condensation in dropwise regime (see next section), as well as the critical heat flux leading to the transition from dropwise to filmwise regime. The drops are pinned on the surface by the force at the triple line. The critical radius $r_{\max }$ is the radius at which another force unbalance this pinning force.

Several forces can displace the drops, the most common ones being the gravity and the shear stress. Rose [38] in 1988 proposed a simple correlation based on capillary length to evaluate $r_{\max }$ for droplet in a gravity field:

$$\begin{aligned} r_{\max }=K\sqrt{\frac{\sigma _{lv}}{\rho _l g}} \end{aligned}$$

(4.18)

where K is equal to 0.4 for steam condensation on a vertical flat plate.

Taking into account the contact angle hysteresis and considering that the triple line is an ellipse, the formulation of the equivalent critical radius for a single drop on a vertical plane is expressed as follows [21]:

$$\begin{aligned} r_{\max }=\sqrt{\frac{6\,c\,(\cos {\theta _{rec}}-\cos {\theta _{adv}})\sin {\theta }}{\pi (2-3\cos {\theta +\cos ^3\theta })}\frac{\sigma _{lv}}{\rho _l g}} \end{aligned}$$

(4.19)

where c is a constant that depends on the shape of the drop and the inclination of the substrate surface. Different values of c were then proposed by several authors, as reported in Table 4.1. $\beta$ in the work of Extrand and Kumagai [17] represents the length to width ratio of the substrate area wetted by the drop, derived from the assumption that the contact line is an ellipse and experimentally validated on several fluid–substrate couples.

Thus, in order to reduce this radius of departure $(\cos {\theta _r}-\cos {\theta _{adv}})$ must be as small as possible. So far, in literature, the smallest values of $r_{\max }$ have been obtained on superhydrophobic surfaces.

Table 4.1 Values of the constant c in Eq. 4.19 according to different authors

When gravity force is too small or does not exist as it is the case for instance in horizontal configuration or in space applications, a wettability gradient on the surface can be used to create an additional driving force. In the case of a 1D wettability gradient in the $\mathbf {x}$ direction, Mancio Reis et al. [27] established the following relation allowing to correlate the driving force to the contact angle hysteresis:

$$\begin{aligned} F_{\theta }(x_{G},t)=\frac{\sigma _{lv}R(x_{G},t)\pi }{2}[\cos \theta _{adv}(x_G+R(x_{G},t))-\cos \theta _{rec}(x_G-R(x_{G},t))] \end{aligned}$$

(4.20)

where $x_{G}$ is the position of the center of mass of the drop and R is the footprint radius. The drop is then set in motion when the footprint radius satisfies $F_{\theta } > 0$.

The use of a wettability gradient to displace a drop has been successfully realized in several studies [25, 26, 32] for drops radius down to 1 mm. Nevertheless several limitations can be highlighted:

• The length of displacement is limited to a few times the footprint diameter of the drops when the contact angle hysteresis is not weak;

• The coating used to obtain the wettability gradient usually exhibits a limited lifetime.

Shear stress on the drop liquid–vapor interface induced by an imposed gas flow is another way to decrease the critical departure radius. Among the pioneering work, one can cite the ones of Tanner et al. [48] and O’Bara et al. [33] who observed significant enhancement of the heat transfer along with an early removal of the drops according to the increase of the vapor velocity. However, O’Bara et al. [33] also shown that high velocities can also change the drop shape and flatten them leading to the reduction of the heat transfer coefficient due to the increase of the surface covered by these big drops.

Over time, several studies on the effect of vapor velocity [11,12,13, 49] have been carried out using various substrates and producing different conclusions. Although it is well accepted that increasing the vapor velocity reduces the departure radius (inducing, most of the time, an improvement in the heat transfer), the extent of the improvement and the dependence of this improvement to the steam velocity remain unclear. It is very difficult to rigorously compare these studies as the drag force depends on the velocity profile in the vicinity of the drops which is usually not measured directly, the usual measured data being flow rate or punctual readings in a cross section. Tancon et al. [47], recently proposed a neat evaluation of the effect of the vapor velocity on the departure radius of the droplets. The experiment were conducted with pure steam, on a vertical sol-gel-coated aluminum substrate leading to an advancing contact angle of around $87$ $^\circ$. The vapor average velocity ranged from 2.7 to 11 m s$^{-1}$ along with the centimetric dimension of the test channels led to turbulent regime. The drag force acting on the drop was classically expressed as the product between the fluid kinetic energy, the drop frontal area and the drag coefficient $C_d$:

$$\begin{aligned} F_d=\frac{1}{2}\rho _v v_v^2 C_d\left( \theta _e-\sin {\theta _e} \cos {\theta _e} \right) r^2 \end{aligned}$$

(4.21)

where $\theta _e=\cos ^{-1}\left( 0.5\cos {\theta _{adv}}+0.5\cos {\theta _{rec}}\right)$ (in radian) and $v_v$ the mean vapor velocity in the cross section.

The drag coefficient $C_d$ of the droplet was obtained from a fit of the data generated using CFD calculations of the flow in the channel for low Reynolds numbers (i.e., in the range 100–1000) in turbulent regime. The expression of $C_d$ was then:

$$\begin{aligned} C_d=5.6053 \left[ \left( L_c/l_{dr} \right) ^{-4/3} Re_{dr}^{-1/6}\right] +0.1754 \end{aligned}$$

(4.22)

where $L_c/l_{dr}$ is the ratio between channel height and droplet height and $Re_{dr}=l_{dr} v_v \rho _v/ \mu _v$. Eq. 4.22 is in agreement with Brown–Lawler equation [6].

Then the balance between gravity force, adhesion force, and drag force allow to express the drop departing radius:

$$\begin{aligned} r_{\max }=\frac{-C+\sqrt{C^2+4AB}}{2B} \end{aligned}$$

(4.23)

with

$$\begin{aligned} A=2c\sigma _{lv} \sin {\theta _e}\left( \cos {\theta _{rec}}-\cos {\theta _{adv}}\right) \end{aligned}$$

(4.24)

$$\begin{aligned} B=\frac{2-3\cos {\theta _e}+\cos ^3{\theta _e}}{3}\pi \rho _l g \end{aligned}$$

(4.25)

$$\begin{aligned} C=\frac{1}{2}\rho _v v_v^2 C_d\left( \theta _e-\sin {\theta _e} \cos {\theta _e} \right) \end{aligned}$$

(4.26)

This mechanical force balance has been validated with direct visualization results. The authors show that for a velocity of 11 m s$^{-1}$ the drag force has the same magnitude as gravity and allows a reduction of the drop departure radius of more than $33\%$

4.1.2 Drops Population Models

The drop population on a substrate is usually described in term of drop-size (mostly the curvature radius) distribution. Several difficulties can then be highlighted to model this drop-size distribution.

• The first one is the huge number of droplets that have to be considered. Indeed, the nucleation sites density is in the order of $10^9$–$10^{15}$ m$^{-2}$. Even if these nucleation sites are not all active simultaneously, the total number of drops per unit of substrate area is expected to be very high.

• The second main difficulty is that the radii of the drops vary on several orders of magnitude, typically from $10^{-8}$ to $10^{-2}$ m.

• The third difficulty is the dynamic nature of the drops life and the very small timescales associated (e.g., interface displacement, sweeping, heat diffusion...) in the range $10^{-9}$–$10^{0}$ s.

Indeed, a given nascent drop can collide with a big one during the first coalescence event and thus reach very quickly the critical drop radius leading to its departure (and maybe other coalescence events). By contrast, another nascent drop can coalesce many times with other small drops before the resulting one reaches $r_{\max }$. The resulting drop-size distribution on the substrate is thus a function of each of the drops’ lifecycle. One should note that “drop population” design in fact a “stationary” or “time averaged” distribution. There are 2 possible ways to tackle these classes of problem: (a) use hypothesis to write a macroscale model (e.g., Population Balance Models) then solve it, (b) use a “tracking of events” strategy over an extended period of time then extract macroscale data; the models of such distribution should take into account a large number of events. Furthermore, the modeling is constrained by the multiple time and space scales that should be respected to calculate the considered phenomena. Consequently, direct CFD-like approaches of dropwise condensation are not feasible. On the other hand, a way to model the drop-size distribution on the substrate by considering drops at individual level remains still possible if strong assumptions can be made. Many papers have been published developing such Individual-Based Models (IBM) [8, 23, 30, 43, 45, 54, 56] (sometimes named lagrangian models). In all these works the following main assumptions are made:

• The nucleation sites density is known a priori and nucleation sites are then randomly distributed on the surface;

• The substrate temperature is supposed to be constant and uniform;

• The contact angle is imposed to the advancing contact angle value during all the drop’s growth process;

• If a nucleation site is not covered by a drop, a nucleus instantaneously appears on it;

• The nuclei are formed with a radius $r_{\min }$ corresponding to the unstable equilibrium radius of a drop forming on a cold substrate with an imposed contact angle $\theta$.

• The individual drop grows according Eq. 4.12 between two successive interactions.

• Only binary drop interactions are considered (either due to growth or to sweeping). Nevertheless, cascading coalescences can take place, i.e., several successive coalescence events can be considered during a time step.

• When two drops collide, they coalesce instantaneously to form a new drop located at the center of mass of the two parent drops.

• When the radius of a drop reaches an imposed value $r_{\max }$, this drop is set in motion in a given direction, and then sweeps the surface of the substrate.

Despite these simplifying assumptions, as well as parallel and adapted numerical implementation, the calculation time is usually very important or even prohibitive. Additionally, as the nucleation sites density is rather high and the number of individuals to consider grows like the square of the domain size, IBM approaches are limited in term of domain size and thus in term of maximal drop radius. Moreover, very small drops imply using an extremely small time step (see Fig. 4.3). As the observation time should be long enough to obtain the “stationary” distribution, a compromise should be made between the number of nucleation sites and the determination of the size distribution of the smallest drops. For these reasons, very few data are available in literature on the distribution including drop-size less than one micrometer; moreover no experimental data are available for validation purpose.

So, most of the literature reported data are limited to the distribution of drop of radius greater than a few micrometers. In that case, the calculated distribution can be compared with the one obtained with the reference law developed by Rose and coworkers. Noticing that experimental observations of drop population remains roughly identical whatever the magnification of the camera, and using geometrical argument on how to pack circles on a plane, Le Fevre and Rose [22] correlated the fraction of the substrate area covered by drops to $\left( r/r_{\max }\right) ^{1/\gamma }$, where $\gamma$ is an empirical constant to determine. Few years later, Rose and Glicksman [40] derived an expression of the drop-size distribution for “visible” drops (i.e., drops greater than few micrometers):

$$\begin{aligned} N(r)= \frac{1}{3 \pi r_{\max } r^2}\left( \frac{r}{r_{\max }} \right) ^{-2/3} \end{aligned}$$

(4.27)

All papers reporting results obtained from individual-based modeling highlight a good adequacy with this law for drops greater than 10 $\upmu$m, whatever are the conditions considered in the simulations or the experiments (wettability, subcooling, ...).

As the objective of the modeling is to access to the drop-size distribution, some authors proposed to not follow each individual drop but to write a balance equation directly in terms of drop population density. These statistical type approaches were first used to determine the drop-size distribution of the smallest drops, i.e., smaller than the ones considered in the Rose and Glicksman correlation. This population balance model (PBM) has been proposed by Wen and Jer [52] in 1976 and is widely used in the literature [1, 21, 31, 44, 51]. The common assumptions associated to PBM are:

• The nucleation sites are regularly placed on the substrate and are separated by a distance equal to the average distance derived from the nucleation sites density: $r_e=\frac{1}{\sqrt{4N_s}}$;

• Only the distribution of drops whose size is in the range $r_{\min }<r< r_{e}$ are modeled. This implies that modeled drops do not move from their nucleation sites and do not coalesce with other pinned drops (i.e., they can coalesce with droplets that sweep the substrate).

• The growth of the modeled drops is only due to the condensation of pure vapor.

• The drops may be swept away by the moving drops of radius equal to $r_{\max }$ with a constant renewal characteristic time.

• The distribution function N(r) of Rose and Glicksman (Eq. 4.27) is used for the large drops ($r>r_e$).

Using these hypotheses, a simple balance equation was established to determine the drop-size distribution n(r) according to the drop radius from the following reasoning. Considering a class of drop-size comprised between $r_1$ and $r_2$, at steady state, the balance of the number of individuals belonging this size class is given by Eq. 4.28:

$$\begin{aligned} A\,n(r_1)\,G(r_1)=A\,n(r_2)\,G(r_2) + S\,\bar{n}\, \delta r \end{aligned}$$

(4.28)

The rate of drops entering this class due to the growth by condensation (left-hand side) is equal to the sum of the rate of drops leaving this class because of the condensation (first right-hand side term) plus the rate of drops’ disappearance (second right-hand side term). This latter term is due to the sweeping of the surface by the moving drops of radius above or equal to $r_{\max }$ (see Sect. 4.1.1.4). In Eq. 4.28, A is the condensing surface area, S is the surface renewal rate by moving drops (m$^2$ s$^{-1}$) and $\bar{n}$ is the average of n over the interval $[r_1, r_2]$.

By reducing the width $\delta r$ between $r_1$ and $r_2$ toward zero, the following differential equation is obtained:

$$\begin{aligned} \frac{d(G(r)n(r))}{dr}+\frac{n(r)}{\tau }=0 \end{aligned}$$

(4.29)

where n(r) is the drop-size distribution (defined only for $r_{\min }<r<r_e$) and $\tau =\frac{A}{S}$ is the renewal characteristic time. This latter is defined as the time required by moving drops to sweep the entire surface area. As the sweeping of the surface affects all the drops whatever are their sizes, this renewal characteristic time is supposed to be independent of the drop radius, and thus is constant.

To solve this differential equation, as $\tau$ is unknown, two additional conditions are needed. For that purpose, the continuity of the drop-size distributions N(r) and n(r), corresponding, respectively, to large and small drops, as well as the continuity of their derivatives are imposed at $r=r_e$, the drop-size distribution of Rose and Glicksman (Eq. 4.27) being used for the large drops:

$$\begin{aligned} n(r_e)=N(r_e)=\frac{1}{3 \pi r_{\max } r_e^2}\left( \frac{r_e}{r_{\max }} \right) ^{-2/3} \end{aligned}$$

(4.30)

$$\begin{aligned} \left( \frac{d\log n(r)}{d\log r}\right) _{r=r_e}=\left( \frac{d\log N(r)}{d\log r}\right) _{r=r_e} = -\frac{8}{3} \end{aligned}$$

(4.31)

Using Eq. 4.12 for the growth rate G(r), along with the associated $A_1$, $A_2$ and $A_3$ constant expressions (Eqs. 4.13–4.15), the resolution of Eq. 4.29 leads to the following expression of the drop-size distribution n(r):

$$\begin{aligned} n(r) = N(r_{e})\frac{G(r_{e})}{G(r)} {{\,\mathrm{e}\,}}^{B(r)+ C(r)} \end{aligned}$$

(4.32)

with:

$$\begin{aligned} B(r)= & {} \frac{A_{2}}{\tau A_{1}}\left[ \frac{r_{e}^{2}-r^{2}}{2}+r_{\min }(r_{e}-r)-r_{\min }^{2}\ln \left( \frac{r_{e}-r_{\min }}{r-r_{\min }}\right) \right] \end{aligned}$$

(4.33)

$$\begin{aligned} C(r)= & {} \frac{A_{3}}{\tau A_{1}}\left[ (r_{e}-r)-r_{\min }\ln \left( \frac{r_{e}-r_{\min }}{r-r_{\min }}\right) \right] \end{aligned}$$

(4.34)

and with:

$$\begin{aligned} \tau =\frac{3 r_e^2(A_2\,r_e + A_3)^2}{A_1(11\,A_2\,r_e^2-14\,A_2\,r_e\,r_{\min }+8\,A_3\,r_e-11\,A_3\,r_{\min })} \end{aligned}$$

(4.35)

It is noteworthy to compare the IBM and PBM. IBM relies on tracking individual drops over space and time until a global stationary state is reached; then the drop-size distribution can be derived by post-processing the results. On the other hand, PBM is based on the a priori construction of a model of drops population and its resolution. However, both models consider the same modeling of the heat transfers through a single droplet (see Sect. 4.1.1.2) and use several other common hypotheses. Indeed, in both approaches:

• The substrate temperature is supposed to be constant and uniform;

• The drops nucleate with a radius $r_{\min }$ and grow with an imposed contact angle (advancing contact angle) during condensation process;

• The drops grow at a rate given by a simplified drop energy balance (e.g., Eq. 4.12) between two successive coalescences;

• When the radius of a drop reaches a given value $r_{\max }$, this drop is set in motion in a given direction, and then sweeps the surface of the substrate.

It is noteworthy to review also the main differences between IBM and PBM:

• IBM use the same mechanisms for all drops, while PBM is constructed by juxtaposing n(r) up to $r_e$ and N(r) above and up to $r_{\max }$, these two latter distributions being obtained from completely different frameworks;

• While drops of any sizes may coalesce in IBM either with a neighboring drop pinned on the surface or with a moving one, the PBM approach prohibits coalescence for the drops of radius smaller than $r_e$ (these ones can interact only with moving drops of radius $r_{\max }$).

The results obtained with both approaches are compared in the following section. Analyses of the effect of some of the assumptions made on the drops life cycle are also proposed for both the drop-size distribution and the heat transfers.

4.2 Drop-Size Distribution According to Individual-Based and Population-Based Models

As already pointed out, IBM and PBM are used to calculate the drop-size distribution. As experimental drop-size distribution for the smallest droplets are not yet available, only cross comparisons are possible. To compare the results obtained using both IBM and PBM, it is mandatory to use configurations as close as possible. Thus, a PBM and a IBM [23] were implemented using the classical assumptions described in previous Sect. 4.1.2 with a specific care taken to limit as much as possible the differences between the two simulated configurations. Thus, for both IBM and PBM, the following assumptions have been used:

• The wall substrate is isothermal;

• The gas phase is constituted by pure vapor at atmospheric pressure;

• The drops form with a radius $r_{\min }$ calculated from Eq. 4.1;

• The nucleation sites density value $N_s$ is set (we emphasize that fixing $N_s$ is equivalent to impose the average distance $2 r_e$ between 2 neighboring nucleation sites);

• For IBM calculations the nucleation sites are randomly distributed with respect to this average value;

• The drop growth model used is the one described in Sect. 4.1.1.2.

Note that one of the mains drawback of IBM is the computation time. Indeed, the necessity of simulating large substrate area to get a sufficient sampling of the biggest drops together with the high value of nucleation sites density lead to a very high number of drops to simulate. Moreover, these drops interact with each other at a very high frequency. So, the time step used in the simulation has to be as small as possible to take into account all coalescence events. Finally, the simulation should be continued until a global stationary regime is obtained.

Fig. 4.5

Comparison of drop-size distributions obtained from both models ($\theta _{adv} =85^\circ$, $\Delta T=1$ K, $T_{sat}=373$ K, $\delta _{coat}=100$ nm, $\mathrm {k}_{coat}=2$ Wm$^{-1}$K$^{-1}$ and $h^i=15.7$ MW m$^{-2}$ K$^{-1}$)

Most of the studies available in the literature consider relatively high maximum radii of the drops (and so large surfaces) in order to compare numerical results with experimental ones. In consequence, the time step $\delta t$ is generally set to a relatively high value and the distribution of the smallest drop-sizes cannot be determined. As the aim is to compare our IBM approach to the PBM one, it is mandatory to use a time step small enough to capture all coalescence events for drops of size as small as $r_{\min }$. At the end of each time step, the next coalescence event is located and the time step is adjusted accordingly; thus all coalescence events are taken into account. However, to keep the computation time reasonable, a minimum value of $\delta t$ is imposed, typically $\delta t_{\min } = 10^{-5}$ s (see [23] for details).

Some differences cannot be bridged between the used IBM and PBM. For instance, the nucleation sites density is the same for both models but for IBM the site are randomly placed to obtain an homogeneous distribution of the distance between two neighboring sites while they are equally spaced for PBM. It can be also noticed that in the IBM, when a drop reaches the radius $r_{\max }$, it is set in motion on the surface at an imposed velocity in a given direction and interacts with other drops until it leaves the modeled domain.

We defined and set a reference case that is suitable for quantitative comparisons between IBM and PBM while maintaining an acceptable computation time (i.e., few days on a simple workstation using a standard Matlab^® code). The computational domain is a square of edge 340 $\upmu$m with 2025 nucleation sites (leading to a nucleation sites density $N_s=1.56 \times 10^{10}$ m$^{-2}$). The advancing contact angle is $\theta _{adv}=85^\circ$ and the subcooling is $\Delta T=1$ K. As the fluid considered is pure water, the condensation coefficient is set to $f=1$. Typical value of coating parameters are arbitrarily imposed, i.e., a thermal conductivity $\mathrm {k}_{coat}=2$ W m$^{-1}$ K$^{-1}$ and a thickness $\delta _{coat}=100$ nm. The maximum drop radius is set to $r_{\max }=65$ $\upmu$m and the velocity of the drops that sweep the surface is fixed at 0.01 ms$^{-1}$.

First, the reproducibility of the IBM results has been checked, as well as their independence to the numerical parameter $\delta t_{\min }$ and the total number of initial nucleation sites $N_{ns}$ (at constant nucleation sites density) [23]. A video showing the behavior of the calculated drops on the surface can be seen on Youtube.¹ It can be noticed that the number of coalescence events is very large, in the order of one million per second, although the modeled domain is limited.

The drop-size distribution obtained from both approaches are reported on Fig. 4.5. It can be pointed out that for the biggest drops (radius greater than 10 $\upmu$m), the IBM results are consistent with the Rose and Glicksman law (Eq. 4.27) that has been experimentally validated many times. This confirms the relevance of the IBM approach, even if it does not ensure that the calculated distribution of the small drops is right.

Below 10 $\upmu$m, the 2 models start to disagree. Overall, the differences between the 2 distributions increase by going towards the small radii and reach more than one order of magnitude for r around hundred nanometers. The IBM exhibits 3 different behaviors. For the smallest drops (below one micron), the drops-size distribution follows a power law with a weak absolute value of the exponent ($-\frac{1}{3}$). Indeed, such very small drops may coalesce only with rather big or moving ones and those events are not very frequent. So, they grow mainly by vapor condensation . For the drops greater than 10 $\upmu$m, the drop-size distribution is almost identical to the one predicted by the Rose and Glicksman law which involves both mechanisms of growing (i.e., coalescence and condensation). However a weak difference can be highlighted in the slopes: −2.4 for IBM while Rose and Glicksman gives $-\frac{8}{3}$ (see Eq. 4.31). Finally, between these sizes, the contribution of the coalescence in the growth dynamic increases progressively and the transition from one driving process of growing to the other is progressive.

Between $r_{\min }$ and $r_e$, PBM results exhibit a N-shaped curve with one maximum at $r_{\min }$ and the other slightly below $r_e$. The IBM gives clearly different results than PBM for drop radius less than $r_e$. This latter approach (Eq. 4.29) assumes a constant renewal characteristic time whatever the drop-size, that only depends of the sweeping rate by the moving drops. This hypothesis seems to be the main reason which can explain the discrepancies between the 2 models. Indeed, this constant value of $\tau$ implies that the small drops ($r<r_e$) do only coalesce with the ones that sweep the surface. But one can reasonably expects that even 2 small drops can coalesce if the distance between their respective nucleation sites is less than $2 r_e$. Also this drop may also coalesce with a second one (small or not) that has already coalesced and is thus no more centered on its nucleation site. So, the second drop could be very close to the first (small) drop.

Using Eq. 4.29, the renewal characteristic time $\tau$ was calculated according to the drop radius r from the IBM results (Fig. 4.6). The value of $\tau$ obtained from Eq. 4.35 is also reported in its definition domain (i.e., from $r_{\min }$ to $r_e$). As it can be seen on the figure, the renewal characteristic time calculated from the IBM results increases from $10^{-4}s$ for the smallest droplets to about $10^{-2}$ s at $r=r_e$, and to more than 1s for the biggest drops. According to Eq. 4.35, as illustrated, $\tau$ should be about $10^{-2}$ s for all drops of radius less than $r_e$. So, taking into account the coalescences of small drops (lower than $r_e$) leads to a smaller renewal characteristic time $\tau$. The difference is important and goes up to 2 orders of magnitude for the smallest drop-sizes.

Fig. 4.6

Global renewal characteristic time obtained from both models ($\theta _{adv} =85^\circ$, $\Delta T=1$ K, $T_{sat}=373$ K, $\delta _{coat}=100$ nm, $\mathrm {k}_{coat}=2$ W m$^{-1}$ K$^{-1}$ and $h^i=15.7$ MW m$^{-2}$ K$^{-1}$)

To continue this analysis and better understand the role of coalescence on the small drops renewal characteristic time, the disappearing term $\frac{n}{\tau }$ in Eq. 4.29 is broken down into two terms according to the involved mechanism. The differential equation which governs the drop-size distribution is rewriten as:

$$\begin{aligned} \frac{d(G(r)n(r))}{dr}+n(r)\left[ \frac{1}{\tau _c (r)}+\frac{1}{\tau _{sw}(r)}\right] =0 \end{aligned}$$

(4.36)

where the renewal characteristic times $\tau _{c}$ and $\tau _{sw}$ related to drop radius r are associated to coalescence events between pinned drops (called “coalescence” in the next §) and to the sweeping loss, i.e., coalescence events between a pinned drop and a moving drop (called “sweeping” in the next §), respectively. These 2 characteristic times were derived from the IBM simulation as we have counted separately the coalescence and sweeping events for each drop-size. When a global stationary regime is reached, the rate of disappearance (or appearance) due to coalescence or sweeping are extracted. Each characteristic time is then simply the ratio between the number of individuals in the considered size-class and this rate of disappearance. The variations of these different characteristic times with respect to the drops radius are reported on Fig. 4.7.

Except for the largest drops, the coalescence characteristic time $\tau _{c}$ is largely smaller than the sweeping one $\tau _{sw}$. This indicates that the coalescence events are much more frequent than the sweeping ones. This is particularly true for small drops. Moreover, the global renewal characteristic time $\tau$ (Fig. 4.6) calculated using Eq. 4.29 is almost identical to the coalescence characteristic time $\tau _c$ (Fig. 4.7). Such a behavior shows that the sweeping is very often negligible in the drops renewal rate, except for the biggest drops (i.e., $r>20$ $\upmu$m). For example, the drop population in the class around 1$\mu m$ is renewed with a characteristic time $\tau _c$ of $10^{-3}$ s while it is about 0.1 s for $\tau _{sw}$. Thus the drops are renewed only one times due to the sweeping when they are renewed one hundred of times due to the coalescence events. The assumption that small droplets do not coalesce in the PBM appears therefore not acceptable in that case.

Fig. 4.7

Characteristic times of coalescence and sweeping obtained thanks to the IBM numerical results as a function of the drop radius ($\theta _{adv}=85^\circ$, $\Delta T=1$ K, $T_{sat}=373$ K, $\delta _{coat}=100$ nm, $\mathrm {k}_{coat}=2$ W m$^{-1}$ K$^{-1}$ and $h^i=15.7$ MW m$^{-2}$ K$^{-1}$)

The influence of the surface wettability on the renewal characteristic time $\tau$ is reported on Fig. 4.8 according to the drop radius. Whatever the advancing contact angle in the range $[45^\circ ;140^\circ ]$, the conclusion made previously about the great importance of coalescence events in the small drops-size distribution remains valid. Indeed, the renewal characteristic time grows by several orders of magnitude when the drops radius is increased from $r_{\min }$ to $r_{\max }$. A vertical shift of the curves is observed with respect to the wettability: more the surface is hydrophilic, more the renewal characteristic time is weak. This is due to the growth dynamics of each single droplet which is faster when the contact angle is small (Fig. 4.3). As a consequence, the frequency of interaction between the drops is greater. In any case, the effect of the sweeping is always negligible, except for the drops of radius close to $r_{\max }$.

Fig. 4.8

Global and sweeping renewal characteristic times obtained for different contact angles as a function of the drop radius ($\Delta T=1$ K, $T_{sat}=373$ K, $\delta _{coat}=100$ nm, $\mathrm {k}_{coat}=2$ W m$^{-1}$ K$^{-1}$ and $h^i=15.7$ MW m$^{-2}$ K$^{-1}$)

So, the 2 approaches allowing to determine the drop-size distribution conduct to differences in the results up to several orders of magnitude, especially for the distribution of the smallest drop radii. These differences can be explained by the use of a constant renewal characteristic time whatever is the drop radius in the PBM. In the following, the influence of the differences between the drop-size distributions obtained with IBM and PBM on the global heat transfer prediction is quantified and analyzed.

4.3 Heat Transfer

4.3.1 Heat Flux Distribution According to Drop-size

From any given drop-size distribution $\bullet (r)$ together with the model of heat transfer through a single droplet described in Sect. 4.1.1.2, it is possible to calculate the heat flux ($\frac{W}{m^2}$) associated to any radius range $[r_1,r_2]$:

$$\begin{aligned} q(r_1,r_2)=\int _{r_{1}}^{r_{2}} \bullet (r)Q_d(r) \, \mathrm {d}r \end{aligned}$$

(4.37)

When related to IBM, $\bullet (r)$ is simply n(r) while with PBM $\bullet (r)$ is a piecewise function: n(r) (Eq. 4.32) below $r_e$ and N(r) (Eq. 4.27) above. For instance, the global heat flux can then be determined by:

$$\begin{aligned} q=\int _{r_{\min }}^{r_{\max }} n(r)Q_d(r)\ dr \text { for IBM} \end{aligned}$$

(4.38)

$$\begin{aligned} q=\int _{r_{\min }}^{r_{e}} n(r)Q_d(r)\ dr + \int _{r_{e}}^{r_{\max }} N(r)Q_d(r)\ dr \text { for PBM} \end{aligned}$$

(4.39)

Fig. 4.9

Heat flux distribution according to r obtained thanks to the 2 different approaches ($\theta _{adv} =85^\circ$, $r_e=4$ $\upmu$m, $r_{\max }=65$ $\upmu$m, $\Delta T=1$ K, $T_{sat}=373$ K, $\delta _{coat}=100$ nm, $\mathrm {k}_{coat}=2$ W m$^{-1}$ K$^{-1}$ and $h^i=15.7$ MW m$^{-2}$ K$^{-1}$)

Fig. 4.10

Comparaison of the the heat flux $q(r_{\min },r)$ obtained by the 2 different approaches ($\theta _{adv} =85^\circ$, $r_e=4$ $\upmu$m, $r_{\max }=65$ $\upmu$m, $\Delta T=1$ K, $T_{sat}=373$ K, $\delta _{coat}=100$ nm, $\mathrm {k}_{coat}=2$ W m$^{-1}$ K$^{-1}$ and $h^i=15.7$ MW m$^{-2}$ K$^{-1}$)

The impact of drop-size distribution on heat flux variation according to drop radius can then be analyzed. As the drop-size distributions obtained using IBM and PBM clearly differ, particularly for the small radii (see Sect. 4.2), significant differences in terms of heat flux are expected. The heat flux associated to each drop radii were computed and results are reported on Fig. 4.9. The frontier between “small” and “large” drops (according to PBM) is represented by the dashed line. The curves behavior is fairly similar, but, as it was expected, an important discrepancy between the 2 approaches for the “small” drops and a relatively good agreement for the “large” drops can be observed.

The contribution of each of the drops’ family (i.e., small drops and large drops) to the global heat flux can be determined by integrating from $r_{\min }$ to r (with r varying from $r_{\min }$ to $r_{\max }$) the curves represented on Fig. 4.9 using Eq. 4.37. We obtain the cumulatives of the heat flux reported on Fig. 4.10. It can be highlighted that in the considered configuration both models predict that the heat flux is mainly evacuated by drops between 1 and 10 $\upmu$m ($70\%$ for the PBM and $60\%$ for the IBM). However, in this drop radius range, the 2 curves plotted on Fig. 4.9, although they both present a maximum in this range, differ significantly: the PBM curve presents a more sharp shape than the IBM one which is more smooth and below the PBM curve. Thus, as these differences lead to important changes on the cumulative heat fluxes (Fig. 4.10), it appears particularly important to use accurate model of the drop population in this drop-size range in order to predict the global heat flux correctly.

Fig. 4.11

Relative deviation (IBM basis) between the cumulative heat fluxes (PBM approach minus IBM one) as a function of drop radius ($\theta _{adv} =85^\circ$, $r_e=4$ $\upmu$m, $r_{\max }=65$ $\upmu$m, $\Delta T=1$ K, $T_{sat}=373$ K, $\delta _{coat}=100$ nm, $\mathrm {k}_{coat}=2$ W m$^{-1}$ K$^{-1}$ and $h^i=15.7$ MW m$^{-2}$ K$^{-1}$)

To go further in the analysis of the effect of the difference between the IBM and PBM drop-size distributions, we calculated the relative deviation between the cumulative heat flux obtained by both approaches. The results are reported on Fig. 4.11. For the small drops, the relative deviation reaches more than −85% for $r \approx 0.1 \upmu$m. This means that for drops below this size, IBM predicts heat flux much higher than PBM. Fortunately, in the considered configuration, these drop-sizes have a relatively low contribution to the total heat flux.

Between approximately $r=1$ $\upmu$m and $r=r_e$, the relative deviation varies sharply because (i) the PBM predicts higher population in the drop classes close to $r_e$ (see Fig. 4.5) and (ii) because these drop classes are those that mainly contribute to the global heat flux (see Fig. 4.9 and/or Fig. 4.10).

Above $r_e$, the relative deviation decreases as the slopes of drop population distributions differ (i.e., $-\frac{8}{3}$ for PBM (Eq. 4.31) and $-2.4$ for IBM). It reaches a value of about 34% when all drop-sizes have been considered (i.e., $q=121.4$ kW m$^{-2}$ for PBM and $q=90.6$ kW m$^{-2}$ for IBM). This value remains relatively low because of compensations between the different drop-size zones. Indeed, it can be observed that the relative difference varies from −85% up to 70% to finally end at 34%. Compared to IBM, PBM strongly overestimates the contribution to the global heat flux of the drops included in the interval [0.1 $\upmu$m, $r_e$] and clearly underestimates this contribution when considering the drops below or above this radius interval.

From these results, several conclusions can be made:

• The 2 approaches are overall disagreeing to each other, especially for the “small” drops. The overall relative deviation in the global heat flux is non-negligible, even if it remains relatively moderate (i.e., 34%) for the considered configuration;

• This moderate global deviation is due to compensations between the different drop-size zones, the “local” deviation being much more important;

• Both approaches predict that the majority of the heat flux is evacuated by drops having a radius close to $r_e$.

4.3.2 Parametric Analysis

In order to go further in the analysis, the influence of 3 main parameters (i.e., the ones that could a priori be adjusted experimentally) has been determined: advancing contact angle $\theta _{adv}$, nucleation sites density $N_s$ and maximum drop radius $r_{\max }$.

The variations of the heat flux obtained thanks to both approaches as a function of the advancing contact angle are reported on Fig. 4.12. Both IBM and PBM predict that decreasing $\theta _{adv}$ leads to a strong increase of the heat flux. For instance, the heat flux value is approximately 3 times higher for $\theta _{adv}=45^\circ$ than for $\theta _{adv}=140^\circ$.

For a given drop radius, the drop volume (and thus the thickness of the liquid layer) is much lower in hydrophilic configuration. As a consequence, the thermal resistance by conduction within the liquid is lower, and the heat flux is thus higher. Note that here, $\theta _{adv}$ and $r_{\max }$ are decoupled and $r_{\max }$ is held constant, which is generally not the case in experiments (see Sect. 4.1.1.4). The differences between PBM and IBM results are found to be significants for $\theta _{adv}$ varying from 60$^\circ$ to 110$^\circ$, with a maximum deviation of about 35%.

Fig. 4.12

Variations of heat fluxes versus advancing contact angle—IBM/PBM comparison. ($r_e=4$ $\upmu$m, $r_{\max }=65$ $\upmu$m, $\Delta T=1$ K, $T_{sat}=373$ K, $\delta _{coat}=100$ nm, $\mathrm {k}_{coat}=2$ W m$^{-1}$ K$^{-1}$ and $h^i=15.7$ MW m$^{-2}$ K$^{-1}$)

Fig. 4.13

Contribution of small droplets to the global heat flux in function of the advancing contact angle—IBM/PBM comparison. ($r_e=4$ $\upmu$m, $r_{\max }=65$ $\upmu$m, $\Delta T=1$ K, $T_{sat}=373$ K, $\delta _{coat}=100$ nm, $\mathrm {k}_{coat}=2$ W m$^{-1}$ K$^{-1}$ and $h^i=15.7$ MW m$^{-2}$ K$^{-1}$)

As pointed out previously, the 2 approaches are mainly in disagreement for the size distribution of the small drops. So, an analysis of the contribution of these small drops to the total heat flux has been conducted for the 2 approaches. The results are reported on Fig. 4.13. PBM predicts that, despite a global heat flux that varies by a factor 3 (see Fig. 4.12), the contribution of the small drops remains constant at about 37% of the total heat flux for any advancing contact angle $\theta _{adv}$. On the other hand, IBM approach shows an increase of the contribution of the small drops with the contact angle (from 20% for $\theta _{adv} = 45 ^\circ$ to almost 45% for $\theta _{adv} = 140 ^\circ$). So, in hydrophilic situation the global heat flux is high but the contribution of small droplets is low. In hydrophobic situation it is the contrary: the global heat flux is low and the contribution of the small drops is much higher. As a result, the heat flux evacuated by the small droplets is higher for low contact angles (i.e., $\theta _{adv}<90 ^\circ$) than for high contact angles (i.e., $\theta _{adv}>90 ^\circ$).

In order to better quantify the deviation between the contributions of the small drops to the total heat flux obtained with the two approaches, the relative deviations of PBM results to IBM results have been determined and are reported on Fig. 4.14. The deviations between the total heat fluxes are also reported on the same figure. As already mentioned, the most important deviation between the global heat fluxes are found at intermediate contact angles (i.e., around $\theta _{adv} = 90 ^\circ$). For small drops, the deviation is large for hydrophilic surfaces (about 70%) and then decreases for hydrophobic surfaces. This remains consistent with the previous results (Fig. 4.13): for hydrophilic surface the contribution of small droplets is weak, so even a great difference between the two approaches leads to a moderate discrepancy between the global heat fluxes. By contrary, for hydrophobic configurations, the contribution of small drops is higher, and thus the two curves on Fig. 4.13 have the same behaviors for $\theta _{adv}>120$ $^\circ$.

To summarize the results of this analysis on the effect of $\theta _{adv}$ on the global heat transfer:

• The highest heat fluxes are obtained for hydrophilic surfaces (about 3 times greater for an advancing contact angle of $45^\circ$ than for a advancing contact angle of $140^\circ$);

• For the considered configuration ($r_{\max } = 65$ $\upmu$m and $N_s = 1.56 \times 10^{10}$ m$^{- 2}$), the contribution of the small droplets remains moderate (i.e., less than 50%) for all contact angles;

• The global deviation between the 2 approaches is the most important for the intermediate contact angles (around $90^\circ$). For small drops, the deviation is particularly important when the contact angle is weak.

Fig. 4.14

Relative deviation (IBM basis) between the global heat fluxes as well as the contribution of small drops in function of the advancing contact angle ($r_e=4$ $\upmu$m, $r_{\max }=65$ $\upmu$m, $\Delta T=1$ K, $T_{sat}=373$ K, $\delta _{coat}=100$ nm, $\mathrm {k}_{coat}=2$ W m$^{-1}$ K$^{-1}$ and $h^i=15.7$ MW m$^{-2}$ K$^{-1}$)

The other parameters on which it is possible a priori to act experimentally are the maximum drop radius (by imposing for instance an external force) and the density of nucleation sites (by realizing micro or nano structures on the surface). The respective deviations between the heat fluxes, as well as between the contributions of small droplets to these heat fluxes, obtained with population balance approach to the ones obtained with individual-based approach are reported on Figs. 4.15 and 4.16. The deviations increase when $r_{\max }$ and $N_s$ increase, with a slight nuance for the $r_{\max }$ parameter where the overall deviation reaches an asymptotic-like value of about 45% for the global heat flux and 70% for the contribution of small droplets.

Fig. 4.15

Relative deviation (IBM basis) between the global heat fluxes and between the contributions of small drops as a function of the maximum drop radius $r_{\max }$ ($\theta _{adv}=85^\circ$, $r_e=4$ $\upmu$m, $\Delta T=1$ K, $T_{sat}=373$ K, $\delta _{coat}=100$ nm, $\mathrm {k}_{coat}=2$ W m$^{-1}$ K$^{-1}$ and $h^i=15.7$ MW m$^{-2}$ K$^{-1}$)

Fig. 4.16

Relative deviation (IBM basis) between the global heat fluxes and between the contributions of small drops as a function of the nucleation sites density $N_S$ ($\theta _{adv}=85^\circ$, $r_{\max }=65$ $\upmu$m, $\Delta T=1$ K, $T_{sat}=373$ K, $\delta _{coat}=100$ nm, $\mathrm {k}_{coat}=2$ W m$^{-1}$ K$^{-1}$ and $h^i=15.7$ MW m$^{-2}$ K$^{-1}$)

Fig. 4.17

Variations of heat fluxes versus maximum drop radius $r_{\max }$—IBM/PBM comparison. ($\theta _{adv} = 85^\circ$, $r_e=4$ $\upmu$m, $\Delta T=1$ K, $T_{sat}=373$ K, $\delta _{coat}=100$ nm, $\mathrm {k}_{coat}=2$ W m$^{-1}$ K$^{-1}$ and $h^i=15.7$ MW m$^{-2}$ K$^{-1}$)

Fig. 4.18

Variations of heat fluxes versus nucleation sites density $N_s$—IBM/PBM comparison ($\theta _{adv} = 85^\circ$, $r_{\max }=65$ $\upmu$m, $\Delta T=1$ K, $T_{sat}=373$ K, $\delta _{coat}=100$ nm, $\mathrm {k}_{coat}=2$ W m$^{-1}$ K$^{-1}$ and $h^i=15.7$ MW m$^{-2}$ K$^{-1}$)

Both approaches show that (i) increasing $N_s$ and (ii) decreasing $r_{\max }$ lead to an important increase of the heat flux (Figs. 4.17 and 4.18). In order to maximize the heat transfers, it is therefore interesting to increase $N_s$ and decrease $r_{\max }$ as much as possible. The heat flux enhancement is more pronounced for the smallest values of $r_{\max }$ which may be difficult to obtain experimentally. Finally, the heat flux improvement is more or less constant with the increase of the nucleation sites density: an increase of one order of magnitude of $N_s$ leads to a gain of more than 100% for the heat flux. However, if the decrease of $r_{\max }$ reduces the deviation between the 2 approaches, conversely, the increase of $N_s$ causes an increase in this deviation. Regarding this latter remark, it must be remembered that variations of $N_s$ lead to a modification of the frontier between small and large drops (the frontier being at $r_e = \frac{1}{\sqrt{4N_s}}$). The increase of $N_s$ leads to a smaller contribution of the small drops to the global heat flux, because the drop-sizes that mainly contribute to the heat flux remain around few $\upmu$m (and therefore gradually belong to the class of large drops when $N_s$ is increased).

4.4 Conclusion

Dropwise condensation allows to reach very high heat transfer coefficients, up to several hundred thousand of W m$^{-2}$ K$^{-1}$. Modeling the heat transfer in such a regime implies to predict the drop-size distribution on the surface, with drop radii spread over 6 or 7 orders of magnitude. Moreover, a heat transfer law through each single drop is needed whatever the size of this single drop. For all these reasons, CFD numerical simulations at drop scale of dropwise condensation are prohibited because of calculation time.

From experimental point of view, the drop-size distribution is very difficult to access because of both small characteristic times and huge difference between the radii that must be measured simultaneously. Only the distribution of drops greater than few microns have been measured up to now, well predicted by the correlation of Rose and Glicksman [40].

So, drastically simplified theoretical approaches have been developed to calculate both the heat flux through a single drop and the size distribution of the smallest drops (population balance model). Unfortunately, results given by these theoretical approaches have not yet been validated since no reference data exist.

So, during last decade, with the increase in computing capabilities, individual-based models were developed as an alternative to the population balance model to compute drop-size and heat transfer. The individual-based model consists in following each drop in its life cycle (born, growth, interaction with other drops and departure), making strong simplifying assumptions in order to limit the calculation time. Comparison of individual-based model and population balance model was thus carried out in the present paper, using a common set of assumptions. Important discrepancies have been highlighted in the drop-size distributions that can be critical from heat transfer point of view especially for radii close to half of the mean distance between two nucleation sites. Without prejudging the accuracy of the individual-based approach. The assumption of a renewal characteristic time due only to sweeping and thus independent of drop radius used in the population balance models has been demonstrated to be main cause of discrepancy and thus is questionable to dropwise condensation modelling. Although the important differences in the drop-size distributions, the prediction of the global heat transfer by both approaches can be fairly close, depending of the input parameter set.

Thus, further works are needed to make the dropwise condensation models more reliable and their predictions more accurate in the future, particularly for situations where the improvement of the heat transfer (by increasing the nucleation sites density and/or reducing the departure radius) will make more crucial the role of the smallest drops in the global heat transfer coefficient.