On the Complexity of Predicting Election Outcomes and Estimating Their Robustness

Abstract

When dealing with election data it is reasonable to assume that the votes are incomplete or noisy. The reasons are manifold and range from cost-intensive elicitation to manipulation. We study the problems of evaluating elections with incomplete data and determining the robustness of elections with noisy data from a computational point of view. To capture a wide variety of motivations, we consider three different models for the distribution of preferences: the uniform distribution over the completions of incomplete preferences inspired by the possible winner problem, the dispersion around complete preferences, also called Mallows noise model, and a model in which the distribution over the votes of each voter is explicitly given. We consider both approval vector preferences and linear order preferences and show that the complexity of the problems can vary greatly depending on the voting rule, the distribution model, and the parameterization. We investigate the problems both in terms of counting complexity as well as decision complexity and discuss the effects of the winner model and tie-breaking on the results.

A preliminary version of this work was published as an extended abstract in the proceedings of AAMAS 2020 (see Baumeister and Hogrebe [3]).

1 Introduction

Elections are an integral part of any democracy, be it for the collective decision-making of a whole country or just for any group of people, a sports club or employees of a company. In addition to these classic applications, elections are also considered in connection with software agents and automation. Here, the applications of elections range from multi-agent planning (see, e.g., Ephrati and Rosenschein [16]) and meta-search engines (see, e.g., Dwork et al. [15]) to recommender systems (see, e.g., Ghosh et al. [18]) and email classification (see, e.g., Cohen et al. [11]). In the classic case, we assume that we have perfect knowledge about the preferences of the voters and are able to use a voting rule to determine the rightful winners with respect to the specific rule.

However, in many realistic scenarios, we can not assume that we have perfect information about voter preferences. Nevertheless, a decision must often be made or at least in some way a result of the election must be presented, for example in the form of the winning probabilities considered here. The reasons for imperfect election data are manifold. First, we often cannot assume that the election data we receive is complete. In the case of actual elections, the collection of complete election data is often cost-intensive, complicated, or simply not possible under the given circumstances. The same holds for the creation of election forecasts based on partial data aggregated from social networks or polls, where a complete collection of election data is not appropriate. On the other hand, even if we receive complete election data, in many situations we cannot assume that it has not been corrupted in transmission, by manipulation, or through the elicitation itself. In these situations the question arises how robust and thereby justified a candidate’s victory is if the data has been corrupted to a certain degree.

Therefore, we study the problem of determining the probability that a particular candidate wins an election for a given distribution over the preferences of the voters. Conitzer and Sandholm [12] were the first to study this problem and referred to it as the evaluation problem. The relevance of the problem is immense, as it captures many different, and in particular the previously presented, scenarios, such as the winner determination on incomplete data, the creation of election forecasts, and the examination of the justification or robustness of a candidate’s victory if corruption of the data is possible. To cover those different motivations, we consider three models for the distribution of preferences: the uniform distribution over the completions of incomplete preferences inspired by the possible winner problem, the dispersion around complete preferences, also called Mallows noise model, and a model in which the distribution over the votes of each voter is explicitly given. The basic definitions of formal elections as well as the formal definition of the evaluation problem, the preference distributions, and computational complexity will be introduced in Sect. 2. In Sect. 3, we study the computational complexity of the evaluation problem regarding those distributions and consider both voting rules on approval vector preferences and linear order preferences, namely positional scoring rules. Our results include both hardness results for $\mathrm {\#P}$ as well as polynomial-time algorithms. We show that the complexity of the problem can vary greatly depending on the voting rule, the distribution model, and the parameterization. Especially, we investigate the problem both in terms of counting complexity as well as decision complexity in Sect. 3.4. Finally, we will examine the relation between our and related work in Sect. 4 and discuss our results in Sect. 5.

2 Preliminaries

Formally an election is given by a tuple $E = (C,V)$, with $C = \{c_1, \dots , c_m\}$ with $m \ge 2$ denoting the set of candidates and $V = (v_1, \dots , v_n)$ with $n \ge 1$ denoting the preference profile consisting of n votes over C. We consider the two most prominent types of votes: approval vectors and linear orders. In the case of approval vectors, each vote is represented by a vector $v_i \in \{0,1\}^m$ in which voter i expresses approval for the candidate $c_j$ by setting the respective entry, denoted by $\mathrm {app}_{v_i}(c_j)$, to 1. In the case of linear orders, each vote $v_i$ is represented by a complete strict linear order ${>}_i$ over C. By $\mathcal {L}(C)$ we denote the set of all strict linear orders over C.

We consider the following voting rules for winner determination. For approval vectors, we use the canonical approval voting (AV). That is, the candidates with the most approvals win. The common variant in which the voters must distribute exactly k approvals is denoted by k-AV with fixed $k \ge 1$ for $m > k$. For linear orders, we focus on positional scoring rules. A positional scoring rule (or scoring rule for short) is characterized by a scoring vector $\boldsymbol{\alpha } = (\alpha _1, \dots , \alpha _m) \in \mathbb {N}^m_{0}$ with $\alpha _1 \ge \alpha _2 \ge \dots \ge \alpha _m$ and $\alpha _1 > \alpha _m$, where $\alpha _j$ denotes the number of points a candidate receives for being placed on position j by one of the voters. Those candidates with the maximum number of points are the winners of the election. A scoring rule covering an arbitrary number of candidates is given by an efficiently evaluable function determining a scoring vector for each number of candidates above a certain minimum. Note that without loss of generality of our results we assume that $\alpha _m = 0$ holds. The most prominent scoring rules are Borda with $\boldsymbol{\alpha } = ( m-1, m-2, \dots , 1, 0 )$, the scoring rule characterized by $\boldsymbol{\alpha } = (2,1,\dots ,1,0)$, k-approval with fixed $k \ge 1$ for $m > k$ characterized by $\boldsymbol{\alpha } = (\alpha _1, \dots , \alpha _m)$ with $\alpha _1 = \dots = \alpha _k = 1$ and $\alpha _{k+1} = \dots = \alpha _m = 0$, and k-veto with fixed $k \ge 1$ for $m > k$ characterized by $\boldsymbol{\alpha } = (\alpha _1, \dots , \alpha _m)$ with $\alpha _1 = \dots = \alpha _{m-k} = 1$ and $\alpha _{m-k + 1} = \dots = \alpha _m = 0$. More specifically, 1-approval is also refereed to as plurality and 1-veto as veto. Note, that k-AV and k-approval essentially describe the same voting rule and differ only in the amount of information we are given about the preferences of the voters. Interestingly, this very distinction leads to differing complexity results in some cases, as we will see later.

In the course of this work we will also encounter elections with partial information. A partial profile $\tilde{V} = (\tilde{v}_1, \dots , \tilde{v}_n)$, in contrast to a normal profile, may contain partial votes. In the case of approval vectors, a partial vote is represented by a partial approval vector $\tilde{v}_i \in \{0,1,\bot \}^m$, where $\bot$ indicates that the approval for the respective candidate is undetermined. An approval vector $v_i$ is a completion of a partial approval vector $\tilde{v}_i$ if for all $j \in \{1,\dots ,m\}$ it holds $\mathrm {app}_{\tilde{v}_i}(c_j) \in \{0,1\} \Rightarrow \mathrm {app}_{v_i}(c_j) = \mathrm {app}_{\tilde{v}_i}(c_j)$. In the case of linear orders, a partial vote consists of a partial order $\tilde{v}_i : {\succ }_i$ over C that is, an irreflexive and transitive, but on the contrary to linear orders, not necessarily connex relation. A linear order $>_i$ is a completion of a partial order ${\succ }_i$ if for all $c_s, c_t \in C$ it holds $c_s \succ _i c_t \Rightarrow c_s >_i c_t$. For both types of votes, a profile $V = (v_1, \dots , v_n)$ is a completion of a partial profile $\tilde{V} = (\tilde{v}_1, \dots , \tilde{v}_n)$, if $v_i$ is a completion of $\tilde{v}_i$ for $1 \le i \le n$. The set of all completions of a vote $\tilde{v}_i$ or a profile $\tilde{V}$ is denoted by $\varLambda (\tilde{v}_i)$ or $\varLambda (\tilde{V})$ respectively.

As mentioned earlier, there may be uncertainty about the votes in elections due to several reasons. Thus we assume some distribution over possible profiles, and investigate the problem of determining the winning probability of a certain candidate. This is formalized in the problem $\mathcal {E}$-Evaluation for a given voting rule $\mathcal {E}$ as follows.

Here we mainly focus on the non-unique winner case where p is considered a winner of election (C, V) with respect to voting rule $\mathcal {E}$, if and only if p is contained in the set of winners $\mathcal {E}(C,V)$. In the unique winner case, we require $\mathcal {E}(C,V) = \{p\}$ for p to be considered a winner of the election. In addition, we also consider random and lexicographic tie-breaking, where in the former the victory of a candidate is weighted according to the total number of winners and in the latter a tie is resolved according to a given order. Unless stated otherwise, the results presented here hold for all four models. Note that regarding the definition of Evaluation, the distribution as part of the input means that the respective distribution is specified by the necessary parameters as part of the input.

In the following we will present the three distribution models for profiles considered in this paper. Note that all the models presented here are products of independent distributions over the preferences for each voter. For a discussion of the properties and relevance of those models considered here and comparable models, we refer to the overview by Boutilier and Rosenschein [8].

PPIC. The first model we consider is the normalized variant of the possible winner motivated model of Bachrach et al. [2]. We will refer to this model as partial profile impartial culture model (PPIC). Given a set of candidates C, a partial profile $\tilde{V} = (\tilde{v}_1, \dots , \tilde{v}_n)$ over C. The probability of a profile $V = (v_1, \dots , v_n)$ over C according to PPIC is given by $\mathrm {Pr}_{\mathrm {PPIC}}( V \mid \tilde{V} ) = {1}/{| \varLambda (\tilde{V}) |}$. Thereby, each completion of the partial profile is equally likely, hence the name ‘impartial culture’. Note, that for partial linear orders, the computation of the probability of a given profile is $\mathrm {\#P}$-hard, since the calculation of the normalization $| \varLambda (\tilde{V}) |$ itself is already a $\mathrm {\#P}$-hard problem as shown by Brightwell and Winkler [9] whereby the normalized variant and the variant considered by Bachrach et al. [2] are not immediately equivalent under polynomial-time reduction. For AV and k-AV, on the other hand, the probability of a given profile can be calculated in polynomial time. For AV it holds that $| \varLambda (\tilde{V}) | = 2^{N_{\bot }}$ where $N_{\bot }$ denotes the total number of undetermined approvals in $\tilde{V}$. For k-AV it holds that $| \varLambda (\tilde{V}) | = \prod _{i = 1}^{n} \left( {\begin{array}{c}u(\tilde{v}_i)\\ k - a(\tilde{v}_i)\end{array}}\right)$ where $u(\tilde{v}_i) = | \{ c \in C \mid \mathrm {app}_{\tilde{v}_i}(c) = \bot \} |$ and $a(\tilde{v}_i) = | \{ c \in C \mid \mathrm {app}_{\tilde{v}_i}(c) = 1 \} |$. For Evaluation under PPIC the parameter is the partial profile $\tilde{V}$. Referring back to the motivations stated at the beginning, PPIC can be used in relation to the evaluation problem to create election forecasts based on partial data about the preferences aggregated from social networks or polls. In terms of robustness, PPIC can be motivated by the possibility that data was partially lost during the collection or transmission. In both scenarios there is a reasonable interest in finding out with which probability which candidate is the winner of the election.

Example 1

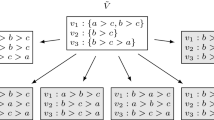
Suppose we are in the run-up to a plurality (1-approval) election over the set of candidates $C = \{a,b,c\}$ and we have received the partial profile $\tilde{V}$ over C shown in Fig. 1 from aggregating social network data. The evaluation problem assuming PPIC with distinguished candidate a asks for the probability that a is a winner, when all possible completions are considered with equal probability. In this case a is only a winner in one of the six possible completions of $\tilde{V}$, whereby the answer to the Evaluation instance is $\varPhi = \nicefrac {1}{6}$.

Fig. 1.

Example for an Evaluation instance assuming PPIC with distinguished candidate a. All possible completions of $\tilde{V}$, each with probability $\nicefrac {1}{6}$. Profiles for which a is not a winner are grayed out.

We now use Example 1 to illustrate the difference between k-approval and k-AV regarding Evaluation. They are essentially the same voting rule and differ only in the amount of information we are given about the preferences and thereby in the expressiveness of the partial preferences. For $v_1$ with partial preference $\{ a> c, b > c \}$ an equivalent partial 1-AV preference could be given by $(\bot ,\bot ,0)$ over (a, b, c). However, for $v_2$ with partial preference $\{b > c\}$ it is not possible to construct a partial approval vector such that b receives the approval with a probability of $\nicefrac {2}{3}$ and a with a probability of $\nicefrac {1}{3}$. It is precisely this difference in the underlying preferences that leads to different complexities for the evaluation problem in Theorem 1 and Theorem 3 for the essentially one and the same voting rule described by k-approval and k-AV.

Mallows. The second model we are considering is the Mallows noise model [28] which is hereinafter mostly referred to as Mallows for short. The basic idea is that some reference profile is given, and the probability of another profile is measured according to its distance to the reference profile. Since the Mallows model is originally defined for linear orders, we will also present a version that applies to approval vectors. Given a set of candidates C, a profile $\hat{V} = (\hat{v}_1, \dots , \hat{v}_n)$ over C and dispersion $\varphi \in (0,1)$. The probability of a profile $V = (v_1, \dots , v_n)$ over C according to the Mallows model is given by $\mathrm {Pr}_{\mathrm {Mallows}}( V \mid \hat{V}, \varphi ) = \nicefrac { \varphi ^{d(V,\hat{V})} }{Z^n}$ with distance d and normalization constant Z chosen according to the vote type. Note, that it is assumed that the dispersion is the same for all voters. In the original case of linear orders, the total swap distance (also known as the Kendall tau distance) $d(V,\hat{V}) = \sum _{i = 1}^{n} \mathrm {sw}(v_i, \hat{v}_i)$ is used, where $\mathrm {sw}(v_i, \hat{v}_i)$ is the minimum number of swaps of pairwise consecutive candidates that are needed to transform $v_i$ into $\hat{v}_i$. The normalization can be written as $Z = Z_{m, \varphi } = 1 \cdot (1\,+\, \varphi )\cdot (1 \,+\, \varphi \,+\, \varphi ^2) \cdots (1 \,+\, \cdots \,+\, \varphi ^{m-1})$ (see, e.g., Lu and Boutilier [27]). In the case of approval vectors, we propose to use the total Hamming distance $d(V,\hat{V}) = \sum _{i = 1}^{n} \mathrm {H}(v_i, \hat{v}_i)$ with $\mathrm {H}(v_i, \hat{v}_i) = |\{ c \in C \mid \mathrm {app}_{v_i}(c) \ne \mathrm {app}_{\hat{v}_i}(c) \}|$. The normalization factor is $Z = Z_{m,\varphi } = \sum _{ j = 0 }^m \left( {\begin{array}{c}m\\ j\end{array}}\right) \cdot \varphi ^j$. Additionally, for k-AV vectors, the normalization becomes . For Evaluation under Mallows, the parameters are the reference profile $\hat{V}$ over C and dispersion $\varphi$. Referring to the motivations, Mallows model captures the scenarios in which the data was corrupted in transmission, by small-scale manipulation, through the elicitation, or the preferences of the voters have changed over time. While the profile obtained in this scenario is the most likely, we have to assume that there is a statistical dispersion. Again, it is natural that, in such scenario, we are interested in how likely and thereby justified and robust the victory of a candidate is.

Fig. 2.

Example for an Evaluation instance assuming Mallows with distinguished candidate b. The probability for each profile is given with respect to its Hamming distance to $\hat{V}$. Profiles for which b is not a winner are grayed out.

Example 2

Suppose we perform a 1-AV election over the set of candidates $C = \{a,b\}$ and the profile $\hat{V}$ over C shown in Fig. 2. We assume that it has been slightly corrupted in transmission with dispersion $\varphi = \nicefrac {1}{2}$. Now, Evaluation assuming Mallows with distinguished candidate b asks for the probability that b is a winner of the election. The profile $\hat{V}$ over (a, b) and the surrounding profiles with their respective total Hamming distance to $\hat{V}$ and probabilities are shown in Fig. 2. The probability that b is a winner, and thereby the answer to the Evaluation instance, is $\varPhi = \nicefrac {(0.25 + 0.25 + 0.0625 + 0.015625)}{ Z^3 } = 0.296$ with $Z^3 = 1.953125$. Whereby, candidate b or the voters could have legitimate concerns about the robustness and thereby the legitimacy of the victory of candidate a under those circumstances.

EDM. Finally, we consider the model introduced by Conitzer and Sandholm [12] and later studied by Hazon et al. [19]. Due to its nature, we refer to it as the explicit distribution model (EDM). Given a set of candidates C, for each voter $i \in \{1, \dots , n\}$ we are given a probability distribution $\pi _i$ over the votes over C through a list of votes paired with their non-zero probabilities. Each unspecified vote has probability 0. The probability of a profile $V= (v_1, \dots , v_n)$ over C according to EDM for $\pi = (\pi _1 ,\dots , \pi _n)$ is given by $\mathrm {Pr}_{\mathrm {EDM}}( V \mid \pi ) = \prod _{i = 1}^{n} \pi _i(v_i)$. The parameters needed for Evaluation under EDM is the list of votes over C paired with their probabilities for each voter. In practice, it can be quite difficult to determine meaningful probabilities for the individual preferences required for EDM. On the other hand, using EDM, one can replicate both PPIC, Mallows and other models by explicitly stating the respective probability distribution for each voter. However, this may require high computational effort as well as a list of exponential length depending on the number of candidates for each voter. Nevertheless, EDM in its generality and flexibility covers the motivations and scenarios of the other models.

Example 3

Suppose we focus on a Borda election over the set of candidates $C = \{ a,b,c \}$ and the probability distribution $\pi$ shown in Fig. 3. The evaluation problem assuming EDM with distinguished candidate b asks for the probability that b is a winner of the election. Here b wins in two profiles with positive probability, $\nicefrac {12}{20}$ and $\nicefrac {3}{20}$, so the answer to the Evaluation instance is $\varPhi = \nicefrac {3}{5}$.

Fig. 3.

Example for an Evaluation instance assuming EDM with distinguished candidate b. The probability for each profile is given with respect to $\pi$. Profiles for which b is not a winner are grayed out.

Computational Complexity. We assume that the reader is familiar with the basics of computational complexity, such as the classes $\mathrm P$, $\mathrm{{NP}}$, $\mathrm{{FP}}$, and $\mathrm {\#P}$. For further information, we refer to the textbooks by Arora and Barak [1] and Papadimitriou [30]. We examine the complexity of the problems presented here mainly in terms of counting complexity as introduced by Valiant [34] using polynomial-time Turing reductions from $\mathrm {\#P}$-hard counting problems to show the hardness of the problems or by presenting polynomial-time algorithms to verify their membership in $\mathrm{{FP}}$. Comparing the complexity of $\mathrm {\#P}$-hard problems to the complexity of decision problems in the polynomial hierarchy, we recognize the immense complexity of just those. According to the theorem of Toda [33], the whole polynomial hierarchy is contained in $\text {P}^\mathrm{{\#P}}$. Therefore, a polynomial-time algorithm for a $\mathrm {\#P}$-hard problem would implicate the collapse of the whole polynomial hierarchy, including $\mathrm{{NP}}$, to $\mathrm P$.

3 Results

In this section we present our results regarding the evaluation problem. Table 1 summarizes our main results for the non-unique winner case. Note that we have omitted several proofs due to the length restrictions but briefly address the ideas.

Table 1. Complexity results for $\mathcal {E}$-Evaluation in the non-unique winner case. The number of voters is denoted by n. For a constant number of candidates, see Theorem 11.

3.1 PPIC

In the following, we present our results regarding PPIC. We start with the results for profiles consisting of linear order votes. Bachrach et al. [2] have shown that the evaluation problem for the non-normalized variant of PPIC is $\mathrm {\#P}$-hard for plurality and veto, even though each preference has at most two completions. It is precisely the latter limitation that makes it possible to easily transfer this result to the normalized variant considered here. Furthermore, by using the circular block votes lemma of Betzler and Dorn [6] it is possible to extend the result to all scoring rules. Note, however, that all these proofs require a variable number of voters. Therefore, we start by showing that $\mathcal {E}$-Evaluation assuming PPIC is $\mathrm {\#P}$-hard for all scoring rules in the non-unique winner case, even if only one voter is participating in the election.

Theorem 1

$\mathcal {E}$-Evaluation is $\mathrm {\#P}$-hard for each scoring rule assuming PPIC, even for one voter.

Proof

We show the $\mathrm {\#P}$-hardness by a polynomial-time Turing reduction from the problem #Linear-Extension, the problem of counting the number of completions (also referred to as linear extensions) of a partial order $\succ _X$ over a set of elements X, which was shown to be $\mathrm {\#P}$-hard by Brightwell and Winkler [9]. Assume we are given a #Linear-Extension instance consisting of a set $X = \{ x_1, \dots , x_t \}$ and a partial order $\succ _X$ over X. First, we determine one completion $>^*_X$ of $\succ _X$ through topological sorting. Set $X_0 = X$. For $i = 0, \dots , t-2$ we perform the following routine.

In the following, we construct an instance for a query to the $\mathcal {E}$-Evaluation oracle. Note that $X_i$ contains $t-i$ elements. Set $C = X_i \cup \{ b_j \mid 1 \le j \le t + i \}$ with $m = 2 t$. We assume that the given scoring rules is defined for 2t candidates. If not, the given linear extension instance can be enlarged using padding elements. Let $\boldsymbol{\alpha } = (\alpha _1, \dots ,\alpha _m)$ with $\alpha _m = 0$ be the scoring vector for m candidates and $k = \min \{ j \in \{1, \dots , m-1\} \mid \alpha _j > \alpha _{j+1} \}$. We distinguish between two cases.

• Case 1 ($k < t - 1$): Let $\tilde{V}$ be a partial profile over C consisting of one partial vote $\tilde{v} : b_1 \succ \dots \succ b_{k-1} \succ X_{i}^{\succ _X} \succ b_k \succ \dots \succ b_{t+i}$ with $X_{i}^{\succ _X}$ being the elements in $X_i$ partially ordered by $\succ _X$. Let $x_s$ be the element in $X_i$ for which $\forall x_j \in X_i \setminus \{ x_s \} : x_s >^*_X x_j$ holds.

• Case 2 ($k \ge t - 1$): Let $\tilde{V}$ be a partial profile over C consisting of one partial vote $\tilde{v} : b_1 \succ \dots \succ b_{k-t+1} \succ X_{i}^{\succ _X} \succ b_{k-t+2} \succ \dots \succ b_{t+i}$ with $X_{i}^{\succ _X}$ being the elements in $X_i$ partially ordered by $\succ _X$. Let $x_s$ be the element in $X_i$ for which $\forall x_j \in X_i \setminus \{ x_s \} : x_j >^*_X x_s$ holds.

We subsequently set $\varTheta _i = \varPhi$ (Case 1) or $\varTheta _i = 1 -\varPhi$ (Case 2) with $\varPhi$ denoting the answer of the $\mathcal {E}$-Evaluation oracle regarding the previously constructed instance consisting of the set of candidates C, partial profile $\tilde{V}$, and candidate $p = x_s$. The routine ends with setting $X_i = X_i \setminus \{x_s\}$.

Finally, after considering each value of i, we return $\prod _{i = 0}^{t-2} \varTheta _i^{-1}$ as the number of completions of $\succ _X$. We now show the correctness of the reduction. By $\succ _{X_i}$ we denote the partial order over $X_i$ induced by $\succ _X$. We show that $\varTheta _i = {|\varLambda (\succ _{X_{i+1}})|}/{|\varLambda (\succ _{X_{i}})|}$ for $i \in \{ 0, \dots , t-2 \}$ holds. For this we consider an arbitrary step i. It holds that $\alpha _1 = \dots = \alpha _k > \alpha _{k+1}$. Note that in both cases, the partiality of $\tilde{v}$ is limited to the partial order $\succ _{X_i}$ embedded in it. In Case 1, $x_s$ is a winner of the election regarding completion $V = (v)$ of $\tilde{V} = (\tilde{v})$ if and only if $x_s$ is placed in position k in v. Candidate $x_s$ being placed in position k in v is equivalent to $\forall x_j \in X_i \setminus \{ x_s \} : x_s >_v x_j$. Thereby, $\varTheta _i = {|\{ {>^*} \in \varLambda (\succ _{X_{i}}) \mid \forall x_j \in X_i \setminus \{ x_s \} : x_s >^* x_j \}|}/{ | \varLambda ( \succ _{X_{i}} )|}$ holds. But if $x_s$ is fixed to the top position regarding $X_i$, it holds that the remaining number of completions equals the number of completions regarding $X_{i+1} = X_i \setminus \{x_s\}$ whereby $|\{ {>^*} \in \varLambda (\succ _{X_{i}}) \mid \forall x_j \in X_i \setminus \{ x_s \} : x_s >^* x_j \}| = | \varLambda (\succ _{X_{i+1}})|$ holds. Thereby, $\varTheta _i = {|\varLambda (\succ _{X_{i+1}})|}/{|\varLambda (\succ _{X_{i}})|}$ follows. In Case 2, $x_s$ is not a winner of the election regarding completions $V = (v)$ of $\tilde{V} = (\tilde{v})$ if and only if $x_s$ is placed in position $k+1$ in v. The proportion of completions in which $x_s$ is not a winner and thus fixed to the last position regarding $X_i$ is given by $\varTheta _i = 1 - \varPhi$ with $\varPhi$ denoting the probability that $x_s$ wins. Thereby, $\varTheta _i = {|\varLambda (\succ _{X_{i+1}})|}/{|\varLambda (\succ _{X_{i}})|}$ can be shown analogous to Case 1.

Finally, it holds that $|X_{t-1}| = 1$ whereby $|\varLambda ( \succ _{X_{t-1}} )| = 1$. Thus, by repeatedly applying $|\varLambda (\succ _{X_{i}})| = \varTheta _i^{-1} \cdot |\varLambda (\succ _{X_{i+1}})|$ for $i \in \{ 0, \dots , t-2 \}$, $|\varLambda (\succ _X)| = |\varLambda (\succ _{X_0})| = \prod _{i = 0}^{t-2} \varTheta _i^{-1}$ follows. As the reduction can be performed in polynomial time, the $\mathrm {\#P}$-hardness follows.    $\square$

Note that the complexity in the unique winner case is much more diverse. For scoring rules fulfilling $\alpha _1 > \alpha _2$ for each number of candidates, for example plurality, $(2,1,\dots ,1,0)$, and Borda, the $\mathrm {\#P}$-hardness of the problem in the case of one voter can be shown using the previous reduction. For 2-approval, the problem is trivial for one voter, but can be shown to be $\mathrm {\#P}$-hard for two voters using a slightly adjusted version of the previous reduction. Finally, for veto, the problem is not hard for any constant number of voters, since the problem is trivial if the number of candidates exceeds the number of voters by more than one.

We now turn to the results regarding approval voting. We start with the result for approval voting with a variable number of approvals per voter, for which the complexity is significantly lower than for scoring rules.

Theorem 2

$\mathcal {E}$-Evaluation is in $\mathrm{{FP}}$ for AV assuming PPIC.

Proof

We show that the problem is in $\mathrm{{FP}}$ using a dynamic programming approach. Assume we are given an AV-Evaluation instance assuming PPIC consisting of a set of candidates $C = \{ p, c_1, \dots , c_{m-1} \}$, partial profile $\tilde{V} = (\tilde{v}_1, \dots ,\tilde{v}_n)$ and candidate p.

First, we define some shorthand notations. By d(c), a(c), and u(c) we denote the number of votes $\tilde{v}_i$ in $\tilde{V}$ with $\mathrm {app}_{\tilde{v}_i}(c) = 0$, 1, or $\bot$ respectively. For a candidate $c \in C$, by R(i, c) for $0 \le i \le n$ we denote the number of combinations to extend the partial entries in $\tilde{V}$ for candidate c such that c has exactly i approvals. It holds that $R(i, c) = \left( {\begin{array}{c} u(c) \\ i - a(c) \end{array}}\right)$ for $0 \le i - a(c) \le u(c)$ and 0 otherwise. By N(s, j, k) we denote the number of combinations to extend the partial entries in $\tilde{V}$ for the candidates $c_1, \dots , c_j$ in a way that exactly k candidates in $\{c_1, \dots , c_j\}$ receive exactly s approvals each while each other candidate in $\{c_1, \dots , c_j\}$ receives less than s approvals. Set $N(s,0,0) = 1$ for $0 \le s \le n$ and $N(s,j,k) = 0$ for $k > j$ or negative s, j, or k. The following relationship applies. $N(s,j,k) = \left[ \sum _{i = 0}^{ s - 1 } R(i, c_j)\right] \cdot N(s, j-1, k) + R(s, c_j) \cdot N(s, j-1, k - 1)$ for $0 \le s \le n$, $1 \le j \le m-1$, and $0 \le k\le m - 1$. The factor in the first term of the formula equals the number of different possibilities for $c_j$ to receive less than s approvals in a completion. The factor in the second term corresponds to the number of different possibilities for $c_j$ in a completion to obtain exactly s approvals, which increases the number of candidates with exactly s approvals by one. Therefore, by summing over all possible numbers of co-winners and each score of p that p could receive considering the different ways p may receive this score we obtain $H = \sum _{k = 0}^{m-1} \sum _{s = 0}^{n}\left( R(s,p) \cdot N( s, m-1, k ) \right)$ denoting the number of completions for which p is a winner of the election. Thereby the probability $\varPhi$ that p is a winner of the election is given by ${ H }/{ 2^{ N_{\bot } } }$ with $N_{\bot }$ denoting the total number of undetermined approvals in $\tilde{V}$. We have to determine $\mathcal {O}(n\cdot m^2)$ different entries with each one requiring at most $\mathcal {O}(n^2)$ steps whereby the whole approach only requires a polynomial bounded number of steps. In the unique winner case we receive the number of completions in which p is the winner of the elections by excluding the possibility of co-winners: $H = \sum _{s = 0}^{n} R(s,p) \cdot N( s, m-1, 0 )$.    $\square$

On the other hand, if the number of approvals is fixed for each voter, the problem becomes hard for approval voting. Interestingly, and contrary to the result for scoring rules, this hardness does not hold for a constant number of voters. This leads to the apparently contradictory result that the complexity of the problem for one and the same voting rule described by k-approval and k-AV is differing. This difference can be traced back to the differing degree of information which was addressed in the explanation after Example 1.

Theorem 3

$\mathcal {E}$-Evaluation is $\mathrm {\#P}$-hard for k-AV for any fixed $k \ge 1$ assuming PPIC, but lies in $\mathrm{{FP}}$ for a constant number of voters.

The first statement can be shown by a reduction from #Perfect-Bipartite-Matching which was shown to be $\mathrm {\#P}$-hard by Valiant [34]. The second statement follows from the observation that there is only a polynomially bounded number of votes per voter and thus for a constant number of voters there is only a polynomially bounded number of profiles with non-zero probability.

3.2 Mallows

In the following, we present our results regarding the Mallows noise model. Note that the Mallows model is generalized by the repeated insertion model (RIM). Therefore, the hardness results in this section also hold for RIM. Again, we first present the results for profiles consisting of linear order votes. Note that our main tool for the hardness results presented here is the observation that the evaluation problem regarding Mallows is equivalent to the counting variant of the unit-cost swap bribery problem (see Dorn and Schlotter [14]) under polynomial-time Turing reduction. We omitted the proof for this result due to the length restrictions. The main idea is to choose the dispersion factor in such a way that it is possible to recalculate the exact number of profiles in a certain total swap distance in which the respective candidate is a (non-)unique winner.

Theorem 4

$\mathcal {E}$-Evaluation is in $\mathrm{{FP}}$ for all scoring rules assuming Mallows for one voter.

We show that Kendall’s approach (see Kendall [22]) of calculating the number of linear orders with an exact given swap distance to a given vote can be formulated as dynamic programming and extended to take into account the position of p.

This result can also be extended to any constant number of voters for a certain class of scoring rules. We call a scoring rule almost constant if the number of different values in its scoring vectors is bounded by a constant, and additionally only one value has an unbounded number of entries. This class of scoring rules was considered by Baumeister et al. [5] and later by Kenig and Kimelfeld [23], the latter of which coined the name. This class contains, for example, scoring rules like k-approval, k-veto and $(2,1,\dots ,1,0)$.

Theorem 5

$\mathcal {E}$-Evaluation is in $\mathrm{{FP}}$ for all almost constant scoring rules assuming Mallows for a constant number of voters.

The result is based on the fact that the number of combinations of relevant prefixes and suffixes of the votes in the profile is bounded by a polynomial with the degree including the number of positions covered by the values with a bounded number of entries and the number of voters. As we will see in Theorem 8, there also exist scoring rules beyond this class for which the problem is hard for a constant number of voters. We proceed with our results for an unbounded number.

Theorem 6

$\mathcal {E}$-Evaluation is $\mathrm {\#P}$-hard for $(2,1,\dots ,1,0)$ and Borda assuming Mallows.

Baumeister et al. [5] showed the NP-hardness of the unit-cost swap bribery problem for $(2,1,\dots ,1,0)$ and Borda through a polynomial-time many-one-reduction from the NP-complete problem X3C. As the respective counting problem #X3C is $\mathrm {\#P}$-hard as shown by Hunt et al. [20] and the previously mentioned reductions by Baumeister et al. are also parsimonious, the counting version of the unit-cost swap bribery problem is $\mathrm {\#P}$-hard for $(2,1,\dots ,1,0)$ and Borda. Therefore, by the results stated at the beginning of this section regarding the polynomial-time Turing equivalence of the problems, the $\mathrm {\#P}$-hardness of $\mathcal {E}$-Evaluation for $(2,1,\dots ,1,0)$ and Borda assuming Mallows follows.

Contrary to Borda and $(2,1,\dots ,1,0)$, it is known that the unit-cost swap bribery problem is in $\mathrm P$ for plurality and veto (Dorn and Schlotter [14]). As we see in the following, however, the respective counting variants and evaluation problems assuming Mallows are $\mathrm {\#P}$-hard.

Theorem 7

$\mathcal {E}$-Evaluation is $\mathrm {\#P}$-hard for k-approval and k-veto with fixed $k \ge 1$ assuming Mallows.

The proof consists of a reduction from #Perfect-Bipartite-Matching for 3-regular graphs which was shown to be $\mathrm {\#P}$-hard by Dagum and Luby [13].

Considering Theorem 4 and Theorem 5, the question arises as to whether a scoring rule exists and, if so, whether a natural scoring rule exists, for which the evaluation problem assuming Mallows is $\mathrm {\#P}$-hard even for a constant number of voters. For this we consider top- Borda characterized by the scoring vector $\boldsymbol{\alpha } = (k, k-1, \dots , 1, 0, \dots , 0)$ for and m candidates.

Theorem 8

$\mathcal {E}$-Evaluation is $\mathrm {\#P}$-hard for top- Borda assuming Mallows, even for a constant number voters.

Again, the proof consists of a reduction from #Perfect-Bipartite-Matching for 3-regular graphs using König’s Line Coloring Theorem (König [24]). The number of voters here is 13. We expect that the problem is already hard for a lower number of voters for scoring rules similar to top- Borda and Borda.

We now turn to the results regarding approval voting.

Theorem 9

$\mathcal {E}$-Evaluation is in $\mathrm{{FP}}$ for AV assuming Mallows and for k-AV assuming Mallows and a constant number of voters.

The proof for the first case consists of a dynamic programming approach similar to that in the proof of Theorem 2. The second case follows from the fact that only a polynomial bounded number of possible profiles exist.

3.3 EDM

We now present our results regarding EDM. Since EDM generalizes both PPIC and Mallows, and, under certain restrictions, even through a polynomial-time Turing reduction, many of the previous results can be transferred to EDM for both scoring rules and approval voting. Note that some results for individual scoring rules and EDM were already known through Hazon et al. [19].

Theorem 10

$\mathcal {E}$-Evaluation is $\mathrm {\#P}$-hard for AV, k-AV, and all scoring rules assuming EDM, but lies in $\mathrm{{FP}}$ for a constant number of voters.

The hardness results follow from the proofs of the hardness results regarding PPIC (see the note on the complexity regarding an unbounded number of voters above Theorem 1 and Theorem 3) in which for the constructed instances the number of completions of a vote is at most two and thus the instance can be efficiently transformed into an EDM instance. The efficiency result follows from the fact that the number of possible profiles is polynomially bounded.

Finally, we present our results for a constant number of candidates.¹

Theorem 11

$\mathcal {E}$-Evaluation is in $\mathrm{{FP}}$ for AV, k-AV, and all scoring rules assuming PPIC, Mallows, or EDM for a constant number of candidates.

The result follows by slight adjustments from the approach for a constant number of candidates by Hazon et al. [19] and the fact that Mallows and PPIC instances can be efficiently transformed to EDM instances for a constant number of candidates.

3.4 Corresponding Decision Problem

Conitzer and Sandholm [12] defined the evaluation problem as a decision problem instead of a weighted counting problem. Assume we are given a rational number r with $0 \le r \le 1$ as part of the input. Here we ask whether the probability that the given candidate is a winner of the election is greater than r. We refer to this problem as $\mathcal {E}$-Evaluation-Dec. The question arises whether the decision problem in some cases is easier to answer than the weighted counting problem. The following result shows that this is not the case for the cases considered here, namely AV, k-AV and scoring rules assuming PPIC, Mallows, and EDM. This result holds for all winner models and parameterized cases considered here.

Theorem 12

For the cases considered here, the problems $\mathcal {E}$-Evaluation and $\mathcal {E}$-Evaluation-Dec are equivalent under polynomial-time Turing reduction.

While the reduction of the decision variant to the probability variant is straightforward, the reduction in the opposite direction uses the decision problem as oracle for the search algorithm of Kwek and Mehlhorn [25]. It follows that $\mathcal {E}$-Evaluation is in $\mathrm{{FP}}$, if and only if $\mathcal {E}$-Evaluation-Dec is in $\mathrm P$. On the other hand, $\mathcal {E}$-Evaluation is $\mathrm {\#P}$-hard, if and only if $\mathcal {E}$-Evaluation-Dec is $\mathrm {\#P}$-hard. While it is unusual to speak of $\mathrm {\#P}$-hardness of decision problems, it is possible to show just that using Turing reductions. The $\mathrm {\#P}$-hardness makes the $\mathrm{{NP}}$-membership of such a problem unlikely (Toda [33]).

An interesting special case of the decision problem is to ask if the probability that the given candidate wins is greater than $r = 0$. By the previous theorem it follows that if the problem for $r = 0$ is $\mathrm{{NP}}$-hard, the $\mathrm{{NP}}$-hardness of the evaluation problem under Turing reduction follows, but not the stronger $\mathrm {\#P}$-hardness. Regarding EDM, the problem is referred to as the Chance-Evaluation problem by Hazon et al. [19]. Regarding PPIC, the problem is equivalent to the well studied possible winner problem (for a recent overview, see Lang [26]). Regarding Mallows, the problem is trivial for the voting rules considered here as each candidate has a non-zero winning probability.

4 Further Related Work

In the following we discuss the related work which has not been sufficiently covered in the paper so far. For a comprehensive overview regarding elections with probabilistic or incomplete preferences, we refer to the overview by Boutilier and Rosenschein [8] and the survey by Walsh [35].

Subsequently to the polynomial-time randomized approximation algorithm with additive error for calculating a candidates’ winning probability assuming PPIC by Bachrach et al. [2], Kenig and Kimelfeld [23] recently presented such an algorithm with multiplicative error for calculating the probability that a candidate loses assuming PPIC or RIM including Mallows.

Wojtas and Faliszewski [37] and recently Imber and Kimelfeld [21] have studied the problem of determining the winning probability for elections in which the participation of candidates or voters is uncertain by examining the complexity of the counting variants of election control problems.

Shiryaev et al. [31] studied the robustness of elections by considering the minimum number of swaps in the profile necessary to replace the current winner for which the evaluation problem under Mallows forms the probabilistic variant. Very recently, Boehmer et al. [7] have further built on these studies and thoroughly investigated the corresponding counting variant considering the parameterized complexity and by experiments based on the election map dataset by Szufa et al. [32], to investigate the practical complexity as well as the actual stability measurement considered by the problem. In comparison to the Mallows model, not all profiles are taken into account, weighted according to their distance, but all profiles up to a given distance limit are equally weighted.

In many cases the Mallows model is used to describe the distribution of votes based on a true general underlying ranking. If one assumes that the assumption regarding the existence of such a ranking is correct, it seems a reasonable approach to determine the winner by determining the most likely underlying ranking or to ask for a voting rule with the output as close as possible to such an underlying ranking. This approach has been examined, beside others, by Caragiannis et al. [10] and de Weerdt et al. [36].

The evaluation problem is also considered in other contexts. For example, in sports, the evaluation problem was studied by Mattei et al. [29] for various tournament formats and subsequently by Baumeister and Hogrebe [4] with a particular focus on predicting the outcome of round-robin tournaments.

5 Conclusion

We studied the computational complexity of the evaluation problem for approval voting and positional scoring rules regarding PPIC, the Mallows noise model, and EDM. We showed that the complexity of the problem varies greatly depending on the voting rule, the distribution model, and the parameterization. While in the general case, and partially even in very restricted cases, the evaluation problem is quite hard, we also identified general cases in which the probability that the given candidate wins the election can be calculated efficiently. Finally, in addition to the more practical motivations we have presented at the beginning, the evaluation problem is essential for the theoretical investigations of probabilistic variants of election interference problems such as manipulation, bribery, and control. As introduced by Conitzer and Sandholm [12] the decision variant of the evaluation problem is essentially the verification problem for just those problems. They show $\mathrm{{NP}}$-hardness for several cases, but also finally point out that these problems do not necessarily lie in $\mathrm{{NP}}$. In Sect. 3.4 we show that this assumption is probably correct by proving the $\mathrm {\#P}$-hardness for several cases. For just those $\mathrm{{NP}}$- and $\mathrm {\#P}$-hard cases, it is unlikely that the interference problem itself lies in $\mathrm{{NP}}$, as the problem of verifying the success of a given intervention is probably not contained in $\mathrm P$.

Besides solving the open cases, namely the complexity regarding Mallows and k-AV in general and Borda for a constant number of voters, it may be interesting to consider multi-winner elections, further distribution models, and the fine-grained parameterized counting complexity as introduced by Flum and Grohe [17]. Of course, the worst-case, and the slightly more practical parameterized worst-case, analysis is only the first but an indispensable step in the complexity analysis of the problems and should, especially for the here identified hard cases, be followed by an average-case or typical-case analysis.