Abstract
We begin our general discussions with the introduction of quadrics in projective space, see, e.g., [Kle1928, Bla1954, Gie1982].
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
We begin our general discussions with the introduction of quadrics in projective space, see, e.g., [Kle1928, Bla1954, Gie1982].
3.1 Projective Geometry
Consider the n-dimensional real projective space

as it is generated via projectivization from its homogeneous coordinate space \(\mathbb {R}^{n+1} \setminus \{0\}\) using the equivalence relation
We denote points in \(\mathbb {R}\mathrm {P}^{n}\) and its homogeneous coordinates by
Affine coordinates are given by normalizing one homogeneous coordinate to be equal to one and then dropping this coordinate, e.g.,
Points with \(x_{n+1}=0\), for which this normalization is not possible, are said to lie on the hyperplane at infinity.
The projectivization operator \(\mathrm {P}\) acts on any subset of the homogeneous coordinate space. In particular, a projective subspace \(\boldsymbol{U} \subset \mathbb {R}\mathrm {P}^n\) is given by the projectivization of a linear subspace \(U \subset \mathbb {R}^{n+1}\),
To denote projective subspaces spanned by a given set of points \(\boldsymbol{a}_1, \ldots , \boldsymbol{a}_k\) with linearly independent homogeneous coordinate vectors we use the exterior product notation
The group of projective transformations is induced by the group of linear transformations of \(\mathbb {R}^{n+1}\) and denoted by \({\text {PGL}}(n+1)\). A projective transformation maps projective subspaces to projective subspaces, while preserving their dimension and incidences. The fundamental theorem of real projective geometry states that this property characterizes projective transformations.
Theorem 3.1
Let \(n \ge 2\), and \(W \subset \mathbb {R}\mathrm {P}^n\) be a non-empty open subset. Let \(f : W \rightarrow \mathbb {R}\mathrm {P}^n\) be an injective map that maps intersections of k-dimensional projective subspaces with W to intersections of k-dimensional projective subspaces with f(W) for some \(1 \le k \le n-1\). Then f is the restriction of a unique projective transformation of \(\mathbb {R}\mathrm {P}^n\).
For a projective subgroup \(G \subset {\text {PGL}}(n+1)\) we denote the stabilizer of a finite number of points \(\boldsymbol{v}_1, \ldots , \boldsymbol{v}_m \in \mathbb {R}\mathrm {P}^n\) by

3.2 Quadrics
Let \(\left\langle \cdot , \cdot \right\rangle \) be a non-zero symmetric bilinear form on \(\mathbb {R}^{n+1}\). A vector \(x\in \mathbb {R}^{n+1}\) is called
-
spacelike if
 ,
, -
timelike if
 ,
, -
lightlike, or isotropic, if
 .
.
There always exists an orthogonal basis with respect to  , i.e. a basis \((e_i)_{i = 1, \ldots , n+1}\) satisfying
, i.e. a basis \((e_i)_{i = 1, \ldots , n+1}\) satisfying  if \(i\ne j\). The triple (r, s, t), consisting of the numbers of spacelike (r), timelike (s), and lightlike (t) vectors in \((e_i)_{i = 1, \ldots , n+1}\) is called the signature of
if \(i\ne j\). The triple (r, s, t), consisting of the numbers of spacelike (r), timelike (s), and lightlike (t) vectors in \((e_i)_{i = 1, \ldots , n+1}\) is called the signature of  . It is invariant under linear transformations. If \(t=0\), the bilinear form \(\left\langle \cdot , \cdot \right\rangle \) is called non-degenerate, in which case we might omit its value in the signature. We alternatively write the signature in the form
. It is invariant under linear transformations. If \(t=0\), the bilinear form \(\left\langle \cdot , \cdot \right\rangle \) is called non-degenerate, in which case we might omit its value in the signature. We alternatively write the signature in the form
The space \(\mathbb {R}^{n+1}\) together with a bilinear form of signature (r, s, t) is denoted by \(\mathbb {R}^{r,s,t}\). The zero set of the quadratic form corresponding to \(\left\langle \cdot , \cdot \right\rangle \)

is called the light cone, or isotropic cone. Its projectivization

defines a quadric in \(\mathbb {R}\mathrm {P}^{n}\) (quadrics in \(\mathbb {R}\mathrm {P}^2\) are called conics).
While we are concerned with quadrics in a real projective space, it is sometimes convenient to consider the complexification

When referring to imaginary points of a quadric \(\mathcal {Q}\subset \mathbb {R}\mathrm {P}^n\), we always mean non-real points on its complexification \(\mathcal {Q}_\mathbb {C}\).
A point \(\boldsymbol{x} \in \mathcal {Q}\) contained in the kernel of the corresponding bilinear form \(\left\langle \cdot , \cdot \right\rangle \), i.e.
is called a vertex of \(\mathcal {Q}\). A quadric is called non-degenerate if it contains no vertices, or equivalently if \(t = 0\). If \(\mathcal {Q}\) is degenerate, i.e. \(t > 0\), its set of vertices is a projective subspace of dimension \(t-1\).
A non-zero scalar multiple of \(\left\langle \cdot , \cdot \right\rangle \) defines the same quadric \(\mathcal {Q}\). Vice versa, if \(\mathcal {Q}\) is non-empty and does not solely consist of vertices it uniquely determines its corresponding symmetric bilinear form up to a non-zero scalar multiple. Upon considering the complexification \(\mathcal {Q}_\mathbb {C}\) of the real quadric \(\mathcal {Q}\) this correspondence holds for all quadrics, and it is thus convenient to generally identify the term quadrics and symmetric bilinear forms up to non-zero scalar multiples.
The signature of a quadric is well-defined up to interchanging r and s. The signature of a projective subspace \(\boldsymbol{U} = \mathrm {P}(U)\) is defined by the signature of the bilinear form restricted to U. After a choice of the sign for the bilinear form of \(\mathcal {Q}\) the signs for the signature of \(\boldsymbol{U}\) are fixed.
A quadric \(\mathcal {Q}\) naturally defines two regions in the projective space \(\mathbb {R}\mathrm {P}^n\),

which we call the two sides of the quadric. Which side is “+” and which side is “-” is only determined after choosing the sign for the bilinear form of \(\mathcal {Q}\).
A projective subspace entirely contained in the quadric \(\mathcal {Q}\) is called an isotropic subspace. A quadric with signature (r, s, t) contains isotropic subspaces of dimension \(\min \{r, s\} + t - 1\) through every point.
Consider the following examples of quadrics in \(\mathbb {R}\mathrm {P}^n\) with different signatures.
Example 3.1
-
(i)
A quadric with signature \((n+1,0)\) is empty in \(\mathbb {R}\mathrm {P}^n\). By either identifying the quadric with its bilinear form up to non-zero scalar multiples or by complexification \(\mathcal {Q}_\mathbb {C}\subset \mathbb {C}\mathrm {P}^n\), we consider this to be an admissible non-degenerate quadric, which only happens to have an empty real part. Note that one side of the quadric \(\mathcal {Q}^+ = \mathbb {R}\mathrm {P}^n\) is the whole space, while the other side \(\mathcal {Q}^- = \varnothing \) is empty.
-
(ii)
A quadric with signature (n, 1) is an “oval quadric”. It is projectively equivalent to the \((n-1)\)-dimensional sphere \(\mathbb {S}^{n-1}\).
-
(iii)
A quadric with signature \((n-1,2)\) is a higher dimensional analogue of a doubly ruled quadric in \(\mathbb {R}\mathrm {P}^3\). It contains lines as isotropic subspaces through every point, but no planes.
-
(iv)
A quadric with signature (r, s, 1) is a cone. It consists of all lines connecting its vertex to a non-degenerate quadric of signature (r, s), given by its intersection with a hyperplane not containing the vertex. Note that if \(r=0\) or \(s=0\) (the real part of) the cone only consists of the vertex. The remaining part of the cone can be considered as imaginary (cf. Example (i)).
-
(v)
A quadric with signature (1, 0, n) is a “doubly counted hyperplane”. Formally, this means the same as just “hyperplane”. The words “doubly counted” indicate that the hyperplane is given by a quadratic equation.
For non-neutral signature, i.e. \(r \ne s\), and \(rs \ne 0\), the subgroup of projective transformations preserving the quadric \(\mathcal {Q}\) is exactly the projective orthogonal group \({\text {PO}}(r,s,t)\), i.e. the projectivization of all linear transformations that preserve the bilinear form \(\left\langle \cdot , \cdot \right\rangle \). For simplicity, we call \({\text {PO}}(r,s,t)\) the “group of transformations that preserve the quadric \(\mathcal {Q}\)” for all signatures.
Remark 3.1
In the case \(r = s\) the statement remains true if we exclude projective transformations that interchange the two sides (3.2) of the quadric. In the case \(rs=0\) the statement remains true upon complexification.
The fundamental theorem of real projective geometry (see Theorem 3.1) may be specialized to quadrics.
Theorem 3.2
Let \(n \ge 3\), \(\mathcal {Q}\subset \mathbb {R}\mathrm {P}^n\) be a non-degenerate non-empty quadric in \(\mathbb {R}\mathrm {P}^n\), and \(W \subset \mathcal {Q}\) be a non-empty open subset of the quadric. Let \(f : W \rightarrow \mathcal {Q}\) be an injective map that maps intersections of k-dimensional projective subspaces with W to intersections of k-dimensional projective subspaces with f(W) for some \(2 \le k \le n-1\). Then f is the restriction of a unique projective transformation of \(\mathbb {R}\mathrm {P}^n\) that preserves the quadric \(\mathcal {Q}\).
For a non-degenerate quadric every such transformation can be decomposed into a finite number of reflections in hyperplanes by the theorem of Cartan and Dieudonné (see, e.g., [Ar1957]).
Theorem 3.3
Let \(\mathcal {Q}\subset \mathbb {R}\mathrm {P}^n\) be a non-degenerate quadric of signature (r, s). Then each element of the corresponding projective orthogonal group \({\text {PO}}(r,s)\) is the composition of at most \(n+1\) reflections in hyperplanes, i.e. transformations of the form
for some \(\boldsymbol{q} \in \mathbb {R}\mathrm {P}^n \setminus \mathcal {Q}\).
Polarity with respect to a conic \(\mathcal {Q}\) with signature \((++-)\) in \(\mathbb {R}\mathrm {P}^2\) (left) and a quadric of signature \((+++-)\) in \(\mathbb {R}\mathrm {P}^3\) (right). The point \(\boldsymbol{x}\) and its polar hyperplane \(\boldsymbol{x}^\perp \) are shown as well as the cone of contact from the point \(\boldsymbol{x}\). Lines through \(\boldsymbol{x}\) that are “inside” (signature \((+-)\)), “on” (signature \((+0)\)), and “outside” (signature \((++)\)) the cone intersect the quadric in 2, 1, or 0 points respectively
3.3 Polarity
A quadric induces the notion of polarity between projective subspaces (see Fig. 3.1). For a projective subspace \(\boldsymbol{U} = \mathrm {P}(U)\subset \mathbb {R}\mathrm {P}^{n}\), where \(U\subset \mathbb {R}^{n+1}\) is a linear subspace, the polar subspace of \(\boldsymbol{U}\) is defined as

If \(\mathcal {Q}\) is non-degenerate, the dimensions of two polar subspaces satisfy the following relation:
A refinement of this statement, which includes the signatures of the two polar subspaces, is captured in the following lemma.
Lemma 3.1
Let \(\mathcal {Q}\subset \mathbb {R}\mathrm {P}^n\) be a non-degenerate quadric of signature (r, s). Then the signature \((\tilde{r}, \tilde{s}, \tilde{t})\) of a subspace \(\boldsymbol{U} \subset \mathbb {R}\mathrm {P}^n\) and the signature \((\tilde{r}_\perp , \tilde{s}_\perp , \tilde{t}_\perp )\) of its polar subspace \(\boldsymbol{U}^\perp \) with respect to \(\mathcal {Q}\) satisfy
In particular, \(\tilde{t} \le \min \{r, s\}\).
For a point \(\boldsymbol{x} \in \mathcal {Q}\) on a quadric, which is not a vertex, the tangent hyperplane of \(\mathcal {Q}\) at \(\boldsymbol{x}\) is given by its polar hyperplane \(\boldsymbol{x}^\perp \). If \(\mathcal {Q}\) has signature (r, s, t) then the tangent plane has signature \((r-1,s-1,t+1)\). Furthermore, for a non-degenerate quadric a projective subspace is tangent to \(\mathcal {Q}\) if and only if its signature is degenerate.
A projective line not contained in a quadric can intersect the quadric in either zero, one, or two points (see Fig. 3.1).
Lemma 3.2
Let \(\mathcal {Q}\subset \mathbb {R}\mathrm {P}^n\) be a quadric, \(\boldsymbol{x}, \boldsymbol{y} \in \mathbb {R}\mathrm {P}^{n}\), \(\boldsymbol{x} \ne \boldsymbol{y}\) be two points, and define
-
If \(\Delta > 0\), then the line \(\boldsymbol{x} \wedge \boldsymbol{y}\) has signature \((+-)\) and intersects \(\mathcal {Q}\) in two points
$$ \boldsymbol{x}_\pm = \left[ \left\langle y, y \right\rangle x + \left( -\left\langle x, y \right\rangle \pm \sqrt{\Delta } \right) y \right] . $$ -
If \(\Delta < 0\), then the line \(\boldsymbol{x} \wedge \boldsymbol{y}\) has signature \((++)\) or \((--)\) and intersects \(\mathcal {Q}\) in no real points, but in two complex conjugate points
$$ \boldsymbol{x}_{\pm } = \left[ \left\langle y, y \right\rangle x + \left( -\left\langle x, y \right\rangle \pm i\sqrt{-\Delta } \right) y \right] . $$ -
If \(\Delta = 0\), then the line \(\boldsymbol{x} \wedge \boldsymbol{y}\) has signature \((+0)\) or \((-0)\) and it is tangent to \(\mathcal {Q}\) in the point
$$ \boldsymbol{\tilde{x}} = \left[ \left\langle y, y \right\rangle x - \left\langle x, y \right\rangle y \right] , $$or it has signature (00) and is contained in \(\mathcal {Q}\) (isotropic line).
The last point of the preceding lemma gives rise to the following definition of the cone of contact (see Fig. 3.1).
Definition 3.1
Let \(\mathcal {Q}\subset \mathbb {R}\mathrm {P}^n\) be a quadric with corresponding bilinear form \(\left\langle \cdot , \cdot \right\rangle \), and \(\boldsymbol{x} \in \mathbb {R}\mathrm {P}^n \setminus \mathcal {Q}\). Define the quadratic form

Then the corresponding quadric

is called the cone of contact, or tangent cone, to \(\mathcal {Q}\) from the point \(\boldsymbol{x}\).
The points of tangency of the cone of contact lie in the polar hyperplane of its vertex.
Lemma 3.3
Let \(\mathcal {Q}\subset \mathbb {R}\mathrm {P}^n\) be a quadric. For a point \(\boldsymbol{x} \in \mathbb {R}\mathrm {P}^n \setminus \mathcal {Q}\) the cone of contact to \(\mathcal {Q}\) from \(\boldsymbol{x}\) is given by
Remark 3.2
For a non-degenerate quadric \(\mathcal {Q}\) the intersection \(\boldsymbol{x}^\perp \cap \mathcal {Q}\) always results in a non-degenerate quadric in \(\boldsymbol{x}^\perp \). If the restriction of the corresponding bilinear form has signature (n, 0) or (0, n) the intersection can be considered as imaginary. The real part of the cone only consists of the vertex in this case (cf. Example 3.1 (iv)).
3.4 Pencils of Quadrics
Let \(\mathcal {Q}_1, \mathcal {Q}_2 \subset \mathbb {R}\mathrm {P}^n\) be two distinct quadrics with corresponding bilinear forms \(\left\langle \cdot , \cdot \right\rangle _1, \left\langle \cdot , \cdot \right\rangle _2\) respectively. Every linear combination of these two bilinear forms yields a quadric. The family of quadrics obtained by all linear combinations of the two bilinear forms is called a pencil of quadrics (see Fig. 4.1):

This is a line in the projective space of quadrics of \(\mathbb {R}\mathrm {P}^n\).
A pencil of quadrics is called non-degenerate if it does not consist exclusively of degenerate quadrics. It contains at most \(n+1\) degenerate quadrics.
A point contained in the intersection of two quadrics from a pencil of quadrics is called a base point. It is then contained in every quadric of the pencil. The variety of base points has (at least) codimension 2.
Example 3.2
The pencil of quadrics \(\mathcal {Q}\wedge C_{\mathcal {Q}}(\boldsymbol{x})\) spanned by a non-degenerate quadric \(\mathcal {Q}\) and the cone of contact \(C_{\mathcal {Q}}(\boldsymbol{x})\) from a point \(\boldsymbol{x} \in \mathbb {R}\mathrm {P}^n\setminus \mathcal {Q}\) contains as degenerate quadrics only the cone \(C_{\mathcal {Q}}(\boldsymbol{x})\) and the polar hyperplane \(\boldsymbol{x}^\perp \). It is comprised of exactly the quadrics that are tangent to \(\mathcal {Q}\) in \(\mathcal {Q}\cap \boldsymbol{x}^\perp \). To make this statement hold in all cases one has to extend the notion of tangency slightly. If \(\mathcal {Q}\cap \boldsymbol{x}^\perp = \varnothing \) in \(\mathbb {R}\mathrm {P}^n\) one should consider the complexification \(\mathcal {Q}_{\mathbb {C}} \subset \mathbb {C}\mathrm {P}^n\). Secondly, any Cayley-Klein sphere which is a (doubly counted) hypersphere should be considered tangent to \(\mathcal {Q}\) in its (possibly imaginary) intersection. Finally, note that the absolute quadric \(\mathcal {Q}\) is tangent to itself in all points, in particular in a hyperplane.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2021 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Bobenko, A.I., Lutz, C.O.R., Pottmann, H., Techter, J. (2021). Quadrics in Projective Space. In: Non-Euclidean Laguerre Geometry and Incircular Nets. SpringerBriefs in Mathematics. Springer, Cham. https://doi.org/10.1007/978-3-030-81847-0_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-81847-0_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-81846-3
Online ISBN: 978-3-030-81847-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


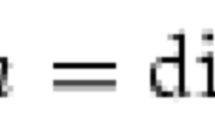

 ,
, ,
, .
.