Effect of Vorticity on Peregrine Breather for Interfacial Waves of Finite Amplitude

Abstract

A third-order nonlinear Schrödinger equation (NLSE) in one space variable has been established for a finite amplitude wave propagating along the interface of the superposition of two finite depth fluids under the circumstance of a basic current shear. Starting from this two-dimensional (1+1) NLSE, we have discussed the stability analysis for a uniform wave train, considering both the cases of air–water interface and the Boussinesq approximation. Later, the effect of shear current on Peregrine breather for both types of aforesaid interfaces has been portrayed.

1 Introduction

The stability of two-dimensional (2D) finite amplitude steady waves to arbitrary small 3D perturbations on the surface of infinite depth of water has been analysed numerically by Maclean et al. [1]. This analysis discloses that there are two different types of instabilities for finite amplitude gravity waves. The first is predominantly 2D and is associated with all the known results for particular cases as for example Benjamin–Feir instability. The second is predominantly 3D and becomes dominant when the steepness of the wave is very large. This work in the case of interfacial waves is then extended by Yuen [2]. The 2D instability of interfacial gravity waves in the particular case of long wave length perturbation and small wave steepness has been studied analytically by Grimshaw and Pullin [3] from the cubic NLSE. Later, Pullin and Grimshaw [4] have extended this analysis for interfacial gravity waves including the effect of basic current shear in the superposition of either or both the inviscid fluids and have reported both the analytical and numerical results. Later on, Dhar and Das [5] analysed the stability of gravity interfacial waves of infinite depth including the effect of shear current. There are many cases in which we observed that currents are not uniform with the water depth. In view of the above, many situations such as air–water interfaces and jet-like ebb flows can be cited, which incorporates non-uniformity of the currents with depth. In the presence of linear shear current for which velocity is uniform, it was theoretically observed that the motion of the wave continues to be irrotational and also constant vorticity can only effect the dispersion relation at first order of approximation. Choi [6] applied a pseudospectral process to analyse the interaction of nonlinear surface gravity waves including linear shear currents and observed that the maximum wave amplitude for positive shear current is much smaller than that in the absence of any shear, while the effect reverse to this is found for a negative shear current. A fully nonlinear boundary integral method to present the interaction between gravity waves and shear currents including the arbitrary distribution of vorticity was suggested by Nwogu [7]. He observed that the vorticity can significantly affect the development of modulated wave trains. It is to be noted that for analysing the nonlinear evolution of water waves, nonlinear Schrodinger equations are generally applied due to its proper reflection of modulational instability. Ever since the experimental validation of the analytical soliton like solution of NLSE, there has been much of an interest shown by the researchers towards the Peregrine Breather [8] like solution of the NLSE. Considering the case of infinite depth superposed fluids, the instances of air–water interface as well as the Boussinesq approximation have been analysed in that paper. According to Liao et al. [9], being a theoretical solution of third-order NLSE, the PB can be viewed as a prototype of Rogue waves and as such the impact of basic current shear for finite amplitude interfacial waves on PB is of considerable interest of this paper. In this chapter, we first derived a third-order NLSE for a gravity wave travelling at the interface of two superposed fluids having finite depths including the effect of basic current shear. From this evolution equation, we then performed a stability analysis in the cases of air–water interface as well as the Boussinesq approximation. Later, the effect of vorticity on Peregrine Breather has also been examined.

2 Governing Equations

We consider the interface between two inviscid and incompressible fluids in the perturbed state by the equation y = ζ(x, t). The two fluids having densities ρ ₁ and ρ ₂ (ρ ₁ < ρ ₂), respectively, are bounded by the horizontal planes at y = h ₁ and y = −h ₂. In each fluid, the basic current has constant vorticity ω ₁ and ω ₂, respectively. As three space dimensional perturbations to the primary wave are not vorticity preserving, the stability analysis presented here is limited to two space dimensional that can be considered as irrotational. Now, we employ the following transformations for dimensionless variables:

(1)

The governing equations can be expressed as

(2)

$$\displaystyle \begin{aligned} \nabla^2\phi=0, ~~~~ \nabla^2\psi=0,~~~\text{in} ~~-h_2<y<\zeta{} \end{aligned} $$

(3)

(4)

$$\displaystyle \begin{aligned} \phi_y-\zeta_t=(\phi_x-\omega_2\zeta)\zeta_x, ~~~ \text{for}~~y=\zeta{} \end{aligned} $$

(5)

(6)

(7)

where and ψ are the stream functions for the upper and lower fluids satisfying the Cauchy–Riemann relations as follows:

(8)

A solution can be found in the following form:

(9)

where P symbolises for , ϕ, , ψ, ζ, and “c.c.” means complex conjugate. Here , ϕ _n, , ψ _n (n = 0, 1, 2) are functions of y, x ₁ = 𝜖x, t ₁ = 𝜖t, whereas the ζ _n are functions of x ₁, t ₁, and 𝜖 is a slow ordering parameter. The linear dispersion relation for a plane progressive wave is given by

$$\displaystyle \begin{aligned} f(\sigma,k)=\sigma_1\sigma^2+r\sigma_2\sigma^2-(\omega_2-r\omega_1)\sigma\sigma_1\sigma_2-k(1-r)\sigma_1\sigma_2,{} \end{aligned} $$

(10)

where $\sigma _i=\tanh {kh_i},~~(i=1,2)$. We assume that the primary wave has the wave number k ₀. Therefore, we have k = 1, and the relation (10) for finding σ thus reduces to

$$\displaystyle \begin{aligned} (\sigma_1+r\sigma_2)\sigma^2-(\omega_2-r\omega_1)\sigma\sigma_1\sigma_2-(1-r)\sigma_1\sigma_2=0.{} \end{aligned} $$

(11)

From the dispersion relation, the group velocity c _g of the primary wave can be found as

$$\displaystyle \begin{aligned} c_g=\frac{-\delta_0\sigma^2+ \{(\omega_2-r\omega_1)\sigma+(1-r) \}\delta_1+(1-r)\sigma_1\sigma_2 }{2(\sigma_1+r\sigma_2)\sigma-(\omega_2-r\omega_1)\sigma_1\sigma_2},{} \end{aligned} $$

(12)

where $\delta _0=h_1(1-\sigma _1^2)+rh_2(1-\sigma _2^2)$ and $\delta _1=\sigma _1 h_2(1-\sigma _2^2)+\sigma _2 h_1(1-\sigma _1^2)$.

3 Derivation of Evolution Equation

By inserting the expansions of (9) into (2) and (3), we obtain the following solutions:

(13)

$$\displaystyle \begin{aligned}\phi_n=\operatorname{\mathrm{sech}}{(h_2k_n)}\cosh{[(y+h_2)k_n]}C_n, ~~ \psi_n=\operatorname{\mathrm{sech}}{(h_2k_n)}\sinh{[(y+h_2)k_n]}D_n,{} \end{aligned} $$

(14)

where , C _n, D _n, (n = 1, 2) are functions of x ₁, t ₁ and $k_n=n-i\epsilon \frac {\partial }{\partial x_1}$. For n = 0, we get the solutions of zeroth harmonic terms after taking Fourier transforms of (2) and (3)

(15)

$$\displaystyle \begin{aligned}\overline{\phi_0}=\operatorname{\mathrm{sech}}{(h_2\epsilon\overline{k})}\cosh{[(y+h_2)\epsilon\overline{k}]}C_0, ~~~ \overline{\psi_0}=\operatorname{\mathrm{sech}}{(h_2\epsilon\overline{k})}\sinh{[(y+h_2)\epsilon\overline{k}]}D_0,{} \end{aligned} $$

(16)

in which , $\overline {\phi _0}$, , $\overline {\psi _0}$ represent the Fourier transforms of the corresponding quantities defined by

(17)

in which , , C ₀, D ₀ are functions of $\overline {k}$, $\overline {\sigma }$.

To solve three sets of equations corresponding to n = 1, 2, 0, we consider the perturbation expansion as follows:

$$\displaystyle \begin{aligned} F_m=\displaystyle\sum_{n=1}^{\infty}\epsilon^n F_{mn},~~(m=0,1),~~ F_2=\displaystyle\sum_{n=2}^{\infty}\epsilon^n F_{2n},{} \end{aligned} $$

(18)

where F _m represents , , C _m, D _m, ζ _m (m = 0, 1, 2).

Inserting (18) in the three sets of equations and equating different powers of 𝜖, we obtain a sequence of equations; from the first set (n = 1) of equations, corresponding to (4) and (5), we obtain solutions of , , C ₁₁, C ₁₂, respectively. Similarly, from second set (n = 2) and third set (n = 0), corresponding to (4), (5) and (2), we obtain solutions of , C ₂₂, ζ ₂₂ and , , C ₀₁, C ₀₂, ζ ₀₁, ζ ₀₂, respectively. It is to be noted that the coefficients of and D _n (n = 1, 2, 0) can be expressed in terms of , C _n by using the Cauchy–Riemann relations (8). Finally, the equation resulting from (2) of the first set of equations can be expressed in the form as follows:

$$\displaystyle \begin{aligned} f(W_1,K_1)\zeta_1=-ir\sigma_2(W_1+\omega_1\sigma_1)a_1-i(W_1-\omega_2\sigma_2)\sigma_1b_1-\sigma_1\sigma_2K_1c_1,{} \end{aligned} $$

(19)

where $W_1=\sigma +i\epsilon \frac {\partial }{\partial t_1}$, $K_1=1-i\epsilon \frac {\partial }{\partial x_1}$ and a ₁, b ₁, c ₁ are quantities due to nonlinear terms. Now, inserting solutions of several perturbed quantities that appear right side of (19), applying the transformations,

$$\displaystyle \begin{aligned} \xi=x_1-c_gt_1, ~~~ \tau=\epsilon t_1{} \end{aligned} $$

(20)

and setting ζ = ζ ₁ = ζ ₁₁ + 𝜖ζ ₁₂, we obtain the following third-order nonlinear evolution equation:

$$\displaystyle \begin{aligned} i\zeta_\tau+\alpha\zeta_{\xi\xi}+\mu\zeta^2\zeta^{*}=0,{} \end{aligned} $$

(21)

in which the coefficients are available in the Appendix. It is to be noted that the nonlinear term μ of (21) comes from the interaction of primary wave with the wave-induced mean flow and the second harmonic, respectively.

4 Modulational Instability analysis

The solution of Eq. (21) is

(22)

where ζ ₀ is a real number, and the frequency shift Δσ due to nonlinearity is

$$\displaystyle \begin{aligned} \varDelta\sigma=(\mu/4)\zeta_0^2.{} \end{aligned} $$

(23)

We now introduce the perturbation on the above solution given by

(24)

in which and are small real perturbations of amplitude and phase, respectively. Next, we assume that . Inserting (24) in (21), linearising with respect to , and taking the Fourier transformation of the resulting equations given by

we obtain the nonlinear dispersion as follows:

$$\displaystyle \begin{aligned} \overline{R_1}=\sqrt{\overline{R_2}(\overline{R_2}-\zeta_0^2\mu/2)},{} \end{aligned} $$

(25)

in which

$$\displaystyle \begin{aligned} \overline{R_1}=\varOmega-c_g\lambda, ~~~~ \overline{R_2}=\alpha\lambda^2.{} \end{aligned} $$

(26)

There is an instability when

$$\displaystyle \begin{aligned} \lambda^2<(\mu/2\alpha)\zeta_0^2.{} \end{aligned} $$

(27)

At marginal stability, the perturbed wave number λ is given as

$$\displaystyle \begin{aligned} \lambda=\sqrt{\mu/2\alpha}\zeta_0.{} \end{aligned} $$

(28)

If this condition (27) is satisfied, then the maximum growth rate is

$$\displaystyle \begin{aligned} G_r=\mu\zeta_0^2/4.{} \end{aligned} $$

(29)

5 Effect of Vorticity on Peregrine Breather

The non-dimensional form of Eq. (21) is

(30)

which is obtained by employing the following transformations on the variables:

(31)

where denotes the normalised coordinate and the normalised time is denoted as . The Peregrine Breather solution of Eq. (30) is

(32)

This solution (32) is localised in both space and time. Applying the transformation (31) in (32), we obtain the Peregrine solution in its dimensional form as

(33)

6 Discussion and Conclusions

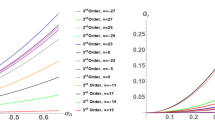
A third-order NLSE is established for gravity waves travelling at the interface of two superposed fluids of finite depth under the circumstance of a shear current. Using this equation, the instability analysis is then investigated for air–water interface (r = 0.00129) as well as the Boussinesq approximation (r → 1). Furthermore, the effect of vorticity on the peregrine breather has been taken into account. For an air–water interface from Fig. 1, we observed that G _r increases as |ω ₁| decreases for fixed depth h ₂ of the lower fluid, that is, the basic current shear in the air decreases G _r for fixed values of h ₂. Also, for fixed |ω ₁|, G _r increases as h ₂ increases. Now, from Fig. 2, we found that G _r increases as ω ₂ decreases, but the reverse effect is observed for −ve vorticity. Also, for fixed +ve vorticity, G _r decreases as h ₂ increases, and the reverse effect is observed for fixed values of −ve vorticity. Here, we found that sufficiently big value of the +ve basic current shear (ω ₂) in the water removes the modulational instability for surface gravity waves of fixed finite depth of water, but −ve basic current shear increases G _r. For the case of Boussinesq approximation, we see from Fig. 3 that G _r increases with the increment of ω ₁ for fixed values of h ₁. In Fig. 4, we have plotted curves for several values of h ₁, h ₂, ω ₁, ω ₂ for both air–water interface and the Boussinesq approximation. As h ₁, h ₂ →∞, the four curves of Fig. 4 are similar as those of Dhar and Das [5]. Here, we see that the basic current shear in the air (ω ₁) decreases G _r for surface waves of infinite depths. Furthermore, for r → 1, which corresponds to potential oceanic or atmospheric application, we found that G _r increases as ω ₁ increases for deep water surface gravity waves. For r = 0.00129 as well as r → 1, wave number λ at marginal stability has been depicted in Fig. 5 for several values of h ₁, h ₂, ω ₁, ω ₂. For the case of air–water interface, from Fig. 6, we see that the breather span increases as h ₂ decreases, while the breather span increases as |ω ₁| increases. From Fig. 7, it is observed that h ₁ has similar influence on breather span as that of the case in Fig. 6 for h ₂ and the breather span increases for increasing +ve values of ω ₂, while the reverse effect is encountered for −ve values of ω ₂. For the Boussinesq approximation, Fig. 8 depicts that the span of the breather decreases as h ₁ increases whereas the breather span decreases as ω ₁ increases. In Fig. 9, we have plotted breather solution for several finite values of h ₁, h ₂, ω ₁, ω ₂. From Figs. 10 and 11 for air–water interface, we find that for fixed value of ω ₁, ω ₂, the breather width increases both in space and in time as h ₂ decreases. In Figs. 12 and 13, we have plotted the breather solution for several finite values of h ₁, h ₂, ω ₁, ω ₂, and we observe that the breather span increases in space when h ₁, h ₂, ω ₁, ω ₂ increases for air–water interface and that the breather amplitude increases in time when h ₁, h ₂, ω ₁, ω ₂ decreases for the Boussinesq approximation.

Fig. 1

G _r vs. ζ ₀ plot for r = 0.00129, h ₁ →∞, ω ₂ = 0 and h ₂ = 2 (left) and h ₂ = 5 (right)

Fig. 2

G _r vs. ζ ₀ plot for r = 0.00129, h ₁ →∞, ω ₁ = 0 and h ₂ = 2 (left) and h ₂ = 5 (right)

Fig. 3

G _r vs. ζ ₀ plot for r = 0.00129, h ₂ →∞, ω ₂ = 0 and h ₁ = 2 (left) and h ₁ = 5 (right)

Fig. 4

G _r vs. ζ ₀ plot for r = 0.00129 (left) and r → 1 (right)

Fig. 5

λ vs. ζ ₀ plot for r = 0.00129 (left) and r → 1 (right). The region above each line indicates stable region and that of the below region indicates unstable region

Fig. 6

$|\zeta (x_1,t_1)|/\tilde {\zeta }$ vs. $\tilde {\zeta }(x_1-c_gt_1)$ plot for r = 0.00129, h ₁ →∞, ω ₂ = 0 and h ₂ = 2 (left) and h ₂ = 5 (right)

Fig. 7

$|\zeta (x_1,t_1)|/\tilde {\zeta }$ vs. $\tilde {\zeta }(x_1-c_gt_1)$ plot for r = 0.00129, h ₁ →∞, ω ₁ = 0 and h ₂ = 2 (left) and h ₂ = 5 (right)

Fig. 8

$|\zeta (x_1,t_1)|/\tilde {\zeta }$ vs. $\tilde {\zeta }(x_1-c_gt_1)$ plot for r → 1, h ₂ →∞, ω ₂ = 0 and h ₁ = 1.4 (left) and h ₁ = 1.5 (right)

Fig. 9

$|\zeta (x_1,t_1)|/\tilde {\zeta }$ vs. $\tilde {\zeta }(x_1-c_gt_1)$ plot for r = 0.00129 (left) and r → 1 (right)

Fig. 10

The Peregrine Breather for r = 0.00129, h ₁ →∞, ω ₂ = 0 and h ₂ = 2, ω ₁ = 20 (left) and h ₂ = 5, ω ₁ = 20 (right)

Fig. 11

The Peregrine Breather for r = 0.00129, h ₁ →∞, ω ₁ = 0 and h ₂ = 3, ω ₂ = 0.65 (left) and h ₂ = 5, ω ₂ = 0.65 (right)

Fig. 12

The Peregrine Breather for r = 0.00129, h ₁ = 2, h ₂ = 4, ω ₁ = 20, ω ₂ = 0.5 (right) and r → 1, h ₁ = 2.3, h ₂ = 3.8, ω ₁ = 20, ω ₂ = 0.7 (left)

Fig. 13

The Peregrine Breather for r = 0.00129, h ₁ = 2.5, h ₂ = 6.5, ω ₁ = 25, ω ₂ = 0.75 (right) and r → 1, h ₁ = 2.1, h ₂ = 3.3, ω ₁ = 15, ω ₂ = 0.69 (left)

Appendix

The coefficients appearing in Eq. (21) are

$$\displaystyle \begin{aligned} \alpha&=\frac{1}{2}\left(\frac{dc_g}{dk} \right)_{k=1} =\frac{1}{f_\sigma}[(\sigma_1+r\sigma_2)c_g^2\\&\quad + \{ 2\sigma h_1(1-\sigma_1^2)+2\sigma rh_2(1-\sigma_2^2)-(\omega_2-r\omega_1)\delta_1 \}c_g & \\ &\quad -\sigma^2\{ \sigma_1h_1^2(1-\sigma_1^2)+r\sigma_2h_2^2(1-\sigma_2^2) \}\\&\quad - \{ (\omega_2-r\omega_1)\sigma+(1-r) \}(\delta_3-\delta_4) -(1-r)\delta_1 ], \end{aligned} $$

$$\displaystyle \begin{aligned}\mu&=\frac{1}{2\sigma_1^3\sigma_2^3f_\sigma}\left[ \frac{ 2\big\{ \sigma^2\sigma_1^2(1-\sigma_2^2)-r\sigma^2\sigma_2^2(1-\sigma_1^2)+ \frac{\sigma_2\sigma_1^2\delta_5(c_g-h_2\omega_2)}{h_2}-\frac{r\sigma_1\sigma_2^2\delta_6(c_g+h_1\omega_1)}{h_1} \big\}^2 }{ \frac{c_g^2}{h_2}+\frac{rc_g^2}{h_1}-\delta_7 } \right.\\ & \quad + \frac{ \{ \sigma^2\sigma_1^2(3-\sigma_2^2)-r\sigma^2\sigma_2^2(3-\sigma_1^2)-\omega_2\sigma_1^2\sigma_2(\delta_5+\sigma+\sigma\sigma_2^2)-r\omega_1(\delta_6+\sigma+\sigma\sigma_1^2) \}^2 }{\sigma^2\sigma_2+r\sigma^2\sigma_1} \\ &\quad -\frac{2\sigma_1^2\sigma_2^2(h_1\delta_5^2\sigma_1^2+rh_2\delta_6^2\sigma_2^2)}{h_1h_2}-\sigma_1\sigma_2\{ 4\sigma^2\sigma_1^3(1-2\sigma_2^2)+4r\sigma^2\sigma_2^3(1-2\sigma_1^2) \\ &\quad -\omega_2\sigma_2\sigma_1^3( 4\sigma(1-\sigma_2^2)-\omega_2\sigma_2(1+\sigma_2^2) ) \\&\quad +r\omega_1\sigma_1\sigma_2^3( 4\sigma(1-\sigma_1^2)+\omega_1\sigma_1(1+\sigma_1^2) ) \} ], & \end{aligned} $$

$$\displaystyle \begin{aligned} \delta_1&=\sigma_1 h_2(1-\sigma_2^2)+\sigma_2 h_1(1-\sigma_1^2), ~~~ \delta_2=\sigma_1+ h_1(1-\sigma_1^2),\\ \delta_3&=h_1h_2(1-\sigma_1^2)(1-\sigma_1^2), \end{aligned} $$

$$\displaystyle \begin{aligned} \delta_4&=\sigma_1\sigma_2\{ h_1^2(1-\sigma_1^2)+h_2^2(1-\sigma_2^2) \}, \delta_5=2\sigma-\sigma_2\omega_2,\delta_6=2\sigma+\sigma_1\omega_1, \\ \delta_7&=1-r+(\omega_2-r\omega_1)c_g. \end{aligned} $$