Keywords

1 Introduction

Studying the dynamics of complex multiphase, multicomponent, or hierarchical media [1, 2], it is necessary, as a rule, to modify the classical equations of continual mechanics in order to include additional degrees of freedom associated with the presence of the internal structure [3,4,5,6,7]. Today, there is a large number of diverse approaches enabling to take into account the influence of the structure of media on their dynamical properties [1, 5, 8, 9]. In this paper, we employ an approach based on the idea of interpenetrating continua [3, 10] leading to improved models of the elastic continuum with inclusions. Previous studies of such models have been mainly dedicated to the linear dynamics [3, 4, 6, 7], 1D problems of wave propagation [10, 11], beam vibrations [3, 12], in particular, when physical nonlinearity [10, 12] and spatio-temporal nonlocal effects [10, 13] were taken into account. Expanding this approach to the 2D problems, we are going to consider the dynamic response of a geometrically nonlinear plate containing elastic inclusions to the action of an external periodic force and to modify along the way the exploration methods applied for homogeneous plates [14,15,16,17]. In this way, our studies encompass resonant, antiresonant and hysteretic phenomena, bifurcation scenario, multi-mode and chaotic oscillations caused by the interaction of nonlinear effects with the dynamics of oscillating inclusions.

2 The Model for the Dynamics of Plate with Oscillating Inclusions and Boundary Value Problem Statement

Based on the approach proposed in the works [3, 4, 12], we describe an elastic medium with oscillatory inclusions by means of a coupled system of PDEs responsible for the description of a bulk medium in the von Karman approximation [14,15,16] and an ODE describing the dynamics of an oscillating inclusion with natural frequency ω. The system under study takes the following form:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \rho h u_{tt}+D \varDelta\varDelta u -h (F_{yy}u_{xx}+F_{xx}u_{yy}-2 F_{xy}u_{xy}) = - m \rho h w_{tt} {} \end{array} \end{aligned} $$
(1)
$$\displaystyle \begin{aligned} \begin{array}{rcl} +\rho h \varOmega^2 \gamma \sin \varOmega t, \\ \varDelta\varDelta F=E((u_{xy})^2-u_{xx}u_{yy}), {} \end{array} \end{aligned} $$
(2)
$$\displaystyle \begin{aligned} \begin{array}{rcl} w_{tt} + \omega^2 (w-u)+ \tau \omega^2 (w-u)_t=0, {} \end{array} \end{aligned} $$
(3)

where u is the plate deflection, F describes the stress field, w is the displacement of a partial oscillator, ρ is the plate density, h is the plate thickness, γ and Ω are the external force’s amplitude and frequency, respectively, m ρ is the mass of an oscillating inclusion τ is the time of relaxation, Δ is the two-dimension Laplace operator, \(D=\frac {E\,h^3}{12(1-\nu ^2)}\), ν is the Poisson’s ratio.

Assume that the plate is the simply supported [15, 17] on all edges of the domain Λ = {0, a}×{0, b}. In this case, the following constrains for the mid-plane displacements S, R hold

(4)

We are looking for the approximate solution to the boundary value problem (1)–(4) in the following form:

$$\displaystyle \begin{aligned} u=U(t) \sin \frac{\pi x}{a} \sin \frac{\pi y}{b},\quad w=W(t) \sin \frac{\pi x}{a} \sin \frac{\pi y}{b}, \quad F=U(t)^2 \varPhi(x,y). \end{aligned} $$
(5)

Substituting (5) into Eq. (2), we get the equation

$$\displaystyle \begin{aligned} \varDelta\varDelta \varPhi=\frac{E\pi^4}{2a^2b^2}\left(\cos \frac{2\pi x}{a}+\cos \frac{2\pi y}{b}\right). \end{aligned} $$
(6)

The solution to this equation takes the form

$$\displaystyle \begin{aligned} \varPhi =\frac{p_x}{2} \left(y - \frac{b}{2} \right)^2 + \frac{p_y}{2} \left(x - \frac{a}{2}\right)^2 + \phi_{01} \cos\frac{2\pi x}{a} + \phi_{10}\cos\frac{2\pi y}{b}, \end{aligned}$$

where

$$\displaystyle \begin{aligned} \phi_{01}=\frac{a^2E}{32b^2},\qquad \phi_{10}=\frac{b^2E}{32a^2}. \end{aligned}$$

From the boundary conditions (4) we can determine the remaining coefficient as follows:

$$\displaystyle \begin{aligned} p_x = \frac{E \pi^2 (b^2 + a^2 \nu)}{ 8 a^2 b^2 ( 1-\nu^2)} , \qquad p_y =\frac{E \pi^2 (a^2 + b^2 \nu) }{ 8 a^2 b^2 (1 - \nu^2)}. \end{aligned} $$
(7)

Inserting expressions (5) into Eqs. (1), (3) and excluding Φ, we finally get the system of ODEs:

(8)

where \(\mu _1=\frac {D \pi ^4 (a^2 + b^2)^2}{\rho h a^4 b^4}\), μ 2 = m, \(\mu _3=\frac {16}{\pi ^2}\), \( \mu _4=\frac {E\pi ^4}{16\rho a^4 b^4 (1-\nu ^2) }(4\nu a^2b^2+(3-\nu ^2)(a^4+b^4))\). Note that dependence of μ 1 and μ 4 on plate size allows one to avoid strong constraints concerning parameter selection. Thus, in the system obtained the parameter μ 2 is regarded as a coupling parameter, μ 4 characterizes the nonlinearity. We also use the scaling Ω t → t, allowing to eliminate the dependence of the external disturbance on the frequency Ω:

(9)

Note that the first equation of the system (9) coincides with the classical Duffing equation as μ 2 = 0. So we can expect that the whole system inherits some features of this equation. Of interest is the question of what additional properties demonstrates the system under consideration.

3 Model’s Multiharmonic Solutions and Their Stability

At first we consider solutions which can be approximated by the trigonometric functions. To do this, the harmonic balance method is utilized. Since the system (9) contains cubic term, the approximate solution possesses the third harmonic in its Fourier expansion. In spite of its smallness, it should be incorporated into the approximation, for this helps to reduce the deviation of phase portrait in the (U, U′) plane from elliptic shape and avoid the discrepancy between numerical and analytical results. Thus, we are looking for a solution to (9) in the following form:

$$\displaystyle \begin{aligned} U(t)= U_1+U_3, \qquad W(t)= W_1+W_3, \end{aligned} $$
(10)

where \(U_j=c_j \sin jt +d_j \cos jt\), \(W_j=s_j \sin jt +q_j \cos jt\), j = 1, 3 are the first and third Fourier harmonics, the parameters c j, d j, s j, and q j are constants.

Substituting formula (10) into the system (9), multiplying the obtained relations in turn by \(\sin t\), \(\cos t\), \(\sin 3t\) or \(\cos 3t\) and then integrating in the interval (0, 2 π), we obtain the following formulas relating hitherto undefined coefficients:

(11)

The second equation of the system (9) yields the explicit relations for the quantities s 1, q 1 and s 3, q 3:

(12)

Thus, taking into account Eqs. (12), we can reduce the system (11) to the cubic polynomial equations with respect to the parameters c 1, d 1, c 3, and d 3 only. Fixing all the parameters but Ω and solving the system obtained, we evaluate the amplitudes of the first and the third harmonics. To reveal the general features of amplitude curves, let us specify the parameters as follows: μ 1 = 0.4, μ 2 = 0.15, μ 4 = 1.0, ω = 0.65, τ = 0.05, γ = 0.3. The plate natural frequencies derived from the linearized problem are 0.526 and 0.781.

Fig. 1a, b exhibits the amplitude curve describing the maximal values of the first harmonic, i.e., \(\max \{c_1 \sin t +d_1 \cos t\} \) = \(\max U_1\) = \(\sqrt {c_1^2+d_1^2}\), when the parameter Ω grows. The local minimum, appeared in the vicinity of Ω = ω, resonant peak, and hysteretic behavior are presented in Fig. 1a. At Ω > ω (Fig. 1b), there are two separated branches of amplitude curves.

Fig. 1
figure 1

The amplitude curves of the first harmonic (a, b) and the third harmonic (c, d). The insets exhibit detailed shape of the amplitude curves in the intervals with hysteresis

Full size image

Fig. 1c, d presents \(\max \{c_3 \sin 3t +d_3 \cos 3t\} \) = \(\max U_3\) = \(\sqrt {c_3^2+d_3^2}\) as a function of the parameter Ω. Note that the local minimum (antiresonance) is located at ω∕3, and two local maxima appear at 0.176 and 0.262.

In studying the scenario of system’s evolution, it is important to investigate the stability of solutions (10). To do this, consider the evolution of small deviations from the functions U 0(t), W 0(t) satisfying the system (9)

$$\displaystyle \begin{aligned} U(t)=U_0(t)+\tilde u(t), W(t)=W_0(t)+\tilde w(t). \end{aligned} $$
(13)

Inserting (13) into (9) and dropping out the higher-order terms, we get the following linear system:

(14)

Now we use the ansatz

$$\displaystyle \begin{aligned} \tilde u=e^{\lambda t}\varphi, \qquad \tilde w=e^{\lambda t}\psi, \end{aligned}$$

which being inserted into (14) produces the following system:

(15)

Suppose that the solution of the system (15) can be found in the form

$$\displaystyle \begin{aligned} \varphi=\sin n t+\alpha_1\cos n t, \qquad \psi = \alpha_2\sin n t+\alpha_3\cos n t, \end{aligned} $$
(16)

where α i = const, i = 1, 2, 3; n ∈ N.

First we restrict ourself to the case n = 1. Inserting (16) into (15) and equating the coefficients of \(\cos t\) and \(\sin t\) to zero, the algebraic system with respect to α i and λ can be cast:

$$\displaystyle \begin{aligned} &\alpha_1 \lambda^2 + 2 \lambda -\alpha_1 +\mu_2\left(\alpha_3 \lambda^2 + 2 \alpha_2 \lambda -\alpha_3\right)+ \frac{\alpha_1 \mu_1}{\varOmega^2}\\&\quad + \frac{3\mu_4}{4\varOmega^2}\left( c_1^2 \alpha_1 + 2 d_1 c_3 + 2 c_1 (d_1 + \alpha_1 c_3 - d_3) \right.\\ &\quad \left.+ \alpha_1 (3 d_1^2 + 2 d_1 d_3 + 2 (c_3^2 + d_3^2)) \right)=0, \\ &\lambda^2 - 2 \alpha_1 \lambda -1+\mu_2\left(\alpha_2 \lambda^2 - 2 \alpha_3 \lambda -\alpha_2\right) + \frac{\mu_1}{\varOmega^2} \\&\quad + \frac{3\mu_4}{4\varOmega^2}\left( 3 c_1^2 + d_1^2 + 2 d_1 (\alpha_1 c_3 - d_3) + 2 (c_3^2 + d_3^2)\right. \\&\quad \left.- 2 c_1 (c_3 + ( d_3-d_1) \alpha_1) \right)=0,\\ &\alpha_2 \lambda^2 - 2 \alpha_3 \lambda -\alpha_2 + \left(\frac{\omega}{\varOmega}\right)^2\left[\alpha_2 - 1\right] + \frac{\omega^2}{\varOmega} \tau\left[ \alpha_1-\alpha_3 +\lambda (\alpha_2-1)\right] =0, \\ &\alpha_3 \lambda^2 + 2 \alpha_2 \lambda -\alpha_3 + \left(\frac{\omega}{\varOmega}\right)^2\left[\alpha_3 - \alpha_1\right] + \frac{\omega^2}{\varOmega} \tau\left[ \alpha_2-1 +\lambda (\alpha_3-\alpha_1)\right] =0. \end{aligned} $$
(17)

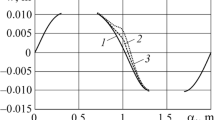
Thus, each point of the amplitude curve depicted in Fig. 1 should be analyzed concerning its stability. Using the λ solutions of system (17), the stability of two-harmonic solution (10) is estimated. The resulting curve partitioning presented in Fig. 2 contains several bifurcation points. To validate the analytical findings, the results of numerical simulations (Fig. 2, solid red line) of parent system (9) at increasing Ω are presented as well. It is evident that two-harmonic approximation (10) fits the numerical periodic solutions, producing the smooth amplitude curve, very good. The upper and lower branches forming the hysteretic transition correspond to stable modes, whereas the middle one relates to the unstable movements. This is quite common case for hysteretic zones, whereas at larger forcing frequency Ω the two zones with unstable solutions are appeared.

Fig. 2
figure 2

Stability of two-harmonic solution (10). The marks “diamond” stand for stable modes, the marks “bullet” correspond to unstable modes. Blue marks and solid red curve correspond to the analytical and numerically derived amplitude curves, respectively. Insets represent the Fourier spectra of the numerical solutions derived at Ω = 0.673 (lower inset) and Ω = 0.8 (upper inset). The value f = 1 stands for the forcing frequency Ω

Full size image

When we fix Ω = 0.673 belonging to the unstable zone, the Fourier spectrum of numerical solution shows the presence of forcing frequency Ω, additional frequency Ω 1 = 0.822Ω, and combination frequency 2Ω − Ω 1 = 1.178Ω (Fig. 2, lower inset). From this it follows that two-dimensional torus exists in the phase space. It is interesting that the stable numerical solution has the same amplitude as the unstable mode of (10).

If we fix Ω = 0.8 from the stable zone, the solution’s Fourier spectrum contains two maxima located at forcing frequency Ω and its tripled 3Ω that corresponds to two-harmonic solution (10).

Thus, in the stability zones, the bi-harmonic solution (10) describes the oscillation modes quite well. But when it losses the stability, the quasiperiodic oscillations with different number of partial and combination frequencies are realized. This produces the irregular deviations from the amplitude curve derived on the basis of solution (10).

4 The Structure of Solutions Approximated by the Four Harmonics

The careful observation of resonant peak with hysteretic zone shows the unstable solution existence at the top of curve. It is reasonable to assume that in case when the two-harmonic solution becomes unstable, the stable regime, enriched by additional harmonics, appears. To describe such a solution, we use the following expression

$$\displaystyle \begin{aligned} U(t)=z_1+\sum_{j=1}^4 U_j(t), \qquad W(t)=z_1+\sum_{j=1}^4 W_j(t),\qquad z_1=const. \end{aligned} $$
(18)

By analogy, inserting this expression into the system (9), the algebraic system with respect to the coefficients is obtained. The resulting amplitude curve at the same parameters as in Fig. 2 is drawn in Fig. 3. So, there is a bifurcational point where solution (18) is cleaved from the two-harmonic regime, which in turn becomes unstable as it is shown in Fig. 2.

Fig. 3
figure 3

Comparison of two- (lower curve) and four-harmonic (upper curve) solutions at μ 2 = 0.15

Full size image

5 Additional Numerical Studies of System (9)

As is shown in Fig. 2, the periodic solutions of the system (9) can be described in detail by different finite harmonic approximations. When the forcing frequency, nonlinearity (μ 4) and connectivity (μ 2) are large, it is instructive to supplement the studies by numerical simulations.

The numerical simulations show that when Ω = O(1), in particular, if Ω = 1.6, the coexistence of periodic and more complex attractors is encountered. Starting from the complex regime and varying Ω, the amplitude curve for this regime is plotted in Fig. 4a.

Fig. 4
figure 4

The amplitude curves at μ 2 = 0.15 (a) and μ 2 = 0.30, when the parameter Ω increases from the leftmost point (blue points) and varies from the value Ω = 1.6 (red line)

Full size image

When we double the parameter μ 2, i.e., take μ 2 = 0.3, and derive the amplitude curves in the same manner, Fig. 4b is obtained. It is observed the increasing of irregularity which is most clear exposed in the vicinity of the resonant peak. The essential separation of zones with different quasiperiodic regimes is seen as well. Auxiliary information on the structure of solutions and their bifurcations can be obtained from the analysis of Poincare sections. Since the model (9) is the harmonically forced system, the Poincare section is defined as a set of points U(t j) : t j = 2πj, j = 1, …, N. Varying Ω and omitting transient processes, the bifurcation diagrams depicted in Fig. 5 are derived at μ 2 = 0.15;0.3. The way of diagram construction is the same to that employed when obtaining Fig. 4.

Fig. 5
figure 5

The bifurcational diagrams at μ 2 = 0.15 (a) and μ 2 = 0.3, blue points correspond to the increasing Ω from the leftmost point (b). The letters stand for the Poincare sections presented below

Full size image

To find out the fine structure and types of existing regimes, the Poincare sections are analyzed in more detail. Specifying the values of forcing frequency Ω = 1;1.3;1.55 and μ 2 = 0.15, at which the complex regimes exist, the Poincare sections (Fig.6a) are derived. Closed forms of the sections tell us about the implementation of quasiperiodic regimes. Furthermore, the doubling torus bifurcation is observed (curve C at Ω = 1.55).

Fig. 6
figure 6

The Poincare sections at (a): Ω = 1 (A); 1.3 (B); 1.55 (C); (b) Ω = 0.8 (A); 0.95 (B, hidden attractor); 1.0 (C); 1.55 (D). The location of Poincare sections is marked in Fig. 5

Full size image

Figure 6b exhibits the Poincare sections of the complex regimes at μ 2 = 0.3. It follows from the diagrams presented that there are three types of quasiperiodic attractors in the given interval of values of the parameter Ω.

6 Conclusions

From the results presented above the following conclusions can be made:

  • the approximate solution comprised of the first and third Fourier harmonics illustrates well enough some features of the dynamics of von Karman plate with inclusions for wide values of forcing frequency and measure of nonlinearity. Moreover, its stability allows one to estimate correctly the bifurcational values of forcing frequency;

  • when two-harmonic solution is unstable, different scenarios of system’s evolution are observed. It is shown, in particular, that the stable four-harmonic regime forming the resonant maximum is developed. Unstability of two-harmonic solution also gives rise to the quasiperiodic regime existence;

  • incorporation of inclusions’ dynamics causes the appearance of additional natural frequencies in the medium, the development of additional regimes and scenario, increasing the hysteretic window.

It is worth noting also that the results outlined above can be useful for improving the ultrasonic diagnostics methods [2, 8], new material (acoustic metamaterial) production [16], as well as in the development of vibro-protection [9, 18] and other civil engineering structures [7].