Keywords

1 Introduction

The ongoing coronavirus disease 2019 (COVID-19) is the first global pandemic caused by a coronavirus. As of 2:45 pm CEST, September 5th, 2020, a total of 26,468,031 cases of new coronary pneumonia have been diagnosed worldwide, with a total of 871,166 deaths, of which 91 countries have confirmed cases over 10,000 [1]. At present, the epidemic has been controlled in China, but it is still spreading around the world, so fighting the epidemic is still the top priority. As of September 23th, 2020, Brazil has reported 4,624,885 confirmed cases [2], ranking third globally and still rising. Before the successful development of new drugs and vaccines, intense non-pharmaceutical interventions are particularly necessary to stop the transmission of COVID-19.

The mathematical model can help understand the nature of outbreaks and plan effective control strategies [3,4,5,6]. Many complicated mathematical models have been used to study asymptomatic infections of other infectious diseases [7,8,9]. These models reveal that changing the proportion of asymptomatic individuals affects mitigation strategies and thus changes the course of the epidemic. There is evidence that asymptomatic and mildly symptomatic individuals are infectious and can promote the rapid spread of the COVID-19 epidemic [10, 11]. For example, the isolation of asymptomatic cases by large-scale testing has led to a rapid decline in the number of new cases in Italian villages [12], indicating that asymptomatic individuals are somewhat infectious. Therefore, asymptomatic individuals should be considered when predicting epidemic trends and evaluating the effectiveness of confinement strategies. If social isolation is combined with individuals, the test-track-isolation strategy will effectively control the epidemic. Particularly, Giordano et al. considered whether the infected person had been diagnosed and the severity of their symptoms and proposed a model with eight infection stages [13]. Because diagnosed individuals are typically isolated, non-diagnosed individuals are more infectious. They found that this distinction helps explain misperceptions about the spread of the COVID-19. The SIDARTHE model distinguishes different groups related to epidemics’ evolution and considers more comprehensively than the SEIR model.

COVID-19 is caused by the infection of the coronavirus SARS-COV-2. Due to the lack of reliable information on the duration of the virus’s acquired immunity, the risk of a surge in infection cannot be assessed [14]. A recent study shows that antibodies to the virus may only last for two months, which has caused speculation that its immunity may not exist for a long time [15]. There are also other studies that reinfection after recovery most often occurs 12 months after infection, indicating that acquired immunity is only short-lived. Particularly, antibodies rapidly decay in mild cases [16, 17]. Therefore, the loss of acquired immunity should be truly considered as a more realistic model. Nevertheless, Giordano et al. [13] omitted the impact of the acquired immunity loss. Motivated by the above discussion, we derive a modified SIDARTH model by introducing the acquired immunity loss.

The organization of this chapter is as follows. In Sect. 2, we present the modified SIDARTH model. Section 3 analyzes the global stability of the disease-free equilibrium and the endemic equilibrium by Lyapunov–LaSalle techniques and graph theory. In Sect. 4, we fit the data from Brazil to analyze the model and perform sensitivity analysis on the parameters. In the end, some concluding remarks are presented to close this chapter in Sect. 5.

2 Model and Preliminaries

2.1 Modified SIDARTH Model

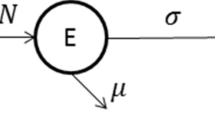
Our model is extended from the work of Giordano et al. [13] but different in the following aspects: we consider the impact of acquired immunity loss; for the sake of convincing in dynamical analysis, we adopt the standard incidence rate and include the recruitment rate Λ and the natural death χ into the model; considering that the mortality rate of the disease is much smaller than the cure rate, we ignore the death rate of diseases. Therefore, the total population of individuals N(t) is divided into seven different epidemic components as shown in Fig. 1. The modified SIDARTH model is as follows:

(1)

where ω is the acquired immunity loss rate. Other parameters and their description can be found in Ref. [13] or Table 1. The above seven components are explained as follows:

  • S: The class of susceptible (uninfected)

  • I: The class of infected (asymptomatic infected, undetected)

  • D: The class of diagnosed (asymptomatic infected, detected)

  • A: The class of ailing (symptomatic infected, undetected)

  • R: The class of recognized (symptomatic infected, detected)

  • T: The class of threatened (infected with life-threatening symptoms, detected)

  • H: The class of healed

Since N(t) = S(t) + I(t) + D(t) + A(t) + R(t) + T(t) + H(t), then

$$\displaystyle \begin{aligned} \frac{dN}{dt}= \varLambda-\chi N\Longrightarrow \lim_{t\rightarrow \infty} \sup N\leq \frac{\varLambda}{\chi}. \end{aligned}$$
Fig. 1
figure 1

Flow chart of the improved SIDARTH model

Full size image
Table 1 Parameters of the model
Full size table

Hence, the feasible region of the model (1) remains in a bounded positive invariant set Γ:

$$\displaystyle \begin{aligned}\varGamma=\left\{(S,I,D,A,R,T,H)\in R_{+}^{7}:0 <S+I+D+A+R+T+H\leq \frac{\varLambda}{\chi}\right\}.\end{aligned}$$

2.2 Basic Reproduction Number

The basic reproduction number R 0 is the key threshold parameter, which can determine whether the infectious disease will die out or spread through the population with time increases. Here, we calculate it through the next-generation matrix method. The infection components in this model are I, D, A, and R. The new infection compartment \(\mathcal {F}\) and the transition terms \(\mathcal {V}\) are given by

The Jacobian matrices F and V  for \(\mathcal {F}\) and \(\mathcal {V}\) at the disease-free equilibrium point \(( \frac {\varLambda }{\chi } , 0, 0, 0, 0, 0, 0)\) are, respectively, given by

The R 0 is defined as the spectral radius of the next-generation matrix FV −1 [18]:

Notice that the R 0 consists of four parts, representing the four modes of transmission of the coronavirus.

3 Stability Analysis

The equilibrium points will provide long-term dynamic information about the epidemic. The model (1) has two equilibrium points: one is the disease-free equilibrium (DFE) \(P_{0} = ( \frac {\varLambda }{\chi } , 0, 0, 0,0, 0,0)\), which exists for all parameter values, and the second is the endemic equilibrium point (EE) P ∗ = (S ∗, I ∗, D ∗, A ∗, R ∗, T ∗, H ∗), which is a positive solution of the following system:

(2)

We can get

(3)

For convenience, we may assume that birth and natural death are balanced (i.e., Λ = χN holds). Thus, we can conclude that when R 0 > χN∕Λ > 1, the model (1) has the unique EE P ∗.

3.1 Global Stability Analysis of the Disease-Free Equilibrium

In this section, the global asymptotic stability of the disease-free equilibrium for model (1) is discussed by a matrix-theoretic method.

Theorem 1

The disease-free equilibrium \(P_{0} = ( \frac {\varLambda }{\chi } , 0, 0, 0, 0, 0, 0)\) of model (1) is globally asymptotically stable if R 0 ≤ 1 or unstable if R 0 > 1.

Proof

We employ the method described in Ref. [19] to construct a Lyapunov function. Let x = (I, D, A, R)T and \(f(x,S):=(F-V)x -\mathcal {F}(x,S)+ \mathcal {V}(x,S)\); then for the disease, compartments can be written as

$$\displaystyle \begin{aligned}x'=(F-V)x-f(x,S).\end{aligned}$$

Let w T ≥ 0 be the left eigenvector of the matrix V −1 F corresponding to the eigenvalue ρ(V −1 F) = ρ(FV −1) = R 0. It is obvious that F ≥ 0, V −1 ≥ 0, and V −1 F is non-negative and irreducible. We construct a Lyapunov function

$$\displaystyle \begin{aligned}L = w^{T}V^{-1}x.\end{aligned}$$

Along the trajectories of system (1), we have

and when R 0 ≤ 1, we see \(\frac {dL}{dt}\leq 0\), and if \(\frac {dL}{dt}=0\) implies that x = 0, i.e., I = D = A = R = T = H = 0, S = S 0. Hence, if R 0 ≤ 1, the invariant set on which \(\frac {dL}{dt}\leq 0\) contains only point x 0. By LaSalle’s invariance principle [20], P 0 is globally asymptotically stable.

If R 0 > 1, \(\frac {dL}{dt}>0\) provided x > 0. From the continuity of the vector field in the neighborhood of P 0, we conclude that \(\frac {dL}{dt}>0\), which means that P 0 is unstable. □

3.2 Global Stability Analysis of the Endemic Equilibrium

To study the global stability of the endemic equilibrium, we use a graph-theoretic method of Ref. [19]. Next, we give the basic knowledge of graph theory. For a more detailed discussion, see Ref. [21].

A directed graph (digraph) \(\mathcal {G} = (V , E)\) contains a set V = 1, 2, …, n of vertices and a set E of arcs (i, j) leading from initial vertex i to terminal vertex j. The in degree d −(i) is the number of arcs in \(\mathcal {G}\) whose terminal vertex is i, and the out degree d +(i) is the number of arcs whose initial vertex is i. Given a weighted digraph \(\mathcal {G}\) with n vertices, define the n × n weight matrix A = [a ij] with entry a ij > 0 equal to the weight of arc (j, i) if it exists and a ij = 0 otherwise. We denote such a weighted digraph by (\(\mathcal {G}\), \(\mathcal {A}\)).

Theorem 2

If R 0 > 1, the unique endemic equilibrium P ∗ = (S ∗, I ∗, D ∗, A ∗, R ∗, T ∗, H ∗) of model (1) is globally asymptotically stable.

Proof

Set

$$\displaystyle \begin{aligned} V_{1}&= I-I^{\ast}-I^{\ast}\log\frac{I}{I^{\ast}}, V_{2}=D-D^{\ast}-D^{\ast}\log\frac{D}{D^{\ast}},\\ V_{3}&=A-A^{\ast}-A^{\ast}\log\frac{A}{A^{\ast}} ,V_{4}=R-R^{\ast}-R^{\ast}\log\frac{R}{R^{\ast}}. \end{aligned} $$

Differentiating along (1) and using formula (2) to get

$$\displaystyle \begin{aligned} \frac{dV_{1}}{dt}&=\left(1-\frac{I^{\ast}}{I}\right)((\alpha I+\beta D+\gamma A+\delta R)\frac{S}{N}-(\varepsilon+\zeta+\lambda+\chi)I) \\&\leq-\frac{\alpha}{N} (I-I^{\ast})^{2}-\beta D\frac{(I-I^{\ast})^{2}}{IN}-\gamma A\frac{(I-I^{\ast})^{2}}{IN}-\delta R\frac{(I-I^{\ast})^{2}}{IN} \\&\quad +\beta D^{\ast}\frac{(\frac{\varLambda}{\chi}-I^{\ast})}{N}\left(\frac{D}{D^{\ast}}-\frac{D I^{\ast}}{I D^{\ast}}-\frac{I}{I^{\ast}}+1\right) \\&\quad +\gamma A^{\ast}\frac{(\frac{\varLambda}{\chi}-I^{\ast})}{N}\left(\frac{A}{A^{\ast}}-\frac{A I^{\ast}}{I A^{\ast}}-\frac{I}{I^{\ast}}+1\right) \\&\quad +\delta R^{\ast}\frac{(\frac{\varLambda}{\chi}-I^{\ast})}{N}\left(\frac{R}{R^{\ast}}-\frac{R I^{\ast}}{I R^{\ast}}-\frac{I}{I^{\ast}}+1\right). \end{aligned} $$

Since \(1-x +\ln x\leq 0\) for x > 0, we get

where

$$\displaystyle \begin{aligned} \frac{dV_{2}}{dt}&=\left(1-\frac{D^{\ast}}{D}\right)(\varepsilon I-(\eta+\rho+\chi)D)\\ &\leq\varepsilon I^{\ast}\left(\frac{I}{I^{\ast}}-\frac{D}{D^{\ast}}-\ln\frac{I}{I^{\ast}}+\ln\frac{D}{D^{\ast}}\right).\\ &:=a_{21}G_{21}, \end{aligned} $$

where

where

$$\displaystyle \begin{aligned}a_{31}=\zeta I^{\ast}, G_{31}=\frac{I}{I^{\ast}}-\frac{A}{A^{\ast}}-\ln\frac{I}{I^{\ast}}+\ln\frac{A}{A^{\ast}}.\end{aligned} $$
$$\displaystyle \begin{aligned} \frac{dV_{4}}{dt}&=\left(1-\frac{R^{\ast}}{R}\right)(\eta D+\theta A-(\nu+\xi+\chi)R)\\ &=\eta D^{\ast}\left(\frac{D}{D^{\ast}}-\frac{DR^{\ast}}{D^{\ast}R}-\frac{R}{R^{\ast}}+1\right) +\theta A^{\ast}\left(\frac{A}{A^{\ast}}-\frac{AR^{\ast}}{A^{\ast}R}-\frac{R}{R^{\ast}}+1\right)\\ &\leq\eta D^{\ast}\left(\frac{D}{D^{\ast}}-\frac{R}{R^{\ast}}-\ln\frac{D}{D^{\ast}}+\ln\frac{R}{R^{\ast}}\right)\\ &\quad +\theta A^{\ast}\left(\frac{A}{A^{\ast}}-\frac{R}{R^{\ast}}-\ln\frac{A}{A^{\ast}}+\ln\frac{R}{R^{\ast}}\right).\\ &:=a_{42}G_{42}+a_{43}G_{43}, \end{aligned} $$

where

The associated weighted digraph (\(\mathcal {G}\), \(\mathcal {A}\)) has four vertices and four cycles in Fig. 2. Simple calculations yield:

$$\displaystyle \begin{aligned}G_{12}+G_{21}=0, G_{13}+G_{31}=0, G_{14}+G_{31}+G_{43}=0,G_{14}+G_{21}+G_{42}=0.\end{aligned}$$

Thus, there exist c i(i = 1, 2, 3, 4) such that \(V = \varSigma _{i=1}^{4}c_{i}V_{i}\) is a Lyapunov function satisfying \(\frac {dV}{dt} \leq 0\). Since d −(2) = 1, d −(3) = 1 and d +(4) = 1, we can calculate that \(c_{2}=c_{1}(\frac {\beta D^{\ast } }{\varepsilon I^{\ast }}+\frac {\delta R^{\ast }}{\varepsilon I^{\ast }(\eta D^{\ast }+\theta A^{\ast })}\eta D^{\ast })\), \(c_{3}=c_{1}(\frac {\gamma A^{\ast } }{\zeta I^{\ast }}+\frac {\delta R^{\ast }}{\zeta I^{\ast }(\eta D^{\ast }+\theta A^{\ast })}\theta A^{\ast })\) and \(c_{4}=\frac {c_{1}\delta R^{\ast } }{\eta D^{\ast }+\theta A^{\ast }}\). We choose c 1 = 1, and then one can verify that

\(\frac {dV}{dt} =0 \Longleftrightarrow (S, I, D, A, R, T, H) = P^{\ast }\) is the only invariant set in int(Γ), obviously. Hence, by LaSalle’s invariance principle [20], the EE P ∗ of system (2) is globally asymptotically stable. □

Fig. 2
figure 2

The weighted digraph (\(\mathcal {G}\), \(\mathcal {A}\)) constructed for the model (1)

Full size image

4 Numerical Analysis of COVID-19 in Brazil

4.1 Parameters Estimation and Numerical Verification of Stability

The numerical analysis is based on the available data of the Ministry of Health of Brazil from July 5th, 2020 (day 1) to August 10th, 2020 (day 37) (diagnosed cumulative infected (\(D+T+R+E+\int _{0}^{t}[\rho D(s)+\xi R(s)+\sigma T(s)]ds\)), and diagnosed current total infected (D + T + R), diagnosed recovered (\(\int _{0}^{t}[\rho D(s)+\xi R(s)+\sigma T(s)]ds\))) [2]. The life expectancy in Brazil is approximately 76.6 [22]. Clearly, we can obtain that the natural death rate χ = 3.5767 × 10−5 per day. Λ is approximately estimated as 2.117 × 108 × χ ≈ 7572. Next, we use the non-linear least-squares fitting function (lsqcurvefit) to minimize the following formula to evaluate other unknown parameters of the model (1) [23]:

$$\displaystyle \begin{aligned}\varSigma_{i=1}^{n}(F(x,xdata_{i})-ydata_{i})^{2},\end{aligned}$$

where xdata and ydata are the given data points. The deterministic model is numerically solved by the Runge–Kutta method. Thus, the parameters of the model can be estimated as shown in Table 1. The reported and predicted number of various infections in Brazil is shown in Fig. 3a, which shows a good fitting effect.

Fig. 3
figure 3

(a) Brazil: reported vs. diagnosed cases of infection. The ordinate axis takes logarithmic form. (b–c) Comparison of model predictions and the official data from August 11th to September 3th, 2020: diagnosed cumulative infected and diagnosed recovered

Full size image

In order to further verify the accuracy of the prediction, we collect the number of diagnosed cumulative infections and the number of diagnosed recovered individuals officially reported by Brazil from August 11th to September 3th, 2020 and compared them with the corresponding data predicted by the model in Fig. 3b and c. It can be seen that the model generally captures the short-term trend of COVID-19, but the long-term prediction requires appropriate adjustment of parameters according to changes in government strategies and medical levels.

So far, the secondary infection due to loss of acquired immunity is a sporadic phenomenon. Therefore, to obtain more accurate fitting parameters, we first assumed the immunity loss rate ω = 0 in the above fitting process. If the loss of acquired immunity is considered, assume that ω = 0.1. Now we verify the global stability analysis result of the equilibrium points using Theorems 1 and 2 in Sect. 3. First, we use the above ω value, other parameters are shown in Table 1, and we can calculate R 0 = 1.0577 > 1, so EE is globally asymptotically stable; second, we reduce α from 0.3372 to 0.2 and get R 0 = 0.6418 < 1, so DFE is globally asymptotically stable. Figure 4 supports our analysis results.

Fig. 4
figure 4

The paths of I(t), D(t), A(t), and R(t) around the DFE (a) and the EE (b)

Full size image

4.2 Sensitivity Analysis

Sensitivity analysis is used to determine the robustness of the parameter values predicted by the model. The sensitivity index allows us to measure the relative change of the basic reproduction number R 0 when the parameter changes, so as to formulate a prevention and control strategy based on the parameter. Here, according to Ref. [24], the normalized sensitivity index of R 0 relative to α is

$$\displaystyle \begin{aligned} \varUpsilon_{\alpha}^{R_{0}}=\frac{\partial R_{0}}{\partial \alpha}\times\frac{ \alpha}{R_{0}}=0.9663, \end{aligned}$$

and the sensitivity index of R 0 to other parameters can also be calculated as follows:

$$\displaystyle \begin{aligned} \varUpsilon_{\beta}^{R_{0}}=0.0023, \varUpsilon_{\gamma}^{R_{0}}=0.0288, \varUpsilon_{\delta}^{R_{0}}=0.0026, \varUpsilon_{\epsilon}^{R_{0}} =-0.2428,\end{aligned}$$
$$\displaystyle \begin{aligned}\varUpsilon_{\zeta}^{R_{0}} =-0.0430, \varUpsilon_{\eta}^{R_{0}} =4.0691e-04, \varUpsilon_{\theta}^{R_{0}} =-0.0248, \varUpsilon_{\mu}^{R_{0}} =-0.0030,\end{aligned}$$
$$\displaystyle \begin{aligned}\varUpsilon_{\rho}^{R_{0}} =-0.0027, \varUpsilon_{\xi}^{R_{0}} =-4.7017e-04,\ \varUpsilon_{\kappa }^{R_{0}} =-0.0011, \varUpsilon_{\chi}^{R_{0}} =-1.1258e-04.\end{aligned}$$

Thus, it can be concluded that R 0 is positively correlated with α, β, γ, δ, η, and negatively correlated with 𝜖, ζ, θ, μ, ρ, ξ, κ, χ.

We specifically analyze the sensitivity of transmission parameters (α, β, γ, δ) and detection parameters (𝜖, θ) related to strategy formulation as shown in Fig. 5(a–f). Interestingly, increasing α and 𝜖 will significantly increase and decrease the number of current total infected (I + D + A + R + T), indicating that the model is more sensitive to changes in α and 𝜖. Similarly, adding other transmission parameters will also increase the number of current total infected, and increasing θ will reduce the number of current total infected, but the sensitivity is relatively small. These simulation results are generally consistent with the corresponding sensitivity index. The above analysis shows that policymakers can effectively reduce the number of infections by enforcing social isolation and distancing measures, and strengthening testing and contact tracing.

Fig. 5
figure 5

(a–f) Sensitivity analysis with respect to transmission parameters (α, β, γ , δ) and detection parameters (𝜖, θ). (g) Current total infected (I + D + A + R + T) at different immunity loss rates ω after day 120. Other parameters are taken from Table 1

Full size image

Next, we analyze the impact of acquired immunity loss. We add the acquired immunity loss item to the epidemic mentioned above prediction after day 120 to simulate the number of diagnosed current total infected. As shown in Fig. 5g, with the addition of ω, a new wave of infections will appear, and the number of infections is positively correlated with ω. Effective vaccination can reduce this hidden danger and achieve long-term immunity.

5 Conclusions

We apply a SIDARTHE model to analyze the COVID-19 outbreak. After calculating the basic reproduction number by the generation matrix method, we cleverly established the global stability of the equilibrium points by combining the Lyapunov–LaSalle techniques and graph theory. Particularly, by fitting the available data of COVID-19 from Brazil, we estimated the model’s parameters and compared the official data with the model’s prediction to illustrate the latter’s effectiveness. Our main findings can be summarized as follows: (1) the DFE is globally asymptotically stable if R 0 ≤ 1 or unstable if R 0 > 1, and the unique EE is globally asymptotically stable if R 0 > 1; (2) through sensitivity analysis, reducing the infection coefficient (α, β, γ, δ) and increasing the detection coefficient (𝜖, θ) play a crucial role in disease control; (3) the loss of acquired immunity might result in another wave of infection. In short, the test-track-isolation strategy and vaccination are effective methods for controlling the epidemic. We believe this research should contribute to continuous monitoring and intervention measures to control the global COVID-19 outbreak.