Keywords

1 Introduction

Dynamics of mechanical systems with impact and friction is a challenging research topic [1]. The strongly nonlinear and numerically stiff nature of the equations of motion necessitates application of special techniques. In engineering, numerical integration techniques were developed along two main avenues. First, a large group of publications focused on models arising by application of the finite element method to elastodynamic problems [2, 3]. Also, a lot of research was devoted to multibody systems [4, 5]. A combination of the methods developed in both of these areas is needed in solving complex engineering problems, like in the discipline of flexible multibody dynamics.

In this study, the attention focused on developing an efficient time-stepping method for the integration of the equations of motion of multibody systems subject to a single unilateral and a set of bilateral motion constraints. This was achieved by seeking a better modeling of the dynamics process. First, a consistent application of Newton’s law is performed in both the impact-free and the impact phases, using concepts of Analytical Dynamics [6, 7]. Moreover, once a potential impact event is detected, an appropriate return map is applied, bringing the state of the system back to the allowable domain [8]. This avoids interpenetration and provides the preimpact conditions. Then, the postimpact state of a system involving frictional impacts is determined by solving a system of three ODEs (Ordinary Differential Equations) only, obtained through a suitable change of coordinates [7]. In this way, the problem of numerical stiffness, which is inherent to impact problems and is related to the large difference in the timescales associated with the dynamics during the free and the impact phase of the motion, is handled in an efficient manner.

Here, the methodology presented in [6] is extended to systems involving a unilateral constraint. The presence of a unilateral constraint, arising from an impact or a friction event (like slip or stick), causes additional difficulties [9, 10]. In essence, the relatively small duration of an impact event induces severe numerical stiffness in the equations of motion. Due to these inherent difficulties, an accurate and efficient numerical integration requires development of special techniques. Here, this is achieved by developing an appropriate time-stepping scheme, involving a return map, which is activated when an impact event is detected. The idea of a return map is similar to that applied earlier to other problems of mechanics [11, 12]. Here, a large modification is necessary since the configuration space is non-Euclidean [8, 13]. In addition, following the detection of an impact, the equations of motion are transformed into a set of three equations, evolving over a much smaller timescale than the others, which are solved separately, until the end of the impact event. This is based on theory presented in earlier work [7] and is a key to overcome numerical stiffness problems in an efficient manner.

The material of this paper is organized as follows. First, the governing equations of motion are presented briefly in Sec. 2. Next, the basic ingredients of the new numerical integration scheme, including the incorporation of a suitable return mapping, are presented in Sec. 3. Selected numerical results are then presented in Sec. 4.

2 Equations of Motion

The configuration of the class of systems examined is described by a set of generalized coordinates, q = (q 1, …,  q n). Their motion is represented by a point p, moving along the configuration manifold M as a function of time t [14]. The generalized velocity \( \underline{v} \) belongs to a vector space T p M. Using the summation convention on repeated indices, \( \underline{v}={v}^I\kern0.1em {\underline{e}}_{\kern0.1em I} \), with I = 1, …, n, where \( {\mathfrak{B}}_e=\left\{{\underline{e}}_{\kern0.1em 1}\kern0.5em \dots \kern0.5em {\underline{e}}_{\kern0.1em n}\right\} \) is a basis of T p M. Employing the duality pairing \( \underset{\sim}{u}^{\ast}\left(\underline{w}\right)\equiv \left\langle \underline{u},\underline{w}\right\rangle \), \( \forall \underline{w}\in {T}_pM \), where 〈⋅, ⋅〉 is the inner product of T p M selected based on the kinetic energy of the system, the elements of the cotangent space \( {T}_p^{\ast }M \) represent generalized momenta. These elements can be expressed in the form \( \underset{\sim}{u}_{\!M}^{\ast }={u}_I\;\underset{\sim}{e}^I \), with respect to a dual basis \( {\mathfrak{B}}_e^{\ast }=\big\{\underset{\sim}{e}^1\ \dots\ \underset{\sim}{e}^n\big\} \).

When there are no motion constraints, the solution is determined by Newton’s law

$$ \underset{\sim}{h}_{\!M}^{\ast}\equiv {\nabla}_{\underline{v}}\underset{\sim}{p}_{\!\!M}^{\ast }-\underset{\sim}{f}_{\!\!M}^{\ast }=\underset{\sim }{0}. $$
(1)

Covectors \( \underset{\sim}{f}_{\!M}^{\ast }={f}_I\kern0.1em \underset{\sim}{e}^I \) and \( \underset{\sim}{p}_{\!M}^{\ast }={p}_I\;\underset{\sim}{e}^I \) represent applied forces and generalized momenta, respectively, with p I = g IJ v J, where g IJ represent the components of the metric tensor at point p. Also, the covariant differential of covector \( \underset{\sim}{p}_{\!M}^{\ast } \), corresponding to tangent vector \( \underline{v} \), takes the form \( {\nabla}_{\underline{v}}\underset{\sim}{p}^{\ast }(t)=\left({\dot{p}}_I-{\Lambda}_{J\kern0em I}^K{p}_K{v}^J\right)\;\underset{\sim}{e}^I \), with I, J, K = 1, …, n, where the quantities \( {\Lambda}_{I\kern0em J}^K \) are known as affinities [15].

The presence of a contact event is signaled by an inequality

$$ \rho (p)\ge 0 $$
(2)

This establishes a new n-dimensional manifold X = {p ∈ M | ρ(p) ≥ 0}, so that the motion of point p is restricted to one side of a hypersurface ∂X of M, defined by ρ = 0 and known as the boundary of X. This makes possible the application of results from the theory of manifolds with a boundary [16]. First, among all smooth vector fields on X, only those tangent to ∂X are allowable. Moreover, the metric and the connection (affinities) are virtually unaffected at points away from the boundary, but they are affected significantly at points near the boundary [7].

The presence of equality motion constraints is expressed in the general form.

$$ {\dot{\psi}}^R\equiv {a}_I^R(q){v}^I=0,I=1,\dots, n\;\mathrm{and}\;R=1,\dots, k. $$
(3)

When a constraint is holonomic, the corresponding equation becomes ϕ R(q) = 0. Then, the equations of motion are obtained by

$$ \underset{\sim}{h}^{\ast}\equiv \underset{\sim}{h}_{\!M}^{\ast }-\underset{\sim}{h}_{\!C}^{\ast }=\underset{\sim}{0}, $$
(4)

in place of Eq. (1), where.

$$ \underset{\sim}{h}_{\!C}^{\ast }={\sum}_{R=1}^k{h}_R{a}_I^R\kern0.1em \underset{\sim}{e}^I\;\mathrm{with}\;{h}_R={({\overline{m}}_{RR}{\dot{\lambda}}^R)}^{\cdotp }+{\overline{c}}_{RR}{\dot{\lambda}}^R+{\overline{k}}_{RR}{\lambda}^R-{\overline{f}}_R. $$
(5)

The convention on repeated indices does not apply to index R, while the quantities \( {\overline{m}}_{RR} \), \( {\overline{c}}_{RR} \), \( {\overline{k}}_{RR} \), and \( {\overline{f}}_R \) are determined by the constraints (for details, see [17]). Also,

$$ \underset{\sim}{h}_{\!M}^{\ast }={h}_I\kern0.1em \underset{\sim}{e}^I\;\mathrm{with}\;{h}_I={({g}_{I\kern0em J}{v}^J)}^{\cdotp }-{\Lambda}_{L\kern0.1em I}^K{g}_{K\kern0.1em J}{v}^J{v}^L-{f}_I $$
(6)

Finally, substitution of Eqs. (5) and (6) into (4) leads to a set of n second-order ODEs in the n + k unknowns \( {q}^{I^{\prime }} \) and λ R. The formulation is completed after including the k equations of the constraints (3), which are also put eventually in a second-order ODE form, providing a natural stabilization effect on the constraints. Namely,

$$ {g}_R={({\overline{m}}_{RR}{\dot{\psi}}^R)}^{\cdotp }+{\overline{c}}_{RR}{\dot{\psi}}^R=0\;\mathrm{or}\;{g}_R={({\overline{m}}_{RR}{\dot{\phi}}^R)}^{\cdotp }+{\overline{c}}_{RR}{\dot{\phi}}^R+{\overline{k}}_{RR}{\phi}^R=0, $$
(7)

for a nonholonomic and a holonomic constraint, respectively [17].

In the absence of significant friction effects, the dominant dynamics during the contact phase is captured by a single ODE with form

$$ {({\overline{g}}_{11}{v}^1)}^{\cdotp }-{\overline{\Lambda}}_{11}^1{\overline{g}}_{11}{v}^1{v}^1-{\overline{f}}_1=0, $$
(8)

along the direction of a special coordinate x 1, starting from the boundary, with a direction normal to it [7]. All terms in Eq. (8) are of order O(1/x 1), while the terms in the remaining equations of motion are O(1). This separation of scales in the equations of motion is exploited to avoid stiffness problems during numerical integration. Finally, the introduction of friction effects causes the appearance of two more equations.

$$ {({\overline{g}}_{22}{v}^2)}^{\cdotp }-{\overline{f}}_2=0\;\mathrm{and}\;{({\overline{g}}_{33}{v}^3)}^{\cdotp }-{\overline{f}}_3=0, $$
(9)

representing action along the tangential directions of the physical space. Then, Eqs. (8) and (9) constitute a set of three coupled ODEs (Ordinary Differential Equations), capturing the dominant dynamic behavior, which is confined in the three-dimensional cotangent distribution in the configuration space affected by the contact action [7].

3 Numerical Integration of the Equations of Motion

The presence of strongly nonlinear terms in the equations of motion and the numerical stiffness in these equations necessitate application of a numerical integration method. In this work, a new time-stepping method is developed, which is set up in a way to avoid them. The basic steps of this numerical procedure are briefly summarized next.

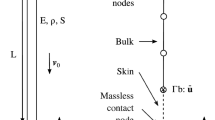
In the absence of impact and friction, a three-field augmented Lagrangian formulation is available [6]. The process starts by putting the equations of motion in a suitable weak form, leading to an efficient temporal discretization. When an impact is detected, some modifications are in order. Figure 1 is used to illustrate the scenario followed in such a case. Specifically, at time t m, the system configuration in the physical space is represented by a point p m, which lies in the interior X o of the constrained configuration manifold X. At the next time t m + 1, the new configuration point p m + 1 is located outside X, indicating that an impact event may have occurred during the current time step. In practice, this is verified by using a suitable contact detection algorithm, which determines both the location of the contact point and the normal contact direction in the physical space [18]. The next step is to return to a point on the boundary ∂X, representing the configuration of the system where the impact event took place. This is achieved through the development and application of an appropriate return mapping (for details, see [6]). Similar maps have also been constructed in other situations [11, 12]. In this work, this step is performed with more care, by taking into account that the configuration manifold M is nonflat [13], in general, as explained briefly next.

Fig. 1
figure 1

Illustration of the total action of the return map

Full size image

The boundary ∂X is locally convex. Then, the task of returning from p m + 1 back to a point on the boundary ∂X in a unique way is reduced to finding the autoparallel starting from point p m + 1 and ending on ∂X, having the shortest length. The iterations are stopped when the final point of this process, say \( {p}_{m+1}^{-} \), is located inside X and sufficiently close to the boundary ∂X. Symbolically, these can be represented by

$$ {p}_{m+1}^{-}=\mathfrak{P}\left({p}_{m+1}\right). $$
(10)

The overall equations of motion are solved in a block-wise manner. This means that, assuming a fixed position, the system’s velocity is calculated, followed by an update to the positions. If the updated positions lead the system’s position outside the boundary, an iteration of the return map procedure takes place, driving the position back to the boundary. This is repeated until both the overall residual and the returned positions converge. The final point \( {p}_{m+1}^{-} \) lies inside the constrained configuration manifold X, sufficiently close to the boundary ∂X. This result provides the updated values at the position level and the equations of motion are solved to provide the corresponding velocity vector \( {\underline{v}}_{\kern0.1em m+1}^{-} \). If this vector points toward the interior X o of the constrained manifold, the solution process continues without considering occurrence of an impact. However, if vector \( {\underline{v}}_{\kern0.1em m+1}^{-} \) points toward the boundary ∂X of the constrained manifold, its value is used as a preimpact velocity and the solution process is continued in the next step, which leads to determination of the postimpact state, say (\( {p}_{m+1}^{+},{\underline{v}}_{\kern0.1em m+1}^{+} \)).

The equations of motion within the boundary layer are first put in a weak form. For their numerical discretization, special curves are selected to approximate the natural trajectory near the boundary of manifold X. The first natural choice is the autoparallel curves [15]. However, using such curves for the geometric discretization of the natural trajectory inside the boundary layer leads to numerical problems since the value of v 1 takes relatively small values. Consequently, such curves tend to become tangent and stay close to the boundary ∂X. For this reason, a higher order set of curves on X is considered, giving rise to a geometric cubic spline on manifold X in the vicinity of the boundary ∂X [19]. The numerical integration advances up until the value of \( {x}_{m+1}^1 \) becomes equal to the value of the boundary layer width b. At that point, the velocity of the system is first transformed from the x-coordinate system, which was employed for performing the evaluations within the boundary layer, back to the original q-coordinate system. In addition, the position of the system is assumed to remain virtually equal to the preimpact position \( {\underline{q}}_{m+1}^{-} \). Using these values as initial conditions, the numerical integration continues according to the process described for impact-free motions.

4 Numerical Results

A set of numerical results is presented next, illustrating the accuracy and effectiveness of the new methodology, applied to systems with rigid members. First, dynamics of the classical problem of a ball bouncing on a rigid plane is considered. Next, a more involved problem, considering impact dynamics of a die with a rigid ground, is examined.

4.1 Bouncing Sphere

The first example is a rigid sphere of unit mass and radius r= 0.1 m, bouncing on a rigid plane. The sphere motion starts with a zero initial velocity when its center is located at a height h = 0.5 m, under the action of gravity, with gravity acceleration g = −9.81 m/s2. The position of its center is determined by a single Cartesian coordinate, χ 1, having its origin on the ground. For this case, an analytical solution is available for both the impact-free phase and the impact phase.

Some typical results are presented in Fig. 2, obtained by employing the new time-stepping scheme. First, Fig. 2a shows the histories of the vertical displacement of the lowest point of the sphere, for two values of the kinematic coefficient of restitution e. Likewise, Fig. 2b depicts the histories of the corresponding mechanical energies. As expected, there is no energy dissipation for the value e = 1, corresponding to an elastic impact and leading to an infinite number of contact events. However, this picture changes for e = 0.8, leading to a gradual loss of mechanical energy at each impact. This is demonstrated by Fig. 2b and is reflected by the decreasing amplitude of the displacement in Fig. 2a.

Fig. 2
figure 2

A sphere bouncing on a rigid ground: (a) vertical displacement and (b) mechanical energy, for e = 1 and 0.8

Full size image

The results of Fig. 2 were compared and found to be in virtual coincidence with the results from the exact solution, in both the free and the impact phases. For example, Fig. 3 presents results determined during the first impact phase. These results were obtained for a value of a maximum penetration ratio δ = 0.8. In general, the values of the parameters δ and e are needed in order to determine the force \( {\overline{f}}_1 \) in Eq. (8). First, Fig. 3a shows histories of the vertical displacement of the sphere, while Fig. 3b depicts the corresponding histories of the vertical velocity, determined for e = 1. The results obtained reveal that application of the new numerical discretization procedure leads to a virtual coincidence with the analytical solution by using a relatively small number of time steps. More specifically, this was achieved by using only two time steps in the case examined. Next, the emphasis was put on a comparison with classical integration methods. In particular, results obtained by employing the HHT- α method are presented next. Several values of the numerical dissipation parameter α were tried, in the range 0 ≤ α ≤ 1/3, with β = (1 + α)2/4 and γ = α + 1/2. The results presented next were obtained for α = 0, but no noticeable differences were detected for other values of α. First, it was found that the impact phase interval should be split to at least seven steps, before the HHT- α method can run and yield a solution. Also, quite a large number of time steps are required in order for the numerical results to be of a reasonable accuracy. This comparison illustrates that the new integration method is more effective, since it leads to the exact solution with a much bigger time step. This, instead, is attributed to the fact that the new method exploits the geometric properties of the system examined during its dynamic evolution in the impact phase.

Fig. 3
figure 3

Histories obtained during the first impact phase by the analytical solution, the new geometric method and the HHT- α method for (a) the vertical displacement and (b) the vertical velocity of the sphere, with e = 1

Full size image

4.2 Die Tossing

The next set of numerical results was obtained for the motion of a die thrown over a rigid ground. This motion is viewed from a coordinate system Oxyz, which is fixed on the ground. It is affected by gravity, acting along the negative z-axis and involves frictional impacts. The die considered is a homogeneous rigid cube, with a mass of 0.016 kg and edge length of 0.02 m. It starts from a position above the ground, with the cube edges parallel to the axes of the Oxyz coordinate system. Moreover, the initial position and velocity are chosen to satisfy two scenarios. In the first, the cube executes a planar motion, taking place in the vertical plane Ozx. In the second scenario, the initial conditions are modified so that the cube exhibits a spatial motion and hits the ground with one of its vertices. In all cases, the value of the kinematic restitution parameter was chosen as e = 0.5 [20]. Moreover, the maximum penetration ratio was selected as δ = 0.20, while the value of the coefficient of friction between the die and the ground was chosen as μ = 0.05 or 0.20.

First, in the results presented in Fig. 4, the initial position of the cube center is at (0, 0, 0.3) m, while its initial velocity is (0.5, 0, −0.5) m/s. Moreover, the initial angular velocity of the cube is (0, 10, 0) rad/s. These initial conditions lead to a subsequent planar motion of the cube. First, Fig. 4a shows the projection of the trajectory executed by the cube center of mass on the vertical plane Ozx for the values selected for μ. Likewise, Fig. 4b shows the projection of the same trajectory on the horizontal plane Oxy. Then, the histories of the two nonzero velocity components of the mass center are shown in Fig. 4c. Finally, the history of angular velocity of the cube is presented in Fig. 4d. A remarkable result is that, for the case with μ = 0.20, the cube starts moving in the opposite direction than it was thrown after the first impact, as it becomes clear by Figs. 4a and c.

Fig. 4
figure 4

Plane die tossing. Projection of the trajectory of the cube center on: (a) the vertical Ozx and (b) the horizontal plane Oxy. Histories of (c) the velocity components of the mass center and (d) the angular velocity of the cube

Full size image

Next, in the set of results presented in Fig. 5, the initial position of the cube center and its initial velocity are kept the same as in the previous case. However, an angular velocity component about the x-axis is added, so that the initial cube angular velocity is (10, 10, 0) rad/s. These initial conditions lead to a general spatial motion of the cube. First, Fig. 5a shows the projection of the trajectory executed by the cube center of mass on plane Ozx for the two values selected for the coefficient of friction. Likewise, Fig. 5b shows the projection of the same trajectory on plane Oxy.

Fig. 5
figure 5

Spatial die tossing. Projection of the trajectory of the cube center on (a) the vertical plane Ozx and (b) the horizontal plane Oxy

Full size image

Finally, the emphasis was placed on investigating the dynamics of the cube arising during the first impact phase. Specifically, the history of the tangential velocity component V x of the cube contact point is presented in Fig. 6a, while the corresponding histories of the tangential velocity V y and the normal velocity V z are included in Fig. 6b, for the plane motion of the die. Similar results were also obtained for the spatial motion of the die. In all cases examined, a smooth change is observed to occur in the velocity components throughout the impact phase.

Fig. 6
figure 6

Velocity components of the cube contact point during the first impact phase: (a) tangential component V x (plane motion), (b) tangential component V y and normal component V z (plane motion)

Full size image

5 Synopsis and Extensions

In the first part of this study, the basic steps of a new time stepping scheme were presented, for capturing dynamics of multibody systems involving impacts and friction. A vital part of that scheme was the development of a new return map. This need arises from the fact that the configuration space of the class of systems examined is non-Euclidean. Specifically, application of this map in order to return a point from the outside to the boundary of the constrained manifold, defined by a unilateral constraint, leads to a curve with the shortest length among a special set of curves emanating from the outer point. In addition, the final curve selected crosses the boundary of the allowable motions in a normal way. In this way, the new return map is a generalization of the classical orthogonal projection operation performed in Euclidean spaces. Based on these ideas, a complete numerical algorithm was set up, providing the means to capture dynamics of multibody systems involving a single impact and several bilateral constraints. Finally, the accuracy and effectiveness of the new time stepping scheme were verified in the second part of this work, by presenting numerical results for two representative mechanical examples.

The methodology developed can be applied to discrete mechanical systems subject to a set of bilateral motion constraints and a single unilateral constraint. A first possible step is to extend it in order to cover cases involving permanent contact. In such cases, the contact is modeled as a bilateral constraint up to a point where separation of the contacting bodies occurs. Another useful extension of this study is to cases with multiple impacts. This is a theoretically challenging subject, involving consideration of configuration manifolds with corners, having a significant engineering importance [5, 16].