Keywords

1 Introduction

Recently, many papers have studied the coupling between mechanical systems, where rigid blocks are combined with devices or structures. An interesting work is [1], where the effectiveness of base anchorages is studied. In [2, 3], the effects of base isolated systems are investigated. Another interesting technique to improve the behaviour of rigid block-like structures is the mass-damper dynamic absorber, as highlighted in [4, 5]. Instead, a safety device can be the mass damper, where in [6, 7] it is modelled as a single degree of freedom that runs on the top of the block. The use of semi-active anchorages was investigated in [8], whereas an active control technique was used to protect the rigid block from overturning [9].

An interesting issue is the protection of frame structures or bridges by using rocking rigid blocks. The paper [10] investigated the effects of a structure placed on a rocking podium, whereas [11] discussed the rocking isolation. An interesting technique to protect frame structures by using a rigid block can be carried out using a rigid coupling between a frame and a rocking wall, as showed in [12]. Instead, [13] studied an elastic link between the frame structure and the block.

Recent papers deal with the use of inerter devices to improve the dynamic and seismic response of structures. For instance in [14, 15], Tuned Mass Damper Inerter devices were used to improve the behaviour of base isolated structures. Instead, in [16, 17], the controlled dynamics of two adjacent structures linked by a spring-dashpot-inerter was investigated.

The coupling between a frame structure and an external rocking wall is examined in this chapter with the purpose of improving the dynamical behaviour. A multi-storey frame structure is modelled by means of an equivalent two-degree-of-freedom linear system, whereas the classical model of rigid block is used to represent the wall. The top of the block is connected to the first storey of the frame structure with an elastic device. The inerter devices considered in this chapter are connected to the vertical sides of block and to the ground as investigated in [18] for stand-alone rigid blocks. The inerter devices possess the ability to increase the inertial mass of the mechanical system introducing apparent inertial mass, which depends only on the acceleration.

The dynamical behaviour of coupled system is analyzed by means of numerical integrations of the equations of motion. Simulations are performed using several earthquakes records as forcing term. A parametric analysis is carried out, and the results are organized in gain maps. The maps show the ratio between the maximum displacements or drifts of coupled and uncoupled systems in the system’s parameters. Wide regions of the maps, where coupling is effective, are found. Results also show that the effectiveness of the coupling can be increased with the use of inerters and makes possible the use of blocks with smaller dimensions.

2 Mechanical System

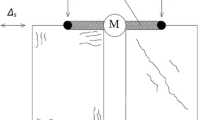
The mechanical system is portrayed in Fig. 1. It is a planar structural system composed of a 2-DOF linear system, which represents the frame structure, and a rocking block whose purpose is to reduce the horizontal displacement derived from a base motion. The mass of the rocking block is M = ρ × 2b × h 1 × s, where ρ = 2500 kg/m3 and s is the length (orthogonal to the plane of the figure). An elastic device represents the connection between the first level of the 2-DOF system and block. Two inerter devices, whose apparent inertial mass is m R, are considered. They connect the ground and the vertical sides of the block. The inerter devices posses the notably ability to behave as virtual added masses since they can transform the rotational inertia of a flywheel in translational inertia.

Fig. 1
figure 1

Coupling of a frame with rocking block: (a) Mechanical and geometrical characteristics of the reduced-order model; (b) Positive directions of the Lagrangian parameters

Full size image

As observed in previous paper [13], the effectiveness of the coupling depends on the ratio between the mass of the block and the mass of the frame, in particular to achieve good results the mass of the block should be about 10–30% of the total mass of the structure to be protected. The introduction of inerter devices is intended to make coupling effective by using relatively small block, since the inerter devices can provide the additional mass needed.

The procedure developed in [19] allows the two-degree-of-freedom system to represent the main dynamic characteristics of a general multi-storey frame structure. Such a dynamic equivalence refers to stand-alone frame structures. It is based on two main assumptions: (i) the frequency of the first mode of the multi-DOF system is the same of the 2-DOF system and (ii) the modal components of the 2-DOF system and those ones associated to the two reference storeys of the multi-DOF system are equal. These assumptions implicitly require that the frame structure has to be sufficiently regular. It is reasonably assumed that, if the dynamic equivalence works correctly for stand-alone structures, it works correctly for the same structures also after the coupling with an external rocking block.

2.1 Equations of Motion

The dynamic response of the reduced-order model is defined by three Lagrangian parameters: two displacements u 1 and u 2, and the rotation θ of the block. In order to represent the motion of the system when block rocks around either left corner or right corner, two sets of three nonlinear equations of motion are derived through a Lagrangian approach, whose positive directions of Lagrangian parameters u 1, u 2, and θ are shown in Fig. 1b. In this section, only the first set of equations, which describes the motion of the system when the block is rocking around left corner, are reported. The second set of equations, which describe the rocking motion around the right corner, can be found in [20]. The two sets of equations that describe the motion of the system without inerter devices are reported in [13].

The introduction of the inerter devices modifies the equations by adding supplemental inertia terms, since they introduce apparent inertial masses in the system (underlined term). The equations of motion are

(1)

where m R is the apparent inertial mass of the inerter devices; \(J_A=J_C+M (b^2+h_b^2)\) and J C are the total polar inertia of block with respect to left base corner and to its centre, respectively; quantity Q 1 reads

(2)

2.2 Uplift and Impact Conditions

When the stabilizing moment M R = M g b, which depends on the weight of the block, is smaller than the overturning moment \(M_{O} =-M\,\ddot {x}_{g} (t)\, h_{b} +k_{C} u_{1} (t) h_{1}\) that depends on inertial forces and elastic reaction of the coupling device, the uplift of the block around left base occurs. If uplift does not take place, the elastic reaction of coupling device depends only on the displacement of the 2-DOF system. By simplifying the sum of two previous moments, the uplift acceleration \(\ddot {x}_{g} =a_{UP} \) around base left corner is obtained. The uplift acceleration reads

$$\displaystyle \begin{aligned} {{a}_{UP}(t)}=\frac{g}{\lambda }+\frac{{{k}_{C}}{{u}_{1}}(t){{h}_{1}}}{M{{h}_{b}}}, \end{aligned} $$
(3)

where λ = h b∕b is the slenderness of the block. If there is no coupling, the same uplift condition of a stand-alone block is obtained. The uplift condition around the right corner can be found in [20].

During rocking motion, when the rotation θ(t) approaches zero, an impact between the block and the support takes place. The impact condition provides the angular velocity as a function of the pre-impact velocity , , where r = (J O − 2bS y∕J O)2 is the restitution coefficient. Quantity J O represents polar inertia of block with respect to one of the two base corners, whereas the static moment of the block with respect to a vertical axis passing through one of the two base corners is defined by S y = ±M b (sign +  refers to a block that re-uplifts around the left corner, sign − refers to a block that re-uplifts around the right corner). The coefficient η represents an additional loss of mechanical energy. In case the impact is perfectly rigid, then η = 1; otherwise, it is less than unity. Such a coefficient can be experimentally obtained as in [5]. In the analyses carried out in this chapter, the value of η is fixed (η = 0.9). Finally, it is worth to notice that the restitution coefficient r is the same as that of the classical stand-alone rigid block model [21].

3 Parametric Analysis

The dynamical behaviour of the coupled mechanical system is investigated by means of an extensive parametric analysis, in which three parameters have been varied: (i) the base dimension of the block 2b, (ii) the coupling stiffness ratio β = k C∕k 1, and (iii) the apparent inertial mass ratio of the inerter devices γ = m R∕M (see Fig. 1).

In the parametric analyses, the 2-DOF system refers to two buildings whose proprieties are shown in Table 1. Considering the values reported in Table 1, the dynamical characteristics of the equivalent model, shown in Table 2, are obtained from the procedure described in [19].

Table 1 Proprieties of the two reference buildings
Full size table
Table 2 Characteristics of the reduced-order models
Full size table

The two modes of the 2-DOF system have a modal damping ratio ξ, that is reported in Table 2.

3.1 Gain Coefficients

The displacement u 1 and the drift u 2 − u 1 of the system with coupling and inerters are compared to those obtained from the stand-alone frame in order to provide an indication of the efficiency of the method. The comparison is carried out introducing two gain coefficients as follows:

$$\displaystyle \begin{aligned} \alpha _{1} =\frac{\max \left|u_{1} (t)\right|}{\max \left|\tilde{u}_{1} (t)\right|} ,\, \, \, \, \alpha _{2} =\frac{\max \left|u_{2} (t)-u_{1} (t)\right|}{\max \left|\tilde{u}_{2} (t)-\tilde{u}_{1} (t)\right|}, \end{aligned} $$
(4)

where the displacements \(\tilde u_1\) and \(\tilde u_2\) refer to the stand-alone frame. Equation (4) shows that the effectiveness of the coupling increases when α 1 and α 2 decrease. Specifically, values of the gain coefficients less than unit represent good performances of the coupling.

The purpose of parametric analysis is to evaluate gain coefficients α 1 and α 2 in a specific parameter plane and summarize the results in gain maps.

3.2 Seismic Excitation

Four earthquake records were used as exciting input. The earthquake records (later called with underlined name) are listed below:

  • Kobe, Takarazuka-000 station, ground motion recorded during the 1995 Japan earthquake

  • L’Aquila, IT.AQV.HNE.D.20090406.013240.X.ACC station, ground motion recorded during the 2009 Italian earthquake

  • Pacoima, Dam-164 ground motion recorded during the 1971 San Fernando, California earthquake

  • Parkfield, CO2-065 ground motion recorded during the California earthquake 1966

4 Discussion of the Results

The gain maps summarize the results of the simulations and represent the contour plots (for a single earthquake) of gain coefficients α 1 and α 2 in a specific parameter plane. When gain parameters are less than unity, the region is coloured in light grey. These regions are named gain regions and define the optimal design parameters.

Figure 2 shows the maps obtained for the three-storey frame (first rows of Tables 1 and 2) in the parameter plane γ-β, whose geometrical scheme is portrayed in Fig. 2a. The maps in Fig. 2b refer to two earthquakes. In particular, the first row refers to Pacoima and the second row to Parkfield earthquakes. The maps show that the ability of coupling with external wall to reduce displacement increases when the apparent inertial mass ratio γ grows up, since the gain regions become wider and the value of gain coefficients reduces. Moreover, when γ = 0 (i.e., when there are no inerters), the coupling is not able to reduce the displacement of the frame because gain coefficients are higher or close to unity. The minimum values of the α 1 gain coefficient are located along the straight dotted lines, whereas the minimum values of the α 2 coefficient are along the dash-dotted straight lines. It is possible to observe that the minimum values of the α 1 coefficient do not depend on the seismic excitation. Several numerical simulations, carried out using many other earthquake records, have confirmed this assertion. Instead, the straight lines of minimum values of the α 2 coefficient change with the earthquake.

Fig. 2
figure 2

Gain maps: (a) Geometrical coupling scheme; (b) Gain maps α 1 and α 2 for a fixed base dimension of the block 2b = 1.0 m and two different earthquakes (Pacoima and Parkfield)

Full size image

The effects of the coupling with an external rocking wall equipped with vertical inerters are investigated by means of the observation of some time histories. In particular, the parameters of the coupled system are indicated with the letters A, B, and C in Fig. 2b. The time histories of displacement u 1 and of rocking angle θ of a system whose proprieties are labelled with A, are shown in Fig. 3a. The point A (γ = 8, β = 0.10) lies on the dotted line and is inside the gain regions of both gain coefficients. The time histories of u 1 and θ (Fig. 3a) reveal that the block and the first storey of frame move in counter phase (see the signs convention of the Lagrangian parameters in Fig. 1b). Therefore, the rocking block behaves as a tuned mass damper with respect to the first storey of the frame and is able to reduce the displacements of the structure. Figure 3b shows the time histories of a coupled frame whose parameters are labelled with B. Point B (γ = 8, β = 0.24) lies on a dash-dotted line and is inside the gain regions of both maps. The examination of the graph of Fig. 3b) reveals that motion of block and first storey is slightly out of phase. Therefore, wall does not behave correctly as a tuned mass damper; nevertheless, it is still able to reduce the displacements. Lastly, point C (γ = 8, β = 0.40) is outside the gain region of the first gain coefficient (but is inside the gain region of the second gain coefficient). In fact, Fig. 3c displays that the block and the first storey are approximately in phase and an increase of the displacement of the first storey with respect to the stand-alone frame occurs.

Fig. 3
figure 3

Time histories under Pacoima earthquake: (a) Point A; (b) Point B; (c) Point C

Full size image

The analyses are carried out also for a five-storey frame as shown in Fig. 4a (second rows of Tables 1 and 2), coupled with a block whose base is 2b = 1.5 m. The α 1 and α 2 gain maps, built for two different earthquakes (Kobe and L’Aquila), are showed in Fig. 4b. The seismic records used in this analysis are different from those used in Fig. 2 to show that the proposed method works correctly with different seismic records. Differently from Fig. 2, the maps of Fig. 4b show the gain coefficient α 2 in the parameter plane 2b-β. The maps on the left column refer to the coupling without inerters, whereas those on the right column consider a coupling with inerters, with apparent mass ratio γ = 20. The performance of the coupled system with rocking block grows up when the apparent inertial mass ratio γ increases; in fact, the gain regions may become larger and the value of the gain coefficients decreases.

Fig. 4
figure 4

Gain maps: (a) Geometrical coupling scheme; (b) Gain maps α 2 for Kobe and L’Aquila (left column γ = 0; right column γ = 20)

Full size image

As further consideration, the oscillation period of rigid blocks depends on the rocking amplitude because of their natural nonlinearity. When the block starts to move in counter-phase motion, it can keep moving in counter phase also if a change of characteristics of motion occurs in time by appropriately adapting the rocking amplitude. The block acts almost as a hysteretic mass damper [22], being able to work properly in wide ranges of frequencies.

5 Conclusions

In this chapter, the coupling between a 2-DOF system and an external rocking block was investigated with the aim to improve the behaviour of the coupled system under base excitations. An inerter device was introduced to add virtual mass to the system. The connection of the top of block to the first level of the of 2-DOF system is carried out by means of an elastic device. Under sufficient regularity of the multi-DOF frame structure, the main dynamical characteristics of such multi-DOF system can be represented by an equivalent 2-DOF model. The behaviour of coupled system was studied by numerically integrating the nonlinear equations of motion. The coupling with block and the use of inerters were considered effective for the structure when there is a reduction in the displacements and drifts of the coupled system with respect to the stand-alone frame. Many analyses were carried out considering four earthquakes records. The gain maps, which provide the ratio between maximum displacement (or the drift) of coupled and uncoupled system, were used to collect the results of an extensive parametric analysis.

The analysis showed that wide gain regions, where the coupling improves the dynamical behaviour of the coupled system with respect to the stand-alone frame, exist in the parameter plane. In these gain regions, the block behaves as a tuned mass damper for the frame system. The size of the gain regions strongly depend on the apparent inertial mass of the inerter devices. In fact, higher is the value of the apparent inertial mass, smaller can be the dimensions of the block to achieve the same reduction of the displacements.