Influence of Model Nonlinearities on the Dynamics of Ring-Type Gyroscopes

Abstract

This paper investigates the nonlinear dynamic response of a rotating ring that forms an essential element in macro ring-based vibratory gyroscopes that utilize oscillatory nonlinear electromagnetic forces. The derivation of the nonlinear equations that represent the motion of a macro ring gyroscope with nonlinear electromagnetic forces is performed. Understanding the effects of model nonlinearities is considered important for characterizing the dynamic behavior of such devices. Dynamic response analysis in the driving and the sensing directions are investigated via time responses, phase diagram, and Poincare’s map when the angular input rate and the nonlinear electromagnetic forces act together.

1 Introduction

The linear and nonlinear dynamic response behavior of rotating rings has been studied in several recent articles. The nonlinear equations of motion considering only the in-plane vibrations of a ring were derived in [1]. The formulation of nonlinear equations of motion of ring-type gyroscope using two vibration modes has been performed employing Galerkin’s procedure in [2]. The influence of rotation and flexible base on the natural frequencies and mode shapes have been investigated in detail in [3]. The modal behavior as well as stability of rotating rings in 3D under magnetic levitation has been studied via an analytical model and validated employing Finite Element Analysis [4]. The Coriolis forces induced in the ring gyroscope due to the ring’s rotation cause the resonant mode to shift vibration into the next resonance mode, as described in [5].

The influences of extensional and shear deformation and inertia on natural frequency differences have been performed in [6]. The plane wave motion to solve the fixed deflection, natural frequency split, and mode contamination of the rotating ring-shaped periodic structures have been analytically examined [7].

In the present paper, the nonlinear dynamic behavior of rotating flexible rings for use in vibratory angular rate sensors has been studied via numerical simulations. A homogenous, isotropic ring is chosen as the resonator. The investigation of dynamic response analysis and the rotating macro ring gyroscope’s stability behavior has been studied by [8] and Gebrel et al. [9] by considering the linearized model associated with the second flexural modes. In [9], a theoretical model for generating nonlinear electromagnetic excitation forces is developed. The schematic of the rotating ring geometry used in the present study has been described in detail in [8, 9].

One of the most critical challenges in constructing ring-based vibratory gyroscopes is the requirement to operate at one of the highly resonant natural frequencies in order to maximize device sensitivity. However, large resonant amplitudes tend to bring out the undesirable nonlinear effects due to geometric as well actuator nonlinearities. Consequently, the dynamic response of thin circular rings and consideration of input nonlinear actuator dynamics is warranted to gain a complete understanding of performance enhancements that can be achieved for this class of gyroscopes.

In the present paper, a mathematical model that represents the nonlinear dynamic behavior of a ring-type gyroscope is formulated. The nonlinear equations of motion are simplified by considering only the highly resonant second flexural mode the device utilizes and by ignoring the presence of extensional modes of vibration. Due to gyroscopic coupling present in the system and angular input rate, the natural frequency variations have been described in the prior study [9]. A suitable electromagnetic actuator model has been developed for the purposes of examining the nonlinear dynamic response.

2 Equation of Motion

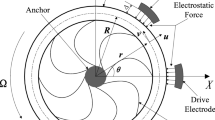
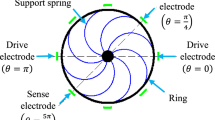
In this study, the nonlinear equations of motion have been obtained by considering that the circumferential strain in the mid-surface is zero, and the equations of motion have been reduced to a suitable discrete form via Galerkin’s procedure and the resulting equations permit the application of dynamic response analysis. The ring used for the present study is assumed to possess isotropic and homogenous material properties. Besides, under the Euler-Bernoulli theory, the transverse shear deformation influence is neglected since it is assumed that plane sections remain plane as well stay normal to the neutral surfaces after deformation [10]. Figure 1a shows the ring geometry and relevant parameters used in this paper. The stiffness components k _r and k _θ, respectively, denote the radial and circumferential components, while u _r and u _θ symbolize the transverse and circumferential displacements. The eight support springs considered to represent the flexible mounting are assumed to possess significantly low stiffness and are expected not to have an influence on the ring dynamics. A body-fixed set of axes X, Y, Z has been assigned to represent the angular motion of the ring with respect to an inertial frame R. In this formulation, the curvilinear surface coordinates α ₁, α ₂, and α ₃ are used for locating the neutral surface elements.

Fig. 1

(a) Ring geometry and parameters. (b) Degenerate second flexural mode shapes

The second flexural mode shapes that possess identical natural frequencies for the ring are known as degenerate modes shapes and are separated by 45 degrees as shown in Fig. 1b. It may be noted that the presence of degenerate mode shapes is due to the ring symmetry. The geometry and parameters used in the present paper have been described in detail in the prior research [9].

In this paper, the nonlinear equations of motion in terms of the generalized coordinates associated with the flexural coordinates A _n and B _n are developed to investigate a ring gyroscope’s nonlinear dynamic behavior. As described in the previous study [9], the nonlinear governing equations for the rotating ring-type gyroscope with the consideration of in-extensional mid-surface when sinusoidal external electromagnetic forces in the radial direction are considered take the form:

$$ {\displaystyle \begin{array}{l}\frac{EA}{br^2}\left({u}_{\theta}^{\hbox{'}}+{u}_r\right)-\frac{EI}{br^4}\left({u}_{\theta}^{\hbox{'}\hbox{'}\hbox{'}}-{u}_r^{\hbox{'}\hbox{'}\hbox{'}\hbox{'}}\right)+\rho h{\varOmega}^2\left(2{u}_{\theta}^{\hbox{'}}-{u}_r^{\hbox{'}\hbox{'}}\right)\\ {}+{k}_r{u}_r+\rho h\left({\ddot{u}}_r-\dot{\varOmega}{u}_{\theta }-2\varOmega {\dot{u}}_{\theta}\right)={f}_{\mathrm{Nem}}\left({A}_n,{B}_n,{\theta}_i\right)\cos \left(\omega t\right),\end{array}} $$

(1)

where $\dot{\left(\ \right)}$ represents time derivative while the spatial derivatives are denoted by ( )^′. In Eq. (1), E represents the Young’s modulus, I indicates area moment of inertia for ring cross-section, ρ is mass density, EI denotes flexural rigidity, A represents the cross sectional area of ring, b is the axial thickness of ring, h indicates radial thickness, r denotes the radius of the ring while ω is the excitation frequency. The term f _Nem(A _n, B _n, θ _i) represents sinusoidal nonlinear external electromagnetic force magnitude, while input angular rate and angular acceleration are, respectively, denoted by Ω and $\dot{\Omega}$.

In this study, the partial differential Eq. (1) is reduced to nonlinear ordinary differential equations by employing Galerkin’s method. The general radial and circumferential displacements that satisfy the continuity conditions are employed in this discretization process. Under these conditions, considering the periodic nature of solutions, the deflection modes can be chosen as [2, 9].

$$ {u}_r={A}_n\cos \left( n\theta \right)+{B}_n\sin \left( n\theta \right)-\frac{n\gamma}{4r}\left[{A}_n^2(t)+{B}_n^2(t)\right] $$

(2)

$$ {\displaystyle \begin{array}{c}{u}_{\theta }=-\frac{1}{n}\left[{A}_n\sin \left( n\theta \right)-{B}_n\cos \left( n\theta \right)\right]+\frac{\gamma }{8r}\left[{A}_n^2(t)+{B}_n^2(t)\right]\sin \left(2 n\theta \right)\\ {}-\frac{\gamma }{4r}{A}_n(t){B}_n(t)\cos \left(2 n\theta \right),\end{array}} $$

(3)

where the mode functions are observed to be composed of time-dependent generalized co-ordinates A _n and B _n, mode number n, ring radius r, and the nonlinear parameter γ. As seen from Eqs. (2) and (3) this parameter has an influence on both homogenous and the non-homogenous part of Eq. (1). Hence, the influence of the parameter γ which results from the in-extensionality of the middle surface is termed as system nonlinearity. In this paper, Eqs. (2) and (3) represent practically any transverse or circumferential deflection where nonlinear additive terms are incorporated in the mode function via the nonlinear term γ. In Eqs. (2) and (3), n takes the value 2 since only the second flexural modes are considered to contribute to the ring vibration. Galerkin’s method is applied by employing Eqs. (2) and (3) in Eq. (1), multiplying by the appropriate weighting function associated with A _n(t) and B _n(t) and integrating with respect to θ from 0 to 2π. The resulting discretized set of nonlinear differential equations take the form:

$$ {\fontsize{9}{11}\selectfont{\displaystyle \begin{array}{l}\left[\rho h\pi +2\rho h\pi {\left(\frac{n\gamma}{2r}\right)}^2{A}_n^2\right]\ddot{A_n}+2\rho h\pi {\left(\frac{n\gamma}{2r}\right)}^2{A}_n{B}_n\ddot{B_n}+2{\zeta \omega}_0{\dot{A}}_n+\left[\frac{EI}{br^4}\left({n}^2-1\right){n}^2+\right.\\ {}\rho h{\Omega}^2\left({n}^2-2\right)+{k}_r\Big]\pi {A}_n+\left[\frac{EA}{br^2}+{k}_r\right]{\left( n\gamma /2r\right)}^2\left[{A}_n^2+{B}_n^2\right]\pi {A}_n+2\rho h\pi {\left( n\gamma /2r\right)}^2\\ {}\left[{\dot{A}}_n^2+{\dot{B}}_n^2\right]{A}_n-\rho h\pi \dot{\Omega}\frac{1}{n}{B}_n-2\rho h\uppi \Omega \frac{1}{n}\dot{B_n}={f}_{\mathrm{Nem}}\left({A}_n,{B}_n,{\theta}_i\right)\cos \left(\omega t\right)\end{array}}} $$

(4)

$$ {\fontsize{9}{11}\selectfont{\displaystyle \begin{array}{l}\left[\rho h\pi +2\rho h\pi {\left(\frac{n\gamma}{2r}\right)}^2{B}_n^2\right]\ddot{B_n}+2\rho h\pi {\left(\frac{n\gamma}{2r}\right)}^2{A}_n{B}_n\ddot{A_n}+2{\zeta \omega}_0{\dot{B}}_n+\left[\frac{EI}{br^4}\left({n}^2-1\right){n}^2+\right.\\ {}\left.\rho h{\Omega}^2\left({n}^2-2\right)+{k}_r\right]\pi {B}_n+\left[\frac{EA}{br^2}+{k}_r\right]{\left(\frac{n\gamma}{2r}\right)}^2\left[{A}_n^2+{B}_n^2\right]\pi {B}_n+2\rho h\pi {\left(\frac{n\gamma}{2r}\right)}^2\\ {}\left[{\dot{A}}_n^2+{\dot{B}}_n^2\right]{B}_n+\rho h\pi \dot{\Omega}\frac{1}{n}{A}_n+2\rho h\pi \Omega \frac{1}{n}\dot{A_n}=0,\end{array}}} $$

(5)

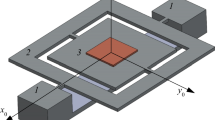
where the parameter ζ is the mechanical damping ratio, and n denotes the number of modes which is taken to be 2 in this study. A nonlinear electromagnetic force f _Nem(A _n, B _n, θ _i) cos (ωt) is considered to provide external sinusoidal excitation which is essential for the operation of the gyroscope where ω represents the excitation frequency. The angular position of electrostatic forces on the system is denoted by θ _i, i = 1, 2, 3, 4. Various configurations for the electromagnetic force are considered for the purposes of designing a ring gyroscope with effective second flexural resonant mode participation. Also, a suitable theoretical formulation of the electromagnetic force magnitude is developed considering the interactions between the electromagnet (em) and permanent magnets (pm) as shown in Fig. 2. The potential energy and force formulations are obtained from a dipole model by the law of Biot and Savart [11]. The expressions for nonlinear electromagnetic forces that affect the system from four positions are derived in the primary coordinate A _n as

$$ \begin{array}{lllll} &{f}_{\mathrm{Nem}}\left({A}_n,{B}_n,{\theta}_i\right)=\frac{\mu_0}{2\pi } kNiA\ {M}_A{V}_A{\sum}_{i=1}^2\left(\cos \left(n{\theta}_i\right)-\frac{n\gamma}{2r}{A}_n\right)\ast\nonumber\\ &\left[\frac{3}{\left\{{\left.d-{A}_n\cos \left(n{\theta}_i\right)-{B}_n\sin \left(n{\theta}_i\right)+\frac{n\gamma}{4R}\Big[{A}_n^2+{B}_n^2\right\}}^4\right.}\right] \end{array} $$

(6)

where μ ₀ = 4π × 10⁻⁷ H/m represents the magnetic permeability of free space, $A=\pi {\overset{\sim }{\ R}}^2$ is the area of the loop, the number of coil turns is denoted by N while i, $\overset{\sim }{\ R\ }$, respectively, represent the coil current and radius of coil circular loop. M _a is the magnetization, and V _a represents the volume of the source magnet. In Eq. (6), consideration for the use of an iron core has been included via a relative permeability constant k. This equation has been employed for studying the effect of nonlinear actuator dynamics employing the system of Eqs. (4) and (5). The distance between electromagnetic (em) and the permanent magnet (pm) is designated as d as shown in Fig. 2.

Fig. 2

Schematic representation of ring dynamics and actuator configurations

3 Results and Discussion

The dynamic response of the system when subjected to an external nonlinear actuator is examined via a numerical solution scheme in the present study. The mathematical model presented in Eqs. (4), (5), and (6) is employed for this purpose. Also, natural frequency variation due to rotation has been quantified and discussed in detail [9]. The operation of ring-based vibratory gyroscopes relies on nonlinear external excitation close to one of the resonant frequencies in order that device sensitivity may be maximized. To this end, variation of the second flexural natural frequency with the input angular rate is quantified using this model. It may be noted that as described in the studies [8, 9], the experimentally predicted natural frequencies agree with those predicted by the mathematical model presented in the present paper.

Furthermore, a nonlinear model which includes complex nonlinear inertia/stiffness terms, as well as a nonlinear electrometric force as depicted in Eqs. (4) and (5), have been employed. Equations (4) and (5) have been solved numerically to predict nonlinear response features of a ring gyroscope. At a nominal input angular rate of 2π rad/sec, the natural frequencies used in the present study have been evaluated as ω ₁= 58.6218 rad/sec, and ω ₂ = 64.8218 rad/sec. In the absence of input angular rate of the ring, two identical natural frequencies are predicted and they take the values ω ₁ = ω ₂ = 61rad/sec. The generalized coordinates q ₁ = A _n/h, q ₂ = B _n/h have been used for the non-dimensional equations. The following typical ring design parameters: radius of r = 92.5 × 10⁻³ m, thickness of h = 0.1016 × 10⁻³ m, and a height of b = 150 × 10⁻³ m with Young’s modulus of E = 2.068 × 10¹¹ N/m ² and the density of ρ = 7833.41 kg/m ³ have been chosen in the present study. Besides, for all time as well as frequency response simulations, a damping ratio, ζ of 0.01 has been assumed for the system. For all numerical simulations, a zero-velocity initial condition together with an initial displacement amplitude of 5 × 10⁻³ m is imposed.

3.1 Nonlinear Dynamic Response in the Driving and Sensing Directions

The time history with long time records in the driving A _n and sensing B _n coordinates of a ring gyroscope shown in Fig. 3a, b are obtained using Eqs. (4), (5), and (6) in the presence of nonlinear term at an excitation frequency 60 rad/sec. The response of the ring in the driving and the sensing directions, respectively, are displayed in Figs. 3a, b. This study concludes that due to the gyroscopic coupling present in the system, a transfer of energy takes place between the two modes in the presence of angular velocity input.

Fig. 3

Radial displacement for Ω = 2 rad/sec in (a) driving and (b) sensing directions

For the same system parameters and initial conditions, when the gyroscope is given an input angular rate of 2π rad/sec, the phase-plane trajectory based on the steady-state response in the driving and sensing directions, respectively, is shown in Fig. 4a, b.

Fig. 4

Phase diagram in (a) driving and (b) sensing directions

Moreover, effects of nonlinearity can be seen in the Poincare’ map plots in Fig. 5a, b and is indicated via multiple equilibrium points. Also, it can be observed that the resulting Poincare’ map appears as a cloud of unorganized points due to the influence of the nonlinear term associated with the system as well as the electromagnetic force.

Fig. 5

Poincare’ map in (a) driving and (b) sensing directions

4 Conclusions

The nonlinear dynamic response of a macro ring-based gyroscope has been investigated for the purpose of quantifying the effects of system as well as actuator nonlinearities inherently present in such systems under operation. The device exhibits high nonlinearity in the presence of nonlinear term in the model which may be attributed to high vibration amplitudes. A suitable electromagnetic actuator model has been developed for the purposes of examining the nonlinear dynamic response. The nonlinear dynamic response obtained via time-response, Phase portraits, and Poincare’ maps indicates that the nonlinearity in the model and actuation play an essential role in shaping the dynamic ring behavior. Comparison with the linear model study [9], revealed that the inclusion of model nonlinearities in the presence of high vibration amplitudes has a strong influence and hence greatly demonstrates its significance.