Constructions of Lagrangian Cobordisms

Abstract

Lagrangian cobordisms between Legendrian knots arise in Symplectic Field Theory and impose an interesting and not well-understood relation on Legendrian knots. There are some known “elementary” building blocks for Lagrangian cobordisms that are smoothly the attachment of 0- and 1-handles. An important question is whether every pair of non-empty Legendrians that are related by a connected Lagrangian cobordism can be related by a ribbon Lagrangian cobordism, in particular one that is “decomposable” into a composition of these elementary building blocks. We will describe these and other combinatorial building blocks as well as some geometric methods, involving the theory of satellites, to construct Lagrangian cobordisms. We will then survey some known results, derived through Heegaard Floer Homology and contact surgery, that may provide a pathway to proving the existence of nondecomposable (nonribbon) Lagrangian cobordisms.

1 Introduction

A contact manifold is an odd-dimensional manifold Y²ⁿ⁺¹ together with a maximally non-integrable hyperplane distribution ξ. In a contact manifold, Legendrian submanifolds play a central role. These are the maximal integral submanifolds of ξ: Λⁿ such that T_p Λ ⊂ ξ, for all p ∈ Λ. In general, Legendrian submanifolds are plentiful and easy to construct. In this article we will restrict our attention to the contact manifold with its standard contact structure $\xi = \ker \alpha$, where α = dz − ydx. In this setting, every smooth knot or link has an infinite number of non-equivalent Legendrian representatives. More background on Legendrian knots is given in Sect. 2.

The even-dimensional siblings of contact manifolds are symplectic manifolds. These are even-dimensional manifolds M²ⁿ equipped with a closed, non-degenerate 2-form ω. In symplectic manifolds, Lagrangian submanifolds play a central role. Lagrangian submanifolds are the maximal dimensional submanifolds where ω vanishes on the tangent spaces: Lⁿ such that ω|_L = 0. When the symplectic manifold is exact, ω = dλ, it is important to understand the more restrictive subset of exact Lagrangians: these are submanifolds where λ|_L is an exact 1-form. Geometrically, L exact means that for any closed curve γ ⊂ L, ∫_γ λ = 0. In this article, we will restrict our attention to a symplectic manifold that is symplectomorphic to with its standard symplectic structure $\omega _{0} = \sum dx_{i} \wedge dy_{i}$. In contrast to Legendrians, Lagrangians are scarce. For example, in with its standard symplectic structure, the torus is the only closed surface that will admit a Lagrangian embedding into . A famous theorem of Gromov [37] states that there are no closed, exact Lagrangian submanifolds of .

There has been a great deal of recent interest in a certain class of non-closed, exact Lagrangian submanifolds, known as Lagrangian cobordisms. These Lagrangian submanifolds live in the symplectization of a contact manifold and have cylindrical ends over Legendrians. In this article, we will focus on exact, orientable Lagrangian cobordisms from the Legendrian Λ₋ to the Legendrian Λ₊ that live in the symplectization of ; this symplectization is equipped with the exact symplectic form ω = d(e^t α), where t is the coordinate on and α = dz − ydx is the standard contact form on . See Fig. 5 for a schematic picture of a Lagrangian cobordism and Definition 1 for a formal definition. Such Lagrangian cobordisms were first introduced in Symplectic Field Theory (SFT) [25]: in relative SFT, we get a category whose objects are Legendrians and whose morphisms are Lagrangian cobordisms. Lagrangian fillings occur when Λ₋ = ∅ and are key objects in the Fukaya category, which is an important invariant of symplectic four-manifolds. A Lagrangian cap occurs when Λ₊ = ∅.

A basic question tied to understanding the general existence and behavior of Lagrangian submanifolds is to understand the existence of Lagrangian cobordisms: Given two Legendrians Λ_±, when does there exist a Lagrangian cobordism from Λ₋ to Λ₊ ? There are known to be a number of obstructions to this relation on Legendrian submanifolds coming from both classical and non-classical invariants of the Legendrians Λ_±. Some of these obstructions are described in Sect. 2.3. To complement the obstructions, there are some known constructions. For example, it is well known [7, 23, 26] that there exists a Lagrangian cobordism between Legendrians Λ_± that differ by Legendrian isotopy. In addition, by Ekholm et al. [23], Chantraine [8], it is known that there exists a Lagrangian cobordism from Λ₋ to Λ₊ if Λ₋ can be obtained from Λ₊ by a “pinch” move or if Λ₊ = Λ₋∪ U, where U denotes a Legendrian unknot with maximal Thurston-Bennequin number of − 1 that is contained in the complement of a ball containing Λ₋. Topologically, between these slices, the cobordism changes by a saddle move (1-handle) and the addition of a local minimum (0-handle); see Fig. 1. It is important to notice that there is not an elementary move corresponding to a local maximum (2-handle) move. By stacking these individual cobordisms obtained from isotopy, saddles, and minimums, one obtains what is commonly referred to as a decomposable Lagrangian cobordism. Through these moves, it is easy to construct Lagrangian cobordisms and fillings; see an example in Fig. 7.

Fig. 1

(a) The pinch move on Λ₊ produces a Lagrangian saddle; (b) Λ₊ obtained by introducing an unknotted component to Λ₋ corresponds to the Lagrangian cobordism having a local min

Towards understanding the existence of Lagrangians, it is natural to ask: Does there exist a Lagrangian cobordism from Λ₋ to Λ₊ if and only if there exists a decomposable Lagrangian cobordism from Λ₋ to Λ₊ ? We know the answer to this question is “No”: by studying the “movies” of the not necessarily Legendrian slices of a Lagrangian, Sauvaget, Murphy, and Lin [42, 59] have shown that there exists a genus two Lagrangian cap of the Legendrian unknot with Thurston-Bennequin number equal to − 3 and rotation number 0. The Lagrangian diagram moves used by Lin [42] to construct a Lagrangian cap are described in Sect. 3.3. The necessity of a local maximum when Λ₊ ≠ ∅ is not currently understood.

To formulate some precise motivating questions, we will use ribbon cobordism to denote a 2n-dimensional manifold that can be built from k-handles with k ≤ n. This idea of restricting the handle index is well known in symplectic topology: Eliashberg [15, 51] has shown that any 2n-dimensional Stein manifold admits a handle decomposition with handles of dimension at most n, and thus any 2n-dimensional Stein cobordism between closed, (2n − 1)-dimensional contact manifolds must be ribbon. Working in the relative setting with submanifolds and using the handle decomposition from the “height” function given by the coordinate on , we see that all decomposable 2-dimensional Lagrangian cobordisms between 1-dimensional Legendrian submanifolds are ribbon cobordisms. We are led to the following natural questions.

Motivating Questions 1

Suppose Λ₊ ≠ ∅ and there exists a connected Lagrangian cobordism L from Λ₋ to Λ₊. Then:

• 1. Does there exist a decomposable Lagrangian cobordism from Λ₋ to Λ₊?

• 2. Does there exist a ribbon Lagrangian cobordism from Λ₋ to Λ₊?

• 3. Is L Lagrangian isotopic to a ribbon and/or decomposable Lagrangian cobordism?

There are some results known about Motivating Question 3 for the special case of the simplest Legendrian unknot. If U denotes the Legendrian unknot with Thurston-Bennequin number − 1, it is known that every (exact) Lagrangian filling is orientable [55], and there is a unique (exact, orientable) Lagrangian filling of U up to compactly supported Hamiltonian isotopy [27]. Moreover, any Lagrangian cobordism from U to U is Lagrangian isotopic, via a compactly supported Hamiltonian isotopy, to one in a countable collection given by the trace of a Legendrian isotopy induced by a rotation [11].

Motivating Questions (1) and (2) are closely related and have deep ties to important questions in topology. Observe that a “yes” answer to (1) implies a “yes” to (2): if the existence of a Lagrangian cobordism implies the existence of a decomposable Lagrangian cobordism, then we also know the existence of a ribbon cobordism. Also note that when Λ₊ is topologically a slice knot and Λ₋ = ∅, (2) is a symplectic version of the topological Slice-Ribbon conjecture: is every Lagrangian slice disk a ribbon disk? Cornwell, Ng, and Sivek conjecture that the answer to Motivating Question (1) and (3) is “No”: using the theory of satellites, we know that there is a Lagrangian concordance between Λ_± shown in Fig. 2, and in [17, Conjecture 3.3] it is conjectured that the concordance between the pair is not decomposable.

Fig. 2

There is a Lagrangian concordance between these Legendrian knots that is conjectured to be non-decomposable. Here Λ₋ is a Legendrian trefoil and Λ₊ is a Legendrian Whitehead double of m(9₄₆)

Very recently, Roberta Guadagni has discovered additional combinatorial moves that can be used to construct a “movie,” meaning a sequence of slice pictures, of a Lagrangian cobordism; Fig. 9 illustrates one of these tangle moves. With one of Guadagni’s moves, it is possible to construct a movie of a Lagrangian cobordism between the Legendrians pictured in Fig. 2; see Fig. 10. Guadagni’s moves are “geometric”: they are developed through proofs similar to those used in the satellite procedure, and thus the handle attachments involved in the cobordism are not obvious. In particular, at this point it is not known if Guadagni’s tangle moves are independent from the decomposable moves.

This survey article is organized as follows. In Sect. 2, we provide some background on Legendrians and Lagrangians, formally define Lagrangian cobordisms, and summarize known obstructions to the existence of Lagrangian cobordisms. In Sect. 3, we describe three “combinatorial” ways to construct Lagrangian cobordisms, and in Sect. 4, we describe more abstract “geometric” ways to construct Lagrangian concordances and cobordisms through satellites. Then in Sect. 5, we describe some potential pathways—through the theory of rulings, Heegaard-Floer homology, and contact surgery—to potentially show the existence of Legendrians that are Lagrangian cobordant but are not related by a decomposable Lagrangian cobordism.

2 Background

2.1 Legendrian Knots and Links

In this section, we give a very brief introduction to Legendrian submanifolds in and their invariants. More details can be found, for example, in the survey paper [28].

In , the standard contact structure ξ is a 2-dimensional plane field given by the kernel of the 1-form α = dz − ydx. In , a Legendrian knot is a knot in that is tangent to ξ everywhere. A useful way to visualize a Legendrian knot is to project it from to . There are two useful projections: the Lagrangian projection

as well as the front projection

An example of a Legendrian trefoil is shown in Fig. 3.

Fig. 3

The front projection (left) and the Lagrangian projection (right) of a Legendrian trefoil

Legendrian submanifolds are equivalent if they can be connected by a 1-parameter family of Legendrian submanifolds. In fact, for each topological knot type there are infinitely many different Legendrian knots. Indeed, we can stabilize a Legendrian knot (as shown in Fig. 4) to get another Legendrian knot of the same topological knot type. We can see that these are not Legendrian equivalent using Legendrian invariants.

Fig. 4

Two ways to stabilize a Legendrian knot in the front projection

Two useful classical invariants of Legendrian knots Λ are the Thurston-Bennequin number tb(Λ) and the rotation number r(Λ). They can be computed easily from front projections. Given the front projection of a Legendrian knot or link Λ, the Thurston-Bennequin number is

where the writhe is the number of crossings counted with sign. Once the Legendrian knot is equipped with an orientation, the rotation number is

One can use these two invariants to see that stabilizations change the Legendrian knot type.

In future sections, we will not assume that our Legendrians Λ_± come equipped with an orientation. In our Motivating Questions described in Sect. 1, our Lagrangian cobordisms are always orientable, so the existence of a Lagrangian cobordism from Λ₋ to Λ₊ will induce orientations on Λ_±.

There are many powerful non-classical invariants that can be assigned to a Legendrian knot. Although this will not be a focus of this paper, we will give a brief description of some of these invariants. One important invariant stems from normal rulings, defined independently by Chekanov and Pushkar [54] and Fuchs [30]. A count of normal rulings leads to ruling polynomials [54]; more details will be discussed in Sect. 5.1. Through the closely related theory of generating families, one can also associate invariant polynomials that record the dimensions of generating family homology groups [32, 40, 58, 61]. In addition, through the theory of pseudo-holomorphic curves, one can associate to a Legendrian Λ a differential graded algebra (DGA), $\mathcal A(\varLambda )$ [13, 24]. An augmentation is a DGA map from $\mathcal A(\varLambda )$ to a field. The count of augmentations is closely related to the count of ruling polynomials [30, 47, 50]. Augmentations can be used to construct finite-dimensional linearized contact homology groups [13], which are often known to be isomorphic to the generating family homology groups [32]. In addition, there are invariants for Legendrian knots coming from Heegaard Floer Homology [43, 52].

2.2 Lagrangian Cobordisms

Lagrangian cobordisms between Legendrian submanifolds always have “cylindrical ends” over the Legendrians, but other conditions vary: sometimes it is specified that the Lagrangian is exact, is embedded (or immersed), is orientable, or has a fixed Maslov class. In this paper, a Lagrangian cobordism is always exact, embedded, and orientable.

Definition 1

Let Λ_± be two Legendrian knots or links in . A Lagrangian cobordism L from Λ₋ to Λ₊ is an embedded, orientable Lagrangian surface in the symplectization such that for some N > 0,

• 1. is compact,

• 2. ,

• 3. , and

• 4. there exists a function and constant numbers $\mathfrak c_\pm$ such that e^t α|_TL = df, where $f|{ }_{(-\infty , -N) \times \varLambda _{-}} = \mathfrak c_{-}$, and $f|{ }_{(N, \infty ) \times \varLambda _{+}} = \mathfrak c_{+}$.

A Lagrangian filling of Λ₊ is a Lagrangian cobordism with Λ₋ = ∅; a Lagrangian cap of Λ₋ is a Lagrangian cobordism with Λ₊ = ∅. A Lagrangian concordance occurs when Λ_± are knots and L has genus 0.

Figure 5 is a schematic representation of a Lagrangian cobordism.

Fig. 5

A Lagrangian cobordism from Λ₋ to Λ₊

Remark 1

In condition (4) of Definition 1, the fact that Λ_± are Legendrian will guarantee that f_± will be locally constant. Using this, it follows that any genus zero Lagrangian surface that is cylindrical over Legendrian knots will be exact. When Λ_± have multiple components, one needs to check that the constant does not vary: this condition guarantees the exactness of the Lagrangian cobordism obtained by “gluing” together Lagrangian cobordisms [10].

Remark 2

In contrast to topological cobordisms, Lagrangian cobordisms form a non-symmetric relationship on Legendrian knots [9]. In this article we will always denote the direction of increasing coordinate by an arrow.

2.3 Obstructions to Lagrangian Cobordisms

The focus of this paper is on constructing Lagrangian cobordisms between two given Legendrians Λ_±. In the smooth world, any two knots are related by a smooth cobordism, but in this more restrictive Lagrangian world, there are a number of obstructions that are important to keep in mind when trying to explicitly construct Lagrangian cobordisms. Here we mention a few that come from classical and non-classical invariants of the Legendrians Λ_±.

Obstructions

• 1. If there exists a Lagrangian cobordism of genus g between Λ₋ and Λ₊, then there must exist a smooth cobordism of genus g between the smooth knot types of Λ₋ and Λ₊. Thus any obstruction of a smooth genus g cobordism between Λ₋ and Λ₊ would obstruct a Lagrangian genus g cobordism.

• 2. Since there are no closed, exact Lagrangian surfaces [37], if there exists a Lagrangian cap (respectively, filling) for Λ, then there cannot exist a Lagrangian filling (respectively, cap) of Λ.

• 3. As shown in [7], if there exists a Lagrangian cobordism L from Λ₋ to Λ₊, then

  $$\displaystyle \begin{aligned} r(\varLambda_{-}) = r(\varLambda_{+}) \quad \text{ and } \quad tb(\varLambda_{+})- tb(\varLambda_{-})= -\chi(L). \end{aligned}$$

  In particular, if a Legendrian knot Λ admits a Lagrangian filling or cap, then r(Λ) = 0. Also, combining this equality on tb and the slice-Bennequin inequality [56], we see that, when Λ is a single component knot, if there exists a Lagrangian cap L of Λ, then tb(Λ) ≤−1 and g(L) ≥ 1.

• 4. If there exists a Maslov 0 ([21]) Lagrangian cobordism Σ from Λ₋ to Λ₊, and Λ₋ has an augmentation, then

  • (a) #Aug(Λ₊;IF₂) ≥ #Aug(Λ₋;IF₂), where IF₂ is the finite field of two elements, and #Aug(Λ;IF₂) denotes the number of augmentations of Λ to IF₂ up to DGA homotopy [6, 53], and

  • (b) the ruling polynomials $R_{\varLambda _{\pm }}(z)$ (see Sect. 5.1 for definitions) satisfy

    $$\displaystyle \begin{aligned} R_{\varLambda_-}(q^{1/2}-q^{-1/2})\leq q^{-\chi(\varSigma)/2}R_{\varLambda_+}(q^{1/2}-q^{-1/2}), \end{aligned}$$

    for any q that is a power of a prime number [53].

• 5. If Λ admits a Maslov 0 Lagrangian filling L, and if 𝜖_L denotes the augmentation of Λ induced by L, then $LCH^{k}_{\epsilon _L}(\varLambda )\cong H_{n-k}(L)$, which is known as the Ekholm-Seidel isomorphism [20], and whose proof was completed by Dimitroglou Rizell in [19]. More generally, if there is a cobordism from Λ₋ to Λ₊, and if Λ₋ admits an augmentation, then [12] provides several long exact sequences relating the homology of the cobordism and the Legendrian contact (co)homologies of its Legendrian ends. A version of this isomorphism and these long exact sequences using generating families are given in [58].

• 6. If Λ admits an augmentation, Λ does not admit a Lagrangian cap, as the augmentation implies the non-acyclicity of the DGA $\mathcal A(\varLambda )$ [22, Theorem 5.5], and from [18, Corollary 1.9] if a Legendrian admits a Lagrangian cap then its DGA $\mathcal A(\varLambda )$ (with IF₂ coefficients) is acyclic.

There are additional obstructions, obtained through Heegaard Floer Theory, that can be used to obstruct Lagrangian concordances and cobordisms [1, 3, 35]. Some of these will be discussed more in Sect. 5.3.

Remark 3

Observe that the Obstructions 4 and 6 assume that the bottom Λ₋ has an augmentation, and stabilized knots will never have an augmentation. It would be nice to have more obstructions when Λ₋ is a stabilized knot. This might be possible using the theory of “satellites” described in Sect. 4.1: it is possible for the satellite of a stabilized Legendrian to admit an augmentation. See Sect. 4.3 for more discussions in this direction.

3 Combinatorial Constructions of Lagrangian Cobordisms

A convenient way of visualizing topological cobordisms is through “movies”: a sequence of pictures that represent slices of the Lagrangian. In this section, we describe three known combinatorial ways to construct Lagrangian cobordisms through such an approach.

3.1 Decomposable Moves

It is well known that if Λ₋ and Λ₊ are Legendrian isotopic, then there exists a Lagrangian cobordism from Λ₋ to Λ₊; see, for example, [7, 23, 26]. Isotopy, together with two types of handle moves, form the basis for decomposable Lagrangian cobordisms.

Theorem 1 ([5, 23])

If the front diagrams of two Legendrian links Λ₋ and Λ₊ are related by any of the following moves, there is a Lagrangian cobordism L from Λ₋ to Λ₊.

Isotopy :

There is a Legendrian isotopy between Λ₋ and Λ₊ ; see Fig. 6 a–c for Reidemeister Moves I–III.

Fig. 6

Decomposable moves in terms of front projections. Arrows indicate the direction of increasing coordinate in the symplectization. The move in (b) only shows the Reidemeister II move in the left cusp case, but there is an analogous move for the right cusp case

1-handle :

The front diagram of Λ₋ can be obtained from the front diagram of Λ₊ by “pinching” two oppositely-oriented strands; see Fig. 6 d. We will also refer to this move as a “Pinch Move.”

0-handle :

The front diagram of Λ₋ can be obtained from the front diagram of Λ₊ by deleting a component of Λ₊ that is the front diagram of a standard Legendrian unknot U with maximal Thurston-Bennequin number of − 1 as long as there exist disjoint disks containing the xz-projection of U and the other components of Λ₊ , respectively. Such an “unknot filling” can be seen in Fig. 6 e.

Definition 2

A Lagrangian cobordism L from Λ₋ to Λ₊ is called elementary if it arises from isotopy, a single 0-handle, or a single 1-handle. A Lagrangian cobordism L from Λ₋ to Λ₊ is decomposable if it is obtained by stacking elementary Lagrangian cobordisms.

Observe that there is not an elementary move corresponding to a 2-handle (maximum). Also note that the elementary 1-handle (saddle) move can be used to connect two components or to split one component into two.

Decomposable cobordisms are particularly convenient as they are easy to describe in a combinatorial fashion, through a list of embedded Legendrian curves,

where the front projection of the Legendrian Λ_i+1 is related to that of Λ_i by isotopy or one of the 0-handle or 1-handle moves.

Example 1

One can construct a Lagrangian filling of a positive Legendrian trefoil with maximal Thurston-Bennequin number using the series of moves shown in Fig. 7: a 0-handle, followed by three Reidemeister I moves, followed by two 1-handles (or pinch moves). This gives a genus 1 (orientable, exact) Lagrangian filling of this Legendrian trefoil. Since we are assuming that Lagrangian fillings and caps are always exact, this implies that this trefoil cannot admit a Lagrangian cap; see Sect. 2.3 Obstruction 2.

Fig. 7

A decomposable Lagrangian filling of a Legendrian trefoil

Example 2

Using elementary moves, one can also construct a Lagrangian concordance from the unknot with tb = −1 to a Legendrian representative of the knot m(9₄₆), as shown on Fig. 8.

Fig. 8

A decomposable Lagrangian cobordism from a Legendrian unknot to a Legendrian m(9₄₆)

3.2 Guadagni Moves

Very recently, Roberta Guadagni has discovered a new “tangle” move; see Fig. 9. This is not a local move: there are some global requirements. In particular, this move cannot be applied if all components of the tangle are contained in the same component of Λ₋: the component of Λ₋ containing the blue strand must be different than the components containing the other strands of the tangle.

Fig. 9

Under some global conditions, there exists a Lagrangian cobordism between these tangles

Example 3

With Guadagni’s tangle move, it is possible to construct a Lagrangian cobordism between the Legendrians pictured in Fig. 2; see Fig. 10. However, at this point it is not known if Guadagni’s tangle move is independent of the decomposable moves.

Fig. 10

A movie, using a Guadagni move, of an (orientable, exact) Lagrangian cobordism from the trefoil to the Whitehead double of m(9₄₆) in Fig. 2

3.3 Lagrangian Diagram Moves

As shown in Sect. 3.1, decomposable cobordisms are constructed from 0-handles and some 1-handles (saddles) but no 2-handles (caps). Based on the work of Sauvaget [59], Lin [42] constructs a genus two cap of a twice stabilized unknot, and thus gives the first explicit example of a non-decomposable Lagrangian cobordism. The construction describes time-slices of a Lagrangian cobordism through a list of moves on “decorated Lagrangian diagrams.”

A decorated Lagrangian diagram is a curve in the xy-plane with the compact regions decorated by a positive number, which is the area of the region. Figure 11 shows some examples: in the illustration of the F move, U is a Lagrangian projection of the Legendrian unknot with maximal Thurston-Bennequin number; in the illustration of the C move, U_m is a decorated Lagrangian diagram, but is not the Lagrangian projection of a Legendrian knot.

Fig. 11

The Lagrangian diagram moves. The labels in the R₀ move represent the change of area through the move, while other labels 0, 𝜖, δ, η, a indicate the area of the corresponding regions; here 0 represents a positive area that is smaller than either the area 𝜖, the area δ or the area η

Theorem 2 ([42])

Let Λ _± be Legendrian links and D _± be their corresponding decorated Lagrangian projections. If one can create a sequence of decorated Lagrangian diagrams

such that each diagram D_i+1 can be obtained from D_i by the following combinatorial moves, then there is a compact Lagrangian submanifold in with boundary Λ₋∪ Λ₊ , where , for some N > 0.

• 1. R₀ : a planar isotopy that changes areas by the amount ± A, for A > 0. This operation can only be done in the direction specified.

• 2. R₂ : a Reidemeister II move. One can either introduce or eliminate two crossings assuming some area conditions are satisfied: it is possible to introduce or remove two crossings as long as the area of the inner region, denoted by 0 in the diagram, is less than either the area δ or the area η. One can also do this move with the lower strand passing under the upper strand.

• 3. R₃ : a Reidemeister III move. One can perform a Reidemeister III move as long as the area of the inner region, denoted by 0 in the diagram, is less than either the area 𝜖, the area δ or the area η. The fixed center crossing can be reversed. Additionally, the moving strand can also occur as an overstrand.

• 4. H₊ : a handle attachment that creates a positive crossing in the diagram.

• 5. H₋ : a handle attachment that removes a negative crossing in the diagram.

• 6. F: a filling that creates the diagram U, which is the Lagrangian projection of an unknot with maximal Thurston-Bennequin number.

• 7. C: a cap that eliminates the diagram U_m , which is the topological mirror of U.

These moves are called Lagrangian diagram moves . Moreover, the constructed Lagrangian will be exact if, in addition,

• (E1) Each move results in a diagram with all components having a total signed area equal to 0. The signed area of a region is determined by the sum of the signed heights of its Reeb chords.

• (E2) If a handle attachment merges two components of a link, the components being merged must be vertically split, meaning that the images of the xy-projections of these components are contained in disjoint disks.

Remark 4

• 1. For condition (E2), the H₋ can never be applied to merge components, and H₊ can only be applied if the components being merged are vertically split.

• 2. A main distinction between the Lagrangian diagram moves and the decomposable moves is that each diagram D_i in the middle of the sequence is not necessarily the Lagrangian projection of a Legendrian link. They are just the xy-projection of some time t_i-slice of the cobordism. Thus the Lagrangian diagram moves are more flexible than the decomposable moves. However, keeping track of the areas is an added complication.

Example 4

Figure 12 illustrates the construction of a Lagrangian torus using the Lagrangian diagram moves. This torus fails to be exact since condition (E1) is violated. Figure 13 gives another construction of a Lagrangian torus. This time, all components have signed area 0, but now condition (E2) is violated.

Fig. 12

A (non-exact) Lagrangian torus constructed using the Lagrangian diagram moves. The middle figure violates (E1)

Fig. 13

A (non-exact) Lagrangian torus constructed using the Lagrangian diagram moves. These figures satisfy (E1) but (E2) is violated in the step labelled by a red arrow

4 Geometrical Constructions of Lagrangian Cobordisms

An important general way to know of the existence of Lagrangian cobordisms without using the constructions described in Sect. 3 comes through the satellite operation. In this section, we review the satellite construction and then state results from [17, 38] about the existence of a Lagrangian concordance/cobordism from Λ₋ to Λ₊ implying the existence of a Lagrangian concordance/cobordism between corresponding satellites.

4.1 The Legendrian Satellite Construction

We begin by reviewing the construction of a Legendrian satellite; see also [48, Appendix] and [17, Sect. 2.2]. To construct a Legendrian satellite, begin by identifying the open solid torus with the 1-jet space of the circle, , equipped with the contact form α = dz − ydx, where x, y are the coordinates in T^∗ S¹ and z is the coordinate in . Similar to the situation for , we can recover a Legendrian knot in J¹ S¹ from its front projection in , which is typically drawn by representing S¹ as an interval with its endpoints identified.

Given an oriented Legendrian companion knot and a oriented Legendrian pattern knot P ⊂ J¹(S¹), the Legendrian neighborhood theorem says that Λ has a standard neighborhood N(Λ) such that there is a contactomorphism κ : J¹(S¹) → N(Λ). The Legendrian satellite, S(Λ, P), is then the image κ(P). The front projection of S(Λ, P) is as shown in Fig. 14. In particular, suppose that the front projection of the pattern P intersects the vertical line at the boundary of the S¹ interval n times. We then make an n-copy of Λ by using n-disjoint copies of Λ that all differ by small translations in the z-direction. Take a point on the front projection of Λ that is oriented from left to right, cut the front of the n-copy open along the n-copy at that point, and insert the front diagram of P. The orientation on the satellite S(Λ, P) is induced by the orientation on P.

Fig. 14

An example of a Legendrian satellite

Remark 5

The satellite operation often makes Legendrian knots “nicer”; for example, in Fig. 14, the companion Λ is stabilized and does not admit an augmentation or a normal ruling. However, the satellite S(Λ, P) does admit a normal ruling and an augmentation.

4.2 Lagrangian Cobordisms for Satellites

In [17, Theorem 2.4], Cornwell, Ng, and Sivek, show that Lagrangian concordance is preserved by the Legendrian satellite operation.

Theorem 3 ([17])

Suppose P ⊂ J¹ S¹ is a Legendrian knot. If there exists a Lagrangian concordance L from a Legendrian knot Λ₋ to a Legendrian knot Λ₊ , then there exists a Lagrangian concordance L_P from S(Λ₋, P) to S(Λ₊, P).

In particular, as shown in Fig. 8, there is a Lagrangian concordance from Λ₋, which is the Legendrian unknot with tb = −1, to Λ₊, which is the Legendrian m(9₄₆) with maximal tb = −1. Using the Legendrian “clasp” tangle P as shown in Fig. 14—which produces the Legendrian Whitehead double—we can conclude that there exists a Lagrangian concordance from S(Λ₋, P) to S(Λ₊, P). In fact, S(Λ₋, P) is the positive trefoil with tb = 1. Thus Theorem 3 implies that there exists a Lagrangian concordance between the Legendrian knots in Fig. 2.

Conjecture 1 ([17, Conjecture 3.3])

The Lagrangian concordance from S(Λ₋, P) to S(Λ₊, P) built through the satellite construction is not decomposable.

Theorem 3 has been extended to higher genus cobordisms by Guadagni, Sabloff, and Yacavone in [38]. To state their theorem, we need to first introduce the notion of “twisting” and then closing a tangle T ⊂ J¹[0, 1]. Given a Legendrian tangle T ⊂ J¹[0, 1], ΔT is the tangle obtained by adding the tangle T and the full twist tangle Δ, which is illustrated in Fig. 15; the tangle Δ^t T can be thought of as T followed by t full twists. Given a Legendrian tangle T ⊂ J¹[0, 1], $\overline {T} \subset J^1(S^1)$ will denote the associated closure to a Legendrian link.

Fig. 15

For an n-stranded tangle, repeating this basic tangle n times produces a full twist

Theorem 4 ([38])

Suppose T ⊂ J¹[0, 1] is a Legendrian tangle whose closure $\overline {T} \subset J^{1}(S^{1})$ is a Legendrian knot. If there exists a Lagrangian cobordism L from Λ₋ to Λ₊ of genus g(L), then there exists a Lagrangian cobordism L_T from $S(\varLambda _{-}, \overline {\varDelta ^{2g(L) + 1} T})$ to $S(\varLambda _{+}, \overline {\varDelta T})$.

In fact, Theorem 4 can be generalized to use the closure of different tangles T₋ and T₊ that are Lagrangian cobordant; for details, see [38].

Remark 6

It is natural to wonder if, along the lines of Conjecture 1, this higher genus satellite procedure can create additional candidates for Legendrians that can be connected by a Lagrangian cobordism but not by a decomposable Lagrangian cobordism. In [38, Theorem 1.5], it is shown that if the cobordism L from Λ₋ to Λ₊ is decomposable and the handles in the decomposition satisfy conditions known as “Property A”, then the corresponding satellites S(Λ₋, Δ^2g(L)+1 P) and S(Λ₊, ΔP) will also be connected by a decomposable Lagrangian cobordism. In particular, if there exists a decomposable cobordism L that does not satisfy Property A and is not isotopic to a cobordism that satisfies Property A, then the satellite construction would lead to a higher genus candidate that generalizes Conjecture 1.

4.3 Obstructions to Cobordisms Through Satellites

In Sect. 2.3, some known obstructions to the existence of a Lagrangian cobordism were mentioned. As mentioned in Remark 3, a number of these obstructions require Λ₋ to admit an augmentation, and thus in particular Λ₋ must be non-stabilized. However, as mentioned in Remark 5, it is possible for the satellite of a Legendrian Λ to admit an augmentation even if Λ does not. So the contrapositive of Theorem 3 provides a potential strategy for further obstructions to the existence of a Lagrangian cobordism when Λ₋ does not admit an augmentation. For example, motivated by Obstruction 4 in Sect. 2.3, one can ask: Can a count of augmentations give an obstruction to the existence of a Lagrangian concordance from S(Λ₋, P) to S(Λ₊, P) and thereby obstruct the existence of a Lagrangian concordance from Λ₋ to Λ₊ ? In fact, this augmentation count will not likely provide a further obstruction: a simple computation shows that when Λ is stabilized enough, the number of augmentations of S(Λ, P) only depends on the Legendrian pattern P. If trying to pursue this path to obtain further obstructions to Lagrangian cobordisms, it is useful to keep in mind the following result of Ng that shows the DGA of the satellite of a Legendrian Λ might only remember the underlying knot type of Λ.

Theorem 5 ([49])

Suppose Λ₁ and Λ₂ are stabilized Legendrian knots that are of the same topological knot type and have the same Thurston-Bennequin and rotation numbers. For a Legendrian pattern P whose front intersects a vertical line by two points, the DGAs of S(Λ₁, P) and S(Λ₂, P) are equivalent.

5 Candidates for Non-decomposable Lagrangian Cobordisms

Now that we have developed some ways to construct a Lagrangian cobordism through combinatorial moves and satellites, we state some theorems that show if a Lagrangian cobordism does exist, then it cannot be decomposable: this addresses Motivating Question 1. While we discuss these theorems, it is useful to keep in mind the known obstructions to Lagrangian cobordisms that were mentioned in Sect. 2.3.

5.1 Candidates for Non-decomposable Lagrangian Cobordisms from Normal Rulings

One simple way to show that two Legendrians Λ_± cannot be connected by a decomposable Lagrangian cobordism comes from a count of “combinatorial” rulings. Roughly, a normal ruling of a Legendrian Λ is a “decomposition” of the front projection into pairs of paths from left cusps to right cusps such that

• 1. each pair of paths starts from a common left cusp and ends at a common right cusp, has no further intersections, and bounds a topological disk whose boundary is smooth everywhere other than at the cusps and certain crossings called switches, and

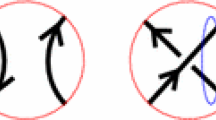
• 2. near a switch, the pair of paths must be arranged as in one of the diagrams in Fig. 16; observe that near the switch, vertical slices of the associated disks are either disjoint or the slices of one are contained in the slices of the other.

  Fig. 16

  

  Normal rulings near a switch

Formal definitions of normal rulings can be found in, for example, [54] and [30].

As an illustration, all normal rulings of a particular Legendrian trefoil are shown in Fig. 17.

Fig. 17

All normal rulings of this max tb positive Legendrian trefoil

For each normal ruling R, let s(R) and d(R) be the number of switches and number of disks, respectively. By Pushkar and Chekanov [54], the ruling polynomial

$$\displaystyle \begin{aligned} R_{\varLambda}(z)= \sum_{R} z^{s(R)-d(R)}, \end{aligned}$$

where the sum is over all the normal rulings, is an invariant of Λ under Legendrian isotopy. Normal rulings and augmentations are closely related even though they are defined in very different ways [30, 31, 50, 57].

We have the following obstruction to decomposable cobordisms in terms of normal rulings.

Theorem 6

If Λ₋ has m normal rulings and Λ₊ has n normal rulings with m > n, then there is no decomposable Lagrangian cobordism from Λ₋ to Λ₊.

Proof

One can compare the number of normal rulings of the two ends for the decomposable moves, as shown in Fig. 18. Thus any normal ruling of Λ₋ induces a normal ruling of Λ₊. Different normal rulings of Λ₋ induce different normal rulings of Λ₊. Therefore the number of normal rulings of Λ₊ is bigger than or equal to the number of normal rulings of Λ₋. □

Fig. 18

Comparison of normal rulings for decomposable moves

Here is a strategy to show the existence of Legendrians that can be connected by a Lagrangian cobordism but not by one that is decomposable.

Strategy 1

Choose Legendrians Λ _± such that:

• 1. Λ ₊ has fewer graded normal rulings than Λ ₋ , and

• 2. it is possible to construct, via a combination of the combinatorial constructions from Sect. 3 or the satellite construction from Sect. 4 , a Lagrangian cobordism from Λ₋ to Λ₊.

Remark 7

If Λ_± admit normal rulings, they will admit augmentations [31, 57]. From Sect. 2.3 Obstruction 4(b), we then know that if there is a Lagrangian cobordism from Λ₋ to Λ₊, their ruling polynomials satisfy

$$\displaystyle \begin{aligned} R_{\varLambda_-}(q^{1/2}-q^{-1/2})\leq q^{-\chi(\varSigma)/2}R_{\varLambda_+}(q^{1/2}-q^{-1/2}), \end{aligned}$$

for any q that is a power of a prime number. Satisfying condition (1) in Strategy 1 means that the polynomial on the right side of the inequality has fewer terms than the polynomial on the left side of the inequality. If following this approach, it may be helpful to start by first finding a pair of positive integer coefficient polynomials that satisfy this inequality and condition (1) at the same time. One can start with checking the ruling polynomials of small crossing number Legendrian knots in [14].

5.2 Candidates for Non-decomposable Lagrangian Concordances from Topology

Observe that any decomposable Lagrangian concordance will be a smooth ribbon concordance. Thus it is potentially possible to use known obstructions to ribbon concordances to find examples of smooth knots whose Legendrian representatives cannot be connected by a decomposable Lagrangian concordance: constructing a Lagrangian concordance between very stabilized Legendrian representatives of these knot types, via the combinatorial techniques of Sect. 3 or geometric techniques of Sect. 4, will give an example of an exact Lagrangian concordance between knots that cannot be connected by a decomposable Lagrangian concordance.

For example, it is known [36, 41, 62] that the only knot that admits a ribbon concordance to the unknot is the unknot itself. This has as a corollary the following obstruction to a decomposable Lagrangian concordance.

Theorem 7 ([17, Theorem 3.2])

If Λ₋ is topologically non-trivial and Λ₊ is topologically an unknot, then there is no decomposable Lagrangian concordance from Λ₋ to Λ₊.

Example 5

To illustrate this theorem, here is a possible low crossing number Legendrian knot to examine as Λ₋. Consider the topological knot 6₁ which is slice and ribbon. Its maximum tb Legendrian representative $\varLambda _{6_1}$ (see Fig. 19) has tb = −5 and r = 0. The DGA of this Legendrian $\mathcal {A}(\varLambda _{6_1})$ admits an augmentation, and thus $\varLambda _{6_{1}}$ does not admit a Lagrangian cap; see Obstruction 6. in Sect. 2.3. Since we are trying to construct a Legendrian Λ₋ that could be Lagrangian concordant to a stabilized unknot, which might have a Lagrangian cap, we will add some stabilizations that will prevent augmentations and thereby allow the possibility of a Lagrangian cap. If we now add a positive and a negative stabilization to $\varLambda _{6_1}$, we get a knot $\varLambda _{6_1}^\pm$ with tb = −7 and r = 0, which has no augmentation and is still topologically the knot 6₁. If, by a sequence of moves in Sect. 3, one can construct a concordance from $\varLambda _{6_1}^\pm$ to the tb = −7 stabilized unknot, then by Theorem 7 this Lagrangian concordance will not be decomposable; see Fig. 20. In fact, one can stabilize $\varLambda _{6_1}$ as many times as we wish resulting in tb(Λ₋) = t and r(Λ₋) = r and try, using the combinatorial constructions of Sect. 3, to construct a Lagrangian concordance to Λ₊, where Λ₊ is a Legendrian unknot with tb(Λ₊) = t and r(Λ₊) = r. If possible, such a construction would prove the existence of a non-decomposable Lagrangian concordance.

Fig. 19

Front diagram of $\varLambda _{6_1}$

Fig. 20

Any Lagrangian concordance from the doubly stabilized $\varLambda _{6_1}$ to the tb = −7, r = 0 Legendrian unknot would necessarily be non-decomposable

There are additional results from topology that give obstructions to the existence of ribbon concordances. For example, as shown by Gilmer [34] and generalized by Friedl and Powell [29], if K₋ is ribbon concordant to K₊, then the Alexander polynomial of K₋ divides the Alexander polynomial of K₊. We can invoke these results in a strategy to show the existence of non-decomposable Lagrangian concordances.

Strategy 2

• 1. Use results from smooth topology to find examples of smooth knots K_± such that K₋ is not ribbon concordant to K₊.

• 2. For any pair of Legendrian representatives Λ_± of the knot type K_± , even highly stabilized, use a combination of the combinatorial moves described in Sect. 3 to construct a Lagrangian concordance from Λ₋ to Λ₊.

The example with the knot 6₁ given above is a concrete example to try to apply this strategy with K₋ = 6₁ and K₊ being an unknot. A possible example when K₊ is non-trivial is the following.

Example 6

Let K₋ be the connect sum of the right- and left-handed trefoils, K₋ = T_r #T_l, and let K₊ be the connect sum of the figure-8 knot, F₈, with itself, K₊ = F₈ #F₈. These knots are concordant but there is no ribbon concordance from K₋ to K₊, as first shown by Gordon [36]. Choose Legendrian representatives Λ_± of K_± such that tb(Λ₋) = tb(Λ₊) and r(Λ₋) = r(Λ₊); note that Λ_± can be very stabilized. If we can construct a Lagrangian concordance from Λ₋ to Λ₊, via the combinatorial moves of Sect. 3, then we will have shown the existence of a pair of Legendrians that are (exactly, orientablility) Lagrangian concordant but cannot be connected by a decomposable Lagrangian concordance.

Remark 8

Some known obstructions to ribbon concordance are, in fact, obstructions to generalizations of ribbon concordance, namely strong homotopy ribbon concordance and homotopy ribbon concordance. A strong homotopy ribbon concordance is one whose complement is ribbon, i.e., can be built with only 1-handles and 2-handles. A homotopy ribbon concordance from K₋ to K₊ is a concordance where the induced map on π₁ of the complement of K₋ (resp. K₊) injects (resp. surjects) into π₁ of the complement of the concordance. Gordon [36] showed that

There have been a number of recent results obstructing (homotopy or strong homotopy) ribbon concordances from Heegaard-Floer and Khovanov homology [39, 41, 45, 62]; these results play an important role in Strategy 2.

5.3 Candidates for Non-decomposable Lagrangian Cobordisms from GRID Invariants

Some candidates for non-decomposable Lagrangian cobordisms of higher genus come from knot Floer homology. Using the grid formulation of knot Floer homology [52], Ozsváth, Szabó, and Thurston defined Legendrian invariants of a Legendrian link , called GRID invariants, which are elements in the hat flavor of knot Floer homology of Λ ⊂−S³:

$$\displaystyle \begin{aligned} \widehat\lambda^+(\varLambda), \widehat\lambda^-(\varLambda) \in \widehat{HFK}(-S^3, \varLambda). \end{aligned}$$

For more background, see [44, 52].

Baldwin et al. [1] have shown that these GRID invariants can be used to obstruct the existence of decomposable Lagrangian cobordisms.

Theorem 8 ([1, Theorem 1.2] )

Suppose that Λ _± are Legendrian links in such that either

• 1. $\widehat \lambda ^+(\varLambda _{+}) = 0$ and $\widehat \lambda ^+(\varLambda _{-}) \neq 0$ , or

• 2. $\widehat \lambda ^-(\varLambda _{+}) = 0$ and $\widehat \lambda ^-(\varLambda _{-}) \neq 0$.

Then there is no decomposable Lagrangian cobordism from Λ₋ to Λ₊.

Remark 9

By Baldwin et al. [4], in the standard contact manifold , the GRID invariants agree with the LOSS invariant [43]. The LOSS invariant is functorial on Lagrangian concordances by Baldwin and Sivek [2, 3]. Thus Theorem 8 would also obstruct the existence of general Lagrangian concordances and not only the decomposable ones. To find non-decomposable cobordisms using obstructions from [1], we should focus on non-zero genus cobordisms.

Using the facts that the GRID invariants are non-zero for the tb = −1 Legendrian unknot and that $\widehat \lambda ^+(\varLambda _{+})$ (resp. $\widehat \lambda ^-(\varLambda _{+})$) vanish for positively (negatively) stabilized Legendrian links, Theorem 8 gives the following corollary.

Corollary 1 ([1, Corollaries 1.3, 1.4])

• 1. If is a Legendrian link such that $\widehat \lambda ^+(\varLambda ) = 0$ or $\widehat \lambda ^-(\varLambda ) = 0$ , then there is no decomposable Lagrangian filling of Λ.

• 2. Suppose Λ _± are Legendrian links such that either

  • (a) $\widehat \lambda ^+(\varLambda _{-}) \neq 0$ and Λ ₊ is the positive stabilization of a Legendrian link, or

  • (b) $\widehat \lambda ^-(\varLambda _{-}) \neq 0$ and Λ ₊ is the negative stabilization of a Legendrian link.

  Then there is no decomposable Lagrangian cobordism from Λ₋ to Λ₊.

This provides another strategy to show the existence of Legendrians Λ_± that are Lagrangian conbordant but cannot be connected by a decomposable Lagrangian cobordism.

Strategy 3

• 1. Find Legendrians Λ_± satisfying the GRID invariants conditions of Corollary 1 and Theorem 8 such that there are no known obstructions, as described in Sect. 2.3 , to the existence of a Lagrangian cobordism from Λ₋ to Λ₊.

• 2. Use a combination of the combinatorial moves described in Sect. 3 to construct a Lagrangian cobordism from Λ₋ to Λ₊.

Example 7

Concrete examples mentioned in [1, Sect. 4.1] can be used for Strategy 3. Let Λ₀, Λ₁ be the Legendrian m(10₁₃₂) knots and Legendrian m(12n₂₀₀) knots shown in [46, Figs. 2 and 3]. Modify them with a pattern shown in [1, Fig. 13] to get $\varLambda ^{\prime }_0$ and $\varLambda ^{\prime }_1$, which are of knot type m(12n₁₉₉) and m(14n₅₀₄₇) (or its mirror), respectively. For i, j = 0, 1 we have $tb(\varLambda ^{\prime }_i)=tb(\varLambda _i)+2$ and $r(\varLambda ^{\prime }_i)=r(\varLambda _i)$. There is no decomposable Lagrangian cobordism from

• 1. Λ₀ to $\varLambda ^{\prime }_1$, or

• 2. Λ₁ to $\varLambda ^{\prime }_0$.

If we can construct, using the combinatorial techniques of Sect. 3, a Lagrangian cobordism (necessarily of genus 1) from Λ₀ to $\varLambda ^{\prime }_{1}$ or from Λ₁ to $\varLambda ^{\prime }_0$, then we will have found a non-decomposable Lagrangian cobordism.

Example 8

In [1, Sect. 4.3], the authors provide an infinite family of pairs of Legendrian knots where there does not exist a decomposable Lagrangian cobordism between them.

Remark 10

In Strategies 2 and 3, we emphasized the construction of Lagrangian cobordisms using the combinatorial techniques of Sect. 3. It would be interesting to know if the geometric constructions of Sect. 4 could also be used to show the existence of a Lagrangian concordance/cobordism from the theory of normal rulings, topology, or grid invariants, that are known to not be decomposable.

5.4 Non-decomposable Candidates Through Surgery

An additional strategy to show the existence of a non-decomposable Lagrangian filling comes from understanding properties of the contact manifold that is obtained from surgery on the Legendrian knot. In particular, Conway, Etnyre, and Tosun [16] have detected a relationship between Lagrangian fillings of a Legendrian and symplectic fillings of the contact manifold obtained by performing a particular type of surgery on the Legendrian.

Theorem 9 ([16, Theorem 1.1])

There is a Lagrangian disk filling of Λ₊ if and only if the contact + 1-surgery on produces a contact manifold that is strongly symplectically fillable. If Λ₊ has a decomposable Lagrangian filling, then the filling can be taken to be Stein.

In fact, [16] also shows that a filling will be a Stein filling if and only if Λ₊ bounds a regular Lagrangian disk: a Lagrangian disk is regular if there is a Liouville vector field that is tangent to the disk. Any decomposable Lagrangian filling is regular.

We now see another strategy to construct a non-decomposable Lagrangian filling.

Strategy 4

Find a Legendrian Λ such that the + 1-surgery on Λ produces a contact manifold that is strongly symplectically fillable but does not admit a Stein filling.

An issue with this approach is a lack of examples: there are very few manifolds which carry strongly fillable but not Stein fillable contact structures. The main examples are the 1∕n surgeries on the positive and negative trefoils; see works by Ghiggini [33] and Tosun [60]. However it is not obvious whether any of these contact structures are a contact + 1-surgery on a Legendrian knot in S³.

6 Conclusion

The desire to understand the flexibility and rigidity of Lagrangian submanifolds has led to a great deal of interesting research in symplectic topology. Similarly, trying to understand constructions of and obstructions to Lagrangian cobordisms has led to many interesting results. At this point, we have few concrete answers to the Motivating Questions stated in our Introduction. In particular, regarding Motivating Question (1), there are presently many candidates for Legendrians Λ_± that can be connected by a Lagrangian cobordism but not by a decomposable Lagrangian cobordism: by understanding all the obstructions to Lagrangian cobordisms, one can come up with some good candidates. When trying and failing to construct a Lagrangian cobordism between a given pair, one may gain intuition for additional obstructions to Lagrangian cobordisms that are waiting to be discovered.