Abstract
Liquid crystals doped with inclusions of other solid or liquid phases possess a number of properties, such as intrinsic anisotropy and extreme responsiveness to external stimuli, that make them particularly attractive for biomedical applications, varying from imaging and spectroscopy to biosensing. One of the hallmarks of such systems is an effective host-mediated interaction between colloidal particles. Building upon similarities between electrostatic potential and small deformations of the nematic director, we show how these anisotropic long-range interactions emerge from the interplay of colloids shape and nematic order and derive general expressions for the long-range interaction potentials for particles of arbitrary shape and size in the presence of confining boundaries and electromagnetic fields. To demonstrate the proposed formalism at work, we consider a series of illustrative examples, ranging from ellipsoids and banana-shaped particles in a sandwich-type cell to nanocolloids in a cylindrical capillary. Our results suggest that one can exploit the interplay of shape, symmetry, and liquid-crystalline order to design particles with prescribed long-range elasticity-mediated interactions, which opens promising pathways to novel mesostructured functional materials.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Nematic liquid crystals combine spatial anisotropy of the orientational order with the fluidity of conventional liquids. Typical NLCs comprise elongated organic molecules with a strong propensity toward aligning their axes along a specific direction characterized by a unit-length vector \(\mathbf {n}\) — the director. Traditionally widely used in information displays, liquid crystalline materials are now rapidly conquering new realms. One of the most mature non-display applications of LCs is in tunable optic filters and light modulators. These components are crucial, in particular, in hyperspectral medical imaging [1, 2], which has tremendous potential in early detection of pathological conditions and disease, such as different types of cancer [3,4,5], diabetic foot ulceration [6], hemorrhagic shock [7]. Real-time hyperspectral imaging augments the surgeon’s field of view and can be used for tumor residue analysis [4, 8]. Due to their strong birefringence in a wide range of frequencies, liquid-crystalline materials are of keen interest to terahertz optics as well [9,10,11]. Unlike X-rays, THz waves do not ionize biological tissues and have energies corresponding to low-frequency vibrational and rotational modes of common biomolecules, making them a powerful non-invasive diagnostic tool with unprecedented spatiotemporal sensitivity [12, 13]. Dispersed nanoscale dopants, ranging from quantum dots [14] to metal nanoparticles [15, 16], can further improve the functionality and efficiency of LC-based devices. At the same time, optical properties of NPs strongly depend on their environment. For instance, surface plasmon resonance in golden nanorods is highly sensitive to their spatial arrangement and the dielectric permittivity of the host medium. These parameters are relatively easy to control with the LC matrix [17], which makes LC-NP composites promising materials for plasmonic applications, including biosensing [18,19,20].
The anisotropy of mechanical properties allows LC-based templates and scaffolds to guide biological cells in specific directions, thereby controlling tissue growth and morphogenesis [21, 22]. Extreme responsiveness to mechanical stimuli endows liquid crystals per se with unsurpassed biosensing capabilities. Chemical binding of biomolecules on the surface or in the bulk of an NLC can disrupt orientational order, thereby changing its optical appearance. This mechanism has been proven successful in detecting different proteins [23, 24], lipids [25], glucose [26], DNA [27]. Recently, Kim et al. designed a self-reporting and self-regulating biosensor using an LC film doped with microdroplets containing an anti-bacterial agent. Shear stresses induced by swimming bacteria shift an intricate balance of elastic and electrostatic forces at the LC-droplet interface and trigger the controlled release of the agent via a feedback loop [28]. One of the major drawbacks of this type of biosensors is comparatively low sensitivity. A growing number of studies suggests that this problem also can be solved with nanodopants [29,30,31,32]. For example, Zhao et al. proposed a thrombin sensor utilizing gold nanoparticles functionalized with \(\sim \)80 binding aptamers each. When loaded with thrombin, the ensuing aggregates are large enough to cause significant distortions of the otherwise uniform director field, thus enabling detection of nanomolar (\(10^{-9}\) mol/L) thrombin concentrations [33].
Nematic liquid crystals doped with nano- and microscale inclusions of other materials are representatives of a broad class of NLC colloids. The world of colloidal particles in an NLC host is dramatically different than in isotropic fluids. Particles suspended in a nematic distort its orientational order even on length scales much larger than the particle size. Distortions overlap and interact with each other, giving rise to effective elastic interactions between colloidal particles. Two hallmarks of such deformation-induced interactions are their long-ranged distance dependence and strong spatial anisotropy. These colloidal interactions generally resemble those between electrostatic multipoles, but the ordered host medium often endows them with distinct traits. The elastic interactions are responsible for the formation of different colloidal structures in liquid crystals. A paradigmatic example is a spherical water droplet accompanied by a point defect (hyperbolic hedgehog) with asymptotic dipole symmetry (see Fig. 5.1a). The ensuing director profile gives rise to the elastic dipole-dipole interaction between the droplets, which then assemble into linear chains parallel to the average director field \(\mathbf{n} _0\) [34,35,36,37]. Droplets of glycerol, on the other hand, induce planar (tangential) anchoring of nematic molecules at the interface, which results in a director field of quadrupole symmetry (Fig. 5.1c) and triggers the aggregation of droplets into inclined chains [36, 38,39,40]. Similarly, solid microspheres with planar anchoring form chains directed at \(30^{\circ }\) to \(\mathbf{n} _0\) [38].
Colloids floating at the nematic-air interface distort the director in the bulk and deform the LC surface. This elasto-capillary coupling leads to the formation of two-dimensional (2D) hexagonal structures with different lattice constants [41, 42]. Photochemical switching between those structures induced by laser light was directly observed in [43, 44]. Transformation of the interfacial hexagonal lattice into linear chains under the action of magnetic field was studied in [45].
One can create a wide variety of 2D crystals in thin nematic cells. In particular, there have been reported hexagonal lattices of glycerol droplets [46], oblique lattices of silica beads [47], antiferroelectrically ordered crystals of dipolar particles [47, 48], and mixed dipole-quadrupole crystals sandwiched between cell walls [49]. The authors of [50] found colloidal superstructures in mixtures of small and large colloids. In these systems, small particles populate a matrix of topological defects surrounding large colloids. One-dimensional structures bound by delocalized topological defects are also of interest. These so-called colloidal wires, whose existence was confirmed in [51], have great potential as optical waveguides. Two-dimensional colloidal crystals assembled from chiral colloidal dimers in a twisted nematic cell were observed in [52]. If the system is sufficiently large, one can even assemble three-dimensional (3D) structures. For instance, Nych et al. developed a step-by-step protocol for the assembly of 3D colloidal crystals of tetragonal symmetry. Surprisingly, these crystals exhibit a highly unusual electro-mechanical response, such as giant electrostriction and collective electro-rotation [53].
Many experimental results were reproduced via numerical minimization of the Landau - de Gennes free energy [47,48,49,50,51,52, 54,55,56,57,58,59,60,61,62] as well as by molecular dynamics [63].
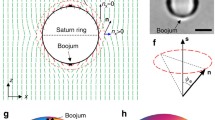
Possible director configurations around spherical colloidal particles: a point defect - hyperbolic hedgehog b line defect — Saturn ring disclination; c pair of point defects — boojums. Dark pink area (coat) contains all topological defects and strong deformations inside. Outside the coat deformations are small; they are governed by Laplace equation and can be expanded in multipoles
In this chapter, we summarise our current understanding of the long-range elastic interactions in NLC colloids. It is worth keeping in mind that short-range interactions are no less important in the context of colloidal assemblies. In NLCs, the short-range interaction is closely intertwined with topological defects emerging in the vicinity of micro-sized colloids, as shown in Fig. 5.1. These singularities in the director field, where it becomes ill-defined, generally have to be studied numerically using Landau-de Gennes formalism. Topological defects and the associated short-range interactions are beyond the scope of this review. For a brief topology oriented discussion of NLC colloids, we refer the reader to [64].
Theoretical understanding of the long-range elastic interactions in NLC colloids is based on their striking similarity to electrostatics. Far from the particle, the director field is governed by the Laplace equation and can be expanded in multipoles. This fact became a starting point for a number of approaches toward the theory of NLC colloids [65,66,67,68,69,70]. However, only one of them, [65], gives analytical results that quantitatively agree with experimental data [71, 72]. The authors of [37] directly measured the elastic interaction between two spherical iron particles by balancing it with a magnetic field and found the predictions of [65] to hold within a few-percent accuracy. Recently, the authors of [60, 61] carried out numerical calculations of the interparticle force between colloids of different sizes. They found their numerical results in good agreement with the experimental data and the predictions of the electrostatic analogy for distances bigger than approximately 3 particle radii.
In practice, liquid crystals are always confined by some surfaces, which can profoundly affect the interparticle interactions. It has been first discovered experimentally that the elastic interactions in a nematic cell are exponentially screened at distances larger than the cell thickness (so-called confinement effect) [54, 73]. Qualitative theoretical investigations of the effects of confinement were performed in [74,75,76,77,78], using the notion of “coat” — introduced in [67] and discussed here in Sect. 5.3 — an area around the particle populated by topological defects and large deformations, as shown schematically in Fig. 5.1. A breakthrough was achieved in Refs. [79,80,81], where external boundaries and fields were incorporated in the form of Green’s functions. Using that approach, the authors derived the interaction potentials for axially symmetric particles in a nematic cell and near one wall with either planar (tangential) or homeotropic (normal) alignment of the LC molecules. The proposed theory [79, 80] is in excellent agreement with the measurements of the confinement effect for two spheres in a homeotropic cell in the range \(1\div 1000~k_BT\) [54] and a planar cell of varying thickness [73].
While theoretical studies were mostly concerned with spherical or axially symmetric particles, experiments and numerical simulations adopted a more diverse set of shapes and topologies. Using lithographically fabricated polygonal platelets, Lapointe et al. were first to demonstrate the relevance of particles’ shape for the interparticle interactions and colloidal self-assembly [82]. In addition to the 2D crystals mentioned above, pentagonal microplatelets in a thin layer of nematic can be assembled into Penrose tilings with quasicrystalline order [83, 84]. Other notable examples of non-spherical colloids include rod-like particles [85], handlebodies of high topological genus [86], micron-sized spheres with nanoscale surface roughness [87], key-lock colloids [88], gourd-shaped dimers [89], colloidal boomerangs [90], and shape-shifting elastomeric rods [91]. Interestingly, the presence of chiral inclusions (e.g., spirals) in an intrinsically achiral nematic can induce spontaneous symmetry breaking evident in chiral defect configurations and director profiles [92].
Here, we describe a theoretical framework applicable to colloids of arbitrary shape and chirality. Building upon [65, 79,80,81, 93,94,95], in Sect. 5.2 we derive general expressions for the pairwise interaction potential in the presence of confining boundaries and electromagnetic fields. Key elements of our model are elastic multipole moments that define the far-field director profile around the particle. In Sect. 5.3, we demonstrate how these coefficients arise from the symmetry of the near-field director, which is dictated by an interplay of the particle shape and the type and strength of nematic anchoring. We thoroughly consider the cases of weak and strong as well as polar and azimuthal anchoring on the particle surface. In the following sections, we apply the proposed formalism to a series of illustrative examples. Namely, Sect. 5.4 discusses in detail the dipole-dipole interaction of banana-shaped particles in a homeotropic and planar nematic cell and contrasts it with that of axially symmetric colloids. In Sect. 5.5, we touch upon elastic monopoles in a confined environment and highlight their distinctive features. The proposed framework is employed to study the behavior of colloids carrying elastic monopole, dipole and/or quadrupole moment in a deformed NLC (nonuniform director field) in Sect. 5.6 and find the distribution of nanoparticles around different types of disclinations in a cylindrical capillary, Sect. 5.7. Finally, Sect. 5.8 elucidates the role of elastic interactions in the coexistence of two quasi-hexagonal structures of glycerol droplets at the nematic-air interface [41, 42].
2 Elastic Interactions in Nematic Liquid Crystal Colloids
Let us first consider a single colloidal particle suspended in a nematic liquid crystal. We will follow the paper [93]. Anchoring of the LC molecules to the particle’s surface distorts the otherwise uniform director field \(\mathbf {n}=\mathbf {n}_0\), so that \(\mathbf {n}\) varies from point to point. The total free energy of the system can be written as the sum of bulk and surface terms \(F=F_{bulk}+F_{surface}\), where the former reads
with K denoting the Frank elastic constant. Two comments are in order. First, we adopt the one-constant approximation, \(K_{11}=K_{22}=K_{33}=K\); implications of this assumption are discussed in [96]. Second, we also omit the \(K_{24}\)-term because it does not play a crucial role in further considerations, as was shown in [80]. Surface energy \(F_{surface}\) penalizes deviations of the director from the preferred orientation at the particle surface. It will be discussed in detail in Sect. 5.3 [for definition see Eq. (5.20)].
Regardless of the particle’s shape, size or anchoring type and strength, deformations of the director field decay with the distance from the particle and eventually become small, \(\mathbf{n} (\mathbf{r} ) \approx (n_{x}, n_{y}, 1)\), where \(|n_{\mu }| \ll 1\), \(\mathbf{n} _{0} = (0, 0, 1)\) is the NLC ground state, and \(\mu = \{ x,y \}\) hereafter. Thus, far from the particle the bulk free energy takes a simple harmonic form
where repeated \(\mu \) implies summation over x and y, i.e. \((\nabla n_{\mu })^{2}=(\nabla n_{x})^{2} + (\nabla n_{y})^{2}\). Hereafter, \(\int dV \) stands for the integration over the whole volume of the system unless otherwise specified, and we do not take into account the volume of the coat(s). This is justified by several reasons: 1) we are interested mainly in the interparticle interactions which are caused by the changes in the director field caused by other particles, and these changes are small inside the coat where the director is governed by strong anchoring to the surface, i.e., the energy of the coat is approximately constant and can be omitted from the theory; 2) the volume inside the coat is much smaller than the volume outside, therefore the replacement of the total energy (5.1) with (5.2) inside the coat does not affect the interparticle interaction considerably (at least when the separation is large enough compared to the particle size); 3) this approximation is in good agreement with experimental data for spherical particles as long as their surfaces are separated by more than \(\sim \)0.2–0.8 radii depending on the system [97,98,99,100]. Note that these studies, in contrast to [60, 61], consider higher-order contributions as explained below.
The Euler-Lagrange equations for \(n_{\mu }\) are of the Laplace type
In analogy to classical electrostatics, solutions to these equations can be expanded in multipoles
where \(\alpha \) and \(\beta \) take values x, y, z and summation over repeated greek indices is assumed. Quantities \(q_{\mu }\), \(p_{\mu }^{\alpha }\), \(Q_{\mu }^{\alpha \beta }\) are called elastic charge (monopole), three components of the dipole moment, and five components of the quadrupole moment for each \({\mu }\), respectively. They are phenomenological far-field characteristics of a given colloidal particle.
Even though we truncated the expansion (5.4) at quadrupolar terms, higher-order contributions may be important as well. It was noticed in [65, 97] that if the leading contribution to \(n_{\mu }\) is dipolar, then anharmonic corrections to \(n_{\mu }\) associated with small variations of \(n_z=\sqrt{1-n_{\mu }n_{\mu }}\) scale as \(r_{\mu }/r^7\), suggesting that high-order terms up to \(1/r^5\) should be considered. Similarly, if the leading contribution to \(n_{\mu }\) is quadrupolar, anharmonic corrections to \(n_{\mu }\) are of the form \(r_{\mu }/r^{10}\) and high-order terms of up to \(1/r^8\) can effectively influence short-range behavior. High-order terms have a profound effect on the spatial anisotropy of the interaction potential at relatively small distances and play an important role in the formation of colloidal crystals [97,98,99,100]. Reference [97] also introduced the concept of three zones: in the first zone (at distances \(\lesssim \)1.1–1.4 particle radii depending on the system) the linear theory is inapplicable; the second zone (between roughly 1.3–1.4 and 2 radii) is where the high-order terms reside; and the third zone (\(\gtrsim \)2 radii) is dominated by the first non-vanishing term in (5.4). In what follows, we will limit ourselves to the first three terms in the multipole expansion (5.4).
As follows from (5.4), director deviations \(n_{x}\) and \(n_{y}\) have a long-range nature. This means that deformations caused by different particles can overlap even if the particles are located at a large distance from each other. In practice, the overlapping manifests itself in the emergence of effective long-range interactions between colloidal particles mediated by the host medium. As we will see below, these interactions are determined precisely by the multipole moments \(q_{\mu }\), \(p_{\mu }^{\alpha }\), \(Q_{\mu }^{\alpha \beta }\).
Imagine that somehow we have found all these multipole coefficients. That is, we know two elastic charges \(q_{\mu }\), six components of the dipole moment \(p_{\mu }^{\alpha }\) and five components of the quadrupole moment \(Q_{\mu }^{\alpha \beta }\) for every \(\mu = \{ x,y \}\) (10 altogether). Note that the quadrupole moment tensor \(\hat{Q}_{\mu }=\{Q_{\mu }^{\alpha \beta }\}\) can be always introduced (with a substitution \(\tilde{Q}_{\mu }^{\alpha \beta }=Q_{\mu }^{\alpha \beta }-\frac{1}{3}\delta _{\alpha \beta }Sp\hat{Q}_{\mu }\)) in such a way that it is symmetric, \(\tilde{Q}_{\mu }^{\alpha \beta } = \tilde{Q}_{\mu }^{\beta \alpha }\), and traceless, \(\text {Sp} \hat{\tilde{Q}}_{\mu }=\tilde{Q}_{\mu }^{\alpha \beta } \delta _{\alpha \beta } = 0\) [101]. Thus, we have 18 multipole parameters. Now we need to build an effective free energy functional, which incorporates these coefficients and gives correct behavior of the director at large distances from the particle.
This aim was first achieved in [65] for the case of axially symmetric particles. The effective free energy functional was written as

where \(P(\mathbf{x} ) = P \delta (\mathbf{x} )\) and \(C(\mathbf{x} ) = C \delta (\mathbf{x} )\) are scalar dipole and quadrupole moment densities and \(\partial _{\mu } n_{\mu }=\partial _{x} n_{x}+\partial _{y} n_{y}\).
The generalization of the free energy (5.5) for particles of arbitrary shape and anchoring strength is quite straightforward:

where \(q_{\mu }(\mathbf{x} )=q_{\mu }\delta (\mathbf{x} ), p_{\mu }^{\alpha }(\mathbf{x} = p_{\mu }^{\alpha }\delta (\mathbf{x} ),Q_{\mu }^{\alpha \beta }(\mathbf{x} )=Q_{\mu }^{\alpha \beta }\delta (\mathbf{x} )\) are point-like densities; \(\alpha \) and \(\beta \) take values x, y, z and summation over repeated greek indices \(\mu =x,y\) is assumed. In the case of axially symmetric particles without helical twisting \(q_{\mu }=0,p_{\mu }^{\alpha }=0\) except for \(p_{x}^{x} = p_{y}^{y} = P\), \(Q_{x}^{xz} = Q_{x}^{zx} = Q_{y}^{yz} =Q_{y}^{zy} =C\) and we arrive at Eq. (5.5).
The Euler-Lagrange equations arising from (5.6) are of Poisson type
If the liquid crystal is confined by some surface \(\varSigma \) such that \(n_{\mu } \Big |_{\varSigma } =0\) then solutions to (5.7) are as follows
where \(G_{\mu }(\mathbf{x} , \mathbf{x} ^{\prime })\) are appropriate Green functions, \(\varDelta G_{\mu }(\mathbf{x} , \mathbf{x} ^{\prime }) = -4 \pi \delta (\mathbf{x} - \mathbf{x} ^{\prime })\) for any \(\mathbf{x} , \mathbf{x} ^{\prime } \in V\) and \(G_{\mu }(\mathbf{x} , \mathbf{s} ) =0\) for any \(\mathbf{s} \in \varSigma \). In the absence of confinement, \(G_{\mu }(\mathbf{x} , \mathbf{x} ^{\prime }) = \frac{1}{| \mathbf{x} - \mathbf{x} ^{\prime }|}\) and (5.8) yields (5.4).
Due to the linearity of the Euler-Lagrange equations (5.7), we can use the superposition principle for the system of N colloidal particles

That is, the resulting director deformation is the sum of distortions caused by every single particle. Substituting (5.8) into (5.6) and implying (5.9), we come to the fact that the free energy of the system can be presented as the sum of the self energy part and pair interactions \(F_{eff}=U^{self}+U^{interaction}\), where \(U^{self}=\sum _{i}U_{i}^{self}\) and
The pairwise elastic interaction \(U^{ij}\), in turn, is the sum of monopole-monopole, monopole-dipole, monopole-quadrupole, dipole-dipole, dipole-quadrupole and quadrupole-quadrupole interactions, \(U^{ij} = U_{\text {qq}} +U_{\text {qd}} +U_{\text {qQ}} +U_{\text {dd}} +U_{\text {dQ}} +U_{\text {QQ}}\), where

Expressions (5.11)–(5.16) give a general form of the pairwise long-range elastic interaction between colloidal particles of arbitrary shape in a confined NLC. They hold in the bulk as well with \(G_{\mu }(\mathbf{x} , \mathbf{x} ^{\prime }) = \frac{1}{| \mathbf{x} - \mathbf{x} ^{\prime }|}\).
Self-energy of the colloid (or the energy of the particle-walls interaction) also can be presented as the sum \(U_{i}^{self} = U_{\text {qq}}^{self} +U_{\text {qd}}^{self} +U_{\text {qQ}}^{self} +U_{\text {dd}}^{self} +U_{\text {dQ}}^{self} +U_{\text {QQ}}^{self}\) where all \(U_{\text {AB}}^{self}\) are given by the formulas (5.11)–(5.16) upon replacing \(G_{\mu }(\mathbf{x} _{i}, \mathbf{x} _{j}^{\prime })\) with \(H_{\mu }(\mathbf{x} _{i}, \mathbf{x} _{j}^{\prime })\), where \(G_{\mu }(\mathbf{x} , \mathbf{x} ^{\prime }) = \frac{1}{|\mathbf{x} - \mathbf{x} ^{\prime }| }+H_{\mu }(\mathbf{x} , \mathbf{x} ^{\prime })\) and \(\varDelta _\mathbf{x }H_{\mu }(\mathbf{x} , \mathbf{x} ^{\prime })=0\). Note that to regularize the self-energy by excluding the divergent part associated with \(\frac{1}{|\mathbf{x} - \mathbf{x} ^{\prime }| }\), it is necessary to set \(\mathbf{x} _{j}^{\prime }=\mathbf{x} _{i}\) after all primed derivatives \(\partial _{\xi }^{\prime }\) are calculated. Employing this procedure we can find


and so forth. We leave the rest of this series as an exercise for the reader. It should be noted that the self-energies (5.17)–(5.19) do not include the energy of nonlinear deformations (i.e., internal energy of the coat). While that contribution cannot be computed within the framework of multipole expansion, it can be treated as an unknown constant, as we argued above. In this context, the self-energy refers only to the difference between the energy of the particle in a confined NLC and its energy in the bulk. In other words, it is the energy of interaction between one particle and all confining boundaries. Hence, \(H_i^{self}\equiv 0\) in the absence of confinement. In a sandwich-type cell, for instance, \(H_i^{self}=H_i^{self}(z)\) with z being normal to the cell walls; minimization of the corresponding self-energy yields an equilibrium position of the particle inside the cell, see [102].
Upon proper substitution of Green’s functions \(G_{\mu }(\mathbf{x} _{i}, \mathbf{x} _{j}^{\prime })\) with \(G_{\mu }^{field}(\mathbf{x} _{i}, \mathbf{x} _{j}^{\prime })\), Eqs. (5.11)–(5.19) remain valid even in the presence of external electric \(\mathbf{E} \) or magnetic \(\mathbf{H} \) fields, as was shown in [81] for axially symmetric particles. Reference [81] also reported the explicit form of Green’s functions \(G_{\mu }^{field}(\mathbf{x} _{i}, \mathbf{x} _{j}^{\prime })\) for different orientations of the field in a nematic cell with homeotropic and planar boundary conditions.
Equations (5.11)–(5.16) show that the energy of interaction depends on both multipole coefficients and Green’s functions. The former originate from the interaction between the particle surface and NLC molecules. The latter are determined by the shape of the confining surface \(\varSigma \) as well as by external fields \(\mathbf{E}/H \).
3 Multipole Coefficients and Particle’s Symmetry
In this section we want to establish a connection between the symmetry of the particle and the director deformations produced at large distances.Footnote 1
As mentioned above these distortions are completely described by a set of multipole coefficients \(q_{\mu }, p_{\mu }^{\alpha }, Q_{\mu }^{\alpha \beta }\). Strictly speaking, we should distinguish two cases here. When the anchoring is weak \(Wr_{0}/K<1\) (\(r_{0}\) being the average size of the particle ) the deformations are small everywhere outside the particle and the coefficients can be found from the mechanical equilibrium condition (we apply this procedure below). If the anchoring is strong \(Wr_{0}/K>1\) the deformations in the particle’s vicinity are large, even topological defects may appear there. So the coefficients cannot be linked directly to the particle’s symmetry. But in this case the notion of the coat suggested in [67] is helpful. The coat is an area, which contains all topological defects and large deformations inside, so that the director field outside is presented in the form of multipole expansion (5.4). The symmetry of the coat matches the symmetry of the director field around the particle and, depending on its size, can be observed experimentally or computed numerically via Landau-de Gennes energy minimization. In fact, one can treat the coat as some imaginary particle with appropriate symmetry and weak anchoring on its surface. Therefore we use only the term “particle” further.
Thus, it is enough to consider one colloidal particle with weak anchoring in a bulk NLC. The free energy of such a system is the sum of two parts: bulk energy (5.2) and the surface anchoring energy. The latter can be presented as
where \(W^{\alpha \beta }(\mathbf{s} )\) is the symmetrical local anchoring tensor at point \(\mathbf{s} \) on the particle’s surface [103]. The tensor description has the covariant form and describes both polar and azimuthal anchoring simultaneously. But a connection between the particle’s symmetry and tensor’s properties is not so clear in general case. In order to make our analysis as transparent as possible we should use the following representation of the surface energy
This is the generalized Rapini-Popular surface energy with \(W^{p}\) and \(W^{a}\) being the strengths of the polar and azimuthal anchoring energies, respectively. Here \(\boldsymbol{\nu }\) is the outer normal to the particle’s surface at the point \(\mathbf{s} \) and \(\boldsymbol{\tau }\) is the unit tangential vector along the local rubbing which also depends on the point \(\mathbf{s} \) of the surface. Azimuthal anchoring \(W^a>0\) makes alignment of the director along vector field \(\boldsymbol{\tau }(\mathbf{s} )\) at the surface. Since the anchoring is weak the total energy can be reduced to

where we neglected terms like \((\nabla n_{z})^{2}\), \(W^{p} n_{\mu } n_{\mu ^{\prime }}\) and \(W^{a} n_{\mu } n_{\mu ^{\prime }}\) because of their smallness. Note that, in fact, \(W^{p} \nu _{z} \nu _{\mu } - W^{a} \tau _{z} \tau _{\mu } = W^{z\mu }\) in (5.20). Note that here \(\int dV\) denotes integration over the LC volume.
At the same time the director field everywhere outside the particle in the bulk NLC is described by (5.4) so that

where the summation over all repeated Greek indices is implied. Then substituting (5.4), (5.23) into (5.22) and performing the integration one can obtain the free energy of the system as a function of the multipole coefficients
where we introduced vector of the coefficients \(\mathbf{m} = (q_{\mu }, p_{\mu }^{\alpha }, Q_{\mu }^{\alpha \beta })=(q_{x},q_{y}, p_{x}^{x}, p_{x}^{y},p_{x}^{z},p_{y}^{x},p_{y}^{y},p_{y}^{z},Q_{x}^{xx},Q_{x}^{xy}...)\). Hence \(m_{u},m_{v}\) denote unknown multipole coefficients. Quantities \(a_{uv}\) arise from the bulk energy, for example,
Apparently, all \(a_{uu}\) are positive and finite, \(a_{uv}\) depend on the particle shape. Each \(c_u\) is the sum of two terms \(c_u^p\) and \(c_u^a\) arising from the polar and azimuthal anchoring, respectively, \(c_u = c_u^p + c_u^a\). So, for instance,
\(c_u\) depends on both the anchoring and the particle’s shape, \(\mathbf{s} =(s_{x},s_{y},s_{z})\) is the radius vector from the center of the particle to the point \(\mathbf{s} \) at the surface (this center of the particle coincides with the center of the coordinate cystem (CS) from which all \(r_{\alpha }\) are measured). In the remainder of this section, we mathematically prove that if a given \(c_u\) vanishes, so does the associated multipole moment. As follows from their definitions (5.25), these quantities, and consequently their corresponding multipoles, vanish if the particle possesses certain symmetries. Table 5.1 summarizes these relations between the particle symmetry and its multipole moments.
Now it is natural to assume that the system under investigation is in equilibrium. Therefore its energy is minimal. Hence one can find the multipole coefficients from the following system of linear equations \(\frac{\partial F_{harm}}{\partial m_{u}}=0\):
or the same in the matrix form:
Here we should make some remarks. First of all this Eq. (5.27) is the exact equation for the multipole coefficients \(\mathbf{m} \) for the weak anchoring case. In this case we know exactly weak anchoring coefficient \(W_{a,p}(\mathbf{s} )\) and vector fields \(\boldsymbol{\nu }(\mathbf{s} )\),\(\boldsymbol{\tau }(\mathbf{s} )\), we can calculate all \(c_{u}\) and \(a_{uv}\) and finally we can solve this matrix equation and find all 18 unknown coefficients.
On the other hand, this lengthy procedure is usually unnecessary. Typically, we do not need to calculate coefficients \(\mathbf{m} \) - we can infer them from experimental or numerical data. It is thus much more valuable to understand which coefficients vanish and which remain finite. We can then find nonzero coefficients as fitting parameters for the director field measured experimentally or simulated numerically. Therefore, our primary strategy is to understand which coefficients vanish and which remain nonzero without solving the system (5.27) based on symmetry considerations only! This strategy is realized in the following subsections.
Since \(\mathbf{c} = \mathbf{c} ^p + \mathbf{c} ^a\), a solution of the system (5.27) can be written as the sum
of two solutions of the following systems
Thus the polar and azimuthal anchorings make their contributions to the coefficients independently and we can consider these two cases separately.
3.1 Polar Anchoring
Suppose that we have a particle with usual polar anchoring on its surface, \(W^a \equiv 0\). Then the multipole coefficients satisfy system (5.29). Here we should say that the phrase “particle symmetry” means that the appropriate symmetry element belongs to the particle shape as well as to the anchoring distribution \(W^p(\mathbf{s} )\). Thus, in terms of symmetry, particles of symmetrical shape with asymmetric anchoring do not differ from those of asymmetrical shape with symmetric \(W^p(\mathbf{s} )\).
Assume first that the particle has one plane of symmetry. Say for instance that it coincides with the coordinate xz-plane. Then for any point \(\mathbf{s} =(x, y, z)\), where \(\boldsymbol{\nu }=(\nu _x, \nu _y, \nu _z)\), there exists point \(\mathbf{s} ^{\prime }=(x, -y, z)\), where \(\boldsymbol{\nu }=(\nu _x, -\nu _y, \nu _z)\), and \(W^p(\mathbf{s} ) = W^p(\mathbf{s} ^{\prime })\). Then using these symmetry relations one can easily ensure that, for example, \(a_{q_x q_x} = K\int dV r^{-4} \ne 0\), \(a_{q_x p_x^y} =4K\int dV y r^{-6} =0\), \(c_{q_y}^p = 2 \int dS\,W^p \nu _{z} \nu _{y} s^{-1} = 0\) etc. In the same way \(a_{q_x p_x^y} = a_{p_x^x p_x^y} = a_{p_x^y p_x^z} = a_{q_y p_y^y} = a_{p_y^x p_y^y} = a_{p_y^y p_y^z} = 0\) and \(c_{q_y}^p = c_{p_y^x}^p = c_{p_y^z}^p = c_{p_x^y}^p = 0\). It is well known that if the leading term in \(n_{\mu }\) decreases as \(r^{-n}\) then the leading anharmonic correction will fall off as \(r^{-3n}\) [65]. Thus, quadrupolar terms can be neglected here as anharmonic corrections to \(n_{\mu }\). Since in vector \(\mathbf{m} \) the multipole coefficients can be arranged in any order, we are able to rewrite the system (5.26) in the following matrix form \(\hat{A}{} \mathbf{m} ^p = -\mathbf{c} ^p\):
Here \(\hat{A}\) is a block diagonal matrix,  . So the system (5.26) splits into two independent subsystems, nonhomogeneous with matrix \(\hat{A}_{nh}\) and homogeneous with matrix \(\hat{A}_{h}\). At the same time \(\hat{A}\) is a positive-definite matrix. Indeed we can treat components of arbitrary nonzero vector \(\mathbf{m} \) as the coefficients of some multipole expansion, then
. So the system (5.26) splits into two independent subsystems, nonhomogeneous with matrix \(\hat{A}_{nh}\) and homogeneous with matrix \(\hat{A}_{h}\). At the same time \(\hat{A}\) is a positive-definite matrix. Indeed we can treat components of arbitrary nonzero vector \(\mathbf{m} \) as the coefficients of some multipole expansion, then
Thus \(\text {det} \hat{A} = \text {det} \hat{A}_{nh}\cdot \text {det} \hat{A}_{h} > 0\). So homogeneous subsystem has only trivial solution. It is easy to ensure that the same scenario occurs for particles of other symmetries. If certain \(c_u^p\) is equal to zero then the related multipole coefficient \(m_u\) vanishes: \(c_u^p =0 \Rightarrow m_u^p =0\).
Accordingly, only those multipole coefficients can exist which are allowed by the particle symmetry from the Table 5.1.
Note that the same classification was obtained in the paper [67] on the basis of gradient expansion \(\partial n_{\mu }\) in the center of the particle. But actually the gradient expansion can not be done exactly as \(\partial n_{\mu }\approx 1\) is not a small parameter. Therefore the current approach can be considered as more consistent and correct.
Here we should remark that multipole coefficients \(\mathbf{m} \) depend on the chosen coordinate system. In one coordinate system CS1 there will be one set of parameters \(\mathbf{m} _{1}\) and in the CS2 (which can be rotated or shifted by some vector \(\mathbf{d} \) with respect to CS1) there will be another set of multipole coefficients \(\mathbf{m} _{2}\), but the total sum (5.4) will be the same in both CSs. In our consideration we have chosen the most appropriate case when symmetry planes coincide with coordinate planes as in this CS the classification is possible and useful. But in any CS the main multipole coefficient \(q_{\mu }\) will be the same as well as in electrostatics - the charge does not depend on the CS [104] while high order moments do depend on the CS.
3.2 Azimuthal Anchoring and Chiral Colloids
As follows from (5.28) and (5.30) the long-ranged director deformations can also arise from the azimuthal anchoring of NLC molecules on the particle surface.
Simple examples of such particles are uniaxial helicoids - axially symmetric particles like cylinders or cones with the helicoidal alignment along their easy axes z (see Figs. 5.2 and 5.3). For this case we need to take \(W^a>0\) and vector \(\tau (\mathbf{s} )\) makes screw thread at the surface of the particle. Then using the method suggested in the previous subsection one can find that multipole coefficients \(\mathbf{m} ^a\) in this case are defined from the Table 5.2. Inasmach as \(p_{hel}\propto \oint dS W^a \tau _{z} \tau _{y} x\) and \(Q_{hel}\propto \oint dS W^a \tau _{z} \tau _{y} xz\), so that \(p_{hel}>0\) and \(Q_{hel}>0\) for right-handed helicity and \(p_{hel}<0\) and \(Q_{hel}<0\) for left-handed helicity (see Fig. 5.2).
3.2.1 Interaction Between Helicoid Cylinders
Consider cylinders (or other symmetric particles like ellipsoid or sphere) with helicoidal alignment at the surface (see Fig. 5.2). This azimuthal helicoid anchoring gives rise to nonzero dipole moments \(p_{y}^{x}=p_{hel}=-p_{x}^{y}\), though the shape of the cylinder does not produce any dipole moments (see Table 5.1). Under these conditions, (5.11) gives the following dipole-dipole elastic interaction between helicoid cylinders (ellipsoids or spheres):
The Green’s functions \(G_{x}\ne G_{y}\) are different only when some external field (electric or magnetic) is applied along the axis x or y [81]. When the external fields are absent in any other cases (like in homeotropic or planar nematic cell) \(G_{x}=G_{y}=G\) and we come to the expression
which coincides with the dipole-dipole interaction between usual axially symmetric dipole particles (\(\partial _{\mu }\partial _{\mu }'=\partial _{x}\partial _{x}'+\partial _{y}\partial _{y}'\)). In the bulk nematic liquid crystal, for example, \(G(\mathbf{x} , \mathbf{x} ^{\prime })=\frac{1}{|\mathbf{x} -\mathbf{x} ^{\prime }|}\) so that
where \(\theta \) is the angle between \(\mathbf{r} \) and \(\textit{z}\) and the director field around the particle has the form:

The formula (5.35) means that helicoids with the same handedness \(p_{hel}p_{hel}'>0\) attract along \(\textit{z}\) axis and repel in perpendicular direction and vice versa for helicoids with different handedness \(p_{hel}p_{hel}'<0\) (see Fig. 5.2). In the nematic cell the interaction, falling off as \(r^{-3}\) in the bulk NLC, becomes exponentially screened at distances comparable to the thickness L of the cell. At the same time the borders between the attraction and repulsion zones transform from straight lines into some parabola like curves. These effects are caused only by the confining walls so they do not depend on the particles shape and anchoring. More detailed consideration of these issues is presented in [79, 80].
3.2.2 Interaction Between Helicoid Cones
Consider cones (or other axially symmetric particles without symmetry plane \(\sigma _{xy}\)) with helicoidal alignment at the surface (see Fig. 5.3). The shape of the particle produces dipole moments \(p_{x}^{x}=p_{y}^{y}=p\) according to the Table 5.1. Azimuthal helicoid anchoring gives rise to nonzero dipole moments \(p_{y}^{x}=p_{hel}=-p_{x}^{y}\). Then substitution of it to the (5.11) gives the dipole-dipole elastic interaction between helicoid cones:

In the absence of the external fields \(G_{x}=G_{y}=G\) and we come to the expression
In the confined nematic this formula gives the same results as in the [80] but with new coefficient \(pp'+p_{hel}p_{hel}'\).
In the bulk nematic liquid crystal \(G(\mathbf{x} , \mathbf{x} ^{\prime })=\frac{1}{|\mathbf{x} -\mathbf{x} ^{\prime }|}\) so that
and the director field around the particle has the form:

Formulas similar to (5.35), (5.36), (5.39), (5.40) were first obtained in [70] but our results predict 3 times stronger interaction. In paper [70] authors made very good classification of different types of dipoles in nematostatics based on the firm fixation of the director field on the surface of the imaginary sphere enclosing the particle and containing all the defects inside. At first glance it seems quite similar to the coat-approach used above. The authors of [70] do not use any anchoring surface energy explicitly and consider the total energy as just the bulk one. But the total energy is the sum of the bulk and surface energies. This, we suppose, is the reason for the discrepancy. The surface terms do play their important role and increase the energy of the system and should be taken into consideration. In the current approach the surface terms are taking into account via terms \(-4 \pi q_{\mu }(\mathbf{x} )n_{\mu } -4 \pi p_{\mu }^{\alpha }(\mathbf{x} )\partial _{\alpha } n_{\mu } -4 \pi Q_{\mu }^{\alpha \beta }(\mathbf{x} ) \partial _{\alpha } \partial _{\beta } n_{\mu }\) in the effective free energy (5.6). These terms in the effective free energy (5.6) replace surface terms in the real free energy (5.22) so they can be effectively considered as surface born.
4 Banana-Shaped Particles in a Nematic Cell
As an example of the interaction between non axially-symmetrical colloids we consider now the interaction between banana-shaped particles (see Fig. 5.4) and as well consider the interaction between axially symmetrical particles including particles with helical screw-thread (see Figs. 5.2 and 5.3). Here let us content ourselves with the dipole-dipole interactions in homeotropic and planar nematic cells.
4.1 Homeotropic Cell
Coordinate system for this case is depicted in Figs. 5.5a and 5.5b. Green’s function then has a form that is well known in electrostatics [104]

where \(I_{m}\), \(K_{m}\) are modified Bessel functions, \(\tan \varphi =\frac{y}{x}\), \(\tan \varphi ^{\prime }=\frac{y^{\prime }}{x^{\prime }}\), \(\lambda _{n}=\frac{n \pi }{L}\), \(\rho _{<}\) is the smaller of \(\rho =\sqrt{x^2+y^2}\) and \(\rho ^{\prime }=\sqrt{x^{\prime 2}+y^{\prime 2}}\).
Every banana-shaped particle has two orthogonal symmetry planes. Suppose first that the particles are oriented in such a way that these planes are parallel to the coordinate xz and yz planes (see Fig. 5.5a), i.e. particles are located primarily perpendicular to the director (we will use symbol \(\bot \) for this case). Then using Table 5.1 one can easily find that the allowed dipole coefficients are \(p_x^x\) and \(p_y^y\). Below we omit the upper indexes and assume \(p_{y} > p_{x}\). Note that \(p_{x} = p_{y}\) for axially symmetric particles. It follows from (5.14) that
where \(\rho =\sqrt{(y-y^{\prime })^{2}+(x-x^{\prime })^{2}}\) is the horizontal projection of the distance between particles, \(\phi \) is the azimuthal angle between \(\rho \) and x-axis,
Before proceeding to a discussion of this interaction in the cell let us consider its features in the bulk liquid crystal. The Green’s function for the bulk NLC is \(G(\mathbf{x} , \mathbf{x} ^{\prime }) = \frac{1}{|\mathbf{x} -\mathbf{x} ^{\prime }|}\) so that \(U_{\text {dd},\bot }^{\text {bulk}}\) is anisotropic as well,
where r is the distance between particles, \(\theta \) is the polar angle between \(\mathbf{r} \) and z-axis, \(\phi \) is the azimuthal angle between \(\rho \) and x-axis.
Note that similar formula for bulk NLC was obtained in [70] but our result predicts three times stronger interaction.
Map of the attraction and repulsion zones between two particles with \(z = z^{\prime }\) and \(p_y = 3 p_x\) in the infinite crystal is depicted by the red dashed lines in Fig. 5.6.
Now assume that the particles are located in the centre of the homeotropic cell \(z = z^{\prime } = \frac{L}{2}\) (solid lines in Fig. 5.6). At small distances \(\rho \ll L\) the interaction is the same as in the bulk nematic \(U_{\text {dd},\bot }^{hom} \rightarrow U_{\text {dd},\bot }^{\text {bulk}}\). But as \(\rho \) increases the lateral zones become closed. So that identical particles attract inside some dumbbell-shaped regions along x axis when \(p_{y}>\sqrt{2}p_{x}\). These regions shrinks as \(|p_y-\sqrt{2}p_x |\) decreases and collapses to the point when \(p_y =\sqrt{2}p_x\). The crossover from the attraction to the repulsion when both particles are located along x axes and \(p_{y}>\sqrt{2}p_{x}\) is shown on the Fig. 5.7.
When \(\frac{p_{x}}{\sqrt{2}}<p_{y}<\sqrt{2}p_{x}\) there will be only repulsion for every \(\phi \) in the perpendicular plane \(\theta =\pi /2\). When \(p_{y}<\frac{p_{x}}{\sqrt{2}}\) there will be attraction inside some dumbbell-shaped regions along y axis and repulsion everywhere along x axis.
Another important issue is the energy dependence on the distance between particles. It follows from (5.46) that in the bulk nematic host the interaction of dipolar colloidal particles decreases as \(\rho ^{-3}\) (see dashed line 4 in Fig. 5.8). But in the cell we see completely different picture. The interaction potential falls off as \(\rho ^{-3}\) only when \(\rho < L\). At larger distances \(\rho > L\) the potential becomes screened by the cell walls (see solid line 2 in Fig. 5.8). Such screening known as confinement effect was first reported experimentally in [54] and theoretically explained in [74, 80] for spherical particles. This phenomena is related only with the confining surfaces and therefore it occurs despite the particles shape.

(reprinted with permission from [93])
Map of the attraction and repulsion zones for two identical banana-shaped particles, \(p_x = p_x^{\prime }\) and \(p_y = p_y^{\prime } = \alpha p_x\), \(\alpha >\sqrt{2}\), according to (5.43). Black line a corresponds to the case \(p_y = 1.5 p_x\), blue line b corresponds to the \(p_y = 2 p_x\) and red line c corresponds to the \(p_y = 3 p_x\). The particles are located in the centre of the homeotropic cell \(z = z^{\prime } = \frac{L}{2}\). Their orientation are shown on the Figs. 5.4b and 5.5a. Sign “-” means attraction (inside of the dumbbell-shaped regions), “-” means repulsion. If \(p_y < \frac{p_x}{\sqrt{2}}\) then the attraction will appear along the y-axis. Dashed lines depict the map of interaction between two particles with \(z = z^{\prime }\) and \(p_y = 3 p_x\) in the absence of confinement

(reprinted with permission from [93])
The crossover from the attraction to the repulsion between two banana-shaped particles located in the middle of the homeotropic cell \(z = z^{\prime }=\frac{L}{2}\) along x axis (see Figs. 5.5a and 5.6), \(p_x = p_x^{\prime }\), \(p_y = p_y^{\prime } = \alpha p_x\) for \(\alpha >\sqrt{2}\). \(\tilde{U} = U_{\text {dd},\bot }^{hom}L^{3} / 8\pi K (p_x p_x^{\prime } + p_y p_y^{\prime })\), where \(U_{\text {dd},\bot }^{hom}\) is given by (5.43) and \(\phi = 0\). Solid black line 1 corresponds to the \(p_y = p_y^{\prime } = 1.5 p_x\), orange line 2 corresponds to the \(p_y = p_y^{\prime } = 1.7 p_x\)
But the particles orientation examined above is not the only possible. Their symmetry planes can be parallel to the coordinate yz and xy planes as well (see Fig. 5.5b), i.e. particles lie primarily parallel to the director (we will use || for this case). Then we have one dipole coefficient \(p_y^z = p \ne 0\) as follows from Table 5.1. Thus
As well as in the previous case the interaction given by (5.48) is screened by the cell walls (solid line 1 in Fig. 5.8). But here it exhibits cylindrical symmetry. In particular, parallel dipoles with \(z = z^{\prime }\) attract each other throughout the cell plane. In the unlimited case \(G = \frac{1}{| \mathbf{x} - \mathbf{x} ^{\prime }|}\) and (5.48) becomes
Similar result for the bulk NLC was obtained in [70] but our result again predicts three times stronger interaction.

(reprinted with permission from [93])
Log-log plot of the dimensionless energy of the dipole-dipole interaction as a function of the distance between two banana-shaped particles located in the middle of the homeotropic cell \(z = z^{\prime }=\frac{L}{2}\). Solid blue line 2 corresponds to the particles repulsion for the orientation along y axis depicted on the Fig. 5.5a, \(p_x = p_x^{\prime }\), \(p_y = p_y^{\prime } = 2 p_x\), \(2\phi = \pi \) and \(\tilde{U} = U_{\text {dd}}L^{3} / 8\pi K (p_x p_x^{\prime } + p_y p_y^{\prime })\), where \(U_{\text {dd}}>0\) is given by (5.43). Dashed line 4 is an appropriate power law asymptotic \(U_{\text {dd}}^{\text {unc}}L^3 / 4\pi K (p_x p_x^{\prime } + p_y p_y^{\prime }) \propto \left( \frac{L}{\rho }\right) ^3\). Solid red line 1 corresponds to the particles attraction along y axis on the Fig. 5.5b, \(p_y^z = p \ne 0\) and \(\tilde{U} = U_{\text {dd}} L^3 / 16\pi K pp^{\prime }\), where \(U_{\text {dd}}<0\) is given by (5.48). Dashed line 3 is the appropriate power law asymptotic \(\frac{1}{4} \left( \frac{L}{\rho } \right) ^3\)
For axially symmetrical particles formula (5.38) with the Green function (5.41) gives the result of dipole-dipole interaction between such particles as
where \(\rho =\sqrt{(y-y^{\prime })^{2}+(x-x^{\prime })^{2}}\) is the horizontal projection of the distance between particles. We see that axially symmetric particles either attract or repel each other independent on \(\phi \) everywhere inside the homeotropic cell, while the dipole-dipole interaction between banana-shaped particles can be either anisotropic or independent of \(\phi \) .
4.2 Planar Cell
Let us choose the coordinate system as shown in Figs. 5.5c and 5.5d. Then the Green’s function is as follows:

where L is the cell thickness, \(I_{m}\), \(K_{m}\) are modified Bessel functions, \(\tan \varphi =\frac{y}{z}\), \(\tan \varphi ^{\prime }=\frac{y^{\prime }}{z^{\prime }}\), \(\lambda _{n}=\frac{n \pi }{L}\), \(\rho _{<}\) is the smaller of \(\rho =\sqrt{z^2+y^2}\) and \(\rho ^{\prime }=\sqrt{z^{\prime 2}+y^{\prime 2}}\). This Green’s function was already used by authors of [80] to describe interactions between axially symmetric particles. Their predictions were found in good agreement with the experimental data for a wide range of L [73].
Imagine first that the particles are oriented as depicted in Fig. 5.5c. Hence the every particle has two symmetry elements affecting on the multipole coefficients existence. They are \(\sigma _{xz}\) and \(\sigma _{xy}\). Therefore, as follows from Table 5.1, director deviations here can be described by the only dipole coefficient \(p_x^z = p \ne 0\). Then

where \(\rho =\sqrt{(y-y^{\prime })^{2}+(z-z^{\prime })^{2}}\) is the horizontal projection of the distance between particles, \(\theta \) is the angle between \(\rho \) and z-axis. As well as in the homeotropic cell the particles do not “feel” the cell walls at small distances \(U_{\text {dd},||}^{plan} \rightarrow -\frac{4\pi K pp^{\prime }}{\rho ^3}(1 - 3 \cos ^2 \theta )\). But if \(\rho \) increases the interaction falls off exponentially (\(K_n(z\rightarrow \infty ) \propto \frac{e^{-z}}{\sqrt{z}}\)) and the borders between zones transform from straight lines into some parabola-like curves (see Fig. 5.9).

(reprinted with permission from [93])
Map of the attraction and repulsion zones for two identical banana-shaped particles, \(p = p^{\prime }\), according to the (5.53). The particles are located in the centre of the planar cell \(x = x^{\prime } = \frac{L}{2}\). Their orientation are shown on the Figs. 5.4b and 5.5c. Sign “-” means attraction, “+” means repulsion
Now suppose that the particles symmetry planes are parallel to the coordinate yz and xz planes (see Fig. 5.5d). The allowed dipole coefficients are \(p_x^x = p_x\) and \(p_y^y = p_y\). Thus
where
At small distances \(B_1 \rightarrow \frac{1}{2} \left( \frac{L}{\rho }\right) ^3\), \(B_2 \rightarrow \frac{1}{4} \left( \frac{L}{\rho }\right) ^3\) and \(B_3 \rightarrow \frac{3}{4} \left( \frac{L}{\rho }\right) ^3\) and we come to the fact that in this case \(U_{\text {dd}} \rightarrow U_{\text {dd}}^{\text {bulk}}\) when \(\rho \ll L\) as well. Note that here \(U_{\text {dd},\bot }^{\text {bulk}}\) is given by (5.46) if we set \(x = x^{\prime }\) (\(\phi =\pi /2\)), that is, \(U_{\text {dd},\bot }^{\text {bulk}} = -\frac{4\pi K}{r^3} \left[ p_x p_x^{\prime } + p_y p_y^{\prime } -\right. \left. 3 p_y p_y^{\prime } \sin ^2\theta \right] \). Say, for instance, \(p_x > p_y\). Then it can be easily found that the interaction between such particles in the bulk nematic is completely repulsive or attractive. In the cell we again have both attraction and repulsion (see Fig. 5.10). In turn, since the summation in (5.56) starts from \(n=2\) \(B_1\) falls off faster than \(B_2\) and \(B_3\). Therefore when \(\rho \gg L\) the interaction is determined only by the coefficients \(p_y\) and \(p_y^{\prime }\). Due to this at large distances these particles will interact as axially symmetrical ones (black lines in Fig. 5.10). On the same grounds, if we set \(p_y > p_x\) no attraction will appear along the y-axis. Map of the interaction in this case will be quite similar to that one for the axially symmetrical particles.

(reprinted with permission from [93])
Map of the attraction and repulsion zones for two identical banana-shaped particles \(p_x = p_x^{\prime }\) and \(p_y = p_y^{\prime }\), according to the (5.55). The particles are located in the centre of the planar cell \(x = x^{\prime } = \frac{L}{2}\). Their orientation are shown on the Figs. 5.4d and 5.5d. Black line a: \(p_x = p_y\). Red line b: \(p_x = 2 p_y\). Blue line c: \(p_x = 5 p_y\). Green line d: \(p_x = 10 p_y\). Sign “-” means attraction, ’“+” means repulsion
For axially symmetrical particles formula (5.38) with the Green function (5.51) gives the result of dipole-dipole interaction between such particles as

where \(\rho =\sqrt{(y-y^{\prime })^{2}+(x-x^{\prime })^{2}}\) is the horizontal projection of the distance between particles and \(\theta \) is the angle between \(\rho \) and z. Formula (5.59) was found to explain very well experimental results [73] where \(\theta =0\) (see Fig. 5.11).

(reprinted with permission from [73])
Dependence of the normalized interparticle force \(FL^4\) on the reduced interparticle distance R/L in nematic cell at various thickness L. The solid line is the theoretically calculated one from Eqs. (5.59) for \(p=p'=2.04a^2\) and \(K=7.05\,\text {pN}\) (NLC MJ032358)

(reprinted with permission from [93])
Ellipsoidal particles in the homeotropic a and planar b nematic cell
5 Elastic Monopoles in a Nematic Cell
In this section, we will consider elastic monopoles in a nematic cell and discover that they are insensitive to the type of confinement. Suppose we have two ellipsoidal particles suspended in the cell (Fig. 5.12). For simplicity, let us assume that their orientation is fixed and such that the long axes make angles \(\omega \) and \(\omega ^{\prime }\) with \(\mathbf{n} _{0}\), \(0< \omega ,\omega ^{\prime } < \frac{\pi }{2}\) and lie in the plane of the figure. In practice, configurations of this symmetry have been realized through asymmetric anchoring conditions [105] and via light-induced rotation of photo-responsive colloids [106]. Since ellipsoids have a centre of symmetry, dominant deformations produced by these particles are elastic monopoles: \(q_{x}=q_{x}^{\prime }=0,q_y = q, q_{y}^{\prime } = q^{\prime }\) in the homeotropic and \(q_x = q\), \(q_{x}^{\prime } = q^{\prime },q_{y}=q_{y}^{\prime }=0\) in the planar cell (see Table 5.1). Then, as follows from (5.41) and (5.11), the monopole-monopole interaction in the homeotropic cell is given by
where \(\rho =\sqrt{(y-y^{\prime })^{2}+(x-x^{\prime })^{2}}\). In the same way we can find from (5.51) and (5.11) that in the planar cell this interaction is described by
where \(\rho =\sqrt{(y-y^{\prime })^{2}+(z-z^{\prime })^{2}}\). Expressions (5.62) and (5.63) demonstrate that the monopole-monopole interaction is the same and does not depend on the type of the nematic cell (see Fig. 5.13) as z on the Fig. 5.12a is the same as x on the Fig. 5.12b. For small distances \(\rho \ll L\) both (5.62) and (5.63) converge to the Coulomb-like law \(U_{\text {qq}}=-4\pi Kqq^{\prime }\frac{1}{r}\) (see Fig. 5.13). Note that opposite elastic charges repel, and like charges attract.

(reprinted with permission from [93])
Monopole-monopole interaction in a nematic cell. Elastic monopoles do not “feel” the type of the cell. Blue line 1 corresponds to \(\tilde{U} = -U_{\text {qq}}^{\text {plan}}L / 16\pi K qq^{\prime }\). Here \(U_{\text {qq}}^{\text {plan}}\) is given by (5.63). The dashed line 2 is the Coulomb-like \(\tilde{U}=\frac{1}{4\rho /L}\) asymptotics for \(\rho \ll L\)
Examples of dipole and quadrupole particles. Pair of vectors \((\mathbf {l}_{||},\mathbf {l}_{\perp })\) lies in a vertical symmetry plane and sets local coordinate system XYZ. Vector \(\mathbf {l}_{||}\) is parallel to \(\mathbf {n}(\mathbf {x})\); a banana-shaped dipole particles with two vertical symmetry planes; b banana-shaped dipole particles with one vertical and one horizontal symmetry planes; c axially symmetric dipole particles with usual elastic moment p and helical elastic moment \(p_{hel}\) d example of triangular particles with two vertical symmetry planes e example of quadrupole particles with two different quadrupole moments
6 Colloidal Particles in a Deformed Nematic
In this section, we derive the free energy of a colloid in a deformed (non-uniform) director field. An alternative approach to this question was developed in [107] and obtained results differ a little bit from ours. Consider again a single particle located at point \(\mathbf {x}\) in a nematic liquid crystal which is deformed by external boundaries or forces, i.e., the director field is intrinsically non-uniform \(\mathbf {n}=\mathbf {n}(\mathbf {r})\). Similarly to the case of two colloids, these intrinsic deformations of the director overlap with those induced by the particle, thereby making its energy position-dependent. If the particle size is much smaller than the characteristic length of the intrinsic director variations, \(\left( \nabla \cdot \mathbf {n}\right) ^{-1}\), the particle can be treated as if it was locally in a uniform director field. In the local Cartesian coordinate system where \(\mathbf{n} (\mathbf{x} )\approx (n_{x},n_{y},1)\), the total energy of the system is as follows:

Here, the first term is the energy of the LC deformations and the sum of three subsequent terms represents the overlap of deformations. If we subtract the particle’s self-energy in the homogeneous director field \(\mathbf{n} (\mathbf{x} )=(0,0,1)\) and the energy of the bulk deformations caused by external forces and fields, we will find the energy of interaction between the particle and the intrinsic deformations of the host medium, or energy of the particle in the deformed director field \(\mathbf{n} (\mathbf{x} )\). In the local Cartesian coordinates:
If a colloidal particle is inclined with respect to the local director field \(\mathbf{n} (\mathbf{x} )\) and has elastic charge \(\mathbf{q} =(q_{x},q_{y},0)\), the first term has the biggest value in comparison with others.
The second term defines the energy of a dipole. Here we will consider dipole particles which have at least two symmetry planes: either two vertical planes xz and yz (Fig. 5.14(a,c,d)) or one vertical plane yz and one horizontal plane xy (Fig. 5.14(b)) in the local coordinate system. Axially-symmetric particles with screw-thread ((Figs. 5.14(c) and 5.2)) also have a helical elastic dipole moment \(p_{hel}\).
The last term represents particles with a quadrupole moment. We will focus on quadrupoles with two symmetry planes or particles with three symmetry planes (Fig. 5.14(a,b,d,e)). Helical quadrupole moment \(Q_{hel}\) characterizes, for instance, axially-symmetric cone-like particles with screw-thread (like those shown in Fig. 5.14(c)). Then, using Tables 5.1 and 5.2, we can explicitly write Eq. (5.65) as follows
Equation (5.66) can be written in an invariant coordinate independent form:
Here,
is valid only in the vicinity of a vector \(\mathbf{n} _0\) such that \((\mathbf{n} -\mathbf{n} _0)\cdot \mathbf{n} _0\approx 0\) and the monopole \(\mathbf{q} \) is perpendicular to \(\mathbf{n} _0\). In fact, vector \(\mathbf{n} _0\) sets the average orientation in this area, the ground state, and defines the elastic charge vector q in this area. For instance if \(\mathbf{n} _0||z\) then \(\mathbf{q} =(q_{x},q_{y},0)\).

where we defined \(p=p_{x}^{x}\), \(p_{hel}=p_{y}^{x}=-p_{x}^{y}\), \(p_{ban}=-p_{y}^{z}\), \(\varDelta p=p_{y}^{y}-p_{x}^{x}\) with the local axes z and y being along \(\mathbf{n} =\mathbf{l} _{||}\) and \(\mathbf{l} _{\bot }\), respectively. Vector \(\mathbf{l} _{||}=\mathbf{n} (\mathbf{x} )\) is along the particle itself and coincides with the local director field \(\mathbf{n} (\mathbf{x} )\), and vector \(\mathbf{l} _{\bot }\) is perpendicular to it and lies in the vertical symmetry plane (Fig. 5.14). Strictly speaking, the direction of \(\mathbf{l} _{\bot }\) is not known a priori and has to be determined by minimizing the total energy (5.67). Equation (5.69) gives the energy of a dipole colloidal particle with two symmetry planes in a non-uniform director field.

where \(Q=2Q_{x}^{xz}\), \(\varDelta Q=2(Q_{x}^{xz}-Q_{y}^{yz})\), \(Q_{hel}=2Q_{y}^{xz}=-2Q_{x}^{yz}\). Expression (5.70) defines the energy of a colloidal dipole with two symmetry planes or a quadrupole particle with three symmetry planes in a non-uniform director field (Fig. 5.14).
Let us now apply the general formulas (5.69) and (5.70) to some specific cases of colloids.
For usual axially-symmetric particles without helical screw-thread (e.g., Fig. 5.1), the energy of the particle in the deformed director field takes the form:
where both terms should be taken into account for dipole particles (see Fig. 5.1a), and only second term remains for symmetrical quadrupole particles (Fig. 5.1b and c). Note that \(Q>0\) for the Saturn ring configuration (Fig. 5.1 (b)), and \(Q<0\) for boojums (Fig. 5.1 (c)). Equation (5.71) coincides with [65] and shows that a dipole particle moves into regions with splay deformations. As a result, small water droplets congregate at the center of a big nematic drop with normal anchoring at the surface and near the poles/boojums in case of planar boundary conditions [34]. Quadrupole particles behave differently depending on the anchoring type. Since \(Q<0\) for planar conditions and \(Q>0\) for homeotropic, quadrupole particles with planar anchoring will move towards regions of strong splay deformations whereas homeotropic particles will be repelled from them.
For axially-symmetric particles with helical screw-thread (Fig. 5.14c), the energy has the form:

where \(p=0\) and \(Q_{hel}=0\) if the particle has horizontal symmetry plane (Fig. 5.2). For axially non-symmetric dipole particles, which have two vertical symmetry planes (Fig. 5.14(a,d)) the energy reads
For axially non-symmetric dipole banana-shaped vertical particles, which have one vertical and one horizontal symmetry planes (Fig. 5.14(b)) the energy is as follows
This framework allows for understanding the behavior of colloids in the vicinity of topological defects in the director field. Following experiment [34], consider a spherical NLC droplet with normal boundary conditions on the surface that induce radial orientation of the director with a defect (radial hedgehog) in the center (Fig. 5.15).
In spherical coordinates, the director can be represented as \(n_{r}=1,n_{\theta }=0,n_{\varphi }=0\), so \(\text {div} \mathbf {n}=\frac{1}{r}\), where r is the distance from the center of the drop. If the particle has dipole moment parallel to the director, the dominant part of the energy reads \(F_{1}=-4 \pi K p\frac{1}{r}+4 \pi K Q\frac{1}{r^{2}}\), and the particle therefore moves to the center, as was observed in [34] for \(p=2.05r_0^2 > 0\) and \(Q=-0.2r_0^3 < 0\). Likewise, quadrupole particles will assemble in the center of the droplet accordingly to the energy
We can also find the energy of the interaction between a particle and a disclination line, another type of defects in nematics. Say, we have a cylinder with homeotropic boundary conditions which give rise to a disclination line along the cylinder axis (Fig. 5.16).
Given the symmetry, the director reads \(\mathbf {n} =(n_{\rho },n_{\varphi },n_{z})=(1,0,0)\) in cylindrical coordinates. Thus, the free energy of a colloid near a radial disclination is as follows
which suggests the attraction of dipoles and negative quadrupoles (for instance, a sphere with boojums) toward the disclination line and repulsion of positive quadrupoles (a sphere with a Saturn ring, for example).
Equation (5.76) can be generalized for disclinations of any topological strength m, which defines the angle \(\theta =m\phi +C\) of the director rotation in the plane perpendicular to the disclination (say, the angle between \(\mathbf{n} \) and axis x). The corresponding energies of dipole and quadrupole particles are, respectively,
and
In most cases, radial configuration considered above is unstable and “escapes in the third dimension” [108], as shown in Fig. 5.17.
The ensuing director field can be written in cylindrical coordinates as \(n_{z}=\cos u(\rho ), n_{\rho }=\sin u(\rho ),n_{\varphi }=0\) with \(u(R)=\frac{\pi }{2}\) and \(u(0)=0\), where, in the one-constant approximation, \(\tan \frac{u(\rho )}{2}=\frac{\rho }{R}\) with R being the cylinder radius [108]. Then the energy of a dipole particle takes the form
which shows that elastic dipoles assemble at the center of the cylinder. For quadrupole particles, we have
Equation (5.80) suggests that positive quadrupoles, \(Q>0\), e.g., spheres with Saturn ring defects (Fig. 5.1 a,b), aggregate at the center of the capillary, which was observed experimentally in [55]. At the same time, particles with negative quadrupole moment \(Q<0\), such as spheres with boojums (Fig. 5.1c) should assemble at a distance \(\rho _{min}=\frac{R}{\sqrt{3}}\) from the center. This result has not been confirmed experimentally yet.
7 Distribution of Nanoparticless in a Deformed Nematic
Thus far, we have focused on micron-sized colloidal particles. In such systems, the energy of the elastic interactions is of the order of hundreds and thousands of \(k_BT\). Hence, the temperature does not play a significant role, except for affecting elastic constants and Brownian motion of the particles. Entropy can be safely neglected under these conditions. In this section, we will consider the case of sub-micron (\(\sim \)0.1 \(\mu \)m) and nano-sized colloids in a nematic LC. For low concentrations, the interactions between such particles typically do not exceed \(\sim \)1 \(k_BT\), and entropic contributions to the free energy become important.
Let us consider a system of N particles with \(f(\mathbf {r})\) being the probability of finding a particle at point \(\mathbf{r} \), \(f\in (0,1)\). Equivalently, one can think of \(f(\mathbf {r})\) as the local volume fraction of particles,
where V and \(v_0\) is the system and particle volume, respectively. Then the configurational entropy of the system reads
For simplicity, we assume that the concentration is small, so that we can neglect the interparticle interactions and retain only the interaction with global nematic deformations. Thus, the internal energy can be defined as
where \(\epsilon (\mathbf{r} )\) is generally given by Eq. (5.67). For axially symmetric colloids with dipole elastic moment p and quadrupole elastic moment Q, it takes the form (5.71),
Note that nanoparticles, because of their size, only weakly distort the NLC. Therefore, the corresponding multipole moments are determined by the particle’s actual shape; for spheres, in particular, \(p=0\). Given (5.82) and (5.83), the grand potential of nanocolloids in a nematic host can be written as follows

where chemical potential \(\mu \) enforces the constraint \(\int dV f(\mathbf{r} ) =v_0N\). Minimizing (5.85), we arrive at the distribution function for nanoparticles in a deformed nematic liquid crystal,
where \(\beta =\frac{1}{k_BT}\), \(f_0=e^{\mu \beta }\ll 1\) for small concentrations and can be found from the condition \(\int dV f(\mathbf{r} ) =v_0N\).
Then, for instance, the distribution of small spherical nano-colloids near a disclination line of strength m is given by
There \(\theta =m\phi +C\) is the director rotation angle in the plane perpendicular to the disclination (say, the angle between \(\mathbf{n} \) and axis x) and \(\phi \) is the azimuthal angle.
Near the cores of disclination lines at nanoscale distances, nematic ordering melts, and the order parameter, as well as the elastic constant K, tend to zero. Our theory is inapplicable in such regions.
Similarly, near an escaped radial disclination but far enough from the core we have
with \(\rho \) being the distance from the particle to the disclination line.
8 Coexistence of Two Colloidal Structures at the NLC-Air Interface
References [41, 42] experimentally observed the coexistence of two structures formed by glycerol droplets at the nematic-air interface. Such droplets form usual quasi-hexagonal (HL) and dense quasi-hexagonal (DL) structures (Fig. 5.18). The experimental setup comprises glycerol droplets of radius \(R=2.5~\mu \)m floating on the NLC-air interface in a cone-like Petri dish (Fig. 5.18a). Glycerol slowly flows out, ad a patch with the HL structure is shrinking. Initially, the average interparticle distance in the HL packing is \(r_3=10~\mu \)m. When it becomes approximately \(r=r_c=\frac{\sqrt{3}r_3}{2}\approx 8.66~\mu \)m, the DL structure with the average lattice constant \(r_1=6~\mu \)m emerges.

(reprinted with permission from [42])
Two equilibrium quasi-hexagonal structures at the nematic-air interface which we refer to as the usual hexagonal (HL) and dense hexagonal (DL), respectively. The DL lattice emerges when the average spacing between the particles becomes smaller than some critical value \(r_{c}\)
Due to planar anchoring of the LC molecules to the droplets surface, they are accompanied by surface boojums residing at their south poles. One can notice, however, that in the dense structure the boojums are shifted from the vertical axis. Indeed, Fig. 5.18(c) demonstrates that in the HL packing boojums show in the center of the droplet under crossed polarizers, whereas in Figs. 5.18(b) and (d) they are rotated equally for all particles in parallel planes. In Ref. [67], it was shown that such a rotation by an angle \(\theta \) gives rise to elastic monopoles and Coulomb-like attraction between the particles, which can be expressed as \(U_{qq}\propto -b^2sin^{2}(2\theta )/r<0\) for small angles. At the same time, the self-energy of the particle scales as \(U_{self}\propto a \sin ^{2}(\theta )>0\). Since Coulomb attraction is proportional to the number of neighbors and inversely proportional to the spacing of the particles, one can conjecture that at some distance both terms will be balanced. Further compression will increase the attraction and cause collapse to the dense structure, which will be eventually stabilized by the elastic dipole-dipole repulsion (5.39), \(U_{elb,thick}\left( r\right) =K\frac{\alpha ^{2}R^{4}}{r^{3}}\) with R denoting the droplet radius. To quantify this transition, recall the total free energy of the system of colloids
where \(F_{i}\) is the average energy per particle, \(F_{i}=U_{i,self}+\frac{1}{2}\sum _{neighbors}U_{ij}\). Taking for simplicity only the nearest 6 neighbors, we can write \(F_i\) as a function of the average particle spacing r and the rotation angle \(\theta \) in the following form
where \(G(r)=\frac{1}{r}-\frac{1}{\sqrt{r^{2}+4h^{2}}}\) is the Green function for a located at a distance h from the interface. G(r) is, in fact, a superposition of the Coulomb attraction between the particles, \(\sim \)1/r, and repulsion between the particle and its mirror reflection, \(\sim \)1\(/\sqrt{r^{2}+4h^{2}}\), which accounts for the presence of the interface. In practice, one could approximate G(r) by \(G_{0}(r) = 1/r \), but it is instructive to keep both contributions. We consider that all particles have the same elastic charge (say \(q_x\) only) as all boojums are rotated equally for all particles in parallel planes. Parameters a, b and \(\alpha \) are unknown dimensionless constants which we need to find from the comparison with experimental data. Self energy of the glycerol droplet with the boojum is proportional to the a, elastic charge of the glycerol droplet with skewed boojum is proportional to the bR and elastic dipole moment of the glycerol droplet is proportional to the \(\alpha R^2\). We know that \(\alpha \) was found to be \(\alpha =0.2\) from the experiment [41] so that only a and b are unknown. The last term in (5.90) describes capillary attraction caused by deformations of the NLC-air interface, the force \(f_{el}\approx 10K\) replaces standard gravitational buoyancy, \(\sigma _{LCA}\) is the surface tension and \(\lambda \approx 2\) mm is the capillary length [41].
Setting \(h\approx 2R\), we see that mechanical equilibrium, \(\frac{\partial F}{\partial \theta }=0\), implies that
where \(r_b\) is the largest critical distance at which boojums start to move from the poles, \(r_b\) can be found from the condition \(\frac{a}{12b^{2}RG(r_b)}=1\). Substituting (5.91) into (5.90), we arrive at the average per particle energy as a function of the particle spacing r only
where
Now we need to to find out under what conditions this function has two local minima and one maximum. In dimensionless units \(x=r/R\), the condition \(\frac{\partial F}{\partial r}=0\) reduces to the equation
where
Calculated per particle energy F(r) given by (5.92) as a function of the average distance between the droplets. Dotted line - Coulomb attraction between skewed boojums, solid line - attraction with Green function from (5.90). Here parameters \(R=2.5~\mu \)m, \(K=7\) pN, \(\sigma _{LCA}=3.8\cdot 10^{-2}\) J/m\(^2\), \(\alpha =0.2\), \(f_{el}=88.4\) pN, \(\lambda =2\) mm are taken from [42]
Experimental data [41, 42] suggests that \(x_1=\frac{r_1}{R}=2.4\), \(x_2=x_c=\frac{r_c}{R}=3.46\), \(x_3=\frac{r_3}{R}=4\) for droplets of radius \(R=2.5\,\upmu \text {m}\), \(\alpha =0.2\). Thus, we need to find such b and \(x_b\) that \(f(x_1)=0\) and \(f(x_2)=0\). This is equivalent to finding necessary a and b. Omitting technicalities, we report that such solutions exist. Namely, for the unscreened Coulomb potential \(G_0(x)=1/x\), we have \(b^2_{Coul}=0.028,x_{b,Coul}=3.7\) (that is, \(a=a_{Coul}=0.091\) and the boojum rotation angle \(\theta _{Coulomb}=24.7^{\circ } \) in the DL), and for the full Green function \(G(x)=\frac{1}{x}-\frac{1}{\sqrt{x^{2}+16}}\), which accounts for the interface, \(b^2=0.023,x_{b,Green}=3.66\) (\(a=a_{Greenl}=0.025\) in this case and the boojum rotation angle \(\theta _{Green}=31.7^{\circ }\) in the DL).
The average per particle energy F(r), calcualted from (5.92) for the experimental data [42], as a function of the average interparticle distance is plotted in Fig. 5.19. It features two distinct minima separated by a \(\sim k_BT\) barrier, consistently with the coexistence of HL and DL lattices.
In the paper [42] another dipolar approach explanation of DL structure has been proposed. We think that the current approach describes the experiment more correctly. In Ref. [42] there is no explanation of the existence of the global minimum with respect to the boojum rotation angle and the particle separation distance both at the same time. Here we have found such global minimum. Therefore, we consider that this approach describes the situation in a more correct way.
Dense packing of glycerol droplets at the nematic-air interface is caused by spontaneous rotational symmetry breaking with the emergence of elastic charges and Coulomb-like elastic attraction between rotated topological defects - boojums at the bottom of glycerol droplets.
9 Conclusions
Colloidal particles suspended in a nematic liquid crystal cause deviations of the director from its ground state. Far from the particle, these distortions can be written in the form of the multipole expansion. The notion of multipoles, well familiar from classical electrostatics, has become one of the cornerstones of our current understanding of the host-mediated interactions in NLC colloids.
Building upon the electrostatic analogy, we developed a general framework of colloidal nematostatics applicable to particles of arbitrary shape, size, chirality, and anchoring strength and type. Unlike many alternative approaches, the formalism we propose in this paper easily incorporates the effects of confinement and the presence of external electric or magnetic fields. Our theory is centered around elastic multipoles — coefficients in the multipole expansion of the far-field director. Considering two limiting cases of anchoring strength, weak (\(Wr_{0} \ll K\)) and strong (\(Wr_{0} \gg K\)), we demonstrated how these coefficients emerge as asymptotics of the near-field solution. In the former case, \(Wr_{0} \ll K\), the proposed approach allows us to find exact analytical expressions for all multipole moments. While that is generally impossible when \(Wr_{0} \gg K\), one can still infer the overall structure of the expansion (that is, which coefficients vanish and which do not) just from the symmetry of the director in the immediate vicinity of the particle. Since this information is typically available in experiments, the formalism we developed here can be readily applied for particles of arbitrary shapes, sizes, and anchoring types.
The proposed framework relies on two assumptions: (i) differences in the NLC elastic constants can be neglected; (ii) deviations of the director field from its ground state are small, \(\mathbf {n}=\mathbf {n}_0+\delta \mathbf {n}\) with \(\left| \mathbf {n}_0\right| \approx 1\) and \(\left| \delta \mathbf {n}\right| \ll 1\). This assumption is well justified for submicron particles but is limited to large interparticle distances in the case of micron and supramicron colloids. The vicinity of a large particle features strong director deformations and topological defects, which render the electrostatic analogy invalid. As such, our theory is inapplicable to entangled and knotted colloidal structures [51, 109,110,111], where disclination loops extend over many particle sizes. These structures are born out of short-range interactions. It is worth noting that even in the case of localized defects, the nature and extent of short-range interactions (in other words, the size and shape of the coat) are not fully understood. Indirectly, this question was addressed in [99]. There was shown that lattice constants and angles of dipolar 2D and 3D structures could be consistently reproduced with multipole interactions incorporating higher-order terms and spherically symmetric hard-core repulsion. Using this model, the authors estimated that the radius of such a sphere-shaped coat around a hedgehog dipole (Fig. 5.1a) is about \(1.2r_0\), where \(r_0\) is the particle size, and roughly matches the distance to the defect. It would be interesting to explore the transition between near-field and far-field director in three dimensions to develop a more detailed idea of the coat’s size and shape and to quantify the limits of electrostatic analogy.
To demonstrate our approach at work, we considered the dipole-dipole interaction between banana-shaped particles in a nematic cell with both planar and homeotropic alignment of the LC molecules at the boundaries. Given that a banana-like colloid possesses two orthogonal planes of symmetry, one can intuitively expect that in the mechanical equilibrium either both of these planes are normal to the cell walls (orientation A) or just one (orientation B). We found that the A-oriented particles placed in the middle of a homeotropic cell interact anisotropically. Each “banana” in this case has two “butterfly wings” on its longer sides within which the interaction is attractive. The less asymmetric the particles are, the smaller the “wings”, so when the axial symmetry is fully restored, the interaction is isotropic. The “wings” have finite size, as \(r \rightarrow \infty \) the interaction becomes completely repulsive. This behavior contrasts with the interaction of banana-like colloids in the bulk LC, where the angular and distance dependencies are completely decoupled. In a planar cell, both axially symmetric colloids and B-oriented “bananas” interact anisotropically. However, the symmetric particles repel along the direction perpendicular to the rubbing, whereas the asymmetric ones attract at small distances.
We have also found that elastic monopoles are insensitive to the type of confinement: nematostatic analog of the Coulomb law has the same form regardless of anchoring at the cell walls and converges to the 1/r scaling in the limit of infinite thickness \(L\rightarrow \infty \).
General expressions for the self-energy of colloidal particles carrying elastic monopole, dipole and/or quadrupole moment in a nonuniform director field were derived within the proposed framework and employed to find the distribution of nanoparticles in a cylindrical capillary. We showed that particles with homeotropic boundary conditions assemble at the center of the escaped radial disclination, whereas those with planar anchoring aggregate at a distance \(\rho _{min}=\frac{R}{\sqrt{3}}\) from the capillary axis.
To elucidate the role of elastic interactions in many-particle systems, we considered the coexistence of two colloidal structures — usual hexagonal and dense hexagonal — formed by glycerol droplets at the nematic-air interface [41, 42]. Our calculations demonstrate how the dense configuration emerges from spontaneous rotational symmetry breaking, which triggers the onset of Coulomb-like attraction between skewed boojums — topological defects at the bottom of glycerol droplets.
These examples strikingly demonstrate how one could exploit the interplay of shape, symmetry, and order to design colloids with prescribed long-range interactions, thereby possibly revealing new types of colloidal superstructures. An interesting and yet unexplored example is that of spheres with conically degenerate surface anchoring — elastic hexadecapoles [100]. These particles appear to have very localized, isotropic short-range interactions and highly anisotropic long-range potential, which underlies the formation of quasi diamond-like assemblies. Such low-symmetric structures have great potential for photonic applications. Another emerging direction, which likely will gain significant attention in the future, focuses on charged colloids. Recently, Everts et al. demonstrated, both theoretically and experimentally, how the interplay of elastic and electrostatic interactions between nearly-spherical particles gives rise to qualitatively different interaction regimes [112].
Abbreviations
- 2D:
-
Two-dimensional
- 3D:
-
Three-dimensional
- LC:
-
Liquid crystal
- NLC:
-
Nematic liquid crystal
- NP:
-
Nanoparticle
- THz:
-
Terahertz (\(10^{12}\) Hz)
- HL:
-
Quasi-hexagonal lattice
- DL:
-
Dense quasi-hexagonal lattice
References
Woltman SJ, Jay GD, Crawford GP (2007) Liquid-crystal materials find a new order in biomedical applications. Nat Mater 6:929–938. https://doi.org/10.1038/nmat2010
Lu G, Fei B (2014) Medical hyperspectral imaging: a review. J Biomed Opt 19:1–24. https://doi.org/10.1117/1.JBO.19.1.010901
Akbari H, Halig L, Schuster DM, Fei B, Osunkoya A, Master V, Nieh P, Chen G (2012) Hyperspectral imaging and quantitative analysis for prostate cancer detection. J Biomed Opt 17:076005. https://doi.org/10.1117/1.JBO.17.7.076005
Panasyuk SV, Yang S, Faller DV, Ngo D, Lew RA, Freeman JE, Rogers AE (2007) Medical hyperspectral imaging to facilitate residual tumor identification during surgery. Cancer Biol Ther 6:439–446. https://doi.org/10.4161/cbt.6.3.4018
Sorg BS, Moeller BJ, Donovan O, Cao Y, Dewhirst MW (2005) Hyperspectral imaging of hemoglobin saturation in tumor microvasculature and tumor hypoxia development. J Biomed Opt 10:044004. https://doi.org/10.1117/1.2003369
Greenman RL, Panasyuk S, Wang X, Lyons TE, Dinh T, Longoria L, Giurini JM, Freeman J, Khaodhiar L, Veves A (2005) Early changes in the skin microcirculation and muscle metabolism of the diabetic foot. The Lancet 366:1711–1717. https://doi.org/10.1016/S0140-6736(05)67696-9
Cancio LC, Batchinsky AI, Mansfield JR, Panasyuk S, Hetz K, Martini D, Jordan BS, Tracey B, Freeman JE (2006) Hyperspectral imaging: a new approach to the diagnosis of hemorrhagic shock. J Trauma Acute Care Surg 60:1087–1095. https://doi.org/10.1097/01.ta.0000217357.10617.3d
Zuzak KJ, Naik SC, Alexandrakis G, Hawkins D, Behbehani K, Livingston EH (2007) Characterization of a near-infrared laparoscopic hyperspectral imaging system for minimally invasive surgery. Anal Chem 79:4709–4715. https://doi.org/10.1021/ac070367n
Abdulhalim I (2011) Non-display bio-optic applications of liquid crystals. Liq Crys Today 20:44–60. https://doi.org/10.1080/1358314X.2011.563975
Wang J, Tian H, Wang Y, Li X, Cao Y, Li L, Liu J, Zhou Z (2018) Liquid crystal terahertz modulator with plasmon-induced transparency metamaterial. Opt Express 26:5769–5776. https://doi.org/10.1364/OE.26.005769
Shen Z, Zhou S, Ge S, Duan W, Ma L, Lu Y, Hu W (2019) Liquid crystal tunable terahertz lens with spin-selected focusing property. Opt Express 27:8800–8807. https://doi.org/10.1364/OE.27.008800
Yang X, Zhao X, Yang K, Liu Y, Liu Y, Fu W, Luo Y (2016) Biomedical applications of terahertz spectroscopy and imaging. Trends Biotechnol 34:810–824. https://doi.org/10.1016/j.tibtech.2016.04.008
D’Arco A, Di Fabrizio M, Dolci V, Petrarca M, Lupi S (2020) Thz pulsed imaging in biomedical applications. Condens Matter 5:25. https://doi.org/10.3390/condmat5020025
Mirzaei J, Reznikov M, Hegmann T (2012) Quantum dots as liquid crystal dopants. J Mater Chem 22:22350–22365. https://doi.org/10.1039/C2JM33274D
Garbovskiy YA, Glushchenko AV (2010) Liquid crystalline colloids of nanoparticles: preparation, properties, and applications. Solid State Phys 62:1–74. https://doi.org/10.1016/B978-0-12-374293-3.00001-8
Shen Y, Dierking I (2019) Perspectives in liquid-crystal-aided nanotechnology and nanoscience. Appl Sci 9:2512. https://doi.org/10.3390/app9122512
Zhang Y, Liu Q, Mundoor H, Yuan Y, Smalyukh II (2015) Metal nanoparticle dispersion, alignment, and assembly in nematic liquid crystals for applications in switchable plasmonic color filters and e-polarizers. Acs Nano 9:3097–3108. https://doi.org/10.1021/nn5074644
Brolo AG (2012) Plasmonics for future biosensors. Nat Photonics 6:709–713. https://doi.org/10.1038/nphoton.2012.266
Špačková B, Wrobel P, Bocková M, Homola J (2016) Optical biosensors based on plasmonic nanostructures: a review. Proc IEEE 104:2380–2408. https://doi.org/10.1109/JPROC.2016.2624340
Si G, Zhao Y, Leong ESP, Liu YJ (2014) Liquid-crystal-enabled active plasmonics: a review. Materials 7:1296–1317. https://doi.org/10.3390/ma7021296
Turiv T, Krieger J, Babakhanova G, Yu H, Shiyanovskii SV, Wei QH, Kim MH, Lavrentovich OD (2020) Topology control of human fibroblast cells monolayer by liquid crystal elastomer. Sci Adv 6:eaaz6485. https://doi.org/10.1126/sciadv.aaz6485
Sung B, Kim MH (2018) Liquid-crystalline nanoarchitectures for tissue engineering. Beilstein J Nanotechnol 9:205–215. https://doi.org/10.3762/bjnano.9.22
Gupta VK, Skaife JJ, Dubrovsky TB, Abbott NL (1998) Optical amplification of ligand-receptor binding using liquid crystals. Science 279:2077–2080. https://doi.org/10.1126/science.279.5359.2077
Aliño VJ, Sim PH, Choy WT, Fraser A, Yang KL (2012) Detecting proteins in microfluidic channels decorated with liquid crystal sensing dots. Langmuir 28:17571–17577. https://doi.org/10.1021/la303213h
Hartono D, Qin WJ, Yang KL, Yung LYL (2009) Imaging the disruption of phospholipid monolayer by protein-coated nanoparticles using ordering transitions of liquid crystals. Biomaterials 30:843–849. https://doi.org/10.1016/j.biomaterials.2008.10.037
Khan M, Park SY (2014) Liquid crystal-based proton sensitive glucose biosensor. Anal Chem 86:1493–1501. https://doi.org/10.1021/ac402916v
Lai SL, Yang KL (2011) Detecting DNA targets through the formation of DNA/CTAB complex and its interactions with liquid crystals. Analyst 136:3329–3334. https://doi.org/10.1039/C1AN15173H
Kim YK, Wang X, Mondkar P, Bukusoglu E, Abbott NL (2018) Self-reporting and self-regulating liquid crystals. Nature 557:539–544. https://doi.org/10.1038/s41586-018-0098-y
Yang S, Liu Y, Tan H, Wu C, Wu Z, Shen G, Yu R (2012) Gold nanoparticle based signal enhancement liquid crystal biosensors for DNA hybridization assays. ChemComm 48:2861–2863. https://doi.org/10.1039/C2CC17861C
Tan H, Yang S, Shen G, Yu R, Wu Z (2010) Signal-enhanced liquid-crystal DNA biosensors based on enzymatic metal deposition. Angew Chem Int 49:8608–8611. https://doi.org/10.1002/anie.201004272
Nandi R, Loitongbam L, De J, Jain V, Pal SK (2019) Gold nanoparticle-mediated signal amplification of liquid crystal biosensors for dopamine. Analyst 144:1110–1114. https://doi.org/10.1039/C8AN02171F
Li X, Li G, Yang M, Chen LC, Xiong XL (2015) Gold nanoparticle based signal enhancement liquid crystal biosensors for tyrosine assays. Sens Actuators B Chem 215:152–158. https://doi.org/10.1016/j.snb.2015.03.054
Zhao D, Peng Y, Xu L, Zhou W, Wang Q, Guo L (2015) Liquid-crystal biosensor based on nickel-nanosphere-induced homeotropic alignment for the amplified detection of thrombin. ACS Appl Mater Interfaces 7:23418–23422. https://doi.org/10.1021/acsami.5b08924
Poulin P, Stark H, Lubensky TC, Weitz DA (1997) Novel colloidal interactions in anisotropic fluids. Science 275:1770–1773. https://doi.org/10.1126/science.275.5307.1770
Poulin P, Cabuil V, Weitz DA (1997) Direct measurement of colloidal forces in an anisotropic solvent. Phys Rev Lett 79:4862–4865. https://doi.org/10.1103/PhysRevLett.79.4862
Poulin P, Weitz DA (1998) Inverted and multiple nematic emulsions. Phys Rev E 57:626–637. https://doi.org/10.1103/PhysRevE.57.626
Noël CM, Bossis G, Chaze AM, Giulieri F, Lacis S (2006) Measurement of elastic forces between iron colloidal particles in a nematic liquid crystal. Phys Rev Lett 96:217801. https://doi.org/10.1103/PhysRevLett.96.217801
Smalyukh II, Lavrentovich OD, Kuzmin AN, Kachynski AV, Prasad PN (2005) Elasticity-mediated self-organization and colloidal interactions of solid spheres with tangential anchoring in a nematic liquid crystal. Phys Rev Lett 95:157801. https://doi.org/10.1103/PhysRevLett.95.157801
Smalyukh II, Kuzmin AN, Kachynski AV, Prasad PN, Lavrentovich OD (2005) Optical trapping of colloidal particles and measurement of the defect line tension and colloidal forces in a thermotropic nematic liquid crystal. Appl Phys Lett 86:021913. https://doi.org/10.1063/1.1849839
Kotar J, Vilfan M, Osterman N, Babič D, Čopič M, Poberaj I (2006) Interparticle potential and drag coefficient in nematic colloids. Phys Rev Lett 96:207801. https://doi.org/10.1103/PhysRevLett.96.207801
Smalyukh II, Chernyshuk S, Lev BI, Nych AB, Ognysta U, Nazarenko VG, Lavrentovich OD (2004) Ordered droplet structures at the liquid crystal surface and elastic-capillary colloidal interactions. Phys Rev Lett 93:117801. https://doi.org/10.1103/PhysRevLett.93.117801
Nych AB, Ognysta UM, Pergamenshchik VM, Lev BI, Nazarenko VG, Muševič I, Škarabot M, Lavrentovich OD (2007) Coexistence of two colloidal crystals at the nematic-liquid-crystal-air interface. Phys Rev Lett 98:057801. https://doi.org/10.1103/PhysRevLett.98.057801
Yamamoto T, Yamamoto J, Lev BI, Yokoyama H (2002) Light-induced assembly of tailored droplet arrays in nematic emulsions. Appl Phys Lett 81:2187–2189. https://doi.org/10.1063/1.1508816
Lev B, Chernyshuk SB, Yamamoto T, Yamamoto J, Yokoyama H (2008) Photochemical switching between colloidal photonic crystals at the nematic-air interface. Phys Rev E 78:020701. https://doi.org/10.1103/PhysRevE.78.020701
Lev B, Nych A, Ognysta U, Reznikov D, Chernyshuk S, Nazarenko V (2002) Nematic emulsion in a magnetic field. JETP Lett 75:322–325. https://doi.org/10.1134/1.1485260
Nazarenko VG, Nych AB, Lev BI (2001) Crystal structure in nematic emulsion. Phys Rev Lett 87:075504. https://doi.org/10.1103/PhysRevLett.87.075504
Muševič I, Škarabot M, Tkalec U, Ravnik M, Žumer S (2006) Two-dimensional nematic colloidal crystals self-assembled by topological defects. Science 313:954–958. https://doi.org/10.1126/science.1129660
Škarabot M, Ravnik M, Žumer S, Tkalec U, Poberaj I, Babič D, Osterman N, Muševič I (2007) Two-dimensional dipolar nematic colloidal crystals. Phys Rev E 76:051406. https://doi.org/10.1103/PhysRevE.76.051406
Ognysta U, Nych A, Nazarenko V, Muševič I, Škarabot M, Ravnik M, Žumer S, Poberaj I, Babič D (2008) 2d interactions and binary crystals of dipolar and quadrupolar nematic colloids. Phys Rev Lett 100:217803. https://doi.org/10.1103/PhysRevLett.100.217803
Škarabot M, Ravnik M, Žumer S, Tkalec U, Poberaj I, Babič D, Muševič I (2008) Hierarchical self-assembly of nematic colloidal superstructures. Phys Rev E 77:061706. https://doi.org/10.1103/PhysRevE.77.061706
Ravnik M, Škarabot M, Žumer S, Tkalec U, Poberaj I, Babič D, Osterman N, Muševič I (2007) Entangled nematic colloidal dimers and wires. Phys Rev Lett 99:247801. https://doi.org/10.1103/PhysRevLett.99.247801
Tkalec U, Ravnik M, Žumer S, Muševič I (2009) Vortexlike topological defects in nematic colloids: Chiral colloidal dimers and 2d crystals. Phys Rev Lett 103:127801. https://doi.org/10.1103/PhysRevLett.103.127801
Nych A, Ognysta U, Škarabot M, Ravnik M, Žumer S, Muševič I (2013) Assembly and control of 3d nematic dipolar colloidal crystals. Nat Commun 4:1489. https://doi.org/10.1038/ncomms2486
Vilfan M, Osterman N, Čopič M, Ravnik M, Žumer S, Kotar J, Babič D, Poberaj I (2008) Confinement effect on interparticle potential in nematic colloids. Phys Rev Lett 101:237801. https://doi.org/10.1103/PhysRevLett.101.237801
Kossyrev P, Ravnik M, Žumer S (2006) Branching of colloidal chains in capillary-confined nematics. Phys Rev Lett 96:048301. https://doi.org/10.1103/PhysRevLett.96.048301
Ji Fukuda, Stark H, Yoneya M, Yokoyama H (2004) Interaction between two spherical particles in a nematic liquid crystal. Phys Rev E 69:041706. https://doi.org/10.1103/PhysRevE.69.041706
Aoki KM, Lev BI, Yokoyama H (2001) Cluster formation of colloids in nematics. Mol Cryst Liq Cryst 367:537–544. https://doi.org/10.1080/10587250108028674
Andrienko D, Tasinkevych M, Dietrich S (2005) Effective pair interactions between colloidal particles at a nematic-isotropic interface. Europhys Lett 70:95. https://doi.org/10.1209/epl/i2004-10455-3
Tasinkevych M, Andrienko D (2010) Colloidal particles in liquid crystal films and at interfaces. Condens Matter Phys 13:33603. https://doi.org/10.5488/CMP.13.33603
Kishita T, Takahashi K, Ichikawa M, Ji Fukuda, Kimura Y (2010) Arrangement dependence of interparticle force in nematic colloids. Phys Rev E 81:010701. https://doi.org/10.1103/PhysRevE.81.010701
Kishita T, Kondo N, Takahashi K, Ichikawa M, Ji Fukuda, Kimura Y (2011) Interparticle force in nematic colloids: Comparison between experiment and theory. Phys Rev E 84:021704. https://doi.org/10.1103/PhysRevE.84.021704
Stark H (1999) Director field configurations around a spherical particle in a nematic liquid crystal. Eur Phys J B 10:311–321. https://doi.org/10.1007/s100510050860
Andrienko D, Tasinkevych M, Patricio P, Allen MP, da Gama MMT (2003) Forces between elongated particles in a nematic colloid. Phys Rev E 68:051702. https://doi.org/10.1103/PhysRevE.68.051702
Muševič I (2018) Nematic liquid-crystal colloids. Materials 11:24. https://doi.org/10.3390/ma11010024
Lubensky TC, Pettey D, Currier N, Stark H (1998) Topological defects and interactions in nematic emulsions. Phys Rev E 57:610–625. https://doi.org/10.1103/PhysRevE.57.610
Lev BI, Tomchuk PM (1999) Interaction of foreign macrodroplets in a nematic liquid crystal and induced supermolecular structures. Phys Rev E 59:591–602. https://doi.org/10.1103/PhysRevE.59.591
Lev BI, Chernyshuk SB, Tomchuk PM, Yokoyama H (2002) Symmetry breaking and interaction of colloidal particles in nematic liquid crystals. Phys Rev E 65:021709. https://doi.org/10.1103/PhysRevE.65.021709
Pergamenshchik VM, Uzunova VO (2007) Coulomb-like interaction in nematic emulsions induced by external torques exerted on the colloids. Phys Rev E 76:011707. https://doi.org/10.1103/PhysRevE.76.011707
Pergamenshchik VM, Uzunova VA (2010) Colloidal nematostatics. Condens Matter Phys 13:33602. https://doi.org/10.5488/CMP.13.33602
Pergamenshchik VM, Uzunova VA (2011) Dipolar colloids in nematostatics: tensorial structure, symmetry, different types, and their interaction. Phys Rev E 83:021701. https://doi.org/10.1103/PhysRevE.83.021701
Yada M, Yamamoto J, Yokoyama H (2004) Direct observation of anisotropic interparticle forces in nematic colloids with optical tweezers. Phys Rev Lett 92:185501. https://doi.org/10.1103/PhysRevLett.92.185501
Takahashi K, Ichikawa M, Kimura Y (2008) Force between colloidal particles in a nematic liquid crystal studied by optical tweezers. Phys Rev E 77:020703. https://doi.org/10.1103/PhysRevE.77.020703
Kondo N, Iwashita Y, Kimura Y (2010) Dependence of interparticle force on temperature and cell thickness in nematic colloids. Phys Rev E 82:020701. https://doi.org/10.1103/PhysRevE.82.020701
Ji Fukuda, Žumer S (2009) Confinement effect on the interaction between colloidal particles in a nematic liquid crystal: An analytical study. Phys Rev E 79:041703. https://doi.org/10.1103/PhysRevE.79.041703
Fukuda J, Lev BI, Yokoyama H (2003) Effect of confining walls on the interaction between particles in a nematic liquid crystal. J Phys Condens Matter 15:3841. https://doi.org/10.1088/0953-8984/15/23/301
Ji Fukuda, Lev BI, KM, Yokoyama H, (2002) Interaction of particles in a deformed nematic liquid crystal. Phys Rev E 66:051711. https://doi.org/10.1103/PhysRevE.66.051711
Oettel M, Dominguez A, Tasinkevych M, Dietrich S (2009) Effective interactions of colloids on nematic films. Eur Phys J E 28:99–111. https://doi.org/10.1140/epje/i2008-10360-1
Pergamenshchik VM, Uzunova VA (2009) Colloid-wall interaction in a nematic liquid crystal: the mirror-image method of colloidal nematostatics. Phys Rev E 79:021704. https://doi.org/10.1103/PhysRevE.79.021704
Chernyshuk SB, Lev BI (2010) Elastic interaction between colloidal particles in confined nematic liquid crystals. Phys Rev E 81:041701. https://doi.org/10.1103/PhysRevE.81.041701
Chernyshuk SB, Lev BI (2011) Theory of elastic interaction of colloidal particles in nematic liquid crystals near one wall and in the nematic cell. Phys Rev E 84:011707. https://doi.org/10.1103/PhysRevE.84.011707
Chernyshuk SB, Tovkach OM, Lev BI (2012) Theory of elastic interaction between colloidal particles in a nematic cell in the presence of an external electric or magnetic field. Phys Rev E 85:011706. https://doi.org/10.1103/PhysRevE.85.011706
Lapointe CP, Mason TG, Smalyukh II (2009) Shape-controlled colloidal interactions in nematic liquid crystals. Science 326:1083–1086. https://doi.org/10.1126/science.1176587
Dontabhaktuni J, Ravnik M, Žumer S (2014) Quasicrystalline tilings with nematic colloidal platelets. Proc Natl Acad Sci USA 111:2464–2469. https://doi.org/10.1073/pnas.1312670111
Senyuk B, Liu Q, Bililign E, Nystrom PD, Smalyukh II (2015) Geometry-guided colloidal interactions and self-tiling of elastic dipoles formed by truncated pyramid particles in liquid crystals. Phys Rev E 91:040501. https://doi.org/10.1103/PhysRevE.91.040501
Tkalec U, Škarabot M, Muševič I (2008) Interactions of micro-rods in a thin layer of a nematic liquid crystal. Soft Matter 4:2402–2409. https://doi.org/10.1039/B807979J
Senyuk B, Liu Q, He S, Kamien RD, Kusner RB, Lubensky TC, Smalyukh II (2013) Topological colloids. Nature 493:200–205. https://doi.org/10.1038/nature11710
Varney MC, Zhang Q, Smalyukh II (2015) Stick-slip motion of surface point defects prompted by magnetically controlled colloidal-particle dynamics in nematic liquid crystals. Phys Rev E 91:052503. https://doi.org/10.1103/PhysRevE.91.052503
Silvestre NM, Tasinkevych M (2017) Key-lock colloids in a nematic liquid crystal. Phys Rev E 95:012606. https://doi.org/10.1103/PhysRevE.95.012606
Senyuk B, Varney MC, Lopez JA, Wang S, Wu N, Smalyukh II (2014) Magnetically responsive gourd-shaped colloidal particles in cholesteric liquid crystals. Soft Matter 10:6014–6023. https://doi.org/10.1039/C4SM00878B
Peng C, Turiv T, Zhang R, Guo Y, Shiyanovskii SV, Wei QH, De Pablo J, Lavrentovich OD (2016) Controlling placement of nonspherical (boomerang) colloids in nematic cells with photopatterned director. J Phys Condens Matter 29:014005. https://doi.org/10.1088/0953-8984/29/1/014005
Evans JS, Sun Y, Senyuk B, Keller P, Pergamenshchik VM, Lee T, Smalyukh II (2013) Active shape-morphing elastomeric colloids in short-pitch cholesteric liquid crystals. Phys Rev Lett 110:187802. https://doi.org/10.1103/PhysRevLett.110.187802
Senyuk B, Pandey MB, Liu Q, Tasinkevych M, Smalyukh II (2015) Colloidal spirals in nematic liquid crystals. Soft Matter 11:8758–8767. https://doi.org/10.1039/C5SM01539A
Tovkach OM, Chernyshuk SB, Lev BI (2012) Theory of elastic interaction between arbitrary colloidal particles in confined nematic liquid crystals. Phys Rev E 86:061703. https://doi.org/10.1103/PhysRevE.86.061703
Terentjev EM (1995) Disclination loops, standing alone and around solid particles, in nematic liquid crystals. Phys Rev E 51:1330–1337. https://doi.org/10.1103/PhysRevE.51.1330
Ruhwandl RW, Terentjev EM (1997) Long-range forces and aggregation of colloid particles in a nematic liquid crystal. Phys Rev E 55:2958–2961. https://doi.org/10.1103/PhysRevE.55.2958
Tovkach O, Chernyshuk S, Lev B (2015) Colloidal interactions in a homeotropic nematic cell with different elastic constants. Phys Rev E 92:042505. https://doi.org/10.1103/PhysRevE.92.042505
Chernyshuk S (2014) High-order elastic terms, boojums and general paradigm of the elastic interaction between colloidal particles in the nematic liquid crystals. Eur Phys J E 37:6. https://doi.org/10.1140/epje/i2014-14006-5
Chernyshuk S, Tovkach O (2016) Colloidal particles as elastic triads in nematic liquid crystals. Liq Cryst 43:2410–2421. https://doi.org/10.1080/02678292.2016.1216619
Chernyshuk SB, Tovkach OM, Lev BI (2014) Elastic octopoles and colloidal structures in nematic liquid crystals. Phys Rev E 89:032505. https://doi.org/10.1103/PhysRevE.89.032505
Senyuk B, Puls O, Tovkach OM, Chernyshuk SB, Smalyukh II (2016) Hexadecapolar colloids. Nat Commun 7:1–7. https://doi.org/10.1038/ncomms10659
Landau LD, Lifshitz EM (1994) The Classical Theory of Fields. Butterworth-Heinemann, Oxford
Xiao K, Chen X, Wu CX (2019) Fréedericksz-like positional transition. Phys Rev Res 1:033041. https://doi.org/10.1103/PhysRevResearch.1.033041
Shiyanovskii SV, Glushchenko A, Reznikov Y, Lavrentovich OD, West JL (2000) Tensor and complex anchoring in liquid crystals. Phys Rev E 62:R1477–R1480. https://doi.org/10.1103/PhysRevE.62.R1477
Jackson LD (1999) Classical Electrodynamics. Hoboken, Wiley
Lee BK, Kim SJ, Kim JH, Lev B (2017) Coulomb-like elastic interaction induced by symmetry breaking in nematic liquid crystal colloids. Sci Rep 7:1–8. https://doi.org/10.1038/s41598-017-16200-z
Yuan Y, Liu Q, Senyuk B, Smalyukh II (2019) Elastic colloidal monopoles and reconfigurable self-assembly in liquid crystals. Nature 570:214–218. https://doi.org/10.1038/s41586-019-1247-7
Pergamenshchik VM (2014) Elastic multipoles in the field of the nematic director distortions. Eur Phys J E 37:1–15. https://doi.org/10.1140/epje/i2014-14121-3
de Gennes PG, Prost J (1993) The Physics of Liquid Crystals. Clarendon Press, Oxford
Tkalec U, Ravnik M, Čopar S, Žumer S, Muševič I (2011) Reconfigurable knots and links in chiral nematic colloids. Science 333:62–65. https://doi.org/10.1126/science.1205705
Jampani VSR, Škarabot M, Ravnik M, Čopar S, Žumer S, Muševič I (2011) Colloidal entanglement in highly twisted chiral nematic colloids: Twisted loops, hopf links, and trefoil knots. Phys Rev E 84:031703. https://doi.org/10.1103/PhysRevE.84.031703
Čopar S, Tkalec U, Muševič I, Žumer S (2015) Knot theory realizations in nematic colloids. Proc Natl Acad Sci USA 112:1675–1680. https://doi.org/10.1073/pnas.1417178112
Everts JC, Senyuk B, Mundoor H, Ravnik M, Smalyukh II (2021) Anisotropic electrostatic screening of charged colloids in nematic solvents. Sci Adv 7(eabd0662). https://doi.org/10.1126/sciadv.abd0662
Acknowledgements
One of the authors (B.I.L) is sincerely grateful for the support of the Department of Physics and Astronomy of the National Academy of Sciences of Ukraine — project (N 120U100857) “Mathematical models of non-equilibrium processes in open systems” and the National Research Foundation of Ukraine — project (N 0120U105146) “Models of non-equilibrium process in colloidal systems”.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Tovkach, O.M., Chernyshuk, S.B., Lev, B.I. (2022). Colloidal Particles in Confined and Deformed Nematic Liquid Crystals: Electrostatic Analogy and Its Implications. In: Bulavin, L., Lebovka, N. (eds) Soft Matter Systems for Biomedical Applications. Springer Proceedings in Physics, vol 266. Springer, Cham. https://doi.org/10.1007/978-3-030-80924-9_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-80924-9_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-80923-2
Online ISBN: 978-3-030-80924-9
eBook Packages: Chemistry and Materials ScienceChemistry and Material Science (R0)