Turbulence Modulation and Energy Transfer in Turbulent Channel Flow Coupled with One-Side Porous Media

Abstract

The microscopic structure of porous walls modulates the turbulent flow above. The standard approach, the volume-averaged modelling of the porous wall, does not resolve the pore structure. To systematically link geometric characteristics with flow properites, direct numerical simulations are conducted which are fully-resolving the microscopic structure. A high-order spectral/hp element solver is adopted to solve the incompressible Navier-Stokes equations. Resolving the full energy-spectra relies on a zonal polynomial refinement based on a conforming mesh. A low and a high porosity case with in-line arrays of cylinders are analysed for two Reynolds numbers. The peak in the streamwise energy spectra is shifted towards the pore unit length for both cases. Proper Orthogonal Decomposition (POD) shows that the fluctuations in the porous wall are linked to the structures above. Q2 structures are linked with blowing events and Q4 structures with suction events in the first pore row. The numerical solver Nektar exhibits an excellent scalability up to 96k cores on “Hazel Hen” where a slightly improved performance is observed on the brand new HPE “Hawk” system. Strong scaling tests indicate an efficiency of 70$\%$ with around 5, 000 mesh-nodes per core, which indicates a high potential for an adequate use of a HPC platform to investigate turbulent flows above porous walls while resolving the pore structure.

1 Introduction

The properties of turbulent flows bounded by porous materials are determined by the microscopic structure of the porous material. This modification of the turbulent flow by a porous structure can be found in natural systems and in various engineering applications. Natural systems are for instance rivers flowing over porous riverbeds or the flow of wind over forests. In engineering the ability of a porous wall to exchange momentum and energy with the turbulent flow is useful for Aerodynamics and Thermodynamics applications. Thermodynamics applications like heat exchangers use the high specific surface area of porous walls to increase the heat transfer. The process of transpiration cooling involves porous walls through which gas is blown to reduce the heat flux into the structure and at the same time to absorb heat from the structure. Aerodynamics investigations show, that it is possible to reduce the noise of an airfoil by applying a porous structure at the trailing edge. All these examples have in common that macroscale properties are determined by the microscopic characteristics of the porous structure or the surface structure. Reducing frictional pressure losses with an increase in heat transfer by the design of a passive structure would be of great commercial value. To enable this it is decisive to understand the influence of the characteristics of porous structures like the pore mophology and topology.

The modulation of turbulence by a permeable surface has been confirmed in early-years experiments with different configurations, e.g. turbulent open channel flows over porous media composed of spheres. A qualitative similar conclusion was drawn that the wall permeability is able to increase turbulent friction. In a recent study, Suga et al. [21] constructed three different kinds of anisotropic porous media to form the permeable bottom wall of the channel. The wall permeability tensor is designed to own a larger wall-normal diagonal component (wall-normal permeability) than the other components and the spanwise turbulent structures are investigated with particle image velocimetry (PIV). They discuss the correlation of streak spacing and integral length with the wall normal distance for different wall permeabilities.

Terzis et al. [22] examined experimentally the hydrodynamic interaction between a regular porous medium and an adjacent free-flow channel at low Reynolds numbers ($Re < 1$). In their study the porous medium consists of evenly spaced micro-structured rectangular pillars arranged in a uniform pattern, while the free-flow channel features a rectangular cross-sectional area. They show that the flow is non-parallel at the interface between the free-flow and the porous media flow. DNS allows microscopic visualization and analysis, which is hardly achvieable within the measurements in such confined and tortuous spaces. The existing experiments provide information about the optically accessible areas. However, because of the difficulty in performing measurements inside the porous media, it is not easy to discuss the turbulent flow physics inside the porous structures.

Direct Numerical Simulation exhibits an edge of observing and analyzing turbulent physics in a confined small space, not only for the canonical cases as channel flows and pipe flows [2, 4, 13,14,15, 17, 19], but also for transitional and turbulent flow in a representative elementary volume (REV) of porous media [5, 7]. Growing interest has been observed regarding the turbulent flow regime inside porous structures, as the studies with direct numerical simulation (DNS) show [5,6,7, 11, 26]. However, an adequate resolution of the smallest length scales of the flow in the interface region (between the pore flow and the turbulent boundary layer) requires enormous computational resources. To limit the computational cost, the size of the computational domain can be reduced. Therefore, appropriate boundary conditions must be chosen. Jimenez et al. [10] performed DNS with a special boundary condition: They imposed no-slip conditions for the streamwise and spanwise velocities, and set the wall-normal velocity for the permeable wall to be proportional to the local pressure fluctuations. The friction is increased by up to $40\%$ over the walls, which was associated with the presence of large spanwise rollers.

Rosti et al. [20] explored the potential of drag reduction with porous materials. They systematically adjusted the permeability tensor on the walls of a turbulent channel flow via VANS-DNS coupling. The total drag could be either reduced or increased by more than 20$\%$ through adjusting the permeability directional properties. Configuring the permeability in the vertical direction lower than the one in the wall-parallel planes led to significant streaky turbulent structures (quasi 1-dimensional turbulence) and hence achieved a drag reduction. Recent studies achieved to resolve the porous media structures coupled with turbulent flows. Kuwata et al. [12] used the Lattice-Boltzmann method (LBM) to resolve porous structures coupled with turbulent flows. The porous media is composed by interconnected staggered cube arrays. The difference between a rough wall and a permeable wall is elucidated.

The current study is intended to establish interface-resolved DNS research about turbulent flows over porous media. Through an adequate resolution of the flow field inside the porous structure and of the turbulent flow above, both the turbulence modulation and the energy exchange across the porous surface is investigated. This physical knowledge can be used to support different levels of modeling like LES or RANS [28]. Furthermore, it will be possible to link the geometrical characteristics of the porous media with the turbulent structures of the flow field. This will enable the design of porous structures that generate specific flow properties.

2 Numerical Method

2.1 Arbitrary High-Order Numerical Solver for Complex Geometries

The three-dimensional incompressible Navier−Stokes equations, given by Eqs. 1–2, are solved in non-dimensional form, where $\varPi$ is the corresponding source term in the momentum equation to maintain a constant pressure gradient in the main flow direction.

$$\begin{aligned} \frac{\partial u_j}{\partial x_j}=0 \end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial u_i}{\partial t}+\frac{\partial u_i u_j}{\partial x_j}=-\frac{\partial p}{\partial x_i}+\frac{1}{Re}\frac{\partial ^2 u_i}{\partial x_i \partial x_j}+\varPi \delta _{i1} \end{aligned}$$

(2)

A spectral/hp element solver Nektar++ [1, 18] is used to perform the DNS and to resolve the wide-spectra of scales in the complex geometrical structures. The high-order solver framework allows arbitrary-order spectral/hp element discretisations and refinement with hybrid shaped elements. Both modal and nodal polynomial functions can be used for the high-order representation. In addition, the homogeneous flow direction can be represented with Fourier-spectral expansions and, therefore, enables the usage of an efficient parallel direct solver. The spectral-accurate discretisation combined with meshing flexibility is optimal to deal with complex porous structures and to resolve the interface region. The time-stepping is treated with a second-order mixed implicit-explicit (IMEX) scheme. The fixed time step is defined by $\varDelta T/(h/\overline{u})=0.0001$ to ensure numerical stability. A run of 10 flow through times for flow development and 5 flow through times for gathering statistics is in general necessary.

Fig. 1

Interface resolved Direct Numerical Simulation. Section of the computational domain in the $x-y$ plane. The spanwise direction is periodic. Depicted is a snapshot of the streamwise velocity fluctuation $u^{\prime }$.

Figure 1 illustrates a two-dimensional sketch of the simulation domain, the spanwise direction is periodic. The domain size $L_x \times L_y \times L_z$ is $100 \times 20 \times 8\pi$, where the lower part $0< y < 10$ is the porous media and the upper part $10< y < 20$ is the free-flow channel. The porous layer consists of circular cylinders arranged in-line. The porous layer consists of 50 porous media elements in streamwise direction and 5 elements in wall-normal direction, which indicates 250 porous elements in total. A no-slip boundary condition is defined for all surfaces of the porous structure (i.g. on the surfaces of the circular cylinders) as well as for the upper wall ($y=20$) and for the lower wall ($y=0$). Periodic boundary conditions are defined in x-direction between $x=0$ and $x=100$. The second pair of periodicity is defined in the spanwise direction $z=0$ and $z=8\pi$.

The geometry is discretizied with full quadrilateral elements on the $x-y$ plane with local refinement near the permeable interface. The third direction (z-direction) is extended with a Fourier-based spectral method. High-order Lagrange polynomials through the modified base are applied on the $x-y$ plane. The numerical solver enables a flexible non-identical polynomial order based on the conforming elements, which offers high meshing flexibility corresponding to laminar, turbulent or interfacial flows according to prior knowledge.

2.2 Simulation Conditions

The simulation cases are summarized in Table 1. Four cases are introduced here covering two porous topologies and two Reynolds numbers. The porous topology is characterised by the porosity $\varphi$, which is defined by the ratio of the void volume $V_{V}$ to the total volume $V_{T}$ of the porous structure. The bulk Reynolds number is defined using the bulk averaged velocity $\overline{u}$, channel height h and kinematic viscosity $\nu$, i.e. $Re=\overline{u}h/\nu$. Additional flow characteristics are the shear Reynolds numbers $Re_\tau ^t = u_\tau ^t h/\nu$ and $Re_\tau ^p = u_\tau ^p h/\nu$. Wherein the superscript t refers to the evaluation at the top wall of the channel and p to the evaluation at the permeable surface. The total mesh resolution ranges from $250\times 10^6$ to $1.1\times 10^9$ for the high Reynolds number condition.

Table 1 Summary of boundary layer parameters for all the cases. Case A1 and A2 are the low porosity cases ($\varphi =0.5$) and case B1 and B2 are the high porosity cases ($\varphi =0.8$)

3 Results

Figure 2 shows the mean streamwise velocity U profiles, where $U=\langle \overline{u} \rangle$ is temporally and spatially averaged. The inner-scaled $U^+$ profiles of both sides are compared in Fig. 2(a), which are normalized by $u_\tau ^p$ and $u_\tau ^t$ correspondingly. All the velocity profiles on the smooth top wall (dashed lines) follow the linear and log law fairly well regardless their difference in porosities and Reynolds numbers, which indicates a marginal influence of the porous media on this side. On the other hand, the velocity profiles above the permeable wall differ significantly from the canonical boundary layer profiles. The $U^+$ profiles of the porous media side are much lower than the smooth wall side, owing to the increase of the friction velocity $u_\tau ^p$. Moreover, the friction velocity $u_\tau ^p$ shows an increase around $32\%$ from the low porosity cases (A1 and A2) to the high porosity ones (B1 and B2), resulting in a much lower magnitude of $U^+$ for the latter.

The velocity profiles $U^{t+}$ in the entire domain are shown in Fig. 2(b), which are normalized by the friction velocity of the smooth wall side $u_\tau ^t$. There are several important differences between the low and the high porosity cases. First, the thickness of the boundary layer is larger for walls with higher permeability, indicating a larger impact area in the channel. Second, the velocity within the porous media increases with porosity $\varphi$. Third, the velocity in the vicinity of the interface is negative with a small value for cases A1 and A2, which is related to the recirculation region between the cylinders. In contrast, the velocity above the smaller cylinders (cases B1 and B2) is monotonic, indicating an absence of a rotational region. This will be more clearly shown in the later discussion. Increasing the Reynolds number, the magnitude of the $U^{t+}$ within the porous media is enhanced, which may indicate more active momentum exchange near the interface.

Fig. 2

Mean streamwise velocity profiles U. a $U^+$ profiles above the porous wall and near the smooth wall normalized by their own inner variables; b $U^{t+}$ profiles of the whole domain normalized by $u_{\tau }^t$

The contours of the time averaged velocities $\overline{u}$ and $\overline{v}$ of the interface region are depicted in Fig. 3. A pair of counter-rotating vortices are observed between two circular cylinders in the low-porosity cases A1 and A2 Fig. 3(a, c), which is absent in the high-porosity cases Fig. 3(b, d). The recirculation induced by the vortices leads to the backflow near the interface of the U profile Fig. 2(b). The upper vortex is driven by the main stream velocity and restricted by the narrow void between cylinders, which results in a classical lid-driven cavity flow here. The upper and lower vortex are separated by the narrow throat between the cylinders, which blocks the convection from below. In comparison, the mean streamwise and vertical velocity within the porous media are higher in case B1 Fig. 3(b) and B2 Fig. 3(d). Between two neighboring cylinders, a blow event (positive $\overline{v}$) is followed by a suction event (negative $\overline{v}$) in the downstream direction, which exchanges fluid between the interface and positions below the cylinder.

The wall normal variation of turbulent kinetic energy (TKE) and Reynolds shear stress, i.e., $\langle \overline{u_i^{\prime }u_j^{\prime }} \rangle ^{t+}_s$, are depicted in Fig. 4, which are averaged in x-z plane and normalized by $u_{\tau }^t$. Note that the subscript s denotes superficial area averaging. For the cases studied, all the components of the TKE and the Reynolds shear stress are intensified on the porous media side compared to its counter part of the non-permeable wall, and the high porosity cases (B1, B2) have even a higher magnitude than the lower ones. Increasing the Reynolds number results in a further increment of all four Reynolds stress components.

Despite sharing similar features above, the high and low porosity cases show clear differences at the interface and below. For cases A1 and A2, the TKE components approach zero quickly as moving from the permeable interface into the porous media domain, which suggests that disturbances in the free-flow result only in a marginal penetration into the porous media domain. In contrast, turbulent fluctuations are still relatively energetic below the interface for cases B1 and B2. The streamwise component $\langle \overline{u^{\prime }u^{\prime }} \rangle ^{t+}_s$ shows a periodic distribution in the porous media domain due to the blockage of the cylinders, while the other two components show a smooth descending trend as moving towards the bottom wall. Nevertheless, the Reynolds shear stress $\langle \overline{u^{\prime }v^{\prime }} \rangle ^{t+}_s$ becomes weak below the first row of cylinders for all the cases.

To show the spatial variation of TKE and Reynolds shear stress, contours of $\overline{u^{\prime }u^{\prime }}$, $\overline{v^{\prime }v^{\prime }}$, $\overline{w^{\prime }w^{\prime }}$, $\overline{u^{\prime }v^{\prime }}$ close to the permeable interface are depicted in Fig. 4. The magnitude of $\overline{u^{\prime }u^{\prime }}$ fades quickly below the porous bed in all four cases. As for $\overline{v^{\prime }v^{\prime }}$, $\overline{w^{\prime }w^{\prime }}$, and $\overline{u^{\prime }v^{\prime }}$, the momentum flux represented by these terms have a deeper impact region in the high porosity cases. A positive peak of the Reynolds shear stress $\overline{u^{\prime }v^{\prime }}$ is observed at the impinging position B in all four cases, which differs from the negative Reynolds shear stress above the porous bed. For cases B1 and B2, an area of positive Reynolds shear stress reaches even below the first layer of cylinders.

Fig. 3

Ensemble averaged velocity fields $\overline{u}$ (row 1) and $\overline{v}$ (row 2). Column a: case A1; Column b: case B1; Column c: case A2; Column d: case B2. The wall normal origin is set at the crest of the cylinders

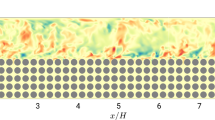
In addition to the one-point statistics, the porous media may also change the energetic scale in the free-flow, which further influences the sustaining process of turbulence. Figure 5 shows one-dimensional pre-multiplied spectra of turbulent kinetic energy $k_x\hat{q}$/$k_z\hat{q}$ as a function of the streamwise/spanwise wave lengths $\lambda _x, \lambda _z$ and wall distance $y^{t+}$. Here, $\hat{\cdot }$ stands for the Fourier coefficients that have been transformed in x- or z-direction. The wave length $\lambda _x$ and $\lambda _z$ are normalized with the distance between two cylinders (pore unit length) D. The streamwise spectra is averaged in time and spanwise dimension, while the spanwise spectra is averaged in time and streamwise dimension. The spectra above the non-permeable wall are flipped upside down and superimposed (as solid lines) on the spectra above of permeable wall (color contour).

Fig. 4

Superficial area averaged Reynolds stresses $\langle \overline{u_i^{\prime }u_i^{\prime } } \rangle ^{t+}_s$ normalized by the friction velocity $u_{\tau }^t$

A series of high-energy spikes are observed in the streamwise spectra of all cases, which are originated from the porous wall and reach as far as $y^{t+}\approx 60$. The wave length of the spikes feature a series of harmonic waves with a maximal wave length of the pore unit length D, which indicates that these spikes stand for the highly regulated fluctuation stemming from the porous medium. In addition to the spikes, the remaining of the spectra represent the energy of ‘background’ turbulence. In cases A1 and A2, the peak of the ‘background’ spectra above the porous wall is $\lambda _x^{t+}\approx 150$ in inner scale at $y^{t+}\approx 20$, which is slightly smaller than $\lambda _x^{t+}\approx 200$ of the smooth wall side. In case A2, with higher Reynolds number, there is a strong trend that the peak the ‘background turbulence’ spectra is synchronized with the porous unit spikes. The energy concentrates between $\lambda _x\approx 2D$ or $\lambda _x^{t+}\approx 400$ and $\lambda _x\approx 0.2D$ or $\lambda _x^{t+}\approx 40$. For the cases B1 and B2, the turbulent spectra also bias towards spikes at $\lambda _x\approx 1\sim 2D$ obviously, especially for the high Reynolds number case B2. Moreover, energetic peaks at large scales $\lambda _x\ge 10D$ are observed for spectra on both sides. It appears that the periodic fluctuations originated from the permeable wall perform as an additional source in the energy cascade of turbulence. By introducing additional energetic modes into the spectra, the porous wall can efficiently biased the peak of streamwise spectra towards the pore unit length.

The TKE spectra show a significant impact of the porous medium on scale energy, especially for the streamwise modes. This indicate that the coherent structures above the porous media can be quite different from those of a canonical wall-bounded flow in terms of length scale and evolution dynamics. Further effort is needed to shed light on this problem.

Proper orthogonal decomposition (POD, [23,24,25]) is applied to the flow fields to extract the most energetic structures. The region is selected to be from the first layer cylinders to the middle of the channel. The first six spatial modes are shown in Fig. 6 The turbulent fluctuation in porous media is one order smaller than that above the interface. The POD modes mainly capture the coherent structure in the TBL. The first two modes are coupled, with large scale Q2 and Q4 structures connected in streamwise direction. These Q2/Q4 zones have a streamwise extent of $\varDelta X \ge 20$, and reach beyond the center of the channel in wall normal direction. Note that there are also smaller scale Q2/Q4 events close to the interface. Modes 3–6 represent coherent structures of smaller scale, which is similar with the results of canonical TBLs. The fluctuation with in the porous media, despite of its small contribution to TKE, has a strong connection with the structures above the interface. It is clearly shown in modes 1 and 2 that large scale Q4 structures are associated with negative $v'$ (i.e., suction) events at the gap between the cylinders, while Q2 events with positive $v'$ (i.e., blow) events. For high order modes, this association is not observed. This provides first-hand information about the interaction mechanism between free-flow and fluid inside the porous medium, which suggests the blow and suction at the interface is more subject to the influence of large scale motions. Figure 7 shows the cumulative energy curve. The first two modes only account for $20\%$ of the total TKE, which is within our exception, since the turbulence above the interface is quite close to a channel flow above a smooth wall. Further POD analysis will be conducted close to the interface region to reveal more about the small scale interaction dynamics.

Fig. 5

Pre-multiplied one-dimensional TKE spectra: $k_x\widehat{q}(\lambda _x)$. Column a–b represent the cases A1, B1, A2, and B2, respectively. The color contours are the energy spectra from the porous media side, while the solid isolines representing spectra of the non-permeable side which are superimposed as a reference

Fig. 6

The first six POD modes from DNS snapshots of coupled porous media and channel flow

Fig. 7

Accumulated modal energy from the first 1000 POD modes

4 Computational Performance

In this section, the parallel computational performance will be discussed. The supercomputing systems utilized were ‘Hazel Hen’ and ‘HAWK’ located at the High-Performance Computer Center Stuttgart (HLRS). ‘Hazel Hen’, a Cray XC40 system, consists of 7,712 compute nodes. Two Intel Haswell processors (E5-2680 v3, 12 cores) and 128 GB memory are deployed at each node. The compute nodes are interconnected by a Cray Aries network with a Dragonfly topology. This amounts to a total of 185,088 cores and a theoretical peak performance of 7.4 petaFLOPS.

The new flagship machine HAWK, based on HPE platform running AMD EPYC 7742 processor code named Rome, will have a theoretical peak performance of 26 petaFLOPs, and consist of a 5,632-node cluster. The AMD EPYC 7742 CPU consists of 64 cores, which leads to 128 cores on a single node sharing 256 GB memory on board. This means that a total of 720,896 cores are available on the HAWK system.

Fig. 8

Scaling behavior of the solver on ‘Hazel Hen’, wall clock time per time step on the left side. On the right side the efficiency for different numbers of MPI ranks

The scalability tests based on two cases are shown in Fig. 8, one with $370 \times 10^6$ mesh element nodes and the other one with $1.1 \times 10^9$. Each MPI rank in the simulations represents one core on Hazel Hen. The total number of MPI ranks tested on the machine ranges from 2,400 to 96,000. A lower number of ranks is not possible due to the memory overload. An approximate linear relationship between the number of MPI ranks and the wall clock time per timestep can be identified on the left hand side. One time step takes about 0.08 s with a load of around 5,000 DOF per core. The strong scaling efficiency on the right hand side exhibits a super linear speedup at low MPI ranks, followed by a slight drop for more than $10^4$ MPI ranks. A minimum efficiency of $70\%$ can be achieved with the maximal number of MPI ranks. Compared to the previously employed open-source FVM code OpenFOAM [3, 4, 8, 16, 27] and the discontinuous-Galerkin spectral-element method (DGSEM) code [9], the open-source spectral/hp element code shows strong scalability on the HPC machine. Due to the recent status of HAWK, the planned scalability test was not conducted. According to real-field usage experience, the per-core performance on HAWK is slightly better than that on Hazel Hen (approximately 20$\%$). The scalability is expected to be at least on the same level of Hazel Hen.

5 Conclusions

We studied turbulent flow over porous media by conducting fully-resolved direct numerical simulations of two porous topologies and two Reynolds numbers cases. The porous wall leads to an asymmetric velocity profile in the channel. This asymmety is more pronounced for higher porosites and leads to a larger boundary layer thickness and lower velocities on the porous wall side. The friction velocity is increased around 32$\%$ for a higher porosity ($\varphi = 0.8$) compared to the lower porosity case ($\varphi =0.5$). But also the low porosity case ($\varphi =0.5$) has an approximatelya 10 $\%$ higher friction velocity than a smooth wall.

Furthermore, the low porosity cases have a lower velocity within the porous media but also recirculation regions between the first row of cylindes. This recirculation can be compared to classical lid-driven cavity flows which blocks the direct convection between the turbulent flow and the first row of pores.

By increasing the Reynolds number, the magnitude of the $U^{t+}$ within the porous medium is enhanced, which indicates a higher momentum near the interface. The TKE and Reynolds shear stress demonstrate that high porosity as well as high Reynolds numbers result in a higher magnitude. For low porosity cases, the turbulent disturbances in the free-flow remains marginal below the interface, while the disturbances are still energetic in the porous media domain for high porosity cases. But these disturbances only penerate the first row of pores where they are one order smaller than in the free turbulent flow. The TKE spectra shows a significant impact of the porous structures on the scale energy, especially for the streamwise modes. For all cases, the turbulent spectra bias towards spikes at $\lambda _x\approx 1\sim 2D$ and are stronger for high Reynolds number cases. Additional energetic peaks at large scales can be found in high porosity cases. The POD analysis shows that the fluctuation within the porous wall, which have a small contribution to the TKE, are linked to the structures above the interface. It is shown that the Q2 structures are linked to blowing events and Q4 structures are linked to suction events in the first row of pores.

We also tested the computational performance of the supercomputing system ‘Hazel Hen’ for the current cases. Scalability test show that the maximum efficiency is achieved at $10^4$ MPI ranks and a minimum efficiency of $70\%$ at 96,000 MPI ranks.