On 3SUM-hard Problems in the Decision Tree Model

Abstract

We describe subquadratic algorithms, in the algebraic decision-tree model of computation, for detecting whether there exists a triple of points, belonging to three respective sets A, B, and C of points in the plane, that satisfy a pair of polynomial equations. In particular, this has an application to detect collinearity among three sets A, B, C of n points each, in the complex plane, when each of the sets A, B, C lies on some constant-degree algebraic curve. In another development, we present a subquadratic algorithm, in the algebraic decision-tree model, for the following problem: Given a pair of sets A, B each consisting of n pairwise disjoint line segments in the plane, and a third set C of arbitrary line segments in the plane, determine whether $A\times B\times C$ contains a triple of concurrent segments. This is one of four 3sum-hard geometric problems recently studied by Chan (2020). The results reported in this extended abstract are based on the recent studies of the author with Aronov and Sharir (2020, 2021).

Work partially supported by NSF CAREER under grant CCF:AF-1553354 and by Grant 824/17 from the Israel Science Foundation.

1 Introduction

In theoretical computer science, analysis of algorithms in non-uniform models is often applied when one is interested in optimizing the number of certain operations, while the remaining operations performed by the algorithm are disregarded in the complexity analysis.

A central problem, which received considerable attention due to its relation to conditional lower bounds on the complexity of fundamental geometric questions, is 3sum, namely, given a set of n real numbers, decide whether there is a triple of them that sums to 0. We sometimes refer to the trichromatic version of 3SUM, where we are given three sets A, B, C of n real numbers each, and the question is to determine whether there is a triple $(a,b,c)\in A\times B \times C$ with $a+b+c=0$.

There is a large family of geometric problems that are known to be 3sum-hard, in the sense that 3sum can be reduced to them. In fact, Gajentaan and Overmars [15], who introduced this concept, initially coined these problems “$n^2$-hard,” as it was strongly believed that 3sum cannot be solved in subquadratic time (it can easily be solved in $O(n^2)$ time). Moreover, Erickson [11] showed a matching quadratic lower bound in the 3-linear decision-tree model (see also [4]),namely, in the linear decision-tree model the only operation allowed to directly access the input data is a sign test of a linear function of the input numbers; these are the operations counted by the model, while all the remaining operations are free. In the 3-linear model, the linear functions are restricted to three parameters, in particular, Erickson [11] used comparisons of the form: “Is $a+b$ greater/smaller/equal to c?”

As a consequence, it was conjectured that there is no subquadratic solution. However, this prevailing conjecture was refuted by Grønlund and Pettie [16], who showed an upper bound close to $O(n^{3/2})$ in the 4-linear decision-tree model (using the so-called Fredman’s trick - see Sect. 2 for this notion in geometric problems), and a slightly subquadratic algorithm in the RAM model. This pioneering work raised the interest of researchers from the entire theoretical computer science community. Soon afterwards, the more general question of k-SUM (deciding whether there is a k-tuple of the input numbers which sum to 0) was studied by Cardinal et al. [8], Kane et al. [19] and by the author and collaborators [13, 14]. The main idea is to reduce the problem to point location in high-dimensional “hyperplane arrangements,” where the challenge is to bring down the query time, so that its dependence on the dimension d is polynomial rather than exponential (see also [20, 21]). In fact, the work of the author in [13] presents a point-location mechanism for arbitrary hyperplanes in the RAM model (whereas the work in [14] considered this problem only in the linear decision-tree model). Very recently Hopkins et al. [18] showed an improvement for such a mechanism, yielding an almost optimal bound in the linear decision-tree model. The approach in [18, 19] uses the concept of inference adapted from active learning. Inference dimension refers to the situation where one considers linear comparisons on a set of items, and the quantity to be measured is, roughly speaking, what is the smallest number of comparisons from which one can deduce the result of another comparison. A key property in the analysis in [19], which eventually led to the near-linear bound for the k-SUM problem, is that the inference dimension is only linear in n in this case.

The seminal work of Gajentaan and Overmars [15] presents a fairly long list of geometric 3sum-hard problems in two and three dimensions (they all have a simple reduction from 3sum), such as: (i) Collinearity testing: Given a set of points in $\mathbb {R}^2$, do they contain a collinear triple? (ii) Covering by strips: Given strips in the plane, does their union cover the unit square? (iii) Separator problems: Given a set of non-intersecting axis-parallel line segments in $\mathbb {R}^2$, is there a line separating them into two non-empty sets? Among geometric 3sum-hard problems, collinearity testing is perhaps the most fundamental one, since many such problems are intrinsically “collinearity-hard”. In this extended abstract we refer to the trichromatic version of collinearity testing, which is described next.

In the sequel we focus on two main developments concerning collinearity testing in the algebraic decision tree model, that is, each comparison is a sign test of some constant-degree polynomial in the coordinates of a constant number of input points. In the first we consider the trichromatic problem in the complex plane, where the input consists of three sets of points A, B, C, each lying on some constant-degree algebraic (complex) curve. We in fact present a more general scheme, for detecting whether there exists a triple of points, belonging to three respective sets A, B, and C of points in the plane, that satisfy two polynomial equations, and show a subquadratic bound in the algebraic decision tree model. These results are briefly described in Sect. 2; we refer the reader to [5] for further details.¹

In the second development we study the segment concurrency problem in the algebraic decision tree model: Given a pair of sets A, B each consisting of n pairwise disjoint line segments in the plane, and a third set C of arbitrary line segments in the plane, determine whether $A\times B\times C$ contains a triple of concurrent segments. When A, B, C are three sets of lines in the plane (rather than line segments as above), the problem is exactly the dual to collinearity testing, which is 3sum-hard. In fact, our restricted setting is still 3sum-hard, and is among four such problems studied by Chan [9], all of which can be reduced to the problem of triangle intersection counting: That is, given two sets A and B, each consisting of n pairwise disjoint line segments in the plane, and a set C of n triangles in the plane, count, for each triangle $\varDelta \in C$, the number of intersection points between the segments of A and those of B that lie inside $\varDelta$. The other two problems are: (i) Intersection of three polygons: Given three simple n-gons A, B, C in the plane, determine whether $A\cap B\cap C$ is nonempty.(ii) Coverage by three polygons: Given three simple n-gons A, B, C in the plane, determine whether $A\cup B\cup C$ covers a given triangle $\varDelta _0$. The property that these problems are 3SUM-hard, as well as the reduction to the problem of triangle intersection counting, are described in [9].

In Sect. 3 we briefly describe a subquadratic solution to the segment concurrency problem in the algebraic decision tree model. This is part of the work in progress of the author with Aronov and Sharir [6] where they presented a subquadratic solution to the triangle intersection counting problem in the algebraic decision tree model.

2 Testing a Pair of Polynomial Equations and Collinearity Testing in the Complex Plane

For simplicity of presentation, we present a solution sketch for the following problem: We are given three sets A, B, and C, each consisting of n points in the plane, and we seek a triple $(a,b,c)\in A\times B\times C$ that satisfies two polynomial equations. We assume that they are of the form $c_1 = F(a,b)$, $c_2 = G(a,b)$, for $c=(c_1,c_2)$, where F and G are constant-degree 4-variate polynomials with good fibers, in the following sense: For any pair of real numbers $\kappa _1$, $\kappa _2$, the two-dimensional surface $\pi _{(\kappa _1, \kappa _2)} := \{(a,b)\in \mathbb {R}^4 \mid F(a,b)=\kappa _1,\; G(a,b) = \kappa _2 \}$ has good fibers².

Polynomial Partitioning. Our analysis relies on planar polynomial partitioning and on properties of Cartesian products of pairs of them. For a polynomial $f :\mathbb {R}^d \rightarrow \mathbb {R}$, for any $d \ge 2$, the zero set of f is . We refer to an open connected component of $\mathbb {R}^d \setminus Z(f)$ as a cell. A fundamental result of Guth and Katz [17] is:

Proposition 1

(Polynomial partitioning [17]). Let P be a finite set of points in $\mathbb {R}^d$, for any $d\ge 2$. For any real parameter D with $1 \le D \le |{P}|^{1/d}$, there exists a real d-variate polynomial f of degree O(D) such that $\mathbb {R}^d \setminus Z(f)$ has $O(D^d)$ cells, each containing at most $|{P}|/D^d$ points of P.

Agarwal et al. [3] presented an algorithm that computes a polynomial partitioning in expected $O(n \mathrm {poly}(D))$ time, whose degree is within a constant factor of that stated in Proposition 1.

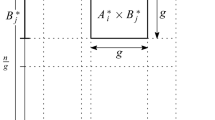
We now proceed as follows. We apply a “block” partitioning for the points in A and in B, using Cartesian products of pairs polynomial partitions, based on the analysis of Solymosi and de Zeeuw [22]. Roughly speaking, we fix a parameter $g\ll n$ (whose value will be set later), and use Proposition 1 in order to form a polynomial partitioning of degree $D = O(\sqrt{n/g})$ for each of the sets A, B. Each connected component in the partition of A (resp., B) contains at most g point of A (resp.,., B). We then form the Cartesian product of the partitioning of A and B. Let $\zeta$ denote a cell in this partition, this cell is the Cartesian product $\tau \times \tau '$ of a cell $\tau$ from the partition of A and a cell $\tau '$ from the partition of B. Since $|A \cap \tau |$, $|B \cap \tau '| \le g$, we have that $\zeta$ contains at most $g^2$ points of $A \times B$, and the overall number of cells in this partition is $O((n/g)^{2 + \varepsilon })$, for any prescribed $\varepsilon > 0$.³

Put $A_\tau := A \cap \tau$ and $B_{\tau '} := B \cap \tau '$. The high-level idea of the algorithm is to sort lexicographically each of the sets $H_{\tau ,\tau '} := \{ (F(a,b), G(a,b)) \mid (a,b) \in A_\tau \times B_{\tau '} \}$, over all pairs of cells $(\tau ,\tau ')$. We then search with each $c=(c_1,c_2)\in C$ through the sorted lists of those sets $H_{\tau ,\tau '}$ that might contain $(c_1,c_2)$. We show that each $c\in C$ has to be searched for in only a small number of sets. Typically to this kind of problems [16], sorting the sets explicitly is too expensive. We overcome this issue by considering the problem in the algebraic decision-tree model, and by using an algebraic variant of Fredman’s trick (extending those used in [7, 16]).

Implicit Sorting and Batched Point Location. Consider the step of sorting $\{F(a,b) \mid (a,b)\in A_\tau \times B_{\tau '}\}$ (the sorting of the values G(a, b) is done in a secondary round and is treated analogously). It has to perform various comparisons of pairs of values F(a, b) and $F(a',b')$, for $a, a'\in A_\tau$, $b, b'\in B_{\tau '}$. We consider $A_\tau \times A_\tau$ as a set of $g^2$ points in $\mathbb {R}^4$, and associate, with each pair $(b,b') \in B_{\tau '}\times B_{\tau '}$, the 3-surface ${\displaystyle \sigma _{b,b'} = \{ (a,a') \in \mathbb {R}^4 \mid F(a,b) = F(a',b') \}}$. Let $\varSigma _{\tau '}$ denote the set of these surfaces. The arrangement $\mathcal {A}(\varSigma _{\tau '})$ has the property that each of its cells $\zeta$ has a fixed sign pattern with respect to all these surfaces. That is, each comparison of F(a, b) with $F(a',b')$, for any (a, b), $(a',b')\in A_\tau \times B_{\tau '}$, has a fixed outcome for all points $(a,a') \in \zeta$ (for a fixed pair $b, b'$). In other words, if we locate the points of $A_\tau \times A_\tau$ in $\mathcal {A}(\varSigma _{\tau '})$, we have available the outcome of all the comparisons needed to sort the set $\{F(a,b) \mid (a,b)\in A_\tau \times B_{\tau '}\}$

Following the above steps is still too expensive, and takes $\varOmega (n^2)$ steps (in the algebraic decision-tree model) if implemented naïvely. We circumvent this issue, in the algebraic decision-tree model, by forming the unions $P := \bigcup _\tau A_\tau \times A_\tau$, and $\varSigma := \bigcup _{\tau '} \varSigma _{\tau '}$; we have $|P|, |\varSigma | = O(g^2\cdot (n/g)^{1+\varepsilon }) = O(n^{1 + \varepsilon } g^{1-\varepsilon })$. By locating each point of P in $\mathcal {A}(\varSigma )$, we get all the signs that are needed to sort all the sets $\{F(a,b) \mid (a,b)\in A_\tau \times B_{\tau '}\}$, over all pairs $\tau$, $\tau '$ of cells, and then the actual sorting costs nothing in algebraic decision tree model. In a main step in [5] we show:

Lemma 1

One can complete the above sorting step, in the algebraic decision tree model, in $O\left( (ng)^{8/5+\varepsilon }\right)$ randomized expected time, for any prescribed $\varepsilon > 0$, where the constant of proportionality depends on $\varepsilon$ and the degree of F and G.

Searching with the Points of C. We next search the structure with every $c=(c_1,c_2)\in C$. We only want to visit subproblems $(\tau ,\tau ')$ where there might exist $a\in \tau$ and $b\in \tau '$, such that $F(a,b)=c_1$ and $G(a,b)=c_2$. To find these cells, and to bound their number, we consider the two-dimensional surface ${\displaystyle \pi _{c=(c_1,c_2)} := \{(a,b)\in \mathbb {R}^4 \mid F(a,b)=c_1,\; G(a,b) = c_2 \}}$, and our goal is to enumerate the cells $\tau \times \tau '$ in the polynomial partition of $A\times B$ crossed by $\pi _c$. By assumption, $\pi _c$ has good fibers, so, by [5, Theorem 3.2], it crosses only $O((n/g)^{1+\varepsilon })$ cells $\tau \times \tau '$, and we can compute them in time $O((n/g)^{1+\varepsilon })$, for any $\varepsilon > 0$ (see [5] for these details).

Summing over all the n possible values of c, the number of crossings between the surfaces $\pi _c$ and the cells $\tau \times \tau '$ is $O(n^{2+\varepsilon }/g^{1+\varepsilon })$, for any $\varepsilon > 0$. Thus computing all such surface-cell crossings, over all $c \in C$, costs $O(n^{2+\varepsilon }/g^{1+\varepsilon })$ time. The cost of searching with any specific c, in the structure of a cell $\tau \times \tau '$ crossed by $\pi _c$, is $O(\log g)$ (it is simply a binary search over the sorted lists). Hence the overall cost of searching with the elements of C through the structure is (with a slightly larger $\varepsilon$) ${\displaystyle O\left( \frac{n^{2+\varepsilon }}{g^{1+\varepsilon }} \right) }$.

The Overall Algorithm. Combining the above costs we get total expected running time of ${\displaystyle O\left( (ng)^{8/5+\varepsilon } + \frac{n^{2+\varepsilon }}{g^{1+\varepsilon }} \right) }$. We now choose $g=n^{2/13}$, and obtain expected running time of $O\left( n^{24/13+\varepsilon }\right)$, where the implied constant of proportionality depends on the degrees of F and G and on $\varepsilon$. In summary, we have shown:

Theorem 1

(Aronov et al. [5]). Let A, B, C be three n-point sets in the plane, and let F, G be a pair of constant-degree 4-variate polynomials with good fibers (in the sense defined at the beginning of this section). Then one can test, in the algebraic decision-tree model, whether there exists a triple $a\in A$, $b\in B$, $c=(c_1,c_2)\in C$, such that $c_1 = F(a,b)$ and $c_2 = G(a,b)$, using only $O\left( n^{24/13 + \varepsilon }\right)$ polynomial sign tests (in expectation), for any $\varepsilon > 0$.

Collinearity Testing in the Complex Plane. In a further development in the Arxiv version of [5], the author with Aronov and Sharir extend Theorem 1 and show that one can test in the same asymptotic time bound (in the algebraic decision tree model) whether there exists a triple $a\in A$, $b\in B$, $c \in C$, such that $F(a,b,c) = 0$, $G(a,b,c)=0$, where now F, G are algebraic functions that satisfy some mild assumptions. Generally speaking, this involves a non-trivial and technical procedure for sorting roots of polynomials in the algebraic decision tree model.

We next apply this property to the problem of collinearity testing in the complex plane, for the following setup. The sets A, B, C are now sets of points in the complex plane $\mathbb {C}^2$, each consisting of n points and lying on a constant-degree algebraic curve, and we wish to determine whether $A\times B\times C$ contains a collinear triple. For simplicity of exposition, we assume that the curves $\gamma _A$, $\gamma _B$, and $\gamma _C$ that contain, respectively, A, B, and C are represented parameterically by equations of the form $(w,z) = (f_A(t),g_A(t))$, $(w,z) = (f_B(t),g_B(t))$, and $(w,z) = (f_C(t),g_C(t))$, where t is a complex parameter and $f_A$, $g_A$, $f_B$, $g_B$, $f_C$, and $g_C$ are constant-degree univariate (complex) polynomials.

With this parameterization the points of A, B, C can be represented as points in the real plane (representing the complex numbers t), and the complex polynomial whose vanishing (that is, once it is compared to zero) asserts collinearity of a triple $a = (z_a,w_a)$, $b = (z_b,w_b)$, $c = (z_c,w_c)$, is

$$\begin{aligned} H(t_a,t_b,t_c) := \begin{vmatrix} 1&f_A(t_a)&g_A(t_a) \\ 1&f_B(t_b)&g_B(t_b) \\ 1&f_C(t_c)&g_C(t_c) \end{vmatrix} , \end{aligned}$$

(1)

where $t_a$, $t_b$, $t_c$ are the parameters that specify a, b, c, respectively, so its real and imaginary components form a pair of real polynomial equations. This is the role assignment of the above polynomials F and G. In summary this shows (once again, refer to the Arxiv version of [5]):

Corollary 1

(Aronov et al. [5]). Let A, B, C be n-point sets in the complex zw-plane, so that A (resp., B, C) lies on a curve $\gamma _A$ (resp., $\gamma _B$, $\gamma _C$) represented by parametric equations of the form $(z,w) = (f_A(t),g_A(t))$ (resp., $(z,w) = (f_B(t),g_B(t))$, $(z,w) = (f_C(t),g_C(t))$), where $f_A$, $g_A$, $f_B$, $g_B$, $f_C$, $g_C$ are constant-degree univariate complex polynomials. Then one can determine, in the algebraic decision-tree model, whether there exists a collinear triple $(a,b,c)\in A\times B\times C$, with $O\left( n^{24/13 + \varepsilon }\right)$ real polynomial sign tests, in expectation, for any $\varepsilon > 0$.

3 Segment Concurrency

We now sketch a subquadratic algorithm, in the algebraic decision tree model, for the segment concurrency problem. We use the notation of Sect. 1.

The Decomposition. Fix a parameter $g \ll n$, put $r := n/g$. We construct a (1/r)-cutting $\varXi _A$ for the segments of A, that is, a partition of the plane into interior-disjoint simplices, the interior of each of which meets at most $n/r = g$ segments of A. Since the segments are pairwise disjoint, we can construct $\varXi _A$ so that it consists of only O(r) trapezoids, each of which is crossed by at most g segments of A. The construction time, in the real-RAM model, is $O(n\log r) = O(n\log n)$; see [10, Theorem 1] for these details. We apply a similar construction for B, and let $\varXi _B$ denote the resulting cutting, with similar properties.

We next overlay $\varXi _A$ with $\varXi _B$, to obtain a decomposition $\varXi$ of the plane into $O(r^2)$ convex polygons of constant complexity. Each cell $\sigma$ of $\varXi$ is identified by a pair $(\tau ,\tau ')$, where $\tau$ and $\tau '$ are the respective cells (simplices) of $\varXi _A$ and $\varXi _B$ whose intersection is $\sigma$. Each cell $\sigma$ of $\varXi$ is crossed by at most $n/r=g$ segments of A and by at most $n/r=g$ segments of B.

Classifying the Segments in a Cell. Let $\sigma = (\tau ,\tau ')$ be a cell of $\varXi$. Call a segment e of A long (resp., short) within $\sigma$ if e crosses $\sigma$ and neither of its endpoints lies in $\sigma$ (resp., at least one endpoint lies in $\sigma$). We apply analogous definitions to the segments of B and to the segments of C.

The high-level structure of the algorithm proceeds as follows. We construct $\varXi _A$ and $\varXi _B$. For each simplex $\tau$ of $\varXi _A$ (resp., $\tau '$ of $\varXi _B$), we compute its conflict list $A_\tau$ (resp., $B_{\tau '}$), which is the set of all segments of A that cross $\tau$ (resp., segments of B that cross $\tau '$). We then form the overlay $\varXi$, and for each of its cells $\sigma = (\tau ,\tau ')$, we compute the set $A_\sigma$ of the segments of $A_\tau$ that cross $\sigma$, and the set $B_\sigma$ of the segments of $B_{\tau '}$ that cross $\sigma$. We partition $A_\sigma$ into the subsets of long and short segments (within $\sigma$), respectively, and apply an analogous partition to $B_\sigma$. We also trace each segment $c\in C$ through the cells of $\varXi$ that it crosses, and form, for each cell $\sigma$ of the overlay, the list $C_\sigma$ of segments of C that cross $\sigma$, partitioned into the subsets of long and short segments. Using standard properties of (1/r)-cuttings, the overall complexity of these sets (of both long and short segments), over all cells $\sigma$, is $O(r^2\cdot n/r) = O(nr) = O(n^2/g)$, and the additional overall cost of constructing them is $O(n^2 \log {n}/g)$.

In this extended abstract we only present the main steps of the analysis for triples in $A \times B \times C$ all of whose segments are long in a cell $\sigma$, the remaining cases (that is, when at least one of these segments is short in $\sigma$) are fairly standard and can be handled by the theory of range search [1]; these steps are presented [6].

Point Location in Planar Arrangements. Passing to the dual plane, the segments of A (resp., B, C), or rather the lines containing them, are mapped to points. We denote the set of points dual to the segments of A (resp., B, C) as $A^*$ (resp., $B^*$, $C^*$). Our goal is to determine whether there exists a collinear triple $(a^*,b^*,c^*) \in A^*\times B^*\times C^*$, so that the corresponding primal segments a, b, c intersect each other (necessarily at the same common point).

We follow the scheme of Sect. 2, let $F(\xi ,\eta ,\zeta )$ be the quadratic 6-variate polynomial whose vanishing expresses collinearity of the three points $\xi$, $\eta$, $\zeta \in \mathbb {R}^2$. Ignoring C for the time being, we preprocess A and B into a data structure that we will then search with the points dual to the (lines containing the) segments of C. For each $a\in A$, $b\in B$, we define the line

$$ \gamma _{a,b} = \{ \zeta \in \mathbb {R}^2 \mid F(a^*,b^*,\zeta ) = 0 \} , $$

which is the line passing through $a^*$ and $b^*$. Let $\varGamma _0$ denote the set of these $O(n^2)$ lines. Our goal is to determine whether any point $c^*\in C^*$ lies on any of the lines $\gamma _{a,b}$, and then also make sure that the corresponding primal segments a, b, c intersect each other (it is possible that a, b, c are long in a cell $\sigma$ but intersect outside $\sigma$; this scenario is handled using range search, as shown in [6]). This requires to preprocess the arrangement $\mathcal {A}(\varGamma _0)$ into a point-location data structure, and then search that structure with each $c^*\in C^*$.

Fredman’s Trick and Batched Point Location. As above, a naïve implementation of this approach would be way too expensive. Instead, we return to the partitions $\varXi _A$, $\varXi _B$ and $\varXi$, and iterate over all cells $\sigma = (\tau ,\tau ')$ of $\varXi$, defining

$$ \varGamma _\sigma = \{\gamma _{a,b} \mid (a,b) \in A_\sigma \times B_\sigma \} . $$

In principle, we want to construct the separate arrangements $\mathcal {A}(\varGamma _\sigma )$, over the cells $\sigma$, preprocess each of them into a point-location structure, and search with each $c^*\in C^*$ in the structures that correspond to the cells of $\varXi$ that c crosses. This is also too expensive if implemented naïvely. We circumvent it, using Fredman’s trick, as follows.

Consider the step of constructing $\mathcal {A}(\varGamma _\sigma )$ for some fixed cell $\sigma$. We observe that it suffices to construct and sort the vertices of $\mathcal {A}(\varGamma _\sigma )$ in the x-direction, and also to sort the lines of $\varGamma _\sigma$ at $x=-\infty$ (see [5, 6] for details). The rest of the construction, including the preprocessing of the arrangement into an efficient point-location data structure, costs nothing in the algebraic decision-tree model, as it is based on a sweeping procedure on the lines of $\varGamma _\sigma$, and all the input-dependent data that the sweep requires has already been computed by the steps just mentioned, so the sweep does not have to access A or B explicitly; Searching the structure with any $c^*\in C^*_\sigma$ (that is, applying a point location query) takes $O(\log g)$ time, since $\varGamma _\sigma$ consists of only $g^2$ lines.

Consider then the step of sorting the vertices of $\mathcal {A}(\varGamma _\sigma )$. In this step we need to compare the x-coordinates of pairs of these vertices. In general, such a comparison involves four pairs $(a_i,b_i) \in A_\sigma \times B_\sigma$, $i=1,\ldots ,4$, where $\gamma _{a_1,b_1}$ and $\gamma _{a_2,b_2}$ intersect at one of the vertices and $\gamma _{a_3,b_3}$ and $\gamma _{a_4,b_4}$ intersect at the other vertex. Roughly speaking, such a comparison can be expressed as testing the sign of some constant-degree 16-variate polynomial $G(a_1,a_2,a_3,a_4;b_1,b_2,b_3,b_4)$.

We now apply Fredman’s trick. We fix a cell $\tau$ of $\varXi _A$. For each quadruple $(a_1,a_2,a_3,a_4) \in A_\tau ^4$, we define the surface

$$ \psi _{a_1,a_2,a_3,a_4} = \{ (b_1,b_2,b_3,b_4) \in \mathbb {R}^8 \mid G(a_1,a_2,a_3,a_4;b_1,b_2,b_3,b_4) = 0 \} , $$

and denote by $\varPsi$ the collection of these surfaces, over all cells $\tau$. We have $|\varPsi | = O((n/g)\cdot g^4) = O(ng^3)$. Similarly, we let P denote the set of all quadruples $(b_1,b_2,b_3,b_4)$, for $b_1,b_2,b_3,b_4 \in B_{\tau '}^4$, over all cells $\tau '$ of $\varXi _B$. We have $|P| = O(ng^3)$.

We apply a batched point location procedure to the points of P and the surfaces of $\varPsi$. The output of this procedure tells us the sign of $G(a_1,a_2,a_3,a_4;b_1,b_2,b_3,b_4)$, for every pair of quadruples $(a_1,a_2,a_3,a_4) \in A_\tau ^4$, $(b_1,b_2,b_3,b_4) \in B_{\tau '}^4$, over all pairs of cells $(\tau ,\tau ')\in \varXi _A\times \varXi _B$, and these signs allow us to sort the vertices of the arrangements $\mathcal {A}(\varGamma _\sigma )$, for all cells $\sigma$ of $\varXi$, at no extra cost in our model. In a main technical step in [6], based on the recent multilevel polynomial partitioning technique of Agarwal et al. [2, Corollary 4.8], we show:

Lemma 2

One can complete the above sorting step, in the algebraic decision tree model, in $O\left( (ng^3)^{16/9+\varepsilon }\right)$ randomized expected time, for any prescribed $\varepsilon > 0$, where the constant of proportionality depends on $\varepsilon$.

Searching with the Elements of C and Wrapping Up. We now need to search the structures computed at the preceding phase with the dual points of $C^*$. Each such point $c^*$ comes from a segment $c\in C$, which crosses only $O(r) = O(n/g)$ cells of $\varXi$ (once again, this follows from standard properties of (1/r)-cuttings). For each of these cells $\sigma$, we need to locate $c^*$ in the arrangement $\mathcal {A}(\varGamma _\sigma )$. There are $O(nr) = O(n^2/g)$ such segment-cell crossings, and each resulting search takes $O(\log g)$ time, using a suitable point-location data structure for each such arrangement, for a total of ${\displaystyle O\left( \frac{n^2\log g}{g} \right) }$ time. The cost of the overall algorithm is thus

$$ O\left( (ng^3)^{16/9+\varepsilon } + \frac{n^2\log g}{g} \right) . $$

We (nearly) balance this bound by taking $g = n^{2/57}$, and conclude that the cost of this procedure, in the algebraic decision-tree model, is $O(n^{112/57+\varepsilon })$, for any $\varepsilon >0$. In summary, we have shown:

Theorem 2

Given three sets A, B, C, each consisting of n line segments in the plane, where the segments of A, B are pairwise disjoint, one can determine whether there exists a concurrent triple of segments $(a,b,c) \in A\times B\times C$, in the algebraic decision-tree model, with $O(n^{112/57+\varepsilon })$ polynomial sign tests (in expectation), for any $\varepsilon > 0$.

Discussion and Open Problems. In spite of the progress in the study of collinearity testing in the algebraic decision tree model [5,6,7], as well as in the RAM model [7, 9], the unrestricted setting of collinearity testing (that is, where A, B, C are collections of arbitrary points in the plane) has still remained elusive in both models of computation. Moreover, we are not aware of subquadratic solutions in either model even for the case where one set of points is one-dimensional and the other two are unrestricted.

Given the subquadratic solutions for 3sum [16, 18] in both models of computation, one may hope that this should also be the case for collinearity testing, as well as other geometric 3SUM-hard problems (see problems (i)–(iii) in Sect. 1). Unfortunately, we are still facing a gap between 3sum and its geometric counterparts. Perhaps, this is because the sign test required for 3sum is a linear function of the input, whereas other geometric 3sum-hard problems do not have this property. In particular, for collinearity testing, the basic operation one needs to apply is orientation testing, which corresponds to a quadratic inequality in the input point coordinates, and thus does not benefit from the linear structural properties of 3sum.