A Comparison of the Model Parameter Estimations from Self-Potential Anomalies by Levenberg-Marquardt (LM), Differential Evolution (DE) and Particle Swarm Optimization (PSO) Algorithms: An Example from Tamış-Çanakkale, Turkey

Abstract

In geophysics, it is particularly important to choose an adequate optimization algorithm for parameter estimation. In this study, the success of Levenberg-Marquardt (LM), Differential Evolution (DE) and Particle Swarm Optimization (PSO) inversion algorithms has been tested by applying to the synthetic and field self-potential (SP) anomalies. Even though it is not preferred to compare derivative-based algorithms with metaheuristics, thanks to a LM-based limitation procedure first proposed in this study, a comparison could be realized. First, a synthetic SP data have been inverted by LM, DE and PSO algorithms. Then, SP field data set collected from Tamış-Çanakkale, Turkey was evaluated by the same algorithms. The estimated model parameters by these algorithms were compared with each other. We also inverted vertical electrical sounding (VES) data set collected from the same region, and an earth model was constructed by using both SP and VES methods. The results from each geophysical method point out the same location for a fault. Based on these studies, it can be concluded that DE, PSO, and LM algorithms may be confidently used in SP modelling studies.

4.1 Introduction

Electrical methods are frequently used to detect the location of systems including the groundwater. Self-potential (SP) and vertical electrical sounding (VES) are proven methods to be successful in groundwater explorations such as groundwater pollution studies, fresh, saltwater interference problems, and geothermal exploration (Ogilvy et al. 1969; Corwin and Hoover 1979; Schiavone and Quarto 1984; Hamzah et al. 2007; Karlık and Kaya 2001).

The VES technique is used to determine the resistivity changes from the surface to the depth. It is mainly based on the principle of measuring the response of the earth to an electric current applied to the ground. The VES method is useful in determining the depth, geometry and resistivity of the layers (Hamzah et al. 2007; Kaya et al. 2015).

Self-potential is an electrical phenomenon that is so easy to measure but it is also so hard to determine the source mechanism. These mechanisms can be specified as electro-kinetic (streaming), thermo-electric, diffusion, and electro-chemical potential. Self-potential method can be applied for determining the possible faults containing fluid in the study area (Yüngül 1950; Fitterman and Corwin 1982; Corwin 1990; Monteiro Santos et al. 2002; Revil et al. 2003). Potential anomalies created by fluid-containing faults are generally generated by electro-chemical sources.

SP anomalies can be analysed by different approaches. Since the use of the graphic-based evaluation methods (Yüngül 1950; Paul 1965; Rao et al. 1970), a new generation numerical methods have been developed for the evaluation of SP data in parallel with developing computer technology: The Fourier, Hartley, Hilbert Transforms and Wavelet analysis (Sundararajan et al. 1990; Asfahani et al. 2001; Gilbert and Pessel 2001; Al-Garni and Sundararajan 2011; Di Maio et al. 2016), Euler Deconvolution (Agarwal and Srivastava 2009; Sındırgı and Özyalın 2019), Gradient and Derivative Analysis (Abdelrahman et al. 1997, 1998, 2006; El-Araby 2004; Essa et al. 2008; Sındırgı et al. 2008; Abedi et al. 2012; Mehanee 2015), tomographic approach (Di Maio and Patella 1994; Patella 1997; Revil et al. 2001; Juliano et al.,2002), Artificial Neural Network algorithms (El-Kaliouby and Al-Garni 2009; Kaftan et al. 2014), and metaheuristic algorithms including Particle Swarm Optimization (PSO) (Juan et al. 2010, Monteiro Santos 2010; Göktürkler et al. 2016; Ekinci et al. 2019; Pekşen et al. 2011), Simulated annealing (SA) (Sharma 2012; Biswas and Sharma 2014, 2015), Genetic Algorithm (GA) and Differential Evaluation (DE) (Abdelazeem and Gobashy 2006; Fernández-Martínez et al. 2010; Göktürkler and Balkaya 2012; Di Maio et al. 2017; Ekinci et al. 2019).

In this study, a synthetic (noise-free and noisy) and a field SP data set (collected from Tamış-Çanakkale, Turkey) have been evaluated by three algorithms including the Levenberg-Marquardt (LM), PSO and DE. Also, to be able to compare LM to the metaheuristics, a new initial model selection process for LM was developed. Then, the estimated parameters have been compared with each other. The VES data set, collected from the same location, is also inverted, and the subsurface model for Tamış-Çanakkale anomaly has been constructed by combining the results from both VES and SP data.

4.2 Materials and Methods

4.2.1 Formulation of the SP Anomaly

Let $V\left( {x,x_0 ,z_0 ,K, \theta , q} \right)$ be the SP anomaly produced by a simple polarized causative body observed at any point on the earth’s surface (Fig. 4.1). Formulation of the SP anomaly (Yüngül 1950; Murty and Haricharan 1985) can be written as;

Fig. 4.1

An infinitely long horizontal cylinder model and its noise-free and noisy anomalies (The model parameters and their corresponding values are listed on the figure)

$$V\left( {x,x_0 ,z_0 ,K, \theta, q} \right) = K\frac{{\left( {x - x_0 } \right)cos\theta + z_0 sin\theta }}{{\left[ {\left( {x - x_0 } \right)^2 + z_0^2 } \right]^q }}$$

(4.1)

where $K$ is the electric dipole moment, $x$ is the horizontal distance, $x_0$ is the distance from the origin, $z_0$ is the depth of the centre of the body, $\theta$ is the polarization angle, and $q$ is the shape factor. The shape factor is dimensionless and its value for a sphere, horizontal cylinder, and semi-infinite vertical cylinder are 1.5, 1.0, and 0.5, respectively. The shape factor becomes near to zero as the structure approaches a horizontal sheet.

4.2.2 Algorithms

4.2.2.1 Levenberg-Marquardt (LM) Inversion Algorithm

Nonlinear least squares problems can be solved using the LM algorithm. The solution from the LM algorithm is not necessarily to be a global minimum. Generally, the LM algorithm is often preferred to Gauss-Newton and Steepest-Descent methods because it guarantees good convergence and non-singularity of the solution. Kenneth Levenberg introduced this algorithm in (1944), and Donald Marquardt (1963) improved it subsequently.

Generalized formulation of forward modelling problems can be written as,

$${\varvec{d}} = {\text{G}}\left( {\varvec{m}} \right)$$

(4.2)

where ${\varvec{d}}$ is the M-dimensional vector of observations and, ${\varvec{m}}$ is a vector of model parameters (in previous study model parameters are $x_0 ,z_0 ,K, \theta, q$) with the size of N×1. ${\text{G}}\left( {\varvec{m}} \right)$ is a nonlinear function predicted by the model. Model parameter ${\varvec{m}}$ can be written by

$${\varvec{m}} = {\varvec{m}}_0 + \Delta {\varvec{m}}$$

(4.3)

where ${\varvec{m}}_0$ is the initial model and $\Delta {\varvec{m}}$ is the model parameters update.

Minimizing the model perturbation to the Gauss-Newton solution can be fulfil via minimizing the objective ${\text{F}}$,

$${\text{F}} = ({\varvec{d}} - {\text{G}}({\varvec{m}}_0 + \Delta {\varvec{m}})) + {{\lambda }}\Delta m^2$$

(4.4)

The sensitivity (Jacobian) matrix $J$(M×N) can be written as,

$$J = \left[ {\begin{array}{*{20}c} {\frac{\partial G_i \left( m \right)}{\partial m_1 }} & \ldots & {\frac{\partial G_i \left( m \right)}{\partial m_N }} \\ \vdots & \ddots & \vdots \\ {\frac{\partial G_M \left( m \right)}{\partial m_1 }} & \ldots & {\frac{\partial G_M \left( m \right)}{\partial m_N }} \\ \end{array} } \right]$$

and using sensitivity matrix, $\Delta {\varvec{m}}$ can be defined as

$$\Delta {\varvec{m}} = \left[ {{\varvec{J}}^{\varvec{T}} {\varvec{WJ}} + {\varvec{I}}} \right]^{ - 1} {\varvec{J}}^{\varvec{T}} {\varvec{W}}\left( {{\varvec{d}} - {\text{G}}\left( {{\varvec{m}}_0 } \right)} \right)$$

(4.5)

where ${\varvec{I}}$ is the identity matrix and $\lambda$ is a damping factor shows the effect of model perturbation. If $\lambda$ is small, Eq. (4.4) will become equal to Gauss-Newton solution equation. Generally, the initial value of $\lambda$ is chosen large. If misfit is smaller than previous iteration ${{\lambda }}$ is reduced, if not it is increased.${\varvec{ W}}$ is a positive definite matrix and defined as (Jupp and Vozoff 1975)

$${\varvec{W}} = \frac{1}{\text{M}}{\varvec{d}}_i^2 ,\,\,\,i = 1,{ 2}, \ldots ,{\text{ M}}$$

(4.6)

RMSE, which means the standard deviation of the residuals, is calculated as follows (Barnston 1992):

$${\text{RMSE}} = \sqrt {\frac{1}{\text{M}}\mathop \sum \limits_{i = 1}^{\text{M}} \left( {{\varvec{d}}_i - {\text{G}}\left( {\varvec{m}} \right)_i } \right)^2 }$$

(4.7)

4.2.2.2 Particle Swarm Optimization (PSO) Algorithm

The PSO was proposed in 1995 by the authors Kennedy and Eberhart. It is a population-based metaheuristic technique and is based on the social behaviour of animals (birds, fishes). While each individual searching for the solution in PSO is called a particle, the population of the particles is called a swarm. Particles move according to two important parameters in the search space. Pbest is the particle’s best position found so far and Gbest is global best position found thus far in the entire swarm. According to these definitions, basic steps of the PSO algorithm can be listed as follows: (1) The algorithm is initialized by placing the particles with random velocities (v) and positions (x) in the search space. (2) The fitness value is used to understand how close a particle is to the solution. It is calculated for each particle. (3) Individual and global bests are updated by comparing them with the previous ones (pbest_i) and equalized to the current value of the fitness. Then the particle’s prior best position ($p_i$) is assumed to be as the current position ($x_i$). The determined position of the particle with the best fitness value so far is assigned as the global best ($g_i$). (4.4) New velocity and position values are updated for each particle. (4.5) Stopping criterion is checked, if could not reach the threshold values, it is continued with step (4.2) (Fig. 4.2).

Fig. 4.2

The flow chart of the particle swarm optimization (Adopted from http://mnemstudio.org/particle-swarm-introduction.htm)

The position and velocity of a particle $i$ can be updated as follows ($i$ =  1, 2, 3, …, N);

$$v_i = \omega v_i + c_1 rand()\left( {p_i - x_i } \right) + c_2 rand()\left( {g_i - x_i } \right)$$

(4.8)

$$x_i = x_i + v_i$$

(4.9)

where $w$ is a weighting factor ($0 < \omega < 1$) known as inertia weight; $c_1$ and $c_2$ are individual and social behaviour coefficients, respectively. rand() is a function to generate pseudo-random numbers within [0, 1]. The updates of position and velocity of each particle end after reaching the stopping criterion (Kennedy and Eberhart 1995; Shi and Eberhart 1998; Poli et al. 2007; Luke 2009; Salmon 2011). In the light of this information, the values of the parameters used in PSO algorithm in this study are listed in Table 4.1.

Table 4.1 The values of the parameters used in PSO and DE algorithms

4.2.3 Differential Evolution (DE) Algorithm

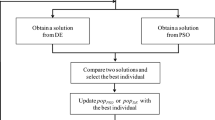
DE algorithm (Storn and Price 1995, 1997) is a population-based optimization algorithm and its applications in geophysics have increased in recent years. Different from the conventional gradient-based inversion methods, a good starting model is not a requirement for the DE algorithm to reach the global minimum. Three control parameters are the only requirements: number of population ($Np$), weighting factor (mutation constant, $F$) and crossover probability ($Cr$). The initial population is generated randomly in the initialization stage of the algorithm, then in the evolution stage population evolves from one generation to the next through mutation, crossover and selection operations until the termination criterion is satisfied (Fig. 4.3) (Li and Yin 2012; Ekinci et al. 2016).

Fig. 4.3

The flow chart of the DE optimization algorithm (from Ekinci et al. 2016)

The target vectors can be defined as $x_{i,G} = \left( {x_{i,G}^1 , x_{i,G}^2 , \ldots , x_{i,G}^D } \right), i = 1,2, \ldots ,Np,$ where $G$ is the current generation, and $D$ is the number of parameters ($j = 1,2, \ldots ,D)$. The  $j$th component of the  $i$th vector can be generated as follows:

$$x_{i,G}^j = x_l^j + rand\left( \right).\left( {x_u^j - x_l^j } \right)$$

(4.10)

where $rand\left( \right)$ symbolizes pseudo-random number between [0,1), also l and u are the lower and upper limits for each parameter.

The evolution cycle includes mutation, crossover and selection operations (Fig. 4.3). Mutation operation is run to form a donor (mutant) vector, $v_{i,G} = \left( {v_{i,G}^1 , v_{i,G}^2 , \ldots ., v_{i,G}^D } \right), i = 1,2, \ldots .,Np,$ for each target vector. Generally, there are five differential mutation strategies (Li and Yin 2012). Previous studies (Balkaya 2013; Ekinci 2016; Ekinci et al. 2017, 2019) are indicated that DE/best/1/bin supplies better solutions with a good estimation accuracy and less computing time for the inversion of geophysical data sets. This strategy is preferred in the DE optimizations of the synthetic and field SP data in this work. Mutation operation for this strategy can be defined as below:

$$v_{i,G} = x_{best,G} + F.\left( {x_{r_{1,G}^i } - x_{r_{2,G}^i } } \right)$$

(4.11)

Here, $x_{best,G}$ is the best individual vector in the population at generation $G$, and ($x_{r_1 }$, $x_{r_2 }$) is a pair of differential vectors.

Then, the trial vector ($u_{i,G}$) is produced by a recombination of the donor vector $\left( {v_{i,G} } \right)$ and the target vector ($x_{i,G}$). The trail vector of the $j$th particle in the $i$th dimension at the $G$ th iteration can be written as:

$$u_{i,G}^j = \left\{ {\begin{array}{*{20}c} {v_{i,G}^j } & {if\,\left( {rand(0,1) \le Cr\,or\,j = j_{rand} } \right)} \\ {x_{i,G}^{jk} } & {otherwise.} \\ \end{array} } \right.,\,\,\,j = 1,2, \ldots ,D$$

(4.12)

where $Cr$ is a crossover rate in the range [0,1] and $j_{rand}$ is a randomly chosen integer in the range [$1,D$].

Selection operator is employed to select the next generation between the trial and target vectors.

$$x_{i,G + 1} = \left\{ {\begin{array}{*{20}c} {u_{i,G} if f(u_{i,G} \le f\left( {x_{i,G} } \right)} \\ {x_{i,G} otherwise.} \\ \end{array} } \right.$$

(4.13)

If the new generated trial vector gives a better fitness value than its previous one, the target vector is updated by using Eq. 13, else it is kept in the present population. The fitness value is calculated for each particle from the objective function, and the particle with the best value is selected as the solution in the current generation.

Evolution cycle ends when a predefined termination criterion is met. This criterion can be error energy, and/or maximum number of $G$. So, the vector yielding the lower error energy value is chosen as an optimum solution for the optimization problem. In this study both termination criteria were used.

For the number of $M$ data, the objective function (Relative Error) can be calculated as follows:

$$\phi = \frac{1}{M}\mathop \sum \limits_{i = 1}^M \left( {g_i^{obs} - g_i^{cal} } \right)^2$$

(4.14)

where $g^{obs}$ and $g^{cal}$ are the observed and calculated data, respectively, and $i$ indicates the observations. The square root of the Eq. (4.14) gives the Root Mean Square (RMS) value.

4.2.4 Parameter Estimation Studies

Synthetic noise-free and noisy (5%) infinitely long horizontal cylinder-shaped SP model anomalies are generated to test the parameter solution quality of the proposed algorithms. Then, to better analyse the pertinence of the suggested algorithms on real data, they applied to four SP profile data, which are selected from Tamış-Çanakkale SP anomaly.

The values of the DE and PSO parameters used during the test and field studies are summarized in Table 4.1. The codes for all algorithms are written in MATLAB^® (ver.R2019a) software with a 3.10 GHz compatible computer with 6 GB memory.

4.2.5 Synthetic Examples

First, to test the parameter solution quality of the proposed algorithms, synthetic noise-free and noisy anomalies based on an infinitely long horizontal cylinder-shaped model were generated. The parameters used for this model were selected as $K$ = 100 000 mV.m, $z_0$ = 500 m, $x_0$ = 950 m, $x_0$ = 145^o, $q$ = 1, and profile length is 2000 m (assuming 50 m sampling interval) (Fig. 4.1). To calculate the noisy synthetic model, 5% Gaussian noise, were added to the synthetic data (Fig. 4.1). Thereafter the proposed algorithms have been applied for estimating the model parameters of the SP source body.

Local optimization (gradient-based) algorithms requires choose the initial parameter values close to the true solution, otherwise the algorithm may end up with a local minimum instead of a global one. To cope with this problem, a new approach to assign the initial values to the LM inversion algorithm has been introduced in this study. For this purpose, similar to the population-based metaheuristic methods, a set including 100 different models for SP have been generated randomly within certain ranges (Table 4.2), then objective function values for each model have been calculated by forward solution. Among these models the one with the lowest error energy has been taken as the initial model for LM. Finally, a LM inversion has been carried based on this initial model. Optionally this procedure may be repeated several times (Göktürkler and Balkaya 2012; Li and Yin 2012; Balkaya 2013), the one with the lowest error energy can be assigned as the solution.

Table 4.2 Parameter ranges used to select LM algorithm initial parameters and generate the initial models by PSO and DE of noise-free and noisy synthetic SP anomalies

Table 4.3 illustrates the initial models by the above mentioned routine for LM algorithm for noise-free and noisy SP data sets. As can be seen from the table the noisy data set produced larger RMS value as expected. The Tables 4.4 and 4.5 give the results of the parameter estimations by the LM, DE and PSO with both the noise-free and noisy SP anomalies. The comparisons of the synthetic and calculated anomalies are illustrated in Fig. 4.4. When Tables 4.4 and 4.5 are compared for noise-free data (Fig. 4.4a–c), it is observed that the algorithms generated similar results in the vicinity of true model parameters. On the other hand, the results for noisy data sets (Fig. 4.4d–f) are deviated from the true model parameters. Based on Fig. 4.4 and Tables 4.4 and 4.5, it can be said that the DE algorithm is relatively better than the others for both noise-free and noisy data sets. The behaviour of parameters and error energy variations of DE solutions are only presented in figure form (Fig. 4.5), in order to save some space in the text.

Table 4.3 Estimated initial SP model parameters for LM algorithm by the proposed approach. This approach has been repeated 10 times, and the model having the lowest error energy has been taken as the initial model

Table 4.4 The best solutions from noise-free synthetic data set by three algorithms at the end of 10 independent runs

Table 4.5 The best solutions from noisy synthetic data set by three algorithms at the end of 10 independent runs

Fig. 4.4

Synthetic data: a–c Noise-free, d–f noisy data. Calculated anomalies from DE, PSO and LM algorithms (The estimated best-fitting parameters are listed on the figures)

Fig. 4.5

The convergence characteristics of the DE algorithm. a Amplitude $K$, b the distance from the origin $x_0$, c depth $z_0$, d polarization angle $\theta$, e Shape factor $q$

Fig. 4.6

Geological map of the study area (adapted and modified from Karacık and Yılmaz 1998; Sözbilir et al. 2018)

4.2.6 Field Example

Çanakkale is tectonically active region on the Alpine-Himalayan Mountain Belt that corresponds to the northward movement of the Arabian plate and located in the middle segment of the NAF zone (Altınok et al. 2012). The main fault systems of the region are Balabanlı, Kestanbol, Tuzla and Edremit Faults. There are a number of geothermal fields (Tuzla, Palamutova, Kestanbol, Küçükçetmi geothermal fields etc.) related with these faults in the study area. The field data sets including SP and VES in this study were collected near a segment of the Tuzla fault system. It represents the transition zone between the Beydağı Horst and Tuzla Basin. Geological units of the study area are the Balabanlı volcanics, Dededağ formations, and Karadağ metamorphics. The Balabanlı volcanics consist of pyroclastic rocks such as rhyodacitic ignimbrites and lavas. The Dededağ formation contains andesitic and trachyandesitic lavas and flow-breccias. The Balabanlı volcanics and Dededağ formation lie over the metamorphic basement (Karacık and Yılmaz 1998; Sözbilir et al. 2018) (Fig. 4.6).

The SP contour map and the superimposed locations of the VES measurements are shown in Fig. 4.7a. The VES method was carried out at five stations using the Schlumberger array. They have been inverted by a software based on a least-squares approach (IPI2WIN), and the inverted resistivity values can be seen in Fig. 4.7b. They indicate two distinct units. The first one is the surface volcanics characterized by low resistivities (10–50 $\Omega {\text{m}}$), and the second one is the metamorphic units (having resistivities of 50–200 $\Omega {\text{m}}$) forming the basement. It is seen that the depth to the basement ranges between approximately 350-600 m from the station VES-1 to VES-4, and the depth to the basement rock is approximately 180 m at the station VES-5. The difference between the depths may be explained as the effect of the Tuzla Fault System.

Fig. 4.7

a SP anomaly map, location of selected SP profiles (P1, P2, P3, and P4), VES stations (VES-1, VES-2, VES-3, VES-4, and VES-5), and estimated SP body locations (stars). b Layered earth models obtained from VES studies

Four different profiles (P1, P2, P3, and P4) were selected for inversion (Fig. 4.7a). They have been evaluated by LM, PSO, and DE algorithms. Search spaces for these algorithms are given in Table 4.6. The procedure of assigning initial values for the LM inversion algorithm introduced in the present study (see Sect. 3.2) has also been applied to the Tamış-Çanakkale data set (Table 4.7). The same values for the algorithm-based parameters as the synthetic data evaluation were also used for the field data set. The measured and calculated data from SP profiles are given in Figs. 4.8, 4.9, 4.10 and 4.11. Tables 4.8, 4.9, 4.10 and 4.11 show the results of the model parameter estimations from the field data sets. Similar to the synthetic data, LM, PSO, and DE algorithms have been executed 10 times and the one has the minimum RMS value has been selected as the best-fitting model (Tables 4.8, 4.9, 4.10 and 4.11). Although DE and PSO algorithms have smaller RMS errors than does LM with the help of the initial model determination procedure developed for the LM algorithm in this study, it is seen that the parameters are also successfully predicted with LM. When the tables are examined, it can be seen that all algorithms provided similar $z_0$ values (~500–700 m) for the SP profiles, except profile P4. On the other hand, the algorithms have determined a smaller $z_0$ values (~185 m) for P4. The calculated average depths ($z_0$) and origin to distances (${\text{x}}_0^{{\text{P}}1}$, ${\text{x}}_0^{{\text{P}}2}$, ${\text{x}}_0^{{\text{P}}3}$ and ${\text{x}}_0^{{\text{P}}4}$) of the SP body using by the algorithms are shown in Fig. 4.12. It is seen that there is a depth difference between the points ${\text{x}}_0^{{\text{P}}3 }$ and ${\text{x}}_0^{{\text{P}}4}$. Considering that the study area is in a horst-graben transition boundary, this difference may be related with the Tuzla Fault System. These findings are accordance with those of VES studies.

Table 4.6 Parameter ranges used in LM, PSO and DE optimizations of the Tamış-Çanakkale anomalies

Table 4.7 The initial SP parameters by the proposed approach in the present study for LM inversion of the Tamış-Çanakkale data set. This approach has been repeated 10 times, and the model having the lowest error energy has been taken as the initial model

Fig. 4.8

a DE, b PSO and, c LM inversions of P1-profile

Fig. 4.9

a DE, b PSO and, c LM inversions of P2-profile

Fig. 4.10

a DE, b PSO and, c LM inversions of P3-profile

Fig. 4.11

a DE, b PSO and, c LM inversions of P4-profile

Table 4.8 The best solutions from Tamış-Çanakkale P1 data set by three algorithms at the end of 10 independent runs

Table 4.9 The best solutions from Tamış-Çanakkale P2 data set by three algorithms at the end of 10 independent runs

Table 4.10 The best solutions from Tamış-Çanakkale P3 data set by three algorithms at the end of 10 independent runs

Table 4.11 The best solutions from Tamış-Çanakkale P4 data set by three algorithms at the end of 10 independent runs

Fig. 4.12

Estimated source depths (dots) from the inversion of the SP profile data

When we combine the geological units of the study area (Fig. 4.6) with the SP and VES findings, we can say that the surface volcanics become thinner and the metamorphic basement units reach the shallower depths in the east and northeast of the study area. In the light of comparison of two geophysical methods we can said that the depth values estimated from SP and VES methods are in good agreements with each other.

4.3 Conclusions

In this study, the model parameters of a polarized body have been determined by a derivative-based (LM), and two population-based optimization algorithms (DE and PSO), and the results are compared. Even though it is not preferred to compare derivative-based algorithms with metaheuristics, a comparison could be realized by a LM-based limitation procedure introduced in this study. By this limitation procedure, the misfit values from the LM algorithm have been observed as being close to those from DE and PSO for both synthetic and field data sets.

In this study, Tamış-Çanakkale SP anomaly from Turkey was also evaluated with the mentioned algorithms and the solutions of them compared to each other. RMS value of the LM solution is relatively higher than the others. Comparison of the estimated SP model parameters to the VES sections has indicated that the surface volcanics become thinner and the metamorphic basement units reach the shallower depths in the east and northeast of the study area.

As a result, the solutions by DE, PSO, and LM (with limitation procedure introduced by the present study) are represented by being in good agreement with each other and they have the ability to converge from local best to the general best, can be successfully applied in determining SP model parameters. The LM algorithm, after the process introduced by the present study, has yielded results comparable with the other algorithms PSO and DE. It also displayed better convergence characteristics after the proposed process.