The Dynamics Analysis of a Spatial Linkage with Flexible Links and Imperfect Revolute Joints

Abstract

The algorithm for generating the dynamics equations of the two-dof spatial linkage is considered in the paper. The presented linkage is composed of the five rigid or flexible links which form a serial closed-loop kinematic chain. It is assumed that revolute joints can be imperfect. The joint coordinates together with homogeneous transformation matrices are applied to generate the equations of motion. The dynamics equations are derived using the Lagrange equations of the second kind. The presented algorithm gives the opportunity to generalize it for any linkages with a tree closed-loop kinematic structure. The flexible links are modelled by means of the Rigid Finite Element Method in the sense of the modified approach. The author’s spatial model of the revolute joint with radial and axial clearance is applied to take into account clearance effects. In this model, a revolute joint is discretized by means of contact elements located on the cylindrical and frontal surfaces of the journal and bearing. Such an approach allows us to detect automatically collisions in many points of the contacting surfaces. The normal contact force is calculated using the Nikravesh-Lankarani formula which is an extension of the classic Hertz model because it additionally takes into account dissipation of the energy. The LuGre friction model is applied to model friction phenomenon in joints. In numerical simulations, an interaction between the links’ flexibility and clearance in the joint during the motion of the linkage is analyzed.

1 Introduction

The clearance in joints can be the result of structural assumptions or the effect of wearing parts. Simulation models of dynamics of linkages with clearance effects allow to better understand their behavior, as well as to estimate the values of impulse forces which increase the dynamic forces acting on the system. In addition, thanks to these models it is possible to determine the limit value of the clearance at which further operation can lead to damage of the system. Paper [1] shows that the flexibility of links has a significant impact on the behavior of linkages with the clearance in joints. The results presented there show that the flexibility can lead to a significant reduction of the impulse forces caused by the impact of the journal and bearing.

In the paper, it is assumed that the clearance can exist only in the revolute joints. There are many papers devoted to the clearance model of the revolute joints [1,2,3,4,5,6,7]. These models can be divided into two main groups: planar [2, 3] and spatial [1, 4,5,6,7], related to how the motion of the journal and bearing is described. Additionally, they can analyze only the radial clearance [2, 3] or they can take into account interaction between the radial and axial clearance [1, 4,5,6,7].

The dynamics model of the two-dof RPSUP linkage is presented in the paper. This model takes into account the flexibility of the link and the clearance in the revolute cut-joint. The kinematics of the linkage is described using the formalism of the joint coordinates and homogeneous transformation matrices. The Rigid Finite Element Method [8] is used to discretize the flexible coupler. The author’s spatial model of the revolute joint with the radial and axial clearance is proposed. In these model contacting surfaces are discretized by means of the contact elements for which the normal and tangent contact forces are calculated. The impulse force in the clearance joint is modeled using the Nikravesh-Lankarani formula [9] and friction is modeled by means of the LuGre friction model [10]. In numerical simulations, the influence of the crank velocity and the clearance in the revolute cut-joint on the slider acceleration is analyzed.

2 Dynamics Model of the Two-dof RPSUP Spatial Linkage

The RPSUP linkage containing five links is shown in Fig. 1. The linkage is divided at cut-joint R and as a result, the two open-loop kinematic chains are obtained (c ∈ {1, 2}). The first chain contains three links $\left({n}_l^{(1)}=3\right)$ whilst the second chain forms two links $\left({n}_l^{(2)}=2\right)$. In the proposed model, it is assumed that the clearance is considered only in the cut-joint R.

Fig. 1

Model of the RPSUP linkage

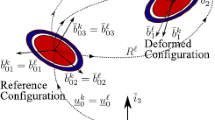
It is also assumed that coupler (1, 3) can be flexible and the Rigid Finite Element Method is used to discretize its. As result, the coupler is replaced by the set of rigid finite elements (rfe) interconnected by means of the set of dimensionless and massless spring-damping elements (sde) (Fig. 2).

Fig. 2

Generalised coordinates

2.1 The Formalism of Generalised Coordinates and Homogeneous Transformation Matrices

The kinematics of the linkage considered is defined by means of the joint coordinates and homogeneous transformation matrices (Fig. 2).

The generalised coordinates vectors defined for each open-loop kinematic chain have the following form:

$$ {\mathbf{q}}^{(1)}={\left({q}_i^{(1)}\right)}_{i=1,\dots, {n}_{dof}^{(1)}}={\left[{\psi}^{\left(1,1\right)}\kern0.5em {z}^{\left(1,2\right)}\kern0.5em {\psi}^{\left(1,3,0\right)}\kern0.5em {\theta}^{\left(1,3,0\right)}\kern0.5em {\varphi}^{\left(1,3,0\right)}\kern0.5em {\tilde{\mathbf{q}}}_f^{\left(1,3\right)}\right]}^T, $$

(1.1)

$$ {\mathbf{q}}^{(2)}={\left({q}_i^{(2)}\right)}_{i=1,\dots, {n}_{dof}^{(2)}}={\left[\begin{array}{cc}{z}^{\left(2,1\right)}& {\psi}^{\left(2,2\right)}\end{array}\right]}^T, $$

(1.2)

where: ${\tilde{\mathbf{q}}}_f^{\left(1,3\right)}=\left\{\begin{array}{cc}\varnothing & \mathrm{if}\kern0.34em \mathrm{coupler}\kern0.17em \mathrm{rigid},\kern0.6em \\ {}{\left[\begin{array}{ccccc}{\tilde{\mathbf{q}}}^{{\left(1,3,1\right)}^T}& \cdots & {\tilde{\mathbf{q}}}^{{\left(1,3,r\right)}^T}& \cdots & {\tilde{\mathbf{q}}}^{{\left(1,3,{n}_{rfe}^{\left(1,3\right)}-1\right)}^T}\end{array}\right]}^T& \mathrm{if}\kern0.34em \mathrm{coupler}\kern0.17em \mathrm{flexible},\end{array}\right.$

$$ {\tilde{\mathbf{q}}}^{\left(1,3,r\right)}={\left[\begin{array}{ccc}{\psi}^{\left(1,3,r\right)}& {\theta}^{\left(1,3,r\right)}& {\varphi}^{\left(1,3,r\right)}\end{array}\right]}^T. $$

The transformation matrices from the local reference frames defined for each link to the global reference frame are defined by:

$$ {\left.{\mathbf{T}}^{\left(c,b\right)}\right|}_{\begin{array}{l}c=1,2\\ {}b=1,\dots, {n}_l^{(c)}\end{array}}=\prod \limits_{j=1}^b{\tilde{\mathbf{A}}}^{\left(c,j\right)}{\tilde{\mathbf{T}}}^{\left(c,j\right)}, $$

(2)

where ${\tilde{\mathbf{A}}}^{\left(c,j\right)}=\mathrm{const}$ is the transformation matrix describing the initial position and orientation of link (c, j) with respect to the preceding link, ${\tilde{\mathbf{T}}}^{\left(c,j\right)}$ is the transformation matrix defining the actual position and orientation of link (c, j) with respect to the initial configuration.

2.2 Dynamics Equations of Motion

The dynamics equations for each open-loop kinematic chain are derived using the Lagrange equations of the second kind [8]:

$$ \frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial {E}_k^{(c)}}{\partial {\dot{\mathbf{q}}}^{(c)}}-\frac{\partial {E}_k^{(c)}}{\partial {\mathbf{q}}^{(c)}}+\frac{\partial {E}_p^{(c)}}{\partial {\mathbf{q}}^{(c)}}+\frac{\partial {R}^{(c)}}{\partial {\dot{\mathbf{q}}}^{(c)}}={\left.{\mathbf{Q}}^{(c)}\right|}_{c=1,2}, $$

(3)

where ${E}_k^{(c)}$ is the kinetic energy of chain c, ${E}_p^{(c)}={E}_{p,g}^{(c)}+{E}_{p,{f}_l}^{(c)}$ is the sum of the potential energy of gravity forces and spring deformation energy of the flexible link, R ^(c) is the Rayleigh function defined for the flexible link and Q ^(c) is the vector of non-potential generalised forces resulting from e.g. the contact forces acting in the clearance joint. The following sections present detailed formulas for determining components of the Eq. (3).

2.2.1 Kinetic Energy and Potential Energy of Gravity Forces

The kinetic energy of the particular subchains can be determined using the concept of the trace of the matrix:

$$ {E}_k^{(1)}=\left\{\begin{array}{c}\frac{1}{2}\sum \limits_{l=1}^{n_l^{(1)}}\mathrm{tr}\left({\dot{\mathbf{T}}}^{\left(1,l\right)}{\mathbf{H}}^{\left(1,l\right)}{\dot{\mathbf{T}}}^{{\left(1,l\right)}^T}\right)\\\mathrm{if}\ \mathrm{coupler}\kern0.17em \mathrm{rigid},\\ {}\frac{1}{2}\sum \limits_{l=1}^{n_l^{(1)}-1}\mathrm{tr}\left({\dot{\mathbf{T}}}^{\left(1,l\right)}{\mathbf{H}}^{\left(1,l\right)}{\dot{\mathbf{T}}}^{{\left(1,l\right)}^T}\right)\\\quad +\frac{1}{2}\sum \limits_{r=1}^{n_{rfe}^{\left(1,3\right)}-1}\mathrm{tr}\left({\dot{\mathbf{T}}}^{\left(1,3,r\right)}{\mathbf{H}}^{\left(1,3,r\right)}{\dot{\mathbf{T}}}^{{\left(1,3,r\right)}^T}\right)\quad \mathrm{if}\ \mathrm{coupler}\kern0.17em \mathrm{flexible},\end{array}\right. \vspace*{-18pt} $$

(4.1)

$$ {E}_k^{(2)}=\frac{1}{2}\sum \limits_{l=1}^{n_l^{(2)}}\mathrm{tr}\left({\dot{\mathbf{T}}}^{\left(2,l\right)}{\mathbf{H}}^{\left(2,l\right)}{\dot{\mathbf{T}}}^{{\left(2,l\right)}^T}\right), $$

(4.2)

where H ^(•) is the pseudo-inertia matrix of link or rfe.

After necessary transformations the Lagrange operator can be written in the matrix form as follows:

$$ \frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial {E}_k^{(c)}}{\partial {\dot{\mathbf{q}}}^{(c)}}-\frac{\partial {E}_k^{(c)}}{\partial {\mathbf{q}}^{(c)}}={\mathbf{M}}^{(c)}{\ddot{\mathbf{q}}}^{(c)}+{\mathbf{h}}^{(c)}, $$

(5)

where: ${\mathbf{M}}^{(c)}={\left({\mathbf{M}}_{i,j}^{(c)}\right)}_{i,j=1,\dots, {n}_l^{(c)}}$, ${\mathbf{M}}_{i,j}^{(c)}=\sum \limits_{l=\max \left\{i,j\right\}}^{n_l^{(c)}}{\mathbf{M}}_{i,j}^{\left(c,l\right)}$, ${\left.{\mathbf{M}}_{i,j}^{\left(c,l\right)}\right|}_{i,j=1,\dots, l}={\left({m}_{n_{dof}^{\left(c,i-1\right)}+v,{n}_{dof}^{\left(c,j-1\right)}+w}^{\left(c,l\right)}\right)}_{\begin{array}{l}v=1,\dots, {\tilde{n}}_{dof}^{\left(c,i\right)}\\ {}w=1,\dots, {\tilde{n}}_{dof}^{\left(c,j\right)}\end{array}}$, ${m}_{i,j}^{\left(c,l\right)}=\mathrm{tr}\left\{{\mathbf{T}}_i^{\left(c,l\right)}{\mathbf{H}}^{\left(c,l\right)}{\mathbf{T}}_j^{{\left(c,l\right)}^T}\right\}{\mathbf{h}}^{(c)}={\left({\mathbf{h}}_i^{(c)}\right)}_{i=1,\dots {n}_l^{(c)}}$, ${\mathbf{h}}_i^{(c)}=\sum \limits_{l=i}^{n_l^{(c)}}{\mathbf{h}}_i^{\left(c,l\right)}$,${\left.{\mathbf{h}}_i^{\left(c,l\right)}\right|}_{i=1,\dots, l}={\left({h}_{n_{dof}^{\left(c,i-1\right)}+v}^{\left(c,l\right)}\right)}_{v=1,\dots, {\tilde{n}}_{dof}^{\left(c,l\right)}}$,${h}_i^{\left(c,l\right)}=\sum \limits_{m=1}^{n_{dof}^{\left(c,l\right)}}\sum \limits_{n=m}^{n_{dof}^{\left(c,l\right)}}\mathrm{tr}\left\{{\mathbf{T}}_i^{\left(c,l\right)}{\mathbf{H}}^{\left(c,l\right)}{\mathbf{T}}_{m,n}^{{\left(c,l\right)}^T}\right\}{\dot{q}}_m^{\left(c,l\right)}{\dot{q}}_n^{\left(c,l\right)}$.

The potential energy of the gravity forces for each subchain can be expressed in a similar way:

$$ { {E}_{p,g}^{(1)}=\left\{\begin{array}{ccc}\sum \limits_{l=1}^{n_l^{(1)}}{m}^{\left(1,l\right)}{\mathbf{j}}_2{\mathbf{T}}^{\left(1,l\right)}{\mathbf{r}}_C^{\left(1,l\right)}& \mathrm{if}& \mathrm{coupler}\kern0.17em \mathrm{rigid},\\ {\!}\sum \limits_{l=1}^{n_l^{(1)}-1}\!{m}^{\left(1,l\right)}{\mathbf{j}}_2{\mathbf{T}}^{\left(1,l\right)}{\mathbf{r}}_C^{\left(1,l\right)}\!+\sum \limits_{l=1}^{n_{rfe}^{\left(1,3\right)}}{m}^{\left(1,l,r\right)}{\mathbf{j}}_2{\mathbf{T}}^{\left(1,l,r\right)}{\mathbf{r}}_C^{\left(1,l,r\right)}& \mathrm{if}& \mathrm{coupler}\kern0.17em \mathrm{flexible},\end{array}\right.,} \vspace*{-18pt}$$

(6.1)

$$ {E}_{p,g}^{(2)}=\sum \limits_{l=1}^{n_l^{(2)}}{m}^{\left(2,l\right)}{\mathbf{j}}_2{\mathbf{T}}^{\left(2,l\right)}{\mathbf{r}}_C^{\left(2,l\right)}, $$

(6.2)

where m ^(•) is the mass of link or rfe, ${\mathbf{r}}_C^{\left(\bullet \right)}$ is the vector of the centre of mass of link or rfe, ${\mathbf{j}}_2=\left[\begin{array}{cccc}0& 1& 0& 0\end{array}\right]$.

The generalized forces due to the gravity forces can be calculated as follows:

$$ \frac{\partial {E}_{p,g}^{(c)}}{\partial {\mathbf{q}}^{(c)}}={\mathbf{g}}^{(c)}, $$

(7)

where: ${\mathbf{g}}^{(c)}={\left({\mathbf{g}}_i^{(c)}\right)}_{i=1,\dots {n}_l^{(c)}}$, ${\mathbf{g}}_i^{(c)}=\sum \limits_{l=i}^{n_l^{(c)}}{\mathbf{g}}_i^{\left(c,l\right)}$,${\left.{\mathbf{g}}_i^{\left(c,l\right)}\right|}_{i=1,\dots, l} ={\left({g}_{n_{dof}^{\left(c,i-1\right)}+v}^{\left(c,l\right)}\right)}_{v=1,\dots, {\tilde{n}}_{dof}^{\left(c,l\right)}}$,

${\left.{\mathbf{g}}_i^{\left(c,l\right)}\right|}_{i=1,\dots, l}={\left({g}_{n_{dof}^{\left(c,i-1\right)}+v}^{\left(c,l\right)}\right)}_{v=1,\dots, {\tilde{n}}_{dof}^{\left(c,i\right)}}$, ${g}_i^{(p)}={m}^{\left(c,l\right)}g{\mathbf{j}}_2{\mathbf{T}}_i^{\left(c,l\right)}{\mathbf{r}}_C^{\left(c,l\right)}$.

2.2.2 Modelling of the Flexibility of Coupler

The Rigid Finite Element Method [8] is used to discretize the coupler. The spring deformation energy and the Rayleigh function of the flexible link takes a form:

$$ {E}_{p,{f}_l}^{(1)}={E}_{p,{f}_l}^{\left(1,3\right)}=\frac{1}{2}\sum \limits_{s=1}^{n_{sde}^{\left(1,3\right)}}{\left({\mathbf{d}}^{\left(1,3,s\right)}\right)}^T{\mathbf{S}}^{\left(1,3,s\right)}{\mathbf{d}}^{\left(1,3,s\right)}, \vspace*{-18pt}$$

(8.1)

$$ {R}_{f_l}^{(1)}={R}_{f_l}^{\left(1,3\right)}=\frac{1}{2}\sum \limits_{s=1}^{n_{sde}^{\left(1,3\right)}}{\left({\dot{\mathbf{d}}}^{\left(1,3,s\right)}\right)}^T{\mathbf{D}}^{\left(1,3,s\right)}{\dot{\mathbf{d}}}^{\left(1,3,s\right)}, $$

(8.2)

where d ^{(1, 3, s)} = q ^{(1, 3, r)}, S ^{(1, 3, s)}, D ^{(1, 3, s)} are stiffness and damping matrices of sde(1,3,s).

These components are introduced to the dynamics equations as the generalized forces which can be calculated as follows:

$$ \frac{\partial {E}_{p,{f}_l}^{(1)}}{\partial \mathbf{q}}+\frac{\partial {R}_{f_l}^{(1)}}{\partial \dot{\mathbf{q}}}={\mathbf{s}}_{f_l}^{(1)}, $$

(9)

where: ${s}_{f_l,i}^{(1)}=\left\{\begin{array}{cc}\sum \limits_{j=1}^{n_{sde}^{\left(1,3\right)}}{\left(\frac{\partial {\tilde{\mathbf{q}}}^{\left(1,3,j\right)}}{\partial {q}_i}\right)}^T{\mathbf{S}}^{\left(1,3,j\right)}{\tilde{\mathbf{q}}}^{\left(1,3,j\right)}&\\+{\left(\frac{\partial {\dot{\tilde{\mathbf{q}}}}^{\left(1,3,j\right)}}{\partial {\dot{q}}_i}\right)}^T{\mathbf{D}}^{\left(1,3,j\right)}{\dot{\tilde{\mathbf{q}}}}^{\left(1,3,j\right)}& \mathrm{if}\kern0.24em {q}_i\in {\mathbf{q}}_f^{\left(1,3\right)},\\ {}0& \mathrm{otherwise}.\end{array}\right.$

2.2.3 Modelling of Contact Forces in Clearance Joint

Fig. 3

Model of revolute joint with radial and axial clearance

In the presented approach, it is assumed that the clearance occurs only in the cut-joint R (Fig. 1). The spatial model of the revolute joint with clearance is proposed (Fig. 3). This model allows considering the radial and axial clearances. In order to take into account the radial clearance, the lateral surface of the journal is discretized into ${n}_{ce}^{(r)}$ radial contact elements (ce _r) located around the perimeter on n _r levels. In the case of the axial clearance, the frontal surface of the journal is discretized into ${n}_{ce}^{(a)}$ axial contact elements (ce _a) located around the perimeter on n _a levels. The contact force of ce _α(i, k) acting on the bearing and journal are determined as follows:

$$ {\left.{\mathbf{f}}_{c,\alpha}^{\left(b,i,k\right)}\right|}_{\alpha \in \left\{r,a\right\}}={f}_{n,\alpha}^{\left(i,k\right)}{\mathbf{n}}_{\alpha}^{\left(i,k\right)}+{f}_{t,\alpha}^{\left(i,k\right)}{\mathbf{t}}_{\alpha}^{\left(i,k\right)}, $$

(10.1)

$$ {\left.{\mathbf{f}}_{c,\alpha}^{\left(j,i,k\right)}\right|}_{\alpha \in \left\{r,a\right\}}= -_b^j{\mathbf{Rf}}_{c,\alpha}^{\left(b,i,k\right)}, $$

(10.2)

where ${f}_{n,\alpha}^{\left(i,k\right)},{f}_{n,\alpha}^{\left(i,k\right)}$ are the normal and tangent forces, ${\mathbf{n}}_{\alpha}^{\left(i,k\right)},{\mathbf{t}}_{\alpha}^{\left(i,k\right)}$ are the normal and tangent unit vectors to the contact surfaces, ${}_b^j\mathbf{R}$ is the rotation matrix from bearing frame {b} to journal frame{j}. Normal force ${f}_{n,\alpha}^{\left(i,k\right)}$ and tangent force${f}_{t,\alpha}^{\left(i,k\right)}$ are calculated using the Lankarani-Nikravesh [9] and LuGre [10] formulas:

$$ {\left.{f}_{n,\alpha}^{\left(i,k\right)}\right|}_{\alpha \in \left\{r,a\right\}}={s}_{\alpha}^{\left( ce,i,k\right)}{\Delta}_{\alpha}^{\left(i,k\right)}+{d}_{\alpha}^{\left( ce,i,k\right)}{\dot{\Delta}}_{\alpha}^{\left(i,k\right)},\vspace*{-18pt} $$

(11.1)

$$ {\left.{f}_{t,\alpha}^{\left(i,k\right)}\right|}_{\alpha \in \left\{r,a\right\}}=\left({\sigma}_0{z}_{\alpha}^{\left(i,k\right)}+{\sigma}_1{z}_{\alpha}^{\left(i,k\right)}+{\sigma}_2{\upsilon}_{t,\alpha}^{\left(i,k\right)}\right){f}_{n,\alpha}^{\left(i,k\right)}, $$

(11.2)

where ${s}_{\alpha}^{\left( ce,i,k\right)},{d}_{\alpha}^{\left( ce,i,k\right)}$ are stiffness and damping coefficients of the contact element [1, 9], ${\Delta}_{\alpha}^{\left(i,k\right)}$ is deformation of the contact element, σ ₀, σ ₁, σ ₂ are stiffness, damping and viscous friction coefficients of the bristles, ${z}_{\alpha}^{\left(i,k\right)}$ is deformation of the bristle, ${\upsilon}_{t,\alpha}^{\left(i,k\right)}$ is a tangent velocity at the contact point.

The forces expressed by Eq. (10) are introduced to the dynamics equations in the form of the generalised forces as follows:

$$\begin{array}{l} \displaystyle {\mathbf{c}}^{(1)}=\sum \limits_{i=1}^{n_r}\sum \limits_{k=1}^{n_{ce}^{(r)}}\left({\mathbf{f}}_{c,r}^{\left(b,i,k\right)}\frac{\partial {\mathbf{r}}_{K_r^{\left(b,i,k\right)}}}{\partial {\mathbf{q}}^{(1)}}+{\mathbf{f}}_{c,r}^{\left(j,i,k\right)}\frac{\partial {\mathbf{r}}_{K_r^{\left(j,i,k\right)}}}{\partial {\mathbf{q}}^{(1)}}\right)\\\displaystyle\qquad\quad +\sum \limits_{i=1}^{n_a}\sum \limits_{k=1}^{n_{ce}^{(a)}}\left({\mathbf{f}}_{c,a}^{\left(b,i,k\right)}\frac{\partial {\mathbf{r}}_{K_a^{\left(b,i,k\right)}}}{\partial {\mathbf{q}}^{(1)}}+{\mathbf{f}}_{c,a}^{\left(j,i,k\right)}\frac{\partial {\mathbf{r}}_{K_a^{\left(j,i,k\right)}}}{\partial {\mathbf{q}}^{(1)}}\right),\end{array}\vspace*{-18pt} $$

(12.1)

$$ {\mathbf{c}}^{(2)}=\sum \limits_{i=1}^{n_r}\sum \limits_{k=1}^{n_{ce}^{(r)}}\left({\mathbf{f}}_{c,r}^{\left(j,i,k\right)}\frac{\partial {\mathbf{r}}_{K_r^{\left(j,i,k\right)}}}{\partial {\mathbf{q}}^{(2)}}\right)+\sum \limits_{i=1}^{n_a}\sum \limits_{k=1}^{n_{ce}^{(a)}}\left({\mathbf{f}}_{c,a}^{\left(j,i,k\right)}\frac{\partial {\mathbf{r}}_{K_a^{\left(j,i,k\right)}}}{\partial {\mathbf{q}}^{(2)}}\right). $$

(12.2)

2.3 Final Dynamics Equations

The dynamics equations of motion together with the state equations formulated for the LuGre friction model take the form:

$$ \dot{\mathbf{z}}=\mathbf{LuGre}\left(t,\mathbf{v},\mathbf{z}\right),\vspace*{-18pt} $$

(13.1)

$$ \left[\begin{array}{cc}{\mathbf{M}}^{(1)}& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{M}}^{(2)}\end{array}\right]\left[\begin{array}{c}{\ddot{\mathbf{q}}}^{(1)}\\ {}{\ddot{\mathbf{q}}}^{(2)}\end{array}\right]=\left[\begin{array}{l}-{\mathbf{h}}^{(1)}-{\mathbf{g}}^{(1)}-{\mathbf{s}}_{f_l}^{(1)}+{\mathbf{c}}^{(1)}\\ {}-{\mathbf{h}}^{(2)}-{\mathbf{g}}^{(2)}+{\mathbf{c}}^{(2)}\end{array}\right], $$

(13.2)

where: M ^(c), h ^(c)|_{c ∈ {1, 2}} are defined by Eq. (5), forces, g ^(c)|_{c ∈ {1, 2}} are described by Eq. (7), ${\mathbf{s}}_{f_l}^{(1)}$ is defined Eq. (9), c ^(c)|_{c ∈ {1, 2}} are defined by Eq. (12).

3 Case Study

The presented model of the RPSUP spatial linkage is applied to analyze the influence of the crank’s velocity on the dynamic response of the linkage. The geometrical and mass properties of the links are gathered in Table 1. It is assumed that the motion of crank and slider (1,2) have to change according to the assumed functions shown in Fig. 4.

Table 1 Parameters of RPSUP linkage

Fig. 4

The assumed time courses of the kinematic inputs: (a) crank (1,1), (b) slider (1,2)

It can be noted that after time 2 s the angular velocity of crank (1,1) is equal to ${\dot{\varphi}}_0^{\left(1,1\right)}\in \left\{5,10,12\ \mathrm{rad}\;{\mathrm{s}}^{-1}\right\}$. The motion of slider (1,2) is intermittent and after each complete cycle, there is a pause in movement, which duration time is equal to 0.5 s.

It is assumed:

• flexible link parameters: Young modulusE = 2.1 × 10¹¹ Pa, Kirchhoff modulusG = 0.8 × 10¹¹ Pa, number of rfes ${n}_{rfe}^{\left(1,3\right)}=4$,

• clearance joint parameters: μ _s = 0.1, μ _k = 0.2, σ ₀ = 100 m⁻¹, σ ₁ = 5  s m⁻¹, σ ₂ = 0  s m⁻¹, v _s = 1 × 10⁻³m s⁻¹, restitution coefficient k _r = 0.9, radius of the bearing r ^(b) = 5 × 10⁻³ m.

Fig. 5

Time courses of the acceleration of slider (2,1) calculated for c _r = 0 mm: (a) rigid coupler, (b) flexible coupler

Fig. 6

Time courses of the acceleration of slider (2,1) calculated for: c _r = 0.25 mm (a) rigid coupler, (b) flexible coupler

In simulations, it is assumed that axial clearance is equal to 0. The dynamics equations are integrated using the 4th order Runge-Kutte scheme. The Baumgarte stabilization method is applied to eliminate kinematic input constraints violations at position and velocity levels. Figure 5 shows acceleration courses of slider (2,1) obtained for the model without clearance effect. Analyzing the plots, it can be observed that the coupler’s flexibility doesn’t have a great impact on the motion of the linkage. As the crank velocity increases, the amplitude of the slider’s acceleration becomes significantly larger. Further, the radial clearance of the revolute joint connecting coupler with link (2,1) is taken into account. Figures 6 and 7 show slider acceleration time courses obtained for the radial clearance equal to c _r = 0.25 mm and c _r = 0.5 mm, respectively. The trajectories of the journal inside the bearing are presented in Figs. 8 and 9. Analyzing the results obtained for c _r = 0.25 mm it can be observed that as velocity ${\dot{\varphi}}_0^{\left(1,1\right)}$ increase from 10 to 15 rad s⁻¹, the maximum acceleration increases 8.5 times if the coupler is rigid and 4 times if the coupler is treated as a flexible.

Fig. 7

Time courses of the acceleration of slider (2,1) calculated for c _r = 0.50 mm: (a) rigid coupler, (b) flexible coupler

Fig. 8

The trajectory of the journal inside the bearing calculated for c _r = 0.25 mm: (a) rigid coupler, (b) flexible coupler

Fig. 9

The trajectory of the journal inside the bearing calculated for c _r = 0.50 mm: (a) rigid coupler, (b) flexible coupler

In the case of c _r = 0.5 mm acceleration increases 3.5 times when the coupler is rigid and 1.25 times if the coupler is treated as a flexible. Additionally, values of acceleration peaks due to the collision between contacting bodies are smaller when the radial clearance equals to 0.5 mm. The presented simulation results confirm that the flexibility compensates for negative effects due to impulse forces existing in the revolute joint.

4 Concluding Remarks

The paper presents the mathematical model of the two-dof RPSUP linkage with the flexible coupler and clearance in the revolute joint. An essential feature of the presented approach is that it can be easily generalized to model dynamics of linkages with a serial open-loop kinematic structure composed of flexible links and revolute frictional joints with clearance, not only at cut-joints. The main advantage of the proposed model of the revolute joint with the clearance is that it allows us to analyze different combinations of contact between the journal and bearing. The simulation results show that the coupler’s flexibility has a great impact on the motion of the linkage with the clearance joint. When the flexibility of the coupler is taken into account the acceleration of the slider is significantly smaller because some part of the energy resulting from the impulse force is transformed into the link’s spring deformation.