Mathematical Analysis of Two Unequal Collinear Cracks in a Piezo-Electro-Magnetic Media

Abstract

In this chapter, we begin our work of studying two unequal collinear semi-permeable cracks in a magneto-electro-elastic media. We employ the Stroh’s formalism and complex variable technique to solve the physical problem. We derive the closed form analytic solutions for various fracture parameters, and study the effect of volume fraction and inter-crack distance on these parameters.

1 Introduction

Piezo-electro-magnetic/Magneto-electro-elastic (MEE) composite materials arewidely used in magnetic field probes, acoustic, medical ultrasonic imaging,hydrophones, electronic packaging, electromagnetic sensors, actuators and transducers etc., due to their multi-field-coupled effects. MEE ceramics are brittle in nature and have low fracture toughness. The presence of defects such as cracks, voids leads to the premature failure of these materials under mechanical/electrical/magnetic loadings. Thus fracture study becomes essential for such materials to predict structural integrity and to advance the design of MEE devices.

This chapter reviews extensive work that has been done to better understand the mechanics of MEE materials in the presence of defects such as cracks. As compared to piezoelectric or anisotropic cases, relatively limited work has been done so far in MEE fracture analysis. A large number of publications for a single crack in a MEE materials are available in the literature [1,2,3,4,5,6]. Further, few work related to multiple cracks in MEE media is available in the literature, also it deserves noting that problems of collinear cracks have been a typical and active topic in fracture mechanics. With the application of MEE ceramics, the collinear-crack problems in them have drawn the attention of many researchers [7,8,9]. The static and dynamic problems of two collinear interfacial cracks in MEE composites [10,11,12,13] have been solved by Zhou and colleagues by using the Schmidt method. Exact solutions for anti-plane collinear cracks in a MEE strip or layer have been derived by Wang et al. [14], Wang and Mai [15], and Singh et al. [16] under different conditions. Most, recently Jangid and Bharagva [17] has derived an analytical solution for two collinear semi-permeable cracks in MEE media using Stroh’s formalism and complex variable technique.

The main objective of this chapter is to show the effect of volume fraction, inter-crack distance and prescribed loadings on the collinear semi-permeable cracks. For this, the problem of two unequal collinear semipermeable cracks weakening a MEE media is studied. Only in-plane electro-magnetic and mechanical loading conditions are considered. The problem is formulated employing Stroh’s formalism and solved using a complex variable technique (see Sects. 4 and 5). Closed form analytical expressions are derived for various fracture parameters (see Sect. 6).

2 Basic Equations for Piezoelectromagnetic Media

The fundamental equations and the boundary conditions for linear piezo-electro-magnetic media are defined as below:

• Constitutive Equations

  $$\begin{aligned} \sigma _{ij}&= C_{ijks}\varepsilon _{ks} - e_{sij}E_{s} - h_{sij}H_{s}, \end{aligned}$$

  (1)
  $$\begin{aligned} D_{i}&= e_{kis}\varepsilon _{ks} + \kappa _{is}E_{s} + \beta _{is}H_{s}, \end{aligned}$$

  (2)
  $$\begin{aligned} B_{i}&= h_{iks}\varepsilon _{ks} + \beta _{is}E_{s} + \gamma _{is}H_{s}. \end{aligned}$$

  (3)

• Kinematic Equations

  $$\begin{aligned} \varepsilon _{ij}=\frac{1}{2}(u_{i, j} + u_{j, i}), E_{i}=\phi _{,i}, H_{i}=\varphi _{,i} . \end{aligned}$$

  (4)

• Equilibrium Equations

  Equilibrium equations for stresses, electric displacements and magnetic inductions in the absence of body forces, free electric charges and free magnetic currents, may, respectively, be written as

  $$\begin{aligned} \sigma _{ij, j}=0, D_{i, i}=0 \,\,\, \text {and} \,\,\, B_{i, i}=0, \end{aligned}$$

  (5)

where $\sigma _{ij}$, $\varepsilon _{ij}$, $D_{i}$, $E_{i}$, $B_{i}$ and $H_{i}$ denote the components of the stress, strain, electric displacement, electric field, magnetic induction and magnetic field, respectively; $C_{ijks}$, $e_{iks}$, $h_{iks}$ and $\beta _{is}$ denote the elastic, piezoelectric, piezo-magnetic and electromagnetic constants; $\kappa _{is}$ and $\gamma _{is}$ denote the dielectric permittivities and magnetic permeabilities, respectively. Comma denotes partial differentiation with respect to argument following it; $\phi$ is the electric potential; and $\varphi$ is the magnetic potential; where i, j, k and $s=1, 2, 3$.

2.1 Crack Face Boundary Conditions

In the literature, mainly three crack face boundary conditions for MEE ceramics are available. These are represented mathematically as:

• Impermeable boundary conditions (proposed by Deeg [18])

  The crack faces are assumed to be traction-free, electrically and magnetically impermeable

  $$\begin{aligned} \sigma _{ij}n_{j}=0; \;\; D_{2}^{+}=D_{2}^{-}=0 \;\; \text {and} \;\; B_{2}^{+}=B_{2}^{-}=0; \end{aligned}$$

  (6)

• Permeable boundary conditions (proposed by Parton [19])

  In this case, crack is traction-free and does not obstruct any electric field from conduction

  $$\begin{aligned} \sigma _{ij}n_{j}=0; \;\; \phi ^{+}=\phi ^{-}; \;\; \varphi ^{+}=\varphi ^{-}; \;\; D_{2}^{+}=D_{2}^{-}\ne 0 \;\; \text {and} \,\, B_{2}^{+}=B_{2}^{-}\ne 0; \end{aligned}$$

  (7)

• Semi-permeable boundary conditions

  This condition, gives a more realistic boundary condition for a open cracks, its modification are proposed by Hao and Shen [20] for piezoelectric solids. These assumption establishes that medium between the crack surfaces partially conducts the electric and magnetic fields and can be expressed as

  $$\begin{aligned} \sigma _{ij}n_{j}=0; \;\; D_{2}^{+}=D_{2}^{-}=D_{2}^{c}=-\kappa _{c}\dfrac{\Delta \phi (x_{1})}{\Delta u (x_{1})} \;\; \text {and} \;\; B_{2}^{+}=B_{2}^{-}=B_{2}^{c}=-\gamma _{c}\dfrac{\Delta \varphi (x_{1})}{\Delta u (x_{1})}, \end{aligned}$$

  (8)

where superscripts $+$ and − represent, respective, values on the upper and lower crack surfaces, considering crack along $x_{1}$-axis; $\kappa _{c}=\kappa _{r}\kappa _{o} (\kappa _{o}=8.85\times 10^{-12}F/m),$ $\kappa _{r}$ is electric permittivity and $\gamma _{c}=\gamma _{r}\gamma _{o} (\gamma _{o}=1.26\times 10^{-6}Ns^{2}/C^{2}),$ $\gamma _{r}$ is magnetic permeability of the medium between the crack faces, respectively; $\Delta \phi$, $\Delta \varphi$ and $\Delta u$ are the jumps of electric potential, magnetic potential and crack opening displacement across the crack, respectively.

3 Fundamental Formulation and Solution Methodology

According to Stroh’s formulation [21] the general solution satisfying Eqs. (1)–(5) may be written as (solution methodology is recapitulated from Jangid and Bhargava [17])

$$\begin{aligned} \mathbf{u}_{,1}=\mathbf{A}{} \mathbf{F}(z)+\overline{\mathbf{A}}\overline{\mathbf{F}(z)},\end{aligned}$$

(9)

$$\begin{aligned} \mathbf{\Phi }_{,1}=\mathbf{B}{} \mathbf{F}(z)+\overline{\mathbf{B}}\overline{\mathbf{F}(z)}, \end{aligned}$$

(10)

where, $\mathbf{A} =(\mathbf{a }_{1}, \mathbf{a }_{2}, \mathbf{a }_{3}, \mathbf{a }_{4}, \mathbf{a }_{5})$, $\mathbf{B} =(\mathbf{b }_{1}, \mathbf{b }_{2}, \mathbf{b }_{3}, \mathbf{b }_{4}, \mathbf{b }_{5})$, $\mathbf{u} =[u_{1},u_{2},u_{3},\phi , \varphi ]^{T}$,   $\mathbf{F }(z)\,{=}\,\dfrac{d\mathbf{f }(z)}{dz}$, $\mathbf{f }(z_{\alpha })\,{=}\,[f_{1}(z_{1}), f_{2}(z_{2}), f_{3}(z_{3}), f_{4}(z_{4}), f_{5}(z_{5})]^{T}$ and $z_{\alpha }\,{=}\,x_{1}+p_{\alpha }x_{2}$, where $p_{\alpha }$ is a non-real root of

$$\begin{aligned} |\mathbf{W} +p(\mathbf{R} +\mathbf{R} ^{T})+p^{2}{} \mathbf{Q} |=0. \end{aligned}$$

(11)

The matrices $\mathbf {W}$, $\mathbf {R}$ and $\mathbf {Q}$ are given by

$$\begin{aligned} \mathbf{W}=\left[ \begin{array}{c@{\quad }c@{\quad }c} C_{1jk1} &{} e_{1j1} &{} h_{1j1} \\ e_{1k1}^{T} &{} -\kappa _{11} &{} -\beta _{11} \\ h_{1k1}^{T} &{} -\beta _{11} &{} -\gamma _{11}\\ \end{array} \right] , \mathbf{R}=\left[ \begin{array}{c@{\quad }c@{\quad }c} C_{1jk1} &{} e_{2j1} &{} h_{2j1} \\ e_{1k2}^{T} &{} -\kappa _{12} &{} -\beta _{12} \\ h_{1k2}^{T} &{} -\beta _{12} &{} -\gamma _{12} \\ \end{array} \right] , \nonumber \\ \mathbf{Q}=\left[ \begin{array}{c@{\quad }c@{\quad }c} C_{2jk2} &{} e_{2j2} &{} h_{2j2} \\ e_{2k2}^{T} &{} -\kappa _{22} &{} -\beta _{22} \\ h_{2k2}^{T} &{} -\beta _{22} &{} -\gamma _{22} \\ \end{array} \right] , { j,k}=1,2,3. \end{aligned}$$

(12)

The column vectors of matrix $\mathbf{B} =\mathbf (b_{1},b_{2},b_{3},b_{4}, b_{5})$ are related to the column vectors of matrix $\mathbf{A} =\mathbf (a_{1},a_{2},a_{3},a_{4}, a_{5})$ in the following form

$$\mathbf{b} _{k}=(\mathbf{R} ^{T}+p_{k}{} \mathbf{Q} )\mathbf{a} _{k}, k=1,2,3,4,5$$

and ${\mathbf \Phi }$ is the generalized stress function such that

$$\begin{aligned} {\mathbf \sigma }_{2}=[\sigma _{2j}, D_{2}, B_{2}]^{T}=\mathbf{\Phi }_{,1}, {\mathbf \sigma }_{1}=[\sigma _{1j},D_{1}, B_{1}]^{T}=-\mathbf{\Phi }_{,2}. \end{aligned}$$

(13)

4 Statement of the Problem

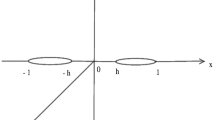
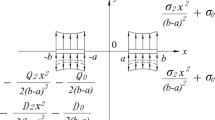
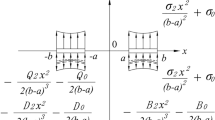
An infinite transversely isotropic piezo-electro-magnetic 2D domain is considered for the analysis in the $ox_{1}x_{2}$-plane. Two unequal collinear cracks $L_{1}$ and $L_{2}$ are taken along the x-axis occupying the intervals [d, c] and [b, a], respectively. The traction free crack face and semipermeable boundary condition are taken for the analysis. The remote boundary of the plate is prescribed in-plane mechanical load $\sigma _{22}^{\infty }$, electric displacement $D_{2}^{\infty }$, and magnetic induction $B_{2}^{\infty }$. The entire configuration is schematically presented in Fig. 1. The physical boundary conditions stated above may be written as

Fig. 1

Schematic representation of the problem

• (i) $\sigma _{2j}^{+}=\sigma _{2j}^{-}=0,$   $D_{2}=D^{c},$   $B_{2}=B^{c}$ on $L=\displaystyle {\bigcup _{1}^{2}}L_{i}$

• (ii) $\sigma _{22}=\sigma _{22}^{\infty },$   $D_{2}=D_{2}^{\infty },$   $B_{2}=B_{2}^{\infty }$   for $|x_{2}|\rightarrow \infty$

• (iii) $u_{j}^{+}=u_{j}^{-}$,   $\sigma _{2j}^{+}=\sigma _{2j}^{-}$,   $D_{2}^{+}=D_{2}^{-}$,   $B_{2}^{+}=B_{2}^{-}$,  $\phi ^{+}=\phi ^{-}$,   $\varphi ^{+}=\varphi ^{-}$ for $|x_{1}|<d$, $c<|x_{1}|<b$, $|x_{1}|>a$

• (iv) ${\boldsymbol{\Phi }}_{,1}^{+}={\boldsymbol{\Phi }}_{,1}^{-}=-\mathbf {V}$,  $\mathbf{V} =[\begin{array}{ccccc} 0&\sigma _{22}^{\infty }&0&D_{2}^{\infty }&B_{2}^{\infty } \end{array}]^{T}$ for $d<|x_{1}|<c$, $b<|x_{1}|<a$.

where $D^{c}$ and $B^{c}$ are the electric and magnetic fluxes through the crack regions (d, c) and (b, a), which can be determined with the help of the Eq. (8).

5 Solution of the Problem

The continuity of ${\boldsymbol{\Phi }}_{,1}(x_{1})$ on the whole real axis implies that

$$\begin{aligned}{}[\mathbf{B} {} \mathbf{F} (x_{1})-\overline{\mathbf{B }}\overline{\mathbf{F }}(x_{1})]^{+}-[\mathbf{B} {} \mathbf{F} (x_{1})-\overline{\mathbf{B }}\overline{\mathbf{F }}(x_{1})]^{-}= & {} \mathbf{0} . \end{aligned}$$

(14)

According to Muskhelishvil [22] its solution may be written as

$$\begin{aligned} {\mathbf {B}}{\mathbf {F}}(z) = {\overline{\mathbf {B}}} {\overline{\mathbf {F}}}(z)=h(z) (say) \end{aligned}$$

(15)

Boundary condition (iv) together with Eqs. (10, 15) yield following vector Hilbert problem

$$\begin{aligned} \mathbf{h }^{+}(x_{1})+\mathbf{h }^{-}(x_{1})=\mathbf{V }^{0}-\mathbf{V },\, \, \mathbf{V }^{0}=[0, 0, 0, D^{c}, B^{c}]^{T} \hbox {on} \,\, L \end{aligned}$$

(16)

Introducing a new complex function vector ${\boldsymbol{\Omega }(z)}=[\Omega _{1}(z), \Omega _{2}(z), \Omega _{3}(z), \Omega _{4}(z),\Omega _{5}(z)]^{T}$ as

$$ {\boldsymbol{\Omega }}(z) = \mathbf{H ^{R}}\mathbf{BF }(z). $$

Which using Eq. (15) gives the relation

$$\begin{aligned} \mathbf{h }(z) ={\boldsymbol{\Lambda }}{\boldsymbol{\Omega }}(z), \end{aligned}$$

(17)

where ${\mathbf {\Lambda }}=[\mathbf{H} ^{R}]^{-1}$,    $\mathbf{H} ^{R}=2Re\mathbf{Y}$,   $\mathbf{Y} =i\mathbf{A} \mathbf{B }^{-1}$.

Consequently Eq. (16) may be written in component form for ${\Omega _{2}}(z), {\Omega _{4}}(z)$ and ${\Omega _{5}}(z)$, yield following scalar Hilbert problems

$$\begin{aligned} \Lambda _{22}[\Omega _{2}^{+}(x_{1})+\Omega _{2}^{-}(x_{1})]+\Lambda _{24}[\Omega _{4}^{+}(x_{1})+\Omega _{4}^{-}(x_{1})] +\Lambda _{25}[\Omega _{5}^{+}(x_{1})+\Omega _{5}^{-}(x_{1})]= & {} -\sigma _{22}^{\infty }, \end{aligned}$$

(18)

$$\begin{aligned} \Lambda _{42}[\Omega _{2}^{+}(x_{1})+\Omega _{2}^{-}(x_{1})]+\Lambda _{44}[\Omega _{4}^{+}(x_{1})+\Omega _{4}^{-}(x_{1})] +\Lambda _{45}[\Omega _{5}^{+}(x_{1})+\Omega _{5}^{-}(x_{1})]= & {} D^{c}-D_{2}^{\infty }, \nonumber \\ \end{aligned}$$

(19)

$$\begin{aligned} \Lambda _{52}[\Omega _{2}^{+}(x_{1})+\Omega _{2}^{-}(x_{1})]+\Lambda _{54}[\Omega _{4}^{+}(x_{1})+\Omega _{4}^{-}(x_{1})] +\Lambda _{55}[\Omega _{5}^{+}(x_{1})+\Omega _{5}^{-}(x_{1})]= & {} B^{c}-B_{2}^{\infty }. \nonumber \\ \end{aligned}$$

(20)

The solution of above Hilbert problems written using According to Muskhelishvil [22] as

$$\begin{aligned} \Omega _{2}(z)= & {} \dfrac{\triangle _{1}}{2\triangle }\left\{ \frac{P_{1}(z)}{(a_{11}a_{22}-a_{12}a_{21})X_{1}(z)} - 1\right\} , \end{aligned}$$

(21)

$$\begin{aligned} \Omega _{4}(z)= & {} \dfrac{\triangle _{2}}{2\triangle }\left\{ 1 - \frac{P_{1}(z)}{(a_{11}a_{22}-a_{12}a_{21})X_{1}(z)}\right\} , \end{aligned}$$

(22)

$$\begin{aligned} \Omega _{5}(z)= & {} \dfrac{\triangle _{3}}{2\triangle }\left\{ 1 - \frac{P_{1}(z)}{(a_{11}a_{22}-a_{12}a_{21})X_{1}(z)}\right\} . \end{aligned}$$

(23)

where $X_{1}(z),$ $P_{1}(z)$ etc. are given in “Appendix A”.

6 Applications

In this section, closed form analytical expressions are derived for crack opening displacement (COD), crack opening potential drop (COPD), crack opening induction drop (COID), stress intensity factor (SIF), electric displacement intensity factor (EDIF) and magnetic induction intensity factor (MIIF).

6.1 Crack Opening Displacement (COD)

The jump displacement vector $\Delta \mathbf{u} _{,1}$ may be given as

$$\begin{aligned} i \Delta \mathbf{u} _{,1}=\mathbf {\Omega }^{+}(x_{1})-\mathbf {\Omega }^{-}(x_{1}). \end{aligned}$$

(24)

Taking the second component of the above equation, we get

$$\begin{aligned} \Delta u_{2,1}(x_{1})= & {} -i[\Omega _{2}^{+}(x_{1})-\Omega _{2}^{-}(x_{1})]. \end{aligned}$$

(25)

Substituting value of $\Omega _{2}(z)$ from Eq. (21) and integrating one obtains

$$\begin{aligned} \Delta u_{2}(x_{1})=\dfrac{\triangle _{1}}{(a_{11}a_{22}-a_{12}a_{21})\triangle } \left\{ C_{0}S_{3}+C_{1}S_{4}+C_{2}S_{5}\right\} , \text {on} \,\, d<|x_{1}|<c \end{aligned}$$

(26)

$$\begin{aligned} \Delta u_{2}(x_{1})=\dfrac{-\triangle _{1}}{(a_{11}a_{22}-a_{12}a_{21})\triangle } \left\{ C_{0}S_{6}+C_{1}S_{7}+C_{2}S_{8}\right\} , \text {on} \,\, b<|x_{1}|<a \end{aligned}$$

(27)

where the symbol $\Delta$ indicates the difference between the values on the upper and lower crack surfaces and $S_{3},$ $S_{4}$ etc. are given in “Appendix B”.

6.2 Crack Opening Potential Drop (COPD)

Comparing the fourth component from Eq. (24) and using the value of $\Omega _{4}(x_{1})$ from Eq. (22) and integrating one obtains the COP drop, $\Delta \phi (x_{1})$, between the two faces of the crack as

$$\begin{aligned} \Delta u_{4}(x_{1})=\dfrac{-\triangle _{2}}{(a_{11}a_{22}-a_{12}a_{21})\triangle } \left\{ C_{0}S_{3}+C_{1}S_{4}+C_{2}S_{5}\right\} ,\text {on} \,\, d<|x_{1}|<c \end{aligned}$$

(28)

$$\begin{aligned} \Delta u_{4}(x_{1})=\dfrac{\triangle _{2}}{(a_{11}a_{22}-a_{12}a_{21})\triangle } \left\{ C_{0}S_{6}+C_{1}S_{7}+C_{2}S_{8}\right\} , \text {on} \,\, b<|x_{1}|<a. \end{aligned}$$

(29)

6.3 Crack Opening Induction Drop (COID)

Comparing the fifth component from Eq. (24) and using the value of $\Omega _{5}(x_{1})$ from Eq. (23) and integrating one obtains the COI drop, $\Delta \varphi (x_{1})$, between the two faces of the crack as

$$\begin{aligned} \Delta u_{5}(x_{1})=\dfrac{-\triangle _{3}}{(a_{11}a_{22}-a_{12}a_{21})\triangle } \left\{ C_{0}S_{3}+C_{1}S_{4}+C_{2}S_{5}\right\} ,\text {on} \,\, d<|x_{1}|<c \end{aligned}$$

(30)

$$\begin{aligned} \Delta u_{5}(x_{1})=\dfrac{\triangle _{3}}{(a_{11}a_{22}-a_{12}a_{21})\triangle } \left\{ C_{0}S_{6}+C_{1}S_{7}+C_{2}S_{8}\right\} , \text {on} \,\, b<|x_{1}|<a. \end{aligned}$$

(31)

The values of electric and magnetic fluxes, $D^{c}$ and $B^{c}$, respectively, are obtained by substituting the required values from Eqs. (26), (28), (30) into Eq. (8) simplifying and solving the system of non-linear equations

$$\begin{aligned} m_{1}{D^{c}}^{2}+D^{c}(m_{4}\sigma _{22}^{\infty }-m_{1}D_{2}^{\infty }-m_{5}B_{2}^{\infty }+m_{2}\kappa _{c})&+B^{c}D^{c}m_{5}+B^{c}m_{3}\kappa _{c} \nonumber \\&= -\kappa _{c}(m_{1}\sigma _{22}^{\infty }-m_{2}D_{2}^{\infty }-m_{3}B_{2}^{\infty }), \end{aligned}$$

(32)

$$\begin{aligned} m_{5}{B^{c}}^{2}+B^{c}(m_{4}\sigma _{22}^{\infty }-m_{1}D_{2}^{\infty }-m_{5}B_{2}^{\infty }+m_{6}\gamma _{c})&+B^{c}D^{c}m_{1}+D^{c}m_{3}\gamma _{c} \nonumber \\&= -\gamma _{c}(m_{5}\sigma _{22}^{\infty }-m_{3}D_{2}^{\infty }-m_{6}B_{2}^{\infty }), \end{aligned}$$

(33)

where,

$$\begin{aligned} m_{1} = \Lambda _{42}\Lambda _{55}-\Lambda _{45}\Lambda _{52}, m_{2} = \Lambda _{22}\Lambda _{55}-\Lambda _{25}\Lambda _{52}, m_{3} = \Lambda _{25}\Lambda _{42}-\Lambda _{22}\Lambda _{45}, \\ m_{4} = \Lambda _{44}\Lambda _{55}-\Lambda _{45}\Lambda _{54}, m_{5} = \Lambda _{25}\Lambda _{44}-\Lambda _{24}\Lambda _{45}, m_{6} = \Lambda _{22}\Lambda _{44}-\Lambda _{24}\Lambda _{42}. \end{aligned}$$

6.4 Stress Intensity Factor (SIF)

Open mode stress intensity factor $K_{I}$ at the crack tips $x_{1}=d,$ c,  b,  and a is obtained using following formulae

$$\begin{aligned} K_{I}(d)= & {} \lim _{x_{1}\rightarrow d^{-}}\sqrt{2\pi (d-x_{1})}\sigma _{22}(x_{1}), \end{aligned}$$

(34)

$$\begin{aligned} K_{I}(c)= & {} \lim _{x_{1}\rightarrow c^{+}}\sqrt{2\pi (x_{1}-c)}\sigma _{22}(x_{1}),\end{aligned}$$

(35)

$$\begin{aligned} K_{I}(b)= & {} \lim _{x_{1}\rightarrow b^{-}}\sqrt{2\pi (b-x_{1})}\sigma _{22}(x_{1}), \end{aligned}$$

(36)

$$\begin{aligned} K_{I}(a)= & {} \lim _{x_{1}\rightarrow a^{+}}\sqrt{2\pi (x_{1}-a)}\sigma _{22}(x_{1}). \end{aligned}$$

(37)

Substituting $\sigma _{22}(x_{1})$ obtained from Eqs. (10), (15), (17) and (20) into above equations and simplifying we obtain

$$\begin{aligned} K_{I}(d)= & {} \dfrac{-\sqrt{2\pi }\left( \Lambda _{25}\triangle _{3}+\Lambda _{24}\triangle _{2}-\Lambda _{22}\triangle _{1}\right) }{\triangle (a_{11}a_{22}-a_{12}a_{21})} \left\{ \dfrac{C_{0}d^{2}+C_{1}d+C_{2}}{\sqrt{(a-d)(b-d)(c-d)}}\right\} , \end{aligned}$$

(38)

$$\begin{aligned} K_{I}(c)= & {} \dfrac{\sqrt{2\pi }\left( \Lambda _{25}\triangle _{3}+\Lambda _{24}\triangle _{2}-\Lambda _{22}\triangle _{1}\right) }{\triangle (a_{11}a_{22}-a_{12}a_{21})} \left\{ \dfrac{C_{0}c^{2}+C_{1}c+C_{2}}{\sqrt{(a-c)(b-c)(c-d)}}\right\} , \end{aligned}$$

(39)

$$\begin{aligned} K_{I}(b)= & {} \dfrac{\sqrt{2\pi }\left( \Lambda _{25}\triangle _{3}+\Lambda _{24}\triangle _{2}-\Lambda _{22}\triangle _{1}\right) }{\triangle (a_{11}a_{22}-a_{12}a_{21})} \left\{ \dfrac{C_{0}b^{2}+C_{1}b+C_{2}}{\sqrt{(a-b)(b-c)(b-d)}}\right\} , \end{aligned}$$

(40)

$$\begin{aligned} K_{I}(a)= & {} \dfrac{-\sqrt{2\pi }\left( \Lambda _{25}\triangle _{3}+\Lambda _{24}\triangle _{2}-\Lambda _{22}\triangle _{1}\right) }{\triangle (a_{11}a_{22}-a_{12}a_{21})} \left\{ \dfrac{C_{0}a^{2}+C_{1}a+C_{2}}{\sqrt{(a-b)(a-c)(a-d)}}\right\} . \end{aligned}$$

(41)

6.5 Electric Displacement Intensity Factor (EDIF)

Similarly, Open mode EDIF, $K_{IV}$, at the crack tips $x_{1}=d,$ c,  b,  and a may be obtain as

$$\begin{aligned} K_{IV}(d)= & {} \dfrac{-\sqrt{2\pi }\left( \Lambda _{45}\triangle _{3}+\Lambda _{44}\triangle _{2}-\Lambda _{42}\triangle _{1}\right) }{\triangle (a_{11}a_{22}-a_{12}a_{21})} \left\{ \dfrac{C_{0}d^{2}+C_{1}d+C_{2}}{\sqrt{(a-d)(b-d)(c-d)}}\right\} , \nonumber \\ \end{aligned}$$

(42)

$$\begin{aligned} K_{IV}(c)= & {} \dfrac{\sqrt{2\pi }\left( \Lambda _{45}\triangle _{3}+\Lambda _{44}\triangle _{2}-\Lambda _{42}\triangle _{1}\right) }{\triangle (a_{11}a_{22}-a_{12}a_{21})} \left\{ \dfrac{C_{0}c^{2}+C_{1}c+C_{2}}{\sqrt{(a-c)(b-c)(c-d)}}\right\} , \end{aligned}$$

(43)

$$\begin{aligned} K_{IV}(b)= & {} \dfrac{\sqrt{2\pi }\left( \Lambda _{45}\triangle _{3}+\Lambda _{44}\triangle _{2}-\Lambda _{42}\triangle _{1}\right) }{\triangle (a_{11}a_{22}-a_{12}a_{21})} \left\{ \dfrac{C_{0}b^{2}+C_{1}b+C_{2}}{\sqrt{(a-b)(b-c)(b-d)}}\right\} , \end{aligned}$$

(44)

$$\begin{aligned} K_{IV}(a)= & {} \dfrac{-\sqrt{2\pi }\left( \Lambda _{45}\triangle _{3}+\Lambda _{44}\triangle _{2}-\Lambda _{42}\triangle _{1}\right) }{\triangle (a_{11}a_{22}-a_{12}a_{21})} \left\{ \dfrac{C_{0}a^{2}+C_{1}a+C_{2}}{\sqrt{(a-b)(a-c)(a-d)}}\right\} .\nonumber \\ \end{aligned}$$

(45)

6.6 Magnetic Induction Intensity Factor (MIIF)

Analogously, MIIF, $K_{V}$, at the crack tips $x_{1}=d,$ c,  b,  and a may be obtain as

$$\begin{aligned} K_{V}(d)= & {} \dfrac{-\sqrt{2\pi }\left( \Lambda _{55}\triangle _{3}+\Lambda _{54}\triangle _{2}-\Lambda _{52}\triangle _{1}\right) }{\triangle (a_{11}a_{22}-a_{12}a_{21})} \left\{ \dfrac{C_{0}d^{2}+C_{1}d+C_{2}}{\sqrt{(a-d)(b-d)(c-d)}}\right\} , \nonumber \\ \end{aligned}$$

(46)

$$\begin{aligned} K_{V}(c)= & {} \dfrac{\sqrt{2\pi }\left( \Lambda _{55}\triangle _{3}+\Lambda _{54}\triangle _{2}-\Lambda _{52}\triangle _{1}\right) }{\triangle (a_{11}a_{22}-a_{12}a_{21})} \left\{ \dfrac{C_{0}c^{2}+C_{1}c+C_{2}}{\sqrt{(a-c)(b-c)(c-d)}}\right\} , \end{aligned}$$

(47)

$$\begin{aligned} K_{V}(b)= & {} \dfrac{\sqrt{2\pi }\left( \Lambda _{55}\triangle _{3}+\Lambda _{54}\triangle _{2}-\Lambda _{52}\triangle _{1}\right) }{\triangle (a_{11}a_{22}-a_{12}a_{21})} \left\{ \dfrac{C_{0}b^{2}+C_{1}b+C_{2}}{\sqrt{(a-b)(b-c)(b-d)}}\right\} , \end{aligned}$$

(48)

$$\begin{aligned} K_{V}(a)= & {} \dfrac{-\sqrt{2\pi }\left( \Lambda _{55}\triangle _{3}+\Lambda _{54}\triangle _{2}-\Lambda _{52}\triangle _{1}\right) }{\triangle (a_{11}a_{22}-a_{12}a_{21})} \left\{ \dfrac{C_{0}a^{2}+C_{1}a+C_{2}}{\sqrt{(a-b)(a-c)(a-d)}}\right\} .\nonumber \\ \end{aligned}$$

(49)

7 Case Study

In this section, the effect of inter-crack distance and volume fraction are shown on the intensity factors (discussed in Sect. 5).

Piezo-electro-magnetic composite BaTiO$_{3}$-CoFe$_{2}$O$_{4}$ is selected for numerical case study considering BaTiO$_{3}$ as inclusion and CoFe$_{2}$O$_{4}$ as matrix. The volume fraction of the inclusion is denoted by $V_{f}$. The proportion of the two phases can be varied by adjusting the volume fraction of inclusion and the matrix. The elastic constants, dielectric permittivities and magnetic permeabilities, as well as piezoelectric and piezo-magnetic constants, are obtained by fraction rule {taken from Wang and Mai [23]}

$$\begin{aligned} \kappa _{is}^{c}=V_{f}.\kappa _{is}^{i} + (1-V_{f}).\kappa _{is}^{m} \end{aligned}$$

(50)

where the superscripts c, i and m represent composite, inclusion and matrix, respectively. $\kappa _{is}$ denotes the dielectric permittivities.

We assume the crack faces as semi-permeable $(\kappa _{r}=\gamma _{r}=1)$. And the length of bigger crack, $L_{1}$, smaller crack, $L_{2}$, prescribed mechanical load, electric displacement and magnetic induction are $2a_{01} (=5~\mathrm{mm})$, $2a_{02} (=4~\mathrm{mm})$, $\sigma _{22}^{\infty }=5~\mathrm{MPa}$, $D_{2}^{\infty }=2(e_{33} / c_{33})\sigma _{22}^{\infty }$ and $B_{2}^{\infty }=2(h_{33} / c_{33})\sigma _{22}^{\infty }$, respectively, till otherwise specified. Material constants for BaTiO$_{3}$-CoFe$_{2}$O$_{4}$ for different volume fraction are given in Table 1, taken from Zhong [24].

Table 1 Material constants for $BaTiO_{3}-CoFe_{2}O_{4}$ for different volume fraction

7.1 Effect of Inter-Crack Distance

Figure 2a, b show the variation of stress intensity factors (SIFs) versus normalized inter-crack distance for different volume fractions. It may be seen, that due to the mutual interactions of two cracks, the SIFs at the crack tips are increased as the inter-crack distance decreases. Also it may be seen, that SIF at the inner crack tips (at $x_{1}=c$ and $x_{1}=b$) is higher as compare to that at the outer crack tips (at $x_{1}=d$ and $x_{1}=a$), which implies that the cracks will open more at the inner tips as compared to that at outer tips. Moreover, $K_{I}$ stabilizes for $d_{0}/a_{02}\ge 3$. Also, SIF is decreased as the volume fraction increases. Similarly, Figs. 3 and 4 show the variations of EDIF and MIIF versus inter-crack distance for different volume fractions.

Fig. 2

Effect of normalized inter-crack distance $d_{0}/a_{02}$ on SIF for different volume fractions

Fig. 3

Effect of normalized inter-crack distance $d_{0}/a_{02}$ on EDIF for different volume fractions

Fig. 4

Effect of normalized inter-crack distance $d_{0}/a_{02}$ on MIIF for different volume fractions

7.2 Effect of Crack Length

Effect of crack length $a_{02}$ on stress intensity factor (SIF), $K_{I}$, for different volume fractions is shown in Fig. 5. It may be seen from the figure that at the interior and exterior tips of the longer crack, $K_{I}$ increases at both the tips as the crack length is increased. Increase in $K_{I}$ at interior tip is more steep vis-a-vis than at exterior tip. The similar variation is observed at the interior and exterior tips of the shorter crack. It is to be noted that for half length of the crack equal to 2.5 mm (i.e., the length of the both cracks is equal), the curves for $K_{I}$ at the interior tips of both cracks and exterior tips of the cracks become equal. Figures 6 and 7 show the same variations for EDIF and MIIF, respectively.

Fig. 5

Effect of crack length $a_{02}$ on SIF for different volume fractions

Fig. 6

Effect of crack length $a_{02}$ on EDIF for different volume fractions

Fig. 7

Effect of crack length $a_{02}$ on MIIF for different volume fractions

8 Conclusions

Considering the aforementioned analytical and numerical studies done on the proposed model, the following points are concluded.

• (i) A complex variable and Stroh’s formalism technique is successfully applied to study the two unequal collinear semi-permeable cracks in a piezo-electro-magnetic media.

• (ii) The closed form analytic expressions are derived for the COD, COPD, COID, SIF, EDIF and the MIIF for the proposed model.

• (iii) Two non-linear equations are derived, to obtain the electric displacement and magnetic induction inside the crack gap media.

• (iv) The effect of volume fraction is observed on the intensity factors(IFs). All the IFs are decreased with the increase in the volume fraction.

• (v) The effect of the inter-crack distance is observed on the IFs. All the IFs are increased with the decrease in the inter-crack distance.

• (vi) The effect of crack length is observed on the IFs. All the IFs are increased with the increase in the crack length.

Appendices

Appendix (A)

$X_{1}(z)=\sqrt{(z-a)(z-b)(z-c)(z-d)},$         $P_{1}(z)=C_{0}z^{2}+C_{1}(z)+C_{2};$

$\triangle =\Lambda _{22}(\Lambda _{44}\Lambda _{55}-\Lambda _{45}\Lambda _{54}) - \Lambda _{24}(\Lambda _{42}\Lambda _{55}-\Lambda _{45}\Lambda _{52}) + \Lambda _{25}(\Lambda _{42}\Lambda _{54}-\Lambda _{44}\Lambda _{52});$

$\triangle _{1}=-\sigma _{22}^{\infty }(\Lambda _{44}\Lambda _{55}-\Lambda _{45}\Lambda _{54}) - (D^{c}-D_{2}^{\infty })(\Lambda _{24}\Lambda _{55}-\Lambda _{25}\Lambda _{54}) + (B^{c}-B_{2}^{\infty })(\Lambda _{25}\Lambda _{44}-\Lambda _{24}\Lambda _{45});$

$\triangle _{2}=\sigma _{22}^{\infty }(\Lambda _{42}\Lambda _{55}-\Lambda _{45}\Lambda _{52}) + (D^{c}-D_{2}^{\infty })(\Lambda _{22}\Lambda _{55}-\Lambda _{25}\Lambda _{52}) + (B^{c}-B_{2}^{\infty })(\Lambda _{25}\Lambda _{42}-\Lambda _{22}\Lambda _{45});$

$\triangle _{3}=\sigma _{22}^{\infty }(\Lambda _{44}\Lambda _{52}-\Lambda _{42}\Lambda _{54}) + (D^{c}-D_{2}^{\infty })(\Lambda _{24}\Lambda _{52}-\Lambda _{22}\Lambda _{54}) + (B^{c}-B_{2}^{\infty })(\Lambda _{22}\Lambda _{44}-\Lambda _{24}\Lambda _{42});$

$C_{0}=a_{11}a_{22}-a_{12}a_{21},$    $C_{1}=a_{20}a_{12}-a_{10}a_{22},$    $C_{2}=a_{21}a_{10}-a_{11}a_{20},$    $k^{2}=\dfrac{(a-b)(c-d)}{(a-c)(b-d)};$

$g=\dfrac{2}{\sqrt{(a-c)(b-d)}},$    $\alpha ^{2}=\dfrac{d-c}{a-c},$    $\beta ^{2}=\dfrac{a-b}{a-c},$    $a_{11}=g[aF(k)+(d-a){{\Pi }}(\alpha ^{2},k)];$

$a_{12}=gF(k),$         $a_{21}=g[cF(k)+(b-c){{\Pi }}(\beta ^{2},k)],$         $a_{22}=gF(k);$

$a_{10}=g\left[ a^{2}F(k)+2a(d-a){{\Pi }}(\alpha ^{2},k)+(d-a)^{2}V_{2}\right] ;$

$a_{20}=g\left[ c^{2}F(k)+2c(b-c){{\Pi }}(\beta ^{2},k)+(b-c)^{2}V_{3}\right] ;$

$V_{2}=\dfrac{1}{2(\alpha ^{2}-1)(k^{2}-\alpha ^{2})}\left\{ \alpha ^{2}E(k)+(k^{2}-\alpha ^{2})F(k)+(2\alpha ^{2}k^{2}+2\alpha ^{2}-\alpha ^{4}-3k^{2}){{\Pi }}(\alpha ^{2},k)\right\} ;$

$V_{3}=\dfrac{1}{2(\beta ^{2}-1)(k^{2}-\beta ^{2})}\left\{ \beta ^{2}E(k)+(k^{2}-\beta ^{2})F(k)+(2\beta ^{2}k^{2}+2\beta ^{2}-\beta ^{4}-3k^{2}){{\Pi }}(\beta ^{2},k)\right\} ;$

where F(k),  E(K) and ${{\Pi }}(\alpha ^{2},k)$ are the complete elliptic integrals of the first, second and third kind, respectively.

Appendix (B)

$\alpha _{1}^{2}=\dfrac{a}{d}\alpha ^{2},$    $\beta _{1}^{2}=\dfrac{c}{b}\beta ^{2},$    $\nu =sin^{-1}\sqrt{\dfrac{(a-c)(y-d)}{(d-c)(a-y)}},$    $\psi =sin^{-1}\sqrt{\dfrac{(a-c)(y-b)}{(a-b)(y-c)}};$

$S_{1}=\alpha ^{2}E(\nu ,k)+(k^{2}-\alpha ^{2})F(\nu ,k)+(2\alpha ^{2}k^{2}+2\alpha ^{2}-\alpha ^{4}-3k^{2}){{\Pi }}(\nu ,\alpha ^{2},k) - \dfrac{\alpha ^{4}\text {sn}{u}\text {cn}{u}\text {dn}{u}}{1-\alpha ^{2}\text {sn}^{2}{u}};$

where snu, cnu and dnu are the Jacobian elliptic functions.

$S_{2}=\beta ^{2}E(\psi ,k)+(k^{2}-\beta ^{2})F(\psi ,k)+(2\beta ^{2}k^{2}+2\beta ^{2}-\beta ^{4}-3k^{2}){{\Pi }}(\psi ,\beta ^{2},k) - \dfrac{\beta ^{4}\text {sn}{u}\text {cn}{u}\text {dn}{u}}{1-\beta ^{2}\text {sn}^{2}{u}};$

$S_{3}=d^{2}g\dfrac{\alpha _{1}^{4}}{\alpha ^{4}}\left\{ F(\nu ,k)+\dfrac{2(\alpha ^{2}-\alpha _{1}^{2})}{\alpha _{1}^{2}}{{\Pi }}(\nu ,\alpha ^{2},k)+ \dfrac{(\alpha ^{2}-\alpha _{1}^{2})^{2}}{2\alpha _{1}^{4}(\alpha ^{2}-1)(k^2-\alpha ^{2})}S_{1}\right\} ;$

$S_{4}=dg\dfrac{\alpha _{1}^{2}}{\alpha ^{2}}\left\{ F(\nu ,k)+\dfrac{\alpha ^{2}-\alpha _{1}^{2}}{\alpha _{1}^{2}}{{\Pi }}(\nu ,\alpha ^{2},k)\right\} ,$         $S_{5}=gF(\nu ,k);$

$S_{6}=b^{2}g\dfrac{\beta _{1}^{4}}{\beta ^{4}}\left\{ F(\psi ,k)+\dfrac{2(\beta ^{2}-\beta _{1}^{2})}{\beta _{1}^{2}}{{\Pi }}(\psi ,\beta ^{2},k)+ \dfrac{(\beta ^{2}-\beta _{1}^{2})^{2}}{2\beta _{1}^{4}(\beta ^{2}-1)(k^2-\beta ^{2})}S_{2}\right\} ;$

$S_{7}=bg\dfrac{\beta _{1}^{2}}{\beta ^{2}}\left\{ F(\psi ,k)+\dfrac{\beta ^{2}-\beta _{1}^{2}}{\beta _{1}^{2}}{{\Pi }}(\psi ,\beta ^{2},k)\right\} ,$         $S_{8}=gF(\psi ,k);$

where F(, k),  E(, k) and ${{\Pi }}(,\,\,k)$ are the incomplete elliptic integrals of first, second and third kinds, respectively.