Keywords

1 Introduction

Rough Set Theory (RST) [11] Reducts are minimal attribute subsets preserving the discernibility capacity of the whole set of attributes [12]. Reducts have been found useful for feature selection [9] and classification [10] among others. The main drawback of reducts is that computing the complete set of reducts for a decision system is an NP-hard problem [18]. However, most of the times, only a subset of reducts is necessary for real applications [4]. The set of all reducts with the minimum length (the shortest reducts) is particularly relevant for such applications, since it is a representative sample of all reducts [19]. Recently, the algorithm MinReduct, for computing all the shortest reducts, was reported [15].

Testor Theory [2] separately developed the concept of Typical Testor. Typical Testor and Reduct concepts are so close [3] that algorithms designed for computing typical testors can be used for computing reducts and vice versa [6]. Typical testors have been used for feature selection [16] and some other real-world applications [20]. Since computing all typical testors is also NP-hard, a significant runtime reduction can be obtained from computing only the set of all the minimum-length typical testors. For this purpose, the Minimum Length Irreducible Testors (MiLIT) algorithm was recently proposed [13]. The authors reported indeed two variants of MiLIT: the first one using an in-place search based on Next Combination (next attribute subset) calculation (NC) and the other one using a search with Pruning based on Feature and Row Contribution (PFRC).

The almost simultaneous publication of these algorithms that solve an equivalent problem deserves a comparative study. Thus, in this work, we present such a study with the aim of providing application suggestions and some foundations for the development of future algorithms. To this end, we will first provide a common theoretical framework for describing the algorithms under study. Then, a description in terms of asymptotic complexity will be presented. Finally, an experimental assessment of the three algorithms will be carried out over synthetic and real-world decision systems.

The rest of this paper is structured in the following way. In Sect. 2, some basic concepts from RST and the pruning properties used by the algorithms under study are presented. In Sect. 3, we describe the algorithms with an special emphasis in their asymptotic time complexity. Then, in Sect. 4, we present our experimental assessment and the discussion of the results. Finally, our conclusions appear in Sect. 5.

2 Theoretical Background

In this section, we introduce the main concepts of Rough Set Theory, as well as the definitions and propositions supporting the pruning strategies used in MiLIT and MinReduct. Notice that although MiLIT algorithms are designed in the top of Testor Theory, we will use concepts from Rough Set Theory for describing these algorithms.

In RST, a decision system (DS) is a table with rows representing objects while columns represent attributes. We denote by U a finite non-empty set of objects \(U=\lbrace x_1,x_2,...,x_n\rbrace \) and A is a finite non-empty set of attributes. For every attribute in A there is a mapping: \(a: U \rightarrow V_a\). The set \(V_a\) is called the value set of a. Attributes in A are further divided into condition attributes C and decision attributes D such that \(A=C \cup D\).

Decision attributes D induce a partition of the universe U into decision classes. Usually, we are interested in those classes induced by an attribute subset B that correspond to the decision classes. To this end, the B-positive region of D, denoted as \(POS_B(D)\), is defined as the set of all objects in U such that if two of them have the same value for every attribute in B, they belong to the same decision class.

A subset \(B \subseteq C\) is a decision reduct of DS relative to D if:

  1. 1.

    \(POS_B(D)=POS_C(D)\).

  2. 2.

    B is a minimal subset (regarding inclusion) fulfilling condition 1.

Decision reducts have the same capability as the complete set of condition attributes for discerning between objects from different classes (Condition 1), and every attribute in a reduct (typical testor) is indispensable for holding Condition 1 (Condition 2). A super-reduct (testor) is a set B that fulfills Condition 1, regardless of Condition 2. Decision reducts are called just reducts, for simplicity.

The Binary Discernibility Matrix is a binary table representing the discernibility information of objects belonging to different classes. The element m(i, j, c) regarding two objects \(x_i\) and \(x_j\) and a single condition attribute \(c \in C\) is defined as:

$$\begin{aligned} m(i, j, c)=\left\{ \begin{array}{cl} 1 &{} \mathrm {if~~}c(x_i) \ne c(x_j) \\ 0 &{} \mathrm {otherwise} \end{array}\right. \end{aligned}$$

The Simplified Binary Discernibility Matrix is a reduced version of the binary discernibility matrix after applying absorption laws. In Testor Theory [5] this concept is called Basic Matrix, and we will adopt this term for the rest of this document, because it is simple and explicit. From the basic matrix of a decision system all reducts can be computed [21].

2.1 Pruning Properties Used by the Algorithms Under Study

The reader can find the proof and a more detailed explanation of the following propositions in [13, 15].

Definition 1

B is a super-reduct iff in the sub-matrix of the basic matrix formed by the columns corresponding to the attributes in B, there is no zero row (a row with only zeros).

The attribute contribution, presented in Definition 2, is used by MinReduct and PFRC-MiLIT.

Definition 2

Given \(B \subseteq C\) and \(x_i \in C\) such that \(x_i \notin B\). \(x_i\) contributes to B iff the sub-matrix of the basic matrix formed with only those attributes in B has more zero rows than that matrix formed with attributes in \(B \cup \lbrace x_i \rbrace \).

The pruning based on Definition 2 is supported by Proposition 1.

Proposition 1

Given \(B \subseteq C\) and \(x_i \in C\) such that \(x_i \notin B\). If \(x_i\) does not contribute to B, then \(B\cup \{x_i\}\) cannot be a subset of any reduct.

The algorithms under study search for super-reducts (testors) instead of reducts (typical testors) supported by the following proposition, which was first introduced in [22]. This simplification reduces the cost of candidate subsets evaluations.

Proposition 2

Let \(B \subseteq C\), if B is one of the shortest super-reducts of a basic matrix, then it is also one of the shortest reducts.

MiLIT and MinReduct, as in many other algorithms for reduct (and typical testor) computation [7, 14, 17] arrange the basic matrix to reduce the search space. The arrangement consist in moving one of the rows with the fewest number of 1’s in the basic matrix to the top, and all columns in which this row has 1, are moved to the left. This arrangement reduces the attribute subsets evaluated by these algorithms which follow a traversing order that resembles the lexicographical order. The search can be stopped after all the attribute subsets that include an attribute of the columns having a 1 in the first row of the basic matrix are evaluated. For the rest of the attribute subsets in the search space (in the lexicographical order), the first row is always a zero row.

For PFRC-MiLIT the following proposition was presented:

Proposition 3

Given \(B \subseteq C\) and \(x_i \in C\) such that \(x_i \notin B\). If there exist a zero row in the sub-matrix of the basic matrix formed by the attributes in \(B\cup \{x_i\}\), that is also a zero row in the sub-matrix formed by the remaining attributes on the right side of \(x_i\). Then \(B\cup \{x_i\}\) cannot be a subset of any reduct.

Proposition 4 is used by MinReduct in order to avoid the unnecessary evaluation of super-sets of a reduct. If a given attribute subset does not hold this proposition, Condition 2 of the reduct definition cannot be met because it has excluding (redundant) attributes. The verification of Proposition 4 is called exclusion evaluation.

Proposition 4

Given \(B \subseteq C\), if B is a subset of a reduct, \(\forall x_i \in B\) exists at least one row in the sub-matrix formed by the attributes in B that has a 1 in the column corresponding to \(x_i\) and 0 in all other columns.

3 MiLIT and MinReduct Algorithms

We present here a brief description of the three algorithms under study. In the subsequent explanation, the asymptotic time complexity of each algorithm is detailed. For this purpose, the number of rows in the basic matrix is denoted by m, the number of columns is denoted by n, the number of 0’s in the first row of the arranged basic matrix is denoted by \(n_0\) and the length of the shortest reducts is denoted by k.

3.1 NC-MiLIT

The key pruning goal of any algorithm designed for computing the shortest reducts consist in evaluating only attribute subsets with a length not higher than that of the shortest reducts (k). Unfortunately, the length of the shortest reducts cannot be known a priori. In fact, the idea of estimating by an approximate algorithm this length and then use it as a parameter for the exact algorithm computing all the shortest reducts was reported in [8].

Both versions of the MiLIT (NC and PFRC) ensure the evaluation of only attribute subsets with a length not higher than k by their traversing order.

For each candidate subset evaluated by NC-MiLIT the super-reduct property is verified by means of Definition 1. This verification has a time cost of \(\varTheta (m\times k)\). The number of evaluations can be precisely determined for this algorithm. To the number of subsets that can be generated with length lower than or equal to k with the n attributes (Eq. 1) we must subtract the avoided evaluations of those attribute subsets that do not include an attribute of the columns having a 1 in the first row (Eq. 2).

$$\begin{aligned} C(n,k) = \sum _{i=1}^{k} \left( {\begin{array}{c}n\\ i\end{array}}\right) \end{aligned}$$
(1)
$$\begin{aligned} C(n_0,k)= \sum _{i=1}^{\mathrm {min}(n_0,k)} \left( {\begin{array}{c}n_0\\ i\end{array}}\right) \end{aligned}$$
(2)

Thus, the time complexity of the NC-MiLIT algorithm can be expressed by Eq. 3

$$\begin{aligned} T_{NC} = \varTheta \left( (m\times k)\left( \sum _{i=1}^{k} \left( {\begin{array}{c}n\\ i\end{array}}\right) - \sum _{i=1}^{\mathrm {min}(n_0,k)} \left( {\begin{array}{c}n_0\\ i\end{array}}\right) \right) \right) \end{aligned}$$
(3)

3.2 PFRC-MiLIT

The PFRC-MiLIT algorithm includes the verification of contribution (Proposition 1) and the zero row remanence (Proposition 3) for each evaluated candidate. The idea is to avoid subsets that are super-sets of any candidate with a non contributing attribute or with remanent zero rows, since they cannot form reducts. Both properties can be verified in time \(\varTheta (m\times k)\) which makes no difference with NC-MiLIT in terms of asymptotic complexity. However, this evaluation process requires more computation time, but a great number of candidates can be avoided in this way. In practical terms, this pruning is achieved by means of a queue data-structure in which those subsets that will not lead to a reduct are not enqueued.

For PFRC-MiLIT, the time complexity computed by Eq. 3 is the upper bound. This can be expressed as it is shown in Eq. 4. The actual number of candidates evaluated depends on the distribution of the data in the basic matrix. The authors of MiLIT claim that in sparse matrices these avoided subsets are very common, which seems obvious after Proposition 3.

$$\begin{aligned} T_{PFRC} = O\left( (m\times k)\left( \sum _{i=1}^{k} \left( {\begin{array}{c}n\\ i\end{array}}\right) - \sum _{i=1}^{\mathrm {min}(n_0,k)} \left( {\begin{array}{c}n_0\\ i\end{array}}\right) \right) \right) \end{aligned}$$
(4)

3.3 MinReduct

MinReduct traverses the search space of attribute subsets using a depth-first search. When a new attribute is added to the current attribute subset candidate, it is verified for contribution as in Definition 2. This verification can be computed in a time \(\varTheta (m)\) by means of a binary cumulative mask. If the new attribute contributes, the current candidate is evaluated for the super-reduct condition, otherwise the new attribute is discarded and several subsets are pruned. Evaluating the super-reduct condition as in Definition 1 requires also a time \(\varTheta (m)\) by means of the same binary cumulative mask. This cumulative computation can be achieved because of the traversing order followed by this algorithm. The disadvantage of this traversing order is that some subsets with a length higher than that of the shortest reducts may be evaluated.

The main pruning property of MinReduct consists in avoiding the evaluation of candidates with length higher than the shortest reduct found so far. Since the length of the shortest reducts is unknown at the beginning of the algorithm, the asymptotic upper bound of the number of candidates evaluated by MinReduct (ss) can be expressed by Eq. 5.

$$\begin{aligned} ss = O\left( \sum _{i=1}^{k} \left( {\begin{array}{c}n\\ i\end{array}}\right) - \sum _{i=1}^{\mathrm {min}(n_0,k)} \left( {\begin{array}{c}n_0\\ i\end{array}}\right) +f(n)\right) \end{aligned}$$
(5)

In Eq. 5, f(n) represents the number of subsets with length higher than k that are evaluated before the first of the shortest reducts is found. There are many algorithms for estimating k in a time proportional to n [8]. However, estimating k a priori makes no significant improvement to MinReduct because the algorithm itself will find a good estimate in a relatively short runtime. Therefore, we can substitute Eq. 5 by Eq. 6, which is the same upper bound of evaluated candidates than PFRC-MiLIT.

$$\begin{aligned} ss = O\left( \sum _{i=1}^{k} \left( {\begin{array}{c}n\\ i\end{array}}\right) - \sum _{i=1}^{\mathrm {min}(n_0,k)} \left( {\begin{array}{c}n_0\\ i\end{array}}\right) \right) \end{aligned}$$
(6)

In MinReduct, the time complexity for the evaluation of subsets that do not include the last column of the arranged basic matrix (\(c_{max}\)) is \(\varTheta (m)\). The worst case time complexity for those subsets including \(c_{max}\) is \(\varTheta (nm)\), because the exclusion evaluation may be required. The number of such subsets (\(ss_{c_{max}}\)) has an asymptotic upper bound as shown in Eq. 7.

$$\begin{aligned} ss_{c_{max}}= O\left( \frac{1}{n-1}\sum _{i=1}^{k} \left( {\begin{array}{c}n\\ i\end{array}}\right) - \frac{1}{n_0-1}\sum _{i=1}^{\mathrm {min}(n_0,k)} \left( {\begin{array}{c}n_0\\ i\end{array}}\right) \right) \end{aligned}$$
$$\begin{aligned} ss_{c_{max}}= O\left( \frac{1}{n}\sum _{i=1}^{k} \left( {\begin{array}{c}n\\ i\end{array}}\right) - \frac{1}{n_0}\sum _{i=1}^{\mathrm {min}(n_0,k)} \left( {\begin{array}{c}n_0\\ i\end{array}}\right) \right) \end{aligned}$$
(7)

Thus, we can compute the upper bound of the asymptotic time complexity (\(T_{MR}\)) for MinReduct by the following expression:

$$\begin{aligned} T_{MR} = O\left( m*ss + mn*ss_{c_{max}}\right) \end{aligned}$$
(8)
$$\begin{aligned} T_{MR} = O\left( m\left[ \sum _{i=1}^{k} \left( {\begin{array}{c}n\\ i\end{array}}\right) - \sum _{i=1}^{\mathrm {min}(n_0,k)} \left( {\begin{array}{c}n_0\\ i\end{array}}\right) \right] +mn\left[ \frac{1}{n}\sum _{i=1}^{k} \left( {\begin{array}{c}n\\ i\end{array}}\right) - \frac{1}{n_0}\sum _{i=1}^{\mathrm {min}(n_0,k)} \left( {\begin{array}{c}n_0\\ i\end{array}}\right) \right] \right) \end{aligned}$$
$$\begin{aligned} T_{MR} = O\left( m\left[ 2\sum _{i=1}^{k} \left( {\begin{array}{c}n\\ i\end{array}}\right) - \left( 1 + \frac{n}{n_0}\right) \sum _{i=1}^{\mathrm {min}(n_0,k)} \left( {\begin{array}{c}n_0\\ i\end{array}}\right) \right] \right) \end{aligned}$$
(9)

4 Experimental Comparison

In this section, an experimental comparison of MiLIT and MinReduct is presented. For this experiment, 500 randomly generated basic matrices with 2000 rows and 30 columns are used. These dimensions were selected as in [14], to keep the runtime for the algorithms within reasonable boundaries. These basic matrices have densities of 1’s uniformly distributed in the range (0.20-0.80). In addition, the algorithms were tested over 13 decision systems taken from the UCI machine learning repository [1] and 15 high dimension synthetic basic matrices. All experiments were run on a PC with a Core i3-7100 Intel processor at 3.90 GHz, with 8 GB in RAM, running GNU/Linux. We thankfully acknowledge the authors of MiLIT [13] for sharing the source code of their Java implementations of the MiLIT algorithm.

Fig. 1.
figure 1

Average runtime vs. density of 1’s for MinReduct and MiLIT.

Full size image
Fig. 2.
figure 2

Runtime for matrices with 1200 rows and density 0.33.

Full size image

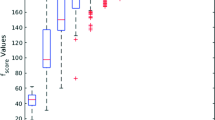
Figure 1 shows the average runtime for MiLIT (NC and PFRC) and MinReduct as a function of the density of 1’s over the 500 synthetic basic matrices. The 500 matrices were divided into 15 bins by discretizing the range of densities, for clarity purposes. As it can be seen in Fig. 1, MinReduct was the fastest in general.

Figure 2 shows the runtime of MiLIT (NC and PFRC) and MinReduct for 13 matrices with 1200 rows and density 0.33 with a number of columns ranging from 30 to 54. These matrices were included in order to explore the performance of the algorithms when the number of attributes increases. For these matrices MinReduct was also the fastest algorithm without any apparent relation to the number of attributes of the basic matrix.

Table 1. Runtime (in seconds) over synthetic and real-world data.
Full size table

Table 1 shows the runtime of MiLIT (NC and PFRC) and MinReduct (MR), in milliseconds, for 13 decision systems taken from the UCI machine learning repository and two high dimension synthetic basic matrices. This is a more heterogeneous experiment in terms of density and dimensions than our two previous experiments. The first columns in Table 1 shows the name of the dataset, the number of attributes (Atts), the number of rows in the basic matrix (Rows), the density of the basic matrix (Dens), the number of shortest reducts (Nsol) and the length of the shortest reducts (Len). Decision systems in Table 1 are sorted in ascending order regarding the density of their basic matrix. Although MinReduct was the fastest in most cases, for the first three matrices, PFRC-MiLIT showed a significant runtime reduction regarding MinReduct and NC-MiLIT. This result corresponds to the benefits expected from the application of Proposition 3 for sparse matrices.

4.1 Discussion

As a result of these experiments carried out over 528 matrices, NC-MiLIT was the fastest algorithm in 11 matrices with no significant runtime reduction in any case. On the contrary, PFRC-MiLIT was the fastest algorithm in only three matrices, but it showed a significant runtime reduction in those matrices.

PFRC-MiLIT incorporates pruning strategies over the feature power set to make fewer evaluations than NC-MiLIT. Although using a breadth-first search for finding all the shortest reducts guarantees that no subset with length higher than k is evaluated, it is less efficient in terms of time and space, than the traditional depth-first search used in most algorithms for reduct computation. Thus, from our experiments we conclude that the evaluation of Proposition 3 for sparse matrices is the main contribution of PFRC-MiLIT. In [13] an upper threshold density of 0.3 was estimated for the application of PFRC-MiLIT. After our experiments, we recommend to reduce this value to 0.15.

5 Conclusions

In this paper we present a comparative study of MiLIT and MinReduct: two recent algorithms for computing all the shortest reducts (minimum length irreducible testors). Although MiLIT comes from the Testor Theory and MinReduct comes from the Rough Set Theory, both algorithms are intended to solve an equivalent algorithmic task. A description of the algorithms in terms of asymptotic complexity was presented. Finally, an experimental comparison over synthetic basic matrices and real-world decision systems taken from the UCI machine learning repository was carried out.

From our experiments, we have concluded that PFRC-MiLIT is the fastest algorithm for sparse basic matrices with densities under 0.15. The main advantage of PFRC-MiLIT relays on the evaluation of the zero row remanence on these sparse matrices. We have also found that the breadth-first search used in MiLIT is less efficient than the traditional depth-first search used in MinReduct, for candidate evaluation. Thus, MinReduct was faster than MiLIT for basic matrices with densities above 0.15 in most cases.

An interesting study for future work would be assessing the performance of verifying the zero row remanence using a depth-first search, for sparse basic matrices. A deeper study involving basic matrices with densities under 0.15 is needed for providing a stronger conclusion on sparse basic matrices.