Efficient Steady Flow Computations with Exponential Multigrid Methods

Abstract

An exponential multigrid framework is developed and assessed with a modal high-order discontinuous Galerkin method in space. The algorithm based on a global coupling, exponential time integration scheme provides strong damping effects to accelerate the convergence towards the steady-state, while high-frequency, high-order spatial error modes are smoothed out with a s-stage preconditioned Runge-Kutta method. Numerical studies show that the exponential time integration substantially improves the damping and propagative efficiency of Runge-Kutta time-stepping for use with the p-multigrid method, yielding rapid and p-independent convergences to steady flows in both two and three dimensions.

1 Introduction

An important requirement for computational fluid dynamics is the capability to predict steady flows such as the case of flow past a body, so that key performance parameters, e.g., the lift and drag coefficients can be estimated. While the classical second-order methods are still being used extensively, high-order spatial discretizations attract more attention. For steady-state computations, most of the spatial discretizations have rested on the use of limited, traditional time discretizations combining with various acceleration methods. Recently, as an alternative to traditional time-marching methods, an exponential time integration scheme, the predictor-corrector exponential time-integrator scheme (PCEXP) [1,2,3,4,5] has been developed and successfully applied to the time stepping of fluid dynamics equations, exhibiting some advantages in terms of accuracy and efficiency for solving the fluid dynamics equations in both time-dependent and time-independent regimes.

In this paper, the exponential time integration is exploited in a multigrid framework which consists of an exponential time marching method and a s-stage preconditioned Runge-Kutta method as an effective way to increase the feasibility of arbitrarily p-order DG for the high-order simulations of steady-state flows. The remainder of this paper is organized as follows. Section 2 presents the multigrid algorithm which combines two stand-alone methods in a V-cycle p-multigrid framework. Section 3 introduces the spatial discretization with a modal high-order DG method. Section 4 discusses how to evaluate the time steps in the p-multigrid framework. Section 5 presents the numerical results including two inviscid flow problems: (a) flow past a circular cylinder; (b) flow flow over a sphere. The numerical results obtained with the exponential p-multigrid method (eMG) are compared directly with a fully implicit method solved with the Incomplete LU preconditioned GMRES (ILU-GMRES) linear solver. Finally, Sect. 6 concludes this work. The Appendix provides the details of Jacobian matrices for the DG space discretization and time-step evaluations.

2 Exponential Multigrid Frame

In this section, a high-order (p) multigrid frame is detailed which is expected to have comparable performance to implicit methods for steady flow computations. The algorithm combines two stand-alone methods: the exponential time integration method and a s-stage preconditioned Runge-Kutta method. The two methods are introduced separately first and are finally integrated into a whole V-cycle multigrid frame.

2.1 Exponential Time Integration

We start with the following semi-discrete system of ordinary differential equations which may be obtained from a spatial discretization:

(1)

where $\mathbf {u} = \mathbf {u}(t) \in \mathbb {R}^K$ denotes the vector of the solution variables and $\mathbf {R}(\mathbf {u}) \in \mathbb {R}^K$ the right-hand-side term which may be the spatially discretized residual terms of the discontinuous Galerkin method used in this work. The dimension K is the degrees of freedom which can be very large for 3-D problems. Without loss of generality, we consider u(t) in the interval of one time step, i.e., t ∈ [t _n, t _n+1]. Applying the term splitting method [6] to (1) leads to a different exact expression

(2)

where the subscript n indicates the value evaluated at t = t _n, J _n denotes the Jacobian matrix and N(u) = R(u) −J _n u denotes the remainder, which in general is nonlinear. Equation (2) admits the following formal solution:

$$\displaystyle \begin{aligned} {\mathbf{u}}_{n+1} = \exp (\Delta t {\mathbf{J}}_n) {\mathbf{u}}_n + \int\limits_{0}^{\Delta t} \exp {\left( (\Delta t-\tau) {\mathbf{J}}_n \right)} \mathbf{N} {\left( \mathbf{u}(t_n + \tau) \right)} {\mathrm{d}\tau} , {} \end{aligned} $$

(3)

where Δt = t _n+1 − t _n and

(4)

If using (3), the stiff linear term and the nonlinear integral term could be computed separately. The linear term could be computed analytically for some specialized equations but the nonlinear term is usually approximated numerically. In this paper, we use its equivalent form (5) instead, in which the linear and nonlinear terms are collected into a single term so that it can be efficiently approximated at one time.

Recently, a two-stage exponential scheme PCEXP [5] is shown to be effective for computing various flow regimes. However, using only the first stage of PCEXP, namely, the EXP1 scheme [1, 3] is shown to be more efficient for steady flows, although it is incapable of solving unsteady flows. Considering the constant approximation of the nonlinear term leads to the EXP1 scheme, namely

$$\displaystyle \begin{aligned} {\mathbf{u}}_{n+1} = \exp(\Delta t {\mathbf{J}}_n) {\mathbf{u}}_n + {\Delta t} \mathbf{\Phi}_1(\Delta t {\mathbf{J}}_n) {\mathbf{N}}_n = {\mathbf{u}}_n + {\Delta t} \mathbf{\Phi}_1(\Delta t {\mathbf{J}}_n) {\mathbf{R}}_n , {} \end{aligned} $$

(5)

where

(6)

and I denotes the K × K identity matrix.

The physical nature of such type of exponential schemes relies on the global coupling feature via the global Jacobian matrix J, so that flow transportation information can be broadcasted to the whole computational domain without a CFL restriction. That is why the exponential schemes behave like a fully implicit method but only depends on the current solution, i.e., in an explicit way as (5). Therefore, the EXP1 scheme is curiously exploited in the p-multigrid framework for steady flow computations.

2.2 Realization of EXP1 with the Krylov Method

The implementation of exponential time integration schemes requires evaluations of matrix-vector products, and in particular, the product of the exponential functions of the Jacobian and a vector, e.g., Φ ₁( Δt J _n)N in (5). They can be approximated efficiently using the Krylov method [7, 8]. Consider a m-dimensional Krylov subspace

(7)

The orthogonal basis matrix satisfies the so-called Arnoldi decomposition [8]:

$$\displaystyle \begin{aligned} \mathbf{J} {\mathbf{V}}_m = {\mathbf{V}}_{m+1} \widetilde{\mathbf{H}}_m , {}\end{aligned} $$

(8)

where . The matrix $\widetilde {\mathbf {H}}_m$ is the (m + 1) × m upper-Hessenberg matrix. Then (8) becomes

$$\displaystyle \begin{aligned} \mathbf{J} {\mathbf{V}}_m = {\mathbf{V}}_m {\mathbf{H}}_m + h_{m+1,m} {\mathbf{v}}_{m+1} {\mathbf{e}}_m^{\mathrm{T}} . {} \end{aligned} $$

(9)

Because ${\mathbf {V}}_m^{\mathrm {T}} {\mathbf {V}}_m = \mathbf {I}$, therefore

$$\displaystyle \begin{aligned} {\mathbf{H}}_m = {\mathbf{V}}^{\mathrm{T}}_m \mathbf{J} {\mathbf{V}}_m , {} \end{aligned} $$

(10)

H _m is thus the projection of the linear transformation of J onto the subspace $\mathbb {K}_m$ with the basis $\mathbb {V}_m$. Since ${\mathbf {V}}_m {\mathbf {V}}_m^{\mathrm {T}} \neq \mathbf {I}$, (10) leads to the following approximation:

$$\displaystyle \begin{aligned} \mathbf{J} \approx {\mathbf{V}}_m {\mathbf{V}}^{\mathrm{T}}_m \mathbf{J} {\mathbf{V}}_m {\mathbf{V}}^{\mathrm{T}}_m = {\mathbf{V}}_m {\mathbf{H}}_m {\mathbf{V}}^{\mathrm{T}}_m , \end{aligned} $$

(11)

and $\exp (\mathbf {J})$ can be approximated by $\exp ( {\mathbf {V}}_m {\mathbf {H}}_m {\mathbf {V}}^{\mathrm {T}}_m )$ as below

$$\displaystyle \begin{aligned} \exp (\mathbf{J}) \mathbf{N} \approx \exp({\mathbf{V}}_m {\mathbf{H}}_m {\mathbf{V}}^{\mathrm{T}}_m) \mathbf{N} = {\mathbf{V}}_m \exp ( {\mathbf{H}}_m ) {\mathbf{V}}^{\mathrm{T}}_m \mathbf{N} . {} \end{aligned} $$

(12)

The first column vector of V _m is and , thus (12) becomes

(13)

Consequently, Φ ₁ can be approximated by

(14)

In general, the dimension of the Krylov subspace, m, is chosen to be much smaller than the dimension of J, K, thus, ${\mathbf {H}}_m \in \mathbb {R}^{m\times m}$ can be inverted easily, so Φ ₁ can be easily computed as the following

(15)

where the matrix-exponential $\exp (\Delta t {\mathbf {H}}_m)$ can be computed efficiently by the Chebyshev rational approximation (cf., e.g., [8, 9]) due to the small size of H _m.

2.3 Preconditioned Runge-Kutta Method

Consider a s-stage preconditioned Runge-Kutta (PRK) method of the following form

(16)

where $\beta _k = 1/ {\left (s-k+1\right )}$. P is taken as the diagonal part of the global residual Jacobian , representing the element-wise wave propagation information. s = 4 is used for all the test cases of this work.

The physical nature of this type of RK method can be interpreted in two different views which are helpful for us to see how does PRK make sense. First, we consider the first-order spatial discretization of finite volume or discontinuous Galerkin method to the i-th element surrounded by adjoined cells j (1 ≤ j ≤ N) with the inter-cell surface area S_ij, and the spatial residual using a upwinding flux can be written as

(17)

So P can be derived as

(18)

A matrix Δt can be defined as

(19)

One can uncover the relationship between the matrix Δt and the traditional definition of time step by considering a cell-constant scalar spectral radius approximation $\lambda _{ij}^{\max }$ to , i.e.,

$$\displaystyle \begin{aligned} \Delta {t} = \frac{2 V_i}{\sum_{j=1}^{N}{{\lambda_{ij}^{\max}}\mathrm{S}_{ij} }} \overset{1D} \longrightarrow \frac{\Delta x_i}{\lambda_{i}^{\max}} \end{aligned} $$

(20)

Therefore, P ⁻¹ is equivalent to a matrix time step and it is consistent to the usual definition of time step in the scalar case. As demonstrated in [10], this matrix is a kind of preconditioner which can provide effective clustering of convective eigenvalues and substantial improvements to the convergence of RK time-stepping. In this work, different from [10], an exact way of evaluating matrix time steps with exact Jacobian is proposed in [3] so that all the stiffness effects from spatial discretizations and boundary conditions can be exactly taken into account. Note that such a matrix time stepping has no temporal order of accuracy, since the traditional scalar, physical time step dose not show up at all. Therefore, the PRK scheme has no temporal order of accuracy. The formula of PRK scheme can be considered as a simplified fully implicit scheme or implicit-explicit Runge Kutta methods, but has it own physical significance. To increase robustness, we recommend to increase diagonal domination to P, namely, , where δτ is a pseudo time step which is computed by (32).

2.4 The V-Cycle p-Multigrid Framework

The use of p-multigrid smoother with explicit RK or preconditioned RK methods is observed inefficient at eliminating low-frequency error modes at lower orders of accuracy. To provide a better smoother with stronger damping effects, the EXP1 scheme that exhibits fast convergence rates for Euler and Navier-Stokes equations is considered. Unlike the explicit RK smoother that only produces weak damping effects in a local, point-wise manner, the exponential scheme is a global method that allows large time steps with strong damping effects to all the frequency modes across the computational domain, as shown in the previous works [3].

In the exponential p-multigrid method (eMG), the EXP1 scheme is utilized on the accuracy level p = 0 and the PRK method is used for accuracy levels p > 0, contributing both memory deduction and efficiency enhancement. The smoothing employs a V-cycle p-multigrid process, where a two-level algorithm is recursively used. To illustrate the algorithm, let us consider a nonlinear problem A(u ^p) = p ^p, where u ^p is the solution vector, A(u ^p) is the nonlinear operator and p denotes the accuracy level of DG. Let v ^p be an approximation to the solution vector u ^p and define the residual r(v ^p) by

$$\displaystyle \begin{aligned} \mathbf{r}({\mathbf{v}}^p) = {\mathbf{f}}^p - {\mathbf{A}}^p({\mathbf{v}}^p) . \end{aligned}$$

In the eMG framework, the solution on the p − 1 level is used to correct the solution of p level in the following steps:

• 1. Conduct a time stepping with the PRK scheme on the highest accuracy level $p_{\max }$.

• 2. Restrict the solution and the residual of p to the p − 1 level ($1 \le p \le p_{\max }$)

  

  (21)

  where $\mathcal {R}_p^{p-1}$ is the restriction operator from the level p to the level p − 1.

• 3. Compute the forcing term for the p − 1 level

  $$\displaystyle \begin{aligned} {\mathbf{s}}^{p-1} = {\mathbf{A}}^{p-1}({\mathbf{v}}^{p-1}_0) - {\mathbf{r}}^{p-1} . \end{aligned} $$

  (22)

• 4. Smooth the solution with the PRK scheme on the p − 1 level but switch to use the EXP1 scheme on the lowest accuracy level p = 0,

  $$\displaystyle \begin{aligned} {\mathbf{A}}^{p-1}({\mathbf{v}}^{p-1}) = \mathcal{R}_p^{p-1} {\mathbf{f}}^p + {\mathbf{s}}^{p-1} . \end{aligned} $$

  (23)

• 5. Evaluate the error of level p − 1

  $$\displaystyle \begin{aligned} {\mathbf{e}}^{p-1} = {\mathbf{v}}^{p-1} - {\mathbf{v}}^{p-1}_0 . \end{aligned} $$

  (24)

• 6. Prolongate the p − 1 error and correct the approximation of level p

  $$\displaystyle \begin{aligned} {\mathbf{v}}^p = {\mathbf{v}}^p + \mathcal{P}_{p-1}^p {\mathbf{e}}^{p-1} ,\end{aligned} $$

  (25)

  where $\mathcal {P}_{p-1}^p$ is the prolongation operator.

3 Spatial Discretization

In this paper, the eMG method is applied to solve three-dimensional Euler equations discretized by a modal discontinuous Galerkin method. Consider the Euler equations in three-dimensional space

$$\displaystyle \begin{aligned} \frac{\partial \mathbf{U}}{\partial t} + \div{\mathbf{F}} = 0 , {} \end{aligned} $$

(26)

where U stands for the vector of conservative variables, F denotes the convective flux

(27)

where $\boldsymbol {v} = {\left (u, v, w\right )}^{\mathrm {T}}$ is the absolute velocity, ϱ, p, and e denote the flow density, pressure, and the specific internal energy; and H = E + p∕ϱ denote the total energy and total enthalpy, respectively; I denotes the 3 × 3 unit matrix; and the pressure p is given by the equation of state for a perfect gas

$$\displaystyle \begin{aligned} p=\varrho {\left(\gamma-1\right)} e , \end{aligned} $$

(28)

where γ = 7∕5 is the ratio of specific heats for perfect gas.

3.1 Modal Discontinuous Galerkin Method

Considering a computational domain Ω divided into a set of non-overlapping elements of arbitrary shape, the modal discontinuous Galerkin method [3] seeks an approximation U _h in each element E ∈ Ω with finite-dimensional space of polynomial P ^p of order p in the discontinuous finite element space

(29)

The numerical solution of U _h can be approximated in the finite element space $\mathbb {V}_h$

$$\displaystyle \begin{aligned} {\mathbf{U}}_h(\mathbf{x},\, t ) = \sum_{j = 1}^n {\mathbf{u}}_j(t) \psi_j( \mathbf{x} ) . {} \end{aligned} $$

(30)

In the weak formulation, the Euler equations (26) in an element E becomes:

(31)

where $\hat {\mathbf {n}}$ is the out-normal unit vector of the surface element σ with respect to the element E, $\widetilde {\mathbf {F}}$ is the Riemann solver [11], which will be approximated by Roe scheme [12], and the Einstein summation convention is used. For an orthonormal basis ${\left \{\psi _i\right \}}$, the term on the left-hand side of (31) becomes diagonal, so the system is in the standard ODE form of (1), thus avoiding solving a a linear system as required for a non-orthogonal basis. More importantly, using an orthogonal basis would yield more accurate solutions, especially for high-order methods, e.g., p = 6.

4 Time-Stepping Strategy

In this section, the time-stepping strategy of the eMG framework is discussed as a time-marching solver to compute the steady solutions of the Euler equations. There are two different time steps needed to be determined. One for the PRK time stepping δτ and the other for EXP1 smoothing which is empirically chosen as large as ${\left (p_{\max }+1\right )} \delta \tau$. As such, only δτ should be determined. δτ is determined by

(32)

where CFL is the global Courant-Friedrichs-Lewy (CFL) number, p the accuracy level, v the velocity vector at the cell center, c the speed of sound, d the spatial dimension, ${\left \vert E\right \vert }$ and ${\left \vert \partial E \right \vert }$ are the volume and the surface area of the boundary of E, respectively; and h _3D represents a characteristic size of a cell in 3D defined by the ratio of its volume and surface area. All the methods mentioned in this paper have been implemented in the HA3D flow solver developed by the author, which is for solving three-dimensional problems as its name indicates. So to support 2-D computations, a 2-D mesh is extruded to a 3-D (quasi-2D) mesh by one layer of cells and we use h _2D instead of h _3D to eliminate the effect of the z dimension on obtaining the truly 2-D time step. Given the cell size Δz in the z direction, h _2D is determined by

$$\displaystyle \begin{aligned} \frac{2}{h_{\mathrm{2D}}} = \frac{3}{{h}_{\mathrm{3D}}} - \frac{1}{\Delta z}. {} \end{aligned} $$

(33)

To enhance the computational efficiency for the steady problems, the CFL number of both schemes are dynamically determined by the following formula

(34a)

(34b)

where R(ϱ _n) denotes the residual of density, $\mathit {CFL}_{\max }$ is the user-defined maximal CFL number, n is the number of iterations, and p is the spatial order of accuracy. Such a variable CFL evolution strategy allows a robust code startup and good overall computational efficiency in practices. In all the test cases considered, the upper-bound CFL number of (34a) is taken as follows: $\mathit {CFL}_{\max }=10^3$ for the implicit BE method; $\mathit {CFL}_{\max }=10^2$ for the eMG method.

5 Numerical Results

In this section, we focus on the investigations of performance and convergence of the eMG framework. The feasibility is of eMG is demonstrated and compared to a fast fully implicit ILU preconditioned GMRES method. Two external flow cases are considered: flows past a circular cylinder in quasi-2D and a sphere in 3D. Since both eMG and GMRES are based on the Krylov subspace, the same Krylov space parameters are used. The Krylov subspace dimension m is 30 and the tolerance of Krylov subspace approximation error is 10⁻⁵, see Saad’s classic works [8, 13] for more details about the error estimations. The fastest first-order backward Euler (BE) discretization solved with the ILU preconditioned GMRES linear solver is used as the performance reference solution.

5.1 Flow Over a Circular Cylinder in Quasi-2D

In this case, the results obtained for flow over a circular cylinder at Mach number Ma = 0.3 is presented. The cylinder has a radius of 1 and is surrounded in a circular computational domain of radius 15, as shown in Fig. 1. The quasi-2D mesh with quadratic curved hexahedral elements is generated by extruding the 2D mesh by one layer of grids. The final 3D mesh is used by the HA3D arbitrarily high-order discontinuous Galerkin flow solver[1,2,3,4,5]. The total degree of freedoms is up to 81,920 with DG at p = 3.

Fig. 1

Flow over a circular cylinder in quasi-2D: quadratic curved elements

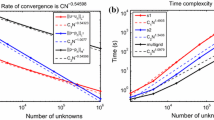
In Fig. 2, the L ₂ norm of density residual R(ϱ _n) is plotted versus the iteration by using the eMG scheme, indicating convergence rates independent of spatial order of accuracy p, or say p-independent. The results obtained with a fast, implicit ILU preconditioned GMRES is computed in Fig. 3, which shows the convergence histories of the implicit method with varying spatial accuracy. The results show rapid quadratic Newton convergences which are dependent on the spatial order of accuracy p. To see how promising is the eMG performance comparing with the fully implicit method, the two results are compared in Fig. 4, where the CPU time is normalized by that of the eMG scheme. As we can see, the implicit method (IMP) is faster for p = 1, 2 cases but is slower than the eMG scheme for the p = 3 case. So for high-order computations, the eMG method is at least comparable to the implicit method in terms of overall performance.

Fig. 2

Flow over a circular cylinder in quasi-2D: p-independent convergences with the eMG method

Fig. 3

Flow over a circular cylinder in quasi-2D: Convergence histories of the implicit method with varying spatial accuracy

Fig. 4

Flow over a circular cylinder in quasi-2D: Performance comparison between the eMG method and the implicit method at different spatial accuracy

5.2 Flow Over a Sphere in 3D

The computational efficiency of the eMG scheme is investigated for the three-dimensional flow past a sphere with the Mach number Ma = 0.3. The radius of the sphere is 1 and the far-field spherical radius is 5. The sphere surface is set as a slip wall boundary condition, and the outer boundary uses a far-field characteristic boundary condition with Riemann invariants. The mesh respects the flow symmetries of the horizontal and vertical planes, on which a symmetry boundary condition is imposed. The generated curved mesh consists of 9778 tetrahedrons and 4248 prisms, 14,026 cells in total. A close-up view of the mesh about the sphere and the velocity contour computed with the eMG scheme at p = 3 is illustrated in Fig. 5.

Fig. 5

Flow contour computed for the flow past a sphere at Ma = 0.3 with eMG and DG p = 3

Figure 6 shows the convergence histories of the eMG method for spatial order of accuracy p = 1, 2, 3. Again, p-independent convergences do appear. In Fig. 7, convergence histories of the implicit method (IMP) are shown with iteration counts. Figure 8 compares both methods measured in CPU time. As one can see that although IMP is fast in terms of iteration counts, the computational cost per iteration is relatively high and the resulting CPU time is penalized. When using high-order spatial schemes along with an implicit method, the high-order global Jacobian matrix consumes a large amount of memory. The most significant part of memory usage (M) of the two methods eMG and IMP are compared as follows

$$\displaystyle \begin{aligned} \mathrm{M}_{\mathrm{emg}} &= \mathrm{NE} {\left[\frac{5}{3}(p+1)(p+2)(p+3) + 150\right]} , \\ \mathrm{M}_{\mathrm{imp}} &= 6 \mathrm{NE} {\left[\frac{5}{6}(p+1)(p+2)(p+3)\right]}^2 . \end{aligned} $$

(35)

For problems sized up to NE = 10⁵ elements at p = 3, fourth-order spatial accuracy, a fully implicit method requires 45 GB memory only for storing the Jacobian matrix, while eMG only requires 0.03 GB memory for storing the solution vectors plus the first-order Jacobian matrix for the same sized problem. Therefore, the eMG method is far more memory friendly compared with a fully implicit method, providing a more practical while efficient strategy for solving steady problems with high-order methods.

Fig. 6

Flow over a sphere in 3D: p-independent convergences with the eMG method

Fig. 7

Flow over a sphere in 3D: convergence histories of the implicit method with varying spatial accuracy

Fig. 8

Flow over a sphere in 3D: performance comparison between the eMG method and the implicit method at different spatial accuracy

6 Conclusions

The first-order exponential time integration scheme, EXP1 has been exploited to increase the feasibility of arbitrarily p-order DG for high-order simulations of steady-state flows. The algorithms and the physical natures of the methods are presented. The performance and memory usage are investigated and compared with a fast backward-Euler ILU preconditioned GMRES fully implicit method for 2-D and 3-D steady flow problems. The results show expected p-independent convergence rates for p = 1, 2, 3 order of accuracy and the eMG method is up to 20 times faster than the p = 3 ILU-GMRES for the 3-D case. Comparing to the fully implicit method, the eMG framework uses less memory but achieves comparable computational efficiency. Although the eMG method shows promising results, the PRK scheme inside has a time step restriction and thus affects the overall efficiency. Further studies are needed to pursue a better high-frequency smoother and a more efficient exponential scheme as well.