Abstract
With view to applications, we here give an explicit correspondence between the following two: (i) the set of symmetric and positive measures ρ on one hand, and (ii) a certain family of generalized Markov transition measures P, with their associated Markov random walk models, on the other. By a generalized Markov transition measure we mean a measurable and measure-valued function P on  , such that for every x ∈ V, P(x;⋅) is a probability measure on
, such that for every x ∈ V, P(x;⋅) is a probability measure on  ). Hence, with the use of our correspondence (i)–(ii), we study generalized Markov transitions P and path-space dynamics. Given P, we introduce an associated operator, also denoted by P, and we analyze its spectral theoretic properties with reference to a system of precise L
2 spaces.
). Hence, with the use of our correspondence (i)–(ii), we study generalized Markov transitions P and path-space dynamics. Given P, we introduce an associated operator, also denoted by P, and we analyze its spectral theoretic properties with reference to a system of precise L
2 spaces.
Our setting is more general than that of earlier treatments of reversible Markov processes. In a potential theoretic analysis of our processes, we introduce and study an associated energy Hilbert space  , not directly linked to the initial L
2-spaces. Its properties are subtle, and our applications include a study of the P-harmonic functions. They may be in
, not directly linked to the initial L
2-spaces. Its properties are subtle, and our applications include a study of the P-harmonic functions. They may be in  , called finite-energy harmonic functions. A second reason for
, called finite-energy harmonic functions. A second reason for  is that it plays a key role in our introduction of a generalized Green function. (The latter stands in relation to our present measure theoretic Laplace operator in a way that parallels more traditional settings of Green functions from classical potential theory.) A third reason for
is that it plays a key role in our introduction of a generalized Green function. (The latter stands in relation to our present measure theoretic Laplace operator in a way that parallels more traditional settings of Green functions from classical potential theory.) A third reason for  is its use in our analysis of path-space dynamics for generalized Markov transition systems.
is its use in our analysis of path-space dynamics for generalized Markov transition systems.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Markov operator
- Standard measure space
- Symmetric measure
- Laplace operator
- Markov chain
- Harmonic function
- Finite energy space
Mathematics Subject Classification (2000)
1 Introduction
In this paper, we continue our study of the graph Laplace and Markov operators, initiated in [1], which was based on the key notion of a σ-finite symmetric measure defined on the product space  for a standard Borel space
for a standard Borel space  .
.
Our goal is to extend the basic definitions and results of the theory of weighted networks (known also as electrical or resistance networks) to the case of measure spaces. We briefly recall that, for a countable locally finite connected graph G = (V, E) without loops, one can identify the edge set E with a subset of the Cartesian product V × V and assign some weight c
xy for every point (x, y) in E where c
xy is a symmetric positive function. It gives us a symmetric atomic measure ρ on E whose projections on V are the counting measure μ. Then, for a weighted network (V, E, c), one defines the Markov transition probability kernel P and the graph Laplacian Δ = c(I − P) which are considered as operators acting either in L
2 spaces with respect to the measures μ and ν = cμ or in the finite energy space  . Their spectral properties are of great interest as well as the study of harmonic functions in the theory of weighted networks.
. Their spectral properties are of great interest as well as the study of harmonic functions in the theory of weighted networks.
Our approach to the measurable theory of weighted networks is based on the concept of a symmetric measure defined on the Cartesian product  where
where  is a standard Borel space. (To stress the existing parallels we use the same notation as in discrete case.) In more detail, in the context of measurable dynamics, the state space V is considered very generally; more specifically
is a standard Borel space. (To stress the existing parallels we use the same notation as in discrete case.) In more detail, in the context of measurable dynamics, the state space V is considered very generally; more specifically  is given, where
is given, where  is a specified σ-algebra for V . From
is a specified σ-algebra for V . From  , we then form the corresponding product space, relative to the product σ-algebra on V × V . It is important that our initial measure ρ is not assumed finite, but only σ-finite. Since ρ is assumed symmetric, the respective two marginal measures coincide, here denoted μ, and they will also not be finite; only σ-finite. The σ-finiteness will be a crucial fact in our computations of a number of Radon-Nikodym derivatives and norms of operators and vectors.
, we then form the corresponding product space, relative to the product σ-algebra on V × V . It is important that our initial measure ρ is not assumed finite, but only σ-finite. Since ρ is assumed symmetric, the respective two marginal measures coincide, here denoted μ, and they will also not be finite; only σ-finite. The σ-finiteness will be a crucial fact in our computations of a number of Radon-Nikodym derivatives and norms of operators and vectors.
We establish an explicit correspondence between (i) symmetric and positive measures ρ on one hand, and (ii) a certain set of generalized Markov transition measures P on the other. More precisely, by a generalized Markov transition measure we mean a measurable and measure-valued function P on  , such that for every x in V , P(x, ⋅) is a probability measure on
, such that for every x in V , P(x, ⋅) is a probability measure on  . From the generalized Markov transition P, we introduce an associated operator, also denoted by P. Its spectral theoretic properties refer to a certain L
2 space, and they will be made precise in Sect. 3.
. From the generalized Markov transition P, we introduce an associated operator, also denoted by P. Its spectral theoretic properties refer to a certain L
2 space, and they will be made precise in Sect. 3.
In addition to the operator P, we shall also consider a natural transfer operator R (the choice of the letter “R” is for David Ruelle who initiated a variant of our analysis in the context of statistical mechanics); and a measure theoretic Laplacian, or Laplace operator. In the special case when V is countably discrete, our Laplace operator will be analogous to a family of more standard discretized classical Laplace operators. For related results on transfer operators, see e.g. [2,3,4,5,6,7,8,9,10,11,12,13].
Among the motivations for our present results are the following: A recent study of a variety of graph limits. This research area has both a general flavor, and an application-focus; see below. The latter includes recent papers on graphons; a current and extremely active area. In addition, we are motivated by a number of new operator-theoretic approaches to the study of graph limits, such as the notion of action convergence (see the recent works by Backhausz and Szegedy, [14, 15] and Pensky [16]). While we mention some of these connections inside our paper, our present emphasis is the theoretic foundations for these related developments.
New Results
It is important to note that our setting is not restricted to the case of finite measures. In fact, in our discussion of Markov transition dynamics, important examples simply will not allow finite covariant measures. We recall that the theory of weighted networks can serve as a discrete analog of our measurable settings, see [1] where this analogy was discussed in detail. The corresponding symmetric measure on the edge set E is σ-finite as well as the counting measure μ on the set of vertices V . Our definitions of the energy space  , Markov operator P, and the graph Laplace operator Δ are direct translations of the corresponding definitions for weighted networks.
, Markov operator P, and the graph Laplace operator Δ are direct translations of the corresponding definitions for weighted networks.
To the best of our knowledge, such interpretations of these objects have not been considered earlier. We stress that our approach to Markov processes generated by σ-finite symmetric measures leads with necessity to the study of Markov transition operators defined on infinite σ-finite measure spaces. The existing literature on Markov processes is devoted mostly to the case of probability measure spaces, see, e.g., [17,18,19].
The notion of Borel equivalence relation defined on a standard Borel space illustrates our setting, and it can be viewed as a rich source of various examples. We refer to the following books and articles: [20,21,22,23,24,25,26,27].
More applications of measurable setting for the study of Markov processes and Laplacians are given in [1]. We mention here the theory of graphons, Dirichlet forms, and the theory of determinantal measures.
With our starting point, a choice of a fixed symmetric and positive measure ρ on a product space, we will then have four natural Hilbert spaces, three are just L
2 spaces, L
2(ρ), and two L
2 spaces referring to the marginal measure μ. The fourth Hilbert space is different. We call it the finite energy Hilbert space  . Its use is motivated by potential theory, and it has a more subtle structure among the considered Hilbert spaces. Given ρ, we introduce an associated energy Hilbert space, denoted
. Its use is motivated by potential theory, and it has a more subtle structure among the considered Hilbert spaces. Given ρ, we introduce an associated energy Hilbert space, denoted  , but depending on the initially given ρ. This energy Hilbert space
, but depending on the initially given ρ. This energy Hilbert space  is not directly linked to the initial L
2 spaces, and its properties are quite different. Nonetheless, the energy Hilbert space
is not directly linked to the initial L
2 spaces, and its properties are quite different. Nonetheless, the energy Hilbert space  will play a key role in our analysis in the main body of our paper. There are many reasons for this. For example, non-constant harmonic functions will not be in L
2; but, in important applications, they may be in
will play a key role in our analysis in the main body of our paper. There are many reasons for this. For example, non-constant harmonic functions will not be in L
2; but, in important applications, they may be in  ; we refer to the latter as finite energy harmonic functions. A second reason for
; we refer to the latter as finite energy harmonic functions. A second reason for  is that it plays a crucial role in our introduction of a generalized Green’s function. The latter stands in relation to our Laplace operator in a way that is parallel to more classical settings of Green’s functions from potential theory. A third reason for
is that it plays a crucial role in our introduction of a generalized Green’s function. The latter stands in relation to our Laplace operator in a way that is parallel to more classical settings of Green’s functions from potential theory. A third reason for  is its use in our analysis of path-space dynamics for the Markov transition system, mentioned above.
is its use in our analysis of path-space dynamics for the Markov transition system, mentioned above.
Organization
Our main results are proved in Theorems 3.10, 4.7, 4.11, 5.3, 6.2, 6.11, and 7.2.
The paper is organized as follows. Section 2 contains our basic definitions and preliminary results. We discuss here the concepts of standard Borel and standard measure spaces, kernels, irreducible symmetric measures, and disintegration. The transfer operator R, Markov operator P, and graph Laplacian Δ are defined in Sect. 3. We collected a number of results about the spectral properties of these operators that were proved in [1]. Also the reader will find the definition of the finite energy Hilbert space  , several results about the structure of the space
, several results about the structure of the space  and the norm of functions from
and the norm of functions from  . We consider also the embedding operator J and prove that J is an isometry. In Sect. 4, we consider the equivalence of Markov operators and the Laplacians generated by equivalent symmetric measures ρ and ρ′. It turns out that, for equivalent symmetric measures ρ and ρ′, there exists an isometry for the corresponding energy Hilbert spaces
. We consider also the embedding operator J and prove that J is an isometry. In Sect. 4, we consider the equivalence of Markov operators and the Laplacians generated by equivalent symmetric measures ρ and ρ′. It turns out that, for equivalent symmetric measures ρ and ρ′, there exists an isometry for the corresponding energy Hilbert spaces  and
and  . The notion of reversible Markov processes is discussed in Sect. 5. We relate various properties of the operator P (such as self-ajointness) to this notion and to the notion of a symmetric measure. A number of results about Markov operators acting in the L
2 spaces and energy space
. The notion of reversible Markov processes is discussed in Sect. 5. We relate various properties of the operator P (such as self-ajointness) to this notion and to the notion of a symmetric measure. A number of results about Markov operators acting in the L
2 spaces and energy space  are proved in this section. Section 6 focuses on the case of a transient Markov processes defined by a Markov operator P. We define the path-space measure
are proved in this section. Section 6 focuses on the case of a transient Markov processes defined by a Markov operator P. We define the path-space measure  and Green’s function G(x, A), and we discuss their properties. Section 7 is devoted to construction of a sequence of discrete weighted networks which can be used to approximate the objects considered for the measurable setting.
and Green’s function G(x, A), and we discuss their properties. Section 7 is devoted to construction of a sequence of discrete weighted networks which can be used to approximate the objects considered for the measurable setting.
In our article we discuss several key notions such as reversible Markov processes, Green’s function, transient processes, limit theory (covering boundaries), potential theory, general Dirichlet forms, graph Laplacians, etc. For the benefit of non-experts in these areas, we included a number of general references in the corresponding sections.
2 Basic Definitions and Symmetric Measures
In this section, we briefly describe our main setting and introduce the most important notation. We also recall several results from [1] which will be used here.
2.1 Standard Borel and Measure Spaces
Suppose V is a Polish space, i.e., V is a separable completely metrizable topological space. Let  denote the σ-algebra of Borel sets generated by open sets of V . Then
denote the σ-algebra of Borel sets generated by open sets of V . Then  is called a standard Borel space. The theory of standard Borel spaces is discussed in many recent books, see e.g., [25, 26, 28, 29] and papers [30, 31]. We recall that all uncountable standard Borel spaces are Borel isomorphic, so that one can use any convenient realization of the space V working in the category of measurable spaces. If μ is a continuous (i.e., non-atomic) positive Borel measure on
is called a standard Borel space. The theory of standard Borel spaces is discussed in many recent books, see e.g., [25, 26, 28, 29] and papers [30, 31]. We recall that all uncountable standard Borel spaces are Borel isomorphic, so that one can use any convenient realization of the space V working in the category of measurable spaces. If μ is a continuous (i.e., non-atomic) positive Borel measure on  , then
, then  is called a standard measure space. Given
is called a standard measure space. Given  , we will call μ a measure for brevity. As a rule, we will deal with non-atomic σ-finite positive measures on
, we will call μ a measure for brevity. As a rule, we will deal with non-atomic σ-finite positive measures on  (unless the opposite is clearly indicated) which take values in the extended real line
(unless the opposite is clearly indicated) which take values in the extended real line  . We use the name of standard measure space for both finite and σ-finite measure spaces. Also the same notation,
. We use the name of standard measure space for both finite and σ-finite measure spaces. Also the same notation,  , is applied for the σ-algebras of Borel sets and measurable sets of a standard measure space. It should be clear from the context what σ-algebra is considered. Working with a measure space
, is applied for the σ-algebras of Borel sets and measurable sets of a standard measure space. It should be clear from the context what σ-algebra is considered. Working with a measure space  , we always assume that
, we always assume that  is complete with respect to μ. By
is complete with respect to μ. By  . we denote the space of real-valued bounded Borel functions on
. we denote the space of real-valued bounded Borel functions on  . For
. For  and a Borel measure μ on
and a Borel measure μ on  , we write
, we write
All objects, considered in the context of measure spaces (such as sets, functions, transformations, etc), are determined modulo sets of zero measure. In most cases, we will implicitly use this mod 0 convention not mentioning the sets of zero measure explicitly.
In what follows, we will use (in most cases implicitly) the notion of measurable fields. Given a measure space  , it is said that
, it is said that  is a measurable field of sets if the set
is a measurable field of sets if the set

Similarly, one can define a measurable field of measuresx → μ
x on  requiring x↦μ
x(A) to be a measurable function for any
requiring x↦μ
x(A) to be a measurable function for any  .
.
Consider a σ-finite continuous measure μ on a standard Borel space  . We denote by
. We denote by

the algebra of Borel sets of finite measure μ. Clearly, any σ-finite measure μ is uniquely determined by its values on  .
.
The linear space of simple function over sets from  is denoted by
is denoted by

will play an important role in our work since simple functions from  form a norm dense subset in L
p(μ)-space, p ≥ 1.
form a norm dense subset in L
p(μ)-space, p ≥ 1.
2.2 Symmetric Measures, Kernels, and Disintegration
Definition 2.1
Let E be an uncountable Borel subset of the Cartesian product  such that:
such that:
-
(i)
(x, y) ∈ E ⇔ (y, x) ∈ E, i.e. θ(E) = E where θ(x, y) = (y, x) is the flip automorphism;
-
(ii)
E x := {y ∈ V : (x, y) ∈ E}≠ ∅, ∀x ∈ X;
-
(iii)
for every x ∈ V ,
 is a standard Borel space where
is a standard Borel space where  is the σ-algebra of Borel sets induced on E
x from
is the σ-algebra of Borel sets induced on E
x from  .
.
We call E a symmetric set.
It follows from (ii) and (iii) that the projection of the symmetric set E on each margin of the product space  is V .
is V .
We observe that conditions (ii) and (iii) are, strictly speaking, not related to the symmetry property; they are included in Definition 2.1 for convenience, so that we will not have to make additional assumptions. Condition (iii) assumes two cases: the Borel space E x can be countable or uncountable. We focus mostly on uncountable Borel standard spaces.
There are several natural examples of symmetric sets related to dynamical systems. We mention here the case of a Borel equivalence relationE on a standard Borel space  . By definition, E is a Borel subset of V × V such that (x, x) ∈ E for all x ∈ V , (x, y) is in E iff (y, x) is in E, and (x, y) ∈ E, (y, z) ∈ E implies that (x, z) ∈ E. Let E
x = {y ∈ V : (x, y) ∈ E}, then E is partitioned into “vertical fibers” E
x. In particular, it can be the case when every E
x is countable. Then E is called a countable Borel equivalence relation.
. By definition, E is a Borel subset of V × V such that (x, x) ∈ E for all x ∈ V , (x, y) is in E iff (y, x) is in E, and (x, y) ∈ E, (y, z) ∈ E implies that (x, z) ∈ E. Let E
x = {y ∈ V : (x, y) ∈ E}, then E is partitioned into “vertical fibers” E
x. In particular, it can be the case when every E
x is countable. Then E is called a countable Borel equivalence relation.
We say that a symmetric set E is decomposable if there exists an uncountable Borel subset A ⊂ V such that
where  .
.
The meaning of this definition can be clarified for Borel equivalence relations: if E satisfies (2.3), then the set A is E-invariant.
We recall several definitions and facts about kernels defined on a measurable space, see e.g. [18, 19]. Given a standard measure space  , we define a σ-finite kernelk as a function
, we define a σ-finite kernelk as a function  (where
(where  is the extended real line) such that
is the extended real line) such that
-
(i)
x↦k(x, A) is measurable for every
 ;
; -
(ii)
for any x ∈ V , k(x, ⋅) is a σ-finite measure on
 .
.
A kernel k(x, A) is called finite if k(x, ⋅) is a finite measure on  for every x. We will also use the notation k(x, dy) for the measure on
for every x. We will also use the notation k(x, dy) for the measure on  .
.
The definition of a finite kernel can be used to define new measures on the measurable spaces  and
and  .
.
Given a σ-finite measure space  and a finite kernel k(x, A), we set
and a finite kernel k(x, A), we set
Then κ is a σ-finite measure on  (which is also called a random measure in the literature).
(which is also called a random measure in the literature).
For a kernel k as above, one can define inductively the sequence of kernels (k n : n ≥ 1) by setting
Following [18], we formulate definitions of main properties of a kernel k. We say that a set is attainable fromx ∈ V if there exists n ≥ 1 such that k
n(x, A) > 0, in symbols, we write x → A. A set
is attainable fromx ∈ V if there exists n ≥ 1 such that k
n(x, A) > 0, in symbols, we write x → A. A set  is called closed for the kernel k if k(x, A
c) = 0 for all x ∈ A. If A is closed, then it follows from (2.4) that k
n(x, A
c) = 0 for any
is called closed for the kernel k if k(x, A
c) = 0 for all x ∈ A. If A is closed, then it follows from (2.4) that k
n(x, A
c) = 0 for any  and x ∈ A. Hence, A is closed if and only if \( x \nrightarrow A^c\).
and x ∈ A. Hence, A is closed if and only if \( x \nrightarrow A^c\).
A kernel k = k(x, A) is called Borel indecomposable on  if there do not exist two disjoint non-empty closed subsets A
1 and A
2.
if there do not exist two disjoint non-empty closed subsets A
1 and A
2.
Let  be the support of the measure k(x, ⋅), that is
be the support of the measure k(x, ⋅), that is  . By \(\widetilde F_x\), we denote the set {x}× K
x ⊂ V × V . Then the formula
. By \(\widetilde F_x\), we denote the set {x}× K
x ⊂ V × V . Then the formula
defines a σ-finite measure on  where \(\widetilde k(x, \cdot ) = (\delta _x \times k)(x, \cdot )\). The support of k is the set
where \(\widetilde k(x, \cdot ) = (\delta _x \times k)(x, \cdot )\). The support of k is the set
We will use below slightly simplified notation identifying the sets F x and \(\widetilde F_x\) and the measures k(x, A) and \(\widetilde k(x, A)\). It will be clear from the context what objects are considered.
As mentioned in Introduction, our approach is based on the study of symmetric measures defined on  , see Definition 2.4. We show that every measure ρ on
, see Definition 2.4. We show that every measure ρ on  generates a kernel
generates a kernel  . This observation is based on the concept of disintegration of the measure ρ. We recall here this construction.
. This observation is based on the concept of disintegration of the measure ρ. We recall here this construction.
Denote by π 1 and π 2 the projections from V × V onto the first and second factor, respectively. Then \(\{\pi _1^{-1}(x) : x \in V\}\) and \(\{\pi _2^{-1}(y) : y \in V\}\) are the measurable partitions of V × V into vertical and horizontal fibers, see [1, 22, 32] for more information on properties of measurable partitions. The case of probability measures was studied by Rokhlin in [32], whereas the disintegration of σ-finite measures has been considered somewhat recently. We refer to a result from [33] whose formulation is adapted to our needs.
Theorem 2.2 ([33])
For a σ-finite measure space
 , let ρ be a σ-finite measure on
, let ρ be a σ-finite measure on
 such that
\(\rho \circ \pi _1^{-1} \ll \mu \)
. Then there exists a unique system of conditional σ-finite measures
\((\widetilde \rho _x)\)
such that
such that
\(\rho \circ \pi _1^{-1} \ll \mu \)
. Then there exists a unique system of conditional σ-finite measures
\((\widetilde \rho _x)\)
such that

In the following remark we collect several facts that clarify the essence of the defined objects.
Remark 2.3
-
(1)
The condition of Theorem 2.2 assumes that a measure μ is prescribed on the Borel space
 . If one begins with a measure ρ on
. If one begins with a measure ρ on  , then the measure μ arises as the projection of ρ on
, then the measure μ arises as the projection of ρ on  , \(\rho \circ \pi _1^{-1} = \mu \).
, \(\rho \circ \pi _1^{-1} = \mu \). -
(2)
Let E be a Borel symmetric subset of
 , and let ρ be a measure on
, and let ρ be a measure on  satisfying the condition of Theorem 2.2. Then E can be partitioned into the fibers {x}× E
x. By Theorem 2.2, there exists a unique system of conditional measures \(\widetilde \rho _x\) such that, for any ρ-integrable function f(x, y), we have $$\displaystyle \begin{aligned} \iint_{V\times V} f(x, y) \; d\rho(x, y) = \int_V \widetilde\rho_x(f) \; d\mu(x). \end{aligned} $$(2.5)
satisfying the condition of Theorem 2.2. Then E can be partitioned into the fibers {x}× E
x. By Theorem 2.2, there exists a unique system of conditional measures \(\widetilde \rho _x\) such that, for any ρ-integrable function f(x, y), we have $$\displaystyle \begin{aligned} \iint_{V\times V} f(x, y) \; d\rho(x, y) = \int_V \widetilde\rho_x(f) \; d\mu(x). \end{aligned} $$(2.5)It is obvious that, for μ-a.e. x ∈ V , \(\mbox{supp}(\widetilde \rho _x) = \{x\} \times E_x\) (up to a set of zero measure). To simplify the notation, we will write

though the measures ρ x and ρ have the supports E x and E, respectively.
-
(3)
It follows from Theorem 2.2 that the measure ρ determines the measurable field of sets x↦E x ⊂ V and measurable field of σ-finite Borel measures x↦ρ x on
 , where the measures ρ
x are defined by the relation $$\displaystyle \begin{aligned} \widetilde\rho_x = \delta_x \times \rho_x. \end{aligned} $$(2.6)
, where the measures ρ
x are defined by the relation $$\displaystyle \begin{aligned} \widetilde\rho_x = \delta_x \times \rho_x. \end{aligned} $$(2.6)Hence, relation (2.5) can be also written in the following form, used in our subsequent computations,
$$\displaystyle \begin{aligned} \iint_{V\times V} f(x, y) \; d\rho(x, y) = \int_V \left(\int_V f(x, y) \; d\rho_x(y)\right)\; d\mu(x). \end{aligned} $$(2.7)In other words, we have a measurable family of measures (x↦ρ x), and it defines a new measure ν on
 by setting
by setting  (2.8)
(2.8)Remark that the measure ρ x is defined on the subset E x of
 , x ∈ V .
, x ∈ V .
Definition 2.4
Let  be a standard Borel space. We say that a measure ρ on
be a standard Borel space. We say that a measure ρ on  is symmetric if
is symmetric if

In other words, ρ is invariant with respect to the flip automorphism θ.
The following remark contains natural properties of symmetric measures. Some of them were proved in [1], the others are rather obvious.
Remark 2.5
-
(1)
If ρ is a symmetric measure on
 , then the support of ρ, the set E = E(ρ), is symmetric mod 0. Here E(ρ) is defined up to a set of zero measure by the relation
, then the support of ρ, the set E = E(ρ), is symmetric mod 0. Here E(ρ) is defined up to a set of zero measure by the relation  .
. -
(2)
We consider the symmetric measures whose supporting sets E satisfy Definition 2.1. In other words, we require that, for every x ∈ V , the set E x ⊂ E is uncountable and therefore is a standard Borel space. The case when E x is countable arises, in particular, when E is a Borel countable equivalence relation on
 . The latter was considered in [1]. For countable sets E
x, x ∈ V , we can take ρ
x as a finite measure which is equivalent to the counting measure, see, e.g. [24, 34, 35] for details.
. The latter was considered in [1]. For countable sets E
x, x ∈ V , we can take ρ
x as a finite measure which is equivalent to the counting measure, see, e.g. [24, 34, 35] for details. -
(3)
In general, the notion of a symmetric measure is defined in the context of standard Borel spaces
 and
and  . But if a σ-finite measure μ is given on
. But if a σ-finite measure μ is given on  , then we need to include an additional relation between the projections of ρ on V and the measure μ. Let π
1 : V × V → V be the projection on the first coordinate. We require that the symmetric measure must satisfy the property \(\rho \circ \pi _1^{-1} \ll \mu \), see Theorem 2.2.
, then we need to include an additional relation between the projections of ρ on V and the measure μ. Let π
1 : V × V → V be the projection on the first coordinate. We require that the symmetric measure must satisfy the property \(\rho \circ \pi _1^{-1} \ll \mu \), see Theorem 2.2. -
(4)
The symmetry of the set E allows us to define a “mirror” image of the measure ρ. Let E y := {x ∈ V : (x, y) ∈ E}, and let \((\widetilde \rho ^y)\) be the system of conditional measures with respect to the partition of E into the sets E y ×{y}. Then, for the measure
$$\displaystyle \begin{aligned}\widetilde \rho = \int_V \widetilde \rho^y d\mu(y), \end{aligned}$$the relation \(\rho = \widetilde \rho \) holds.
-
(5)
It is worth noting that, in general, when a measure μ is defined on
 , the set E(ρ) do not need to be a set of positive measure with respect to the product measure μ × μ. In other words, we admit both cases: (a) ρ is equivalent to μ × μ, (b) ρ and μ × μ are mutually singular.
, the set E(ρ) do not need to be a set of positive measure with respect to the product measure μ × μ. In other words, we admit both cases: (a) ρ is equivalent to μ × μ, (b) ρ and μ × μ are mutually singular.
Assumption 1
In this paper, we consider the class of symmetric measures ρ on  which satisfy the following property:
which satisfy the following property:
where x↦ρ x is the measurable field of measures arising in Theorem 2.2.
Moreover, in most statements, we will assume that  , i.e.,
, i.e.,

This property of the function c(x) is natural because it corresponds to local finiteness of graphs in the theory of weighted (electric) networks. In several statements, we will require that

We observe also that the case when the function c is bounded leads to bounded Laplace operators and is not interesting for us.
Relation (2.8) defines the measure ν such that the measures μ and ν are equivalent. It is stated in Lemma 2.6 that c(x) is the Radon-Nikodym derivative of ν with respect to μ. If we want to reverse the definition and use ν as a primary measure, then we need to require that the function c(x)−1 is locally integrable with respect to ν.
The following (important for us) fact follows from the definition of symmetric measures. We emphasize that formula (2.10) will be used repeatedly in many proofs.
Lemma 2.6
-
(1)
For a symmetric measure ρ and any bounded Borel function f on
 , $$\displaystyle \begin{aligned} \iint_{V \times V} f(x, y) \; d\rho(x, y) = \iint_{V \times V} f(y, x) \; d\rho(x, y). \end{aligned} $$(2.10)
, $$\displaystyle \begin{aligned} \iint_{V \times V} f(x, y) \; d\rho(x, y) = \iint_{V \times V} f(y, x) \; d\rho(x, y). \end{aligned} $$(2.10)Equality (2.10) is understood in the sense of the extended real line, i.e., the infinite value of the integral is allowed.
-
(2)
Let ν be defined as in (2.8). Then
$$\displaystyle \begin{aligned}d\nu(x) = c(x) d\mu(x). \end{aligned}$$
2.3 Irreducible Symmetric Measures
We now relate the notions of symmetric measures and kernels. It turns out that one can associate a finite kernel  to any symmetric measure ρ on
to any symmetric measure ρ on  . For this, we use the disintegration of ρ according to Theorem 2.2, ρ =∫V
ρ
xdμ(x), and set
. For this, we use the disintegration of ρ according to Theorem 2.2, ρ =∫V
ρ
xdμ(x), and set  .
.
The definition of sets attainable from x ∈ V and that of decomposable sets, given above in the context of Borel spaces, can be translated to the case of measure spaces. Below we define the notion of an irreducible symmetric measure which will be extensively used in the paper.
Definition 2.7
-
(1)
A kernel x → k(x, ⋅) is called irreducible with respect to aσ-finite measureμon
 (μ-irreducible) if, for any set A of positive measure μ and μ-a.e. x ∈ V , there exists some n such that k
n(x, A) > 0, i.e., any set A of positive measure is attainable from μ-a.e. x, x → A.
(μ-irreducible) if, for any set A of positive measure μ and μ-a.e. x ∈ V , there exists some n such that k
n(x, A) > 0, i.e., any set A of positive measure is attainable from μ-a.e. x, x → A. -
(2)
A symmetric measureρ on
 is called irreducible if the corresponding kernel
is called irreducible if the corresponding kernel  is μ-irreducible where μ is the projection of measure ρ.
is μ-irreducible where μ is the projection of measure ρ. -
(3)
A symmetric measure ρ (or the kernel x → ρ x(⋅)) is called μ-decomposable if there exists a Borel subset A of V of positive measure μ such that
$$\displaystyle \begin{aligned} E \subset (A\times A) \cup (A^c \times A^c) \end{aligned} $$(2.11)where
 is also of positive measure. Otherwise, ρ is called indecomposable.
is also of positive measure. Otherwise, ρ is called indecomposable.
Every kernel k, defined on  , generates the potential kernel
, generates the potential kernel
where k 0(x, A) = χ A(x). In general, the kernel G may be degenerated admitting only the values 0 and ∞. We will discuss below the role of G in the case of transient Markov processes.
Lemma 2.8
Let ρ be a symmetric measure on with the kernel
with the kernel . Suppose that the support of ρ, the set E, satisfies relation (2.11) where μ(A) > 0 and μ(A
c) > 0, i.e. the kernel x↦ρ
x(A) is μ-decomposable. Then the sets A and A
care closed and x↦ρ
x(A) is a μ-reducible kernel. The converse statement also holds.
. Suppose that the support of ρ, the set E, satisfies relation (2.11) where μ(A) > 0 and μ(A
c) > 0, i.e. the kernel x↦ρ
x(A) is μ-decomposable. Then the sets A and A
care closed and x↦ρ
x(A) is a μ-reducible kernel. The converse statement also holds.
Proof
The first result follows directly from the definitions given above in this subsection. To see that the converse is true, it suffices to note that, for any set B of positive measure, the compliment \(\widehat B^c\) of the set
is either of zero measure, or closed (recall that x → B means that there exists n such that  ). If ρ is reducible, then there exists a set A, μ(A) > 0, such that the closed set \(\mu (\widehat A^c)\) has positive measure. The existence of such a set implies that the measure ρ is decomposable. □
). If ρ is reducible, then there exists a set A, μ(A) > 0, such that the closed set \(\mu (\widehat A^c)\) has positive measure. The existence of such a set implies that the measure ρ is decomposable. □
It is obvious from this lemma that a decomposable symmetric measure ρ cannot be irreducible. It was proved in [1] that the definitions of an irreducible measure and irreducible kernel agree, see Theorem 6.2 below.
By definition, the projection of the support of an irreducible measure ρ is the set V . Irreducibiliity of symmetric measures means irreducibility of a corresponding Markov process, see details in [1].
In the following statement, we give another approach to the notion of irreducible symmetric measures. Let ρ be a symmetric measure on  . We use the support of the fiber measure ρ
x, x ∈ V , to characterize an irreducible measure in different terms.
. We use the support of the fiber measure ρ
x, x ∈ V , to characterize an irreducible measure in different terms.
For any fixed x ∈ V , we define a sequence of subsets: A 0(x) = {x}, A 1(x) = E x,
Recall that E
x is the support of the measure ρ
x, and E
x can be identified with the vertical section of the symmetric set E. Note that all the sets A
n(x) are in  as x → E
x is a measurable field of sets.
as x → E
x is a measurable field of sets.
Lemma 2.9
Given , a symmetric measure ρ is irreducible if and only if for μ-a.e. x ∈ V and any set
, a symmetric measure ρ is irreducible if and only if for μ-a.e. x ∈ V and any set of positive measure there exists n ≥ 1 such that
of positive measure there exists n ≥ 1 such that
Proof
Indeed, the property formulated in (2.12) is another form of k n(x, B) > 0 where the kernel k is defined by x → ρ x. □
Various aspects of symmetric measures are also discussed in [36, 37]. In particular, one can observe that if symmetric measures ρ and \(\overline \rho \) are equivalent, then they are simultaneously either irreducible or not.
3 Linear Operators and Hilbert Spaces Associated to Symmetric Measures
While the main structures of our paper (symmetric measures, transfer operators R, Markov transition densities P, and associated Laplace operators Δ) may be naturally formulated in the general context of measurable functions, their spectral theory, and their dynamic-systems properties, only take a precise form after suitable Hilbert spaces are introduced. We will show that the initial structures, reversible Markov processes, and associated Laplace operators, etc., in turn dictate their own natural Hilbert space theoretic context. More precisely, in the section below, we identify the particular L 2 spaces, having the property that respective operators R, P, and Δ become self-adjoint. In addition to these L 2 spaces, we also identify two other Hilbert spaces (details below). They are motivated by parallels to classical potential theory, and to the study of diffusion processes. Moreover, they have discrete counterparts in the study of infinite networks, and of graph Laplacians. But presently, we introduced these two Hilbert spaces in a general measure space context. Continuing conventions from our earlier papers, we shall denote these Hilbert spaces (i) the energy Hilbert space, and (ii) the dissipation Hilbert space. The latter refers to a certain path-space construction, which in turn is built directly from the initial structure, mentioned above, symmetric measure, transfer operator, and Markov transition densities.
3.1 Symmetric Operator R, Markov Operator P, and Laplacian Δ
Suppose  is a finite kernel defined on a standard Borel space
is a finite kernel defined on a standard Borel space  . Then it defines a linear positive (see Remark 3.3) operator P(k) which is determined by the kernel k:
. Then it defines a linear positive (see Remark 3.3) operator P(k) which is determined by the kernel k:
It can be easily seen that, for the kernels k n (see (2.4)), the operator P(k n), defined as in (3.1), satisfies the property:

We consider in this section the kernel  generated by a symmetric measure ρ, i.e.,
generated by a symmetric measure ρ, i.e.,  .
.
Let  be a σ-finite measure space, and ρ a symmetric measure on
be a σ-finite measure space, and ρ a symmetric measure on  supported by a symmetric set E. Let x↦ρ
x be the measurable family of measures on
supported by a symmetric set E. Let x↦ρ
x be the measurable family of measures on  that disintegratesρ. Recall that, by Assumption 1, the function c(x) = ρ
x(V ) is finite for μ-a.e. x. As discussed above in Sect. 2.2, the measure ρ produces a finite kernel
that disintegratesρ. Recall that, by Assumption 1, the function c(x) = ρ
x(V ) is finite for μ-a.e. x. As discussed above in Sect. 2.2, the measure ρ produces a finite kernel  which we use to define the following operators.
which we use to define the following operators.
Definition 3.1
For a symmetric measure ρ on  , we define three linear operators R, P and Δ acting on the space of bounded Borel functions
, we define three linear operators R, P and Δ acting on the space of bounded Borel functions  .
.
-
(i)
The symmetric operatorR:
$$\displaystyle \begin{aligned} R(f)(x) := \int_V f(y) \; d\rho_x(y) = \rho_x(f). \end{aligned} $$(3.2) -
(ii)
The Markov operatorP:
$$\displaystyle \begin{aligned}P(f)(x) = \frac{1}{c(x)}R(f)(x) \end{aligned}$$or
$$\displaystyle \begin{aligned} P(f)(x) := \frac{1}{c(x)} \int_V f(y) \; d\rho_x(y) = \int_V f(y) \; P(x, dy) \end{aligned} $$(3.3)where P(x, dy) is the probability measure obtained by normalization of dρ x(y), i.e.
$$\displaystyle \begin{aligned}P(x, dy) := \frac{1}{c(x)}d\rho_x(y). \end{aligned}$$In other words, the Markov operator P defines the measurable field x↦P(x, ⋅) of transition probabilities on the space
 , or a Markov process.
, or a Markov process. -
(iii)
The graph Laplace operator Δ:
$$\displaystyle \begin{aligned} \Delta(f)(x) := \int_V (f(x) - f(y)) \; d\rho_x(y) \end{aligned} $$(3.4)or
$$\displaystyle \begin{aligned} \Delta(f) = c(I - P)(f) = (cI - R)(f). \end{aligned} $$(3.5)Using (2.9), we can write the operator Δ in more symmetric form:

where
 is a function identically equal to 1,
is a function identically equal to 1,
Remark 3.2 (R as a Transfer Operator)
It is worth noting that the operator R can be treated as a transfer operator (see e.g. [38] and the literature cited there).
Let  be a standard measure space, and let σ be a surjective endomorphism of X. Consider the partition ξ of X into the orbits of σ: y ∈ Orb
σ(x) if there are non-negative integers n, m such σ
n(y) = σ
m(x). Let the partition η be the measurable hull of ξ. Take the system of conditional measures {μ
C}C ∈ ξ corresponding to the partition η (see Theorem 2.2).
be a standard measure space, and let σ be a surjective endomorphism of X. Consider the partition ξ of X into the orbits of σ: y ∈ Orb
σ(x) if there are non-negative integers n, m such σ
n(y) = σ
m(x). Let the partition η be the measurable hull of ξ. Take the system of conditional measures {μ
C}C ∈ ξ corresponding to the partition η (see Theorem 2.2).
We define a transfer operator R on the standard measure space  by setting
by setting
where C x is the element of η containing x. The domain of R is L 1(μ) in this example.
As was shown in [38], the operator R : L 1(μ) → L 1(μ) defined by (3.6) is a transfer operator, i.e., it satisfies the relation
To see that our definition of the operator R given in (3.2) agrees with (3.6), it suffices to take the measurable partition η of V × V into subsets \(\{\pi _1^{-1}(x) : x \in V\}\) where π 1 is the projection of V × V onto V .
Remark 3.3
In this remark we make several comments about the basic properties of the operators R, P, and Δ.
-
(1)
The definition of each of the operators R, P, and Δ depends on a symmetric measure ρ, and, strictly speaking, they must be denoted as R(ρ), P(ρ), and Δ(ρ). Since most of our results are proved for a fixed measure ρ, we will drop this variable. Below in this section, we discuss the relationships between P(ρ) and P(ρ′) when ρ and ρ′ are equivalent symmetric measures.
-
(2)
The operators R and P are positive in the sense that R(f) ≥ 0 and P(f) ≥ 0 whenever f ≥ 0. Moreover, if
 , then
, then  because every measure P(x, ⋅) is probability. Hence, P is a Markov operator.
because every measure P(x, ⋅) is probability. Hence, P is a Markov operator.
-
(3)
The properties of the graph Laplace operator Δ are formulated in Proposition 3.7, which is given below. All statements from this theorem are proved in [1] (see also [39, 40]). Other aspects of graph Laplace operators in the context of measure spaces are discussed in [41, 42].
-
(4)
Since every measure ρ on V × V is uniquely determined by its values on a dense subset of functions, it suffices to define ρ on the set of the so-called “cylinder functions” (f ⊗ g)(x, y) := f(x)g(y). This observation will be used below when we prove a relation for cylinder functions first.
-
(5)
In general, a positive operator R in
 is called symmetric if it satisfies the relation: $$\displaystyle \begin{aligned} \int_V f R(g)\; d\mu = \int_V R(f) g\; d\mu, \end{aligned} $$(3.7)
is called symmetric if it satisfies the relation: $$\displaystyle \begin{aligned} \int_V f R(g)\; d\mu = \int_V R(f) g\; d\mu, \end{aligned} $$(3.7)for any
 . It turns out that any symmetric operator R defines a symmetric measure ρ. Indeed, the functional
. It turns out that any symmetric operator R defines a symmetric measure ρ. Indeed, the functional  (3.8)
(3.8)determines a measure on
 such that $$\displaystyle \begin{aligned}\rho(A\times B) = \int_V \chi_A(x) R(\chi_B)(x)\; d\mu(x). \end{aligned}$$
such that $$\displaystyle \begin{aligned}\rho(A\times B) = \int_V \chi_A(x) R(\chi_B)(x)\; d\mu(x). \end{aligned}$$As shown in [1], the operator R is symmetric if and only if the measure ρ, defined in (3.8), is symmetric.
In Definition 3.1, we do not discuss domains of the operators R, P, and Δ. It depends on the space where an operator is considered. In the current paper, we work with L
2-Hilbert spaces defined by the measures μ, ν, and ρ. But the most intriguing is the case of the finite energy space Hilbert space h
E. We discuss the properties of this space as well as those of operators Δ and P acting in  in the forthcoming paper [43]. On the other hand, we have already proved a number of results about these objects in [1]. We find it useful to give here the definitions and some formulas which are used below.
in the forthcoming paper [43]. On the other hand, we have already proved a number of results about these objects in [1]. We find it useful to give here the definitions and some formulas which are used below.
We remark that the finite energy space  , see Definition 3.4 can be viewed as a generalization of the energy space considered for discrete weighted networks. They have been extensively studied during last decades.
, see Definition 3.4 can be viewed as a generalization of the energy space considered for discrete weighted networks. They have been extensively studied during last decades.
Definition 3.4
Let  be a standard measure space with σ-finite measure μ. Suppose that ρ is a symmetric measure on the Cartesian product
be a standard measure space with σ-finite measure μ. Suppose that ρ is a symmetric measure on the Cartesian product  . We say that a Borel function
. We say that a Borel function  belongs to the finite energy space
belongs to the finite energy space if
if
Remark 3.5
-
(1)
It follows from Definition 3.4 that
 is a vector space containing all constant functions. We identify functions f
1 and f
2 such that f
1 − f
2 = const and, with some abuse of notation, the quotient space is also denoted by
is a vector space containing all constant functions. We identify functions f
1 and f
2 such that f
1 − f
2 = const and, with some abuse of notation, the quotient space is also denoted by  . So that, we will call elements f of
. So that, we will call elements f of  functions assuming that a representative of the equivalence class f is considered.
functions assuming that a representative of the equivalence class f is considered. -
(2)
Definition 3.4 assumes that a symmetric irreducible measure ρ is fixed on
 . This means that the space of functions f on
. This means that the space of functions f on  satisfying (3.9) depends on ρ, and, to stress this fact, we will use also the notation
satisfying (3.9) depends on ρ, and, to stress this fact, we will use also the notation  .
.
Define the norm in  by setting
by setting

As proved in [1],  is a Hilbert space with respect to the norm
is a Hilbert space with respect to the norm  .
.
The description of the structure of the Hilbert space  is a very intriguing problem. We give here a few results proved in [1].
is a very intriguing problem. We give here a few results proved in [1].
Theorem 3.6
Let ρ be a symmetric measure on such that\(\mu = \rho \circ \pi _1^{-1}\)
. Suppose c(x) = ρ
x(V ) is locally integrable with respect to μ.
such that\(\mu = \rho \circ \pi _1^{-1}\)
. Suppose c(x) = ρ
x(V ) is locally integrable with respect to μ.
-
(1)
For the measure dν(x) = c(x)dμ(x), we have

Moreover, if
 , then
, then (3.11)
(3.11)where
 .
. -
(2)
For every
 , one has
, one has . The function χ
Ais in
. The function χ
Ais in if and only if either μ(A) < ∞ or μ(A
c) < ∞.
if and only if either μ(A) < ∞ or μ(A
c) < ∞.
-
(3)
The finite energy space
 admits the decomposition into the orthogonal sum
admits the decomposition into the orthogonal sum (3.12)
(3.12)where the closure of
 is taken in the norm of the Hilbert space
is taken in the norm of the Hilbert space .
.
In the following statement we return to the L
2-spaces, and following [1], we formulate a number of properties of the operators, R, P, and Δ that clarify their essence. Here, we focus on the properties of these operators related to L
2-spaces. In the next paper [43], we will mostly consider these operators acting in the finite energy space  .
.
Proposition 3.7
Let dν(x) = c(x)dμ(x) be the σ-finite measure on where μ and c(x) = ρ
x(V ) are defined as above. Let the operators R, P, and Δ be defined as in Definition3.1.
where μ and c(x) = ρ
x(V ) are defined as above. Let the operators R, P, and Δ be defined as in Definition3.1.
-
(1)
Suppose that the function x↦ρ x(A) ∈ L 2(μ) for any
 . Then R is a symmetric unbounded operator in L
2(μ), i.e.,$$\displaystyle \begin{aligned}\langle g, R(f) \rangle_{L^2(\mu)} = \langle R(g), f \rangle_{L^2(\mu)}. \end{aligned}$$
. Then R is a symmetric unbounded operator in L
2(μ), i.e.,$$\displaystyle \begin{aligned}\langle g, R(f) \rangle_{L^2(\mu)} = \langle R(g), f \rangle_{L^2(\mu)}. \end{aligned}$$If c ∈ L ∞(μ), then R : L 2(μ) → L 2(μ) is a bounded operator, and
$$\displaystyle \begin{aligned}||R||{}_{L^2(\mu) \to L^2(\mu)} \leq ||c||{}_{\infty}. \end{aligned}$$ -
(2)
The operator R : L 1(ν) → L 1(μ) is contractive, i.e.,
$$\displaystyle \begin{aligned}||R(f)||{}_{L^1(\mu)} \leq ||f||{}_{L^1(\nu)}, \qquad f \in L^1(\nu). \end{aligned}$$Moreover, for any function f ∈ L 1(ν), the formula
$$\displaystyle \begin{aligned} \int_V R(f) \; d\mu(x) = \int_V f(x) c(x) \; d\mu(x) \end{aligned} $$(3.13)holds. In other words, ν = μR, and
$$\displaystyle \begin{aligned}\frac{d(\mu R)}{d\mu}(x) = c(x). \end{aligned}$$ -
(3)
The bounded operator P : L 2(ν) → L 2(ν) is self-adjoint. Moreover, νP = ν where dν(x) = c(x)dμ(x).
-
(4)
The operator P considered in the spaces L 2(ν) and L 1(ν) is contractive, i.e.,
$$\displaystyle \begin{aligned}|| P(f) ||{}_{L^2(\nu)} \leq || f ||{}_{L^2(\nu)}, \qquad || P(f) ||{}_{L^1(\nu)} \leq || f ||{}_{L^1(\nu)}. \end{aligned}$$ -
(5)
Spectrum of P in L 2(ν) is a subset of [−1, 1].
-
(6)
The graph Laplace operator Δ : L 2(μ) → L 2(μ) is a positive definite essentially self-adjoint operator with domain containing
 . Moreover,
. Moreover,
when the integral in the right hand side exists.
Definition 3.8
A function  is called harmonic, if Pf = f. Equivalently, f is harmonic if Δf = 0 or R(f) = cf. Similarly, h is harmonic for a kernel x → k(x, ⋅) if
is called harmonic, if Pf = f. Equivalently, f is harmonic if Δf = 0 or R(f) = cf. Similarly, h is harmonic for a kernel x → k(x, ⋅) if
Question
As was mentioned above, the definition of operators R(ρ), P(ρ), and Δ(ρ) is based on a symmetric measure ρ defined on  . Suppose that another symmetric measure, ρ′, which is equivalent to ρ, is defined on
. Suppose that another symmetric measure, ρ′, which is equivalent to ρ, is defined on  . It would be interesting to find out what relations between (R(ρ), P(ρ), Δ(ρ)) and (R(ρ′), P(ρ′), Δ(ρ′)) exist. Possibly, this question can be made more precise if we require that both ρ and ρ′ are supported by the same symmetric set E and disintegrated with respect to the same measure μ on
. It would be interesting to find out what relations between (R(ρ), P(ρ), Δ(ρ)) and (R(ρ′), P(ρ′), Δ(ρ′)) exist. Possibly, this question can be made more precise if we require that both ρ and ρ′ are supported by the same symmetric set E and disintegrated with respect to the same measure μ on  .
.
Remark 3.9
In our further results, the following sets of functions will play an important role. Let  be a σ-measure space, and ρ a symmetric measure on
be a σ-measure space, and ρ a symmetric measure on  satisfying Assumption 1. Then the measure dν(x) = c(x)dμ(x) is defined on
satisfying Assumption 1. Then the measure dν(x) = c(x)dμ(x) is defined on  and is equivalent to μ where
and is equivalent to μ where  . We define
. We define  as in (2.2), and, similarly, we set
as in (2.2), and, similarly, we set


It is straightforward to check that Assumption 1 implies

In general, the converse does not hold. But these two sets coincide if and only if Assumption 1 is extended by adding the reverse implication
3.2 Embedding Operator J
We define now a natural embedding J of bounded Borel functions over  into bounded Borel functions over
into bounded Borel functions over  . The operator J will be considered later acting on the corresponding L
2-spaces.
. The operator J will be considered later acting on the corresponding L
2-spaces.
Let

If  is equipped with a σ-finite measure μ (or ν = cμ), we can specify J as an operator with domain L
2(μ) or L
2(ν)).
is equipped with a σ-finite measure μ (or ν = cμ), we can specify J as an operator with domain L
2(μ) or L
2(ν)).
Theorem 3.10
For given , let ρ be a symmetric measure ρ on
, let ρ be a symmetric measure ρ on and c(x) = ρ
x(V ). Then:
and c(x) = ρ
x(V ). Then:
-
(1)
the operator J : L 2(ν) → L 2(ρ) is an isometry where dν(x) = c(x)dμ(x);
-
(2)
the co-isometry J ∗ : L 2(ρ) → L 2(ν) acts by the formula
$$\displaystyle \begin{aligned}(J^*g)(x) = \int_V g(x,y)\; P(x, dy), \qquad g\in L^2(\rho); \end{aligned}$$ -
(3)
the operator J : L 2(μ) → L 2(ρ) is densely defined (in L 2(μ)) and is, in general, unbounded.
Proof
-
(1)
This fact is proved by the following computation: for any f ∈ L 2(ν), one has
$$\displaystyle \begin{aligned} || (Jf) ||{}^2_{L^2(\rho)} = & \iint_{V\times V} (Jf)^2(x, y) \; d\rho(x, y)\\ =& \iint_{V\times V} f^2(x) \; d\rho_x (y)d\mu(x)\\ =& \int_{V} f^2(x) c(x)\; d\mu(x)\\ =& || f ||{}^2_{L^2(\nu)}. \end{aligned}$$ -
(2)
To find the co-isometry J ∗, we take arbitrary functions f ∈ L 2(ν) and g ∈ L 2(ρ) and compute the inner product using the equality c(x)P(x, dy) = dρ x(y):
$$\displaystyle \begin{aligned} \langle Jf, g\rangle_{L^2(\rho)} = & \iint_{V\times V} (Jf)(x, y) g(x, y)\; d\rho(x, y)\\ = & \int_{V} f(x) \left(\int_{V} g(x, y)\; d\rho_x(y)\right) d\mu(x)\\ = & \int_{V} f(x) \left(\int_{V} g(x, y)\; P(x, dy)\right) d\nu(x)\\ = &\langle f, J^*g\rangle_{L^2(\nu)}, \end{aligned}$$where J ∗ g =∫V g(x, y) P(x, dy). This proves (2).
-
(3)
To show that (3) holds, we take a Borel function f ∈ L 2(μ) and note that
$$\displaystyle \begin{aligned} || Jf ||{}^2_{L^2(\rho)} = \iint_{V\times V} f^2(x) \; d\rho_xd\mu(x) = \int_V f^2(x)c(x) \; d\mu(x). \end{aligned} $$(3.15)In particular, we have, for
 , $$\displaystyle \begin{aligned}|| J(\chi_A) ||{}^2_{L^2(\rho)} = \int_A c(x) \; d\mu(x), \end{aligned}$$
, $$\displaystyle \begin{aligned}|| J(\chi_A) ||{}^2_{L^2(\rho)} = \int_A c(x) \; d\mu(x), \end{aligned}$$that is, assuming that c is locally integrable, we see that J is well defined on a dense subset of L 2(μ). Formula (3.15) shows that, for general c, the operator J : L 2(μ) → L 2(ρ) is not bounded.
□
4 Equivalence of Symmetric Measures
In this section we focus on the question about relations of Markov operators, and Laplacians, arising from equivalent symmetric measures.
4.1 Equivalence of Markov Operators
Let ρ be a symmetric measure on  which is disintegrated by fiber measures x↦ρ
x over the measure μ = ρ ∘ π
−1. As above, define transition probabilities x↦P(x, ⋅) by setting c(x)−1
dρ
x(⋅) = P(x, ⋅) where c(x) = ρ
x(V ). In other words, P(x, A) = P(χ
A)(x) where P is the Markov operator, see (3.3).
which is disintegrated by fiber measures x↦ρ
x over the measure μ = ρ ∘ π
−1. As above, define transition probabilities x↦P(x, ⋅) by setting c(x)−1
dρ
x(⋅) = P(x, ⋅) where c(x) = ρ
x(V ). In other words, P(x, A) = P(χ
A)(x) where P is the Markov operator, see (3.3).
Having the operator P defined, one can construct a stationary Markov process. Let  . For ω = (ω
n) ∈ Ω, set
. For ω = (ω
n) ∈ Ω, set

These notions are studied in detail in Sect. 5. Here we mention only the notion of reversibility, one of the most important properties of Markov operators (processes).
Definition 4.1
-
(1)
A kernel x↦k(x, ⋅) is called reversible with respect to a measure μ on
 , if for any bounded Borel function f(x, y), $$\displaystyle \begin{aligned}\iint_{V\times V} f(x, y) k(x, dy)d\mu(x) = \iint_{V\times V} f(y, x) k(x, dy)d\mu(x). \end{aligned}$$
, if for any bounded Borel function f(x, y), $$\displaystyle \begin{aligned}\iint_{V\times V} f(x, y) k(x, dy)d\mu(x) = \iint_{V\times V} f(y, x) k(x, dy)d\mu(x). \end{aligned}$$ -
(2)
Suppose that x↦P(x, ⋅) is a measurable family of transition probabilities on the space
 , and let P be the Markov operator determined by x↦P(x, ⋅). It is said that the corresponding Markov process is reversible with respect to a measurable functions c : V → (0, ∞) if, for any sets
, and let P be the Markov operator determined by x↦P(x, ⋅). It is said that the corresponding Markov process is reversible with respect to a measurable functions c : V → (0, ∞) if, for any sets  , the following relation holds: $$\displaystyle \begin{aligned} \int_B c(x) P(x, A)\; d\mu(x) = \int_A c(x) P(x, B)\; d\mu(x). \end{aligned} $$(4.1)
, the following relation holds: $$\displaystyle \begin{aligned} \int_B c(x) P(x, A)\; d\mu(x) = \int_A c(x) P(x, B)\; d\mu(x). \end{aligned} $$(4.1)Denoting dν(x) = c(x)dμ(x), we can rewrite (4.1) in the form that will be used below.
$$\displaystyle \begin{aligned}\int_V \chi_B(x) P(x, A) \; d\nu(x) = \int_V \chi_A(x) P(x, B) \; d\nu(x). \end{aligned}$$
The following result clarifies relationship between symmetric measures ρ and reversible Markov processes. This lemma is a part of more general statement, see Theorem 5.3.
Lemma 4.2
Let ρ =∫V
ρ
xdμ be a measure on such that c(x) = ρ
x(V ) < ∞ for all x. Suppose that the Markov operator P is defined according to (3.3). Then the following are equivalent:
such that c(x) = ρ
x(V ) < ∞ for all x. Suppose that the Markov operator P is defined according to (3.3). Then the following are equivalent:
-
(i)
ρ is symmetric;
-
(ii)
(P, c) is reversible.
In what follows, we will focus on the following question: suppose that ρ and ρ′ are two equivalent symmetric measures such that the corresponding Markov processes (P, c) and (P′, c′) are reversible. How are they related? More generally, we can ask about relations between all objects whose definition was based on a symmetric measure. They are the Laplacian Δ, symmetric operator R, and finite energy Hilbert space. Some partial answers are given in this and subsequent sections.
Definition 4.3
Let (P, c) be a pair consisting of a positive measurable function c(x) on  and a reversible Markov process P(x, ⋅) satisfying Definition 4.1. We will say that two such pairs (P, c) and (P′, c′) are equivalent if the corresponding symmetric measures ρ and ρ′ are equivalent as measures on
and a reversible Markov process P(x, ⋅) satisfying Definition 4.1. We will say that two such pairs (P, c) and (P′, c′) are equivalent if the corresponding symmetric measures ρ and ρ′ are equivalent as measures on  (see Theorem 5.3). The latter means that there exists a positive measurable function r(x, y) such that
(see Theorem 5.3). The latter means that there exists a positive measurable function r(x, y) such that
If the equivalent measures ρ and ρ′ satisfy the property \(\mu = \rho \circ \pi _1^{-1} = \rho '\circ \pi _1^{-1}\), then we call the pairs (P, c) and (P′, c′) strongly equivalent. In this case, we also call the measures ρ and ρ′strongly equivalent.
Remark 4.4
-
(1)
The symmetry of equivalent measures ρ and ρ′ implies that the function r(x, y) is symmetric, r(x, y) = r(y, x).
-
(2)
Let the measures ρ and ρ′ be strongly equivalent. Then these measures are disintegrated as follows:
$$\displaystyle \begin{aligned}\rho' = \int_V \rho^{\prime}_x\ d\mu(x), \qquad \rho = \int_V \rho_x\ d\mu(x). \end{aligned}$$It can be seen that the equivalence of ρ and ρ′ implies that the measures ρ x and \(\rho ^{\prime }_x\) are equivalent μ-a.e. Moreover,
$$\displaystyle \begin{aligned} \frac{d\rho^{\prime}_x}{d\rho_x}(y) = r_x(y) \end{aligned} $$(4.2)where r x(⋅) is obtained from r(x, ⋅) by fixing the variable x.
-
(3)
Conversely, given two (strongly) equivalent measures ρ and ρ′, we can construct (strongly) equivalent pairs (P, c) and (P′, c′) according to the properties formulated in Lemma 4.2 and Theorem 5.3. In other words, if (P, c) defines a reversible Markov process with the symmetric measure ρ, then, for any symmetric measure ρ′ equivalent to ρ, we can construct a reversible Markov process (P′, c′) which is equivalent to (P, c). Note that the functions c(x) = ρ x(V ) and \(c'(x) = \rho ^{\prime }_x(V)\) are determined by ρ and ρ′ uniquely.
One can prove a more general statement than that given in Remark 4.4 (2).
Lemma 4.5
Let ρ and ρ′ be two symmetric measures on such that dρ′(x, y) = r(x, y)dρ(x, y). Suppose that
such that dρ′(x, y) = r(x, y)dρ(x, y). Suppose that
and the measures μ and μ′ on are equivalent, i.e., m(x)dμ′(x) = dμ(x) for some positive Borel function m(x). Then the measures\(\rho ^{\prime }_x\)and ρ
xare equivalent a.e. on V , and
are equivalent, i.e., m(x)dμ′(x) = dμ(x) for some positive Borel function m(x). Then the measures\(\rho ^{\prime }_x\)and ρ
xare equivalent a.e. on V , and
Proof (Sketch)
The result is deduced as follows:
On the other hand,
Comparing the above formulas, we obtain that (4.3) holds.
□
Consider a particular case when the Radon-Nikodym derivative r(x, y) of two equivalent measures ρ and ρ′ is the product p(x)q(y).
Lemma 4.6
Let
\(\rho = \int \rho _x \; d\mu (x)\)
and
\(\rho ' = \int \rho ^{\prime }_x \; d\mu '(x)\)
be two measures on
 such that
such that
for some positive Borel functions p and q. Then, for μ-a.e. x ∈ V , the Radon-Nikodym derivative\(\dfrac {d\rho ^{\prime }_x(y)}{d\rho _x(y)}\)satisfies the relation
where
Proof
The result can be easily deduced from the formula
We leave the details to the reader. □
Relation (4.4) means that the Radon-Nikodym derivative \(\dfrac {d\rho ^{\prime }_x}{d\rho _x}(y)\) is proportional to the function q(y) where the coefficient of proportionality is given by φ(x). If ρ and ρ′ are symmetric measures, then \(\dfrac {d\rho '}{d\rho }(x, y) = p(x)p(y)\).
Theorem 4.7
Let ρ and ρ′ be two strongly equivalent measures on such that\(d\rho ^{\prime }_x = r_x(y) d\rho _x(y)\)for all x ∈ V . Then the corresponding Markov processes (P, c) and (P′, c′) are strongly equivalent and
such that\(d\rho ^{\prime }_x = r_x(y) d\rho _x(y)\)for all x ∈ V . Then the corresponding Markov processes (P, c) and (P′, c′) are strongly equivalent and
Proof
We first find P(r x):
Next, we compute
Now, the result follows from (4.6). □
Remark 4.8
-
(1)
Let the symmetric measures ρ and ρ′ be strongly equivalent, \(d\rho ^{\prime }_x(y)= r_x(y) d\rho _x(y)\). As in (4.6), we can obtain that
$$\displaystyle \begin{aligned}P'\left(\frac{1}{r_x}\right)(x) = \frac{c(x)}{c'(x)}. \end{aligned}$$Therefore, the following property holds:
$$\displaystyle \begin{aligned}P(r_x)(x) P'\left(\frac{1}{r_x}\right)(x) = 1 \end{aligned}$$ -
(2)
Since the notion of equivalence of measures ρ and ρ′ is symmetric, we note that the roles of P and P′ can be interchanged and the following relation holds:
$$\displaystyle \begin{aligned}P(f)(x) = \frac{P'\left( f \frac{1}{r_x} \right) (x)} {P'\left(\frac{1}{r_x} \right)(x)}. \end{aligned}$$ -
(3)
It follows from the strong equivalence of ρ and ρ′ that r x(y) is integrable with respect to ρ x and
$$\displaystyle \begin{aligned}c'(x) = \int_V r_x(y) \; d\rho_x(y). \end{aligned}$$ -
(4)
Several useful formulas can be easily deduced from Theorem 4.7. Firstly, formula (4.5) can be rewritten in the form
$$\displaystyle \begin{aligned} P(f r_x)(x) = c'(x) P'(f)(x) c(x)^{-1},\end{aligned} $$(4.7)and equivalently, the latter is represented as a relation between Markov kernels:
$$\displaystyle \begin{aligned}c'(x) P'(x, dy) = c(x) r_x(y) P(x, dy).\end{aligned} $$ -
(5)
The same proof as in Theorem 4.7 shows that
$$\displaystyle \begin{aligned}R'(f)(x) = R(fr_x)(x).\end{aligned} $$ -
(6)
In more general setting, assuming that \(d\rho ^{\prime }_x(y) = m(x) r_x(y) d\rho _x(y)\) where m(x) is as in (4.3), we deduce that
$$\displaystyle \begin{aligned}P(f r_x)(x) m(x)= c'(x) P'(f)(x) c(x)^{-1}.\end{aligned} $$Similarly, one can show that
$$\displaystyle \begin{aligned}R'(f)(x) = m(x) R(f r_x)(x)\end{aligned} $$where the operator R′ is defined by \(x \mapsto \rho ^{\prime }_x\).
-
(7)
Suppose that, for given pair (P, c), the operator P′ is defined by (4.7), and let dν′(x) = c′(x)dμ(x). Then we claim that ν′P′ = ν′:
$$\displaystyle \begin{aligned} \int_V P'(f)(x)\; d\nu'(x) = & \ \int_V c(x) P(f r_x)(x) c'(x)^{-1} c'x) \; d\mu(x) \\ = & \ \int_V P(fr_x)(x) \; d\nu(x)\\ = &\ \int_V\left( \int_V (fr_x)(y) P(x, dy) \right)\; d\nu(x)\\ = & \ \iint_{V\times V} f(y) \frac{d\rho^{\prime}_x}{d\rho_x}(y) c(x)^{-1} d\rho_x(y) c(x) d\mu(x)\\ = & \ \iint_{V\times V} f(y) \; d\rho^{\prime}_x(y) d\mu(x) \\ = & \ \iint_{V\times V} f(x) \; d\rho'(x,y)\\ = & \int_V f(x) c'(x)\; d\mu(x)\\ = & \ \int f(x) \; d\nu'(x). \end{aligned}$$
4.2 On the Laplacians Δ and Δ′
In the remaining part of this section, we will discuss relations between the Laplace operators Δ and Δ′ acting in the finite energy Hilbert spaces  and
and  respectively.
respectively.
Let Δ′(f) be the Laplace operator defined by a symmetric measure ρ′ on  . We can find out how Δ′ and Δ are related.
. We can find out how Δ′ and Δ are related.
Proposition 4.9
Let ρ and ρ′ be two equivalent symmetric measures on such that dρ′(x, y) = q(x)q(y)dρ(x, y). Then
such that dρ′(x, y) = q(x)q(y)dρ(x, y). Then
In particular, when q is harmonic for P, then
Moreover,
and assuming that P(q) = q, we have

Proof
-
(1)
By definition of the operator Δ, we have
$$\displaystyle \begin{aligned} \Delta'(f)(x) = & \ \int_V (f(x) - f(y)) \; d\rho^{\prime}_x(y) \\ = &\ \int_V (f(x) - f(y))q(x) q(y) \; d\rho_x(y) \\ = &\ \int_V (f(x) - f(y)) c(x)q(x) q(y) \; dP(x, dy) \\ = & \ c(x) q(x) f(x) \int_V q(y) \; P(x, dy) - c(x) q(x) \int_V q(y) f(y)\; P(x, dy)\\ = & \ c(x)q(x) \left[ f(x) P(q)(x) - P(qf)(x) \right]. \end{aligned} $$(4.9)Add and subtract cq 2 f to the right hand side of (4.9). Then, regrouping the terms, we obtain
$$\displaystyle \begin{aligned}\Delta'(f) = c q [qf - P(qf)] + cqf (P(q) - q) = q \Delta (qf) + cqf (P(q) - q). \end{aligned}$$This means that, in case when P(q) = q, the Laplace operators Δ and Δ′ are related as in (4.8).
-
(2)
Now we can apply (1) to prove the formulas given in (2). From the last expression in (4.9), we see that f is harmonic with respect to Δ′ if and only if P(qf) = fP(q). □
Corollary 4.10
Let ρ be a symmetric measure on , and let q be a harmonic function for the Markov operator P generated by ρ. Define the symmetric measure ρ′ such that dρ′(x, y) = q(x)q(y)dρ(x, y). Let P′ be the corresponding Markov operator produced by ρ′. Then we have the map
, and let q be a harmonic function for the Markov operator P generated by ρ. Define the symmetric measure ρ′ such that dρ′(x, y) = q(x)q(y)dρ(x, y). Let P′ be the corresponding Markov operator produced by ρ′. Then we have the map

Proof
It follows from the definition of the measure ρ′ that
Since q is harmonic, i.e., R(q) = cq, we obtain that
Let f be any function harmonic with respect to the operator P′. Then
It follows from (4.10) that f = q −1 P(qf), and we are done. □
We remark that in the proved statement we temporarily extended the notion of symmetric measures to the case of signed symmetric measures assuming that the P-harmonic function q can be negative.
Theorem 4.11
Suppose that ρ′ and ρ are two symmetric measures such that dρ′(x, y) = q(x)q(y)dρ(x, y). If q is harmonic for the Laplace operator Δ, then the operator

is an isometry.
Proof
We need to show that, for any  ,
,

In the computation given below, we use the following: the definition of the norm in the finite energy space, the symmetry of the measures ρ and ρ′, and the relation R(q) = cq that holds for harmonic functions because
Then we compute

This computation shows that  and Q preserves the norm. □
and Q preserves the norm. □
Continuing the above theme, consider the Laplace operator Δ acting in L 2(μ). We recall that Δ : L 2(μ) → L 2(μ) is a positive definite self-adjoint operator according to Proposition 3.7.
Proposition 4.12
Suppose ρ is a symmetric measure on and the Laplacian Δ = Δ(ρ) is defined by (3.4). Let q and f be functions on
and the Laplacian Δ = Δ(ρ) is defined by (3.4). Let q and f be functions on from the domain of Δ such that qf is also in the domain of Δ. Then
from the domain of Δ such that qf is also in the domain of Δ. Then
If q and f are in L 2(μ), then ∫V Δ(qf) dμ = 0.
Proof
By definition of Δ, we have
Then
and (4.11) is proved.
If the functions q and f are in L
2(μ) (in particular, q and f can be taken from the dense subset  ), then we can use the fact that Δ is essentially self-adjoint and conclude that
), then we can use the fact that Δ is essentially self-adjoint and conclude that
□
We immediately deduce the following fact from Proposition 4.12.
Corollary 4.13
-
(1)
If functions f and f 2 are in the domain of Δ, then
$$\displaystyle \begin{aligned}\int_V \Delta(f^2)\; d\mu =0. \end{aligned}$$ -
(2)
If f is a harmonic function for Δ, then Δ(f 2) = 0, and therefore f 2is also harmonic.
Proof
-
(1)
is an obvious consequence of Proposition 4.12. To show that (2) holds, we use that Δ(f) = c(f − P(f)) and P is a positive operator. This means that P(f) ≥ 0 whenever f ≥ 0. By Schwarz’ inequality for positive operators, we have P(f 2)(x) ≥ P(f)2(x), and therefore
$$\displaystyle \begin{aligned} \Delta(f^2) & = c(f^2 - P(f^2))\\ & \leq c(f^2 - P(f)^2)\\ &= c (f - P(f))(f+P(f))\\ &=0. \end{aligned}$$The fact that f 2 is harmonic follows from (1) and the proved inequality in (2).
□
5 Reversible Markov Process Generated by Symmetric Measures
In this section, we consider Markov processes generated by a Markov operator which is determined by a symmetric irreducible measure ρ on the standard Borel space  such that the margin measure μ on
such that the margin measure μ on  is σ-finite. Our first theme is reversible Markov processes. For the benefit of non-specialist readers, we cite the following sources: [44,45,46]. We refer also to [47,48,49]. In the second part of this section, we will assume that this Markov process is transient (see the definition below). The reader can find vast literature on the theory of transient Markov processes, we refer to [17,18,19, 50,51,52,53,54,55,56,57].
is σ-finite. Our first theme is reversible Markov processes. For the benefit of non-specialist readers, we cite the following sources: [44,45,46]. We refer also to [47,48,49]. In the second part of this section, we will assume that this Markov process is transient (see the definition below). The reader can find vast literature on the theory of transient Markov processes, we refer to [17,18,19, 50,51,52,53,54,55,56,57].
5.1 Reversible Markov Processes
Let  be a σ-finite measure space, and let ρ be a symmetric measure on
be a σ-finite measure space, and let ρ be a symmetric measure on  which is disintegrated with respect to (ρ
x, x ∈ V ) and μ according to (2.5). By assumption, c(x) = ρ
x(V ) is locally integrable. We recall (see Definition 3.1) that, in this setting, a Markov operator P is defined on
which is disintegrated with respect to (ρ
x, x ∈ V ) and μ according to (2.5). By assumption, c(x) = ρ
x(V ) is locally integrable. We recall (see Definition 3.1) that, in this setting, a Markov operator P is defined on  by the probability kernel x↦P(x, ⋅). This operator P acts by the formula
by the probability kernel x↦P(x, ⋅). This operator P acts by the formula
where P(x, dy) = c(x)−1
dρ
x(y). Then the operator P is positive and normalized, i.e.,  . As mentioned above in Proposition 3.7, the fact that ρ is symmetric is equivalent to self-adjointness of P as an operator in L
2(ν). It follows also that P preserves the measure ν = cμ. Furthermore, we can use the kernel x → P(x, ⋅) = P
1(x, ⋅) to define the sequence of probability kernels (transition probabilities)
. As mentioned above in Proposition 3.7, the fact that ρ is symmetric is equivalent to self-adjointness of P as an operator in L
2(ν). It follows also that P preserves the measure ν = cμ. Furthermore, we can use the kernel x → P(x, ⋅) = P
1(x, ⋅) to define the sequence of probability kernels (transition probabilities)  in accordance with (2.4). These kernels satisfy the equality
in accordance with (2.4). These kernels satisfy the equality

Therefore one has

and this relation defines the sequence of probability measures (P n) by setting P 0(x, A) = δ A(x) = χ A(x) and

We use the notation P(x, A) for P 1(x, A).
For the Markov operator P, one can define one more sequence of measures. We use the formula
to define the measures  on the Borel space
on the Borel space  (here ρ
1 = ρ).
(here ρ
1 = ρ).
Lemma 5.1
-
(1)
Every measure
 is symmetric on
is symmetric on
 , and ρ
n
is equivalent to ρ.
, and ρ
n
is equivalent to ρ.
-
(2)
 .
. -
(3)
$$\displaystyle \begin{aligned} d\rho_n(x,y) = c(x) P_n(x, dy)d\mu(x)= P_n(x, dy)d\nu(x). \end{aligned} $$(5.3)
-
(4)
$$\displaystyle \begin{aligned}\rho_n( A\times B) = \langle \chi_A, RP^{n-1}(\chi_B) \rangle_{L^2(\mu)}. \end{aligned}$$
Proof
The assertions of the lemma are rather obvious. We only mention two simple facts: ρ n(A × V ) = ρ(A × V ) for every n, and, since the operator P n is self-adjoint in L 2(ν), the measure ρ n is symmetric. □
Definition 5.2
Suppose that x↦P(x, ⋅) is a measurable family of transition probabilities on the space  , and let P be the Markov operator determined by x↦P(x, ⋅). It is said that the corresponding Markov process is reversible with respect to a measurable function c : x → (0, ∞) on
, and let P be the Markov operator determined by x↦P(x, ⋅). It is said that the corresponding Markov process is reversible with respect to a measurable function c : x → (0, ∞) on  if, for any sets
if, for any sets  , the following relation holds:
, the following relation holds:
As shown in [1], the reversibility for the Markov process (P n) is equivalent to the following properties (here we give an extended and more comprehensive formulation):
Theorem 5.3
Let be a standard σ-finite measure space, x↦c(x) ∈ (0, ∞) a measurable function,
be a standard σ-finite measure space, x↦c(x) ∈ (0, ∞) a measurable function, . Suppose that x↦P(x, ⋅) is a probability kernel. The following are equivalent:
. Suppose that x↦P(x, ⋅) is a probability kernel. The following are equivalent:
-
(i)
x↦P(x, ⋅) is reversible (i.e., it satisfies (5.4) ;
-
(ii)
x → P n(x, ⋅) is reversible for any n ≥ 1;
-
(iii)
the Markov operator P defined by x → P(x, ⋅) is self-adjoint on L 2(ν) and νP = ν where dν(x) = c(x)dμ(x);
-
(iv)
$$\displaystyle \begin{aligned}c(x) P(x, dy) d\mu(x) = c(y) P(y, dx)d\mu(y); \end{aligned}$$
-
(v)
the operator R defined by the relation R(f)(x) = c(x)P(f)(x) is symmetric (see Remark3.3);
-
(vi)
the measure ρ on
 defined by$$\displaystyle \begin{aligned}\rho(A \times B) = \int_V \chi_A R(\chi_B)\; d\mu = \int_V c(x) \chi_A P(\chi_B)\; d\mu \end{aligned}$$
defined by$$\displaystyle \begin{aligned}\rho(A \times B) = \int_V \chi_A R(\chi_B)\; d\mu = \int_V c(x) \chi_A P(\chi_B)\; d\mu \end{aligned}$$is symmetric;
-
(vii)
for every
 , the measure ρ
ndefined by (5.2) is symmetric;
, the measure ρ
ndefined by (5.2) is symmetric;
-
(viii)
for any Borel sets
 ,
, 
where the random variables X 1, …, X nare defined below in Remark5.4(5) and the sets A 0, A 1, …, A nare written in the reverse order in the right hand side.
Proof
We refer to [1] where most of these properties are discussed. We prove (viii) here. Indeed, it can be seen that

Since P is self-adjoint on L 2(ν), we can repeatedly use the relation ∫V fP(g)dν =∫V P(f)gdν and rewrite (5.5) as follows:

The fact that property (viii) implies that P is reversible is proved by using the density of simple functions in L 2(ν). □
We discuss the notion of reversibility in the following Remark where we included several direct consequences of Definition 4.1 and Theorem 5.3.
Remark 5.4
-
(1)
Let x↦P(x, ⋅) be a Borel field of probability measures over a standard Borel space
 . This field of transition probabilities generates the Markov operator P such that
. This field of transition probabilities generates the Markov operator P such that  . It follows from Theorem 5.3 that one can define the notion of reversible Markov process x↦P(x, ⋅) with respect to a σ-finite measure ν: It is said that ((x↦P(x, ⋅)), ν) is reversible if P is a self-adjoint operator in L
2(ν). This definition is equivalent to the property $$\displaystyle \begin{aligned}\int_A P(x, B) \; d\nu = \int_B P(x, A)\; d\nu. \end{aligned}$$
. It follows from Theorem 5.3 that one can define the notion of reversible Markov process x↦P(x, ⋅) with respect to a σ-finite measure ν: It is said that ((x↦P(x, ⋅)), ν) is reversible if P is a self-adjoint operator in L
2(ν). This definition is equivalent to the property $$\displaystyle \begin{aligned}\int_A P(x, B) \; d\nu = \int_B P(x, A)\; d\nu. \end{aligned}$$Equally, one can consider the notion of reversibility for P(x, ⋅) with respect to a symmetric measure ρ. Theorem 5.3 states the equivalence of these approaches.
-
(2)
Based on (1), the following question is raised naturally: Givenx↦P(x, ⋅) as above, under what condition the set

is non-empty?
-
(3)
The following observation is a direct consequence of Theorem 5.3. Let P(x, A) = P(χ A)(x) be the probability kernel defined by a normalized Markov operator P acting on Borel functions over
 . To answer the question about the existence of a P-invariant measure ν ∼ μ such that (P, ν) is reversible, it suffices to construct a locally integrable function c satisfying (5.4). It can be done by pointing out a symmetric measure ρ such that ρ
x(V ) = c(x) and the projection of ρ onto V is the measure μ.
. To answer the question about the existence of a P-invariant measure ν ∼ μ such that (P, ν) is reversible, it suffices to construct a locally integrable function c satisfying (5.4). It can be done by pointing out a symmetric measure ρ such that ρ
x(V ) = c(x) and the projection of ρ onto V is the measure μ. -
(4)
There exists a stronger version of reversible Markov processes. Let P be a Markov operator acting on
 such that, for any
such that, for any  , $$\displaystyle \begin{aligned}\chi_A P(\chi_B) = \chi_B P(\chi_A). \end{aligned}$$
, $$\displaystyle \begin{aligned}\chi_A P(\chi_B) = \chi_B P(\chi_A). \end{aligned}$$Then, for any positive Borel function
 , the measure dν(x) = c(x)dμ(x) belongs to
, the measure dν(x) = c(x)dμ(x) belongs to  . Indeed, it suffices to define the symmetric measure ρ according to Theorem 5.3 (vi) and then apply statement (ii).
. Indeed, it suffices to define the symmetric measure ρ according to Theorem 5.3 (vi) and then apply statement (ii). -
(5)
We give here one more interpretation of the definition of reversible Markov processes. For this, we use the notation to be introduced in Sect. 6. Let
$$\displaystyle \begin{aligned}\Omega = V \times V \times V \cdots\end{aligned}$$be the path space of the Markov process (P n), and let X n : Ω → V be the random variable defined by X n(ω) = ω n. Given a measure ν on V , we can reformulate the definition of reversible Markov operator as follows:
$$\displaystyle \begin{aligned}dist( X_0\ |\ X_1 \in A) = dist(X_1\ |\ X_0 \in A). \end{aligned}$$The meaning of the above formula is clarified in Proposition 6.4.
-
(6)
Suppose now that a non-symmetric measure ρ is given on the space
 , i.e, ρ(A × B) ≠ ρ(B × A), in general. However, we will assume that ρ is equivalent to ρ ∘ θ where θ(x, y) = (y, x). Then, using the same approach as above, we can define the following objects: margin measures \(\mu _i := \rho \circ \pi _i^{-1}, i =1,2,\), fiber measures dρ
x(⋅) and dρ
x(⋅) (see Remark 2.5), and functions c
1(x) = ρ
x(V ), c
2(x) = ρ
x(V ).
, i.e, ρ(A × B) ≠ ρ(B × A), in general. However, we will assume that ρ is equivalent to ρ ∘ θ where θ(x, y) = (y, x). Then, using the same approach as above, we can define the following objects: margin measures \(\mu _i := \rho \circ \pi _i^{-1}, i =1,2,\), fiber measures dρ
x(⋅) and dρ
x(⋅) (see Remark 2.5), and functions c
1(x) = ρ
x(V ), c
2(x) = ρ
x(V ).
Define now the symmetric measureρ # generated by ρ as follows
Then
Clearly, ρ # is equivalent to ρ.
Let E ⊂ V × V be the support of ρ. Then E # = E ∪ θ(E) is the support of the symmetric measure ρ #. The disintegration of ρ =∫V ρ xdμ 1(x) with respect to the partition {x}× E x defines the disintegration of ρ #. For \(\mu ^{\#} := \dfrac {1}{2}(\mu _1 + \mu _2) \), we obtain that
Having the symmetric measure ρ
# defined on  , we can introduce the operators R
# and P
# as in (3.2) and (3.3). It turns out that, for
, we can introduce the operators R
# and P
# as in (3.2) and (3.3). It turns out that, for  ,
,
where
Similarly,
where
Then we can define the measure dν #(x) = c #(x)dμ(x) such that the operator
is self-adjoint in L 2(ν #). By Theorem 5.3, we obtain that the Markov process generated by x↦P #(x, ⋅) is reversible where P #(x, A) = P #(χ A)(x).
5.2 Properties of Markov Operators
In this subsection, we discuss some properties of the Markov operator P, which is defined by relation (3.3). The operator P is considered acting in Hilbert spaces L
2(μ), L
1(ν), and  where dν(x) = c(x)dμ(x) and
where dν(x) = c(x)dμ(x) and  is the energy space.
is the energy space.
We begin with the following simple observations whose proofs are obvious and can be omitted. Remind that  is the family of Borel subsets of finite measure μ, and
is the family of Borel subsets of finite measure μ, and  is the linear subspace generated by the characteristic functions χ
A,
is the linear subspace generated by the characteristic functions χ
A,  .
.
Remark 5.5
-
(1)
If
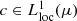 , then
, then 
The converse is not true.
-
(2)
We observe that if both functions, c(x) and c(x)−1 are in
 , then
, then 
-
(3)
The following property holds for
 :
:  (5.6)
(5.6)(this should be understood that functions from
 are representatives of elements from
are representatives of elements from  ).
). -
(4)
We recall that
 (5.7)
(5.7)where ρ is a symmetric measure used in the definition
 . This fact is proved in [1].
. This fact is proved in [1].
Lemma 5.6
If , then
, then is dense in L
1(ν) and L
2(ν).
is dense in L
1(ν) and L
2(ν).
Proof (Sketch)
We show the density of  in L
1(ν) only. It suffices to check that, for every
in L
1(ν) only. It suffices to check that, for every  , the characteristic function χ
B can be approximated in L
1(ν) by simple functions from
, the characteristic function χ
B can be approximated in L
1(ν) by simple functions from  , i.e., for every ε > 0, there exists some
, i.e., for every ε > 0, there exists some  such that \(|| \chi _B - s ||{ }_{L^1(\nu )} < \varepsilon \). Without loss of generality, we can assume that s(x) ≤ χ
B(x). Then
such that \(|| \chi _B - s ||{ }_{L^1(\nu )} < \varepsilon \). Without loss of generality, we can assume that s(x) ≤ χ
B(x). Then
Since c is μ-integrable on B, one can take a subset B 0 ⊂ B such that
The result follows. □
Next, let ρ be a symmetric measure on  , and let P be the operator acting on bounded Borel functions by the formula
, and let P be the operator acting on bounded Borel functions by the formula
where c(x)P(x, dy) = dρ x(y).
In the next statement we collect several properties of the Markov operator P considered in various spaces.
Proposition 5.7
Let , ν, and ρ be as above. Then, for any
, ν, and ρ be as above. Then, for any ,
,
-
(a)
\(P(\chi _A) \in L^1(\mu ) \ \Longleftrightarrow \ \dfrac {\rho _x(A)} {c(x)} \in L^1(\mu ) \ \Longrightarrow \ P(\chi _A) \in L^2(\mu )\);
-
(b)
if the function x↦∫V c(y)−1dρ x(y) is locally integrable, then P is a densely defined operator in L 2(μ);
-
(c)
if
 , then
$$\displaystyle \begin{aligned}P(\chi_A) \in L^1(\nu) \cap L^2(\nu); \end{aligned}$$
, then
$$\displaystyle \begin{aligned}P(\chi_A) \in L^1(\nu) \cap L^2(\nu); \end{aligned}$$ -
(d)
the measures μ and μP are equivalent if and only if the function c −1is integrable on (E x, ρ x) for μ-a.e. x ∈ V . The Radon-Nikodym derivative can be found by the formula:
$$\displaystyle \begin{aligned}\frac{d(\mu P)}{d\mu}(x) = \int_V \frac{1}{c(y)} \; d\rho_x(y). \end{aligned} $$
Proof (Sketch)
-
(a)
The fact that P(χ A) is in L 2(μ) follows from the Schwarz inequality for positive operators,
$$\displaystyle \begin{aligned}P(\chi_A)^2 \leq P(\chi_A^2) = P(\chi_A). \end{aligned}$$The criterion for integrability of the function P(χ A) is proved as follows:
$$\displaystyle \begin{aligned} \int_V P(\chi_A)(x)\; d\mu(x) = & \iint_{V\times V} \chi_A(y) P(x, dy)\; d\mu(x) \\ = & \iint_{V\times V} \frac{\chi_A(y)}{c(x)}\; d\rho_x(y)d\mu(x)\\ = &\int_V \frac{\rho_x(A)}{c(x)}\; d\mu(x). \end{aligned}$$It follows from (a) that the same computation can be used to show that P(χ A) is in L 2(μ) whenever
$$\displaystyle \begin{aligned}\dfrac{\rho_x(A)} {c(x)} \in L^1(\mu).\end{aligned} $$ -
(b)
To prove this result, we refer to the proof of (b) and use the symmetry of the measure ρ:
$$\displaystyle \begin{aligned}P(\chi_A) \in L^2(\mu) \ \Longleftarrow \ P(\chi_A) \in L^1(\mu)\end{aligned} $$and
$$\displaystyle \begin{aligned} \int_V P(\chi_A)(x) \; d\mu(x) = & \iint_{V\times V} \frac{\chi_A(y)} {c(x)}\; d\rho_x(y)d\mu(x)\\ = & \iint_{V\times V} \frac{\chi_A(x)}{c(y)}\; d\rho_x(y)d\mu(x)\\ =& \int_A\left( \int_V \frac{\chi_A(x)}{c(y)}\; d\rho_x(y) \right) d\mu(x). \end{aligned}$$It gives the desired statement.
-
(c)
Suppose
 . Then, using the symmetry of the measure ρ and relation (2.7), we obtain $$\displaystyle \begin{aligned} \int_V P(\chi_A)(x)\; d\nu(x) =& \int_V \left(\int_V \chi_A (y) \frac{1}{c(x)} \; d\rho_x(y) \right) \; c(x) d\mu(x)\\ =& \iint_{V\times V}\chi_A(x) \; d\rho_x(y)d\mu(x)\\ =& \int_V \chi_A(x) c(x)\; d\mu(x) \\ = & \int_A c(x)\; d\mu(x) < \infty, \end{aligned}$$
. Then, using the symmetry of the measure ρ and relation (2.7), we obtain $$\displaystyle \begin{aligned} \int_V P(\chi_A)(x)\; d\nu(x) =& \int_V \left(\int_V \chi_A (y) \frac{1}{c(x)} \; d\rho_x(y) \right) \; c(x) d\mu(x)\\ =& \iint_{V\times V}\chi_A(x) \; d\rho_x(y)d\mu(x)\\ =& \int_V \chi_A(x) c(x)\; d\mu(x) \\ = & \int_A c(x)\; d\mu(x) < \infty, \end{aligned}$$i.e., P(χ A) ∈ L 1(ν). The fact that P(χ A) ∈ L 2(ν) is proved as in (a).
-
(d)
The statement will follow from the following chain of equalities:
$$\displaystyle \begin{aligned} (\mu P)(A) = & \int_V \chi_A \; d(\mu P)\\ = & \int_V P(\chi_A) \; d\mu\\ = & \int_V \left( \int_V \chi_A(y) P(x, dy)\right) d\mu(x)\\ = & \iint_{VtV} \chi_A(y) \frac{1}{c(x)} \; d\rho_x(y) d\mu(x)\\ = & \int_{V} \chi_A(x)\left( \int_V \frac{1}{c(y)} \; d\rho_x(y)\right) d\mu(x)\\ = & \int_{A} \left( \int_V \frac{1}{c(y)} \; d\rho_x(y)\right) d\mu(x)\\ = & \int_A \frac{d(\mu P)}{d\mu}(x) \; d\mu(x) \end{aligned}$$where
$$\displaystyle \begin{aligned}\frac{d(\mu P)}{d\mu}(x) = \int_V \frac{1}{c(y)} \; d\rho_x(y). \end{aligned}$$
□
Clearly, Proposition 5.7 can be extended to functions from  .
.
Lemma 5.8
-
(1)
Let P be a self-adjoint Markov operator in L 2(ν). Suppose that
 . Then, for
. Then, for ,
,  (5.8)
(5.8)where measures ρ nare defined in (5.2).
-
(2)
Moreover, for all
 ,
, 
Proof
-
(1)
We recall that if P is a self-adjoint operator in the space L 2(ν), then νP = ν. Hence,
$$\displaystyle \begin{aligned} || P^n(\chi_A) ||{}^2_{L^2(\nu)} = & \langle P^n(\chi_A), P^n(\chi_A) \rangle_{L^2(\nu)}\\ = & \langle \chi_A, P^{2n}(\chi_A) \rangle_{L^2(\nu)}\\ = & \rho_{2n}(A\times A). \end{aligned}$$ -
(2)
Since \(\rho _x^{(n)}(V) = c(x)\) for all
 , we can easily deduce from (1) the following equality (we use here formula (5.7)):
, we can easily deduce from (1) the following equality (we use here formula (5.7)): 
□
Remark 5.9
It is interesting to compare formula (5.8) with a similar result for  proved in [1], see also (3.11) in Theorem 3.6.
proved in [1], see also (3.11) in Theorem 3.6.

Hence, it follows that

5.3 More on the Embedding Operator J
In this subsection, we return to the study of the operator J defined in (3.14), see Sect. 3.2. We recall that the operator J is an isometry if considered acting from L 2(ν) to L 2(ρ), and it is an unbounded operator from L 2(μ) to L 2(ρ). Here we focus on relations between J and other operators we study in the paper.
Lemma 5.10
For any
 , we have
, we have
Proof
Indeed, we use Schwarz’ inequality for P to show that
□
As an illustration of properties of this embedding J, we note that the function J(c −1)(x, y) is not integrable with respect to ρ but is locally integrable.
Another useful relation that compares norms of functions is contained in the following inequality.
Lemma 5.11
Let f be a function from the finite energy space such that f and Δ(f) belong to L 2(μ). Then

Proof
The proof follows from [1, Corollary 7.4] and Proposition 3.7 (6):

□
In the remaining part of this section, we consider the Markov operator P as an operator acting on functions from the energy space  .
.
Proposition 5.12
Assume that
 . Then, for every
. Then, for every
 , we have
, we have

Proof
We need to show that the energy norm of J(P(χ A)) is finite. By Theorem 3.6, we find that
To see that the last integral is finite, we first show that (JP)(χ A) is in L 2(ρ):
The latter is finite.
Similarly, one can check that ∬V ×V P(χ A)(x)P(χ A)(y) dρ(x, y) is also finite. We leave the proof for the reader. □
Consider a new operator, denoted by ∂, which acts from the energy space  to L
2(ρ):
to L
2(ρ):

Remark that in the theory of electrical networks the analogous transformation is called a voltage drop operator.
Lemma 5.13
The operator defined by (5.9) is an isometry.
defined by (5.9) is an isometry.
Proof
The proof is obvious because

□
Since J : L 2(ν) → L 2(ρ) is an isometry, then the co-isometry J ∗ sends L 2(ρ) to L 2(ν) according to the formula
where g ∈ L 2(ρ).
In the following proposition, we formulate a relation between operators P, J ∗, and ∂.
Proposition 5.14
The following diagram commutes:

where\(\widetilde \Delta = (\sqrt {2} c)^{-1} \Delta = (\sqrt {2})^{-1} (I - P)\).
Proof
The proof is mainly based on Theorem 3.10 and the definition of ∂. We have
□
In the next statement, we present several properties of the operator I − P.
Corollary 5.15
-
(1)

-
(2)
The operator I − P acting from
 to L
2(ν) is contractive.
to L
2(ν) is contractive.
-
(3)
For the operator Δ = c(I − P), the following holds

Proof
Assertion (1) is a direct consequence of Proposition 5.14 (this result was already mentioned in [1]).
To see that (2) holds, we recall the formula for the norm of a function in the finite energy space  :
:

where the meaning of random variables X n is explained in Sect. 6 below.
(3) is obvious. □
6 Transient Markov Processes and Symmetric Measures
Transient Markov processes and Green’s functions are central themes in the theory of Markov chains that have been studied in a numerous books and papers. For the benefit of non-specialist readers, we cite the following sources [17, 58,59,60]. More interesting results can be found in [61,62,63].
In this section we consider Green’s functions G A(x) of transient Markov processes and relate the symmetric measures ρ n to the norm of G A in the finite energy space.
6.1 Path-space Measure
We denote by Ω the infinite Cartesian product  . Let (X
n(ω) : n = 0, 1, …) be the sequence of random variables X
n : Ω → V such that X
n(ω) = ω
n. We call Ω as the path space of the Markov process (P
n). Let Ωx, x ∈ V, be the set of infinite paths beginning at x:
. Let (X
n(ω) : n = 0, 1, …) be the sequence of random variables X
n : Ω → V such that X
n(ω) = ω
n. We call Ω as the path space of the Markov process (P
n). Let Ωx, x ∈ V, be the set of infinite paths beginning at x:
Clearly, Ω =∐x ∈ V Ωx.
A subset {ω ∈ Ω : X
0(ω) ∈ A
0, …X
k(ω) ∈ A
k} is called a cylinder set defined by Borel sets A
0, A
1, …, A
k taken from  ,
,  . The collection of cylinder sets generates the σ-algebra
. The collection of cylinder sets generates the σ-algebra  of Borel subsets of Ω, and
of Borel subsets of Ω, and  is a standard Borel space. Then the functions X
n : Ω → V are Borel.
is a standard Borel space. Then the functions X
n : Ω → V are Borel.
Define a probability measure  on Ωx. For this, denote by
on Ωx. For this, denote by  the increasing sequence of σ-subalgebras such that
the increasing sequence of σ-subalgebras such that  is the smallest subalgebra for which the functions X
0, X
1, …, X
n are Borel. For a cylinder set (A
1, …, A
n) from
is the smallest subalgebra for which the functions X
0, X
1, …, X
n are Borel. For a cylinder set (A
1, …, A
n) from  we set
we set

Then  extends to the Borel sets on Ωx by the Kolmogorov extension theorem [64].
extends to the Borel sets on Ωx by the Kolmogorov extension theorem [64].
The values of  can be written as
can be written as

The joint distribution of the random variables X i is given by

Lemma 6.1
The measure space is a standard probability measure space for μ-a.e. x ∈ V .
is a standard probability measure space for μ-a.e. x ∈ V .
On the measurable space  , define a σ-finite measure λ by
, define a σ-finite measure λ by

(λ is infinite if and only if the measure ν is infinite).
By  , we denote the σ-subalgebra
, we denote the σ-subalgebra  . Since
. Since  is a σ-subalgebra of
is a σ-subalgebra of  , there exists a projection
, there exists a projection

The projection E
n is called the conditional expectation with respect to  and satisfies the property:
and satisfies the property:
We proved in [1] that the Markov process P n is irreducible if the initial symmetric measure is irreducible. More precisely, the statement is as follows.
Theorem 6.2
Let ρ be a symmetric measure on
 , and let A and B be any two sets from
, and let A and B be any two sets from
 . Then
. Then

The Markov process (P n) is irreducible if and only if the measure ρ is irreducible.
In other words, relation (6.6) can be interpreted in the following way: for the Markov process (P n), the “probability” to get in B for n steps starting somewhere in A is exactly ρ n(A × B) > 0.
To see that (6.6) holds, one uses the definition of the measure λ and formulas (6.1) and (6.2).
Corollary 6.3
Let A
0, A
1, …, A
nbe a finite sequence of subsets from . Then
. Then

for i = 1, …, n.
It is worth noting that the concept of reversible Markov processes can be formulated in terms of the measure λ, roughly speaking λ must be a symmetric distribution.
Proposition 6.4
Let the measure λ on Ω be defined by (6.4). The Markov operator P is reversible if and only if, for any sets A
0, …, A
nfrom and any
and any ,
,
Proof
The proof uses Theorem 5.3 (viii). In the proof we assume for simplicity that n = 2; the general case is proved similarly. We recall that P is reversible if and only is the Markov operator P is self-adjoint in L 2(ν). We compute applying (6.1):

It proves the statement. □
In the next statement we relate harmonic functions to martingales. Recall first the definition of a martingale.
Let  be the Markov chain on Ω with values in
be the Markov chain on Ω with values in  defined by X
n(ω) = ω
n. We recall that the space Ω is represented as the disjoint union of subsets Ωx := {ω ∈ Ω : ω
0 = x}, x ∈ V . Let
defined by X
n(ω) = ω
n. We recall that the space Ω is represented as the disjoint union of subsets Ωx := {ω ∈ Ω : ω
0 = x}, x ∈ V . Let  be a sequence of real-valued random variables defined on Ω. Then it generates a sequence of measurable fields of random variables x → Φn(x), x ∈ V, defined on the corresponding subset Ωx. Let
be a sequence of real-valued random variables defined on Ω. Then it generates a sequence of measurable fields of random variables x → Φn(x), x ∈ V, defined on the corresponding subset Ωx. Let  be the σ-algebra of subsets of Ω generated by
be the σ-algebra of subsets of Ω generated by  . Denote by
. Denote by  the smallest σ-subalgebra such that the functions Φi, i = 1, …n, are Borel measurable. These σ-algebras induce σ-algebras
the smallest σ-subalgebra such that the functions Φi, i = 1, …n, are Borel measurable. These σ-algebras induce σ-algebras  on every Ωx.
on every Ωx.
It is said that the sequence ( Φn) is a martingale if

Here  is the conditional expectation with respect to the probability path measure
is the conditional expectation with respect to the probability path measure  , see (6.1).
, see (6.1).
Proposition 6.5
Let P be the Markov operator defined by a symmetric measure ρ. For the objects defined above, the following are equivalent:
-
(i)
a Borel function h on
 is harmonic with respect to the Markov operator P;
is harmonic with respect to the Markov operator P;
-
(ii)
the sequence
 is a martingale.
is a martingale.
Proof
It follows from the definition of the Markov chain (X
n), path space measure  , and [2, Proposition 2.24] that, for any Borel function f,
, and [2, Proposition 2.24] that, for any Borel function f,

Hence, we see that a function h is harmonic if and only if

i.e., (h ∘ X n) is a martingale. □
6.2 Green’s Functions
In this section, we will work with transient Markov processes. We first define a Green’s function G(x, A). Our main goal is to study Green’s functions as elements of the energy space.
Definition 6.6
Let

The Markov process is called transient if, for every  , the function G(x, A) is finite μ-a.e. on V .
, the function G(x, A) is finite μ-a.e. on V .
In this subsection, we will always assume that the Markov process (P n) is transient.
Lemma 6.7
Let ρ be an irreducible symmetric measure. Suppose be a set such that G(x, A) is finite a.e. Then, for any
be a set such that G(x, A) is finite a.e. Then, for any , the function G(x, B) is finite for μ-a.e. x ∈ V .
, the function G(x, B) is finite for μ-a.e. x ∈ V .
Proof
The proof of this result is straightforward and mainly based on the definition of irreducible measure, see also Lemma 2.9. □
Lemma 6.8
Let and let P be a Markov operator defined by a symmetric measure ρ. Then the function x↦P
n(x, A) = P
n(χ
A)(x) belongs to
and let P be a Markov operator defined by a symmetric measure ρ. Then the function x↦P
n(x, A) = P
n(χ
A)(x) belongs to and
and

Proof
The proof is based on the facts that ν is P-invariant, ρ is symmetric, and on the definition of the norm in the energy space which are used in the following computation:

□
Remark 6.9
As a curious observation, we mention that, for any  ,
,
It is worth noting that the above formula cannot be extended to direct products of sets A and B from  . In particular, one can prove that the relation
. In particular, one can prove that the relation
implies that P(χ B − P(χ B)) > 0 a.e. Therefore there would exist a harmonic function in L 2(ν) which is a contradiction.
Fix a set  , then we have the family of measurable functions G
A(x) := G(x, A) indexed by sets of finite measure.
, then we have the family of measurable functions G
A(x) := G(x, A) indexed by sets of finite measure.
Lemma 6.10
For a set
 , the equality
, the equality
holds. Equivalently,
Proof
We compute using the definition of Green’s function and the fact that the series ∑n
P
n(x, A) is convergent for all x and all  :
:
□
Theorem 6.11
For the objects defined above, we have the following properties.
-
(1)
For any sets
 , we have
, we have
 (6.7)
(6.7)and, in particular,
 (6.8)
(6.8) -
(2)
For any
 and
and ,
, 
Furthermore, if
 (6.9)
(6.9)then
 is dense in the energy space
is dense in the energy space .
.
Proof
-
(1)
We prove (6.8) here. Relation (6.7) is proved similarly. One has

For (2),

It follows from the proved relation that if
 for all
for all  , then f = 0, and
, then f = 0, and  is dense in
is dense in  . □
. □
Let  denote, as usual, the space spanned by characteristic functions, and let
denote, as usual, the space spanned by characteristic functions, and let  be as in (6.9). Then the following two operators, J and K, are densely defined
be as in (6.9). Then the following two operators, J and K, are densely defined

where  .
.
Proposition 6.12
The operators J and K form a symmetric pair, i.e.,

where and
and .
.
Proof
To prove (6.11) it suffices to check that it holds for φ = χ
A and f = G
B where  . For these functions, we show that the both inner products are equal to ν(A ∩ B).
. For these functions, we show that the both inner products are equal to ν(A ∩ B).
By Lemma 6.10, we have
On the other hand, for the same functions φ and f, we compute the inner product in the finite energy Hilbert space using the symmetry of ρ:

□
Corollary 6.13
The finite energy Hilbert space admits the orthogonal decomposition

In particular, for every , we have G
B = G
1 ⊕ G
2
, where
, we have G
B = G
1 ⊕ G
2
, where is always non-zero.
is always non-zero.
Proof
Indeed, if one assumed that G
1 = 0, then we would have that G
B is orthogonal to  . This contradicts Theorem 6.11. □
. This contradicts Theorem 6.11. □
We conclude this section with the following result that was proved in [1]:
Theorem 6.14
Let (P
n) be a transient Markov process, and let G(x, A) be the corresponding Green’s function. Then, for any , we have the decomposition
, we have the decomposition
where h is a harmonic function and φ ∈ L 2(ν).
7 Discretization of the Graph 
In this section, we show that our basic setting (a symmetric measure on the Cartesian product  ) can be realized as a limit of discrete graphs. This approach naturally leads to the notion of graphons. The reader can find necessary information in the following books [65,66,67] and articles [68,69,70].
) can be realized as a limit of discrete graphs. This approach naturally leads to the notion of graphons. The reader can find necessary information in the following books [65,66,67] and articles [68,69,70].
Let  be a σ-finite measure space, and let ρ be a symmetric measure on
be a σ-finite measure space, and let ρ be a symmetric measure on  . We will associate with
. We will associate with  and ρ a sequence of countably infinite graphs
and ρ a sequence of countably infinite graphs  equipped with conductance functions c
n such that the weighted graphs
equipped with conductance functions c
n such that the weighted graphs  can be viewed as a discretization of of the uncountable graph
can be viewed as a discretization of of the uncountable graph  considered in [1].
considered in [1].
We first recall a few facts from [1].
Lemma 7.1
Suppose that . Then, for any set
. Then, for any set ,
,
where
 . The converse is not true, in general.
. The converse is not true, in general.
We can view at the set  as an uncountable graph
as an uncountable graph  whose vertices are sets A from
whose vertices are sets A from  and edges are defined as follows. For a symmetric measure ρ defined on
and edges are defined as follows. For a symmetric measure ρ defined on  , we say that two sets A and B from
, we say that two sets A and B from  are connected by an edge e if ρ(A × B) > 0.
are connected by an edge e if ρ(A × B) > 0.
This definition is extended to get finite paths in the graph  . It is said that there exists a finite path in the graph
. It is said that there exists a finite path in the graph  from A to B if there exists a sequence {A
i : i = 0, …, n} of sets from
from A to B if there exists a sequence {A
i : i = 0, …, n} of sets from  (vertices of
(vertices of  ) such that A
0 = A, A
n = B and ρ(A
i × A
i+1) > 0, i = 0, …n − 1.
) such that A
0 = A, A
n = B and ρ(A
i × A
i+1) > 0, i = 0, …n − 1.
Theorem 7.2
Let
 be as above, and let ρ be a symmetric irreducible measure on
be as above, and let ρ be a symmetric irreducible measure on
 . Then any two sets A and B from the graph
. Then any two sets A and B from the graph
 are connected by a finite path, i.e., the graph
are connected by a finite path, i.e., the graph
 is connected.
is connected.
Proof
We will show that there exists a finite sequence (A
i : 0 ≤ i ≤ n) of disjoint subsets from  such that A
0 = A, ρ(A
i × A
i+1) > 0, and ρ(A
n × B) > 0, i = 0, …, n − 1.
such that A
0 = A, ρ(A
i × A
i+1) > 0, and ρ(A
n × B) > 0, i = 0, …, n − 1.
If ρ(A × B) > 0, then nothing to prove, so that we can assume that ρ(A × B) = 0.
Let  be a partition of V into disjoint subsets of positive finite measure such that
be a partition of V into disjoint subsets of positive finite measure such that  for all i. Without loss of generality, we can assume that the sets A and B are included in ξ. Let for definiteness, A = C
0.
for all i. Without loss of generality, we can assume that the sets A and B are included in ξ. Let for definiteness, A = C
0.
Since ρ(A × A c) > 0 (by Lemma 7.1), there exists a set \(C_{i_1}\in \xi \) such that \(\rho (A \times C_{i_1}) > 0\) and ρ(A × C j) = 0 for all 0 < j < i 1. Set
It is clear that  and ρ(A
0 × A
1) > 0. If ρ(A
1 × B) > 0, then we are done. If not, we proceed as follows. Because of the property \(\rho (A_1 \times A_1^c)> 0\), there exists some i
2 > i
1 such that \(\rho (A_1 \times C_{i_2}) > 0\) and ρ(A
1 × C
j) = 0 for all i
1 < j < i
2. Set
and ρ(A
0 × A
1) > 0. If ρ(A
1 × B) > 0, then we are done. If not, we proceed as follows. Because of the property \(\rho (A_1 \times A_1^c)> 0\), there exists some i
2 > i
1 such that \(\rho (A_1 \times C_{i_2}) > 0\) and ρ(A
1 × C
j) = 0 for all i
1 < j < i
2. Set
Then ρ(A 1 × A 2) > 0, and we check whether ρ(A 2 × B) > 0. If not, we continue in the same manner by constructing consequently disjoint sets A i satisfying the property ρ(A i × A i+1) > 0. Since B is an element of ξ, this process will terminate. This means that there exists some n such that A n ⊃ B. This argument proves the proposition. □
Given a σ-finite measure space  , consider a sequence of measurable partition
, consider a sequence of measurable partition  such that
such that
-
(i)
 ;
; -
(ii)
ξ n+1 refines ξ n, i.e., every element A n(i) of the partition ξ n is the union of some elements of ξ n+1: \(A_n(i) = \bigcup _{j \in \Lambda _n(i)} A_{n+1}(j)\) where Λn(i) is a finite subset of
 ;
; -
(iii)
the set
 generates the Borel σ-algebra
generates the Borel σ-algebra  .
.
If for every i, the cardinality of the set Λi is bigger than one, we say that ξ n+1 refines ξ n strictly.
It is well known, see e.g. [26], that, for any point x ∈ V , there exists a sequence i n(x) such that A n+1(i n+1(x)) ⊂ A n((i n)(x)) and

Suppose ρ is a symmetric measure on  . We define a sequence of non-negative Borel functions c
(n) on
. We define a sequence of non-negative Borel functions c
(n) on  by setting
by setting
for any x, y from V . Clearly, \(c^{(n)}_{xy}\) is a piecewise constant function.
Lemma 7.3
For a given sequence of strictly refining partitions (ξ n), the sequence of functions\((c^{(n)}_{xy})\)is monotone decreasing.
Proof
The proof is straightforward. For x, y ∈ V , let the sequences (A n(i n(x))) and (A n(j n(y))) shrink to the points x and y, respectively, according to (7.2). By assumption of the lemma, A n+1(i n+1(x)) is a proper subset of A n(i n(x)). Hence,
□
We now can define a sequence of discrete graphs (weighted networks) G
n = (V
n, E
n, w
n). The vertex set V
n is formed by the atoms of the partition ξ
n, i.e., by the sets  ; therefore V
n can be identified with
; therefore V
n can be identified with  . The set of edges E
n consists of pairs (i, j) such that
. The set of edges E
n consists of pairs (i, j) such that
The weight function is w n(i, j) = ρ(A n(i) × A n(j)).
Lemma 7.4
Let ρ be a symmetric irreducible measures on
 . Then the weighted graph G
n
is connected for every n.
. Then the weighted graph G
n
is connected for every n.
It follows from Lemma 7.3 that
exists and is a Borel non-negative function. Since the measure ρ is symmetric, we conclude that c xy = c yx.
Next, we define
where x ∼n y if and only if \(c^{(n)}_{xy} > 0\). It can be seen that
Using the proved results, we can deduce the following statement.
Theorem 7.5
The sequence (c (n)(x)) is monotone decreasing for every x ∈ V and
Proof
Indeed, we see from (7.3) that
Hence, the Borel function c(x) is well defined for every x. Because ⋂n A n(i n(x)) = {x}, we obtain that c(x) = ρ x(V ). □
References
S. Bezuglyi, P.E.T. Jorgensen, Graph Laplace and Markov operators on a measure space. ArXiv e-prints (2018)
D. Alpay, P. Jorgensen, I. Lewkowicz, W-Markov measures, transfer operators, wavelets and multiresolutions, in Frames and Harmonic Analysis. Contemporary Mathematics, vol. 706 (American Mathematical Society, Providence, 2018), pp. 293–343
L.W. Baggett, N.S. Larsen, K.D. Merrill, J.A. Packer, I. Raeburn, Generalized multiresolution analyses with given multiplicity functions. J. Fourier Anal. Appl. 15(5), 616–633 (2009)
L.W. Baggett, K.D. Merrill, J.A. Packer, A.B. Ramsay, Probability measures on solenoids corresponding to fractal wavelets. Trans. Am. Math. Soc. 364(5), 2723–2748 (2012)
O. Bratteli, P.E.T. Jorgensen, Convergence of the cascade algorithm at irregular scaling functions, in The Functional and Harmonic Analysis of Wavelets and Frames (San Antonio, TX, 1999). Contemporary Mathematics, vol. 247 (American Mathematical Society, Providence, 1999), pp. 93–130
L. Cioletti, M. Denker, A.O. Lopes, M. Stadlbauer, Spectral properties of the Ruelle operator for product-type potentials on shift spaces. J. Lond. Math. Soc. (2) 95(2), 684–704 (2017)
D.E. Dutkay, P.E.T. Jorgensen, The role of transfer operators and shifts in the study of fractals: encoding-models, analysis and geometry, commutative and non-commutative, in Geometry and Analysis of Fractals. Springer Proceedings of the Mathematical Statistics, vol. 88 (Springer, Heidelberg, 2014), pp. 65–95
Y. Jiang, Y.-L. Ye, Convergence speed of a Ruelle operator associated with a non-uniformly expanding conformal dynamical system and a Dini potential. Discrete Contin. Dyn. Syst. 38(9), 4693–4713 (2018)
P. Jorgensen, F. Tian, Transfer operators, induced probability spaces, and random walk models. Markov Process. Related Fields 23(2), 187–210 (2017)
P.E.T. Jorgensen, Ruelle operators: functions which are harmonic with respect to a transfer operator. Mem. Am. Math. Soc. 152(720), viii+60 (2001)
P.E.T. Jorgensen, S. Pedersen, Dense analytic subspaces in fractal L 2-spaces. J. Anal. Math. 75, 185–228 (1998)
D. Ruelle, The thermodynamic formalism for expanding maps. Commun. Math. Phys. 125(2), 239–262 (1989)
D. Ruelle, Spectral properties of a class of operators associated with conformal maps in two dimensions. Commun. Math. Phys. 144(3), 537–556 (1992)
Á. Backhausz, B. Szegedy, On large-girth regular graphs and random processes on trees. Random Struct. Algoritm. 53(3), 389–416 (2018)
Á. Backhausz, B. Szegedy, On the almost eigenvectors of random regular graphs. Ann. Probab. 47(3), 1677–1725 (2019)
M. Pensky, Dynamic network models and graphon estimation. Ann. Statist. 47(4), 2378–2403 (2019)
R. Lyons, Y. Peres, Probability on trees and networks, in Cambridge Series in Statistical and Probabilistic Mathematics, vol. 42 (Cambridge University, New York, 2016)
E. Nummelin, General irreducible Markov chains and nonnegative operators, in Cambridge Tracts in Mathematics, vol. 83 (Cambridge University, Cambridge, 1984)
D. Revuz, Markov chains, in North-Holland Mathematical Library, vol. 11, 2nd edn. (North-Holland Publishing Co., Amsterdam, 1984)
C.T. Conley, B.D. Miller, A bound on measurable chromatic numbers of locally finite Borel graphs. Math. Res. Lett. 23(6), 1633–1644 (2016)
C.T. Conley, B.D. Miller, Measurable perfect matchings for acyclic locally countable Borel graphs. J. Symb. Log. 82(1), 258–271 (2017)
I.P. Cornfeld, S.V. Fomin, Y.G. Sinaı̆, Ergodic Theory. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 245 (Springer, New York, 1982). Translated from the Russian by A. B. Sosinskiı̆
N.T. Do, P. Kuchment, B. Ong, On resonant spectral gaps in quantum graphs, in Functional Analysis and Operator Theory for Quantum Physics. EMS Series Congress Report (European Mathematical Society, Zürich, 2017), pp. 213–222
J. Feldman, C.C. Moore, Ergodic equivalence relations, cohomology, and von Neumann algebras. I. Trans. Am. Math. Soc. 234(2), 289–324 (1977)
V. Kanovei, Borel equivalence relations, in University Lecture Series, vol. 44 (American Mathematical Society, Providence, RI, 2008). Structure and classification
A.S. Kechris, Classical descriptive set theory, in Graduate Texts in Mathematics, vol. 156 (Springer, New York, 1995)
J. Lehn, Remark on measurable graph theorems. Proc. Am. Math. Soc. 63(1), 46–48 (1977)
S. Gao, Invariant descriptive set theory, in Pure and Applied Mathematics (Boca Raton), vol. 293 (CRC Press, Boca Raton, 2009)
A.S. Kechris, Global aspects of ergodic group actions, in Mathematical Surveys and Monographs, vol. 160 (American Mathematical Society, Providence, RI, 2010)
F. Chersi, An ergodic decomposition of invariant measures for discrete semiflows on standard Borel spaces, in Advanced Topics in the Theory of Dynamical Systems (Trento, 1987). Notes Reports Mathematical Science Engineering, vol. 6, pp. 75–87 (Academic Press, Boston, 1989)
P.A. Loeb, Conversion from nonstandard to standard measure spaces and applications in probability theory. Trans. Am. Math. Soc. 211, 113–122 (1975)
V.A. Rohlin, On the fundamental ideas of measure theory. Mat. Sbornik N.S. 25(67), 107–150 (1949)
D. Simmons, Conditional measures and conditional expectation; Rohlin’s disintegration theorem. Discrete Contin. Dyn. Syst. 32(7), 2565–2582 (2012)
J. Feldman, C.C. Moore, Ergodic equivalence relations, cohomology, and von Neumann algebras. II. Trans. Am. Math. Soc. 234(2), 325–359 (1977)
A.S. Kechris, B.D. Miller, Topics in orbit equivalence, in Lecture Notes in Mathematics, vol. 1852 (Springer, Berlin, 2004)
Z.-Q. Chen, Y.-X. Ren, T. Yang, Law of large numbers for branching symmetric Hunt processes with measure-valued branching rates. J. Theoret. Probab. 30(3), 898–931 (2017)
D.H. Alimorad, J.A. Fakharzadeh, A theoretical measure technique for determining 3D symmetric nearly optimal shapes with a given center of mass. Comput. Math. Math. Phys. 57(7), 1225–1240 (2017)
S. Bezuglyi, P.E.T. Jorgensen, Transfer operators, endomorphisms, and measurable partitions. Lecture Notes in Mathematics, vol. 2217 (Springer, Cham, 2018)
P.E.T. Jorgensen, E.P.J. Pearse, Continuum versus discrete networks, graph Laplacians, and reproducing kernel Hilbert spaces. J. Math. Anal. Appl. 469(2), 765–807 (2019)
B. Landa, Y. Shkolnisky, The steerable graph Laplacian and its application to filtering image datasets. SIAM J. Imaging Sci. 11(4), 2254–2304 (2018)
S. Smale, D.-X. Zhou, Learning theory estimates via integral operators and their approximations. Constr. Approx. 26(2), 153–172 (2007)
S. Smale, D.-X. Zhou, Geometry on probability spaces. Constr. Approx. 30(3), 311–323 (2009)
S. Bezuglyi, P.E.T. Jorgensen, Finite Energy Space, Graph Laplace Operator, and Symmetric Measures
M.F. Chen, From Markov Chains to Nonequilibrium Particle Systems (World Scientific Publishing Co. Inc., River Edge, 1992)
K. Lange, Applied probability, in Springer Texts in Statistics (Springer, New York, 2003)
T. Komorowski, C. Landim, S. Olla, Fluctuations in Markov processes. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 345 (Springer, Heidelberg, 2012). Time symmetry and martingale approximation
Y. Chen, M.-P. Qian, J.-S. Xie, On characterization of reversible Markov processes by monotonicity of the fluctuation spectral density. J. Math. Phys. 47(10), 103301, 9 (2006)
M. Longla, Remarks on limit theorems for reversible Markov processes and their applications. J. Statist. Plann. Inference 187, 28–43 (2017)
M. Peligrad, Asymptotic properties for linear processes of functionals of reversible or normal Markov chains, in High Dimensional Probability VI. Program of Probability, vol. 66 (Birkhäuser/Springer, Basel, 2013), pp. 195–210
J.R. Artalejo, On the transient behavior of the maximum level length in structured Markov chains, in Modern Mathematical Tools and Techniques in Capturing Complexity. Understand Complex System (Springer, Berlin, 2011), pp. 379–390
V.T. Cyr, Transient Markov shifts (ProQuest LLC, Ann Arbor, MI, 2010). Thesis (Ph.D.)–The Pennsylvania State University
D. Korshunov, The key renewal theorem for a transient Markov chain. J. Theoret. Probab. 21(1), 234–245 (2008)
S. Wei, R.J. Kryscio, Semi-Markov models for interval censored transient cognitive states with back transitions and a competing risk. Stat. Methods Med. Res. 25(6), 2909–2924 (2016)
W. Woess, Denumerable Markov chains, in EMS Textbooks in Mathematics (European Mathematical Society (EMS), Zürich, 2009). Generating functions, boundary theory, random walks on trees
M.B. Marcus, J. Rosen, Necessary and sufficient conditions for the continuity of permanental processes associated with transient Lévy processes. Electron. Commun. Probab. 20(57), 6 (2015)
J. Peterson, G. Samorodnitsky, Weak weak quenched limits for the path-valued processes of hitting times and positions of a transient, one-dimensional random walk in a random environment. ALEA Lat. Am. J. Probab. Math. Stat. 9(2), 531–569 (2012)
P. Lherminier, E. Sanchez-Palencia, Remarks and examples on transient processes and attractors in biological evolution, in Proceedings of the 2014 Madrid Conference on Applied Mathematics in Honor of Alfonso Casal. Electronic Journal of Differential Equations Conference, vol. 22 (Texas State University, San Marcos, 2015), pp. 63–77
A.N. Borodin, P. Salminen, Handbook of Brownian Motion—Facts and Formulae. Probability and its Applications, 2nd edn. (Birkhäuser, Basel, 2002)
G.F. Lawler, V. Limic, Random walk: a modern introduction. Cambridge Studies in Advanced Mathematics, vol. 123 (Cambridge University, Cambridge, 2010)
V.N. Kolokoltsov, Markov processes, semigroups and generators, in De Gruyter Studies in Mathematics, vol. 38 (Walter de Gruyter and Co., Berlin, 2011)
A. Beveridge, A hitting time formula for the discrete Green’s function. Combin. Probab. Comput. 25(3), 362–379 (2016)
Z.-Q. Chen, P. Kim, Green function estimate for censored stable processes. Probab. Theory Related Fields 124(4), 595–610 (2002)
I.T. Dimov, T.V. Gurov, Estimates of the computational complexity of iterative Monte Carlo algorithm based on Green’s function approach. Math. Comput. Simulation 47(2–5), 183–199 (1998). IMACS Seminar on Monte Carlo Methods (Brussels, 1997)
A.N. Kolmogorov, Foundations of the Theory of Probability (Chelsea Publishing Company, New York, 1950)
L. Lovász, Large networks and graph limits, in American Mathematical Society Colloquium Publications, vol. 60 (American Mathematical Society, Providence, 2012)
S. Chatterjee, Large deviations for random graphs, in Lecture Notes in Mathematics, vol. 2197 (Springer, Cham, 2017). Lecture notes from the 45th Probability Summer School held in Saint-Flour, June 2015, École d’Été de Probabilités de Saint-Flour. [Saint-Flour Probability Summer School]
S. Janson, Graphons, cut norm and distance, couplings and rearrangements, in New York Journal of Mathematics. NYJM Monographs, vol. 4 (State University of New York, University at Albany, Albany, NY, 2013)
H. Chuangpishit, M. Ghandehari, J. Janssen, Uniform linear embeddings of graphons. European J. Combin. 61, 47–68 (2017)
L. Lovász, B. Szegedy, The automorphism group of a graphon. J. Algebra 421, 136–166 (2015)
A. Shojaei-Fard, Graphons and renormalization of large Feynman diagrams. Opuscula Math. 38(3), 427–455 (2018)
Acknowledgements
The authors are thankful to colleagues and collaborators, especially the members of the seminars in Mathematical Physics and Operator Theory at the University of Iowa, where versions of this work have been presented. We acknowledge very helpful conversations with among others Professors Paul Muhly, Wayne Polyzou; and conversations at distance with Professors Daniel Alpay, and his colleagues at both Ben Gurion University, and Chapman University. We wish to thank the referee for useful suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Bezuglyi, S., Jorgensen, P.E.T. (2021). Symmetric Measures, Continuous Networks, and Dynamics. In: Alpay, D., Peretz, R., Shoikhet, D., Vajiac, M.B. (eds) New Directions in Function Theory: From Complex to Hypercomplex to Non-Commutative. Operator Theory: Advances and Applications(), vol 286. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-76473-9_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-76473-9_6
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-76472-2
Online ISBN: 978-3-030-76473-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)




 is a standard Borel space where
is a standard Borel space where  is the σ-algebra of Borel sets induced on E
x from
is the σ-algebra of Borel sets induced on E
x from  .
. ;
; .
. . If one begins with a measure ρ on
. If one begins with a measure ρ on  , then the measure μ arises as the projection of ρ on
, then the measure μ arises as the projection of ρ on  ,
,  , and let ρ be a measure on
, and let ρ be a measure on  satisfying the condition of Theorem
satisfying the condition of Theorem 
 , where the measures ρ
x are defined by the relation
, where the measures ρ
x are defined by the relation  by setting
by setting 
 , x ∈ V .
, x ∈ V . , then the support of ρ, the set E = E(ρ), is symmetric mod 0. Here E(ρ) is defined up to a set of zero measure by the relation
, then the support of ρ, the set E = E(ρ), is symmetric mod 0. Here E(ρ) is defined up to a set of zero measure by the relation  .
. . The latter was considered in [
. The latter was considered in [ and
and  . But if a σ-finite measure μ is given on
. But if a σ-finite measure μ is given on  , then we need to include an additional relation between the projections of ρ on V and the measure μ. Let π
1 : V × V → V be the projection on the first coordinate. We require that the symmetric measure must satisfy the property
, then we need to include an additional relation between the projections of ρ on V and the measure μ. Let π
1 : V × V → V be the projection on the first coordinate. We require that the symmetric measure must satisfy the property  , the set E(ρ) do not need to be a set of positive measure with respect to the product measure μ × μ. In other words, we admit both cases: (a) ρ is equivalent to μ × μ, (b) ρ and μ × μ are mutually singular.
, the set E(ρ) do not need to be a set of positive measure with respect to the product measure μ × μ. In other words, we admit both cases: (a) ρ is equivalent to μ × μ, (b) ρ and μ × μ are mutually singular. ,
,  (μ-irreducible) if, for any set A of positive measure μ and μ-a.e. x ∈ V , there exists some n such that k
n(x, A) > 0, i.e., any set A of positive measure is attainable from μ-a.e. x, x → A.
(μ-irreducible) if, for any set A of positive measure μ and μ-a.e. x ∈ V , there exists some n such that k
n(x, A) > 0, i.e., any set A of positive measure is attainable from μ-a.e. x, x → A. is called irreducible if the corresponding kernel
is called irreducible if the corresponding kernel  is μ-irreducible where μ is the projection of measure ρ.
is μ-irreducible where μ is the projection of measure ρ. is also of positive measure. Otherwise, ρ is called indecomposable.
is also of positive measure. Otherwise, ρ is called indecomposable. , or a Markov process.
, or a Markov process.
 is a function identically equal to 1,
is a function identically equal to 1, , then
, then  because every measure P(x, ⋅) is probability. Hence, P is a Markov operator.
because every measure P(x, ⋅) is probability. Hence, P is a Markov operator.
 is called symmetric if it satisfies the relation:
is called symmetric if it satisfies the relation:  . It turns out that any symmetric operator R defines a symmetric measure ρ. Indeed, the functional
. It turns out that any symmetric operator R defines a symmetric measure ρ. Indeed, the functional 
 such that
such that  is a vector space containing all constant functions. We identify functions f
1 and f
2 such that f
1 − f
2 = const and, with some abuse of notation, the quotient space is also denoted by
is a vector space containing all constant functions. We identify functions f
1 and f
2 such that f
1 − f
2 = const and, with some abuse of notation, the quotient space is also denoted by  . So that, we will call elements f of
. So that, we will call elements f of  functions assuming that a representative of the equivalence class f is considered.
functions assuming that a representative of the equivalence class f is considered. . This means that the space of functions f on
. This means that the space of functions f on  satisfying (
satisfying ( .
.
 , then
, then
 .
. , one has
, one has . The function χ
Ais in
. The function χ
Ais in if and only if either μ(A) < ∞ or μ(A
c) < ∞.
if and only if either μ(A) < ∞ or μ(A
c) < ∞.
 admits the decomposition into the orthogonal sum
admits the decomposition into the orthogonal sum
 is taken in the norm of the Hilbert space
is taken in the norm of the Hilbert space .
. . Then R is a symmetric unbounded operator in L
2(μ), i.e.,
. Then R is a symmetric unbounded operator in L
2(μ), i.e., . Moreover,
. Moreover,
 ,
,  , if for any bounded Borel function f(x, y),
, if for any bounded Borel function f(x, y),  , and let P be the Markov operator determined by x↦P(x, ⋅). It is said that the corresponding Markov process is reversible with respect to a measurable functions c : V → (0, ∞) if, for any sets
, and let P be the Markov operator determined by x↦P(x, ⋅). It is said that the corresponding Markov process is reversible with respect to a measurable functions c : V → (0, ∞) if, for any sets  , the following relation holds:
, the following relation holds:  is symmetric on
is symmetric on
 , and ρ
n
is equivalent to ρ.
, and ρ
n
is equivalent to ρ.
 .
. defined by
defined by , the measure ρ
ndefined by (
, the measure ρ
ndefined by ( ,
, 
 . This field of transition probabilities generates the Markov operator P such that
. This field of transition probabilities generates the Markov operator P such that  . It follows from Theorem
. It follows from Theorem 
 . To answer the question about the existence of a P-invariant measure ν ∼ μ such that (P, ν) is reversible, it suffices to construct a locally integrable function c satisfying (
. To answer the question about the existence of a P-invariant measure ν ∼ μ such that (P, ν) is reversible, it suffices to construct a locally integrable function c satisfying ( such that, for any
such that, for any  ,
,  , the measure dν(x) = c(x)dμ(x) belongs to
, the measure dν(x) = c(x)dμ(x) belongs to  . Indeed, it suffices to define the symmetric measure ρ according to Theorem
. Indeed, it suffices to define the symmetric measure ρ according to Theorem  , i.e, ρ(A × B) ≠ ρ(B × A), in general. However, we will assume that ρ is equivalent to ρ ∘ θ where θ(x, y) = (y, x). Then, using the same approach as above, we can define the following objects: margin measures
, i.e, ρ(A × B) ≠ ρ(B × A), in general. However, we will assume that ρ is equivalent to ρ ∘ θ where θ(x, y) = (y, x). Then, using the same approach as above, we can define the following objects: margin measures 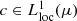 , then
, then 
 , then
, then 
 :
: 
 are representatives of elements from
are representatives of elements from  ).
).
 . This fact is proved in [
. This fact is proved in [ , then
, then
 . Then, using the symmetry of the measure ρ and relation (
. Then, using the symmetry of the measure ρ and relation ( . Then, for
. Then, for ,
, 
 ,
, 
 , we can easily deduce from (1) the following equality (we use here formula (
, we can easily deduce from (1) the following equality (we use here formula (

 to L
2(ν) is contractive.
to L
2(ν) is contractive.

 is harmonic with respect to the Markov operator P;
is harmonic with respect to the Markov operator P;
 is a martingale.
is a martingale.
 , we have
, we have


 and
and ,
, 

 is dense in the energy space
is dense in the energy space .
.

 for all
for all  , then f = 0, and
, then f = 0, and  is dense in
is dense in  . □
. □
 ;
; ;
; generates the Borel σ-algebra
generates the Borel σ-algebra  .
.