Modelling the Three-Stage of Creep

Abstract

Over the last years, several studies have addressed the time-dependent mechanical behaviour of polymeric composites. When subjected to a constant stress, viscoelastic materials experience a time-dependent increase in strain. This phenomenon is known as viscoelastic creep and manifests as a tendency of a solid material to deform permanently under the influence of constant stress: tensile, compressive, shear or flexural. When applied to polymers, creep is the result of the inherent viscoelastic nature that causes time dependency of behavior. As well known, the initial strain in a material is roughly predicted by its stress-strain modulus. Then, the material will continue to deform slowly with time indefinitely or until rupture or yielding causes failure. A typical creep curve reveals a three-stage behavior, (1) the transient stage, where the deformation rate decreases with time, (2) the steady-state, characterized by a “relatively” uniform rate gradient and (3) the accelerated phase, where the strain rate increases until rupture. In polymers at low strains (nearly to 1%), creep is essentially recoverable after unloading. However, in certain cases, creep failure is the most important degradation mode of a structure (turbine blades, aircraft parts). Furthermore, in civil engineering works, this kind of deformations may be substantial throughout the required service life. The investigation of the creep response of selected engineering materials should integrate the design of structures subjected to mechanical loads over a long time of operation (self-weight, static loads). The aim of “creep modeling for structural analysis” is the development of methods to simulate and analyze the time-dependent changes of stress and strain states in engineering structures up to the critical stage of creep rupture, passing through service state. In particular, the key in identifying these three stages above described lies in the location of the transition points between stages. This work presents a study conducted to estimate the 4 instants of time of the creep curve: (1) the first transition point, that is the transition point between transient and steady creep; (2) the secondary point, that is the inflexion point of the creep curve where the strain rate reaches its minimum; (3) the second transition point, that is the transition point between steady and accelerated creep; and (4) the instability point. This research follows the work publish by Crevecoeur [3] and is based on a combination of an exponential and a power law approach to the creep test data of HDPE pipe sample.

1 Introduction

Creep is a slow, continuous deformation of a material under a constant stress and temperature. As a result of its inherent viscoelastic nature, polymers present a time-dependent deformation that occurs under any temperature. Creep of polymeric solids can be subdivided into several stages, where instantaneous creep takes place upon loading, followed by transient creep where the strain-rate reaches its minimum. It then increases and approaches an asymptotic limit and rupture occurs.

Therefore, the study on the process of creep is essential and significant for engineering applications concerning temperature and stress and has been a challenge in the design of structures subjected to loads for long periods of time. According to Monfared [14], predicting creep behaviour is of utmost importance on advanced reinforced or non-reinforced materials design, such as polymeric composite.

In fact, to define parameters to prevent unsafe and undesired events such as progressive deformations and local reduction of material strength, may be an important tool in development of more slender and durable structures. In this context, estimating of transition points between stages of creep may help in linear and non-linear analysis of the structure behaviour.

On the other hand, Crevecoeur [6] shows a non-linear kinetics in the ageing of biological systems, which is characterized by three successive stages such as observed in a creep curve of polymeric composite. Crevecoeur shows that a model useful for the follow-up of operating inert systems allows to find back typical curves and laws related to the ageing of biological systems.

Based on the work of Crevecoeur and through a combination of an exponential and a power law approach to the creep test data of FRP sample, this paper proposes a simple approach to modelling the three-stages of polymer creep.

2 Theoretical Background

The combination of mechanical behavior of elastic and viscous materials characterizes the response of a viscoelastic material.

According to Barra [1], due its molecular nature, the polymeric mass may be seen formed from a twisted or tangled chains in its undeformed state. Subjected to constant tension, molecules exert a retractive response to this tension in order to maintain their stable (folded) conformation. Under continuous tension, the chains slide relatively to each other and the tangled structure is deformed into an extended conformation. When the applied load is released before the creep rupture occurs, an immediate elastic recovery equal to the elastic deformation, followed by a period of slow recovery is observed.

Within certain limits, the graphic tension versus deformation will take the shape of an ellipse. This format tends to be maintained to the extent that the amplitudes of tension and deformation grow (Fig. 1).

Fig. 1

Stress-strain relationship of viscoelastic materials

The viscoelastic behaviour manifests itself in several ways, which comprise: (a) creep under constant load; (b) relaxation of tension under constant deformation; (c) recovery of time dependent deformation after complete removal of load; (d) rupture due to time-dependent creep; (e) fatigue resistance dependent on the excitation frequency.

Basically, there are three principal ways to describe the viscoelastic behavior [19] in time domain. The first one is the Boltzmann superposition principle so-called the integral representation expressed by the convolution integral (1).

$$\varepsilon \left( {\text{t}} \right) = \mathop \smallint \limits_{ - \infty }^{\text{t}} {\text{J}}\left( {{\text{t}} -\uptau_{\text{n}} } \right){\text{d}}\upsigma\left( {\uptau_{\text{n}} } \right)$$

(1)

The second way, represented by a differential equation (2), uses assemblages of Hookean springs and Newtonian viscous elements (dashpots) as models through several forms of combinations. For a Maxwell rheological model, total strain yields:

$$\frac{{\partial\upvarepsilon}}{{\partial {\text{t}}}} = {\eta \dot{\varepsilon }}$$

(2)

The third method is based on assumptions about the molecules themselves which dynamic tests are more convenient to be used for. This last method will not be described in this paper.

2.1 Creep

Depending on the level of excitation applied, the material may not recover to its original shape, and then a permanent deformation becomes installed. The magnitude of this permanent deformation will depend on the duration and the amount of tension applied, as well as the temperature [8].

For a constant temperature, this creep description is illustrated by Fig. 2 and translated by expression (3).

Fig. 2

Creep and recovery description

$${\text{J}}\left( {\text{t}} \right) = \in \left( {\text{t}} \right)/\upsigma_{0}$$

(3)

For most applications, composite structures may be designed using linear elastic analysis. However, due to the effects of environment, there are instances where time dependent phenomena such as creep may be important long-term design considerations.

In these cases, creep failure is the most important degradation mode of a structure (turbine blades, aircraft parts) and its behavior must be known until its failure. An example showing importance of the creep phenomenon is the creep behavior of epoxy-based structural adhesives. Compared to other joining methods, welding or bolting for example, epoxy-based structural adhesives provide advantages, such as its high strength-to-weight ratio [10].

2.2 The Three-Stages of Creep

As known, viscoelastic material is a rheological material that exhibits time-temperature rate of loading dependence, with the response being a function of the current input and also of the current and past input history.

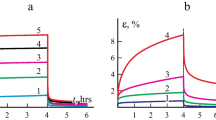
Under a sustained load over a long period of time, viscoelastic materials undergo three stages of strain evolution (Fig. 3).

Fig. 3

Three-stages of creep

The typical creep curve showed in Fig. 3 may be described as follow:

• (a) First stage: so-called Primary or Transient creep, in which creep occurs at a decreasing rate;

• (b) Second stage: so-called Second or Steady-state creep, in which strain rate reaches its minimum and shows a nearly constant value;

• (c) Third stage: so-called Tertiary or Accelerated creep, where the strain rate increases quickly and its end the rupture occurs.

Figure 4 shows the strain rate of creep behavior and the total relationship of an ideal creep curve, the so-called creep bathtub. The bathtub curve usually gives the failure rate for an operating system.

Fig. 4

Strain rate bathtub

According to Naumenko and Altenbach [15], the secondary creep is for many applications the most important creep model. The relative equilibrium, i.e., a uniform rate of strain gradient, enables the long-term behavior of the structure to be analyzed assuming stationary creep processes. The extent of this stage depends on the combination of applied stress and system temperature. For relatively low stresses, the secondary stage may have a considerable extent before the onset of tertiary creep [2].

However, for components with a close fit, the primary creep needs to be taken into account. Bolts and copper canisters for the storage of spent nuclear fuel are an example of this [16].

On its turn, the tertiary creep leads to an unstable crack propagation and materials failure at end. The point where the accelerated creep starts is known as flow time and is defined as the time at which the shear deformation under constant volume starts, i.e., wherein the volume does not change. In an idealized curve of creep, tertiary stage only occurs at high stress or for ductile materials.

Furthermore, stress impacts significantly the strain rate where the increase of the stress by one order causes an increase of strain rate about four orders approximately [11].

Thus, to provide a better understanding of the structure behavior over time, these three-stages of creep should be known in order to avoid undesired behavior and even irreversible failure.

In particular, the key to determining these three-stages is in the fact that how to locate the transition points between stages along the creep curve. At last instance, it translates in the determination of secondary stage boundaries and in the predicting a creep safe envelope.

2.3 Biological Ageing Analogy

As defined in Luder [13], biological ageing is usually considered the continuous accumulation of damage or deterioration, at the level of the cells, tissues, organs or organism, which reduces vitality and ultimately leads to death.

Crevecoeur [6] shows that ageing could be seen as a multifactorial process. According to that, there is a widely observed non-linear kinetics in the ageing of biological systems, which is characterised by three successive stages, (1) firstly the ageing rate is high, but it decreases quickly to a minimum, from which (2) it remains nearly constant during the major part of the process until (3) it starts increasing again up to the final collapse of the system.

Concerning to this, taking ageing in the broad sense, as the whole process of going from birth to death, non-linearities appear. Those can be found in nature as reflecting successive periods in the life of biological systems, such as in the “survival, mortality or growth curves” (see Van Voorhies [20], Luder [13] and Fotsis et al. [9], respectively).

Selye [17] described the three stages of a system reaction, termed General Adaptative Syndrome (GAS) where “there is an integrated syndrome of closely interrelated adaptive reactions to non-specific stress itself”. The first stage of GAS is the “Alarm Reaction”, which can be corresponding to an elastic response of polymer under static load; the second stage is called “Stage of Resistance”, in which “a certain resistance is built up against the damaging stimulus” that could be translated in terms of steady creep rate; at last, the tertiary stage, called “Stage of Exhaustion”, where the system loses its resistance and fails with several internal changes.

Thus, the parallel between biological ageing and polymeric creep behavior can be explained by assuming that a polymeric structure is composed of interconnected microstructures operating together under an input stress.

In this way, Crevecoeur [4] shows the similarity between creep behavior and mechanical system ageing, where the failure rate of mechanical repairable systems that deteriorate with time due to ageing can usually be visualized by a bathtub curve, as shown in the creep rate curve.

3 Modeling Approach

Crevecoeur [5] suggests a differential equation to synthesize the strain rate behavior of creep expressed by the bathtub curve:

$$\frac{{{\dot{\varepsilon }}\left( {\text{t}} \right)}}{{\upvarepsilon_{e} \left( {\text{t}} \right)}} =\upalpha + \frac{\upbeta}{{{\text{t}}_{\text{i}} }}$$

(4)

where:

• $\dot{\varvec{\varepsilon }}\left( \varvec{t} \right)$ is the strain rate

• $\varvec{\varepsilon}_{\varvec{e}} \left( \varvec{t} \right)$ is the measured strain from creep test

• $\varvec{\alpha},\varvec{ \beta }$ are constants to be fitted, where $\varvec{\alpha}> {\mathbf{0}}$ and $\beta < {\mathbf{1}}$ and $\alpha \ll\varvec{\beta}$.

Once (4) is integrated, it gives a combination of an exponential and a power law function (5).

$$\upvarepsilon_{e} \left( {\text{t}} \right) = {\text{k}}. {\text{e}}^{{\upalpha.{\text{t}}}} .{\text{t}}^{\upbeta}$$

(5)

where:

• $\varvec{k}$ is a constant for a given temperature and load.

The three parameters $\varvec{\alpha}$, $\varvec{\beta}$ and $\varvec{k}$ are constant as long as the physical constraints on the system remain constant, i.e., while the stress and temperature remain constant, these three parameters stay constant.

Crevecoeur [6] introduces a third system constraint which is called the internal “organisation” of the system. In the case of a polymer, this can be understood as the molecular arrange of the polymer and the micromechanical assemblage of the composite material.

According to Smith [18], the values of the parameter $\varvec{\beta}$ will typically range between 0.15 and 0.65. However, this quantity can have values between 0 and 1 [3].

In (5) the quantity $\left( {1/\varvec{\alpha}} \right)$ gives the order of magnitude of the time scale for the creep process. Physically, this quantity corresponds to a time called “instability time”, $\varvec{t}_{\varvec{i}}$, [6], i.e.:

$$\frac{1}{\upalpha} = {\text{t}}_{\text{i}}$$

(6)

The instability time is one that from it there is a risk that the system starts to fail. At $\varvec{t}_{\varvec{i}}$, if the load is not removed or operating conditions are not relaxed, the system will become impaired. It means that the system will usually continue after $\varvec{t}_{\varvec{i}}$ but the process leading to the collapse is irreversibly started.

According to Crevecoeur [6], it is noticeable that the instability time occurs in tertiary creep and it is possible to divide the third stage into two parts, (1) before $\varvec{t}_{\varvec{i}}$ (the predictable ageing) and (2) after $\varvec{t}_{\varvec{i}}$ (the statistically predictable ageing).

The system failure takes place about 20–40% of life after $\varvec{t}_{\varvec{i}}$.

Applying (6) into (5), yields (7).

$$\upvarepsilon_{\text{e}} \left( {\text{t}} \right) = {\text{k}}. {\text{e}}^{{\left( {\frac{\text{t}}{{{\text{t}}_{\text{i}} }}} \right)}} .{\text{t}}^{\upbeta}$$

(7)

where:

• $\varvec{\varepsilon}_{\varvec{e}} \left( \varvec{t} \right)$ is the creep strain measured at $\varvec{t}$.

From Eq. (7), at some given time $\varvec{t}_{\varvec{n}}$, it is expectable that:

$${\text{t}} = {\text{t}}_{\text{i}} \ldots {\text{that means}} \ldots \upvarepsilon_{\text{e}} \left( {\text{t}} \right) =\upvarepsilon\left( {{\text{t}}_{\text{i}} } \right)$$

(8)

From the equality (8), Eq. (7) yields (8).

$$\upvarepsilon_{i} \left( {{\text{t}}_{\text{i}} } \right) = {\text{k}}. {\text{e}}^{1} .{\text{t}}_{\text{i}}^{\upbeta}$$

(9)

where:

• $\varvec{\varepsilon}_{\varvec{i}} \left( {\varvec{t}_{\varvec{i}} } \right)$ is the strain at $\varvec{t}_{\varvec{i}}$.

The quotient between (7) and (9) yields (10):

$$\frac{{\upvarepsilon_{\text{e}} \left( {\text{t}} \right)}}{{\upvarepsilon_{\text{i}} \left( {{\text{t}}_{\text{i}} } \right)}} = { \exp }\left( {\frac{\text{t}}{{{\text{t}}_{\text{i}} }} - 1} \right) .\left( {\frac{\text{t}}{{{\text{t}}_{\text{i}} }}} \right)^{\upbeta}$$

(10)

From data pairs ($\varvec{\varepsilon}_{\varvec{e}} ,\varvec{ t}$), it is expectable that ($\varvec{\varepsilon}_{\varvec{i}} ,\varvec{ t}_{\varvec{i}} ,\varvec{ \beta }$) converge from a successive iteration of (10).

Moreover, according to Crevecoeur [7] the use of $\varvec{\varepsilon}_{\varvec{e}} \left( \varvec{t} \right)/\varvec{\varepsilon}_{\varvec{i}} \left( {\varvec{t}_{\varvec{i}} } \right)\varvec{ }$ and $\varvec{t}/\varvec{t}_{\varvec{i}}$ allows to normalize the shape of the creep curve, independently of how long the process lasts. In fact, for a given $\varvec{\beta}$ and making $\varvec{\varepsilon}_{\varvec{e}} \left( \varvec{t} \right) =\varvec{\varepsilon}_{\varvec{i}} \left( {\varvec{t}_{\varvec{i}} } \right)$, the creep curve will look similar for a small $\varvec{t}_{\varvec{i}}$ (tests at higher stress or temperature) as well as for a larger $\varvec{t}_{\varvec{i}}$ (tests at lower stress or temperature).

To find the time of steady creep, Crevecoeur [6] suggests the following relation:

$${\text{t}}_{{2{\text{ary}}}} = {\text{t}}_{\text{i}} .\left( {\sqrt \beta -\upbeta} \right)$$

(11)

Expression (11) gives the point where the strain rate reaches its minimum and corresponds to the point of inflexion on the creep curve.

From (11), the secondary strain point, $\varvec{\varepsilon}_{{2\varvec{ary}}}$, is estimated using (7).

It must to be warned that the 2ary stage (the steady-state stage) has visually the aspect of a straight line but in fact it is an approximate linearization for practical applications and shows a quasi-straight linear zone.

The point ($\varvec{\varepsilon}_{{2\varvec{ary}}} ,\varvec{ t}_{{2\varvec{ary}}}$) is somewhere in the 2ary stage where the creep curve turns from concave (from below) to convex (from below) form.

Furthermore, it is possible to mark several periods of time on the creep curve. Comparing biological and inert systems, Crevecoeur [6] distinguishes some periods of time:

• (1) the instability time—$\varvec{t}_{\varvec{i}}$;

• (2) the actual time of collapse—$\varvec{t}_{\varvec{r}}$ (the ‘lifespan’);

• (3) the maximum possible lifetime—$\varvec{t}_{\varvec{m}}$ (the ‘longevity’); and

• (4) the statistical average of lifetimes—$\varvec{t}_{\varvec{\mu}}$, (the ‘life expectancy’).

These periods of time are shown in Fig. 5

Fig. 5

Periods of time on a hypothetical creep curve

where:

• $\varvec{t}_{{1\varvec{ary}}}$ is the transition point between transient and steady creep

• $\varvec{t}_{{2\varvec{ary}}}$ is the inflexion point of the creep curve

• $\varvec{t}_{{3\varvec{ary}}}$ is the second transition point (flow time)

• $\varvec{t}_{\varvec{i}}$ is the instability time

• $\varvec{t}_{\varvec{r}}$ is the actual time of failure

• $\varvec{t}_{\varvec{m}}$ is the maximum possible lifetime.

Applying $\varvec{t}_{{2\varvec{ary}}}$ to the derivative of (5) and comparing its straight line to creep data curve, it is expectable to determine $\varvec{t}_{{1\varvec{ary}}}$ and $\varvec{t}_{{3\varvec{ary}}}$ taking the difference between the straight line and creep data less than to 1%.

3.1 Creep Safety Envelope

Once defined the critical points on the creep curve (for a given temperature and load), it is possible to determine different critical points for a spectral of different values of stress for a specific temperature or different levels of temperature for a range of stress values. Fig. 6 shows a creep safety envelope for an aleatory polymeric sample at a given temperature.

Fig. 6

Creep envelope for a given temperature

4 Material Testing

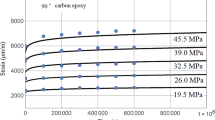
In order to simulate the above described fitting, sampled points from the creep curves identified by Liu et al. [12] are used as the actual experimental values to be matched.

4.1 Liu’s Creep Data

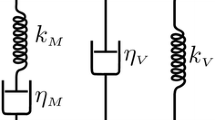
The creep experimental data are obtained for creep testing of a sample extracted from HDPE (high-density polyethylene) pipes at 5 stress levels. From a Generalized Kelvin Model (Fig. 7), a Dirichlet Series with three terms were used to represent the resulting strain (12). The tests were conducted at room temperature of about 22 ℃.

Fig. 7

Generalized kelvin model

Table 1 shows the fitted values of experimental data from Eq. (12).

Table 1 Fitted values from Eq. (12)

$$\upvarepsilon_{\text{D}} \left( {\text{t}} \right) = \frac{{\upsigma\left( {\text{t}} \right)}}{{{\text{k}}_{0} \left(\upsigma \right)}} + \mathop \sum \limits_{{{\text{i}} = 1}}^{3} \frac{{\upsigma\left( {\text{t}} \right)}}{{{\text{k}}_{\text{i}} \left(\upsigma \right)}}\left[ {1 - { \exp }\left( { - \frac{\text{t}}{{\uptau_{\text{i}} }}} \right)} \right]$$

(12)

where the respective relaxion times are:

• $\varvec{\tau}_{1} = 500\,\varvec{s}$

• $\varvec{\tau}_{2} = 10000\,\varvec{s}$

• $\varvec{\tau}_{3} = 200000\,\varvec{s}$

The sampled points from the creep curves identified in Table 1 are used to simulate the actual experimental values to be matched and the resulted strain-time curves are depicted in Fig. 8.

Fig. 8

Creep curves until end of measurements

5 Application of Crevecoeur Fitting Methodology

From the data spectra generated by Eq. (12), Crevecoeur equation coefficients are fitted for each stress level and presented in Table 2.

Table 2 Crevecoeur equation coefficients

5.1 Fitting Quality

In order evaluate the quality of the fitted values, the relationship diagram between $\varvec{log}\,\varvec{\sigma}$ versus $\varvec{log}\,\varvec{t}_{\varvec{i}}$ and $\varvec{\varepsilon}\left( {\varvec{t}_{\varvec{i}} } \right)$ versus $\varvec{log}\,\varvec{t}_{\varvec{i}}$ is shown in Fig. 9.

Fig. 9

Evaluation diagram

The linear relation plotted is similar to a typical failure mode of HDPE Pipe, the so-called Mode–1, where the pipe fails mainly in a ductile manner under mechanical overload at higher stresses (see Xu et al. [21]), that indicates an acceptable correlation between data test and the approach.

6 Results and Comments

Figure 10 and Table 3. Strain Correlation show the relationship between the strain at $\varvec{t}_{\varvec{i}}$ and $\varvec{t}_{{2\varvec{ary}}}$, $\varvec{\varepsilon}_{\varvec{i}} \left( {\varvec{t}_{\varvec{i}} } \right)$ and $\varvec{\varepsilon}_{{2\varvec{ary}}} \left( {\varvec{t}_{{2\varvec{ary}}} } \right)$. This one reveals a constant ratio between the instability time and the time of steady creep, over the stress increment.

Fig. 10

Strain correlation

Table 3 Strain correlation

6.1 Transition Points

In order to exemplify the strain rate bathtub the strain rate for 12,19 MPa is depict in Fig. 11.

Fig. 11

Strain bathtub for 12,19 MPa.

From derivative of (5) and applying the $\varvec{t}_{{2\varvec{ary}}}$, it is expectable to find the values of $\varvec{t}_{{1\varvec{ary}}}$ and $\varvec{t}_{{3\varvec{ary}}}$ where the difference between the strain rate line from (4) and the creep data curve is less than or equal to 1%. Tables 4 and 5. Pairs of Transition Points (2/2) shows the values of each pairs of fitted points.

Table 4 Pairs of transition points (1/2)

Table 5 Pairs of transition points (2/2)

From expression (5) and the values from Tables 4 and 5. Pairs of Transition Points (2/2), the theoretical creep curves for each step of stress are depicted in Fig. 12

Fig. 12

Transition points

Once defined the critical points on the creep curve shown in Table 4, creep safety envelope is created and the shape of the curve is given in Fig. 13.

Fig. 13

Creep safety envelope

7 Conclusions

This paper presented a study conducted to estimate the 4 instants of time characterizing the creep curve: (1) the first transition point, that is the transition point between transient and steady creep; (2) the secondary point, that is the inflexion point of the creep curve where the strain rate reaches its minimum; (3) the second transition point, that is the transition point between steady and accelerated creep; and (4) the instability point.

The creep curve used in this study was constructed using data resulting from a numerical simulation of an experiment of Liu et al. [12], where a sample cut from a 24’’ HDPE-Pipe was tested for five different stress levels.

A brief review of the fitting methodology was first presented concerning the creep behavior and its three-stages. This methodology was applied then to the numerical description of the creep behavior of a PE. The time-dependent and stress-dependent approach was easily applied to a viscoelastic material. The transition points were calculated and a creep safety envelope was defined and a lifetime prediction could be made.

Although there was no comparative analysis of the useful life of the material based on standards, the creep curves obtained by the Crevecoeur adjustment methodology evidenced a good fitting.