Maintaining Consistency with Constraints: A Constrained Deep Clustering Method

Abstract

Constrained clustering has been intensively explored in the data mining. Popular clustering algorithms such as k-means and spectral clustering are combined with prior knowledge to guide the clustering process. Recently, constrained clustering with deep neural network gains superior performance by jointly learning cluster-oriented feature representations and cluster assignments simultaneously. However, these methods face a common issue that they have poor performance when only minimal constraints are available because of their single way to mine constraint information. In this paper, we propose an end-to-end clustering method that learns unsupervised information and constraint information in two consecutive modules: an unsupervised clustering module to obtain feature representations and cluster assignments followed by a constrained clustering module to tune them. The constrained clustering module is composed of a Siamese or triplet network to maintain consistency with constraints. To capture more information from minimal constraints, the consistency is maintained from two perspective simultaneously: embedding space distance and cluster assignments. Extensive experiments on both pairwise and triplet constrained clustering validate the effectiveness of the proposed algorithm.

This work was supported by National Science Foundation of China (No.61632019; No.61876028; No.61972065; No.61806034).

1 Introduction

Clustering with deep neural networks has extensively explored due to the inherent property of highly non-linear transformation of DNNs. These methods effectively combine the neural network with popular clustering algorithms, such as k-means [7, 14, 22], spectral clustering [17], subspace clustering [10], agglomerative clustering [23] to joint dimensionality reduction and clustering-oriented representation learning. These unsupervised methods refer to unlabeled data, however, some prior knowledge such as pairwise constraints or triplet constraints could be obtained automatically in many clustering tasks.

Constrained clustering is a kind of task that few auxiliary information is provided to guide clustering. Some constrained clustering methods are explored with pairwise constraints (must-link and cannot-link) [8, 16]. SDEC [16] decreases the embedding distance between must-link pairs and increases distance between cannot-link pairs. But the distance in the embedding space between cannot-link pairs have already been large at the beginning of training due to the good separation of the pre-trained network, which leads to the inefficiency of its objective. Hsu et al. [8] present their objective on softmax output with KL divergence but abandon the contribution of instances without constraints. Zhang et al. [25] explore more complex constraints. They enforce the must-link pairs with similar assignment probability and cannot-link pairs oppositely. But when the number of constraints is not enough to mitigate the negative effect of imbalance (which means very few must-link assignments can be referred to, e.g. approximately $10\%$ in Fashion dataset), this method that only mines constraint information from the perspective of cluster assignments is sensitive to the reduction of the number of constraints. For these reasons, these methods face a common issue that they have poor performance when the number of constraints is small.

In this paper, we propose a Constrained Deep Clustering method (CDC) that aims to maintain consistency with constraints. To be effective even if minimal constraints are available, our method learns unsupervised information and constraint information in two consecutive modules: an unsupervised clustering module followed by a constrained clustering module. Inspired by the metric learning, we construct the network based on a Siamese network or triplet network in the constrained clustering module. For the purpose of capturing more information from minimal constraints, the consistency is maintained from two perspective simultaneously: embedding space distance and cluster assignments. The model is trained by cosine function as the similarity metric avoiding the inefficiency when embedding distance between cannot-link pairs is large and weighted cross entropy objective to tune cluster assignments. The main contributions of this paper are summarized as follows:

• We propose an end-to-end clustering method that learns unsupervised information and constraint information in two consecutive modules: an unsupervised clustering module to obtain feature representations and cluster assignments followed by a constrained clustering module to tune them.

• We propose effective objective function to maintain consistency with constraints from two perspective: embedding space distance and cluster assignments.

• Extensive experiments are conducted on both image and text datasets. The results show competitive performance on both pairwise and triplet constrained clustering, validating the effectiveness of CDC algorithm.

2 Related Work

Deep clustering is a category of clustering in recent years that combine deep neural network to learn cluster-friendly features. There are approaches [6, 7, 21, 22] obtaining feasible feature space based on autoencoder (AE). Other novel methods adopt deep generative model to perform clustering task, such as VAE-based [5, 11] and GAN-based [3, 15, 24] methods. In addition, some clustering methods recently has shifted to handle high-dimensional data, including spectral clustering [9, 17] and subspace clustering [10, 26, 27].

Constrained clustering has been widely studied to lead an auxiliary guidance to clustering. Some methods explore strategies for improving clustering performance with pairwise constraints [1, 2, 18, 19]. Other methods with deep neural network gains better performance. Hsu et al. [8] view the outputs of the softmax layer as the distribution of possible clusters given a sample and evaluate the similarity with KL divergence. Zhang et al. [25] explore more complex constraints generated from new types of side information. Although these methods capture the point that similar samples should output similar assignment distribution, there is no work noticing consistency of embedding space distance and cluster assignments simultaneously.

3 Proposed Method

Consider a task about clustering a data set X containing n unlabeled instances, each sample $\{ x_i\in \mathbb {R}^d\}^n_{i=1}$ should be assigned to one of k clusters. Except these unlabeled data, two types of user-specified prior information is also provided to guide the clustering process, including pairwise constraints and triplet constraints. A pairwise constraint indicates that a pair of samples $\{(x_i,x_j):x_i,x_j\in X \}$ have a relationship of must-link ($x_i$ and $x_j$ belong to the same clusters) or cannot-link ($x_i$ and $x_j$ belong to different clusters). A triplet constraint consists of a triple of samples $\{(\widetilde{x},x_p,x_n):\widetilde{x},x_p,x_n \in X \}$, where the positive sample $x_p$ is closer to the anchor $\widetilde{x}$ than the negative sample $x_n$ in the embedding space.

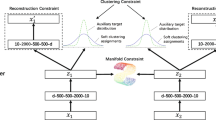
We propose to find a non-linear mapping $f_ {\varvec{\theta }} : X \rightarrow Z$ that transforms the original data into latent space Z, in which the embedding distance is consistent with the original semantic distance and cluster assignments are consistent with constraints. The model contains two consecutive modules: the unsupervised clustering module followed by our constrained clustering module. The whole structure of CDC is illustrated in Fig. 1.

Fig. 1.

The process of CDC algorithm. The method learns unsupervised information and constraint information in two consecutive modules: an unsupervised clustering module to obtain feature representations and cluster assignments followed by a constrained clustering module to tune them.

We introduce the referred method in unsupervised clustering module in Sect. 3.1. Then we propose two types of constrained clustering module with pairwise constraints and triplet constraints respectively in Sect. 3.2 and Sect. 3.3.

3.1 Unsupervised Clustering Module

The first module aims to learn cluster-oriented feature representations. We refer the DEC [21] to learn feature representations and cluster assignments.

The DEC method initializes the centroids $\{ \mu _j \} _{j=1} ^k$ through k-means on the embedding space of the autoencoder pre-trained by a stacked autoencoder (SAE), then computes the soft assignments $q_{ij}$ as:

$$\begin{aligned} q_{ij} = \frac{(1 + \Vert z_i-\mu _j\Vert ^2/\alpha )^{-\frac{\alpha + 1}{2}}}{\sum \nolimits _{j^{'}=1}^{k} (1 + \Vert z_i-\mu _{j^{'}} \Vert ^2/\alpha )^{-\frac{\alpha + 1}{2}}}, \end{aligned}$$

(1)

where $q_{ij}$ measures the similarity between embedded data $z_i$ and centroids $\mu _j$ with Student’s t-distribution being the kernel, $\alpha$ is a constant, e.g. $\alpha = 1$.

The auxiliary distribution P is defined to refine the cluster assignments . By squaring the soft assignments $q_{ij}$ and then normalizing it, $p_{ij}$ is formulated as:

$$\begin{aligned} p_{ij} = \frac{q^2_{ij}/\sum \nolimits _i q_{ij}}{\sum \nolimits _{j^{'}=1}^{k} (q^2_{ij'}/\sum \nolimits _i q_{ij'})}. \end{aligned}$$

(2)

The loss function is defined as the reconstruction loss added to the KL divergence between soft assignments Q and auxiliary distribution P as follows:

$$\begin{aligned} L = KL(P\Vert Q) + L_R = \sum \nolimits _i \sum \nolimits _j p_{ij} \log \frac{p_{ij}}{q_{ij}} + \sum \nolimits _i \Vert x_i - x'_i\Vert ^2. \end{aligned}$$

(3)

The clusters are iteratively refined during this self-training process. Constrained clustering module inherits the parameters and centroids and then learn from pairwise constraints or triplet constraints.

3.2 Clustering with Pairwise Constraints

The pairwise constraints are learned in our constrained clustering module based on a Siamese architecture, which is a popular network in metric learning. Two samples with pairwise constraints are required as inputs at the same step. Each group of inputs can be expressed as a triad $((x_1, x_2), y )$, where y is an indicator that $y = 1$ when given $x_1$ and $x_2$ with must-link relationship while $y = 0$ with cannot-link constraint. The structure of pairwise constrained clustering module is illustrated in Fig. 2. For the purpose of maintaining consistency with constraints, we define the objective function in two parts: embedding space distance and cluster assignments.

Fig. 2.

The structure of constrained clustering module on pairwise constrained clustering based on a Siamese network. Constrained pairs are transformed into embedded features $Z_1$ and $Z_2$. Soft assignments $Q_1$ and $Q_2$ are normalized to compute assignment objective. The shared parameters are optimized by Eq. (7).

Consistency of Embedding Space Distance. The main idea of this part is to seek a mapping that transforms pairs of inputs into a embedding space, in which a similarity measure approximates the semantic information in the original space. To this end, the distance loss for all m groups of $((x_1, x_2), y )$ is defined as:

$$\begin{aligned} L_{dist} = -\frac{1}{m} \sum \nolimits _{i=1}^m \left( y^{(i)} \lambda _1 \sigma (z_1^{(i)},z_2^{(i)}) - (1 - y^{(i)}) \lambda _2 \sigma (z_1^{(i)},z_2^{(i)}) \right) , \end{aligned}$$

(4)

where $z_1^{(i)}$ and $z_2^{(i)}$ are corresponding embedded features of the $i^{th}$ group of inputs, $\sigma (\cdot )$ is a similarity function, $\lambda _1$ and $\lambda _2$ are trade-off parameters. In summary, the embedded features with the same label prefer larger similarity, while points with different labels obtain smaller similarity by minimizing the objective function.

Consistency of Cluster Assignments. The main idea of this part is to tune cluster assignments with given constraints. Soft assignments are learned from its high confidence assignments in the unsupervised clustering module. We expect to tune cluster assignments to maintain the consistency with constraints. Specifically, must-link pairs are expected to have similar cluster assignments distribution, while assignment differences of cannot-link pairs are strengthened. The assignment loss is formulated as:

$$\begin{aligned} L_{assign} = -\frac{1}{m} \sum \nolimits _{i=1}^m \left( y^{(i)} \lambda _3 w^{(i)} \log (q_1^{(i)}\cdot q_2^{(i)}) + (1 - y^{(i)}) w^{(i)} \log (1 - q_1^{(i)}\cdot q_2^{(i)}) \right) . \end{aligned}$$

(5)

This process is treated as a binary classification problem that whether or not two constrained samples belong to the same cluster. The inner product of corresponding normalized soft assignments $q_1^{(i)}$ and $q_2^{(i)}$ reflects the probability that two inputs $x_1^{(i)}$ and $x_2^{(i)}$ are assigned into the same cluster. By minimizing the cross entropy loss, the must-link pairs prefer to be allocated into the same cluster and the cannot-link pairs are the opposite. In addition, we introduce a weight w to pay more attention to those pairs whose distances in the embedding space are not consist with constraints. Precisely speaking, the weights increase for those must-link pairs with large differences in embedded features and those cannot-link pairs with small differences. The weight formulas are defined as:

$$\begin{aligned} w^{(i)} =\left\{ \begin{aligned}&\frac{1}{1 + e^{-d^{(i)}}},&if (x_1,x_2)^{(i)} \in must-link, \\&\frac{3 + e^{d^{(i)}}}{2(1 + e^{d^{(i)}})},&if (x_1,x_2)^{(i)} \in cannot-link, \end{aligned} \right. \end{aligned}$$

(6)

where $d^{(i)} = \alpha \Vert z_1^{(i)} - z_2^{(i)}\Vert _2$ reflects the difference between a pair of embedded features, $\alpha$ is an adjustment parameter to control the distance. We set $\alpha = 0.01$ in all experiments because the great masses of samples are well-separated. The weight w is a monotonically increasing function for must-link, while monotonically decreasing function in the opposite case.

In summary, we define the objective function in constrained clustering module for pairwise constraints as:

$$\begin{aligned} L_{pair} = L_{dist} + L_{assign} + L_{recon}, \end{aligned}$$

(7)

$$\begin{aligned} L_{recon} = \frac{1}{m} \sum \nolimits _{i=1}^m y^{(i)} (\Vert x_1 - x'_1\Vert ^2 + \Vert x_2 - x'_2\Vert ^2)^{(i)}, \end{aligned}$$

(8)

where $L_{recon}$ is the sum of reconstruction losses of two instances, which is added to the must-link cases to avoid a large scale cluster.

3.3 Clustering with Triplet Constraints

Triplet constraints are weaker constraints and easily accessible with only a trained embedding space. They could replace the stronger constraints in some constrained clustering tasks that lack ground truth labels or partition-based constraints, e.g. pairwise constraints. Different from these stronger constraints coming from specific partitions, triplet constraints convey the differences in distance level.

Fig. 3.

The structure of constrained clustering module on triplet constrained clustering based on a triplet network. A triple of samples are input into the network at the same step. The similarities are obtained in the embedding space. Parameters are shared among the triplet network and are optimized by Eq. (9).

We construct a triplet network for training triplet constraints. As we can see in Fig. 3, a triple of samples $(\widetilde{x},x_p,x_n)$ are input to the network simultaneously. The similarities $\sigma (\widetilde{z}, z_n)$ and $\sigma (\widetilde{z}, z_p)$ are calculated in the embedding space output by the network with shared parameters. The objective function in constrained clustering module for triplet constraints is formulated as:

$$\begin{aligned} L_{trip} = \max (\sigma (\widetilde{z}, z_n) - \sigma (\widetilde{z}, z_p) + m, 0), \end{aligned}$$

(9)

where $\sigma (\widetilde{z}, z_n)$ and $\sigma (\widetilde{z}, z_p)$ represent similarities between positive and negative samples against the anchor respectively. Those positive samples are pulled close to their anchor and negative samples are separated from them. A hyperparameter margin m is introduced as a threshold that tries to widen the gap in $\sigma (\widetilde{z}, z_n)$ and $\sigma (\widetilde{z}, z_p)$. Due to the partition uncertainty of triplet constraints, some cases cannot be avoided that some positive samples and their anchors come from different classes, or some negative samples have the same labels with their anchors, which we call imperfect triplet constraints. The margin m also works by preventing $x_p$ being too close or $x_n$ being too separated from $\widetilde{x}$ in these cases. The parameter study about m is illustrated in Sect. 4.4.

In summary, our method learns feature representations and cluster assignments in the unsupervised clustering module and then tunes them in the constrained clustering module in one epoch. The procedure is summarized in Algorithm 1.

4 Experiments

4.1 Datasets

To verify the effectiveness and efficiency of the proposed CDC on constrained clustering tasks, we evaluate it on five benchmark datasets:

• MNIST [12]: A dataset composed of 70000 handwritten digits of 10 types. Each sample is a $28\times 28$ gray image.

• Fashion-MNIST [20]: A dataset of Zalando’s article images with the same size as MNIST. Each sample is a $28\times 28$ gray image, divided into 10 classes.

• USPS: A handwritten digits dataset that contains 9298 images (7291 for training, 2007 for test) with size of $16\times 16$ pixels.

• KMNIST [4]: Kuzushiji-MNIST is a dataset which focuses on cursive Japanese, composed of $28\times 28$ images of 10 types. Train and test set sizes are 6,000 and 1,000 per class.

• Reuters10K [13]: A subset consist of 10000 examples of Reuters. Each sample is composed of the 2000 most frequently occurring word stems in an English news story.

All datasets are preprocessed for each element before being fed into the algorithms. Precisely, we normalize all datasets to approach $\frac{1}{d} \Vert x_i\Vert ^2_2$ to 1 for each $x_i \in \mathbb {R}^d$ in X.

4.2 Experimental Setting

The structure of the encoder network is set in the same way as DEC [21], SDEC [16] and FDCC [25] to be comparable with them. Concretely, we set the encoder network with dimensions of d - 500 - 500 - 2000 - 10 and the decoder with a symmetrical structure, where d is the dimension of input data. All layers are fully connected and activated by ReLU function except for the input, output, and embedding layers.

Table 1. Clustering performance of pairwise constraints in terms of accuracy (ACC %) and normalized mutual information (NMI %) over 5 datasets. The results of baseline models are obtained by running the released code except the ones marked by (*), which are reported from the corresponding papers. The mark (-) represents that the result is unavailable.

The parameters and centroids are initialized with a SAE and k-means in the same way as DEC [21]. Cosine similarity $\cos (a,b) = \frac{a \cdot b}{\Vert a\Vert \Vert b\Vert }$ is selected in Eq. (4, 9) for all experiments. In each iteration, we train the network with Adam optimizer. The learning rate and batch-size are set to 0.001 and 256 respectively. We investigate the influence of trade-off parameter in Eq. (5) with grid search and set it as 10. The whole training process will stop when breaks the threshold in stopping criterion $\delta = 0.001$ or reach the maximum epoch.

4.3 Experimental Results

Evaluation of Experiments on Pairwise Constraints. Our method is compared with both unsupervised clustering algorithms and constrained clustering methods. Unsupervised algorithms include k-means [14], k-means on latent feature space obtained by SAE (SAE-KM), DEC [21] and IDEC [6]. Constrained clustering algorithms include flexible CSP [19], COP-kmeans [18], MPC-kmeans [2], SDEC [16] and FDCC [25].

For the purpose of simulating human-guided constraints, we construct constraints from existing labeled data sets. We pick a set of randomly selected pairwise samples from training set and generate must-link or cannot-link constraints according to their ground truth labels. The number of constraints N is set to 3600 on MNIST, Fashion and KMNIST that accounts for merely 0.0002% of the number of possible constraints $C_n^2$, and 1000 on USPS and Reuters10K that accounts for 0.0038% and 0.002% respectively. Besides, transitive constraints are also added to the known constraints. For instance, given must-link (a, b), (a, c) and cannot-link (a, d), we can easily deduce addable constraint: must-link (b, c) and cannot-link (b, d), (c, d). This conduction may cause an explosion of the constraint quantity when N is large, but can be ignored with a small amount of constraints.

Fig. 4.

Clustering ACC and NMI on MNIST and Fashion with different numbers of triplet constraints.

The evaluation of ACC and NMI are reported in Table 1. As we can see, the performance of CDC outperforms the unsupervised algorithms with just minimal pairwise constraints. This shows that our algorithm of maintaining consistency with constraints has a positive effect on clustering. The constrained methods below are set with the same ratio of number of constraints as ours for fair comparison. The results show obvious improvement, especially on Fashion, KMNIST and Reuters10K, validating the superiority of CDC algorithm.

Evaluation of Experiments on Triplet Constraints. We evaluate the clustering performance of our method on triplet constraints by comparative experiment with FDCC [25] that put forwards triplet constraints first. To be comparable fairly with it, we introduce the same embedding space to compute Euclidean Metric among triples. Figure 4 plots the results of comparative experiment with different numbers of constraints. The results show clearly that the increase of constraint number reflects positive feedback in performance. On MNIST, minimal constraints bring about obvious improvement and then performance becomes stable, which means enough prior information has been captured. On Fashion-MNIST, the performance enhances continuously and leads to a sharp improvement in range [3000, 6000]. Comparing with FDCC, our method brings slight improvements on MNIST and obvious enhancement on Fashion-MNIST. The results validate the effectiveness of our algorithm for weak constraint information.

4.4 Parameter Analysis

We evaluate the performance with different settings of m in Eq. (9) by grid search in range [0.3, 0.6]. Figure 5 shows the parameter study results on Fashion-MNIST. Two interesting observations can be obtained: (1) The larger m produce better performance than a smaller one when given less constraints. (2) As the number of constraints increases, the results of larger m are not significantly improved or even decreased. The first observation can be explained that our objective tends to widen the difference in the similarity between positive and negative samples against the anchor, larger m enforces larger threshold to be broken down, which can promote the optimization when constraints are not enough. The second consequence occurs because our method learns enough information when more constraints are provided, a smaller m reduce the inefficiency of imperfect triplet constraints, which we illustrate in Sect. 3.3.

Fig. 5.

The performance of our method across different settings of m on Fashion.

5 Conclusion

In this paper, we propose a Constrained Deep Clustering method (CDC) that aims to maintain consistency with constraints. The CDC method learns unsupervised information and constraint information in two consecutive modules. Effective objective function are proposed to maintain the consistency from two perspective simultaneously: embedding space distance and cluster assignments. Extensive experimental results on both pairwise and triplet constrained clustering validate the effectiveness of our method even if only minimal constraints are provided. Our future work will be explored from the perspective of exploring more complex similarity metric or addressing the imbalance of the constraints.