Signed Diffie-Hellman Key Exchange with Tight Security

Abstract

We propose the first tight security proof for the ordinary two-message signed Diffie-Hellman key exchange protocol in the random oracle model. Our proof is based on the strong computational Diffie-Hellman assumption and the multi-user security of a digital signature scheme. With our security proof, the signed DH protocol can be deployed with optimal parameters, independent of the number of users or sessions, without the need to compensate any security loss. We abstract our approach with a new notion called verifiable key exchange.

In contrast to a known tight three-message variant of the signed Diffie-Hellman protocol (Gjøsteen and Jager, CRYPTO 2018), we do not require any modification to the original protocol, and our tightness result is proven in the “Single-Bit-Guess” model which we known can be tightly composed with symmetric cryptographic primitives to establish a secure channel.

1 Introduction

Authenticated key exchange (AKE) protocols are protocols where two users can securely share a session key in the presence of active adversaries. Beyond passively observing, adversaries against an AKE protocol can modify messages and adaptively corrupt users’ long-term keys or the established session key between users. Hence, it is very challenging to construct a secure AKE protocol.

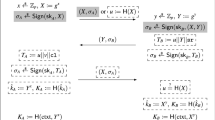
The signed Diffie-Hellman (DH) key exchange protocol is a classical AKE protocol. It is a two-message (namely, two message-moves or one-round) protocol and can be viewed as a generic method to transform a passively secure Diffie-Hellman key exchange protocol [14] into a secure AKE protocol using digital signatures. Figure 1 visualizes the protocol. The origin of signed DH is unclear to us, but its idea has been used in and serves as a solid foundation for many well-known AKE protocols, including the Station-to-Station protocol [15], IKE protocol [19], the one in TLS 1.3 [32], and many others [7, 18, 22, 23, 25].

Fig. 1.

Our signed Diffie-Hellman key exchange protocol and the tight variant of Gjøsteen and Jager [18]. The functions $\mathsf {H}$ and $\mathsf {G}$ are hash functions. Operations marked with a gray are for our signed DH protocol, and dashed are for Gjøsteen and Jager’s. Operations without a box are performed by both protocols. All signatures are verified upon arrival with the corresponding messages, and the protocol aborts if any verification fails.

Tight Security. Security of a cryptographic scheme is usually proven by constructing a reduction. Asymptotically, a reduction reduces any efficient adversary $\mathcal {A}$ against the scheme into an adversary $\mathcal {R}$ against the underlying computational problem. Concretely, a reduction provides a security bound for the scheme, $\varepsilon _\mathcal {A}\le \ell \cdot \varepsilon _\mathcal {R}$, where $\varepsilon _\mathcal {A}$ is the success probability of $\mathcal {A}$ and $\varepsilon _\mathcal {R}$ is that of $\mathcal {R}$. We say a reduction is tight if $\ell$ is a small constant and the running time of $\mathcal {A}$ is approximately the same as that of $\mathcal {R}$. For the same scheme, it is more desirable to have a tight security proof than a non-tight one, since a tight security proof enables implementations without the need to compensate a security loss with increased parameters.

Multi-challenge Security for AKE. An adversary against an AKE protocol has full control of the communication channel and, additionally, it can adaptively corrupt users’ long-term keys and reveal session keys. The goal of an adversary is to distinguish between a (non-revealed) session key and a random bit-string of the same length, which is captured by the $\textsc {Test}$ query. We follow the Bellare-Rogaway (BR) model [5] to capture these capabilities, but formalize it with the game-based style of [21]. Instead of weak perfect forward secrecy, our model captures the (full) perfect forward secrecy.

Unlike the BR model, our model captures multi-challenge security, where an adversary can make $T$ many $\textsc {Test}$ queries which are answered with a single random bit. This is a standard and well-established multi-challenge notion, and [21] called it “Single-Bit-Guess” (SBG) security. Another multi-challenge notion is the “Multi-Bit-Guess” (MBG) security where each $\textsc {Test}$ query is answered with a different random bit. Although several tightly secure AKE protocols [2, 18, 28, 35] are proven in the MBG model, we stress that the SBG model is well-established and allows tight composition of the AKE with symmetric cryptographic primitives, which is not the case for the non-standard MBG model. Thus, the SBG multi-challenge model is more desirable than the MBG model. More details about this have been provided by Jager et al.[21, Introduction] and Cohn-Gordon et al. [10, Section 3].

The Non-tight Security of Signed DH. Many existing security proofs of signed DH-like protocols [7, 22, 23] lose a quadratic factor, $O(\mu ^2 S^2)$, where $\mu$ and $S$ are the maximum numbers of users and sessions. In the SBG model with $T$ many $\textsc {Test}$ queries, these proofs also lose an additional multiplicative factor $T$.

At CRYPTO 2018, Gjøsteen and Jager [18] proposed a tightly secure variant of it by introducing an additional message move into the ordinary signed DH protocol. They showed that if the signature scheme is tightly secure in the multi-user setting then their protocol is tightly secure. They required the underlying signature scheme to be strongly unforgeable against adaptive Corruption and Chosen-Message Attacks ($\mathsf {StCorrCMA}$) which is a notion in the multi-user setting and an adversary can adaptively corrupt some of the honest users to see their secret keys. Moreover, they constructed a tightly multi-user secure signature scheme based on the Decisional Diffie-Hellman (DDH) assumption in the random oracle model [4]. Combining these two results, they gave a practical three message fully tight AKE. We note that their tight security is proven in the less desirable MBG model, and, to the best of our knowledge, the MBG security can only non-tightly imply the SBG security [21]. Due to the “commitment problem”, the additional message is crucial for the tightness of their protocol. In particular, the “commitment problem” seems to be the reason why most security proofs for AKEs are non-tight.

1.1 Our Contribution

In this paper, we propose a new tight security proof of the ordinary two-message signed Diffie-Hellman key exchange protocol in the random oracle model. More precisely, we prove the security of the signed DH protocol tightly based on the multi-user security of the underlying signature scheme in the random oracle model. Our proof improves upon the work of Gjøsteen and Jager [18] in the sense that we do not require any modification to the signed DH protocol and our tight multi-challenge security is in the SBG model. This implies that our analysis supports the optimal implementation of the ordinary signed DH protocol with theoretically sound security in a meaningful model.

Our technique is a new approach to resolve the “commitment problem”. At the core of it is a new notion called verifiable key exchange protocols. We first briefly recall the “commitment problem” and give an overview of our approach.

Technical Difficulty: The “commitment problem”. As explained in [18], this problem is the reason why almost all proofs of classical AKE protocols are non-tight. In a security proof of an AKE protocol, the reduction needs to embed a hard problem instance into the protocol messages of $\textsc {Test}$ sessions so that in the end the reduction can extract a solution to the hard problem from the adversary $\mathcal {A}$. After the instance is embedded, $\mathcal {A}$ has not committed itself to which sessions it will query to $\textsc {Test}$ yet, and, for instance, $\mathcal {A}$ can ask the reduction for $\textsc {Reveal}$ queries on sessions with a problem instance embedded to get the corresponding session keys. At this point, the reduction cannot respond to these $\textsc {Reveal}$ queries. A natural way to resolve this is to guess which sessions $\mathcal {A}$ will query $\textsc {Test}$ on, and to embed a hard problem instance in those sessions only. However, this introduces an extremely large security loss. To resolve this “commitment problem”, a tight reduction should be able to answer both $\textsc {Test}$ and $\textsc {Reveal}$ for every session without any guessing. Gjøsteen and Jager achieved this for the signed DH by adding an additional message.

In this paper, we show that this additional message is not necessary for tight security.

Our Approach: Verifiable Key Exchange. In this work we, for simplicity, use the signed Diffie-Hellman protocol based on the plain Diffie-Hellman protocol [14] (as described in Fig. 1) to explain our approach. In the technical part, we abstract and present our idea with a new notion called verifiable key exchange protocols. Our approach is motivated by the two-message non-tight AKE in [10].

Let $\mathbb {G}:=\langle g \rangle$ be a cyclic group of prime-order p where the computational Diffie-Hellman (CDH) problem is hard. Let $(g^\alpha ,g^\beta )$ (where ) be an instance of the CDH problem. By its random self-reducibility, we can efficiently randomize it to multiple independent instances $(g^{\alpha _i},g^{\beta _i})$, and, given a $g^{\alpha _i \beta _i}$, we can extract the solution $g^{\alpha \beta }$.

For preparation, we assume that a $\textsc {Test}$ session does not contain any forgeries. This can be tightly justified by the $\mathsf {StCorrCMA}$ security of the underlying signature scheme which can be implemented tightly by the recent scheme in [12].

After that, our reduction embeds the randomized instance $(g^{\alpha _i},g^{\beta _i})$ into each session. Now it seems we can answer neither $\textsc {Test}$ nor $\textsc {Reveal}$ queries: The answer has the form $K:=\mathsf {H}(\text {ctxt},g^{xy})$, but the term $g^{xy}$ cannot be computed by the reduction, since $g^x$ is from either adversary $\mathcal {A}$ or the CDH problem challenge. However, our reduction can answer this by simulating the random oracle $\mathsf {H}$. More precisely, we answer $\textsc {Test}$ and $\textsc {Reveal}$ queries with a random K, and we carefully program the random oracle $\mathsf {H}$ so that adversary $\mathcal {A}$ cannot detect this change. To achieve this, when we receive a random oracle query $\mathsf {H}(\text {ctxt},Z)$, we answer it consistently if the secret element Z corresponds to the context $\text {ctxt}$ and $\text {ctxt}$ belongs to one of the $\textsc {Test}$ or $\textsc {Reveal}$ queries. This check can be efficiently done by using the strong DH oracle [1].

The approach described above can be abstract by a notion called verifiable key exchange (VKE) protocols. Roughly speaking, a VKE protocol is firstly passively secure, namely, a passive observer cannot compute the secret session key. Additionally, a VKE allows an adversary to check whether a session key belongs to some honestly generated session, and to forward honestly generated transcripts in a different order to create non-matching sessions. This VKE notion gives rise to a tight security proof of the signed DH protocol. We believe this is of independent interest.

On the Strong CDH Assumption. Our techniques require the Strong CDH assumption [1] for the security of our VKE protocol. We refer to [11, Appendix B] for a detailed analysis of this assumption in the Generic Group Model (GGM). Without using the GGM, we can use the twinning technique [9] to remove this strong assumption and base the VKE security tightly on the (standard) CDH assumption. This approach will double the number of group elements. Alternatively, we can use the group of signed Quadratic Residues (QR) [20] to instantiate our VKE protocol, and then the VKE security is tightly based on the factoring assumption (by [20, Theorem 2]).

Real-World Impacts. As mentioned earlier, the signed DH protocol serves as a solid foundation for many real-world protocols, including the one in TLS 1.3 [32], IKE [19], and the Station-to-Station [15] protocols. We believe our approach can naturally be extended to tighten the security proofs of these protocols. In particular, our notion of VKE protocols can abstract some crucial steps in a recent tight proof of TLS 1.3 [11].

Another practical benefit of our tight security proof is that, even if we implement the underlying signature with a standardized, non-tight scheme (such as Ed25519 [8] or RSA-PKCS $\#$1 v1.5 [31]), our implementation does not need to lose the additional factor that is linear in the number of sessions. In today’s Internet, there can be easily $2^{60}$ sessions per year.

1.2 Protocol Comparison

We compare the instantiation of signed DH according to our tight proof with the existing explicitly authenticated key exchange protocols in Fig. 2. For complete tightness, all these protocols require tight multi-user security of their underlying signature scheme. We implement the signature scheme in all protocols with the recent efficient scheme from Diemert et al. [12] whose signatures contain 3 $\mathbb {Z}_p$ elements, and whose security is based on the DDH assumption. The implementation of TLS is according to the recent tight proofs in [11, 13], and we instantiate the underlying signature scheme with the same DDH-based scheme from [12].

Fig. 2.

Comparison of $\mathsf {AKE}$ protocols. We denote $\mathbf{Comm}.$ as the communication complexity of the protocols in terms of the number of group elements, hashes and $\mathbb {Z}_p$ elements (which is due to the use of the signature scheme in [12]). The column Model lists the $\mathsf {AKE}$ security model and distinguishes between multi-bit guessing (MBG) and the single-bit-guessing (SBG) security.

We note that the non-tight protocol from Cohn-Gorden et al. [10], whose security loss is linear in the number of users, has better communication efficiency (2, 0, 0). However, its security is weaker than all protocols listed in Fig. 2, since their protocol is only implicitly authenticated and achieves weak perfect forward secrecy.

We detail the comparison with $\textsf {JKRS}$ [21]. Using the DDH-based signature scheme in [12], the communication complexity of our signed DH protocol is (2, 0, 6), while that of $\textsf {JKRS}$ is (5, 1, 3). We suppose the efficiency of our protocol is comparable to $\textsf {JKRS}$.

Our main weakness is that our security model is weaker that of $\textsf {JKRS}$. Namely, ours does not allow adversaries to corrupt any internal secret state. We highlight that our proof does not inherently rely on any decisional assumption. In particular, if there is a tightly multi-user secure signature scheme based on only search assumptions, our proof directly gives a tightly secure AKE based on search assumptions only, which is not the case for [21].

Open Problems. We do not know of any tightly multi-user secure signature schemes with corruptions based on a search assumption, and the schemes in [30] based on search assumptions do not allow any corruption. It is therefore insufficient for our purpose, and we leave constructing a tightly secure AKE based purely on search assumptions as an open problem.

2 Preliminaries

For $n \in \mathbb {N}$, let $[n] = \{1, \ldots , n\}$. For a finite set $\mathcal {S}$, we denote the sampling of a uniform random element x by . By we denote the bit that is 1 if the evaluation of the Boolean statement B is and 0 otherwise.

Algorithms. For an algorithm $\mathcal {A}$ which takes x as input, we denote its computation by $y \leftarrow \mathcal {A}(x)$ if $\mathcal {A}$ is deterministic, and if $\mathcal {A}$ is probabilistic. We assume all the algorithms (including adversaries) in this paper to be probabilistic unless we state it. We denote an algorithm $\mathcal {A}$ with access to an oracle $\textsc {O}$ by $\mathcal {A}^\textsc {O}$.

Games. We use code-based games [6] to present our definitions and proofs. We implicitly assume all Boolean flags to be initialized to 0 ( ), numerical variables to 0, sets to $\emptyset$ and strings to $\bot$. We make the convention that a procedure terminates once it has returned an output. $G^\mathcal {A}\Rightarrow b$ denotes the final (Boolean) output b of game G running adversary $\mathcal {A}$, and if $b=1$ we say $\mathcal {A}$ wins G. The randomness in $\Pr [G^\mathcal {A}\Rightarrow 1]$ is over all the random coins in game G. Within a procedure, “ ” means that we terminate the run of an adversary $\mathcal {A}$.

Digital signatures. We recall the syntax and security of a digital signature scheme. Let $\mathsf {par}$ be some system parameters shared among all participants.

Definition 1

(Digital Signature). A digital signature scheme is defined as follows.

• The key generation algorithm returns a public key and a secret key . We assume that implicitly defines a message space $\mathcal {M}$ and a signature space $\varSigma$.

• The signing algorithm returns a signature $\sigma \in \varSigma$ on $m$.

• The deterministic verification algorithm returns 1 (accept) or 0 (reject).

${\mathsf {SIG}}$ is perfectly correct, if for all and all messages $m \in \mathcal {M}$, .

In addition, we say that ${\mathsf {SIG}}$ has $\alpha$ bits of (public) key min-entropy if an honestly generated public key is chosen from a distribution with at least $\alpha$ bits min-entropy. Formally, for all bit-strings we have

Definition 2

($\mathsf {StCorrCMA}$ Security [12, 18]). A digital signature scheme ${\mathsf {SIG}}$ is $(t,\varepsilon ,\mu , {Q}_{s}, {Q}_{\textsc {Cor}})\text {-}\mathsf {StCorrCMA}$ secure (Strong unforgeability against Corruption and Chosen Message Attacks), if for all adversaries $\mathcal {A}$ running in time at most t, interacting with $\mu$ users, making at most ${Q}_{s}$ queries to the signing oracle $\textsc {Sign}$, and at most ${Q}_{\textsc {Cor}}$ (${Q}_{\textsc {Cor}}<\mu$) queries to the corruption oracle $\textsc {Corr}$ as in Fig. 3, we have

$$\Pr [\mathsf {StCorrCMA}^\mathcal {A}\Rightarrow 1] \le \varepsilon .$$

Fig. 3.

$\mathsf {StCorrCMA}$ security game for a signature scheme ${\mathsf {SIG}}$. $\mathcal {A}$ has access to the oracles $\textsc {O}:= \{\textsc {Sign}, \textsc {Corr}\}$.

Security in the Random Oracle Model. A common approach to analyze the security of signature schemes that involve a hash function is to use the random oracle model [4] where hash queries are answered by an oracle $\mathsf {H}$, where $\mathsf {H}$ is defined as follows: On input x, it first checks whether $\mathsf {H}(x)$ has previously been defined. If so, it returns $\mathsf {H}(x)$. Otherwise, it sets $\mathsf {H}(x)$ to a uniformly random value in the range of $\mathsf {H}$ and then returns $\mathsf {H}(x)$. We parameterize the maximum number of hash queries in our security notions. For instance, we define $(t,\varepsilon ,\mu , {Q}_{s}, {Q}_{\textsc {Cor}},Q_{\mathsf {H}})\text{- }\mathsf {StCorrCMA}$ as security against any adversary that makes at most $Q_{\mathsf {H}}$ queries to $\mathsf {H}$ in the $\mathsf {StCorrCMA}$ game. Furthermore, we make the standard convention that any random oracle query that is asked as a result of a query to the signing oracle in the $\mathsf {StCorrCMA}$ game is also counted as a query to the random oracle. This implies that ${Q}_{s}\le Q_{\mathsf {H}}$.

Signature Schemes. The tight security of our authenticated key exchange (AKE) protocols are established based on the $\mathsf {StCorrCMA}$ security of the underlying signature schemes. To obtain a completely tight AKE, we use the recent signature scheme from [12] to implement our protocols.

By adapting the non-tight proof in [17], the standard unforgeability against chosen-message attacks ($\mathsf {UF}\text{- }\mathsf {CMA}$) notion for signature schemes implies the $\mathsf {StCorrCMA}$ security of the same scheme non-tightly (with security loss $\mu$). Thus, many widely used signature schemes (such as the Schnorr [33], Ed25519 [8] and RSA-PKCS $\#$1 v1.5 [31] signature schemes) are non-tightly $\mathsf {StCorrCMA}$ secure. We do not know any better reductions for these schemes. We leave proving the $\mathsf {StCorrCMA}$ security of these schemes without losing a linear factor of $\mu$ as a future direction. However, our tight proof for the signed DH protocol strongly indicates that the aforementioned non-tight reduction is optimal for these practical schemes. This is because if we can prove these schemes tightly secure, we can combine them with our tight proof to obtain a tightly secure AKE with unique and verifiable private keys, which may contradict the impossibility result from [10].

For the Schnorr signature, we analyze its $\mathsf {StCorrCMA}$ security in the generic group model (GGM) [29, 34]. We recall the Schnorr signature scheme below and show the GGM bound of its $\mathsf {StCorrCMA}$ security in Theorem 1.

Let $\mathsf {par}= (p,g,\mathbb {G})$, where $\mathbb {G}= \langle g\rangle$ is a cyclic group of prime order p with a hard discrete logarithm problem. Let $\mathsf {G}:\{0,1\}^* \rightarrow \mathbb {Z}_p$ be a hash function. Schnorr’s signature scheme, $\mathsf {Schnorr}:=({\mathsf {Gen}},{\mathsf {Sign}},{\mathsf {Ver}})$, is defined as follows:

Theorem 1

($\mathsf {StCorrCMA}$ Security of $\mathsf {Schnorr}$ in the GGM). Schnorr’s signature ${\mathsf {SIG}}$ is $(t, \varepsilon , \mu , {Q}_{s}, {Q}_{\textsc {Cor}}, {Q}_\mathsf {G})$-$\mathsf {StCorrCMA}$-secure in the $\mathrm {GGM}$ and in the programmable random oracle model, where

$$\begin{aligned} \varepsilon&\le \frac{({Q}_{\mathbb {G}}+\mu +1)^2}{2p} + \frac{(\mu - {Q}_{\textsc {Cor}})}{p} + \frac{{Q}_\mathsf {G}{Q}_{s}+1}{p}, \quad \text {and} \quad t'\approx t. \end{aligned}$$

Here, $Q_\mathbb {G}$ is the number of group operations queried by the adversary.

The proof of Theorem 1 is following the approach in [3, 24]: We first define an algebraic interactive assumption, ${\mathsf {CorrIDLOG}}$, which is tightly equivalent to the $\mathsf {StCorrCMA}$ security of $\mathsf {Schnorr}$, and then we analyze the hardness of ${\mathsf {CorrIDLOG}}$ in the GGM. ${\mathsf {CorrIDLOG}}$ stands for Interactive Discrete Logarithm with Corruption. It is motivated by the ${\mathsf {IDLOG}}$ (Interactive Discrete Logarithm) assumption in [24]. ${\mathsf {CorrIDLOG}}$ is a stronger assumption than ${\mathsf {IDLOG}}$ in the sense that it allows an adversary to corrupt the secret exponents of some public keys. Due to space limit, we leave the detailed proof of Theorem 1 in our full version.

3 Security Model for Two-Message Authenticated Key Exchange

In this section, we use the security model in [21] to define the security of two-message authenticated key exchange protocols. This section is almost verbatim to Sect. 4 of [21]. We highlight the difference we make for our protocol: Since our protocols do not have security against (ephemeral) state reveal attacks (as in the extended Canetti-Krawczyk (eCK) model [26]), we do not consider state reveals in our model.

A two-message key exchange protocol $\mathsf {AKE}:= (\mathsf {Gen_{AKE}}, \mathsf {Init}_{\textsc {I}}, \mathsf {Der_{R}}, \mathsf {Der}_{\textsc {I}})$ consists of four algorithms which are executed interactively by two parties as shown in Fig. 4. We denote the party which initiates the session by $\mathsf {P}_i$ and the party which responds to the session by $\mathsf {P}_r$. The key generation algorithm $\mathsf {Gen_{AKE}}$ outputs a key pair for one party. The initialization algorithm $\mathsf {Init}_{\textsc {I}}$ inputs the initiator’s long-term secret key and the responder’s long-term public key , and outputs a message $m_{i}$ and a state st. The responder’s derivation algorithm $\mathsf {Der_{R}}$ takes as input the responder’s long-term secret key, the initiator’s public key and a message $m_{i}$. It computes a message $m_{r}$ and a session key K. The initiator’s derivation algorithm $\mathsf {Der}_{\textsc {I}}$ inputs the initiator’s long term key , the responder’s long term public key , the responder’s message $m_{r}$ and the state st. Note that the responder is not required to save any internal state information besides the session key K.

Fig. 4.

Running an authenticated key exchange protocol between two parties.

We give a security game written in pseudocode. We define a model for explicit authenticated protocols achieving (full) forward secrecy instead of weak forward secrecy. Namely, an adversary in our model can be active and corrupt the user who owns the $\textsc {Test}$ session $\text {sID}^*$, and the only restriction is that if there is no matching session to $\text {sID}^*$, then the peer of $\text {sID}^*$ must not be corrupted before the session finishes.

Here explicit authentication means entity authentication in the sense that a party can explicitly confirm that he is talking to the actual owner of the recipient’s public key. The key confirmation property is only implicit [16], where a party is assured that the other identified party can compute the same session key. The game $\mathsf {IND}\text {-}\mathsf {FS}$ is given in Figs. 5 and 6.

Fig. 5.

Game $\mathsf {IND}\text {-}\mathsf {FS}$ for $\mathsf {AKE}$. $\mathcal {A}$ has access to oracles . Helper procedures $\textsc {Fresh}$ and $\textsc {Valid}$ are defined in Fig. 6. If there exists any test session which is neither fresh nor valid, the game will return b.

Fig. 6.

Helper procedures $\textsc {Fresh}$ and $\textsc {Valid}$ for game $\mathsf {IND}\text {-}\mathsf {FS}$ defined in Fig. 5. Procedure $\textsc {Fresh}$ checks if the adversary performed some trivial attack. In procedure $\textsc {Valid}$, each attack is evaluated by the set of variables shown in Table 1 and checks if an allowed attack was performed. If the values of the variables are set as in the corresponding row, the attack was performed, i.e. $\text {attack}=\mathbf{true}$, and thus the session is valid.

Execution Environment. We consider $\mu$ parties $\mathsf {P}_1,\dotsc ,\mathsf {P}_\mu$ with long-term key pairs , $n\in [\mu ]$. Each session between two parties has a unique identification number $\text {sID}$ and variables which are defined relative to $\text {sID}$:

• $\text {init}[\text {sID}]\in [\mu ]$ denotes the initiator of the session.

• $\text {resp}[\text {sID}]\in [\mu ]$ denotes the responder of the session.

• $\text {type}[\text {sID}]\in \{\text {``In''},\text {``Re''}\}$ denotes the session’s view, i.e. whether the initiator or the responder computes the session key.

• $I[\text {sID}]$ denotes the message that was computed by the initiator.

• $R[\text {sID}]$ denotes the message that was computed by the responder.

• $\text {state}[\text {sID}]$ denotes the (secret) state information, i.e. ephemeral secret keys.

• $\text {sKey}[\text {sID}]$ denotes the session key.

To establish a session between two parties, the adversary is given access to oracles $\textsc {Session}_{\textsc {I}}$ and $\textsc {Session}_{\mathsf {R}}$, where the first one starts a session of type $\text {``In''}$ and the second one of type $\text {``Re''}$. The $\textsc {Session}_{\mathsf {R}}$ oracle also runs the $\mathsf {Der_{R}}$ algorithm to compute it’s session key and complete the session, as it has access to all the required variables. In order to complete the initiator’s session, the oracle $\textsc {Der}_{\textsc {I}}$ has to be queried.

Following [21], we do not allow the adversary to register adversarially controlled parties by providing long-term public keys, as the registered keys would be treated no differently than regular corrupted keys. If we would include the key registration oracle, then our proof requires a stronger notion of signature schemes in the sense that our signature challenger can generate the system parameters with some trapdoor. With the trapdoor, the challenger can simulate a valid signature under the adversarially registered public keys. This is the case for the Schnorr signature and the tight scheme in [12], since they are honest-verifier zero-knowledge and the aforementioned property can be achieved by programming the random oracles. However, for readability, we treat the registered keys as corrupted keys.

Finally, the adversary has access to oracles $\textsc {Corr}$ and $\textsc {Reveal}$ to obtain secret information. We use the following boolean values to keep track of which queries the adversary made:

• $\text {corrupted}[n]$ denotes whether the long-term secret key of party $\mathsf {P}_n$ was given to the adversary.

• $\text {revealed}[\text {sID}]$ denotes whether the session key was given to the adversary.

• $\text {peerCorrupted}[\text {sID}]$ denotes whether the peer of the session was corrupted and its long-term key was given to the adversary at the time the session key is computed, which is important for forward security.

The adversary can forward messages between sessions or modify them. By that, we can define the relationship between two sessions:

• Matching Session: Two sessions $\text {sID}$ and $\text {sID}'$ match if the same parties are involved ($\text {init}[\text {sID}]=\text {init}[\text {sID}']$ and $\text {resp}[\text {sID}]=\text {resp}[\text {sID}']$), the messages sent and received are the same ($I[\text {sID}]=I[\text {sID}']$ and $R[\text {sID}]=R[\text {sID}']$) and they are of different types ($\text {type}[\text {sID}]\ne \text {type}[\text {sID}']$).

Our protocols use signatures to preserve integrity so that any successful no-match attacks described in [27] will lead to a signature forgery and thus can be excluded.

Finally, the adversary is given access to oracle $\textsc {Test}$, which can be queried multiple times and which will return either the session key of the specified session or a uniformly random key. We use one bit b for all test queries, and store test sessions in a set $\mathcal {S}$. The adversary can obtain information on the interactions between two parties by querying the long-term secret keys and the session key. However, for each test session, we require that the adversary does not issue queries such that the session key can be trivially computed. We define the properties of freshness and validity which all test sessions have to satisfy:

• Freshness: A (test) session is called fresh if the session key was not revealed. Furthermore, if there exists a matching session, we require that this session’s key is not revealed and that this session is not also a test session.

• Validity: A (test) session is called valid if it is fresh and the adversary performed any attack which is defined in the security model. We capture this with attack Table 1.

Table 1. Distilled table of attacks for adversaries against explicitly authenticated two-message protocols without ephemeral state reveals. An attack is regarded as an AND conjunction of variables with specified values as shown in the each line, where “–” means that this variable can take arbitrary value and $\mathbf {F}$ means “false”.

Attack Tables. We define validity of different attack strategies. All attacks are defined using variables to indicate which queries the adversary may (not) make. We consider three dimensions:

• whether the test session is on the initiator’s ($\text {type}[\text {sID}^*]=$“In”) or the responder’s side ($\text {type}[\text {sID}^*]=$“Re”),

• all combinations of long-term secret key reveals, taking into account when a corruption happened ($\text {corrupted}$ and $\text {peerCorrupted}$ variables),

• whether the adversary acted passively (matching session) or actively (no matching session).

This way, we capture all kind of combinations which are possible. From the 6 attacks in total presented in Table 2, two are trivial wins for the adversary and can thus be excluded:

• Attack (3.)+(4.): If there is no matching session, and the peer is corrupted, the adversary will trivially win, as he can forge a signature on any message of his choice, and then compute the session key.

Other attacks covered in our model capture forward secrecy (FS) and key compromise impersonation (KCI) attacks. An attack was performed if the variables are set to the corresponding values in the table.

Table 2. Full table of attacks for adversaries against explicitly authenticated two-message protocols. The trivial attacks where the session’s peer is corrupted when the key is derived, and the corresponding variables are set to $\mathbf {T}$, are marked with . The $\bot$ symbol indicates that the adversary cannot query anything from this party, as he already possesses the long-term key.

However, if the protocol does not use appropriate randomness, it should not be considered secure. Thus, if the adversary is able to create more than one matching session to a test session, he may also run a trivial attack. We model this in row (0.) of Table 2.

Note that we do not include reflection attacks, where the adversary makes a party run the protocol with himself. For the $\mathsf {KE}_{\mathsf {DH}}$ protocol, we could include these and create an additional reduction to the square Diffie-Hellman assumption (given $g^x$, to compute $g^{x^2}$), but for simplicity of our presentation we will not consider reflection attacks in this paper.

How to read the tables. As an example, we choose row (5.) of Table 2. Then, if the test session is an initiating session (namely, $\text {type}[\text {sID}^*]=\text {``In''}$), the responder is not corrupted when the key is computed, and there does not exist a matching session (namely, $|\mathfrak {M}(\text {sID}^*)|=0$), this row will evaluate to true. In this scenario, the adversary is allowed to query both long-term secret keys. Note that row (6.) denotes a similar attack against a responder session. Since the session’s type does not change the queries the adversary is allowed to make in this case, we merge these rows in Table 1. For the same reason, we also merge lines (1.) and (2.).

The purpose of these tables are to make our proofs precise, by listing all the possible attacks. We note that while in our case it would have been possible to simply write out the attacks, the number of possible combinations get too large if state-reveals are considered. As we adopt our model from [21], which does include state-reveals, we stuck to their notation.

For all test sessions, at least one attack has to evaluate to true. Then, the adversary wins if he distinguishes the session keys from uniformly random keys which he obtains through queries to the $\textsc {Test}$ oracle.

Definition 3

(Key Indistinguishability of AKE). We define game $\mathsf {IND}\text {-}\mathsf {FS}$ as in Figs. 5 and 6. A protocol $\mathsf {AKE}$ is $(t,\varepsilon , \mu , S, T, {Q}_{\textsc {Cor}})\text{- }\mathsf {IND}\text {-}\mathsf {FS}$-secure if for all adversaries $\mathcal {A}$ attacking the protocol in time t with $\mu$ users, $S$ sessions, $T$ test queries and ${Q}_{\textsc {Cor}}$ corruptions, we have

$$\begin{aligned} \left| \Pr [\mathsf {IND}\text {-}\mathsf {FS}^{\mathcal {A}} \Rightarrow 1] - \frac{1}{2}\right| \le \varepsilon . \end{aligned}$$

Note that if there exists a session which is neither fresh nor valid, the game outputs the bit b, which implies that $\Pr [\mathsf {IND}\text {-}\mathsf {FS}^{\mathcal {A}} \Rightarrow 1] = 1/2$, giving the adversary an advantage equal to 0. This captures that an adversary will not gain any advantage by performing a trivial attack.

4 Verifiable Key Exchange Protocols

A key exchange protocol $\mathsf {KE}:=(\mathsf {Init}_{\textsc {I}}, \mathsf {Der_{R}}, \mathsf {Der}_{\textsc {I}})$ can be run between two (unauthenticated) parties $i$ and $r$, and can be visualized as in Fig. 4, but with differences where (1): parties does not hold any public key or private key, and (2): public and private keys in algorithms $\mathsf {Init}_{\textsc {I}}, \mathsf {Der_{R}}, \mathsf {Der}_{\textsc {I}}$ are replaced with the corresponding users’ (public) identities.

The standard signed Diffie-Hellman (DH) protocol can be viewed as a generic way to transform a passively secure key exchange protocol to an actively secure AKE protocol using digital signatures. Our tight transformation does not modify the construction of the signed DH protocol, but requires a security notion (i.e. One-Wayness against Honest and key Verification attacks, or $\mathsf {OW\text{- }HV}$) that is (slightly) stronger than passive security: Namely, in addition to passive attacks, an adversary is allowed to check if a key corresponds to some honestly generated transcripts and to forward transcripts in a different order to create non-matching sessions. Here we require that all the involved transcripts must be honestly generated by the security game and not by the adversary. This is formally defined by Definition 4 with security game $\mathsf {OW\text{- }HV}$ as in Fig. 7.

Fig. 7.

Game $\mathsf {OW\text{- }HV}$ for $\mathsf {KE}$. $\mathcal {A}$ has access to oracles .

Definition 4

(One-Wayness against Honest and key Verification attacks ($\mathsf {OW\text{- }HV}$)). A key exchange protocol $\mathsf {KE}$ is $(t, \varepsilon , \mu , S, Q_{V}) \text{- }\mathsf {OW\text{- }HV}$ secure, where $\mu$ is the number of users, $S$ is the number of sessions and $Q_{V}$ is the number of calls to $\textsc {KVer}$, if for all adversaries $\mathcal {A}$ attacking the protocol in time at most t, we have

$$\begin{aligned} \Pr [\mathsf {OW\text{- }HV}^{\mathcal {A}} \Rightarrow 1] \le \varepsilon . \end{aligned}$$

We require that a key exchange protocol $\mathsf {KE}$ has $\alpha$ bits of min-entropy, i.e. that for all messages $m'$ we have $\Pr [m = m'] \le 2^{-\alpha },$ where m is output by either $\mathsf {Init}_{\textsc {I}}$ or $\mathsf {Der_{R}}$.

4.1 Example: Plain Diffie-Hellman Protocol

We show that the plain Diffie-Hellman (DH) protocol over prime-order group [14] is a $\mathsf {OW\text{- }HV}$-secure key exchange under the strong computational DH ($\mathsf {StCDH}$) assumption [1]. We use our syntax to recall the original DH protocol $\mathsf {KE}_{\mathsf {DH}}$ in Fig. 8.

Let $\mathsf {par}=(p, g ,\mathbb {G})$ be a set of system parameters, where $\mathbb {G}:=\left\langle g\right\rangle$ is a cyclic group of prime order p.

Definition 5

(Strong CDH Assumption). The strong CDH ($\mathsf {StCDH}$) assumption is said to be $(t, \varepsilon , Q_{\textsc {Dh}})$-hard in $\mathsf {par}=(p, g ,\mathbb {G})$, if for all adversaries $\mathcal {A}$ running in time at most t and making at most $Q_{\textsc {Dh}}$ queries to the DH predicate oracle $\textsc {Dh}_{a}$, we have:

where the DH predicate oracle $\textsc {Dh}_{a}(C,D)$ outputs 1 if $D=C^{a}$ and 0 otherwise.

Fig. 8.

The Diffie-Hellman key exchange protocol, $\mathsf {KE}_{\mathsf {DH}}$, in our syntax definition.

Lemma 1

Let $\mathsf {KE}_{\mathsf {DH}}$ be the DH key exchange protocol as in Fig. 8. Then $\mathsf {KE}_{\mathsf {DH}}$ has $\alpha = \log _2{p}$ bits of min-entropy, and for every adversary $\mathcal {A}$ that breaks the $(t, \varepsilon , \mu , S, Q_{V})\text{- }\mathsf {OW\text{- }HV}$-security of $\mathsf {KE}_{\mathsf {DH}}$, there is an adversary $\mathcal {B}$ that breaks the $(t',\varepsilon ', Q_{\textsc {Dh}})\text{- }\mathsf {StCDH}$ assumption with

$$\begin{aligned} \varepsilon '=\varepsilon , \quad t' \approx t, \quad \text{ and } \quad Q_{\textsc {Dh}}=Q_{V}+1. \end{aligned}$$

(1)

Proof

The min-entropy assertion is straightforward, as the DH protocol generates messages by drawing exponents uniformly as random.

We prove the rest of the lemma by constructing a reduction $\mathcal {B}$ which inputs the $\mathsf {StCDH}$ challenge $(A, B)$ and is given access to the decisional oracle $\textsc {Dh}_{a}$. $\mathcal {B}$ simulates the $\mathsf {OW\text{- }HV}$ security game for the adversary $\mathcal {A}$, namely, answers $\mathcal {A}$’s oracle access as in Fig. 9. More precisely, $\mathcal {B}$ uses the random self-reducibility of $\mathsf {StCDH}$ to simulate the whole security game, instead of using the $\mathsf {Init}_{\textsc {I}}$ and $\mathsf {Der_{R}}$ algorithms. The most relevant codes are highlighted with bold line numbers.

Fig. 9.

Reduction $\mathcal {B}$ that breaks the $\mathsf {StCDH}$ assumption and simulates the $\mathsf {OW\text{- }HV}$ game for $\mathcal {A}$, when $A=g^{a}$ and $B=g^{b}$ for some unknown $a$ and $b$.

We show that $\mathcal {B}$ simulates the $\mathsf {OW\text{- }HV}$ game for $\mathcal {A}$ perfectly:

• Since $X$ generated in line 26 and $Y$ generated in line 37 are uniformly random, the outputs of $\textsc {Session}_{\textsc {I}}$ and $\textsc {Session}_{\mathsf {R}}$ are distributed as in the real protocol. Note that the output of $\textsc {Der}_{\textsc {I}}$ does not get modified.

• For $\textsc {KVer}(\text {sID},K)$, if K is a valid key that corresponds to session $\text {sID}$, then there must exist sessions $\text {sID}_1$ and $\text {sID}_2$ such that $\text {type}[\text {sID}_1]=\text {``In''}$ (defined in line 24) and $\text {type}[\text {sID}_2]=\text {``Re''}$ (defined in line 34) and

  $$\begin{aligned} K = (B\cdot g^{\alpha [\text {sID}_2]})^{(a+\alpha [\text {sID}_1])} =Y^{a} \cdot Y^{\alpha [\text {sID}_1]}. \end{aligned}$$

  (2)

  where $I[\text {sID}]=I[\text {sID}_1]=A\cdot g^{\alpha [\text {sID}_1]}$ (defined in line 26) and $R[\text {sID}]=R[\text {sID}_2]=Y:=B\cdot g^{\alpha [\text {sID}_2]}$ (defined in line 37). Thus, the output of $\textsc {KVer}(\text {sID},K)$ is the same as that of $\textsc {Dh}_{a}(Y, K/Y^{\alpha [\text {sID}_1]})$.

Finally, $\mathcal {A}$ returns $\text {sID}^* \in [\text {cnt}_{\text {S}}]$ and a key $K^*$. If $\mathcal {A}$ wins, then $\textsc {KVer}(\text {sID}^*, K^*)=1$ which means that there exists sessions $\text {sID}_1$ and $\text {sID}_2$ such that $\text {type}[\text {sID}_1] = \text {``In''}$, $\text {type}[\text {sID}_2]=\text {``Re''}$ and

$$K^*= g^{(a+\alpha [\text {sID}_1]) (b+\alpha [\text {sID}_2])}=g^{ab} \cdot A^{\alpha [\text {sID}_2]} \cdot B^{\alpha [\text {sID}_1]} g^{\alpha [\text {sID}_1]\alpha [\text {sID}_2]}=g^{ab} \cdot A^{\alpha [\text {sID}_2]} \cdot Y^{\alpha [\text {sID}_1]}, $$

where $Y=R[\text {sID}_2]=B\cdot g^{\alpha [\text {sID}_2]}$. This means $\mathcal {B}$ breaks the $\mathsf {StCDH}$ with $g^{ab}=K^*/(Y^{\alpha [\text {sID}_1]}\cdot A^{\alpha [\text {sID}_2]})$ as in line 08, if $\mathcal {A}$ break the $\mathsf {OW\text{- }HV}$ of $\mathsf {KE}_{\mathsf {DH}}$. Hence, $\varepsilon =\varepsilon '$. The running time of $\mathcal {B}$ is the running time of $\mathcal {A}$ plus one exponentiation for every call to $\textsc {Session}_{\textsc {I}}$ and $\textsc {Session}_{\mathsf {R}}$, so we get $t \approx t'$. The number of calls to $\textsc {Dh}_{a}$ is the number of calls to $\textsc {KVer}$, plus one additional call to verify the adversary’s forgery, and hence $Q_{\textsc {Dh}}=Q_{V}+1$.

Group of Signed Quadratic Residues. Our construction of a key exchange protocol in Fig. 8 is based on the $\mathsf {StCDH}$ assumption over a prime order group. Alternatively, we can instantiate our $\mathsf {VKE}$ portocol in a group of signed quadratic residues $\mathbb {QR}_N^+$ [20]. As the $\mathsf {StCDH}$ assumption in $\mathbb {QR}_N^+$ groups is tightly implied by the factoring assumption (by [20, Theorem 2]), our $\mathsf {VKE}$ protocol is secure based on the classical factoring assumption.

5 Signed Diffie-Hellman, Revisited

Following the definition in Sect. 3, we want to construct a $\mathsf {IND}\text {-}\mathsf {FS}$-secure authenticated key exchange protocol $\mathsf {AKE}=(\mathsf {Gen_{AKE}}, \mathsf {Init}_{\textsc {I}}, \mathsf {Der}_{\textsc {I}}, \mathsf {Der_{R}})$ by combining a $\mathsf {StCorrCMA}$-secure signature scheme ${\mathsf {SIG}}=({\mathsf {Gen}},{\mathsf {Sign}},{\mathsf {Ver}})$, a $\mathsf {OW\text{- }HV}$-secure key exchange protocol $\mathsf {KE}=(\mathsf {Init}_{\textsc {I}}', \mathsf {Der}_{\textsc {I}}',\mathsf {Der_{R}}')$, and a random oracle $\mathsf {H}$. The construction is given in Fig. 10, and follow the execution order from Fig. 4.

Fig. 10.

Generic construction of $\mathsf {AKE}$ from ${\mathsf {SIG}}$, $\mathsf {KE}$ and a random oracle $\mathsf {H}$.

We now prove that this construction is in fact a secure $\mathsf {AKE}$ protocol.

Theorem 2

For every adversary $\mathcal {A}$ that breaks the $(t,\varepsilon , \mu , ST, Q_\mathsf {H},, {Q}_{\textsc {Cor}})\text{- }\mathsf {IND}\text {-}\mathsf {FS}$-security of a protocol $\mathsf {AKE}$ constructed as in Fig. 10, we can construct an adversary $\mathcal {B}$ against the $(t',\varepsilon ', \mu , {Q}_{s}, {Q}_{\textsc {Cor}}') \text{- }\mathsf {StCorrCMA}$-security of a signature scheme ${\mathsf {SIG}}$ with $\alpha$ bits of key min-entropy, and an adversary $\mathcal {C}$ against the $(t'',\varepsilon '', \mu , S', Q_{V})\text{- }\mathsf {OW\text{- }HV}$ security of a key exchange protocol $\mathsf {KE}$ with $\beta$ bits of min-entropy, such that

$$\begin{aligned} \varepsilon&\le 2\varepsilon ' +\frac{\varepsilon ''}{2} + \frac{\mu ^2}{2^{\alpha +1}} +\frac{S^2}{2^{\beta +1}} \\ t'&\approx t, \quad {Q}_{s}\le S, \quad {Q}_{\textsc {Cor}}'={Q}_{\textsc {Cor}}\\ t''&\approx t, \quad S' = S, \quad Q_{V}\le Q_\mathsf {H}. \end{aligned}$$

Proof

We will prove this by using the following hybrid games, which are illustrated in Fig. 11.

Fig. 11.

Games ${G}_0 \text{- }{G}_2$. $\mathcal {A}$ has access to oracles , where $\textsc {Reveal}$ and $\textsc {Corr}$ are simulated as in the original $\mathsf {IND}\text {-}\mathsf {FS}$ game in Fig. 5. Game ${G}_0$ implicitly assumes that there is no collision between long term keys or messages output by the experiment.

Game ${G}_0$: This is the $\mathsf {IND}\text {-}\mathsf {FS}$ security game for the protocol $\mathsf {AKE}$. We assume that all long term keys, and all messages output by $\mathsf {Init}_{\textsc {I}}$ and $\mathsf {Der_{R}}$ are distinct. If a collision happens, the game aborts. To bound the probability of this happening, we use that ${\mathsf {SIG}}$ has $\alpha$ bits of key min-entropy, and $\mathsf {KE}$ has $\beta$ bits of min-entropy. We can upper bound the probability of a collision happening in the keys as $\mu ^2/2^{\alpha +1}$ for $\mu$ parties, and the probability of a collision happening in the messages as $S^2/2^{\beta +1}$ for $S$ sessions, as each session computes one message. Thus we have

$$\begin{aligned} \Pr [\mathsf {IND}\text {-}\mathsf {FS}^{\mathcal {A}} \Rightarrow 1] = \Pr [{G}_{0}^\mathcal {A}\Rightarrow 1] + \frac{\mu ^2}{2^{\alpha +1}} +\frac{S^2}{2^{\beta +1}}. \end{aligned}$$

(3)

Game ${G}_1$: In this game, when the oracles $\textsc {Der}_{\textsc {I}}$ and $\textsc {Session}_{\mathsf {R}}$ try to derive a session key, they will abort if the input message does not correspond to a previously sent message, and the corresponding signature is valid w.r.t. an uncorrupted party (namely, $\mathcal {A}$ generates the message itself).

This is the preparation step for reducing an $\mathsf {IND}\text {-}\mathsf {FS}$ adversary of $\mathsf {AKE}$ to an $\mathsf {OW\text{- }HV}$ adversary of $\mathsf {KE}$. Note that in this game we do not exclude all the non-matching $\textsc {Test}$ sessions, but it is already enough for the “$\mathsf {IND}\text {-}\mathsf {FS}$-to-$\mathsf {OW\text{- }HV}$” reduction. For instance, $\mathcal {A}$ can still force some responder session to be non-matching by reusing some of the previous initiator messages to query $\textsc {Session}_{\mathsf {R}}$, and then $\mathcal {A}$ uses the non-matching responder session to query $\textsc {Test}$.

The only way to distinguish ${G}_0$ and ${G}_1$ is to trigger the new abort event in either line 19 (i.e. $\mathsf {AbortDer_{R}}$) or line 39 (i.e. $\mathsf {AbortDer_{I}}$) of Fig. 11. We define the event $\mathsf {AbortDer}:=\mathsf {AbortDer_{I}}\vee \mathsf {AbortDer_{R}}$ and have that

$$\begin{aligned} \left| {\Pr [{G}_{0}^\mathcal {A}\Rightarrow 1]-\Pr [{G}_{1}^\mathcal {A}\Rightarrow 1]}\right| \le \Pr [\mathsf {AbortDer}]. \end{aligned}$$

To bound this probability, we construct an adversary $\mathcal {B}$ against the $(t',\varepsilon ', \mu , {Q}_{s}, {Q}_{\textsc {Cor}}') \text{- }\mathsf {StCorrCMA}$-security of ${\mathsf {SIG}}$ in Fig. 12.

Fig. 12.

Adversary $\mathcal {B}$ against the $(t',\varepsilon ', \mu , {Q}_{s}, {Q}_{\textsc {Cor}}') \text{- }\mathsf {StCorrCMA}$-security of ${\mathsf {SIG}}$. The $\mathsf {StCorrCMA}$ game provides oracles $\textsc {Sign}', \textsc {Corr}'$. The adversary $\mathcal {A}$ has access to oracles , where $\textsc {Reveal}$ and $\textsc {Test}$ remain the same as in Fig. 4. We highlight the most relevant codes with bold line numbers.

We note that $\mathsf {AbortDer}$ is only if $\mathcal {A}$ performs attacks 5 + 6 in Table 1 which may lead to a session without any matching session. If then $\varSigma$ is defined in lines 26 and 42 of Fig. 12 and $\varSigma$ is a valid $\mathsf {StCorrCMA}$ forge for ${\mathsf {SIG}}$. We only show that for the case when here, and the argument is similar for the case when . Given that $\mathsf {AbortDer_{R}}$ happens, we have that and . Due to the criteria in line 40, the pair $(X,\sigma _{i})$ has not been output by $\textsc {Session}_{\textsc {I}}$ on input $(i, r)$ for any $r$, and hence $(i, X)$ has never been queried to the $\textsc {Sign}'$ oracle. Therefore, $\mathcal {B}$ aborts $\mathcal {A}$ in the $\mathsf {IND}\text {-}\mathsf {FS}$ game and returns $(i,X,\sigma _{i})$ to the $\mathsf {StCorrCMA}$ challenger to win the $\mathsf {StCorrCMA}$ game. Therefore, we have

$$\begin{aligned} \Pr [\mathsf {AbortDer_{R}}] \le \varepsilon ', \end{aligned}$$

(4)

which implies that

$$\begin{aligned} \left| {\Pr [{G}_{0}^\mathcal {A}\Rightarrow 1] -\Pr [{G}_{1}^\mathcal {A}\Rightarrow 1]}\right| \le \Pr [\mathsf {AbortDer_{I}}]+ \Pr [\mathsf {AbortDer_{R}}] \le 2 \varepsilon '. \end{aligned}$$

(5)

The running time of $\mathcal {B}$ is the same as that of $\mathcal {A}$, plus the time used to run the key exchange algorithms $\mathsf {Init}_{\textsc {I}}', \mathsf {Der_{R}}', \mathsf {Der}_{\textsc {I}}'$ and the signature verification algorithm ${\mathsf {Ver}}$. This gives $t' \approx t$. For the number of signature queries we have ${Q}_{s}\le S$, since $\textsc {Session}_{\mathsf {R}}$ can abort before it queries the signature oracle, and the adversary can reuse messages output by $\textsc {Session}_{\textsc {I}}$. For the number of corruptions, we have ${Q}_{\textsc {Cor}}' = {Q}_{\textsc {Cor}}$.

Game ${G}_2$: The $\textsc {Test}$ oracle always returns a uniformly random key, independent on the bit b.

Since we have excluded collisions in the messages output by the experiment, it is impossible to create two sessions of the same type that compute the same session key. Hence, an adversary must query the random oracle $\mathsf {H}$ on the correct input of a test session to detect the change between ${G}_1$ and ${G}_2$ (which is only in case $b=0$). More precisely, we have $\Pr [G_2^\mathcal {A}\Rightarrow 1\mid b=1]=\Pr [G_1^\mathcal {A}\Rightarrow 1\mid b=1]$ and

$$\begin{aligned} \left| \Pr [G_2^\mathcal {A}\Rightarrow 1]-\Pr [G_1^\mathcal {A}\Rightarrow 1]\right| \nonumber&= \frac{1}{2} \left| \Pr [G_2^\mathcal {A}\Rightarrow 1\mid b=0]+\Pr [G_2^\mathcal {A}\Rightarrow 1\mid b=1]\right. \nonumber \\&\quad - \left. \Pr [G_1^\mathcal {A}\Rightarrow 1\mid b=0]-\Pr [G_1^\mathcal {A}\Rightarrow 1\mid b=1]\right| \nonumber \\&=\frac{1}{2} \left| \Pr [G_2^\mathcal {A}\Rightarrow 1\mid b=0]-\Pr [G_1^\mathcal {A}\Rightarrow 1\mid b=0]\right| . \end{aligned}$$

(6)

To bound Eq. (6), we construct an adversary $\mathcal {C}$ to $(t'',\varepsilon '', \mu , S', Q_{V})$-break the $\mathsf {OW\text{- }HV}$ security of $\mathsf {KE}$. The input to $\mathcal {C}$ is the number of parties $\mu$, and system parameters $\mathsf {par}$. In addition, $\mathcal {C}$ has access to oracles $\textsc {Session}_{\textsc {I}}', \textsc {Session}_{\mathsf {R}}',\textsc {Der}_{\textsc {I}}'$ and $\textsc {KVer}$.

We firstly show that the outputs of $\textsc {Session}_{\textsc {I}}$, $\textsc {Session}_{\mathsf {R}}$ and $\textsc {Der}_{\textsc {I}}$ (simulated by $\mathcal {C}$) are distributed the same as in ${G}_1$. Due to the abort conditions introduced in ${G}_1$, for all sessions that has finished computing a key without making the game abort, their messages are honestly generated, although they may be in a different order and there are non-matching sessions. Hence, $\textsc {Session}_{\textsc {I}}$, $\textsc {Session}_{\mathsf {R}}$ and $\textsc {Der}_{\textsc {I}}$ can be perfectly simulated using $\textsc {Session}_{\textsc {I}}'$, $\textsc {Session}_{\mathsf {R}}'$ and $\textsc {Der}_{\textsc {I}}'$ of the $\mathsf {OW\text{- }HV}$ game and the signing key.

It is also easy to see that the random oracle $\mathsf {H}$ simulated by $\mathcal {C}$ has the same output distribution as in ${G}_1$. We stress that if line 66 is executed then adversary $\mathcal {A}$ may use the $\text {sID}$ to distinguish ${G}_2$ and ${G}_1$ for $b=0$, which is the only case for $\mathcal {A}$ to see the difference. At the same time, we obtain a valid attack $\varSigma :=(\text {sID}, K^*)$ for the $\mathsf {OW\text{- }HV}$ security. Thus, we have

$$ \left| \Pr [G_2^\mathcal {A}\Rightarrow 1\mid b=0]-\Pr [G_1^\mathcal {A}\Rightarrow 1\mid b=0]\right| \le \varepsilon ''. $$

As before, the running time of $\mathcal {C}$ is that of $\mathcal {A}$, plus generating and verifying signatures, and we have $t'' \approx t$. Furthermore, $S' = S$, as the counter for the $\mathsf {OW\text{- }HV}$ game increases once for every call to $\textsc {Session}_{\textsc {I}}$ and $\textsc {Session}_{\mathsf {R}}$.

Fig. 13.

Reduction $\mathcal {C}$ against the $(t'',\varepsilon '', \mu , S', Q_{V}) \text{- }\mathsf {OW\text{- }HV}$-security of $\mathsf {KE}$. The $\mathsf {OW\text{- }HV}$ game provides oracles . The adversary $\mathcal {A}$ has access to oracles , where $\textsc {Reveal}, \textsc {Corr}$ and $\textsc {Test}$ are defined as in ${G}_2$ of Fig. 11. We highlight the most relevant codes with bold line numbers. The center dot ‘$\cdot$’ in this figure means arbitrary value.

At last, for game ${G}_2$ we have $\Pr [{G}_{2}^\mathcal {A}\Rightarrow 1] =\frac{1}{2}$, as the response from the $\textsc {Test}$ oracle is independent of the bit b. Summing up all the equations, we obtain

$$\begin{aligned} \varepsilon&\le \left| \Pr [\mathsf {IND}\text {-}\mathsf {FS}^{\mathcal {A}} \Rightarrow 1] - \frac{1}{2}\right| \\&= \left| {\Pr [{G}_{0}^\mathcal {A}\Rightarrow 1]+ \frac{\mu ^2}{2^{\alpha +1}} +\frac{S^2}{2^{\beta +1}} -\Pr [{G}_{2}^\mathcal {A}\Rightarrow 1]}\right| \\&= \left| {\Pr [{G}_{0}^\mathcal {A}\Rightarrow 1] -\Pr [{G}_{1}^\mathcal {A}\Rightarrow 1] + \Pr [{G}_{1}^\mathcal {A}\Rightarrow 1] -\Pr [{G}_{2}^\mathcal {A}\Rightarrow 1] + \frac{\mu ^2}{2^{\alpha +1}} +\frac{S^2}{2^{\beta +1}}}\right| \\&\le \left| {\Pr [{G}_{0}^\mathcal {A}\Rightarrow 1] -\Pr [{G}_{1}^\mathcal {A}\Rightarrow 1]}\right| + \left| {\Pr [{G}_{1}^\mathcal {A}\Rightarrow 1] -\Pr [{G}_{2}^\mathcal {A}\Rightarrow 1]}\right| + \frac{\mu ^2}{2^{\alpha +1}} +\frac{S^2}{2^{\beta +1}} \\&\le 2\varepsilon ' +\frac{\varepsilon ''}{2} + \frac{\mu ^2}{2^{\alpha +1}} +\frac{S^2}{2^{\beta +1}} , \end{aligned}$$

and $t' \approx t, \quad {Q}_{s}\le S, \quad {Q}_{\textsc {Cor}}'={Q}_{\textsc {Cor}}, \quad t'' \approx t, \quad S' = S, \quad Q_{V}\le Q_\mathsf {H}$.