1 Introduction

Based on the results in [11], the authors of [13] have considered the ratio-dependent predator–prey system with the Michaelis–Menten functional response

$$\displaystyle \begin{aligned} \left.\begin{array}{lll} \displaystyle\dot{x} & = & \displaystyle rxg(x,K)-\sum_{i=1}^ny_ip_i\left(\frac{y_i}{x}\right),\\ \\ \displaystyle\dot{y}_i & = & \displaystyle y_ip_i\left(\frac{y_i}{x}\right)-d_iy_i,\quad (i\in\{1,\ldots,n\}) \end{array} \right\}, \end{aligned} $$
(1)

where the dot means differentiation with respect to time t; x(t) ≥ 0 denotes the quantity of the prey at time t and y i(t) ≥ 0 are the numbers or densities of the ith predator (i ∈{1, …, n}) at time t. It was assumed that the per capita growth rate of prey in the absence of predators is rg(x, K) where r > 0 denotes the maximal growth rate of prey and K > 0 is the carrying capacity of environment with respect to the prey; furthermore, the death rate d i > 0 of the ith predator is constant, and the per capita birth rate of the same predator is \(p_i\left (\frac {y_i}{x}\right )\), where the functions g and p i have the following forms:

$$\displaystyle \begin{aligned} g(x,K):\equiv1-\frac{x}{K} \qquad \mbox{and}\qquad p_i\left(\frac{y_i}{x},a_i\right):\equiv\frac{m_ix}{a_iy_i+x}, \end{aligned}$$

and a i is the ith half-saturation constant, namely, in the case where p i is a bounded function for fixed

$$\displaystyle \begin{aligned} a_i>0,\qquad m_i:=\sup\limits_{x,y_i>0}p_i(x,y_ia_i) \end{aligned}$$

is the maximal birth rate of the ith predator (i ∈{1, …, n}). For the survival of the predator, it is clearly necessary that the maximal birth rate be larger than the death rate: m i > d i (i ∈{1, …, n}). This will be assumed in the sequel.

In order to have more realism, the authors of paper [13] took into account that the predator’s growth rate at present depends on past quantities and, therefore, a continuous density function ρ was introduced whose role is to weight moments of the past (cf. [8]). Thus, they replaced the quantity x by

$$\displaystyle \begin{aligned} q(t):=\int_{-\infty}^tx(\tau)\rho(t-\tau)\,\mathrm{d}\tau\qquad (t\in[0,\infty)), \end{aligned} $$
(2)

where the density function ρ satisfies the requirements

$$\displaystyle \begin{aligned} \rho(s)\geq0\quad (s\in[0,\infty)),\qquad \int_0^\infty \rho(s)\,\mathrm{d}s=1. \end{aligned}$$

Note that it is necessary to assume that the function ρ is smooth: \(\rho \in \mathfrak {C}^1\). Thus, the system governing the dynamics of the predator–prey community is taken up in the form

$$\displaystyle \begin{aligned} \left.\begin{array}{lll} \displaystyle\dot{x} & = & \displaystyle rxg(x,K)-\sum_{i=1}^ny_ip_i\left(\frac{y_i}{x}\right),\\\\ \displaystyle\dot{y}_i & = & \displaystyle y_ip_i\left(\frac{y_i}{q}\right)-d_iy_i\quad (i\in\{1,\ldots,n\}). \end{array} \right\} \end{aligned} $$
(3)

In [13], the authors could give in the case of one prey and two predators, i.e., when n = 2, parameter values for which the above system loses its stability, and they conjectured that there may be periodic solution occurrence.

This chapter is organized as follows. In the next section, assuming that the density function ρ is a solution of homogeneous linear differential equations with constant coefficients, i.e., it has the form

$$\displaystyle \begin{aligned} \rho_m(s):=\frac{h^{m+1}s^{m} e^{-hs}}{m!}\qquad (s\in[0,+\infty)) \end{aligned} $$
(4)

where \(m\in \mathbb {N}_0\), we perform linear stability analysis of the interior equilibrium in the case of m ∈{0, 1}. In the section that follows, the conjecture in [13] is proved. We show that if the parameter is varied and crosses a critical value, periodic solutions arise via Hopf bifurcation. Finally, a numerical simulation for supporting the theoretical analysis is also given.

2 The System with Delay

In case of m = 0, the weight function is exponentially decaying (“exponential fading memory”) and has the form

$$\displaystyle \begin{aligned} \rho_0(s)=h e^{-hs}\qquad (s\in[0,+\infty)), \end{aligned} $$
(5)

and in case of m = 1, it takes the form

$$\displaystyle \begin{aligned} \rho_1(s)=h^2s e^{-hs}\qquad (s\in[0,+\infty)), \end{aligned} $$
(6)

where for both cases we have h > 0 (cf. Fig. 1). Fargue has shown in [3] that if the density ρ has the form (4), then system (3) is equivalent to a system of ordinary differential equations of higher dimension. The exponential fading memory was used by several authors (cf. e.g., [1, 2, 4, 6, 15, 17, 18]). The authors of [5, 7, 9] used the memory with hump in order to make their model more realistic.

Fig. 1
figure 1

The density functions: blue exponential fading memory and red memory with a hump

Full size image

2.1 Exponential Fading Memory

Assuming that the influence of the past is fading away exponentially, i.e., for arbitrary h > 0 (5) and

$$\displaystyle \begin{aligned} h\int_{-\infty}^t\rho_0(-h(t-\tau))\,\mathrm{d}\tau=\int_0^{\infty}\exp(-hs)\,\mathrm{d}s=1 \end{aligned}$$

holds, we have for the quantity q in (2)

$$\displaystyle \begin{aligned} \dot{q}(t)=h(x(t)-q(t))\qquad (t\in[0,+\infty)). \end{aligned}$$

The smaller the h the longer is the time interval in the past in which the values of x are taken into account, i.e., 1∕h is the “measure of the influence of the past.” Hence, system (3) is equivalent in its qualitative dynamical behavior to the following system of ordinary differential equations:

$$\displaystyle \begin{aligned} \left.\begin{array}{lll} \displaystyle\dot{x} & = & \displaystyle rxg(q,K)-\sum_{i=1}^ny_ip_i\left(\frac{y_i}{x}\right),\\\\ \displaystyle\dot{y}_i & = & \displaystyle y_ip_i\left(\frac{y_i}{q}\right)-d_iy_i\quad (i\in\{1,\ldots,n\}),\\\\ \displaystyle\dot{q} & = & \displaystyle h(x-q). \end{array} \right\} \end{aligned} $$
(7)

We note that the equivalence above takes place over the time interval [0, ∞); furthermore, if \((x,y_1,\ldots ,y_n):[0,\infty )\rightarrow \mathbb {R}^{n+1}\) is the solution of (3) corresponding to the continuous and bounded initial function \(\widetilde {x}:(-\infty ,0]\rightarrow \mathbb {R}\) and the initial values \(y_i^0:=y_i(0)\) (i ∈{1, …, n}) (i.e., \(x(t):=\widetilde {x}(t)\) (t < 0)), then

$$\displaystyle \begin{aligned} (x,y_1,\ldots,y_n,q):[0,\infty)\rightarrow\mathbb{R}^{n+2} \end{aligned}$$

is the solution of (3) satisfying the initial values

$$\displaystyle \begin{aligned} x(0)=\widetilde{x}(0),\quad y_i(0)=y_i^0\qquad (i\in\{1,\ldots,n\}) \end{aligned}$$

and

$$\displaystyle \begin{aligned} q(0)=q^0:=h\int_{-\infty}^0\widetilde{x}(\tau)\exp(h\tau)\,\mathrm{d}\tau \end{aligned}$$

and vice versa. (Clearly, if the initial values x(0), \(y_i^0\), and q 0 related to system (3) are prescribed, then the function \(\widetilde {x}\) is not uniquely determined.)

2.2 Memory with a Hump

Assume now that the weight function is given by (6) and for t ∈ [0, +∞) introduces notations

$$\displaystyle \begin{aligned} \begin{array}{l} \displaystyle q(t):=h^2\int_{-\infty}^t(t-\tau)x(\tau)\exp(-h(t-\tau))\,\mathrm{d}\tau, \\\\ \displaystyle r(t):=h\int_{-\infty}^tx(\tau)\exp(-h(t-\tau))\,\mathrm{d}\tau. \end{array} \end{aligned} $$
(8)

Then, we have

$$\displaystyle \begin{aligned} \dot{q}=h(r-q),\qquad \text{resp.}\qquad \dot{r}=h(x-r), \end{aligned}$$

and furthermore, it is easy to see that system (3) is equivalent on [0, +∞) in the sense described following (7) to the system

$$\displaystyle \begin{aligned} \left.\begin{array}{lll} \displaystyle\dot{x} & = & \displaystyle rxg(x,K)-\sum_{i=1}^ny_ip_i\left(\frac{y_i}{x}\right),\\\\ \displaystyle\dot{y}_i & = & \displaystyle y_ip_i\left(\frac{y_i}{q}\right)-d_iy_i\quad (i\in\{1,\ldots,n\}),\\\\ \displaystyle\dot{q} & = & \displaystyle h(r-q),\\\\ \displaystyle\dot{r} & = & \displaystyle h(x-r). \end{array} \right\} \end{aligned} $$
(9)

3 The Case of One Prey and Two Predators

As it was done in [13], we also assume that the community consists of one prey and two predators, i.e., n = 2 holds. This means that that system (7) takes the form

$$\displaystyle \begin{aligned} \left.\begin{array}{lll} \dot{x}&=&rx\left(1-\displaystyle\frac{x}{K}\right)-m_1\displaystyle\frac{xy_1}{a_1y_1+x}-m_2\displaystyle\frac{xy_2}{a_2y_2+x},\\\\ \dot{y}_1&=&m_1\displaystyle\frac{xy_1}{a_1y_1+x}-d_1y_1,\\\\ \dot{y}_2&=&m_2\displaystyle\frac{xy_2}{a_2y_2+x}-d_2y_2. \end{array}\right\} \end{aligned} $$
(10)

In [11], it was showed that system (10) is dissipative, i.e., all of its solutions are bounded and the positive octant of the phase space \(\mathbb {R}^3\) is an invariant region; furthermore, if we extend it for

$$\displaystyle \begin{aligned} \mathbb{R}^3_+:=\left\{(x,y_1,y_2)\in\mathbb{R}^3:\;x\geq0,\,y_1\geq0,\,y_2\geq0\right\} \end{aligned}$$

by \(\dot {x}=0\), \(\dot {y}_i=0\) if \(x^2+y_i^2=0\) for any i (i ∈{1;2}), then the extended system has four equilibria on the boundary of the positive octant of the phase space, namely

$$\displaystyle \begin{aligned} E^0(0,0,0),\qquad E^1(K,0,0),\qquad E_i^2(\widehat{x}_i,\widehat{y}_1,\widehat{y}_2)\quad (i\in\{1;2\}), \end{aligned}$$

where for i, j ∈{1;2}: j ≠ i we have

$$\displaystyle \begin{aligned} \hat{x}_i:=K\left(1-\displaystyle\frac{1}{r}\frac{m_i-d_i}{a_i}\right),\qquad \hat{y}_i:=\frac{m_i-d_i}{d_ia_i}\hat{x},\quad \hat{y}_j=0, \end{aligned}$$

and it has one interior equilibrium \(E^*(x^*,y_1^*,y_2^*)\) where for i ∈{1;2} we have

$$\displaystyle \begin{aligned} x^*:=K\left(1-\frac{1}{r}\sum_{i=1}^{2}\frac{m_i-d_i}{a_i}\right)\qquad \text{and}\qquad y_i^*:=\frac{m_i-d_i}{d_ia_i}x^*. \end{aligned}$$

Note that equilibria E 0 and E 1 always exist. The equilibria \(E_i^2\) (i ∈{1;2}) and E ∗ may or may not exist. In particular, \(E_i^2\) exists (i ∈{1;2}) if

$$\displaystyle \begin{aligned} \frac{m_i-d_i}{a_i}<r\qquad \text{and}\qquad m_i>d_i \end{aligned}$$

hold. The interior equilibrium E ∗ that represents the coexistence of all species exists if maximal growth rates m i − d i of the predators are positive and the sum of the ratios of the growth rates and half-saturation constants of the predators is less than the intrinsic growth rate of the prey, i.e.,

$$\displaystyle \begin{aligned} m_i>d_i\qquad \text{and}\qquad \sum_{i=1}^{2}\frac{m_i-d_i}{a_i}<r \end{aligned} $$
(11)

hold.

Introducing delays with density functions (5) and (6), system (10) goes into

$$\displaystyle \begin{aligned} \left.\begin{array}{lll} \dot{x}&=&rx\left(1-\displaystyle\frac{x}{K}\right)-m_1\displaystyle\frac{xy_1}{a_1y_1+x}-m_2\displaystyle\frac{xy_2}{a_2y_2+x},\\\\ \dot{y}_1&=&m_1\displaystyle\frac{qy_1}{a_1y_1+q}-d_1y_1,\\\\ \dot{y}_2&=&m_2\displaystyle\frac{qy_2}{a_2y_2+q}-d_2y_2,\\\\ \displaystyle\dot{q} & = & \displaystyle h(x-q) \end{array} \right\} \end{aligned} $$
(12)

and into

$$\displaystyle \begin{aligned} \left.\begin{array}{lll} \dot{x}&=&rx\left(1-\displaystyle\frac{x}{K}\right)-m_1\displaystyle\frac{xy_1}{a_1y_1+x}-m_2\displaystyle\frac{xy_2}{a_2y_2+x},\\\\ \dot{y}_1&=&m_1\displaystyle\frac{qy_1}{a_1y_1+q}-d_1y_1,\\\\ \dot{y}_2&=&m_2\displaystyle\frac{qy_2}{a_2y_2+q}-d_2y_2,\\\\ \displaystyle\dot{q} & = & \displaystyle h(r-q),\\\\ \displaystyle\dot{r} & = & \displaystyle h(x-r). \end{array} \right\} \end{aligned} $$
(13)

From the biological point of view, we are only interested in the case when the interior equilibrium exists because the other equilibria are unstable when no delay is concerned (cf. [11]). If condition (11) holds, then interior equilibria of (10), resp. (12) and of (13) are

$$\displaystyle \begin{aligned} E^*:=(x^*,y_1^*,y_2^*), \end{aligned}$$

resp.

$$\displaystyle \begin{aligned} E_{d0}^*:=(x^*,y_1^*,y_2^*,x^*)\qquad \text{and}\qquad E_{d1}^*:=(x^*,y_1^*,y_2^*,x^*,x^*). \end{aligned}$$

In order to determine the stability of equilibria E ∗, resp. \(E_{d0}^*\) and \(E_{d1}^*\) of systems (10), resp. (12) and (13) one has to compute the Jacobians

$$\displaystyle \begin{aligned} J(x,y_1,y_2):=\left[ \begin{array}{ccc} \displaystyle j_{11} & \displaystyle-\frac{m_1x^2}{(a_1y_1+x)^2} & \displaystyle-\frac{m_2x^2}{(a_2y_2+x)^2} \\ \displaystyle\frac{a_1m_1y_1^2}{(a_1y_1+x)^2} & \displaystyle\frac{m_1x^2}{(a_1y_1+x)^2}-d_1 & \displaystyle 0 \\ \displaystyle\frac{a_2m_2y_2^2}{(a_2y_2+x)^2} & \displaystyle 0 & \displaystyle \frac{m_2x^2}{(a_2y_2+x)^2}-d_2 \\ \end{array} \right] \end{aligned}$$

resp.

$$\displaystyle \begin{aligned} J(x,y_1,y_2,q):=\left[\begin{array}{cccc} \displaystyle j_{11} & \displaystyle-\frac{m_1x^2}{(a_1y_1+x)^2} & \displaystyle-\frac{m_2x^2}{(a_2y_2+x)^2} &\displaystyle 0\\ \displaystyle 0 & \frac{m_1q^2}{(a_1y_1+q)^2}-d_1 & \displaystyle 0 & \displaystyle\frac{a_1m_1y_1^2}{(a_1y_1+q)^2} \\ \displaystyle 0 & \displaystyle 0 & \displaystyle\frac{m_2q^2}{(a_2y_2+q)^2}-d_2 & \displaystyle\frac{a_2m_2y_2^2}{(a_2y_2+q)^2} \\ \displaystyle h & \displaystyle 0 & \displaystyle 0 & \displaystyle-h \\ \end{array} \right] \end{aligned}$$

and

$$\displaystyle \begin{aligned} J(x,y_1,y_2,q,p):=\left[\begin{array}{ccccc} \displaystyle j_{11} & \displaystyle -\frac{m_1x^2}{(a_1y_1+x)^2} & \displaystyle -\frac{m_2x^2}{(a_2y_2+x)^2} & \displaystyle 0 & \displaystyle 0 \\ \displaystyle 0 & \displaystyle \frac{m_1q^2}{(a_1y_1+q)^2}-d_1 & \displaystyle 0 & \displaystyle \frac{a_1m_1y_1^2}{(a_1y_1+q)^2} & \displaystyle 0 \\ \displaystyle 0 & \displaystyle 0 & \displaystyle\frac{m_2q^2}{(a_2y_2+q)^2}-d_2 & \displaystyle \frac{a_2m_2y_2^2}{(a_2y_2+q)^2} & \displaystyle 0 \\ \displaystyle 0 & \displaystyle 0 & \displaystyle 0 & \displaystyle -h & \displaystyle h \\ \displaystyle h & \displaystyle 0 & \displaystyle 0 & \displaystyle 0 & \displaystyle -h \\ \end{array} \right] \end{aligned}$$

at these equilibria, where

$$\displaystyle \begin{aligned} j_{11}:=r-\frac{2rx}{K}-\frac{a_1m_1y_1^2}{(a_1y_1+x)^2}-\frac{a_2m_2y_2^2}{(a_2y_2+x)^2}. \end{aligned}$$

If we take parameter values (cf. [13])

$$\displaystyle \begin{aligned} m_1:=16,\;\, m_2:=18,\;\, d_1:=8,\;\, d_2:=12,\;\, a_1:=4,\;\, a_2:=2,\;\, K:=0.1, \end{aligned} $$
(14)

then the dependence of E ∗, resp. \(E_{d0}^*\) and \(E_{d1}^*\), on the parameter r (in fact on the maximal growth rates from the prey) is as follows:

$$\displaystyle \begin{aligned} E^*:=\left(0.1\left(1-\frac{5}{r}\right),\frac{1}{40}\left(1-\frac{5}{r}\right),\left(1-\frac{5}{r}\right)\right), \end{aligned}$$

resp.

$$\displaystyle \begin{aligned} E_{d0}^*:=\left(0.1\left(1-\frac{5}{r}\right),\frac{1}{40}\left(1-\frac{5}{r}\right),\frac{1}{40}\left(1-\frac{5}{r}\right),0.1\left(1-\frac{5}{r}\right)\right) \end{aligned}$$

and

$$\displaystyle \begin{aligned} E_{d1}^*:=\left(0.1\left(1-\frac{5}{r}\right),\frac{1}{40}\left(1-\frac{5}{r}\right),\frac{1}{40}\left(1-\frac{5}{r}\right),0.1\left(1-\frac{5}{r}\right),0.1\left(1-\frac{5}{r}\right)\right). \end{aligned}$$

Under this restriction, we have

$$\displaystyle \begin{aligned} J:=J(E^*):=\left[\begin{array}{ccc} 8-r & -4 & -8 \\ 1 & -4 & 0 \\ 1 & 0 & -4 \end{array} \right] \end{aligned}$$

resp.

$$\displaystyle \begin{aligned} J_0:=J(E_{d0}^*):=\left[\begin{array}{cccc} 8-r & -4 & -8 & 0 \\ 0 & -4 & 0 & 1 \\ 0 & 0 & -4 & 1 \\ h & 0 & 0 & -h \end{array} \right] \end{aligned}$$

and

$$\displaystyle \begin{aligned} J_1:=J(E_{d1}^*):=\left[\begin{array}{ccccc} 8-r & -4 & -8 & 0 & 0 \\ 0 & -4 & 0 & 1 & 0 \\ 0 & 0 & -4 & 1 & 0 \\ 0 & 0 & 0 & -h & h\\ h & 0 & 0 & 0 & -h \end{array} \right]. \end{aligned}$$

We calculate the characteristic polynomials of J, resp. J 0 and J 1, using Faddeev–Leverrier method (cf. [10]) and with the help of block matrices. The characteristic polynomial of the Jacobian J has the form

$$\displaystyle \begin{aligned} \chi_J(z):=z^3+a_2z^2+a_1z+a_0\qquad (z\in\mathbb{K}), \end{aligned}$$

where

$$\displaystyle \begin{aligned} \begin{array}{lll} \displaystyle a_2 & = & \displaystyle-\mathrm{Tr}(J)=r,\\\\ \displaystyle a_1 & = & \displaystyle\frac{1}{2}\left\{(\mathrm{Tr}(J))^2-\mathrm{Tr}(J^2)\right\}=8r-36,\\\\ \displaystyle a_0 & = & \displaystyle-\det(J)=16r-80. \end{array} \end{aligned}$$

The equilibrium E ∗ is feasible if and only if r > 5 holds. In this case, χ J is a stable polynomial since it fulfills the Routh–Hurwitz condition (cf. [8]): its coefficients have the same sign and

$$\displaystyle \begin{aligned} a_1a_2-a_0=(8r-36)r-16r+80=8r^2-52r+80=4(r-4)(r-5/2)>0. \end{aligned}$$

As a consequence, E ∗ is asymptotically stable if it exists. The characteristic polynomial \(\chi _{J_0}\) is calculated as follows. From the definition, we have

Since A and B commute, we get (cf. [16])

$$\displaystyle \begin{aligned} \begin{array}{lll} \displaystyle\det(zI_4-J_0) & = & \displaystyle-\frac{1}{8}\det\left[DA-CB\right]\\\\ & = & \displaystyle-\frac{1}{8}\det\left[\left[\begin{array}{cc} -4-z & 1 \\ 0 & -h-z \end{array} \right]\left[\begin{array}{cc} r+z-8 & 4 \\ 0 & -32-8z \end{array} \right]-8h\left[\begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array} \right]\right]\\\\ & = & \displaystyle-\frac{1}{8}\det\left[\left[\begin{array}{cc} (4+z)(r-8+z) & 4(4+z)-4-z\\ 0 & (h+z)(4+z) \end{array} \right]-8h\left[\begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array} \right]\right]\\\\ & = & \displaystyle-\frac{1}{8}\det\left[\begin{array}{cc} -(4+z)(r-8+z) & -4(4+z)-8(4+z)\\ -8h & 8(h+z)(4+z) \end{array} \right]\\\\ & = & \displaystyle(4+z)(r-8+z)(h+z)(4+z)-12h(4+z)\\\\ & = & \displaystyle(4 + z)\left\{z^3+(h+r-4)z^2+((h+4)r-4(h+8))z+4h(r-5)\right\}. \end{array} \end{aligned}$$

The characteristic polynomial \(\chi _{J_1}\) can be computed as follows.

$$\displaystyle \begin{aligned} \begin{array}{lll} \displaystyle\chi_{J_1}(z) & := & \displaystyle\det(zI_5-J_1)=(-1)^5\det(J_1-zI_5)\\\\ & = & \displaystyle-\det\left[\begin{array}{ccccc} 8-r-z & -4 & -8 & 0 & 0 \\ 0 & -4-z & 0 & 1 & 0 \\ 0 & 0 & -4-z & 1 & 0 \\ 0 & 0 & 0 & -h-z & h\\ h & 0 & 0 & 0 & -h-z \end{array} \right]\\\\ & = & \displaystyle -(h+z)^2(4+z)^2(8-r-z). \end{array} \end{aligned}$$

It is easy to see that J 1 is stable only if r > 8, whereas the stability of J 0 depends on the third-order polynomial

$$\displaystyle \begin{aligned} z^3+\alpha(h)z^2+\beta(h)z+\gamma(h)\qquad (z\in\mathbb{K}), \end{aligned} $$
(15)

where

$$\displaystyle \begin{aligned} \alpha(h):=h + r-4,\qquad \beta(h):=(h+4) r-4 (h+8),\qquad \gamma(h):=4h(r-5). \end{aligned}$$

In order to have Hopf bifurcation in case of J 0, one has to show that a pair of complex conjugate eigenvalues of J 0 crosses the imaginary axis with non-zero velocity, while the rest of the eigenvalues continue to have negative or positive real parts. This is fulfilled if (cf. [8, 14])

  • the so-called eigenvalue crossing condition holds, i.e., the characteristic polynomial \(\chi _{J_0}\) has a pair of pure imaginary roots μ(h) ± ıν(h) and no other roots with zero real parts, for which at a critical value h ∗ of the bifurcation parameter h

    $$\displaystyle \begin{aligned} \mu(h_*)=0,\qquad \nu(h_*)\neq0;\qquad \left(\sigma(J_0)\backslash\{\pm\imath\nu(h_*)\}\right)\cap\imath\mathbb{R}=\emptyset, \end{aligned}$$

    hold;

  • the transversality condition holds, i.e., μ′(h ∗) ≠ 0 is fulfilled.

Clearly, for every h > 0, we have γ(h) > 0 because r > 5 holds.

Next, we use a lemma for which a proof is given in Appendix of [12].

Lemma 3.1

Let \(I\subset \mathbb {R}\) an open interval \(\alpha ,\beta ,\gamma :I\rightarrow \mathbb {R}\) smooth functions. Then, the polynomial

$$\displaystyle \begin{aligned} P(z):=z^3+\alpha z^2+\beta z+\gamma\qquad (z\in\mathbb{K}) \end{aligned}$$

fulfills at some h = h ∗∈ I the eigenvalue crossing condition and the transversality condition if

$$\displaystyle \begin{aligned} \alpha(h^*)\neq 0,\qquad \beta(h^*)>0,\qquad \gamma(h^*)=\alpha(h^*)\beta(h^*) \end{aligned} $$
(16)

and

$$\displaystyle \begin{aligned} \frac{\mathrm{d}}{\mathrm{d}h}\left.\left\{\alpha(h)\beta(h)-\gamma(h)\right\}\right|{}_{h=h^*}\neq0 \end{aligned} $$
(17)

hold.

Thus, the eigenvalue crossing condition holds for the polynomial in (15) if and only if

$$\displaystyle \begin{aligned} \beta(h):=(h+4) r-4 (h+8)>0,\qquad \alpha(h):=h + r-4\neq0 \end{aligned}$$

and

$$\displaystyle \begin{aligned} \alpha(h)\beta(h)-\gamma(h):=(h + r-4)\left\{(h+4) r-4 (h+8)\right\}-4h(r-5)\neq0. \end{aligned}$$

The authors in [13] have chosen for r := 7 the value h ∗ := 1 that is seemingly not critical. No wonder that they could not observe and prove periodic oscillation. Solving equation α(h)β(h) = γ(h), we have

$$\displaystyle \begin{aligned} h_H:=h_*=\frac{1+\sqrt{17}}{2}. \end{aligned}$$

Because

$$\displaystyle \begin{aligned} \alpha(h_*)=\frac{\sqrt{17}+7}{2}\neq0 \qquad \text{and}\qquad \beta(h_*)=\frac{3\sqrt{17}-5}{2}>0, \end{aligned}$$

the eigenvalue crossing condition holds at this value of the parameter h. Thus, we are able to prove the occurrence of limit cycles from the interior equilibrium \(E_{d0}^*\) of the system (12).

Theorem 3.1

Suppose that conditions in (14) hold and r = 7, then at the critical value h H of the bifurcation parameter h the equilibrium \(E_{d0}^*\) of the system (12) undergoes a Hopf bifurcation: \(E_{d0}^*\) loses its stability and a branch of periodic solutions emerges from \(E_{d0}^*\) near h = h H.

Proof

We need to check whether the transversality condition (17) holds. Indeed, at the critical value h = h H, we have

$$\displaystyle \begin{aligned} \frac{\mathrm{d}}{\mathrm{d}h}(\alpha\beta-\gamma)(h_H)=-[8 - 3 (3 + h) - 7 (4 + h) + 4 (8 + h)]_{h=h_H}=3\sqrt{17}\neq0, \end{aligned}$$

which proves our statement. □

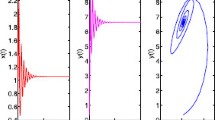
Figure 2 shows the time evolution of system (12) if Hopf bifurcation occurs.

Fig. 2
figure 2

The periodic solution of system (12) near h = h H

Full size image

4 Stability of the Bifurcating Periodic Solution

In this section, we shall present a very brief summary of the projection method (cf. [14]) in order to decide whether the bifurcation is super- or subcritical. Under supercritical bifurcation, we mean the case when the equilibrium \(E_{d0}^*\) has lost its stability with occurrence of periodic solutions that are orbitally asymptotically stable (i.e., for values of the bifurcation parameter h less than h H), while in the subcritical case, the periodic solutions are unstable and exist for hs when the equilibrium \(E_{d0}^*\) is still asymptotically stable (i.e., for values of h greater than h H).

Clearly, system (12) has the form

$$\displaystyle \begin{aligned} (\dot{u},\dot{v},\dot{w},\dot{z})=\mathbf{F}(u,v,w,z,h), {} \end{aligned} $$
(18)

where

$$\displaystyle \begin{aligned} \begin{array}{lll} \displaystyle F_1(u,v,w,z,h) & := & \displaystyle ru\left(1-\displaystyle\frac{u}{K}\right)-m_1\displaystyle\frac{uv}{a_1v+u}-m_2\displaystyle\frac{uw}{a_2w+u},\\\\ \displaystyle F_2(u,v,w,z,h) & := & \displaystyle m_1\displaystyle\frac{zv}{a_1v+z}-d_1v,\\\\ \displaystyle F_3(u,v,w,z,h) & := & \displaystyle m_2\displaystyle\frac{zw}{a_2w+z}-d_2w,\\\\ \displaystyle F_4(u,v,w,z,h) & := & \displaystyle h(u-z) \end{array} \end{aligned}$$

and h is the bifurcation parameter. Define the bilinear, resp. trilinear functions

$$\displaystyle \begin{aligned} \mathfrak{B}=(B_1,B_2,B_3,B_4):\mathbb{K}^4\times\mathbb{K}^4\rightarrow\mathbb{K}^4, \end{aligned}$$

resp.

$$\displaystyle \begin{aligned} \mathfrak{C}=(C_1,C_2,C_3,C_4):\mathbb{K}^4\times\mathbb{K}^4\times\mathbb{K}^4\rightarrow\mathbb{K}^4 \end{aligned}$$

by

$$\displaystyle \begin{aligned} B_i(\mathbf{x},\mathbf{y}):=\left.\sum\limits_{j,k=1}^4\frac{\partial^2F_i(\boldsymbol{\xi}, h_H)}{\partial\xi_j\partial\xi_k}\right|{}_{{\boldsymbol{\xi}}=E_{d0}^*}x_jy_k, \qquad (i\in\{1,2,3,4\}), \end{aligned}$$

resp. by

$$\displaystyle \begin{aligned} C_i(\mathbf{x},\mathbf{y},\mathbf{z}):=\left.\sum\limits_{j,k,l=1}^4\frac{\partial^3F_i(\boldsymbol{\xi}, h_H)}{\partial\xi_j\partial\xi_k\partial\xi_l}\right|{}_{{\boldsymbol{\xi}}=E_{d0}^*}x_jy_kz_l \qquad (i\in\{1,2,3,4\}). \end{aligned}$$

The Jacobian J 0 at the critical parameter value h = h H will be denoted by \(\mathfrak {A}\):

$$\displaystyle \begin{aligned} \mathfrak{A}:=\left.\frac{\partial\mathbf{F}(\boldsymbol{\xi},h_H)}{\partial(u,v,w,z)}\right|{}_{{\boldsymbol{\xi}}=E_{d0}^*}. \end{aligned}$$

Clearly, ıω and − ıω are eigenvalues of \(\mathfrak {A}\) with left and right eigenvectors \(\mathbf {p},\mathbf {q}\in \mathbb {K}^4\), i.e., satisfying

$$\displaystyle \begin{aligned} \mathfrak{A}\mathbf{q}=\imath\omega\mathbf{q},\qquad \mathfrak{A}^T\mathbf{p}= -\imath\omega\mathbf{p} {} \end{aligned} $$
(19)

and normalized by setting

$$\displaystyle \begin{aligned} \langle\mathbf{p},\mathbf{q}\rangle=1 {} \end{aligned} $$
(20)

where 〈⋅, ⋅〉 is the standard scalar product in \(\mathbb {C}^4\), antilinear in the first argument.

To examine the supercriticality, resp. subcriticality, of the bifurcating solution, one has to compute the sign of the first Poincaré–Lyapunov coefficient

$$\displaystyle \begin{aligned} l_1=\frac{1}{2\omega}\cdot\Re\left(\left\langle\mathbf{p},\mathcal{H}_{21}\right\rangle\right), \end{aligned} $$
(21)

where

$$\displaystyle \begin{aligned} \mathcal{H}_{21}:=\mathfrak{C}(\mathbf{q},\mathbf{q},\overline{\mathbf{q}})+2\mathfrak{B}\left(\mathbf{q},{\mathbf{h}}_{11}\right)+ \mathfrak{B}(\overline{\mathbf{q}},{\mathbf{h}}_{20}), \end{aligned}$$

resp.

$$\displaystyle \begin{aligned} {\mathbf{h}}_{11}:=\mathfrak{A}^{-1} \mathfrak{B}(\mathbf{q},\overline{\mathbf{q}})\qquad \text{and}\qquad {\mathbf{h}}_{20}:=\left(2\imath\omega I_3-\mathfrak{A}\right)^{-1}\mathfrak{B}(\mathbf{q},\mathbf{q}). \end{aligned}$$

In case of l 1 < 0 (resp. l 1 > 0), we have supercritical (resp. subcritical) bifurcation.