Keywords

1 Introduction

Mathematical models play an essential role to describe the dynamics of many infectious diseases. The first models usually use three main populations that are the susceptible S(t), the infectious I(t), and the removed individuals R(t) at a specific time t. The basic SIR formulation is introduced in the pioneer work [1]; but, when an individual is incubated but still not yet infectious, another class should be added; this class is called latent compartment noted by L(t). A mutation process was observed in many infections such as tuberculosis [2], human immunodeficiency virus [3], dengue fever [4], influenza [5], and other sexually transmitted diseases. This phenomenon can result in the observation on two or more strains of the studied pathogen. Hence, multi-strain model can better describe different type of diseases.

Recently, two-strain SLIR epidemic model has been tackled [6], the authors consider two incidence rates, the first is bilinear while the second is non-monotonic. More recently, the same problem with two strains is treated by choosing both the incidences as non-monotonic [7]. The generalization of a multi-strain SLIR epidemiological model with general incidence rates is studied in [8]; the authors compare the numerical simulations with COVID-19 clinical data. In this work, we continue the investigation of this last kind of problems by taking into consideration the effect of quarantine measures on SLIR model with two non-monotonic incidence rates. The two-strains SLIR epidemiological model that we consider is formulated as follows:

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} \frac{dS}{dt} &= \; \Lambda-\frac{\alpha (1-u_1) S I_{1}}{1+m I_{1}^{2}}-\frac{\beta (1-u_2) S I_{2}}{1+ k I_{2}^{2}}- \delta S \;, \\\\ \frac{dL_{1}}{dt} &= \; \frac{\alpha (1-u_1) S I_{1}}{1+m I_{1}^{2}}-(\gamma_{1}+\delta)L_{1}\;, \\\\ \frac{dL_{2}}{dt} &= \;\frac{\beta (1-u_2)S I_{2}}{1+ k I_{2}^{2}}-(\gamma_{2}+\delta)L_{2}\;, \\\\ \frac{dI_{1}}{dt} &= \; \gamma_{1} L_{1}-(\mu_{1}+\delta)I_{1}\;, \\\\ \frac{dI_{2}}{dt} &= \; \gamma_{2} L_{2}-(\mu_{2}+\delta)I_{2}\;,\\ {} \frac{dR}{dt} &= \; \mu_{1}I_{1}+\mu_{2}I_{2}-\delta R\;, \end{aligned} \right. \end{aligned} $$
(1)

with

$$\displaystyle \begin{aligned} S(0)\geq0,\ L_{1}(0)\geq0,\ L_{2}(0)\geq0 ,\ I_{1}(0)\geq0 ,\ I_{2}(0)\geq0 ,\ R(0)\geq0. \end{aligned}$$

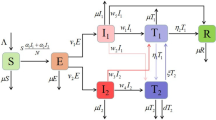
This model contains six variables, that are, susceptible individuals (S), two categories of latent individuals: (L 1) and (L 2), two categories of infectious individuals: (I 1) and (I 2), and removed individuals (R). The parameters of the model (1) are described in Table 1 and the two-strain SLIR diagram is illustrated in Fig. 1; the parameters are given in Table 1. The last two new parameters to the model u 1 and u 2 represent the efficiency of quarantine in reducing the first strain infection and the second strain infection, respectively.

Fig. 1
figure 1

The diagram of SLIR two-strain model

Full size image
Table 1 Description of parameters of the model (1)
Full size table

The present work is organized as follows. In the next section, we will prove the positivity and the boundedness results. In Sect. 3, we fulfilled the global analysis of our model. In Sect. 4, we will give some results of the numerical simulations. Short conclusion is given in the last section.

2 Positivity and Boundedness of Solutions

Since our problem is related to the population dynamics, we will prove that all model variables are positive and bounded. First, we will assume that all the parameters in our model are positive.

Proposition 2.1

For any positive initial conditions S(0), L 1(0), L 2(0), I 1(0), I 2(0), R(0), the variables of the model (1) S(t), L 1(t), L 2(t), I 1(t), I 2(t), and R(t) will remain positive for all t > 0.

Proof

First, let

$$\displaystyle \begin{aligned} T = sup\{&\displaystyle {\tau \geq 0 \;|\; \; \forall t, 0 \leq t \leq \tau} \;\text{such that}\; S(t) \geq 0, \; L_{1}(t) \geq0, \; L_{2}(t) \geq 0,\\ &I_{1}(t)\geq 0, I_{2}(t)\geq 0\; , R(t) \geq 0\}. \end{aligned} $$

Let us now demonstrate that T = +∞.

Assume that 0 < T < +∞; by continuity, we will have S(T) = 0 or L 1(T) = 0 or L 2(T) = 0 or I 1(T) = 0 or I 2(T) = 0 or R(T) = 0. If S(T) = 0 before the other variables L 1, L 2, I 1, I 2, R, become zero. Therefore

$$\displaystyle \begin{aligned}\displaystyle{ \frac{ dS(T)}{dt}=\lim_{t\rightarrow T^{-}} \frac{S(T)-S(t)}{T-t}=\lim_{t\rightarrow T^{-}}} \frac{-S(t)}{T-t} \leq 0.\end{aligned}$$

From the first equation of the system (1), we have

$$\displaystyle \begin{aligned}\displaystyle{ \frac{dS(T)}{dt}=\Lambda > 0}. \end{aligned}$$

If L 1(T) = 0 before S, L 2, I 1, I 2, and R. Then

$$\displaystyle \begin{aligned}\displaystyle{ \frac{ dL_{1}(T)}{dt}=\lim_{t\rightarrow T^{-}} \frac{L_{1}(T)-L_{1}(t)}{T-t}=\lim_{t\rightarrow T^{-}}} \frac{-L_{1}(t)}{T-t} \leq 0. \end{aligned}$$

From the second equation of the system (1) with the fact L 1(T) = 0, which gives

$$\displaystyle \begin{aligned}\displaystyle{ \frac{ dL_{1}(T)}{dt}= \frac{\alpha (1-u_1) S I_{1}}{1+m I_{1}^{2}}}.\end{aligned}$$

Since u 1 and u 2 reflect the effectiveness of quarantine, we have u i ∈ [0, 1], i = 1, 2. Therefore, α(1 − u 1) and m are positive, and we have

$$\displaystyle \begin{aligned} \displaystyle{ \frac{ dL_{1}(T)}{dt}} > 0. \end{aligned}$$

Also, if I 1 = 0 before S, L 1, L 2, I 2, R become zero, then

$$\displaystyle \begin{aligned}\displaystyle{ \frac{ dI_{1}(T)}{dt}=\lim_{t\rightarrow T^{-}} \frac{I_{1}(T)-I_{1}(t)}{T-t}=\lim_{t\rightarrow T^{-}}} \frac{-I_{1}(t)}{T-t} \leq 0.\end{aligned}$$

But from the fourth equation of the system (1) with I 1(T) = 0, we will have

$$\displaystyle \begin{aligned}\displaystyle{ \frac{ dI_{1}(T)}{dt}}= \gamma_{1} L_{1}.\end{aligned}$$

Since γ 1 > 0, we have

$$\displaystyle \begin{aligned}\displaystyle{ \frac{ dI_{1}(T)}{dt}}= \gamma_{1} L_{1} > 0. \end{aligned}$$

Similar proofs for L 2(t), I 2(t), and R(t).

We conclude that T could not be finite; this completes the proof.

Proposition 2.2

The biologically feasible region is represented by

$$\displaystyle \begin{aligned}\mathcal{H}=\{(S,L_{1},L_{2},I_{1},I_{2}, R)\in \mathbb{R}^{6}_{+} \mathit{\text{ such that }} S + L_{1} + L_{2} + I_{1} + I_{2}+ R \leq \displaystyle{\frac{\Lambda}{\delta}} \}\end{aligned}$$

is positively invariant.

Proof

Let the total acting population

$$\displaystyle \begin{aligned} N(t)= S(t) + L_{1}(t) + L_{2}(t) + I_{1}(t) + I_{2}(t) + R(t). \end{aligned}$$

By adding all equations in system (1), we will have

$$\displaystyle \begin{aligned} \displaystyle{\frac{dN(t)}{dt} = \Lambda - \delta N(t)}, \end{aligned}$$

therefore,

$$\displaystyle \begin{aligned} N(t)= \displaystyle{\frac{\Lambda}{\delta}} + C e^{-\delta t}, \end{aligned} $$
(2)

when t = 0, we will have

$$\displaystyle \begin{aligned} N(0)= \displaystyle{\frac{\Lambda}{\delta}} + C. \end{aligned}$$

Therefore

$$\displaystyle \begin{aligned} N(t)= \displaystyle{\frac{\Lambda}{\delta}} + (N(0) - \displaystyle{\frac{\Lambda}{\delta}})e^{-\delta t}, \end{aligned}$$

hence,

$$\displaystyle \begin{aligned} \displaystyle{ \lim_{t\rightarrow +\infty} N(t)= \frac{\Lambda}{\delta}}. \end{aligned}$$

Consequently, we conclude that \(\mathcal {H}\) is positively invariant which completes the proof.

3 Analysis of the Model

This section is devoted to the equilibria global stability by using some suitable Lyapunov functionals [9, 10]. Since the first five equations of the system (1) are not dependent of R and since the total population verifies Eq. (2), thus we can omit the sixth equation and the system (1) can be reduced to

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} \frac{dS}{dt} &= \; \Lambda-\frac{\alpha (1-u_1) S I_{1}}{1+m I_{1}^{2}}-\frac{\beta (1-u_2) S I_{2}}{1+ k I_{2}^{2}}- \delta S\; , \\\\ \frac{dL_{1}}{dt} &= \; \frac{\alpha (1-u_1) S I_{1}}{1+m I_{1}^{2}}-(\gamma_{1}+\delta)L_{1}\; , \\\\ \frac{dL_{2}}{dt} &= \;\frac{\beta (1-u_2) S I_{2}}{1+ k I_{2}^{2}}-(\gamma_{2}+\delta)L_{2}\; , \\\\ \frac{dI_{1}}{dt} &= \; \gamma_{1} L_{1}-(\mu_{1}+\delta)I_{1}\; , \\\\ \frac{dI_{2}}{dt} &= \; \gamma_{2} L_{2}-(\mu_{2}+\delta)I_{2}\;, \end{aligned} \right. \end{aligned} $$
(3)

with

$$\displaystyle \begin{aligned} R=N-S-L_{1}-L_{2}-I_{1}-I_{2}. \end{aligned}$$

3.1 The Basic Reproduction Number

It is well known that the basic reproduction number can be defined as the average number of new cases of an infection caused by one infected individual, in a population consisting of susceptible individuals only. We use the next generation matrix FV −1 to calculate the basic reproduction number R 0. Indeed, the formula that gives us the basic reproduction number is R 0 = ρ(FV −1), where ρ stands for the spectral radius, F is the nonnegative matrix of new infection cases, and V is the matrix of the transition infections associated with model (3).

Then,

This implies that

$$\displaystyle \begin{aligned}R_{0}=\max\{R^{1}_{0}, R^{2}_{0}\},\end{aligned}$$

with

$$\displaystyle \begin{aligned}R^{1}_{0}=\displaystyle{\frac{\alpha (1-u_1) \Lambda \gamma _{1}}{\delta (\gamma_{1}+\delta) (\mu_{1}+\delta)}}\end{aligned}$$

and

$$\displaystyle \begin{aligned}R^{2}_{0}=\displaystyle{\frac{\beta (1-u_2) \Lambda \gamma _{2}}{\delta (\gamma_{2}+\delta)(\mu_{2}+\delta)}}\;.\end{aligned}$$

Denoting

$$\displaystyle \begin{aligned} a = \gamma_{1}+\delta, \; b = \gamma_{2}+\delta, \; c = \mu_{1}+\delta, \; e= \mu_{2}+\delta, \end{aligned}$$

then,

$$\displaystyle \begin{aligned}R^{1}_{0}=\displaystyle{\frac{\alpha (1-u_1) \Lambda \gamma _{1}}{\delta ac}}\end{aligned}$$

and

$$\displaystyle \begin{aligned}R^{2}_{0}=\displaystyle{\frac{\beta (1-u_2) \Lambda \gamma _{2}}{\delta be}}\;. \end{aligned}$$

3.2 Steady States

The model (3) has four equilibrium points, one called disease-free equilibrium and the others called endemic equilibria given as follows:

  • The disease-free equilibrium \(\mathcal {E}_{f}=\left (\displaystyle {\frac {\Lambda }{\delta }},0,0,0,0\right ).\)

  • The strain 1 endemic equilibrium \(\displaystyle {\mathcal {E}_{s_{1}}=\left (S^{*}_{s_{1}},L^{*}_{1,s_{1}},L^{*}_{2,s_{1}},I^{*}_{1,s_{1}},I^{*}_{2,s_{1}}\right )},\)

    where

    $$\displaystyle \begin{aligned} &S^{*}_{s_{1}}\; =\displaystyle{\frac{ac}{\alpha (1-u_1)\gamma_{1}}(R^{1}_{0}-\frac{\alpha (1-u_1)}{\delta}I^{*}_{1,s_{1}})}\; , \; L^{*}_{1,s_{1}}=\displaystyle{\frac{c}{\gamma_{1}}I^{*}_{1,s_{1}}} \;,\\ &I^{*}_{1,s_{1}}=\displaystyle{\frac{2 \delta (R^{1}_{0}-1)}{\sqrt{\alpha (1-u_1)^{2}+4m\delta^{2}(R^{1}_{0}-1)}+\alpha (1-u_1)}} \;,\\ &I^{*}_{2,s_{1}}=0 \; ,\; L^{*}_{2,s_{1}}=0 \;. \end{aligned} $$

  • The strain 2 endemic equilibrium \(\displaystyle {\mathcal {E}_{s_{2}}=\left (S^{*}_{s_{2}},L^{*}_{1,s_{2}},L^{*}_{2,s_{2}},I^{*}_{1,s_{2}},I^{*}_{2,s_{2}}\right )},\)

    where

    $$\displaystyle \begin{aligned} &S^{*}_{s_{2}} \; =\displaystyle{\frac{be}{\beta (1-u_2) \gamma_{2}}(R^{2}_{0}-\frac{\beta (1-u_2)}{\delta}I^{*}_{2,s_{2}} )} \; ,\; L^{*}_{2,s_{2}}=\displaystyle{\frac{e}{\gamma_{2}}I^{*}_{2,s_{2}}}\; , \\ &I^{*}_{2,s_{2}}=\displaystyle{\frac{2 \delta (R^{2}_{0}-1)}{\sqrt{\beta (1-u_2)^{2}+4k\delta^{2}(R^{2}_{0}-1)}+\beta (1-u_2)}} \;, \\ &I^{*}_{1,s_{2}}= 0 \; , \; L^{*}_{1,s_{2}}=0 \;. \end{aligned} $$

  • The endemic equilibrium \(\displaystyle {\mathcal {E}_{t}=\left (S^{*}_{t},L^{*}_{1,t},L^{*}_{2,t},I^{*}_{1,t},I^{*}_{2,t}\right )},\) where

    $$\displaystyle \begin{aligned} \qquad \qquad &S^{*}_{t} \;=\displaystyle{\frac{\Lambda}{\delta}(1-\frac{\alpha (1-u_1) I^{*}_{1,t} }{\delta R^{1}_{0}}- \frac{\beta (1-u_2) I^{*}_{2,t}}{\delta R^{2}_{0}})} \;,\\ \qquad \qquad &L^{*}_{1,t}= \displaystyle{\frac{c}{\gamma_{1}}I^{*}_{1,t}} \; , \; L^{*}_{2,t} = \displaystyle{\frac{e}{\gamma_{2}}I^{*}_{2,t}} \; ,\\ \qquad \qquad &I^{*}_{1,t}=\displaystyle{ \sqrt{\frac{1}{m}(R^{1}_{0} \;S^{*}_{t} \frac{\delta}{\Lambda}-1)}} \; , \; I^{*}_{2,t}=\displaystyle{ \sqrt{\frac{1}{k}(R^{2}_{0}\; S^{*}_{t} \frac{\delta}{\Lambda}-1)}} \;. \end{aligned} $$

Remark 3.1

  1. (1)

    From the components of the equilibrium point \(\mathcal {E}_{s_{1}}\) (respectively, \(\mathcal {E}_{s_{2}}\)), we conclude that this strain 1 endemic equilibrium (respectively strain 2 endemic equilibrium) exists when \(R^{1}_{0}>1\) (respectively, \(R^{2}_{0}>1\)).

  2. (2)

    From the last equilibrium point \(\mathcal {E}_{t}\) components, we can conclude that this endemic equilibrium exists when \(R^{1}_{0}>1\) and \(R^{2}_{0}>1\).

3.3 Global Stability

Theorem 1

If \(R^{1}_0\leq 1\) and \(R^{2}_0 \leq 1\) . Then the disease-free equilibrium point \(\mathcal {E}_{f}\) is globally asymptotically stable.

Proof

First, we consider the following Lyapunov function in \(\mathbb {R}^{5}_{+}\):

$$\displaystyle \begin{aligned} \mathcal{L}_f(S,L_{1},L_{2},I_{1},I_{2})&=S^{*}\displaystyle{\bigg(\frac{S}{S^{*}}-\ln\left(\frac{S}{S^{*}}\right)-1\bigg)+ L_{1}+ L_{2}+ \frac{a}{\gamma_{1}} I_{1}+ \frac{b}{\gamma_{2}} I_{2}}. \end{aligned} $$

The time derivative is given by

$$\displaystyle \begin{aligned} &\dot{\mathcal{L}}_f(S,L_{1},L_{2},I_{1},I_{2})\\ &\quad = \dot{S}-\displaystyle{\frac{S}{S^{*}} \dot{S}+\dot{L_{1}}+\dot{L_{2}}+\frac{a}{\gamma_{1}}\dot{I_{1}}+ \frac{b}{\gamma_{2}}\dot{I_{2}}},\\ &\quad =\delta S^{*}_{0}\left(2-\displaystyle{\frac{S^{*}_{0}}{S}-\frac{S}{S^{*}_{0}}}\right)+\frac{\alpha (1-u_1) S^{*}_{0} I_{1}}{1+mI^{2}_{1}}+\frac{\beta (1-u_2) S^{*}_{0} I_{2}}{1+kI^{2}_{2}}-\frac{ac}{\gamma_{1}}I_{1}-\frac{be}{\gamma_{2}}I_{2},\\ &\quad \leq \delta S^{*}\left(2-\displaystyle{\frac{S^{*}_{0}}{S}-\frac{S}{S^{*}_{0}}}\right)+I_{1}\left(\alpha (1-u_1) S^{*}_{0}-\frac{ac}{\gamma_{1}}\right)+ I_{2}\left(\beta (1-u_2) S^{*}_{0}-\frac{be}{\gamma_{2}}\right),\\ &\quad \leq \displaystyle{\delta S^{*}\left(2-\frac{S^{*}_{0}}{S}-\frac{S}{S^{*}_{0}}\right)+\frac{ac}{\gamma_{1}} I_{1}(R^{1}_{0}-1)+ \frac{be}{\gamma_{2}}I_{2}(R^{2}_{0}-1)}, \end{aligned} $$

since the arithmetic mean is greater than or equal to the geometric mean, it follows

$$\displaystyle \begin{aligned} 2-\displaystyle{\frac{S^{*}_{0}}{S}-\frac{S}{S^{*}_{0}}} \leq 0. \end{aligned}$$

Therefore when \(R^{1}_{0}\leq 1\) and \( R^{2}_{0}\leq 1\), we will have \(\dot {\mathcal {L}}_f \leq 0,\) then the disease-free equilibrium point \(\mathcal {E}_{f}\) is globally asymptotically stable. In order to establish the global stability of the endemic steady state \(\mathcal {E}_{s_{1}}\), \(\mathcal {E}_{s_{2}}\), and \(\mathcal {E}_{s_{t}}\), we will need the following numbers:

$$\displaystyle \begin{aligned} R_{m}= \frac{\Lambda}{\delta} \sqrt{m}\end{aligned}$$
$$\displaystyle \begin{aligned} R_{k}= \frac{\Lambda}{\delta} \sqrt{k}.\end{aligned}$$

We call R m (respectively R k) the strain 1 inhibitory effect reproduction number (respectively the strain 2 inhibitory effect reproduction number).

Theorem 2

If \( R^{2}_0 \leq 1< R^{1}_0\) and R m ≤ 1. Then the strain 1 endemic equilibrium point \(\mathcal {E}_{s_{1}}\) is globally asymptotically stable.

Proof

First, we consider the Lyapunov function \(\mathcal {L}_1\) defined by

$$\displaystyle \begin{aligned} \mathcal{L}_1(S,L_{1},L_{2},I_{1},I_{2}) =& S^{*}_{s_1}\displaystyle{\left(\frac{S}{S^{*}_{s_1}}-\ln\left(\frac{S}{S^{*}_{s_1}}\right)-1\right)} +L^{*}_{1}\left(\frac{L_{1}}{L^{*}_{1,s_{1}}}-\ln\left(\frac{L_{1}}{L^{*}_{1,s_{1}}}\right)-1\right)\\ &+L_{2} +\displaystyle{\frac{a}{\gamma_{1}}I^{*}_{1,s_{1}}\left(\frac{I_{1}}{I^{*}_{1,s_{1}}}-\ln\left(\frac{I_{1}}{I^{*}_{1,s_{1}}}\right)-1\right)+\frac{b}{\gamma_{2}} I_{2}}. \end{aligned} $$

The time derivative is given by

$$\displaystyle \begin{aligned} &\dot{\mathcal{L}}_1(S,L_{1},L_{2},I_{1},I_{2})\\ &\quad = \displaystyle{\left(1-\frac{S^{*}_{s_1}}{S}\right)\left(\Lambda-\frac {\alpha (1-u_1) SI_{1}}{1+mI_{1}^{2}}-\frac{\beta (1-u_2) S I_{2}}{1+ k I_{2}^{2}}- \delta S\right)} \\ &\qquad +\displaystyle{\left(1-\frac{L^{*}_{1,s_{1}}}{L_{1}}\right)\left(\frac{\alpha (1-u_1) SI_{1}}{1+mI_{1}^{2}}-aL_{1}\right)} +\displaystyle{\frac{\beta (1-u_2) SI_{2}} {1+kI_{2}^{2}}}-bL_{2}\\ &\qquad +\displaystyle{\frac{a}{\gamma_{1}} \left(\gamma_{1}L_{1}-cI_{1}\right) \left(1-\frac{I^{*}_{1,s_{1}}}{I_{1}}\right)}+\displaystyle{\frac{b}{\gamma_{2}}}\left(\gamma_{2}L_{2}-eI_{2}\right). \end{aligned} $$

We have

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} &\Lambda= \delta S^{*}_{s_1}+\frac{\alpha (1-u_1) S^{*}_{s_1} I^{*}_{1,s_{1}}}{1+m I^{*^{2}}_{1}},\\ & \frac{\alpha (1-u_1) S^{*}_{s_1} I^{*}_{1,s_{1}}}{1+m I^{*^{2}}_{1,s_{1}}}= aL^{*}_{1,s_{1}},\\ &\dfrac{L^{*}_{1,s_{1}}}{I^{*}_{1,s_{1}}}=\dfrac{\gamma_{1}}{c}. \end{aligned} \right. \end{aligned}$$

Therefore

$$\displaystyle \begin{aligned} &\dot{\mathcal{L}}_1(S,L_{1},L_{2},I_{1},I_{2})\\ &\quad = \;\displaystyle{\delta S^{*}_{s_1}}\left(2-\displaystyle{\frac{S^{*}_{s_1}}{S}} -\displaystyle{\frac{S}{S^{*}_{s_1}}}\right)+3 aL^{*}_{1,s_{1}} +\displaystyle{ \frac{\alpha (1-u_1) S^{*}_{s_1} I_{1}}{1+m I^{2}_{1}}}+\displaystyle{\frac{\beta (1-u_2) S^{*}_{s_1} I_{2}}{1+kI^{2}_{2}}}\\ &\qquad -\displaystyle{\frac{\alpha (1-u_1) S I_{1} L^{*}_{1,s_{1}}}{L_{1}(1+m I^{2}_{1})}}-\displaystyle{\frac{\alpha (1-u_1) S^{*}_{s_1}}{1+m I^{*^{2}}_{1,s_{1}}}\frac{S^{*}_{s_1} I^{*}_{1,s_{1}}}{S}}-\displaystyle{\frac{\alpha (1-u_1) S^{*}_{s_1} I_{1}}{1+m I^{*^{2}}_{1,s_{1}}}}\\ &\qquad -\displaystyle{ \frac{aL_{1}I_{1}}{I_{1}}}-\displaystyle{ \frac{be}{\gamma_{2}}I_{2}}. \end{aligned} $$

Then,

$$\displaystyle \begin{aligned} &\dot{\mathcal{L}}_1(S,L_{1},L_{2},I_{1},I_{2})\\ &\quad = \; aL^{*}_{1,s_{1}}\left(4-\dfrac{S^{*}_{s_1}}{S}-\dfrac{I^{*}_{1,s_{1}}}{I_1} \dfrac{L_1}{L^{*}_{1,s_{1}}} - \dfrac{S}{S^{*}_{s_1}} \dfrac{L^{*}_{1,s_{1}}}{L_1}\dfrac{I_1}{I^{*}_{1,s_{1}}} \dfrac{1+m I^{*^{2}}_{1}}{1+m I^{2}_{1}} - \dfrac{1+m I^{2}_{1}}{1+m I^{*^{2}}_{1}}\right)\\ &\qquad + \delta S^{*}_{s_1}\left(2-\displaystyle{\dfrac{S^{*}_{s_1}}{S}} -\dfrac{S}{S^{*}_{s_1}}\right)+ \beta (1-u_2) I_2 \left( \dfrac{ S^{*}_{s_1}}{1+kI^2_2}- \frac{be}{\beta (1-u_2) \gamma_{2}}\right) \\ &\qquad + \frac{\alpha (1-u_1) S^{*}_{s_1} I^{*}_{1,s_{1}}}{1+m I^{*^{2}}_{1,s_{1}}}\left( \dfrac{1+m I^{2}_{1}}{1+m I^{*^{2}}_{1}}+ \dfrac{1+m I^{*^{2}}_{1}}{1+m I^{2}_{1}}\frac{I_1}{I^{*}_{1,s_{1}}}-\dfrac{I_1}{I^{*}_{1,s_{1}}}-1 \right). \end{aligned} $$

Therefore,

$$\displaystyle \begin{aligned} &\dot{\mathcal{L}}_1(S,L_{1},L_{2},I_{1},I_{2})\\ &\quad = \; aL^{*}_{1,s_{1}}\left(4-\dfrac{S^{*}_{s_1}}{S}-\dfrac{I^{*}_{1,s_{1}}}{I_1} \dfrac{L_1}{L^{*}_{1,s_{1}}} - \dfrac{S}{S^{*}_{s_1}} \dfrac{L^{*}_{1,s_{1}}}{L_1}\dfrac{I_1}{I^{*}_{1,s_{1}}} \dfrac{1+m I^{*^{2}}_{1,s_{1}}}{1+m I^{2}_{1}} - \dfrac{1+m I^{2}_{1}}{1+m I^{*^{2}}_{1,s_{1}}}\right)\\ &\qquad + \delta S^{*}_{s_1}\left(2-\displaystyle{\dfrac{S^{*}_{s_1}}{S}} -\dfrac{S}{S^{*}_{s_1}}\right)+\beta (1-u_2) I_2 \left(\dfrac{ S^{*}_{s_1}}{1+kI^2_2}- \frac{be}{\beta (1-u_2) \gamma_{2}}\right) \\ &\qquad - \frac{amc}{\gamma_{1}}\left(1-m I_{1}I^{*}_{1,s_{1}}\right) \dfrac{(I+I^{*}_{1,s_{1}})(I-I^{*}_{1,s_{1}})^{2}}{(1+m I^{*^{2}}_{1,s_{1}})(1+m I^{2}_{1})}. \end{aligned} $$

By the relation between arithmetic and geometric means we have

$$\displaystyle \begin{aligned}2-\displaystyle{\frac{S^{*}_{s_1}}{S}}-\displaystyle{\frac{S}{S^{*}_{s_1}}} \leq 0\end{aligned}$$

and

$$\displaystyle \begin{aligned} 4-\dfrac{S^{*}_{s_1}}{S}-\dfrac{I^{*}_{1,s_{1}}}{I_1} \dfrac{L_1}{L^{*}_{1,s_{1}}} - \dfrac{S}{S^{*}_{s_1}} \dfrac{L^{*}_{1,s_{1}}}{L_1}\dfrac{I_1}{I^{*}_{1,s_{1}}} \dfrac{1+m I^{*^{2}}_{1,s_{1}}}{1+m I^{2}_{1}} - \dfrac{1+m I^{2}_{1}}{1+m I^{*^{2}}_{1,s_{1}}}\leq 0.\end{aligned}$$

If \(R^{2}_0\leq 1\). Then

$$\displaystyle \begin{aligned} \dfrac{ S^{*}_{s_1}}{1+kI^2_2} \leq \frac{be}{\beta (1-u_2) \gamma_{2}}. \end{aligned}$$

Since R m ≤ 1, we have that \(m (\frac {\Lambda }{\delta })^{2} \leq 1\)

which implies, \(1-m I_{1}I^{*}_{1,s_{1}}\geq 0\)

Consequently,

$$\displaystyle \begin{aligned} \dot{\mathcal{L}}_1\leq 0.\end{aligned}$$

We conclude that the point \(\mathcal {E}_{s_{1}}\) is globally asymptotically stable when \(R^{2}_0\leq 1\), \(1<R^{1}_0 \), and R m ≤ 1.

Theorem 3

If \( R^{1}_0 \leq 1< R^{2}_0\) and R k ≤ 1. Then the strain 2 endemic equilibrium point \(\mathcal {E}_{s_{2}}\) is globally asymptotically stable.

Proof

Let us consider the following Lyapunov function:

$$\displaystyle \begin{aligned} &\mathcal{L}_2(S,L_{1},L_{2},I_{1},I_{2})\\ &\quad =\displaystyle{S^{*}_{s_2}\left(\frac{S}{S^{*}_{s_2}}-\ln\left(\frac{S}{S^{*}_{s_2}}\right)-1\right)}+L_{1}+L^{*}_{2}\left(\frac{L_{2}}{L^{*}_{2}}-\ln\left(\frac{L_{2}}{L^{*}_{2}}\right)-1\right)\\ &\qquad +\displaystyle{\frac{a}{\gamma_{1}}I_{1}+\frac{b}{\gamma_{2}}I^{*}_{2,2}\left(\frac{I_{2}}{I^{*}_{2,2}}-\ln\left(\frac{I_{2}}{I^{*}_{2,s_{2}}}\right)-1\right)}. \end{aligned} $$

It easy to verify that

$$\displaystyle \begin{aligned} &\dot{\mathcal{L}_2}(S,L_{1},L_{2},I_{1},I_{2})\\ &\quad = \displaystyle{\left(1-\frac{S^{*}_{s_2}}{S}\right)}\left(\Lambda-\frac{\alpha (1-u_1) S I_{1}}{1+mI_{1}^{2}} -\frac{\beta (1-u_2) S I_{2}}{1+ k I_{2}^{2}}-\delta S\right)\\ &\qquad +\left(1-\displaystyle{\frac{L^{*}_{2}}{L_{2}}}\right)\left(\frac{\beta (1-u_2) S I_{2}}{1+k I_{2}^{2}}-bL_{2}\right)+\left(\frac{\alpha (1-u_1) S I_{1}}{1+ m I_{1}^{2}} -aL_{1} \right)\\ &\qquad +\frac{b}{\gamma_{2}}\left(\gamma_{2} L_{2}-e I_{2}\right) \left(1-\frac{I^{*}_{2,s_{2}}} {I_{2}} \right)+\frac{a}{\gamma_{a}}(\gamma_{1}L_{1}-cI_{1}). \end{aligned} $$

It is easy to see that

$$\displaystyle \begin{aligned} \left\{ \begin{aligned} &\Lambda= \delta S^{*}_{s_2}+\frac{\beta (1-u_2) S^{*}_{s_2} I^{*}_{2,s_{2}}}{1+k I^{*^{2}}_{2,s_{2}}}\\ &\frac{\beta (1-u_2) S^{*}_{s_2} I^{*}_{2,s_{2}}}{1+k I^{*^{2}}_{2,s_{2}}}= bL^{*}_{2,s_2},\\ &\dfrac{L^{*}_{2,s_{2}}}{I^{*}_{2,s_{2}}}=\dfrac{\gamma_{2}}{e}. \end{aligned} \right. \end{aligned}$$

We have

$$\displaystyle \begin{aligned} &\dot{\mathcal{L}}_2(S,L_{1},L_{2},I_{1},I_{2})\\ &\quad = \displaystyle{\delta S^{*}_{s_2}} (2-\displaystyle{\frac{S^{*}_{s_2}}{S}} -\displaystyle{\frac{S}{S^{*}_{s_2}}})+3 bL^{*}_{2,s_2} + \displaystyle{ \frac{\beta (1-u_2) S^{*}_{s_2} I_{2}}{1+k I^{2}_{2}}}\\ &\qquad +\displaystyle{\frac{\alpha (1-u_1) S^{*}_{s_2} I_{2}}{1+mI^{2}_{1}}}-\displaystyle{\frac{\beta (1-u_2) S I_{2} L^{*}_{2}}{L_{2}(1+k I^{2}_{2})}}-\displaystyle{\frac{\beta (1-u_2) S^{*}_{s_2}}{1+k I^{*^{2}}_{2}}.\frac{S^{*}_{s_2} I^{*}_{2,s_{2}}}{S}}\\ &\qquad -\displaystyle{\frac{\beta (1-u_2) S^{*}_{s_2} I_{2}}{1+k I^{*^{2}}_{2}}}-\displaystyle{ \frac{bL_{2}I_{2}}{I_{2}}}-\displaystyle{ \frac{ac}{\gamma_{1}}I_{1}}. \end{aligned} $$

Then,

$$\displaystyle \begin{aligned} \dot{\mathcal{L}}_2(S,L_{1},L_{2},I_{1},I_{2}) = & \; \delta S^{*}_{s_2}\left(2-\displaystyle{\frac{S^{*}_{s_2}}{S}} -\displaystyle{\frac{S}{S^{*}_{s_2}}}\right)+\dfrac{\alpha (1-u_1) S^{*}_{s_2} I_1}{1+mI^2_1}-\frac{ac}{\gamma_{1}}I_{1}\\ &+bL^{*}_{2,s_{2}}\left(3-\dfrac{S^{*}_{s_2}}{S}-\dfrac{I^{*}_{2,s_{2}}}{I_2}\dfrac{L_2}{L^{*}_{2,s_{2}}}-\dfrac{S}{S^{*}_{s_2}}\dfrac{L^{*}_{2,s_{2}}}{L_2}\dfrac{I_2}{I^{*}_{2,s_{2}}}\right)\\ &+\dfrac{\beta (1-u_2) S^{*}_{s_2} I^{*}_{2,s_{2}}}{1+k I^{*^{2}}_{2,s_{2}}}\dfrac{S}{S^{*}_{s_2}}\dfrac{L^{*}_{2,s_{2}}}{L_2}\dfrac{I_2}{I^{*}_{2,s_{2}}}+\dfrac{\beta (1-u_2) S^{*}_{s_2} I_2}{1+k I^{2}_{2}} \\ &-\dfrac{\beta (1-u_2) S I_2}{1+k I^{2}_{2}}\dfrac{L^{*}_{2,s_{2}}}{L_2}-\dfrac{be}{\gamma_2}I_2. \end{aligned} $$

Therefore

$$\displaystyle \begin{aligned} &\dot{\mathcal{L}}_2(S,L_{1},L_{2},I_{1},I_{2})\\ &\quad \leq \displaystyle{\delta S^{*}_{s_2}}\left(2-\displaystyle{\frac{S^{*}_{s_2}}{S}} -\displaystyle{\frac{S}{S^{*}_{s_2}}}\right)+\left(\dfrac{\alpha (1-u_1) S^{*}_{s_2} }{1+mI^2_1}- \frac{ac}{\gamma_{1}}\right) I_{1}\\ &\qquad +\dfrac{be}{\gamma_2}I_2\left(\dfrac{S}{S^{*}_{s_2}}\dfrac{L^{*}_{2,s_{2}}}{L_2}-1\right)+ \dfrac{\beta (1-u_2) S^{*}_{s_2} I_2}{1+k I^{2}_{2}} \left(1-\dfrac{S}{S^{*}_{s_2}}\dfrac{L^{*}_{2,s_{2}}}{L_2}\right)\\ &\qquad +bL^{*}_{2,s_{2}}\left(3-\dfrac{S^{*}_{s_2}}{S}-\dfrac{I^{*}_{2,s_{2}}}{I_2}\dfrac{L_2}{L^{*}_{2,s_{2}}}-\dfrac{S}{S^{*}_{s_2}}\dfrac{L^{*}_{2,s_{2}}}{L_2}\dfrac{I_2}{I^{*}_{2,s_{2}}}\right). \end{aligned} $$

The hypothesis (H 2) implies that

$$\displaystyle \begin{aligned} \dfrac{be}{\gamma_2}I_2\left(\dfrac{S}{S^{*}_{s_2}}\dfrac{L^{*}_{2,s_{2}}}{L_2}-1\right)+ \dfrac{\beta (1-u_2) S^{*}_{s_2} I_2}{1+k I^{2}_{2}} \left(1-\dfrac{S}{S^{*}_{s_2}}\dfrac{L^{*}_{2,s_{2}}}{L_2}\right)\leq 0. \end{aligned}$$

Then,

$$\displaystyle \begin{aligned} \dot{\mathcal{L}}_2(S,L_{1},L_{2},I_{1},I_{2}) \; \leq & \; \displaystyle{\delta S^{*}_{s_2}}\left(2-\displaystyle{\frac{S^{*}_{s_2}}{S}} -\displaystyle{\frac{S}{S^{*}_{s_2}}}\right)+\left(\dfrac{\alpha (1-u_1) S^{*}_{s_2} }{1+mI^2_1}- \frac{ac}{\gamma_{1}}\right) I_{1}\\ &+bL^{*}_{2,s_{2}}\left(3-\dfrac{S^{*}_{s_2}}{S}-\dfrac{I^{*}_{2,s_{2}}}{I_2}\dfrac{L_2}{L^{*}_{2,s_{2}}}-\dfrac{S}{S^{*}_{s_2}}\dfrac{L^{*}_{2,s_{2}}}{L_2}\dfrac{I_2}{I^{*}_{2,s_{2}}}\right), \end{aligned} $$

hence,

$$\displaystyle \begin{aligned} \dot{\mathcal{L}}_2(S,L_{1},L_{2},I_{1},I_{2}) \; \leq & \; \displaystyle{\delta S^{*}_{s_2}}\left(2-\displaystyle{\frac{S^{*}_{s_2}}{S}} -\displaystyle{\frac{S}{S^{*}_{s_2}}}\right)+\left(\alpha (1-u_1) S^{*}_{s_2} - \frac{ac}{\gamma_{1}}\right) I_{1}\\ &+bL^{*}_{2,s_{2}}\left(3-\dfrac{S^{*}_{s_2}}{S}-\dfrac{I^{*}_{2,s_{2}}}{I_2}\dfrac{L_2}{L^{*}_{2,s_{2}}}-\dfrac{S}{S^{*}_{s_2}}\dfrac{L^{*}_{2,s_{2}}}{L_2}\dfrac{I_2}{I^{*}_{2,s_{2}}}\right). \end{aligned} $$

If \(R^{1}_0\leq 1\). Then

$$\displaystyle \begin{aligned} \alpha (1-u_1) S^{*}_{s_2} \leq \frac{ac}{\gamma_{1}}. \end{aligned}$$

By the relation between arithmetic and geometric means we have

$$\displaystyle \begin{aligned}2-\displaystyle{\frac{S^{*}_{s_2}}{S}} -\displaystyle{\frac{S}{S^{*}_{s_2}}} \leq 0\end{aligned}$$

and

$$\displaystyle \begin{aligned} 3-\dfrac{S^{*}_{s_2}}{S}-\dfrac{I^{*}_{2,s_{2}}}{I_2}\dfrac{L_2}{L^{*}_{2,s_{2}}}-\dfrac{S}{S^{*}_{s_2}}\dfrac{L^{*}_{2,s_{2}}}{L_2}\dfrac{I_2}{I^{*}_{2,s_{2}}}\leq 0. \end{aligned}$$

Then

$$\displaystyle \begin{aligned} \dot{\mathcal{L}}_2\leq 0.\end{aligned}$$

We conclude that the point \(\mathcal {E}_{s_{2}}\) is globally asymptotically stable when \( R^{1}_0\leq 1<R^{2}_0 \).

Theorem 4

If \(R^{1}_0 > 1, \ R^{2}_0 > 1\) , R m ≤ 1, and R k ≤ 1. Then the endemic equilibrium point \(\mathcal {E}_{s_{t}}\) is globally asymptotically stable.

Proof

For the proof of this last result it will be enough to consider the following Lyapunov function \(\mathcal {L}_3\):

$$\displaystyle \begin{aligned} &\mathcal{L}_3(S,L_{1},L_{2},I_{1},I_{2})\\ &\quad =\displaystyle{S^{*}_{t}\left(\frac{S}{S^{*}_{t}}-\ln\left(\frac{S}{S^{*}_{t}}\right)-1\right)}+L^{*}_{1,t}\left(\frac{L_{1}}{L^{*}_{1,t}}-\ln\left(\frac{L_{1}}{L^{*}_{1,t}}\right)-1\right) \\ &\qquad +L^{*}_{2,t}\left(\frac{L_{2}}{L^{*}_{2,t}}-\ln\left(\frac{L_{2}}{L^{*}_{2,t}}\right)-1\right)+ \frac{a}{\gamma_{a}}I^{*}_{1,t}\left(\frac{I_{1}}{I^{*}_{1,t}}-\ln\left(\frac{I_{1}}{I^{*}_{1,t}}\right)-1\right)\\ &\qquad +\frac{b}{\gamma_{2}}I^{*}_{2,t}\left(\frac{I_{2}}{I^{*}_{2,t}}-\ln\left(\frac{I_{2}}{I^{*}_{2,t}}\right)-1\right). \end{aligned} $$

4 Numerical Simulations

In this section, we will perform some numerical simulations in order to check the impact of quarantine measures in reducing the spread of COVID-19. Indeed, Fig. 2 shows the evolution of infection for λ = 1, α = 0.9, β = 1.45, γ 1 = 0.5, γ 2 = 0.3, μ 1 = 0.15, μ 2 = 0.15, δ = 0.2, m = 1.75, k = 2.85 and different values of u 1 and u 2.

Fig. 2
figure 2

The effect of quarantine strategy on the SLIR model dynamics

Full size image

In the case when no quarantine strategy is undertaken, i.e. u 1 = u 2 = 0, we observe that the disease persists and the infected cases stay at very high level. When the effectiveness of the quarantine measures is increased, u 1 = u 2 = 0.25 or u 1 = u 2 = 0.75, a significant reduce of the infection cases is observed; we can also observe a considerable reduce of the latent individuals. Finally, when the quarantine measures are fully established, i.e. u 1 = u 2 = 1, an interesting result is observed. In this last case, the disease dies out, which is represented by the vanishing of all strains infected individuals and also the latent ones. The susceptible individuals will reach in this situation their maximal level. We conclude that the quarantine measures reduce significantly the spread of COVID-19.

5 Conclusion

Modeling epidemiological phenomena makes it possible to better understand several mechanisms that influence the spread of many diseases. In this work, we have studied the effectiveness of quarantine against the spread of COVID-19. Indeed, we have established the problem via six-compartment SLIR model, in which the dynamics of the COVID-19 epidemic is modeled by a system of six nonlinear differential equations, describing the interactions between susceptible, exposed, infected, and healed. First, we have calculated the basic reproduction number depending on the quarantine efficacy. Next, we have given the disease-free equilibrium and three other endemic equilibria, and then we have discussed, according to the value of the basic reproduction number, the global stability of each equilibrium. Numerical simulations are presented in order to discuss the effectiveness of quarantine measures in reducing the spread of COVID-19 pandemic.