Keywords

1 Introduction

The adoption of EVs has been growing rapidly over the past decade, mainly as a result of ambitious government policies to reduce environmental pollution and advances in the EV industry. In 2019, worldwide EV sales reached 2.1 million, bringing the global EV fleet to 7.2 million, an increase of 40% compared to 2018 [6]. However, the future large-scale adoption of EV raises concerns about charging service quality since charging an EV is time-consuming and requires a considerable amount of electrical power. Nowadays, EV drivers tend to choose the nearest available CPs to plug in their EVs and start charging immediately. This can easily overload charging infrastructures in a large-scale scenario resulting in poor service quality and EV drivers’ dissatisfaction.

Recently, there has been growing interest in the development of EV charging scheduling strategies that focus on economical objectives such as minimizing the electricity costs or on power grid reliability by minimizing the power losses [3] and voltage deviations [7]. However, many studies assume that there is a sufficient number of CPs thus focus on the power allocation and neglect the assignment of EV to a suitable CP. Besides, they assume an identical output power of CPs. Yet, in real life, CPs with different charging output power are installed in the same charging station to meet the various type of charging demands and improve the quality of service [12].

In this work, we consider a charging station that regroups several CPs with different charging power levels. Moreover, this charging station has a maximum power capacity that the distribution-level transformer poses. Each EV driver can submit a charging reservation before arriving to avoid queuing. We developed a heuristic based on interval scheduling [9] and a Simulated Annealing (SA) to assign each EV to a suitable CP and allocate the electrical power over the plugin time. The objective of the scheduling is to ensure a final state-of-charge at the departure that is as close as possible to the requested state-of-charge.

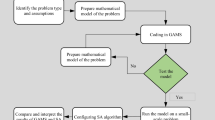
The remainder of this paper is organized as follows. In Sect. 2, we present a brief review of the main works on electric vehicle charging scheduling problems. In Sect. 3, we describe in detail the investigated problem and formulate it as a mixed-integer linear programming (MILP). We then propose our optimization methods in Sect. 4 and evaluate their performance in Sect. 5. Finally, we conclude the paper in Sect. 6.

2 Related Work

Several studies have been conducted on the EV charging scheduling problem (EVCSP). Here, we discuss some of the relevant literature that addresses the EVCSP in charging stations and parking lots. From the perspective of these charging service providers, the main objectives are to reduce costs [21,22,23, 25], improve service quality charging by maximizing the energy delivered [14, 16, 23], or maximizing charging incomes [14] while maintaining the physical constraints of the charging infrastructure. One largely used constraint is the charging infrastructure capacity that defines the overall power limit to avoid potential transformer overload and feeder congestion [14, 16, 21, 25]. For the charging power of CPs, some papers consider variable power in which the charging rate varies over time [14, 16, 25] others consider fixed constant power [4].

EV charging demands are usually defined by arrival and departure times and the requested charging energy. [4, 22, 23] consider uncertainly in the arrival time. [21] consider that EVs may arrive with or without an appointment. Departure times can be provided by the EVs drivers [4, 21, 24, 25] or it can be estimated based on historical behavior [23]. In [16], an EV is allowed to leave before its initially provided departure time. Regarding the requested charging energy, [23] assumes that the EVs drivers will provide their desired state-of-charge when they plug-in their EVs. [20, 21] assume that the EV owners will directly request the energy demand expressed in kWh. Other papers consider charging EVs to the rated battery capacity [14, 16, 24, 25]. The requested charging energy can either be a hard constraint where the desired energy must be reached [4, 20, 21] or a soft constraint where the scheduler tries to achieve satisfactory energy by the departure time [25].

Different optimization methods were used for tackling these problems. [24] developed a charging scheme based on binary programming for demand respond application and a convex relaxation method is proposed to solve the charging scheduling problem in real-time. Authors in [25] propose a two-stage approximate dynamic programming strategy for charging a large number of EVs. [20] provide a model predictive control based algorithm. We can also find different metaheuristics, for example, particle swarm optimization [16, 21], a GRASP-like algorithm [4], memetic algorithm [4].

Although the above-mentioned studies have examined various aspects of the EV charging scheduling, they have essentially assumed there are a sufficient number of chargers for all EVs and thus the scheduler doesn’t decide to which CP each EV is assigned. In this paper, hybrid heuristics and meta-heuristic are proposed to jointly assign the EVs to CP and schedule the EV charging. We consider different charging levels.

3 Problem Description and Formulation

We consider a charging station with m charging points (CPs). The switching on and off of each CP can be controlled. An electric vehicle (EV) can be connected to the CP but does not necessarily have to charge immediately. Each charging point i, \(i = {1,.., m}\) has a constant output power \(p_i\) (kW). We also consider the variable power model where the output power of each CP i can vary over time from 0 to \(p_i\). The charging station has a maximum power supply of \(P^{max}\) (kW) which is insufficient to sustain simultaneous activation of all CPs. Thus, the sum of the output power of the CPs cannot exceed \(P^{max}\) (kW) at any time. The scheduling time horizon of one day and is divided into H time slots of length \(\tau \) (minutes). A set of n EVs that need charging in the whole day. Each EV j, \(j={1,.., n}\), submits a charging demand by providing the following information: the desired arrival time to the station \(r_j\), the estimated initial state-of-charge at the arrival (\(e^0_j\)), the desired state-of-charge at the departure (\(e^{d}_j\)), the battery capacity \(B_j\) (kWh), and the departure time \(d_j\). The scheduler collects all charging demands and determines a day ahead optimized charging schedule by assigning EV to each CP. Since there are a limited number of CP, the actual starting time for each EV can exceed the desired arrival time. An EV will occupy a CP from the assigned stating time until its departure time and cannot be plugged out during this period. The preemption of charging operation is allowed. Ideally, each EV should be charged to its desired state-of-charge by the departure time, however, this may not be possible due to the limited number of CP and the charging station capacity limit. So, the objective of the scheduler is to minimize the difference between the desired state-of-charge and the final state-of-charge at the departure time.

In the following, a MILP model is proposed to jointly optimize the assigned of the EV to CP and the power allocation at each time slot.

In the case of a constant power model, the decision variables are:

$$ x^t_{ij}= \left\{ \begin{array}{ll} 1 &{} \text{ if } \text{ EV } \text{ j } \text{ is } \text{ charging } \text{ by } \text{ the } \text{ CP } \text{ i } \text{ at } \text{ time } \text{ slot } \text{ t } \\ 0 &{} \text{ otherwise. } \end{array} \right. $$
$$ e^f_j: \text{ final } \text{ state-of-charge } \text{ of } \text{ EV } \text{ j } \text{ at } \text{ it } \text{ departure } \text{ time } $$

  • Objective: minimize the difference between the state-of-charge at the departure (\(e^f_j\)) and the desired state-of-charge \(e^d_j\).

    $$ \min \qquad \sum _{j=1}^{n} (e^{d}_j - e^f_j) $$

  • Constraints:

    $$\begin{aligned} \sum _{i=1}^{m} x^t_{ij} \le 1 \qquad \forall j,t \end{aligned}$$
    (1)

    Constraints (1) ensure that each EV j is assigned to one CP at each time slot t.

    $$\begin{aligned} \sum _{j=1}^{n} x^t_{ij} \le 1 \qquad \forall i,t \end{aligned}$$
    (2)

    Constraints (2) ensure that each CP i charges one EV at each time slot t.

    $$\begin{aligned} x^{t'}_{i'j} \le 1 - x^t_{ij} \qquad \forall i,j,t, i' \ne i \quad and \quad t' < t \end{aligned}$$
    (3)

    Constraints (3) ensure that each EV j is charged by one CP i i.e., The EV assigned to a CP cannot be moved to another CP.

    $$\begin{aligned} e^0_j \le e^f_j \le e^{d}_j \qquad \forall j \end{aligned}$$
    (4)
    $$\begin{aligned} e^f_j = e^0_j + \frac{\tau \sum _{t=r_j}^{d_j} p_i \times x^t_{ij} }{B_j}\qquad \forall j \end{aligned}$$
    (5)

    Constraints (4) and (5) calculate the final state-of-charge of each EV j.

    $$\begin{aligned} x^t_{ij} = 0 \qquad \forall i,j \quad \forall t, t< r_j \quad and \quad t \ge d_j \end{aligned}$$
    (6)

    Constraints (6) ensure each EV j can only be charged between its desired arrival time \(r_j\) and departure time \(d_j\).

    $$\begin{aligned} x^t_{ij} + x^{t'}_{ij'} \le 1 \qquad \forall i,j,t, j' : j' \ne j, t' \in [t,d_j] \end{aligned}$$
    (7)

    Constraints (7) ensure that the CP i is reserved to the EV j from the time it begins to charge to its departure time \(d_j\).

    $$\begin{aligned} \sum _{i=1}^{m} \sum _{j=1}^{n} p_i \times x^t_{ij} \le P^{max} \qquad \forall t \end{aligned}$$
    (8)

    Constraints (8) ensure that the total output power doesn’t exceed the charging station limit at each time slot.

When considering variable power model, we add the decision variables \(p^t_{ij}\) that represent the power delivered by the CP i to EV j at time t. The constraints (5) and (8) will be replaced by the following constraints:

$$\begin{aligned} e^f_j = e^0_j + \frac{\tau \sum _{t=r_j}^{d_j} p^t_{ij} }{B_j}\qquad \forall j \end{aligned}$$
(9)
$$\begin{aligned} \sum _{i=1}^{m} \sum _{j=1}^{n} p^t_{ij} \le P^{max} \qquad \forall t \end{aligned}$$
(10)

We also add the following constraints to ensure that the delivered power to an EV j by CP i doesn’t exceed its maximum output power \(p_i\) :

$$\begin{aligned} p_i \times x^t_{ij} \ge p^t_{ij} \qquad \forall i,j,t \end{aligned}$$
(11)

4 Proposed Methods

Solving the optimal charging scheduling problem with an exact method cannot be done in polynomial time [18]. Thus, heuristics and the Simulated Annealing (SA) metaheuristic combined with an exact method were developed.

4.1 Solution Representation

Solving the scheduling problem consists of determining the assignment of each Ev to CP and then, in case of a constant charging model, choose the appropriate time slots of charging. In the case of a variable power model, choose the appropriate charging rate at each time slot. Therefore, a feasible solution consists of the assignment of EVs to the CPs and the power allocation. The assignment of EVs to CPs is represented as a vector \((\pi _1,.., \pi _n)\) where \(\pi _i\) is the sequence of EVs assigned to CP i. Once we have the EV-CP assignment, we solve the power allocation by determining the amount of power delivered by each CP to each EV at each time slot. To this end, we define the solution variables \(a^t_{ij}\) of the EV-CP assignment, which is equal to 1 if the EV j is plugged to the CP i at time t. The \(a^t_{ij}\) values will be used as inputs for solving the power allocation problem. To get \(a^t_{ij}\) from \((\pi _1,.., \pi _n )\), we simply schedule all EVs sequentially without idles times while respecting their arrival times. For each EV j in the sequence \(\pi _i\), we select the earliest possible starting time \(st_j = \max (r_j, d_{j'}) \) where \(j'\) is the EV scheduled before the EV j in \(\pi _i\). In this case, the variable \(a^t_{ij}\) will be equal to 1 for all \(t \in [st_j, d_j] \). If \(st_j > d_j\), the charging demand of EV j will be rejected but penalized in the objective function.

The proposed heuristics and neighborhood search in the SA deals with the EV-CP assignment problem. Then, for each solution, the power allocation problem is formulated as a linear programming model.

4.2 Heuristics for Solving the Assignment of EVs to CPs

In the following, we define greedy rules for the assignment of EVs to CPs.

First Come Fist Served (FCFS) Heuristic. First-come-fist-served (FCFS) rule is a popular approach to schedule the EVs charging. It assigns the EV with the smallest arrival time to the first available CP.

Interval Graph Coloring Based Heuristic (IGCH). Consider the interval graph \(G =(V,E)\) where each vertex \(v \in V\) represents a charging demand of an EV j, \(j\in n\) defined by its arrival time \(r_j\) and its departure time \(d_j\). There is an edge \(e \in E\) between two vertices if and only if their associated intervals have a nonempty intersection i.e. \((j,j') \in E\) if \([r_j,d_j] \cap [r_{j'},d_{j'}] \ne \emptyset \). Assigning a set of EVs to a given CP is equivalent to the k-coloring problem of the graph G. The k-coloring problem is to assign a color \(c \in \{1,..,k\}\) to each vertex of G so that no adjacent vertices have the same color. The set of vertices colored with the same color corresponds to the set of EVs assigned to the same CP and it is called a color class. Since an interval graph is a chordal graph, the greedy coloring algorithm delivers an optimal coloring on a chordal graph following the perfect elimination orderings [5]. A perfect elimination ordering in a graph is an ordering of the vertices of the graph such that, for each vertex v and the neighbors of v that occur after v in the order form a clique. We use the lexicographic breadth-first (LexBFS) search proposed by [17] to find the perfect elimination ordering in linear time. We add randomness to the algorithm to generate difference perfect elimination orders by adding a random weight w to each vertex. Therefore, when two vertices have the same label, we choose the vertex with maximum weight w. Algorithm 1 shows the pseudocode of LexBFS ordering.

In the case where we have the chromatic number k, i.e. the number of color classes is less than or equal to the number of CP, we assign the EVs with the same color class to the same CP. We start with the color classes that have the greater cardinally (the highest number of vertices with the same color) and assign them to the CP with the greater charging output power. Otherwise, when \(k > m\), each remaining non assigned EV j will be assigned to the CP that has the largest available time from \(r_j\) to \(d_j\). The overall procedure of the IGCH algorithm is depicted in Algorithm 2.

figure a
figure b

4.3 Exact Methods for Solving the Power Allocation Problem

After determining the assignment of the EVs to CPs, the objective here is to decide the amount of electric power delivered by each CP at each time slot. We formulate both constant and variable power models as an integer linear programming (ILP) model.

A Linear Programming for Constant Power Model: We define the binary decision variables \(y^t_{ij}\).

$$ y^t_{ij}= \left\{ \begin{array}{ll} 1 &{} \text{ if } \text{ EV } \text{ j } \text{ is } \text{ charging } \text{ by } \text{ the } \text{ CP } \text{ i } \text{ at } \text{ time } \text{ t } \\ 0 &{} \text{ otherwise. } \end{array} \right. $$

Let \(H_j = \{t | t \in H, a^t_{ij} = 1\}\). We set \( y^t_{ij} = 0 \qquad \forall t \notin {H_j} \)

  • Objective :

    $$ \min \qquad \sum _{j=1}^{m} (e^{d}_j - e^f_j) $$

  • Constraints:

    $$\begin{aligned} e^0_j \le e^f_j \le e^{d}_j \qquad \forall j \end{aligned}$$
    (12)
    $$\begin{aligned} e^f_j = e^0_j + \frac{\sum _{t=r_j}^{d_j} y^t_{ij} \times \tau \times p_i }{B_j}\qquad \forall j \end{aligned}$$
    (13)

    Constraints (12) and (13) calculate the final state-of-charge of each EV j.

    $$\begin{aligned} \sum _{i=1}^{n} \sum _{j=1}^{m} y^t_{ij} \times p_i \le P^{max} \qquad \forall t \end{aligned}$$
    (14)

    Constraints (14) ensure that the total output power doesn’t exceed the charging station limit at each time slot.

A Linear Programming for the Variable Power Model: We define the continuous decision variables \(p^t_{ij}\) which represents the power delivered by the CP i to EV j at time t.

$$ \min \qquad \sum _{j=1}^{m} (e^d_j - e^f_j) $$

Constraints :

$$\begin{aligned} e^0_j \le e^f_j \le e^{d}_j \qquad \forall j \end{aligned}$$
(15)
$$\begin{aligned} e^f_j = e^0_j + \frac{\sum _{t=r_j}^{d_j} p^t_{ij} \times \tau }{B_j}\qquad \forall j \end{aligned}$$
(16)

Constraints (15) and (16) calculate the final state-of-charge of each EV j.

$$\begin{aligned} a^t_{ij} \times p_i \ge p^t_{ij} \qquad \forall i,j,t \in H_j \end{aligned}$$
(17)

Constraints (17) ensure that the delivered power by each CP i doesn’t exceed its maximum rated power \(p_i\) at each time t.

$$\begin{aligned} \sum _{i=1}^{n} \sum _{j=1}^{m} p^t_{ij} \le P^{max} \qquad \forall t \end{aligned}$$
(18)

Constraints (18) ensure that the total output power doesn’t exceed the charging station limit.

4.4 Simulated Annealing

Simulated annealing algorithm, initially proposed by [8], has been successfully adapted to address several optimal resource scheduling problems. The pseudo-code of the SA algorithm is shown in Algorithm 3.

A candidate solution for SA represents the EV-CP assignment part described in Sect. (4.1). We obtain its objective value by solving the LP problem representing the power allocation as described in Sect. (4.3). In preliminary experiments, the population-based meta-heuristics turned out to be worse than SA and time-consuming due to solving an LP for each newly generated solution in the population. Thus, we pursue with SA only.

First, an initial solution \(S_0\) is generated using the FCFS rule. Starting from the initial solution \(S_0\), SA generates a neighborhood solution \(S'\). The difference in the objective value between the new solution \(S'\) and the current solution S is calculated as \(\varDelta f = f(S') -f(S) \). The neighborhood solution \(S'\) replaces the current solution based on the Metropolis criteria; It will replace the current solution if there is an improvement i.e. \(\varDelta f <0\). If it also improves the best solution found so far, it will become the new global best solution \(S_{best}\). Otherwise, a random number r is generated following the uniform distribution U[0, 1] and the neighborhood solution \(S'\) will become the current solution if \( r \le e^{-\varDelta f/T}\) where T is a parameter called temperature, which regulates the probability of accepting worsening solutions. The temperature is initially set to a value \(T_0\) proportional to the objective function value of the initial solution \(T_0 = \mu f(S_0) \) where \(\mu \) is a fixed parameter.

At each iteration l, the temperature is gradually decreased by a cooling scheme. The authors in the original SA paper [8] propose the following decreasing geometric cooling scheme:

$$ T_{l+1} = \alpha T_{l} $$

Where \(0<\alpha < 1\). Typically, when \(\alpha \) is set to high implying a slow decrease of the temperature. We also consider the Lundy-Mees cooling scheme proposed by [11]:

$$ T_{l+1} = \frac{T_{l}}{a+ b T_{l}}$$

Connolly in [1] develops a variant of the Lundy-Mees scheme that set the parameter a to 1 and b in dependence of the initial temperature \(T_0\), the final temperature \(T_f\) and the size of the neighborhood M:

$$b = \frac{T_0-T_f}{M T_0 T_f} $$

The algorithm will stop if it reaches the maximum number of iteration or after a fixed number of moves that did not result in accepted solutions. When the stopping criterion is met, the algorithm terminates returning the best solution \(S_{best}\) found so far.

Neighborhood Generation. A neighborhood solution is obtained through a perturbation on the assignment of Evs to CPs in the current solution by one of the following moves:

  • Swap in the same CP: a neighborhood solution is generated by randomly choosing a CP and interchange the position of two EVs scheduled in this CP. The positions of EVs are randomly selected.

  • Swap from two different CP: a neighborhood solution is generated by randomly swapping two EVs between two CPs. The CPs and EVs are randomly selected.

  • Insert: a neighborhood solution is generated by randomly choosing an EV in a CP and move it to another position in another CP. The CPs and the position of the EV are randomly selected.

  • Shift left: a neighborhood solution is generated by moving an EV at position \(p_1\) from a CP to position \(p_2\) in the same CP where \(p_2 < p1\). The positions \(p_1\) and \(p_2\) are randomly selected.

  • Shift right: a neighborhood solution is generated by moving an EV at position \(p_1\) from a CP to position \(p_2\) in the same CP where \(p_2 > p_1\). The positions \(p_1\) and \(p_2\) are randomly selected.

After each move, the power allocation is solved using the ILP models described in Sect. 4.3.

figure c

5 Experimental Analysis

To evaluate the performance of the proposed methods, several simulations are conducted, and the relevant results are discussed in this section. Note that all algorithms are implemented in C++ programming language. We use CPLEX 12.7 as a solver for the LP models in our heuristics and SA. Note that the CPLEX was not used to solve the MILP presented in Sect. (3) since we couldn’t get results for small instances vehicles even after turning for several days due to out of memory errors.

5.1 Parameters Tuning for SA

The tuning of the particular optimization problem is essential to obtain good results. We use the IRACE (Iterated Racing for Automatic Algorithm Configuration) package [10] which allows an automatic parameter configuration using the Iterated F-race method. Two scenarios of each case were selected to be the training instances for IRACE. Table 1 presents the parameters of the SA along with the range of values that tested for each parameter. The final choices of the parameter values are also presented and they are used in all experiments in the following sections.

Table 1. Values tested for the SA parameters tuning.
Full size table
Table 2. Comparison of results with \(m=10\).
Full size table
Table 3. Comparison of results with \(m=20\).
Full size table
Table 4. Comparison of results with \(m=40\).
Full size table

5.2 Scenarios Generation

Regarding the charging station, we consider three cases with different number of CPs \(m=\{10,20,40\}\). For each case, 30% of CPs deliver 3.7 kW, 30% deliver 11 kW, 30% deliver 22 kW and 10% deliver 43 kW. This charging rates are chosen from the standard IEC 61851 [19] that defines the classification of the different charging modes. The charging station maximum capacity \(P^{max}\) is set to 70% of \( \sum _{i=1}^{n} p_i\). The scheduling time horizon is one day and the time slot \(\tau \) is set to 6 min.

To test the model implemented, we need to model the stochastic EVs charging demands. The EV arrivals are randomly occurring and independent events. Therefore, the arrival time is modeled using a non-homogeneous Poisson Process with an arrival rate that varies \(\lambda (h)\) at each hour \(h=\{1,...,24\}\). The arrivals are likely high in the morning and low in the afternoon. The parking times \(pr_j\) follow an exponential distribution with a mean parking duration that also varies over time. There is no correlation between the arrival time and the parking time so the two variables can be generated independently [15]. The departure time \(d_j\) of each EV can be directly obtained \(d_j = r_j + pr_j \). The initial state-of-charge at the arrival (\(e^0_j\)) is considered uniformly distributed in the range of [20,70]. The desired state-of-charge of each EV j (\(e^{d}_j\)) is uniformly chosen from [\(e^0_j\),100]. The battery capacities are chosen randomly from the list of current real-world EVs battery capacities [2].

We generate 15 scenarios for each case. In the first 10 scenarios, the chromatic number (k) of the interval graph of the scenario is greater than the number of CPs while it is less or equal in the last five scenarios.

5.3 Simulation Results

Due to the stochastic nature of the IGCH and the SA algorithm, 30 independent executions were done for each scenario to obtain statistically significant results. The objective value is calculated for each scenario and we collect the mean, best, the standard deviation (std), and average execution time in seconds of each algorithm. Table 2, Table 3 and Table 4 shows the comparison of results obtained with \(m=10\), \(m=20\) and \(m=40\) respectively. We highlight in bold the best solution found.

About comparison between the model with constant power and the model with variable power, the objective value in the second one was averagely lower by 26.6% by the IGCH and by 20% by the SA than the first model. Thus, charging demands can be satisfied more using the variable power model.

For all scenarios, the best solutions found by the SA and IGCH always outperform the FCFS heuristic. For the scenarios with \(m=10\), the SA algorithm outperforms the IGCH in all scenarios whereas it outperforms the IGCH in 18 scenarios out of 30 with \(m=20\) and in 2 scenarios out of 30 when \(m=40\).

We perform the Mann-Whitney U test [13] to compare the results between the IGCH and the SA for each case. The Mann-Whitney U test is a non-parametric statistical test for determining whether two independent samples were drawn from a population with the same distribution. We compare the p-value to a significance level of 0.05. The p-value found was 0.0001, 0.3661 and 0.0038 for results with \(m=10\), \(m=20\) and \(m=40\), respectively. It suggests that there is no significant difference between the results with \(m=20\) of SA and IGCH algorithms. However, we can conclude that the difference between the SA and IGCH results with \(m=10\) and \(m=40\) are statistically significant. The average time taken by the three methods is always greater in scenarios with \(m=40\) when there are more EV charging demands. Also, the IGCH uses an average of 99.5% less computational time than SA. It is also noted that increment of computation time in the SA algorithm is due to solving multiple LP with CPLEX at each neighbor generation while there are one LP solved for each IGCH execution. In conclusion, the proposed IGCH is significantly better than the FCFS mechanism and it is preferable to the SA regarding the execution time. Moreover, it can handle large scenario better than the SA.

6 Conclusion

In this paper, we addressed the electric vehicle charging scheduling problem (EVCSP) in a charging station with different charging modes to maximize the final state-of-charge of each EV by the departure time. To solve the optimization problem, we designed a heuristic based on interval scheduling and Simulated Annealing (SA) combined with linear programming. Variable power and constant power models were both studied and compared. Different scenarios were presented to evaluate the performance of the proposed algorithms. The results show that the variable power model is better for allocating power. The results also show that the proposed heuristic and SA can achieve an optimal solution and outperform the SA algorithm, and the performance is significantly better than the First Come First Serve (FCFS) mechanism. In this paper, we have assumed that the data on vehicle recharging (arrival time, departure time, state of charge, etc.) are known in advance. This assumption is realistic since many recharging service operators require a reservation of the recharging in advance to avoid queues. However, it is interesting to study the dynamic case of vehicle arrival. In future work, we will consider multi-objective optimization to reduce the charging cost.