Fast Preconditioned Iterative Method for the Space Fractional Complex Ginzburg-Landau Equation

Abstract

In this work, we give an effective preconditioned numerical method to solve the discreted linear system, which is obtained from the space fractional complex Ginzburg-Landau equation. The coefficient matrix of the linear system is the sum of a symmetric tridiagonal matrix and a complex Toeplitz matrix. The preconditioned iteration method has computational superiority since we can use the fast Fourier transform (FFT) and the circulant preconditioner to solve the discreted linear system. Numerical examples are tested to illustrate the advantage of the proposed preconditioned numerical method.

Supported by the “Peiyu” Project from Xuzhou University of Technology (Grant Number XKY2019104).

1 Introduction

In this paper, we solve the space fractional complex Ginzburg-Landau equation as follows [39]

$$\begin{aligned} \displaystyle&\frac{\partial v}{\partial t}+(\nu _1+\mathbf {i}\eta _1)(-\varDelta )^{\frac{\beta }{2}}v +(\kappa _1+\mathbf {i}\zeta _1)|v|^2v-\gamma _1 v=0,\end{aligned}$$

(1)

$$\begin{aligned} \displaystyle&v(x,0)=v_{0}(x) , \end{aligned}$$

(2)

where $x\in \mathbb {R}$, $1<\beta \leqslant 2$, $\mathbf {i}$ is the imaginary unit, $0<t\leqslant T_1$, v(x, t) is a complex-value function, $\nu _1>0,\;\kappa _1>0$, $\eta _1$, $\zeta _1$, and $\gamma _1$ are real constants, and $v_{0}(x)$ is an initial function. Furthermore, the operator $(-\varDelta )^{\frac{\beta }{2}}v(x,t)$ ($1<\beta \leqslant 2$) in (1) is defined [9] as follows

$$\begin{aligned} -(-\varDelta )^{\frac{\beta }{2}}v(x,t) =-\frac{\frac{\partial ^2}{\partial x^2}\int _{-\infty }^{\infty }|x-\xi |^{1-\beta }v(\xi ,t)\text {d}\xi }{2\cos (\frac{\beta \pi }{2})\varGamma (2-\beta )}. \end{aligned}$$

(3)

The operator $(-\varDelta )^{\frac{\beta }{2}}$ is equivalent to

$$\begin{aligned} -(-\varDelta )^{\frac{\beta }{2}}v(x,t) = -\frac{{-\infty }\hat{D}_x^{\beta }v(x,t)+ _x\hat{D}_{+\infty }^{\beta }v(x,t)}{2\cos (\frac{\beta \pi }{2})}, \end{aligned}$$

where the two operators $_{-\infty }\hat{D}_x^{\beta }$ and $_x\hat{D}_{+\infty }^{\beta }$ are defined in [32].

The fractional Ginzburg-Landau equation has been used to describe a lot of physical phenomena; see [29, 30, 35]. However, there are few works on the numerical methods for the fractional complex Eq. (1)–(2) [10, 13, 33, 38, 39]. Based on the extensive application background of this equation, it is interesting to study the numerical methods for solving the fractional complex Eq. (1)–(2).

Recently, some new approaches are proposed to improve network routing and measurement [14, 37, 41]. Based on effective user behavior and traffic analysis methods [4, 5, 17, 19], new scheduling strategies are designed to raise resources utilization [6, 18, 20, 36] and energy-efficiency [21, 22]. To test these new scheduling strategies, traffic Reconstruction is important [15, 16, 23, 24, 27, 40]. Fluid model is effective model to reconstruct the bursty data traffic. Moreover, fractional differential equation can be used to build the fluid model. In our paper, we develop an effective preconditioned numerical method to solve the linear system, which is discreted from the fractional complex Eq. (1)–(2). Compared to the direct method, the complex linear systems can be fast solved by the circulant matrix and the FFT at each step due to the Toeplitz structure of coefficient matrices.

2 A Finite Difference Scheme

In this part, we exploit the fourth-order finite difference scheme [39] to discretize the fractional complex Eq. (1)–(2). For the two operators $_{-\infty }\hat{D}_x^{\beta }$ and $_x\hat{D}_{+\infty }^{\beta }$, the WSGD method [12] is used to approximate them. The shifted Grunwald formulae [28] is defined as

$$_{L}\mathcal {\tilde{A}}_{\hat{h},p_1}^{\beta }v(x)=\frac{\sum _{i=0}^{+\infty }d_{i}^{(\beta )}v(x-(i-p_1)\hat{h})}{\hat{h}^{\beta }},$$

$$_{R}\mathcal {\tilde{A}}_{\hat{h},q_1}^{\beta }v(x)=\frac{\sum _{i=0}^{+\infty }d_{i}^{(\beta )}v(x+(i-q_1)\hat{h})}{\hat{h}^{\beta }},$$

where $p_1$, $q_1$ are positive integers and the coefficients $d_{i}^{(\beta )}$ are computed as follows

$$d_{0}^{(\beta )}=1,~d_{i}^{(\beta )}=\frac{i-\beta -1}{i}d_{i-1}^{(\beta )},~i\in \mathbb {Z^{+}}.$$

According to the reference [12] and using the shifted Grunwald formulae, the WSGD operator is of the following form:

$$_{L}\mathcal {\tilde{D}}_{h}^{\beta }v(x)=\frac{\sum _{i=0}^{+\infty }z_{i}^{(\beta )}v(x-(i-1)\hat{h})}{\hat{h}^{\beta }},$$

$$_{R}\mathcal {\tilde{D}}_{h}^{\beta }v(x)=\frac{\sum _{i=0}^{+\infty }z_{i}^{(\beta )}v(x+(i-1)\hat{h})}{\hat{h}^{\beta }},$$

where

$$\begin{aligned} \begin{array}{cc} {\left\{ \begin{array}{ll} z_{0}^{(\beta )}=\tilde{\lambda }_{1}d_{0}^{(\beta )}, ~z_{1}^{(\beta )}=\tilde{\lambda }_{1}d_{1}^{(\beta )}+\tilde{\lambda }_{0}d_{0}^{(\beta )},\\ z_{i}^{(\beta )}=\tilde{\lambda }_{1}d_{i}^{(\beta )}+\tilde{\lambda }_{0}d_{i-1}^{(\beta )}+\tilde{\lambda }_{-1}d_{i-2}^{(\beta )},~i\geqslant 2, \end{array}\right. } \end{array} \end{aligned}$$

(4)

and

$$\tilde{\lambda }_{1}=\frac{\beta ^{2}}{12}+\frac{\beta }{4}+\frac{1}{6},~\tilde{\lambda }_{0}=\frac{2}{3}-\frac{\beta ^{2}}{6},~\tilde{\lambda }_{-1}=\frac{\beta ^{2}}{12}-\frac{\beta }{4}+\frac{1}{6}.$$

Let the operator $\mathcal {B}$ be

$$\mathcal {B}v(x)=c^{\beta }v(x-\hat{h})+(1-2c^{\beta })v(x)+c^{\beta }v(x+\hat{h}),$$

where $c^{\beta }=-\frac{\beta ^{2}}{24}+\frac{\beta }{24}+\frac{1}{6}$. Therefore, the fourth-order approximation to the operator $(-\varDelta )^{\frac{\beta }{2}}$ can be obtained by

$$\begin{aligned} \varDelta _{\hat{h}}^{\beta }v(x) =&\;\frac{_{L}\mathcal {\tilde{D}}_{\hat{h}}^{\beta }v(x)+_{R}\mathcal {\tilde{D}}_{\hat{h}}^{\beta }v(x)}{2\cos (\frac{\beta \pi }{2})} \end{aligned}$$

(5)

$$\begin{aligned} =&\;\mathcal {B}(-\varDelta )^{\frac{\beta }{2}}v(x)+\mathcal {O}(\hat{h}^{4}). \end{aligned}$$

(6)

In the following, we will give the numerical discretization of (1)–(2) in the domain $\Pi = [a_1, b_1]$. Let $\hat{\tau }=\frac{T_1}{N_1}$ and denote $t_{i}=i\hat{\tau }$, where $N_1$ is a positive integer, $0\leqslant i \leqslant N_1$. Given a grid function $u=\{u^{i}|0\leqslant i \leqslant N_1\}$, denote

$$\tilde{D}_{t}u^{i+1}=\frac{3u^{i+1}-4u^{i}+u^{i-1}}{2\hat{\tau }},$$

$$\tilde{u}^{i+1}=2u^{i}-u^{i-1}.$$

Let $\hat{h}=\frac{b_1-a_1}{M_1}$ and $x_{i}=a_1+i\hat{h}$, where $M_1$ is a positive integer, $0\leqslant i \leqslant M_1$. Moreover, we denote $\mathfrak {F}_{M_1}=\{i|i=1,2,\ldots ,M_1-1\}$. According to the method of [39], we can obtain the following finite difference scheme for the fractional complex Eq. (1) and (2):

$$\begin{aligned} \displaystyle&\mathcal {B}\tilde{D}_{t}v_{j}^{i+1}+(\nu _1+\mathbf {i}\eta _1)\varDelta _{\hat{h}}^{\beta }v_{j}^{i+1}+ (\kappa _1+\mathbf {i}\zeta _1)\mathcal {B}|\tilde{v}_{j}^{i+1}|^2\tilde{v}_{j}^{i+1}-\gamma _1\mathcal {B}\tilde{v}_{j}^{i+1}=0,\nonumber \\ \displaystyle&j\in \mathfrak {F}_{M_1}, \; 1\leqslant i \leqslant N_1-1,\end{aligned}$$

(7)

$$\begin{aligned} \displaystyle&v_{j}^{0}=v_{0}(x_{j}), j\in \mathbb {Z}, \end{aligned}$$

(8)

$$\begin{aligned} \displaystyle&v_{j}^{i}=0, j\in \mathbb {Z}\setminus \mathfrak {F}_{M_1},\; 0\leqslant i \leqslant N_1 . \end{aligned}$$

(9)

In the practical computation, we can calculate $u^{1}$ as follows [39]

$$\begin{aligned} \begin{array}{cc} {\left\{ \begin{array}{ll} \mathcal {B}(\frac{v_{j}^{1}-v_{0j}}{\hat{\tau }})+(\nu _1+\mathbf {i}\eta _1)\varDelta _{\hat{h}}^{\beta }\frac{v_{j}^{1}+v_{0j}}{2}+(\kappa _1+\mathbf {i}\zeta _1)\mathcal {B}|v_{j}^{(1)}|^2v_{j}^{(1)}=\gamma _1 \mathcal {B}v_{j}^{(1)},\\ \mathcal {B}(\frac{v_{j}^{(1)}-v_{0j}}{\hat{\tau }/2})+(\nu _1+\mathbf {i}\eta _1)\varDelta _{\hat{h}}^{\beta }v_{0j}+(\kappa _1+\mathbf {i}\zeta _1)\mathcal {B}|v_{0j}|^2v_{0j}=\gamma _1 \mathcal {B}v_{0j},j\in \mathfrak {F}_{M_1}. \end{array}\right. } \end{array} \end{aligned}$$

(10)

Let

$$v^{i+1}=[v_{1}^{i+1},\ldots ,v_{M_1-1}^{i+1}]^{T},$$

$$\begin{aligned} \ D_{1}=\hat{\tau }(\kappa _1+\mathbf{i} \zeta _1)\left[ \begin{array}{cccc} |v_{01}|^{2}&{}0&{}\ldots &{}0\\ 0&{}|v_{02}|^{2}&{}\ldots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\ldots &{}|v_{0,M_1-1}|^{2} \end{array}\right] -(2+\gamma _1\hat{\tau })I, \end{aligned}$$

$$\begin{aligned} \ D_{2}=(\kappa _1+\mathbf{i} \zeta _1)\left[ \begin{array}{cccc} |v_{1}^{(1)}|^{2}&{}0&{}\ldots &{}0\\ 0&{}|v_{2}^{(1)}|^{2}&{}\ldots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\ldots &{}|v_{M_1-1}^{(1)}|^{2} \end{array}\right] -\gamma _1I, \end{aligned}$$

$$\begin{aligned} \ D_{3}=(\kappa _1+\mathbf{i} \zeta _1)\left[ \begin{array}{cccc} |\tilde{v}_{1}^{i+1}|^{2}&{}0&{}\ldots &{}0\\ 0&{}|\tilde{v}_{2}^{i+1}|^{2}&{}\ldots &{}0\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}\ldots &{}|\tilde{v}_{M_1-1}^{i+1}|^{2} \end{array}\right] -\gamma _1I, \end{aligned}$$

$$\begin{aligned} Z=\left[ \begin{array}{cccccc} z_{1}^{(\beta )}&{} z_{0}^{(\beta )}&{}0&{}\cdots &{}0&{}0\\ z_{2}^{(\beta )}&{} z_{1}^{(\beta )}&{}z_{0}^{(\beta )}&{}0&{}\cdots &{}0\\ \vdots &{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\vdots \\ \vdots &{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}0\\ z_{M_1-2}^{(\beta )}&{}\ddots &{}\ddots &{}\ddots &{}z_{1}^{(\beta )}&{}z_{0}^{(\beta )}\\ z_{M_1-1}^{(\beta )}&{}z_{M_1-2}^{(\beta )}&{}\cdots &{}\cdots &{}z_{2}^{(\beta )}&{}z_{1}^{(\beta )} \end{array}\right] , \end{aligned}$$

(11)

and

$$A_{\beta }=\text {tridiag}\left( c^{\beta },1-2^{\beta },c^{\beta }\right) ,$$

then the fourth-order finite difference scheme (7)–(10) has the following form

$$\begin{aligned} \displaystyle&2A_{\beta }v^{(1)}=-A_{\beta }D_{1}v^{0}-\omega Cv^{0}, \end{aligned}$$

(12)

$$\begin{aligned} \displaystyle&(A_{\beta }+\frac{\omega _1}{2}C)v^{1}=(A_{\beta }-\frac{\omega _1}{2}C)v^{0}-\hat{\tau } A_{\beta }D_{2}v^{(1)}, \end{aligned}$$

(13)

$$\begin{aligned} \displaystyle&(\frac{3}{2}A_{\beta }+\omega _1 C)v^{i+1}=A_{\beta }(2v^{i}-\frac{1}{2}v^{i-1}-\hat{\tau } D_{3}\tilde{v}^{i+1} ), 1\leqslant i \leqslant N_1-1 . \end{aligned}$$

(14)

where $C=Z+Z^{T}$ and $\omega _1=\frac{(\nu _1+\mathbf {i}\eta _1)\hat{\tau }}{2\hat{h}^{\beta }\cos (\frac{\beta \pi }{2})}$.

3 A Fast Preconditioned Numerical Method

In this part, we give an effective preconditioned generalized minimum residual (PGMRES) method [34] to solve the discreted linear system of the finite difference scheme (7)–(10), in which the preconditioned matrix is Strang’s circulant preconditioner proposed in [2].

3.1 Toeplitz Matrix and GMRES Method

The Toeplitz linear system is as follows

$$B_{n_1}u=\tilde{b},$$

where $B_{n_1}$ is a Toeplitz matrix, $\tilde{b}$ is a given vector. Toeplitz systems are widely used in various fields; see [1, 3, 7, 11, 25, 26, 31]. The elements of an $n_1\times n_1$ Toeplitz matrix $B_{n_1}$ satisfy $(B_{n_1})_{ij}=b_{i-j}$ for $i,j=1,2,\ldots ,n_1$. The elements of a circulant matrix $C_{n_1}$ satisfy $c_{-i}=c_{n_1-i}$ for $1\leqslant i \leqslant n_1-1$ [2].

It is well-known that [8] the computation cost will be $\mathcal {O}(n_1\log n_1)$ operations if one wants to compute the matrix-vector products $C_{n_1}u$ and $C_{n_1}^{-1}u$ by the fast Fourier transform. In addition, we can calculate the matrix-vector product $B_{n_1}u$ in $\mathcal {O}(2n_1\log ( 2n_1))$ by the FFT [2]. These important properties can be exploited to fast solve the discreted linear system in the form (12)–(14).

Consider the following non-Hermitian linear systems

$$Bu=\tilde{b},$$

where B is a non-Hermitian matrix. As we know, the GMRES method [34] is a very effective iterative method for solving these linear systems. Under normal circumstances, the convergent rate of the this method is very slow because of the very large condition number of the matrix B. To deal with this drawback, we could exploit the preconditioned matrix to speed up the convergent rate of the GMRES method. Please refer to [34] for the PGMRES method.

3.2 A Preconditioner for the Implicit-Explicit Difference Scheme

It can be seen that $A_{\beta }$ and C are Toeplitz matrices in the matrix-vector form (12)–(14). According to Sect. 3.1, we can store an $M_1\times M_1$ Toeplitz matrix $B_{M_1}$ in $\mathcal {O}(M_1)$ of memory, and we can compute the matrix-vector product $B_{M_1}u$ in $\mathcal {O}(M_1\log M_1)$ by the FFT. Moreover, the coefficient matrices of the complex linear systems (13) and (14) are non-Hermitian.

In this section, we exploit Strang’s circulant matrix as a preconditioner to speed up the GMRES method. For the matrix $A_{\beta }$ in (12), the preconditioned matrix is

$$S_{1}=s(A_{\beta }),$$

where $s(A_{\beta })$ is the Strang circulant matrix for the matrix $A_{\beta }$. For the matrix $A_{\beta }+\frac{\omega _1}{2}C$ in (13), the preconditioned matrix is

$$S_{2}=s(A_{\beta })+\frac{\omega _1}{2}s(C).$$

For the matrix $\frac{3}{2}A_{\beta }+\omega _1 C$ in (14), the preconditioned matrix is

$$S_{3}=\frac{3}{2}s(A_{\beta })+\omega _1 s(C).$$

It easily knows that $S_{1}$, $S_{2}$ and $S_{3}$ are circulant matrices. In the following, we will see that the proposed preconditioners are very efficient to speed up the GMRES method.

4 Numerical Experiments

In this part, we show the computational advantage of the PGMRES algorithm by two numerical examples for the fractional complex equation. We denote “GaE” by the direct method, which is implemented by left divide in MATLAB. For the PGMRES method with Strang’s circulant preconditioner, we denote by “cPGMRES”. We stop the cPGMRES method if the condition satisfies

$$\frac{\Vert \text {res1}^{k}\Vert _{2}}{\Vert \text {res1}^{0}\Vert _{2}}< 10^{-7},$$

where $\text {res1}^k$ denotes the k-th residual vector for the cPGMRES method. In all tables, “Icpu” denotes the computational time in seconds for GaE and cPGMRES, and “Ite” is the iteration numbers for cPGMRES.

Example 1

In this example, the parameters in the fractional complex Eq. (1) and (2) are same as these in [39].

Furthermore, according to [39], the numerical exact solution v is calculated with $\hat{\tau }= 10^{-4}$ and $\hat{h} = 1.25\times 10^{-2}$. Let $v_{\hat{h}}$ be the numerical solution. We compute the error $\text {ERR}=v-v_{\hat{h}}$ as the numerical accuracy at $T_1 = 2$ with the $l_{\hat{h}}^{\infty }$ norm.

Table 1. Numerical results for Example 1

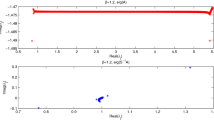
We report the numerical results in Table 1. In this table, $\text {ERR}_{1}$ and $\text {ERR}_{2}$ denote the errors for the cPGMRES method and the GaE method, respectively. We can see that there is little difference between numerical errors of the two methods. But, if the size of the matrix in the complex linear systems (12)–(13) is large, the computational times of GaE are much more than the computational times of cPGMRES. Furthermore, Figs. 1, 2 and 3 show the distribution of the eigenvalues for the matrix $\frac{3}{2}A_{\beta }+\omega _1 C$ and $S_{3}^{-1}(\frac{3}{2}A_{\beta }+\omega _1 C)$ at $T_1=2$, respectively, when the size of the matrix is 320, and $\beta =1.3,~1.6,~1.9$. In the figures, the blue points indicate that most of the eigenvalues of the matrix $S_{3}^{-1}(\frac{3}{2}A_{\beta }+\omega _1 C)$ approach to 1, while the eigenvalues of the matrix $\frac{3}{2}A_{\beta }+\omega _1 C$ do not approach to 1. Therefore, the figures show that our new preconditioner is very effective for solving the linear systems (12)–(14).

Fig. 1.

Example 1: Spectrum of $\frac{3}{2}A_{\beta }+\omega _1 C$ (upper) and $S_{3}^{-1}(\frac{3}{2}A_{\beta }+\omega _1 C)$ (lower), when $\beta =1.3$.

Fig. 2.

Example 1: Spectrum of $\frac{3}{2}A_{\beta }+\omega _1 C$ (upper) and $S_{3}^{-1}(\frac{3}{2}A_{\beta }+\omega _1 C)$ (lower), when $\beta =1.6$.

Fig. 3.

Example 1: Spectrum of $\frac{3}{2}A_{\beta }+\omega _1 C$ (upper) and $S_{3}^{-1}(\frac{3}{2}A_{\beta }+\omega _1 C)$ (lower), when $\beta =1.9$.

Example 2

In this example, we take the parameters which are same as these in [39]. Moreover, we compute the exact solution v with $\hat{\tau }= 10^{-4}$ and $\hat{h} = 1.25\times 10^{-2}$.

Table 2 gives the numerical results and Figs. 4, 5 and 6 show the distribution of the eigenvalues for the matrices $\frac{3}{2}A_{\beta }+\omega _1 C$ and $S_{3}^{-1}(\frac{3}{2}A_{\beta }+\omega _1 C)$ at $T_1=2$, respectively, when the size of the matrix is 320, and $\beta =1.3,~1.6,~1.9$. Similar to Example 1, the computational results and figures indicate the superiority of the preconditioned numerical method.

Fig. 4.

Example 2: Spectrum of $\frac{3}{2}A_{\beta }+\omega _1 C$ (upper) and $S_{3}^{-1}(\frac{3}{2}A_{\beta }+\omega _1 C)$ (lower), when $\beta =1.3$

Fig. 5.

Example 2: Spectrum of $\frac{3}{2}A_{\beta }+\omega _1 C$ (upper) and $S_{3}^{-1}(\frac{3}{2}A_{\beta }+\omega _1 C)$ (lower), when $\beta =1.6$.

Fig. 6.

Example 2: Spectrum of $\frac{3}{2}A_{\beta }+\omega _1 C$ (upper) and $S_{3}^{-1}(\frac{3}{2}A_{\beta }+\omega _1 C)$ (lower), when $\beta =1.9$.

Table 2. Numerical results for Example 2

5 Conclusion and Future Work

In this work, we have given a fast preconditioned numerical method to solve the linear system, which is discreted from the space fractional complex Ginzburg-Landau equation. We propose a circulant preconditioner due to the Toeplitz structure of the coefficient matrix of the linear system. Numerical examples show that the preconditioned numerical method is very efficient.