Keywords

1 Introduction

Retrial queue (RQ) systems are adequate models of processes arising from real world applications. Main fields where such models are used are telecommunication networks, computer networks, call centers, wireless communication systems, cognitive networks, cloud computing. An extensive review of recent developments and methods related to RQ systems one can find in, for example, Artalejo, Falin [2], Artalejo, Gomez-Corral [3], Gomez-Corral, Phung-Duc [16], Falin, Templeton [13], Kim, Kim [17], Nobel [24], Phung-Duc [26].

The waiting time distribution, the time a request spends in the orbit, is very complicated problem in the retrial queue system theory. Different approaches to the investigation of the waiting time can be found in Artalejo, Chakravarthy, Lopez-Herrero [1], Artalejo, Gomez-Corral [4], Choi, Chang [6], Falin, Artalejo [8], Gharbi, Dutheillet [14], Sudyko, Nazarov, Sztrik [27], Tóth, Bérczes, Sztrik [28], Zhang, Feng, Wang [29] for finite retrial group of sources and Chakravarthy, Dudin [7], Falin, Fricker [9], Falin [1, 10, 12], Gomez-Corral, Ramalhoto [15], Neuts [20], Nobel, Tijms [25], Lee, Kim, Kim [18] for infinite number of sources.

Since a request waiting time distribution and the number of returns distribution are connected to each other, in this paper we investigate both of them. We use the method of asymptotic analysis under a heavy load condition and a low rate of retrials condition following approach applied in, for example, Moiseeva, Nazarov [19], Nazarov, Moiseeva [21], Nazarov, Semenova [22], Nazarov, Sztrik, Kvach [23].

The rest of the paper is organized as follows. In Sect. 2 the RQ-system mathematical model and the waiting time characteristic function are presented. In Sect. 3 we derive Kolmogorov’s equations for the system states. Section 4 is connected with the asymptotic analysis of the distribution of the number of requests in the orbit, which is needed for further research. In Sect. 5 asymptotic analysis of characteristic functions for the number of request returns to the orbit is provided. In Sect. 6 the asymptotic distribution of the waiting time in the orbit is derived for two different conditions. In Sect. 7 we found the approximation of the waiting time distribution in prelimit situation. Also, several sample results obtained by numerical methods showing that proposed approximation is effective. The paper ends with a Conclusion.

2 Mathematical Model

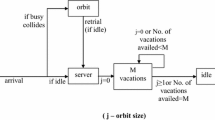
Let us consider a M/M/1 retrial queuing (RQ) system. The system input receives a Poisson flow of requests which is given by a scalar intensity \(\lambda \). When incoming request arrive at the system the server can be idle or busy. In the first case this request occupies the server and the service starts immediately. Served request leaves the system. In second case, the request joins to the orbit. Each request from the orbit after a random delay retries to get accesses to the server. At the retrial moment server again can be idle or busy. In the first case this request occupies the server for a random service time; otherwise, it instantly returns to the orbit for a next random delay. Service time and random delay time are independent and exponentially distributed with parameters \(\mu \) and \(\sigma \), respectively.

We assume the system being in stationary mode. Let’s define W – waiting time of the tagged request in the orbit as the length of the interval from the moment the request arrives in the system till the start of the service. Let’s denote by \(\tilde{\nu }\) the number of transitions of the tagged request to the orbit. Also we denote by r the probability that the server is busy at the moment the request arrives at the system. Obviously \(\tilde{\nu }=0\), with the probability \((1-r)\) that the request finds the server idle at the moment of the arrival to the system. In addition, we denote by \(\nu (t)\) the number of returns of the tagged request to the orbit from the moment t until the start of the service. Using above notations:

$$\begin{aligned} \tilde{\nu }= \left\{ \begin{array}{l} 0,\quad {\text {with probability }} (1 - r),\;\\ 1 + \nu (t),\quad {\text {with probability }} r.\;\quad \end{array} \right. \end{aligned}$$

The characteristic function for W can be written as follows:

$$\begin{aligned} \begin{gathered} G(u)=E\left\{ {{e}^{juW}} \right\} =(1-r)+r\sum \limits _{n=0}^{\infty }{E\left\{ {{{e}^{juW}}}/{\nu =1+n}\; \right\} }P\left\{ \nu (t)=n \right\} \\ =(1-r)+r\sum \limits _{n=0}^{\infty }{{{\left( \frac{\sigma }{\sigma -ju} \right) }^{1+n}}P\left\{ \nu (t)=n\right\} .} \end{gathered} \end{aligned}$$
(1)

The aim of our study is to find the asymptotic distribution of W the waiting time of the tagged request in the orbit. As can be seen from (1), for that purpose it is enough to find the probability r and the probability distribution \(P\left\{ \nu (t)=n \right\} \) under limiting conditions. First, we conduct our research under a heavy load condition and then under a low rate of retrials condition. As a result, two different asymptotic distributions of W were obtained.

3 Kolmogorov’s Equations

Let’s denote by i(t) the number of requests in the orbit at time t and by k(t) - the state of the server at time t:

$$\begin{aligned} k(t) = \left\{ \begin{array}{l} 0,\quad {\text {if the server is idle,}}\;\\ 1,\quad {\text {if the server is busy.}}\;\quad \end{array} \right. \end{aligned}$$

The system state at time t can be described by means of a markov chain \(\left\{ k(t),i(t) \right\} \) with stationary probability distribution:

$$\begin{aligned} {{P}_{k}}(i)=P\left\{ k(t)=k,i(t)=i \right\} \end{aligned}$$

Probability distribution \({{P}_{k}}(i)\) satisfy the following Kolmogorov equations:

$$\begin{aligned} \begin{gathered} (\lambda +i\sigma ){{P}_{0}}(i)=\mu {{P}_{1}}(i),\\ (\lambda +\mu ){{P}_{1}}(i)=\lambda {{P}_{0}}(i)+(i+1)\sigma {{P}_{0}}(i+1)+\lambda {{P}_{1}}(i-1). \end{gathered} \end{aligned}$$
(2)

Steady-state partial characteristic functions \({{H}_{k}}(u)\) for i(t) can be written in the following form:

$$\begin{aligned} {{H}_{k}}(u)=\sum \limits _{i=0}^{\infty }{{{e}^{jui}}{{P}_{k}}(i)}, \end{aligned}$$
(3)

where \(j=\sqrt{-1}\) is the imaginary unit.

According to (2) and (3) we obtain the system of equations for \({{H}_{k}}(u)\):

$$\begin{aligned} \begin{gathered} -\lambda {{H}_{0}}(u)+j\sigma \frac{\partial {{H}_{0}}(u)}{\partial u}+\mu {{H}_{1}}(u)=0,\\ -(\lambda +\mu ){{H}_{1}}(u)+\lambda {{H}_{0}}(u)-j\sigma {{e}^{-ju}}\frac{\partial {{H}_{0}}(u)}{\partial u}+\lambda {{e}^{ju}}{{H}_{1}}(u)=0. \end{gathered} \end{aligned}$$
(4)

Steady-state characteristic functions for \(\nu (t)\) can be written in the following form:

$$\begin{aligned} G(u)=E\left\{ {{e}^{juv(t)}} \right\} =\sum \limits _{i=0}^{\infty }{\left[ {{G}_{0}}(i,u){{P}_{0}}(i)+{{G}_{1}}(i,u){{P}_{1}}(i) \right] }. \end{aligned}$$

Let’s consider:

$$\begin{aligned} {{G}_{k}}(i,u,t)=E\left\{ {{{e}^{juv(t)}}}/{k(t)=k,i(t)=i}\; \right\} , \end{aligned}$$

where \({{G}_{k}}(i,u,t)\) - conditional partial characteristic functions for \(\nu (t)\). Taking into account that the system is in a stationary mode, for \({{G}_{k}}(i,u)\) we obtain the system of inverse Kolmogorov equations:

$$\begin{aligned} -(\lambda +i\sigma ){{G}_{0}}(i,u)+\lambda {{G}_{1}}(i,u)+(i-1)\sigma {{G}_{1}}(i-1,u)+\sigma =0, \end{aligned}$$
(5)
$$\begin{aligned} -(\lambda +\mu +\sigma ){{G}_{1}}(i,u)+\mu {{G}_{0}}(i,u)+\lambda {{G}_{1}}(i+1,u)+{{e}^{ju}}\sigma {{G}_{1}}(i,u)=0. \end{aligned}$$
(6)

4 Asymptotic Analysis of the Number of Requests in the Orbit

Heavy Load Condition. Denote \(\rho =\frac{\lambda }{\mu }\), \(\varepsilon =1-\rho \), making substitutions \(u=\varepsilon w\), \({{H}_{0}}(u)=\varepsilon {{F}_{0}}(\omega ,\varepsilon )\), \({{H}_{1}}(u)={{F}_{1}}(\omega ,\varepsilon )\) and deviding (4) by \(\mu \) we get:

$$\begin{aligned} \begin{gathered} {{F}_{1}}(w,\varepsilon )-(1-\varepsilon )\varepsilon {{F}_{0}}(w,\varepsilon )+j\frac{\sigma }{\mu }\frac{\partial {{F}_{0}}(w,\varepsilon )}{\partial w}=0,\\ (1-\varepsilon )\varepsilon {{F}_{0}}(w,\varepsilon )+\left[ (1-\varepsilon )({{e}^{jw\varepsilon }}-1)-1 \right] {{F}_{1}}(w,\varepsilon )\\ -j\frac{\sigma }{\mu }{{e}^{-jw\varepsilon }}\frac{\partial {{F}_{0}}(w,\varepsilon )}{\partial w}=0. \end{gathered} \end{aligned}$$
(7)

The beforelimited characteristic function under a heavy load condition can be determined approximately by the equation: \(H(u)={{H}_{0}}(u)+{{H}_{1}}(u)\approx h(w)={{F}_{1}}(w)\).

Step 1. Let \(\varepsilon \rightarrow 0\) in (7). Denote

$$\begin{aligned} \underset{\varepsilon \rightarrow 0}{\mathop {\lim }}\,{{F}_{k}}(\omega ,\varepsilon )={{F}_{k}}(\omega ). \end{aligned}$$

For functions \({{F}_{k}}(w)\) we obtain the system of equations:

$$\begin{aligned} \begin{gathered} {{F}_{1}}(w)+j\frac{\sigma }{\mu }\frac{\partial {{F}_{0}}(w)}{\partial w}=0,\\ -{{F}_{1}}(w)-j\frac{\sigma }{\mu }\frac{\partial {{F}_{0}}(w,\varepsilon )}{\partial w}=0. \end{gathered} \end{aligned}$$

This system consists of two equivalent equations.

Step 2. Let’s rewrite \({{F}_{k}}(w,\varepsilon )\) from (7) as follows:

$$\begin{aligned} {{F}_{k}}(w,\varepsilon )={{F}_{k}}(w)+\varepsilon {{f}_{k}}(w)+o({{\varepsilon }^{2}}), \end{aligned}$$

and devide equations of the system (7) by \(\varepsilon \). With respect to step 1 results and after taking \(\varepsilon \rightarrow 0\), we obtain:

$$\begin{aligned} \begin{gathered} {{f}_{1}}(w)-{{F}_{0}}(w)+j\frac{\sigma }{\mu }\frac{\partial {{f}_{0}}(w)}{\partial w}=0,\\ -{{F}_{1}}(w)+{{f}_{1}}(w)+j\frac{\sigma }{\mu }\frac{\partial {{f}_{0}}(w)}{\partial w}+\frac{\sigma }{\mu }w\frac{\partial {{F}_{0}}(w)}{\partial w}=0. \end{gathered} \end{aligned}$$

Combining resulting equations of steps 1 and 2, we get the following system:

$$\begin{aligned} \begin{gathered} {{F}_{1}}(w)+j\frac{\sigma }{\mu }\frac{\partial {{F}_{0}}(w)}{\partial w}=0, \\ {{f}_{1}}(w)-{{F}_{0}}(w)+j\frac{\sigma }{\mu }\frac{\partial {{f}_{0}}(w)}{\partial w}=0, \\ -{{F}_{1}}(w)+{{f}_{1}}(w)+j\frac{\sigma }{\mu }\frac{\partial {{f}_{0}}(w)}{\partial w}+\frac{\sigma }{\mu }w\frac{\partial {{F}_{0}}(w)}{\partial w}=0. \end{gathered} \end{aligned}$$

Solving the obtained system as it is shown in [19] the following expression can be got:

$$\begin{aligned} h(w)={{(1-jw)}^{-\left( \frac{\mu +\sigma }{\sigma } \right) }}, \end{aligned}$$
(8)

where h(w) is a characteristic function of gamma distribution \(\gamma \left( x \right) \) with parameters \(\beta =\frac{\mu +\sigma }{\sigma }\) and \(\alpha =1\).

Low Rate of Retrials Condition. Making substitutions \(\sigma =\varepsilon \), \(u=\varepsilon w\), \({{H}_{k}}(u)={{F}_{k}}(\omega ,\varepsilon )\) in (4), we obtain:

$$\begin{aligned} \begin{gathered} -\lambda {{F}_{0}}(\omega ,\varepsilon )+j\frac{\partial {{F}_{0}}(\omega ,\varepsilon )}{\partial \omega }+\mu {{F}_{1}}(\omega ,\varepsilon )=0,\\ -(\lambda +\mu ){{F}_{1}}(\omega ,\varepsilon )+\lambda {{F}_{0}}(\omega ,\varepsilon )-j{{e}^{-j\varepsilon \omega }}\frac{\partial {{F}_{0}}(\omega ,\varepsilon )}{\partial \omega }+\lambda {{e}^{j\varepsilon \omega }}{{F}_{1}}(\omega ,\varepsilon )=0. \end{gathered} \end{aligned}$$
(9)

Step 1. Let \(\varepsilon \rightarrow 0\) in (9). Denote

$$\begin{aligned} \underset{\varepsilon \rightarrow 0}{\mathop {\lim }}\,{{F}_{k}}(\omega ,\varepsilon )={{F}_{k}}(\omega ). \end{aligned}$$

For functions \({{F}_{k}}(w)\) we obtain the system of equations:

$$\begin{aligned} \begin{gathered} -\lambda {{F}_{0}}(\omega )+j\frac{\partial {{F}_{0}}(\omega )}{\partial \omega }+\mu {{F}_{1}}(\omega )=0,\\ \lambda {{F}_{0}}(\omega )-j\frac{\partial {{F}_{0}}(\omega )}{\partial \omega }-\mu {{F}_{1}}(\omega )=0. \end{gathered} \end{aligned}$$

Note that equations of this system are equivalent.

Step 2. Adding equations in system (9), we get:

$$\begin{aligned} j(1-{{e}^{-j\varepsilon \omega }})\frac{\partial {{F}_{0}}(\omega ,\varepsilon )}{\partial \omega }+\lambda ({{e}^{j\varepsilon \omega }}-1){{F}_{1}}(\omega ,\varepsilon )=0. \end{aligned}$$

Let’s decompose exponential function and rewrite above expression:

$$\begin{aligned} j(j\varepsilon \omega +o(\varepsilon ))\frac{\partial {{F}_{0}}(\omega ,\varepsilon )}{\partial \omega }+\lambda (j\varepsilon \omega +o(\varepsilon )){{F}_{1}}(\omega ,\varepsilon )=0. \end{aligned}$$

Taking \(\varepsilon \rightarrow 0\), we obtain:

$$\begin{aligned} j\frac{\partial {{F}_{0}}(\omega )}{\partial \omega }+\lambda {{F}_{1}}(\omega )=0. \end{aligned}$$

Combining with the result of Step 1, we get the system similar to system obtained in [22]:

$$\begin{aligned} \begin{gathered} -\lambda {{F}_{0}}(\omega )+j\frac{\partial {{F}_{0}}(\omega )}{\partial \omega }+\mu {{F}_{1}}(\omega )=0,\\ j\frac{\partial {{F}_{0}}(\omega )}{\partial \omega }+\lambda {{F}_{1}}(\omega )=0. \end{gathered} \end{aligned}$$
(10)

Lets find the solution in the following form:

$$\begin{aligned} {{F}_{k}}(\omega )=R(\kappa ){{e}^{jwk}}, \end{aligned}$$
(11)

where \(R(\kappa )=P(k=\kappa )\) - stationary probabilities of Markov chain k(t), \(\kappa =0,1\).

Substituting (11) in (10), we obtain a homogeneous system of two equations for the probability distribution R(k):

$$\begin{aligned} \begin{gathered} -(\lambda +\kappa )R(0)+\mu R(1)=0\\ -\kappa R(0)+\lambda R(1)=0. \end{gathered} \end{aligned}$$
(12)

Equation

$$\begin{aligned} \lambda (\lambda +\kappa )-\mu \kappa =0 \end{aligned}$$
(13)

determines the value of \(\kappa \) for (11). Solving (13) we obtain:

$$\begin{aligned} \kappa = \frac{{{\lambda ^2}}}{{\mu - \lambda }} \end{aligned}$$
(14)

Taking into account the normalization condition \(R(0)+R(1)=1\) and (12) the probability distribution R(k) can be calculated as:

$$\begin{aligned} R(0) = \frac{{\mu - \lambda }}{\mu }, R(1) = \frac{\lambda }{\mu }. \end{aligned}$$

5 Asymptotic Analysis of the Number of Returns of the Tagged Request to the Orbit

Heavy Load Condition. Denote \(\rho =\frac{\lambda }{\mu }\), \(\varepsilon =1-\rho \), making substitutions \(u=\varepsilon w\), \(i\varepsilon =x\), \({{G}_{k}}(i,u)={{g}_{k}}(x,w,\varepsilon )\) and multiplying (5) by \(\varepsilon \) we obtain:

$$\begin{aligned} \begin{gathered} - (\varepsilon \lambda + \sigma ){g_0}(,w,\varepsilon ) + \varepsilon \lambda {g_1}(,w,\varepsilon ) + (x - \varepsilon )\sigma {g_1}( - \varepsilon ,w,\varepsilon ) + \varepsilon \sigma = 0\\ - (\lambda + \mu + \sigma (1 + {e^{j\varepsilon w}})){g_1}(,w,\varepsilon ) + \mu {g_0}(,w,\varepsilon ) + \lambda {g_1}( + \varepsilon ,w,\varepsilon ) = 0 \end{gathered} \end{aligned}$$
(15)

Step 1. Let \(\varepsilon \rightarrow 0\) in (15). Denote

$$\begin{aligned} \mathop {\lim }\limits _{\varepsilon \rightarrow 0} {g_k}(x,w,\varepsilon ) = {g_k}(x,w). \end{aligned}$$

We obtain the following system for \({{g}_{k}}(x,w)\):

$$\begin{aligned} \begin{gathered} -x\sigma {{g}_{0}}(x,w)+x\sigma {{g}_{1}}(x,w)=0,\\ -(\mu +\sigma ){{g}_{1}}(x,w)+(\mu +\sigma ){{g}_{0}}(x,w)=0. \end{gathered} \end{aligned}$$
(16)

Note that equations of this system are equivalent and \({{g}_{0}}(x,w)={{g}_{1}}(x,w)=g(x,w)\). Step 2. Let’s rewrite \({{g}_{k}}(x,w,\varepsilon )\) from (15) as follows:

$$\begin{aligned} {{g}_{k}}(x,w,\varepsilon )=g(x,w)+\varepsilon {{f}_{k}}(x,w)+o(\varepsilon ), \end{aligned}$$
(17)

and then rewrite (15):

$$\begin{aligned} \begin{gathered} -(\varepsilon \lambda +x\sigma ){{g}_{0}}(x,w,\varepsilon )+\left( \varepsilon \lambda +x\sigma \right) {{g}_{1}}(x,w,\varepsilon )\\ -\,\varepsilon \frac{\partial \left[ x\sigma {{g}_{1}}(x,w,\varepsilon ) \right] }{\partial x}+\varepsilon \sigma =O({{\varepsilon }^{2}}),\\ -\,(\mu +\sigma ){{g}_{1}}(x,w,\varepsilon )+\mu {{g}_{0}}(x,w,\varepsilon )\\ +\,\varepsilon \frac{\partial \left[ \lambda {{g}_{1}}(x,w,\varepsilon ) \right] }{\partial x}+{{e}^{j\varepsilon w}}\sigma {{g}_{1}}(x,w,\varepsilon )=O({{\varepsilon }^{2}}). \end{gathered} \end{aligned}$$
(18)

Substituting decomposition (17) in (18), taking \(\varepsilon \rightarrow 0\) and after performing some actions on the equations, we get the following system:

$$\begin{aligned} x\left[ {{f}_{1}}(x,w)-{{f}_{0}}(x,w) \right] =g(x,w)+x\frac{\partial g(x,w)}{\partial x}-1, \end{aligned}$$
$$\begin{aligned} \left[ {{f}_{1}}(x,w)-{{f}_{0}}(x,w) \right] =jw\frac{\sigma }{\mu }g(x,w)+\frac{\partial g(x,w)}{\partial x}-\frac{\sigma }{\mu }{{f}_{1}}(x,w). \end{aligned}$$

Adding equations in the system (18) and taking \(\varepsilon \rightarrow 0\), we get the following expression:

$$\begin{aligned} (x-\frac{\mu }{\sigma })\left[ {{f}_{1}}(x,w)-{{f}_{0}}(x,w) \right] =\left( 1-jw \right) g(x,w)+\left( x-\frac{\mu }{\sigma } \right) \frac{\partial g(x,w)}{\partial x}-1. \end{aligned}$$

Combining obtained expressions we get the system of three equations:

$$\begin{aligned} x\left[ {{f}_{1}}(x,w)-{{f}_{0}}(x,w) \right] =g(x,w)+x\frac{\partial g(x,w)}{\partial x}-1, \end{aligned}$$
$$\begin{aligned} \left[ {{f}_{1}}(x,w)-{{f}_{0}}(x,w) \right] =jw\frac{\sigma }{\mu }g(x,w)+\frac{\partial g(x,w)}{\partial x}-\frac{\sigma }{\mu }{{f}_{1}}(x,w), \end{aligned}$$
$$\begin{aligned} (x-\frac{\mu }{\sigma })\left[ {{f}_{1}}(x,w)-{{f}_{0}}(x,w) \right] =\left( 1-jw \right) g(x,w)+\left( x-\frac{\mu }{\sigma } \right) \frac{\partial g(x,w)}{\partial x}-1. \end{aligned}$$

Eliminating \({{f}_{1}}(x,w),{{f}_{0}}(x,w)\) from this system, we obtain the equation for the function g(x, w), solving which we find:

$$\begin{aligned} g(x,w)=\frac{\frac{\mu }{\sigma }}{\frac{\mu }{\sigma }-jw}, \end{aligned}$$
(19)

where g(x, w) is a conditional characteristic function of exponential distribution with parameter \(\alpha =\frac{\mu }{\sigma }\).

Let’s pass from the conditional characteristic function g(x, w) to the characteristic function g(w):

$$\begin{aligned} g(w)=\int \limits _{0}^{+\infty }{g(x,w)\gamma \left( x \right) dx}. \end{aligned}$$

It is easy to show that the inverse Fourier transform has the form of the probability distribution density of the limiting value of \(\nu (t)\):

$$\begin{aligned} P(z)=\int \limits _{0}^{\infty }{\gamma \left( x \right) \frac{\mu }{x\sigma }}\exp \left\{ -\frac{\mu }{x\sigma }z \right\} dx. \end{aligned}$$
(20)

Low Rate of Retrials Condition. Making substitutions \(\sigma =\varepsilon \), \(i\varepsilon =x\), \({{G}_{k}}(i,u)={{g}_{k}}(x,u,\varepsilon )\) in (5), (6) we obtain:

$$\begin{aligned} \begin{gathered} -(\lambda +x){{g}_{0}}(x,u,\varepsilon )+\lambda {{g}_{1}}(x,u,\varepsilon )\\ +\,(x-\varepsilon ){{g}_{1}}(x-\varepsilon ,u,\varepsilon )+\varepsilon =0,\\ - (\lambda +\mu +\varepsilon ){{g}_{1}}(x,u,\varepsilon )+\mu {{g}_{0}}(x,u,\varepsilon )\\ +\,\lambda {{g}_{1}}(x+\varepsilon ,u,\varepsilon )+{{e}^{ju}}\varepsilon {{g}_{1}}(x,u,\varepsilon )=0. \end{gathered} \end{aligned}$$
(21)

Step 1. Let \(\varepsilon \rightarrow 0\) in (21). Denote

$$\begin{aligned} \underset{\varepsilon \rightarrow 0}{\mathop {\lim }}\,{{g}_{k}}(x,w,\varepsilon )={{g}_{k}}(x,w). \end{aligned}$$

We obtain the following system for \({{g}_{k}}(x,w)\):

$$\begin{aligned} \begin{gathered} -(\lambda +x){{g}_{0}}(x,u)+(\lambda +){{g}_{1}}(x,u)=0,\\ -\mu {{g}_{1}}(x,u)+\mu {{g}_{0}}(x,u)=0. \end{gathered} \end{aligned}$$

This system consist of two equivalent equations and \({{g}_{0}}(x,w)={{g}_{1}}(x,w)=g(x,w)\). Step 2. Let’s rewrite \({{g}_{k}}(x,w,\varepsilon )\) from (21) as follows:

$$\begin{aligned} {{g}_{k}}(x,w,\varepsilon )=g(x,w)+\varepsilon {{f}_{k}}(x,w)+o(\varepsilon ), \end{aligned}$$
(22)

and then rewrite (21):

$$\begin{aligned} \begin{gathered} - (\lambda +x){{g}_{0}}(x,u,\varepsilon )+\lambda {{g}_{1}}(x,u,\varepsilon )+x{{g}_{1}}(x,u,\varepsilon )\\ -\,\varepsilon \frac{\partial \left[ x{{g}_{1}}(x,u,\varepsilon ) \right] }{\partial x}+\varepsilon =o(\varepsilon ),\\ - (\lambda +\mu +\varepsilon ){{g}_{1}}(x,u,\varepsilon )+\mu {{g}_{0}}(x,u,\varepsilon )+\lambda {{g}_{1}}(x,u,\varepsilon )\\ +\,\varepsilon \frac{\partial \left[ \lambda {{g}_{1}}(x,u,\varepsilon ) \right] }{\partial x}+{{e}^{ju}}\varepsilon {{g}_{1}}(x,u,\varepsilon )=o(\varepsilon ). \end{gathered} \end{aligned}$$
(23)

Substituting decomposition (22) in (23), taking \(\varepsilon \rightarrow 0\) and after performing some actions on the equations, we get the following system:

$$\begin{aligned} \begin{gathered} (\lambda +x)({{f}_{1}}(x,u)-{{f}_{0}}(x,u))=\frac{\partial \left[ xg(x,u) \right] }{\partial x}-1\\ \mu ({{f}_{1}}(x,u)-{{f}_{0}}(x,u))=\frac{\partial \left[ \lambda g(x,u) \right] }{\partial x}+({{e}^{ju}}-1)g(x,u). \end{gathered} \end{aligned}$$

Thus, for the function g(x, u) we obtain the following equation:

$$\begin{aligned} \left[ \lambda (\lambda +x)-\mu \right] \frac{\partial g(x,u)}{\partial x}+\left[ (\lambda +x)({{e}^{ju}}-1)-\mu \right] g(x,u)+\mu =0 \end{aligned}$$
(24)

In limiting case \(k=i\varepsilon =x\) and k is the solution of the Eq. (13). This equation is equal to the coefficient of the derivative \(\frac{\partial g(x,u)}{\partial x}\). Then the coefficient is zero in (24) and \(k=x\):

$$\begin{aligned} \left[ (\lambda +k)({{e}^{ju}}-1)-\mu \right] g(x,u)+\mu =0. \end{aligned}$$

Solving this system for g(x, u) we obtain:

$$\begin{aligned} g(u)=\frac{1-\frac{\lambda }{\mu }}{1-{{e}^{ju}}\frac{\lambda }{\mu }}. \end{aligned}$$

Thus, probability distribution of \(\nu (t)\) the number of returns of the tagged request to the orbit is geometric

$$\begin{aligned} P(\nu (t)=n)\approx (1-p){{p}^{n}}, \end{aligned}$$
(25)

where \(\rho =\frac{\lambda }{\mu }\), \(n=0,1,2,\ldots \)

6 Distribution of the Waiting Time in the Orbit

Using results obtained in previous sections, we derive expressions for waiting time asymptotic distributions under considered conditions.

Heavy Load Condition. Using the found distribution density, let’s get an approximation of the asymptotic discrete probability distribution of the number of returns of the tagged request to the orbit:

$$\begin{aligned} {{P}_{1}}(n)=P((1-\rho )n)\cdot {{\left( \sum \limits _{m=0}^{\infty }{P((1-\rho )m)} \right) }^{-1}}. \end{aligned}$$
(26)

Substituting above distribution into (1), we obtain:

$$\begin{aligned} \begin{gathered} G(u)=E\left\{ {{e}^{juW}} \right\} =(1-r)+r\sum \limits _{n=0}^{\infty }{E\left\{ {{{e}^{juW}}}/{\nu =1+n}\; \right\} }P\left\{ \nu (t)=n \right\} \\ =(1-r)+r\sum \limits _{n=0}^{\infty }{{{\left( \frac{\sigma }{\sigma -ju} \right) }^{1+n}}{{P}_{1}}(n)}. \end{gathered} \end{aligned}$$

As a result, we have found the limiting characteristic function of the waiting time of the request in a M/M/1 RQ system under a heavy load condition. Applying the inverse Fourier transform of the obtained G(u), we find the asymptotic distribution of the waiting time of the request in the orbit.

Low Rate of Retrials Condition. In previous section we found that probability distribution of \(\nu (t)\) under low rate of retrials condition is geometric with parameter \(\rho =\frac{\lambda }{\mu }\). Substituting this distribution in (1), we obtain:

$$\begin{aligned} \begin{gathered} G(u)=E\left\{ {{e}^{juW}} \right\} =(1-r)+r\sum \limits _{n=0}^{\infty }{E\left\{ {{{e}^{juW}}}/{\nu =1+n}\; \right\} }P\left\{ \nu (t)=n \right\} \\ =(1-r)+r\sum \limits _{n=0}^{\infty }{{{\left( \frac{\sigma }{\sigma -ju} \right) }^{1+n}}(1-p){{p}^{n}}}=(1-r)\\ +\, r\frac{\sigma }{\sigma -ju}(1-p){{\sum \limits _{n=0}^{\infty }{\left( \frac{\sigma }{\sigma -ju}p \right) }}^{n}}=(1-r)+r\frac{\sigma (1-p)}{\sigma (1-p)-ju} \end{gathered} \end{aligned}$$

Obtained G(u) is the limiting characteristic function of the waiting time of the request in a M/M/1 RQ system under a low rate of retrials condition. The distribution of W in this case is two-phase hyper exponential distribution with an infinite parameter in the first phase and a parameter \(\sigma (1-p)\) in the second phase.

7 Numerical Results

Probability distributions \({{P}_{1}}(n)\) and \(P(\nu (t)=n)\) given in (26) and (25) have been obtained by the method of asymptotic analysis under a heavy load and a low rate of retrials conditions respectively.

We compare the resulting asymptotic distribution and the numerical solution of the system of Eq. (5), (6) in order to investigate the applicability of these asymptotic results for prelimit situations. Also, for that purpose Kolmogorov distances between distributions were found:

$$\begin{aligned} \begin{gathered} {{\varDelta }_{1}}=\underset{0\le n<\infty }{\mathop {\max }}\,\left| \sum \limits _{j=0}^{n}{{{P}_{1}}(j)}-\sum \limits _{j=0}^{n}{\pi \left( j \right) } \right| ,\\ \varDelta =\underset{0\le n<\infty }{\mathop {\max }}\,\left| \sum \limits _{j=0}^{n}{P(j)}-\sum \limits _{j=0}^{n}{\pi \left( j \right) } \right| . \end{gathered} \end{aligned}$$

Let us denote the prelimit probability distribution of the number of returns of the tagged request to the orbit by \(\pi (n)\). We obtain it by numerical methods similar as it is shown in [27]. Using the law of total probability, \(\pi (n)\) can be written in the following form:

$$\begin{aligned} \pi \left( n \right) =\sum \limits _{i=0}^{\infty }{\left[ {{\varPi }_{0}}\left( n,i \right) {{P}_{0}}(i)+{{\varPi }_{1}}\left( n,i \right) {{P}_{1}}(i) \right] }, \end{aligned}$$
(27)

where unconditional probabilities \({{P}_{k}}(i)\) are solutions of (2) and normalization condition. In order to find conditional probabilities \({{\varPi }_{k}}\left( n,i \right) =P\left( {\nu (t)=n}/{k(t)=k,i(t)=i}\; \right) \), let’s write conditional characteristic function \({{G}_{k}}(i,u)\) as follows:

$$\begin{aligned} {{G}_{k}}(i,u)=\sum \limits _{n=0}^{\infty }{{{e}^{jun}}{{\varPi }_{k}}\left( n,i \right) }, \end{aligned}$$

and substitute this representation into inverse Kolmogorov Eq. (5), (6) for \({{G}_{k}}(i,u)\):

$$\begin{aligned} \begin{gathered} -(\lambda +i\sigma )\sum \limits _{n=0}^{\infty }{{{e}^{jun}}{{\varPi }_{0}}\left( n,i \right) }+\lambda \sum \limits _{n=0}^{\infty }{{{e}^{jun}}{{\varPi }_{1}}\left( n,i \right) }\\ +(i-1)\sigma \sum \limits _{n=0}^{\infty }{{{e}^{jun}}{{\varPi }_{1}}\left( n,i-1 \right) }+\sigma =0\\ -(\lambda +\mu +\sigma )\sum \limits _{n=0}^{\infty }{{{e}^{jun}}{{\varPi }_{1}}\left( n,i \right) }+\mu \sum \limits _{n=0}^{\infty }{{{e}^{jun}}{{\varPi }_{0}}\left( n,i \right) }\\ +\lambda \sum \limits _{n=0}^{\infty }{{{e}^{jun}}{{\varPi }_{1}}\left( n,i+1 \right) }+\sigma \sum \limits _{n=1}^{\infty }{{{e}^{jun}}{{\varPi }_{1}}\left( n-1,i \right) }=0. \end{gathered} \end{aligned}$$

Equating coefficients of corresponding powers of the exponent the following systems of equations for probabilities \({{\varPi }_{k}}\left( n,i \right) \) were obtained:

For \(n=0:\)

$$\begin{aligned} \begin{gathered} -(\lambda +i\sigma ){{\varPi }_{0}}\left( 0,i \right) +\lambda {{\varPi }_{1}}\left( 0,i \right) +(i-1)\sigma {{\varPi }_{1}}\left( 0,i-1 \right) +\sigma =0\\ -(\lambda +\mu +\sigma ){{\varPi }_{1}}\left( 0,i \right) +\mu {{\varPi }_{0}}\left( 0,i \right) +\lambda {{\varPi }_{1}}\left( 0,i+1 \right) =0, \end{gathered} \end{aligned}$$
(28)

For \(n\ge 1:\)

$$\begin{aligned} \begin{gathered} -(\lambda +i\sigma ){{\varPi }_{0}}\left( n,i \right) +\lambda {{\varPi }_{1}}\left( n,i \right) +(i-1)\sigma {{\varPi }_{1}}\left( n,i-1 \right) =0,\\ -(\lambda +\mu +\sigma ){{\varPi }_{1}}\left( n,i \right) +\mu {{\varPi }_{0}}\left( n,i \right) +\lambda {{\varPi }_{1}}\left( n,i+1 \right) +\sigma {{\varPi }_{1}}\left( n-1,i \right) =0. \end{gathered} \end{aligned}$$
(29)

We find exact values of \({{P}_{k}}(i)\) and \({{\varPi }_{k}}\left( 0,i \right) \) by solving (2) and (28) for some given parameters \(\lambda \), \(\mu \), \(\sigma \) using numerical methods. Then we substitute found \({{P}_{k}}(i)\) and \({{\varPi }_{k}}\left( 0,i \right) \) values into (27) and get the probability \(\pi \left( 0 \right) \). Solving (29) by numerical methods for some given parameters \(\lambda \), \(\mu \), \(\sigma \) we similarly find \({{\varPi }_{k}}\left( n,i \right) \) for \(n=1,2,3,...\) (Table 2).

Table 1. The difference between the numerical distribution \(\pi \left( n \right) \) and asymptotic distribution \(P(\nu (t)=n)\) under a low rate of retrials condition for various parameters
Full size table
Table 2. The difference between the numerical distribution \(\pi \left( n \right) \) and asymptotic distribution \({{P}_{1}}(n)\) under a heavy load condition for various parameters
Full size table

By substituting these values in (27) we can find the numerical probability distribution \(\pi \left( n \right) \).

We consider different parameters setup of \(\lambda \), \(\mu \), \(\sigma \) for each asymptotic distribution. In Fig. 1 prelimit probabilities \(\pi \left( n \right) \) and asymptotic probabilities \({{P}_{1}}(n)\) are compared to each other. In Fig. 2 prelimit probabilities \(\pi \left( n \right) \) and asymptotic probabilities \(P(\nu (t)=n)\) are shown. Table 1 present Kolmogorov distances between the numerical and asymptotic distributions for various parameters. The analysis of obtained numerical results shows that under these parameters obtained asymptotic distributions and prelimit distributions are very close to each other and asymptotic method is very effective.

Fig. 1.
figure 1

The difference between the numerical \(\pi \left( n \right) \) and asymptotic \({{P}_{1}}(n)\) distributions under a heavy load condition, \(\lambda =0.95\), \(\mu =1\), \(\sigma =0.1\)

Full size image
Fig. 2.
figure 2

The difference between the numerical \(\pi \left( n \right) \) and asymptotic \(P(\nu (t)=n)\) distributions under a low rate of retrials condition, \(\lambda =0.5\), \(\mu =1\), \(\sigma =0.1\)

Full size image

8 Conclusion

In this paper was presented an asymptotic analysis of the waiting time and the number of returns of a M/M/1 retrial queueing system. Two different cases were considered. First we conducted analysis under a heavy load condition and then under a low rate of retrials condition. Numerical illustrations and results show the effectiveness of asymptotic method for the considered retrial queuing system.