Stable Periodic Economic Cycles from Controlling

Abstract

When a system becomes unstable or noise becomes excessive, often regulations of the form of limiters (barriers obstructing excursion into undesired areas of the phase space) are imposed. It is hoped that by the influence of this element, the system can be calmed and its behaviour can be optimised. In what follows below, we consider a simple noisy nonlinear economics model that self-organises towards criticality. We demonstrate that the inherent effect of limiters is the emergence of stable cycles and that limiters need to be implemented with care in order to obtain an optimised system response. In particular, the implementation of the limiter around the maximal system response has generally a suboptimal effect, whereas the placement of the limiter in the vicinity of a period-one cycle will generally yield the optimal effect. We also show that, as a downside of the proposed approach, in order to control on period-one cycles, generally strong interventions are required. In democratic countries, a transparent control policy would therefore be an indispensable for its implementation. The discussed framework may prove helpful for this purpose.

1 Introduction into Control Fundamentals

The emergence of periodic economic cycles in western economies is a ubiquitous undesired, puzzling and still poorly understood, observation. Even against the large noise component in the data, a relatively simple spectral analysis suggests the presence of different periodic components. Among the most remarkable cycles in the annual GDP growth rates, the Kitchin [19], the Juglar [16], and, less prominent, the Kuznets [22] cycles stand out. As economic booms and bouts affect modern societies with a strong and direct impact on individual biographies, there have been considerable efforts to prevent them or at least to smoothen their effects. Until the 1970s, as the legacy of Keynes [18], cycles were regarded as primarily due to variations in demand (company investments and household consumptions). Unfortunately, this theory offered very little explanation for the observed wavelength of the periodicities. Despite, under its influence, economic analysis focused on monetary and fiscal measures to offset demand shocks. During the 1970s, it became obvious that stabilisation policies based on this theory failed. Shocks on the supply side, in the form of rising oil prices and declining productivity growth, emerged to be equally crucial for the generation of cycles. In 1982, Kydland and Prescott [23] finally offered new approaches to the control of macroeconomic developments. One of their conclusions was that the control should be kept constant throughout a cycle, in order to minimise negative effects.

The remarkable stability of the observed oscillatory behaviour shown in resisting not only against all occurred technological transformations but even against all the attempts to eliminate them, points to a simple, fundamental origin of the phenomenon. It also nourishes the hope that if the origin of the phenomenon could be understood, this insight might be used to engineer towards a softer course of the oscillations. An extreme form of this approach was already taken in the former socialist countries by following the Marxist [26] interpretation of economy, leading to the centrally planned economies. To deal with this problem in democratic societies, it is, however, necessary to be able to communicate a sufficiently simple optimality policy. For this, an understanding of the fundamental nature of the phenomenon and of the response that can be expected from control attempts is necessary. For this, simple models may provide important guidelines [24].

Stability of the oscillations with cycles of nearly doubled wavelength from Kitchin, to Juglar, to Kuznets (roughly 4, 8, and 16 years, the last obviously to be taken with a grain of salt) suggests that the prediction problem of economics might closely be related to chaotic processes. Although the question to which extent real economies can be classified as chaotic can readily be disputed, low-dimensional chaotic models might yield insight into the mechanisms that rule economics and how economics respond to control policies. In particular, for chaotic processes, strategies of control and for prediction have been developed that offer to be adapted for economics. Note that already in early implementations of optimal control programs, it was found that control mechanisms themselves may induce chaotic behaviour [6, 7, 28] and render optimal control impossible. As a general mechanism inherent in many of these examples, chaos is induced by a preference function that depends on past experience. This delay mechanism naturally makes a dynamical system infinite-dimensional, which has the tendency of resulting in a chaotic behaviour. Despite these insights, the quest for a fundamental simple dynamical model for economic cycles is still open.

A connected and very natural goal in economics is the desire to control economic behaviour, in particular when economics develop wave-like fluctuation tendencies. We shall suppose in the following that we are given a ‘temporally stable’ system—meaning by this that we have a behaviour following fixed equations of dynamics, at least over a considered time span, be them periodic or chaotic. That equations may change, expressed in a dependence of system parameters, may be reasonable to assume, but only beyond a relatively long time span compared to the time horizon needed to establish and to maintain control. Getting control over a dynamical systems into a desired system behaviour can be achieved by the so-called control algorithms.

2 Problem Setting

In chaotic systems, all trajectories are unstable. The aim of chaos control is to stabilise chosen natural trajectories, using additional control structures, in order to render them robust against external perturbations from a large interval of perturbation strength. In the Handbook of Chaos Control,Schuster1999, the interested reader will find the following passage from the excellent introductory article by Lai and Grebogi:

Besides the occurrence of chaos in a large variety of natural processes, chaos may also occur because one may wish to design a physical, biological or chemical experiment, or to project an industrial plant, to behave in a chaotic manner.

In many-particle systems, often the collective behavior is more ordered than the individual behavior (e.g., in biology (neurons, flocks of animals), economics, etc.), so that hidden control mechanisms seem to be at work. From a similar perspective, if a system request is to be able to respond with selectable periodic behavior, it may be simpler to build first a chaotic system and then to exploit control mechanisms to produce the desired response. To identify the control mechanisms and, in particular, to stabilise the desired simpler behaviours, is the task of chaos control. To realise the full power of this concept, one has to remark that chaos control is also applicable to systems that are not inherently chaotic. The only difference here is that if control is abandoned, the trajectories will settle on the stable solution instead of a chaotic solution in the former case. In what follows, we will provide such examples.

A remarkable illustration of this concept is gait-control, i.e., the control of the motion pattern displayed by living systems. It is well-known that animals (amphibia, horses, even humans) change their gate depending on the environmental conditions. Depending on the weight a human is carrying and on the roughness or steepness of the environment, humans dance, march, set on foot after another, etc. It is similarly imaginable that horses have an essentially chaotic gait generator that is controlled by environment, by body weight (changing with age), and by the rider on the horseback, to change from trod, gallop, backward motion, etc. A similar simple control can be expected to be at work in macroeconomics, which is the major theme in this chapter. In principle, on a more general level, chaos control is the resurrection of the old classical problem of the control of a dynamical system seen under a novel angle. In the following, we provide a short overview of chaos control, before we focus on one particular control mechanism where we explore its relevance in the context of economics.

We may distinguish five groups of control mechanisms.

• (1) OGY-parametric control

• (2) Local stabilisation control

• (3) Delay-coordinate control

• (4) Feedback control

• (5) Limiter control

Below we will present but an introductory outline of these methods mostly using 1-d iterated map applications; for a broader and deeper view on this subject we may, e.g., recommend Ref. [35] to the reader. Throughout Sect. 15.2, we will use the letter a to denote the monitored system parameter [43].

1. Parametric Control

This most popular control method was put forward by E. Ott, C. Grebogi and J.E Yorke around 1990 (the ‘OGY’- method [30]). Let us expose the working principle first in dimension one, using the quadratic parabola f :  x _n+1 = a ₀ x _n (x _n − 1) as the example, and let us consider, to start with, an unstable periodic orbit {x(1), x(2), …, x(n)} of period n. Because of the orbits’ instability, after i iterations, the real orbit x _i will not coincide with the ‘ideal’ point x(i). We thus have

$$\displaystyle \begin{aligned} \begin{array}{rcl} x_{i+1}-x(i+1) & \approx &\displaystyle \frac{\partial f}{\partial x}|{}_{x=x(i), a=a_0} (x_i-x(i))+ \frac{\partial f}{\partial a}|{}_{x=x(i), a=a_0}\varDelta a_i\\ & =&\displaystyle a_0 (1-2 x(i))(x_i-x(i))+ x(i) (1-x(i)) \varDelta a_i. \end{array} \end{aligned} $$

If we want x _i+1 to stay ultimately close in a neighbourhood of x(i + 1), we should have |x(i + 1) − x _i+1|≈ 0. From this it follows that we need to choose

$$\displaystyle \begin{aligned}\varDelta a_i=a_0 \frac{(2 x(i)-1)({x}_i-x(i))}{x(i) (1-x(i))}. \end{aligned}$$

In higher dimensions, we have

$$\displaystyle \begin{aligned} \begin{array}{rcl} {\mathbf{x}}_{i+1}=\mathbf{F}({\mathbf{x}}_i, a), \end{array} \end{aligned} $$

where a again denotes an external parameter. Similarly to above we will have

$$\displaystyle \begin{aligned} {\mathbf{x}}_{i+1} -\mathbf{x}(i+1)(a_0) & \approx {\mathbf{D}}_{\mathbf{x}} \mathbf{F}(\mathbf{x},a)|{}_{\mathbf{ x}(i)(a_0), a_0}({\mathbf{x}}_{i} -\mathbf{x}(i)(a_0)) \\ & \quad + {\mathbf{D}}_a \mathbf{F}(\mathbf{x},a)|{}_{\mathbf{x}(i)(a_0), a_0} (a-a_0) . \end{aligned} $$

From the first contribution we obtain a n × n-matrix applied to a vector of dimension n, and from the second contribution we get a vector of length n. Using the ansatz

$$\displaystyle \begin{aligned} \begin{array}{rcl} a-a_0\approx -{\mathbf{K}}^T ({\mathbf{x}}_{i} -\mathbf{x}(i)(a_0)), \end{array} \end{aligned} $$

to render the behaviour at x(i)(a) stable, the 1 × n Matrix K ^T needs to be modified accordingly. This goal is achieved if

$$\displaystyle \begin{aligned} \begin{array}{rcl} ({\mathbf{x}}_{i+1} & -&\displaystyle \mathbf{x}(i)(a_0)) \\ & =&\displaystyle \big({\mathbf{D}}_{\mathbf{x}} \mathbf{F}(\mathbf{x},a)|{}_{\mathbf{x}(i)(a_0), a_0} - {\mathbf{D}}_a \mathbf{F}(\mathbf{x},a)|{}_{\mathbf{x}(i)(a_0), a_0} \mathbf{ K}^T\big) ({\mathbf{x}}_{i} -\mathbf{x}(i)(a_0))\\& =:&\displaystyle \mathbf{J}({\mathbf{x}}_{i} -\mathbf{ x}(i)(a_0)) ({\mathbf{x}}_{i} -\mathbf{x}(i)(a_0)) \end{array} \end{aligned} $$

is asymptotically stable, which is the case if all eigenvalues of the n × n matrix J are of absolute size smaller than unity.

For the two-dimensional dissipative Hénon map written in the form F : {x, y}→{a + by − x ², x} we obtain for the period-1 orbit {x ₁, y ₁} ${\mathbf {D}}_{\mathbf {x}}\mathbf {F}=\left ( \begin {array}{rr} -2 x_1 & b\ \\ 1\quad \quad & 0\quad \end {array}\right ),$with eigenvalues $\mu _{s/u}=-x_1 \pm (b+x_1 ^2)^{1/2}$ and eigenvectors {μ _s∕u, 1} and D _a F = (1, 0). Hence, the control matrix obtains the form $\mathbf {K}= \left ( \begin {array}{rr} -2x_1-k_1 & b-k_2\\ 1\quad \quad \quad & 0\quad \quad \end {array}\right ).$

The determination of the control matrix K so that all eigenvalues are of absolute size smaller than unity is a well-known procedure in control theory (called ‘pole placement’). The OGY-method chooses to set the unstable eigenvalues of the matrix K ^T to zero while letting the stable eigenvalues unchanged. The consequence of this is that after control has been switched on, the trajectories approach the fixed point of the periodic orbit along its stable manifold (in principle, also other, less natural, choices are possible).

More generally, let for parametric control a ₀ be the parameter value at which an orbit should be stabilised. Then we may write

$$\displaystyle \begin{aligned} {\mathbf{x}}_{i+1}-\mathbf{x}(i+1)(a_0) &\approx \mathbf{D}\mathbf{F}(\mathbf{ x}(i)(a),a) ({\mathbf{x}}_i- \mathbf{ x}(i)(a_0))\\ &\approx {\mathbf{D}}_{\mathbf{x}} \;\mathbf{F}(\mathbf{x}(i))|{}_{\mathbf{ x}(i)=\mathbf{x}(i)(a_0)} ({\mathbf{x}}_{i}-\mathbf{x}(i)(a_0)) \\ & \quad + {\mathbf{D}}_a{\mathbf{D}}_{\mathbf{x}(i)} \;\mathbf{F}(\mathbf{x}(i)(a), a)|{}_{a=a_0}\varDelta a_i. \end{aligned} $$

From this we get

$$\displaystyle \begin{aligned}{\mathbf{x}}_{i+1}-\mathbf{x}(i+1)(a_0) \approx \mathbf{g} \varDelta a_i+ \mathbf{D}\mathbf{F}(\mathbf{x}(i)(a_0)) ({\mathbf{x}}_i- \mathbf{x}(i)(a_0)-\mathbf{g} \varDelta a_i ), \end{aligned}$$

where $\mathbf {g}=\frac {\partial \mathbf {x}(i)(a)}{\partial a}|{ }_{a=a_0} \approx \frac {\mathbf {x}(i)(a)-\mathbf {x}(i)(a_0)}{\varDelta a_i}$. Let {f _i}, i = 1, …, n denote the contravariant vector basis to the eigenvectors {e ₁, …, e _n} (f _j e _i = δ _ji). Then we have

$$\displaystyle \begin{aligned} \begin{array}{rcl} {\mathbf{D}}_{\mathbf{x}}\mathbf{F}(\mathbf{x}(i)(a_0))=\mu_{u} {\mathbf{e}}_{u} {\mathbf{f}}_{u}+\mu_{s} {\mathbf{e}}_{s} {\mathbf{f}}_{s}, \end{array} \end{aligned} $$

where μ _u,s describes the unstable/stable eigenvalues. From this we get

$$\displaystyle \begin{aligned}{\mathbf{f}}_u ({\mathbf{x}}_{i+1}-\mathbf{x}(i)(a_0))=0, \end{aligned}$$

which implies

$$\displaystyle \begin{aligned}{\mathbf{f}}_u (\mathbf{g} \varDelta a_i+ \mathbf{D}\mathbf{ F}(\mathbf{x}(i)(a_0)) ({\mathbf{x}}_i- \mathbf{x}(i)(a_0)-\mathbf{g} \varDelta a_i)=0. \end{aligned}$$

As a consequence, we obtain

$$\displaystyle \begin{aligned}\mathbf{g} \varDelta a_i \approx \mathbf{D}\mathbf{F}(\mathbf{ x}(i)(a_0))({\mathbf{x}}_i-\mathbf{x}(i)(a_0))- \mathbf{g} \varDelta a_i), \end{aligned}$$

which implies that, at time i, we need to choose the parametric control

$$\displaystyle \begin{aligned}\varDelta a_i \approx \frac{{\mathbf{D}}_{\mathbf{x}}\mathbf{F}(\mathbf{x}(i)(a_0))( \mathbf{ x}_i-\mathbf{x}(i)(a_0))} {\mathbf{g}(\mathbf{Id}- {\mathbf{D}}_{\mathbf{x}}\mathbf{F}(\mathbf{ x}(i)(a_0)))}, \end{aligned}$$

or, expressed in terms of stable/unstable manifolds, we need to take

$$\displaystyle \begin{aligned} \varDelta a_i \approx \frac{{\mathbf{f}}_u \mu_u ({\mathbf{x}}_i-\mathbf{ x}(i)(a_0))}{\mathbf{g}(1-\mu_u) {\mathbf{f}}_u}. \end{aligned} $$

(15.1)

From a general point of view, this control only makes sense if the actual orbits are already in the neighbourhood of the orbit that we want to control, which may, in particular initially, take a substantial consumption of time. To speed the process up, targeting algorithms have been designed.

Control Time

The time needed to control on a chosen orbit (called ‘control time’) is of particular interest in applications. For the chosen control strategy, in dimension d = 1, the ansatz

$$\displaystyle \begin{aligned}\langle \tau \rangle\sim \delta^{ -\gamma} \end{aligned}$$

defines the corresponding scaling exponent γ > 0. From

$$\displaystyle \begin{aligned}P(\varepsilon, x(i))= \int_{x(i)-\varepsilon}^{x(i)+\varepsilon} \rho(x(i)) dx \approx 2 \varepsilon \rho(x(i)), \end{aligned}$$

we get

$$\displaystyle \begin{aligned}\langle \tau \rangle= \frac{1}{p(\varepsilon)} \sim \varepsilon^{-1}=\delta^1, \end{aligned}$$

from which one concludes that γ = 1.

In higher dimensions, matters become substantially more complicated. For a class of 2d-maps, the exponent becomes [33]

$$\displaystyle \begin{aligned}\gamma= 1+ \frac{\ln|\mu_u|}{2 \ln(1/|\mu_s|)}. \end{aligned}$$

Control of the dissipative Hénon map, using easy to read elementary Mathematica code, is achieved as follows:

2. Local Stabilisation Control

We return to the one-dimensional case. Let ε be the error made after running through a ‘quasiperiod’ (an imprecise orbit) of length n. This error will, after additional t = n time steps, grow to

$$\displaystyle \begin{aligned}\varepsilon^{\prime} = \varepsilon \prod_{i=1} ^{n} | f^{' }(x_{i})|. \end{aligned}$$

This implies that the value of x _i should be corrected by

$$\displaystyle \begin{aligned}c=\frac{c ^{\prime}} {\prod_{i=1} ^{n} | f^{' }(x_{i})|} \end{aligned}$$

to stabilise the original orbit (see Fig. 15.1 for an illustration). For higher-dimensional systems, the same procedure can be followed, where the correction has to be applied in the direction of the unstable manifold.

Fig. 15.1

Stabilised period 3 in the chaotic regime of the inhibitory interaction to pyramidal neurons. The numerical function was extracted from experimentally measured phase response curves (cf. [41])

This method can be seen as a variant of the parametric control using a particularly simple control parameter. Control is achieved by means of a change of the slope in the orbit point by the increase of the y-coordinate by a value of c:

Control of neural interaction map f(x) in the stable period 2 regime on a period 3 (see Fig. 15.2):

Fig. 15.2

Stabilised period 3 for the inhibitory chaotic neural interaction function

In Fig. 15.3 we demonstrate that control on an unstable periodic orbit can be achieved not only in the domain of chaotic, but also in the regime of stable system behavior.

Fig. 15.3

Stabilised period 5 in the stable regime of the neuron interaction map where the natural motion would be a stable period 2

3. Delay-Coordinate Control

This control method can be particularly simple in experimental applications. Starting from m-dimensional vectors

$$\displaystyle \begin{aligned}\mathbf{x}(t)=(u(t), u(t-t_D), u(t-2 t_D),\ldots), \end{aligned}$$

and the dynamical map of the form

$$\displaystyle \begin{aligned}{\mathbf{x}}_{i+1}=\mathbf{G}({\mathbf{x}}_i, a_i, a_{i-1},\ldots,a_{i-\mu}), \end{aligned}$$

we use again the ansatz

$$\displaystyle \begin{aligned}({\mathbf{x}}_{i+1} -\mathbf{x}(i)(a_0))= \big({\mathbf{D}}_{\mathbf{ x}} \mathbf{G}(\mathbf{x},a)|{}_{\mathbf{x}(i)(a_0), a_0} - {\mathbf{D}}_a \mathbf{G}(\mathbf{x},a)|{}_{\mathbf{x}(i)(a_0), a_0} \mathbf{ K}^T\big) ({\mathbf{x}}_{i} -\mathbf{x}(i)(a_0)) \end{aligned}$$

that leads to

$$\displaystyle \begin{aligned}({\mathbf{x}}_{i+1} -\mathbf{x}(i)(a_0))= \mathbf{ A}({\mathbf{x}}_{i} - \mathbf{x}(i)(a_0))+{\mathbf{B}}_a (a(i)-a_0)+{\mathbf{B}}_b (a_{i-1}-a_0) \end{aligned}$$

with partial derivatives at x _i(a ₀) and μ ₀, respectively. The linear control

$$\displaystyle \begin{aligned}a_i-a_0=-{\mathbf{K}}^T({\mathbf{x}}_i-\mathbf{ x}(i)(a_0))-k(a_{i-1}-a_0), \end{aligned}$$

with k as the control parameter, can, using

$$\displaystyle \begin{aligned}{\mathbf{y}}_{i+1}=({\mathbf{x}}_{i+1},a_i), \end{aligned}$$

be written in a simpler way as

$$\displaystyle \begin{aligned}{\mathbf{y}}_{i+1}-\mathbf{y}(i)(a_0)= \big({\mathcal A}-{\mathcal B \mathbf{K}}^T\big) ({\mathbf{y}}_{i}-\mathbf{y}(i)(a_0)), \end{aligned}$$

where ${\mathcal A}=(\{\mathbf {A}, {\mathbf {B}}_b\},\{0,0\})$, ${\mathcal B}=(\mathbf { B}_a, 1)$, and ${\mathcal K}=(\mathbf {K}, k)$ are the quantities in the generated product space. Again, this equation can be stabilised using the method of pole placement; matrix ${\mathcal A}$ can again be found by a method of numerical linear approximation. For obtaining the experimental vectors B _a and B _b, one has to rely on the system parameter a. In Fig. 15.4 we demonstrate that control on an unstable periodic orbit can be achieved with varying time delay.

Fig. 15.4

Delay-coordinate control (system: neuronal interaction). A portion of the signal with a fixed delay (varying in 11 steps) was added to the signal

4. Feedback Control

This method can be seen as a special case if the delay-coordinate control, where we add to the dynamical system the by a factor c down-tuned system output of time t − τ. The combined system (again for simplicity we constrain our presentation to one-dimensional systems) can then be written as

$$\displaystyle \begin{aligned} \begin{array}{rcl} f(x,c): \;\;\; x_{i+1}=\tilde{f}(x_{i})+c x_{i-\tau}. \end{array} \end{aligned} $$

The method depends on the two parameters c and τ. The variational equation has the form

$$\displaystyle \begin{aligned}\frac{dv}{dt}= D_x f(x(t),0) \ v(t) +c D_c f(x(t),0) \ D g(x(t)) \ (v(t)-v(t-\tau)), \end{aligned}$$

where g(t) is the (generally scalar) measurement at time t. The boundary of stabilisation can be explored by using Floquet methods.

Feedback control program outline:

As will have emerged from our presentation so far, a general problem with the described control mechanisms is that they require considerable knowledge of the system to be controlled and that the system needs to be carefully led towards the desired solution. For many systems, this may not be easily available, and the control process may be rather slow. In the next section, we will present the limiter control method that avoids these complications and will be seen to be pretty close to the control mechanisms that are applied in macroeconomics. With this, for economics most relevant, control method we can easily achieve control on orbits of the original system, as well as, additionally, on desired orbits of the system plus controller.

3 Controlling Economics by Thresholds

In economics, controls are applied according to economics goals that the controller (state, federal banks, governments) wants to achieve. This is generally done by defining limits or bandwidths, after whenever crossing them, control actions take place. We will present in the following a chaos control method that is more realistic seen from the point of view of economics, using the quadratic map as the fundamental example of complex nonlinear dynamics. Later, we will motivate why the example of the logistic map is very appropriate and essential for describing the evolution of macroeconomic processes. Our derivation will provide conditions for optimal stabilisation of economic dynamics and then we will explain why exactly the desire to control the fluctuations will even enhance periodic cycles, if not even the control itself is at their origin.

Let us thus describe how simple control mechanisms in economics may affect the evolution of the dynamics. Let us describe the threshold of the control threshold by x _th, above which the economy no longer develops according to its intrinsic dynamics. For a quadratic parabola, threshold control can be described by the equation

$$\displaystyle \begin{aligned} x_{n+1} = \begin{cases} \mu x_n (1-x_n) & \text{if} \quad \mu x_n(1-x_n)\leq x_{th} \\ (1-\alpha) \mu x_n(1-x_n)+\alpha x_{th} & \text{if} \quad \mu x_n(1-x_n)>x_{th}. \end{cases} {} \end{aligned} $$

(15.2)

Here, x _n and x _n+1 denote the state variable at time n and n + 1, respectively. − α is the proportionality factor of the perturbation by the applied control, whereas x _th defines the threshold for the state variable above which the correction is applied control, see Fig. 15.5a.

Fig. 15.5

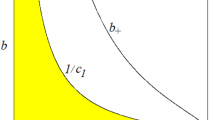
Modified maps used for limiter control of the period-1 orbit (a) and the period-2 orbit (b) of the logistic map, see (15.2). (a) Full line α _min = 0.75 and dashed line α _max = 1.5 indicate two intervention thresholds that can be seen as a chosen intervention bandwidth. Superstable orbits are obtained for α = 1 (dotted line). (b) Full line: α _min = 0.93750; dashed line: α _max = 1.24999; fine dashes: α = 1. Note that the present use of α differs from the later use of the symbol for describing the ‘scaling constant’

For general maps f, period-k unstable periodic orbits (’UPO’) are determined by the fixed points of the k-fold iterated map f ^k (cf. Fig. 15.5b), with their stability being given by the derivative of this map at the fixed points. If the absolute value of the derivative of the control map is less than unity, the system can be stabilised on the UPO. We will show that based on this condition, the control mechanism can be optimised. Figure 15.5 shows the map when modified by the control, for different values of α. Without loss of generality, we have set the system parameter to μ = 4, the fully developed chaos case (maximal chaos). There are two limiting values within which the map can be controlled: a maximal value α _max > 1 (dashed line) and a minimal value α _min < 1 (full line). The special case α = 1 provides superstable UPOs; this case already has been analysed by L. Glass et al. [12]. As the simplest example for our theoretical analysis, we focus on the unstable period-1 orbit. The derivative of the unperturbed system is μ(1 − 2x ^∗) = −2, where x ^∗ = 0.75 denotes the fixed point; the absolute slope larger than 1 refers to an unstable orbit. First we consider the case where α < 1, cf. Fig. 15.5. Driving the system slightly out of the fixed point x ^∗, the trajectory alternates between the two branches of the map that meet at the fixed point. In order to make the fixed point attractive, the absolute value of the product of the derivatives of the two branches at the fixed point must be smaller than 1. This leads to a condition for the minimal value of α,

$$\displaystyle \begin{aligned}\mid (1-\alpha)(\mu (1-2x^{*}))^2 \mid<1.\end{aligned}$$

Thus, the lower threshold becomes α _min = 0.75. In the case of α > 1, (long dashes), the trajectory propagates only along the perturbed branch after pushing the system out of the fixed point. Therefore, the corresponding condition is

$$\displaystyle \begin{aligned}\mid (1-\alpha)(\mu(1-2x^{*}))\mid<1,\end{aligned}$$

which yields the upper limit α _max = 1.5. These results can readily be generalised to stabilise orbits of higher periodicity.

Note that this procedure can also be applied to the control of natural systems (cf. Ref. [8], first experiment) and for higher-dimensional maps. For α = 1, the derivative becomes zero at the fixed point and the periodic orbits are superstable (Fig. 15.5, short dashes). Experimentally, this corresponds to a limiter x _th that is rigid, i.e., cannot be modified at all. At this point, the periodic orbits become optimally stable and therefore almost insensitive to noise (as a matter of fact, the diode used as limiter in the second experiment of Ref. [8] approximates this case). Because of these properties, this method is called ‘hard limiter’ control (HLC) [43,44,45].

This procedure of stabilising UPOs can be adapted for two-dimensional maps, as is shown by the example of the Hénon map, see Fig. 15.6. For the controlled Hénon map $x_{n+1}=\tilde {x}_{n+1}:=a+b y_{n}-x^{2}$, if $\tilde {x}_{n+1} \leq x_{th}$ and $x_{n+1}= (1-\alpha ) \tilde {x}_{n+1}+ \alpha x_{th}$, if $\tilde {x}_{n+1} \leq x_{th}$, with y _n+1 = x _n for both cases, the effectivity-range of the stability parameter α can be determined analogously. For the standard parameters a = 1.4 and b = 0.3 we obtain for the period-1 and the period-2 orbit α = 0.79011 < α < 1.68129 and 0.80090 < α < 1.20408, respectively. Since the cutoff algorithm requires no computational effort in experiments, optimised control is provided in a the most simple way. A minor drawback of the presented control method is that the perturbations can be quite large, if not assisted by targeting procedures.

Fig. 15.6

Fast switching of the dissipative Hénon map between periodicities p = 1, 2, 4, 8, 16 using HLC. x-coordinates are shown over t = 250 iteration steps each, where a slightly thickened line marks the position of the limiter. Control of high periodicities is at least as fast as the control of low periodicities

Whereas a substantial effort in the earlier presented control methods is that they require the identification of the orbits one might want to control on, here the effort is to identify the bifurcation points of the combined dynamical-and-controller system: Only for these values of the controller, true orbits of the original system are obtained. This happens on a set of measure zero, but a similar characterisation applies to the periodic orbits seen in a space of all potential orbits. The simplicity of the threshold control drastically reduces the latency of the controller. As has been shown above, the limiter control can be optimised by using ‘hard limiters’, leading in the 1-d case to a description by the class of flat-topped maps. Earlier, Glass and Zeng had suggested these maps for regularising cardiac rhythms [12], in a more general context a chain of flat-topped map was used by Sinha and Biswas to investigate adaptive dynamics [39]. Moreover, Sinha and Ditto presented a simple network of flat-topped logistic maps which encodes numbers and performs arithmetic computations [40].

One may ask oneself whether flat-topped maps could, similarly to their relatives with of quadratic nonlinearities, also display a kind of universal behaviour. In contrast to the latter family, it is to be noted first that flat-topped unimodal maps—due to their flat tops—cannot show chaotic motion. As an ergodic chaotic trajectory would explore the entire attractor of the system, it eventually will land on the flat segment, from which it will continue on a periodic orbit. If we consider (non-ergodic) maps having separated attractors, the periodic motion can only be observed if the orbit visits the attractor which is associated with the flat segment of the map. Flat-topped maps can, however, undergo a period doubling cascade, as a function of the height of the top, as we show in Fig. 15.7 for three variants of the implementation of this concept.

Fig. 15.7

(a) Flat-topped tent, (b) spread tent, (c) spread logistic map, with corresponding generated bifurcation diagrams (d)–(f)

It comes as little surprise that these processes can be treated in full parallel to the Feigenbaum treatment. In the first step, we therefore determine the properties of the bifurcation cascade and then will compare it with the Feigenbaum case. We will show that, generically, in flat-topped maps the single scaling for the opening of the forks of the Feigenbaum case is replaced by two different scaling factors. One of them is a trivial scaling by α = 1, which is associated with the scaling of the top. The other scaling by $\tilde {\alpha }$ depends on the derivatives of the map and can therefore not be universal, which is why for this splited scaling, we propose the term “partial” universality. In the course of period doubling, flat-topped maps show an exponential convergence towards the period doubling accumulation point. As a consequence, the value of the scaling exponent d diverges. Of practical interest is the observation that the convergence onto the asymptotic periodic orbit is exponential and usually reached within a few iterations when starting from arbitrary initial conditions.

To render life as easy as possible, we shall first switch to the flat-topped symmetric tent map. As the curvature of the side branches that the flap-topped parabola would introduce is of limited variation, this has no further influence on the generic behaviour. The flat-topped symmetric tent map is given by

$$\displaystyle \begin{aligned} x_{i+1} = \begin{cases} 1-\mid 2(x_i -0.5)\mid & \text{for}\ 1-|2(x_{i} -0.5)|< h \\ h & \text{otherwise}. \end{cases} \end{aligned} $$

(15.3)

Threshold h denotes our limiter, which is the natural choice of the bifurcation parameter. Figure 15.7a, d shows the HLC-controlled tent map along with its bifurcation diagram, where the threshold h is increased from h = 0.5 to h = 1. For the diagram, the last 100 of a trajectory of 500 points were plotted, showing that the associated orbits are periodic, except for h = 1. Upon this increase of h, the length of the flat interval shrinks from I _h=0.5 = 0.5 to I _h=1.0 = 0. In Fig. 15.7d, for each h the interval end points are shown as thin lines. In the bifurcation diagram, a period doubling bifurcation occurs whenever an end point collides with a 2ⁿ-periodic fixed point. Therefore, a new controlled orbit is born whenever the diagonal x _n+1 = x _n first hits a flat interval of the 2ⁿ-fold iterated map. When h is increased further, the intersection point moves along the flat interval to the other end point, where the next period doubling bifurcation is generated. Because of the constant absolute slope of the map, all branches in the bifurcation diagram are straight lines. For an orbit of length 2ⁿ, the slope of the bifurcation branch that contains x = 0.5 can be written as $s_n =2^{ 2 ^{n - 1}}$, n > 0. The sequence of period doubling bifurcation can now be calculated as the intersections of this branch with the lines corresponding to the end points of the flat top. For n > 1 this leads to

$$\displaystyle \begin{aligned}h_{n}=1- \frac {\prod_{k=0}^{n-2}\big(2^{2^k}-1\big)}{2^{2^{n-1}}+1},\end{aligned}$$

where 2ⁿ denotes the periodicity of the cycle. The location of the threshold at which the periodicity becomes infinite can numerically be determined to be at h _∞≃ 0.82490806728021.

The scaling behaviour of 1-d unimodal maps is characterised by two constants α and δ. The constant α describes asymptotically the scaling of the fork opening by subsequent period doubling, whereas δ represents the scaling of the intervals of period 2ⁿ to that of period 2ⁿ⁻¹ near the period doubling accumulation point, i.e., at the transition to chaos. Both values depend on the leading order of the maximum of the map (the second order is of course the generic case). The usual Feigenbaum constants correspond to the prominent class of maps with non-vanishing curvature at the hump. Therefore, it is not a surprise that for flat-topped maps, Feigenbaum scaling results are changed. The value of α can be determined from the fixed point of the period doubling operator T (e.g., [36])

$$\displaystyle \begin{aligned} g(x)=Tg(x)= - \alpha g\left(g\left(-\frac{x}{\alpha}\right)\right),{}\end{aligned} $$

(15.4)

where g(x) denotes the fixed point function. Following the Feigenbaum ansatz, we study the renormalised function

$$\displaystyle \begin{aligned}g_{n,1} (x)=(-\alpha)^n f^{2^{n}}_{h_{n+1}} \left(\frac {x}{(-\alpha)^{n}}\right),\end{aligned}$$

at h _n, where 2ⁿ denotes the periodicity of the orbit. The scaling function g(x) then is obtained as g(x) =lim_i→∞lim_n→∞ g _n,i(x). The form of the rescaled functions g _n,1(x) for n = 0, 1, 2, 3 motivates that g(x) will be a square wave. Therefore, we make the ansatz

$$\displaystyle \begin{aligned}g(x)=1+b(1+\varTheta (x - 1) - \varTheta(x+1)),{}\end{aligned} $$

(15.5)

where Θ(x) represents the Heaviside function. Insertion of 15.5 into 15.4 leads to

$$\displaystyle \begin{aligned}1+b(1+\varTheta(x - 1) - \varTheta(x+1))&= - \alpha\left(1+b\left(1+\varTheta\left(g\left(\frac{x}{-\alpha}\right)-1\right)\right.\right.\\&\quad \left.\left.- \varTheta\left(g\left(\frac{x}{-\alpha}\right)+1\right)\right)\right).\end{aligned} $$

This equation allows for α = 1 and b = −2 as solutions.¹ The value of α = 1 implies that in the vicinity of the accumulation point h _∞, the opening of the bifurcation fork does not change under subsequent period doubling bifurcations. However, as the map has everywhere a nonzero slope of absolute value 2, the ratio of the fork openings within a 2ⁿ periodic orbit is $\tilde {\alpha }=2$.² This is illustrated in Fig. 15.8 which shows the location of the forks in the bifurcation diagram versus the periodicity of the orbit. Each circle represents a bifurcation fork, the openings of which can be calculated by multiplying all factors along the path, starting at the period 2 orbit. For example, in order to calculate the opening size of the from top fourth fork of period 16, we follow the bold path in Fig. 15.8 and obtain

$$\displaystyle \begin{aligned}1 \circ \tilde{\alpha}^{-1} \circ 1 \circ 1 \circ \tilde{\alpha}^{-4}=\tilde{\alpha}^{-5}.\end{aligned}$$

Note, that the value of α = 1 is only exact close to the accumulation point, whereas the value of $\tilde {\alpha }=2$ is always exact. Instead of considering the bifurcation points h _n at which periods of order 2ⁿ are born, the value of δ can be determined by using the values H _n where the periodic orbits contain the point x = 0.5, as both sequences converge with the same behaviour to the accumulation point h _∞. The value of the bifurcation parameter H _n is given by

$$\displaystyle \begin{aligned}H_n=1-\frac{\prod_{k=0}^{n-1}\big(2^{2^{k}} -1\big)}{2^{2^n}}.{}\end{aligned} $$

(15.6)

Fig. 15.8

Split scaling of forks: The horizontal scaling (α = 1) is universal. The vertical scaling ($\tilde {\alpha }$) depends on the derivatives of the map

Equation 15.6 can be written recursively as

$$\displaystyle \begin{aligned}H_n =1-(1-H_{n+1} ) \frac{1}{1-2^{-2^{n}}},\end{aligned}$$

which leads to

$$\displaystyle \begin{aligned} H_n =1-(1-h_{\infty}) \prod_{k=0}^{\infty}\frac{1}{1-2^{-2^{k}}}.{} \end{aligned} $$

(15.7)

Using

$$\displaystyle \begin{aligned}\prod_{k=0}^{\infty}\big(1-2^{2^{-k}}\big)^{-1} \approx \left(1-\sum_{k=n}^{\infty}2^{-2^{k}}\right)^{-1}\approx 1+ 2^{-2^n},\end{aligned}$$

Eq. 15.7 reduces to

$$\displaystyle \begin{aligned}H_n=h_\infty -c\,\,2^{-2^n},{} \end{aligned} $$

(15.8)

where c = 1 − h _∞. Equation 15.8 reveals an exponential convergence towards the fixed point. Therefore, the ratio between two subsequent intervals H _n − h _∞ and H _n+1 − h _∞, which asymptotically determines the value of δ, depends on n as

$$\displaystyle \begin{aligned}\delta(n)^{-1}=2^{-2^{n}}.\end{aligned}$$

This result means that in the case of the flat-topped tent map, the occurrence of period doubling does not follow a power law as in the Feigenbaum case. Rather, it is of exponential nature.

Unstable periodic orbits can only be controlled when the system is already in the vicinity of the orbit. As the initial transients can become very large, targeting algorithms have been designed [21, 37] that efficiently push the system onto the selected orbit. The flat-topped tent map and the corresponding tent map share the same orbit if the threshold of the flat-topped tent map coincides with the largest fixed point of the tent map. Due to the flat top, this orbit becomes stable. Initial conditions that lead to the flat top are on the selected orbit within one iteration. Iterating backwards, we can determine the intervals that lead to the orbit in two iterations, and so on. This approach is similar to the strange repeller escape problem. The relationship suggests that in our case, the convergence onto the selected orbit is exponential, which makes a targeting algorithm idle. The exact convergence onto the selected orbit depends on the size of the flat top. The larger the horizontal segment is, the faster is the convergence. As the size of the flat top is determined by the threshold, the time constant of convergence varies with the latter. We calculated the time constant for h _∞ by propagating back the interval associated with the flat top. For each back-iteration, 2k new intervals of half the size of the intervals obtained by the previous step join the already recruited intervals (Fig. 15.9).

Fig. 15.9

Split scaling of forks: The horizontal scaling (α = 1) is universal. The vertical scaling ($\tilde {\alpha }$) depends on the derivatives of the map

This property is due to the slope of the map, which in the present case equals 2. Figure 15.9 gives the number of back-iterations versus half of the number of the added intervals k. Let the differences between two subsequent values of k be denoted by Δ(i), where i denotes the order of the backward iteration. From their values, it is seen that k can be calculated iteratively as

$$\displaystyle \begin{aligned}k(i)=k(i - 1)+\varDelta(i- 1),\end{aligned}$$

where i ≥ 2, k(1) = 1, Δ(1) = 1, Δ(2i) = k(i) and Δ(2i − 1) = k(i).

If L denotes the measure of naturally, i.e., equally distributed, initial conditions that do not lead to the selected orbit, the reduction of L due to i-fold back-iteration can be written recursively as

$$\displaystyle \begin{aligned}L(i+1)=L(i) - 2k(i)\frac{l_0} {2^i},{}\end{aligned} $$

(15.9)

where l ₀ denotes the initial size of the flat top. If properly scaled, 1 − L(i) is the probability measure for initial conditions to be controlled onto the selected orbits in i steps. Figure 15.10a shows the convergence onto the orbit for h = 2∕3, h = h _∞. and h = 0.85 (full line, dashed line, and broken line, respectively). The squares represent calculations using Eq. 15.9. For the system to be controlled, it needs to visit the flat segment of the graph. The determination of the measure of orbits that reach the horizontal fragment after n iterations is equivalent to the escape problem of a (hyperbolic) strange repeller. Indeed, the average rates either for landing on the controlled orbit or for the escape are given by the decreasing number of chaotic orbits as a function of iterations. For the numerical treatment of hyperbolic repellers, one standard method is cycle expansion [2, 3]. We used this approach to check our brute-force results for h = 2∕3, cf. Fig. 15.10. The cycle expansion of the dynamical ζ-function is then governed by the cycle that corresponds to the fixed point at x = 0 and reads

$$\displaystyle \begin{aligned}1/\zeta=1-z \frac{1}{2}.\end{aligned} $$

Fig. 15.10

Convergence onto orbits versus steps. (a) Flat-topped tent map (h = 0.85, h = h _∞, h = 2∕3). Circles and squares from back-iteration [Eq. 15.9] and from zeta function (Eq. 15.11), respectively. (b) Spread tent map (h = 1, h = 0.8, h = 0.6); circles: results from ζ-function (Eq. 15.11)

The escape rate γ is determined by the zero of the dynamical ζ-function using $z=\exp (\gamma )$. For our case, this yields γ = ln(2), implying that for arbitrary initial conditions the probability of landing on the period 1-orbit within 5 iterations is p = 0.95.

The scalings induced by HLC also explain the large-scale repetitive star-like bifurcation structures and the adjacent repetitive empty bands (positions indicated in Fig. 15.11b by the large and the small circles, respectively). It is easy to see that the asymptotic scaling of these repetitive structures stars are both given by the derivative of the leftmost fixed point of the map. As a consequence, both scalings are again non-universal.

Fig. 15.11

(a) Generic bifurcation diagram of flat-topped maps. The (for display reasons: tent) map is drawn over the vertical axis x (broken lines). To obtain the controlled map at control parameter h, replace the (rightwards pointing) peak of the map by a vertical segment positioned at h. The asymptotic controlled orbit points are also displayed with abscissa h, giving rise to a bifurcation diagram. (b) Relation between the n-fold iterates of F (graphs F ⁿ, n = 1, 2, 3, shown by dashed-dotted, dashed, and full lines) and the scaling of the ‘stars’ (large circles): Back-iterations (arrows) of the period-one fixed point x = 2∕3 yield successive star locations. Their scaling is therefore determined by the derivative F′(0). A similar argument applies for the size of the ‘windows’ (whose x-values are located around the small circles)

This ends our excursion on the statistical properties of the hard limiter controlled tent map. By generalising the fully analysed tent map example of HLC, we can, however, obtain insight into the behaviour and properties of more general systems. We demonstrate this by choosing a family of what we shall call ‘spread maps’: unimodal, and symmetric hard limiter controlled maps that are additionally characterised by a segment of fixed size 2d. Why this is convenient will be apparent in a moment. We start for simplicity with family of maps that are close to the previous tent map example, in which case we deal with the equation

$$\displaystyle \begin{aligned} x_{n+1} = \begin{cases} x_n \frac{ h} {(0.5 - d )} \, & \text{for} \; x_n \leq 0.5-d \\ (1-x_n)\frac{ h} {(0.5-d )} & \text{for} \; x_n\geq 0.5+d \\ h & \text{elsewhere}. \end{cases} \end{aligned} $$

(15.10)

Choosing the height h at which we place the controller now entrains a change in the slope of the piecewise linear sides of the maps, yielding further insight into the properties of hard limiter control. As has already been promised at the beginning our explorations, the influence of the slope at the two sides is rather small and leaves the scaling properties and essentially also the bifurcation diagrams unchanged (cf. Fig. 15.7b, e). Since the flat top is symmetric about the line x = 0.5 and of constant size, the corresponding envelopes are obtained as two parallel horizontal lines at 0.5 + d and 0.5 − d. Bifurcation can only occur at these two lines. The effect of the changed slopes of the map is reflected in the curved bifurcation branches shown in Fig. 15.7e, in comparison with the straight lines of the flat-topped tent map (Fig. 15.7d).

Due to the salient role of the horizontal segment for occurrence of bifurcations, the scaling by α remains unchanged. In contrast, the scaling by $\tilde {\alpha }$ changes from one period doubling to the next. Upon a decrease of h, we observe two effects that emerge related to orbit convergence. On the one hand, some of the orbits are lost, which reduces the number of intervals added by back-iteration. On the other hand, due to the decreased slope of the map, individual intervals become larger (except for the central one). The trade-off between these effects leads to an optimal convergence case at h ≈ 0.8. Figure 15.10b shows the time constants obtained for decreasing heights (h = 1 (full line), h = 0.8 (dashed line), and h = 0.6 (broken line)), using d = 0.1. For h = 1, the exponential decay constant can again be calculated using the cycle expansion. The dynamical ζ-function then is

$$\displaystyle \begin{aligned} 1/\zeta=1- \frac{1} {1-2d} z, \end{aligned} $$

(15.11)

which leads to the escape rate γ = ln(1∕(1 − 2d)). In Fig. 15.10b, the calculated values are shown as circles.

To emphasise the origin of this phenomenon, we finally consider a last family of spread maps on the interval [0, 1], characterised by horizontal flat top of a fixed length 2d. We choose

$$\displaystyle \begin{aligned} x_{i+1} = \begin{cases} \mu x_i(1-x_i -2d) \, & \text{for} \; x_i \leq (0.5 - d ) \\ \mu(x_i -2d)(1-x_i) & \text{for} \; x_i \geq (0.5+d) \\ \mu (0.5 - d )^ 2 & \text{elsewhere} \end{cases} \end{aligned} $$

(15.12)

where d again denotes half of the flat segment size, and μ controls the opening of the underlying parabola (cf. Fig. 15.7c). This example, in distinction of the previous cases, is now differentiable on the interval [0, 1]. In this way, the height of the graph becomes a function of μ (and the fixed chosen d), as h = μ(0.5 − d)². Given d, this restricts the range of μ to 0 < μ ≤ 1∕(0.5 − d)². Upon increasing μ, also this family exhibits a nontrivial bifurcation diagram (shown in Fig. 15.7f for d = 0.1). The shape of this diagram differs greatly from those of the previous two families and is closer to the ordinary period doubling bifurcation diagram of the logistic map. This property is due to the smooth connections between the horizontal segment and the two branches of the map. Figure 15.12a and b illustrate the differing mechanisms at the first period doubling bifurcation for the flat-topped tent and the spread logistic maps. In the former case, the bifurcation abruptly emerges from the single flat segment of the second iteration. In contrast, the second iteration of the spread logistic map already has two different flat segments, and the bifurcation occurs along the smooth inter-segment connection. At the period doubling accumulation point these smooth transitions turn into step like transitions, conserving the scaling of α = 1.

Fig. 15.12

Bifurcation mechanisms of flat-topped spread tent (left panel) and logistic maps (right panel). Second iteration maps before, at, and after bifurcations. Parameters: tent: h = 0.65, h = 2∕3, h = 0.68, logistic: μ = 4.65, μ = 4.74, μ = 4.85

Wrapping these results up, for flat-topped maps, the scaling function g(x) is a square wave with a scaling factor α = 1 for subsequent period doubling bifurcation. The ratio of bifurcation fork openings within orbits of order 2ⁿ depends on the derivative of the map and therefore does not follow a universal behaviour. The scaling factor δ diverges. Close to the transition point, this kills the power law behaviour for the occurrence of bifurcation, and an exponential law appears, which renders the observation of orbits of higher periodicity increasingly difficult.

We have shown that the limiter based control algorithm also works with the Hénon map, cf. Ref. [43]. This ends our excursion into natural control of nonlinear dynamical systems. In conclusion, we have demonstrated that control by threshold induces a number of naively unexpected phenomena that may be well worth to be taken into account when monitoring macroeconomic systems by the most fundamental control measures applied in economics dynamics.

4 Application to a Simple Model of Macroeconomics

‘Greed and Control Rule Macroeconomics’

We first motivate the principles that advocate more specifically to use the quadratic iterated map as a simple, but generic, model of macroeconomic development. In this model, a primary source of cycles can be identified. We then demonstrate a detailed mechanism of how cycles are additionally introduced when applying even the simplest control strategies. The principles of applying the simplest and most natural control method are explained, and the laws underlying the generation of (super)stable cycles by means of the control, are outlined. Finally, we propose an optimal control mechanism, work out its main properties and highlight the difficulties of its application in economics. The obtained insights add a new facet to the control advice by Kydland and Prescott [23]: The optimal system behaviour is not obtained by controlling on the natural cycle, but is achieved by a controlled period-one orbit. This not only requires a control policy that is kept fixed through time. To acquire the period-one state, a strong initial control effort is generally required, and control must permanently be maintained. In order to control the system on a period-one orbit, it may be advantageous if the system is in the chaotic regime. Finally we show how the regime of the dynamics can be identified by the system’s response to control.

Chaos is composed of an infinite number of unstable periodic cycles of increasing periodicities. In order to exploit this reservoir of characteristic system behaviours, elaborate methods have been developed to stabilise (or ‘control’) intrinsically unstable orbits, using only small control signals [11, 25, 30, 34]. By the more detailed study of the potential of these control methods in economics [4, 14, 15, 17, 20], several limiting factors were identified. As a first shortcoming, the inherent latency of most of the above control approaches emerged. In the context of quickly changing economics, control, however, is required to be fast. As a second problem, some economic data cannot be collected in a continuous fashion. This renders the application of the standard control methods, that are based on the explicit knowledge of the geometry of the economic dynamics, tedious, and targeting methods, designed to improve the speed of convergence towards the desired solutions, inefficient. Moreover, the large amount of strong noise that is characteristic for economics tends to veil these structures. As a third requirement, the control should permit to be formulated in terms of a simple economics policy. For control strategies that are based on past observations (e.g., statistical data from the preceding year), this is not easily achievable. Moreover, these control strategies lead to policy functions involving time delays [24], which often entrain chaotic behaviour, as in the above-mentioned pioneering examples [6, 7, 28]. These observations apply in particular to time-delayed feedback control methods [14, 32] that for some time were proposed as a means of controlling financial markets. Due to these problems, the interest in the application of dynamical systems methods for the control of economic dynamics, has decreased thereupon.

Economies naturally tend towards the recruitment of all available resources. In the following let us explain how human greed drives their economics towards the boundaries and fosters a natural tendency of the system to evolve towards maximally developed nonlinearities. While occasionally also animals are said to be greedy, human greed takes things further than just acquiring resources for one’s self. The basis for this is in human society, in its ability to store and trade virtually unlimited amounts of goods. This has been triggered by the human’s change from hunters to agriculture (manifested in the bible’s and other tales’ expel of humans from the paradise) and is fostered by the development of the necessary technological basis (wheel, communication, building). For humans, the distinction between constant, constant and exponential improvement of a state is, from the perceptional point; difficult (the focus is just on different observables that are constant (state, additive gain, gain factor)). Moreover, if the changes are small and slow enough, the three cases can hardly be distinguished. Only when the limits of economic systems are approached, the distinction between the last two models becomes important. In this case, nonlinearities matter, as they are required to keep the system within its boundaries.

For our modelling of the dynamics of such systems, we choose the iterative picture. The evolution of a simple model of economics takes place on three time scales: At the lowest level, perturbations affect a deterministically changing variable x that will be considered to represent a momentary degree of system exploitation (second level). This setting is completed (third level) by a greed-driven parameter μ, expressing to what extent the corresponding system conformation covers the full theoretically available system size. For states far from the maximal exploitation of the resources allowed by parameter μ, we allow the dynamics to grow almost linearly. Close to maximal exploitation, the next value consumption is required to be small, implementing in this way a kind of system recovery.

A corresponding simple and generic model of such dynamics is again provided by the iterated logistic map on a space that we may rescale to be the unit interval

On a time scale much slower than the one responsible for the iterative dynamics, the principle of economic greed will gradually drive the system, via the increase of the order parameter μ, towards the ‘critical’ value μ = 4, allowing for an ever-growing exploitation of the phase-space [0, 1]. As can easily be seen at ‘criticality’ μ = 4, it is the nonlinearity that keeps the system states x away from the boundary: Starting with a small value x ₀, upon iteration the value of x first increases in an almost linear fashion (the approximate proportionality factor being μ), but soon as x _n approaches the upper phase-space boundary (at x _n = a∕4 = 1), this behaviour is annihilated by the factor 1 − x _n that sends the dynamics back to small values.

On the human greed-driven pathway towards the globalisation of resources (μ → 4), the asymptotic system state (obtained for n →∞) converges initially to a fixed state increasing in its value with μ, then suddenly changes into a period-2 behaviour (two alternating values of x), and then undergoes a continued period doubling bifurcation route, where a cascade of stable periodic orbits of increasing orders 2ⁿ (where n = 2, 3, 4…) characterises the asymptotic solutions [10]. Using renormalisation theory, it can be shown that in order to reach the next bifurcation, μ progresses geometrically, with factor q ≈ 1∕4.67. This implies that the transition point to period infinity is reached within a finite interval of μ (cf. Fig. 15.13). Beyond this period doubling accumulation point, chaos is possible and abundant, but while the value of parameter μ can still be increased, we observe a succession of windows of periodic behaviour and chaotic behaviours [42], rendering a statement how much weight the parameters μ leading to chaotic behaviour have, a highly nontrivial one [5]. The properties exhibited by the logistic map have been found to be characteristic for a large universality class of nonlinear processes (of which the logistic map is the simplest representative, see, e.g., [36]). Our model thus characterises a whole class of systems subject to such a process of self-organisation. The quadratic parabola has therefore been used in economics in a number of approaches. In particular, in an early example by Benhabib and Day [6], under suitable conditions, economics were found to follow the behaviour of the logistic map, providing an early indication for why economics could eventually become chaotic. In their model, there is a competition between the demand for two goods. The preference for one good is a function of past experience (this is taken account of by an iterative implementation) and of a constraint formulated in terms of a fixed budget. The nonlinearity parameter μ is as a decreasing function of the prices.

Fig. 15.13

State sequences are obtained, upon increasing parameter μ, from a logistic map as a model of economics. For small values of μ, stable regular behavior emerges. As μ is increased, the behavior becomes increasingly complicated, until chaotic behavior emerges. The figure insets represent the fractions of the maximally available environments that are accessible to the process

One might ask what happens if μ is driven beyond the critical value of μ = 4. In this case, large-scale erratic behavior may be expected, as the process is no longer confined to the previously invariant interval (cf. Fig. 15.14). Seen from the model side, the process that now can leave the confinement of the unit interval, will leave behind a Cantor structure of initial conditions that have not yet managed to explore new lands outside the interval. After a potentially chaotic transient, the system settles in a new area of stability, where the same scenario takes place anew, starting at rescaled small μ. We believe that in particular the effects by technical shocks may adequately be described in this framework. A simple thought experiment, taking place in a sub-domain of economy, provides us with an illustrative practical model. Consider, e.g., fishing in Norway, starting in a fjord with a single boat, focusing, say, on salmon. The annual catch x _n will be small in this case and will only mildly affect the fish population (captured by a parameter μ ≪ 1). Twice as large or a doubled number of boats will roughly double the catch $\bar {x}$, but will still have a small effect on the fish population. This situation that can be captured by a roughly doubled parameter μ. Guided by greed, this process holds on. The initially observed fixed point behaviour will finally lose its stability and a period doubling process is initiated, captured by μ → 4 (such processes have indeed been observed in different ecological systems, like fish farms or sheep breeding). This is, because after a too large capture (x _n ≈ a∕4), the system needs to recover. Finally, the fjord gets overfished, fishing enters a state of crisis (term ‘crisis’ is used in nonlinear dynamics in a closely corresponding context [13]), that holds on until a small number of larger ships equipped with novel technologies permit to exploit the whole of the Atlantic Ocean, fishing larger prey. The same pathway is then followed on this scaled-up environment, until fishing on this scale starts to have a profound environmental effect, this time on the ecological system of the Atlantic. After break down of fishing at this scale, swimming fish factories permit to do world-wide fishing, and the same process restarts on the world-wide scale. Finally, all oceans are overfished, where some of the fish species are endangered to the point of extinction. Traditional fishing then breaks down, forcing economics to develop novel technologies such as fish farms and leaving behind residuals of Cantor-set type of the traditional fishing (for an illustration see the sketch in Fig. 15.14).

Fig. 15.14

Mechanism of a crisis: Upon the increase of μ, the previously stable fixed point (open circle) loses its stability. Later, the map leaves the unit-square confinement, and trajectories finally settle in another regime (box II) offering stable dynamics (full circle). The same mechanism will lead the process to yet another regime of stability, and so on

5 Effects of Threshold (Limiter) Control

In real economics, the system state x (representing, e.g., demand or GDP) exhibits strong short-term fluctuations, often of local or external origin. Whereas in the case of small μ such perturbations are stabilised by the system itself, for larger μ they may lead to ever more long-lived erratic excursions. To incorporate these fluctuations into our model, we perturb x by multiplicative noise, for simplicity chosen uniformly distributed over a finite interval. The size str of the interval from which we sample the noise, is a measure for the amount of noise. To improve the predictability of economics under these circumstances, it is natural to apply control mechanisms to x; to study the fundamental effects such a control has on the system behaviour, we have to choose the simplest control tool available that does not additionally complicate the behaviour of the system and the properties of which are well understood. The most natural control candidate with these properties is hard limiter control HLC [8, 9, 29, 43, 45]. This control mechanism simply acts by simply asking the value of x to not exceed a certain limit, a control mechanism that is simple and in reality often is imposed. In Fig. 15.15, three time series were generated by this model at fixed parameter μ leading, in absence of noise, to superstable period-four orbit (for the definition of (super)stability of orbits see, e.g., [36]). Whereas the first time series represents the uncontrolled case, for the second series, a limiter at the highest cycle point was inserted, which is compared to a third series where the control was on the unstable period-one orbit. Even by the eye and quite against intuition, it is seen that the period-one orbit yields the highest average value $\bar {x}$.

Fig. 15.15

Noisy (str = 0.02) time series x of a superstable period-four orbit. Red: uncontrolled; dark green: controlled in the maximal cycle point; light green: controlled in the unstable period-one orbit. Period-one orbit control yields the highest average $\bar {x}$

Exact results for the hard limiter control (HLC) have already been presented in this chapter. For reasons of convenience, we will once more exhibit the nontrivial features of this control: By introducing a limiter, orbits that sojourn into the forbidden area are eliminated (see Fig. 15.16). Modified in this way, the system tends to replace previously chaotic with periodic behaviour. By gradually restricting the phase-space, it is possible to transfer initially chaotic into ever simpler periodic motion. When the modified system is tuned in such a way that the control mechanism is only marginally effective, the controlled orbit runs in the close neighbourhood of an orbit of the uncontrolled system. In a series of papers [8, 9, 29, 43, 45], this control approach was successfully applied in different experimental settings, and its properties were fully analysed.

Fig. 15.16

HLC for time-continuous and discrete dynamical systems with noise. Limiter positions are indicated by dashed lines. (a) HLC changes chaotic into period-one behaviour (modified from Corron et al. [9]). (b) HLC for the noisy logistic map. Placement of the limiter around the maximum of the map preserves the natural noisy period-two orbit (red). For lower placement, a modified period-one behaviour is obtained (green). Continuous dynamical systems can be mapped into discrete dynamical systems by using the method of Poincaré sections [31]

The model demonstrates two interesting aspects of the control of dynamical systems. First, to some extent surprisingly from a naive physics point of view (d’Alembert’s principle, for example), the natural system behaviour does not need to provide the economically most efficient working mode. Additional constraints can improve efficiency. Secondly, more surprisingly from an economics point of view, giving away—at absolutely no request in return, even without effects of feedback—can improve the efficiency of an economic system.

As has been already mentioned the time required to arrive in a close neighbourhood of the target orbit is an important characteristic of the control method. With the classical methods, unstable periodic orbits can only be controlled when the system is already in the vicinity of the target orbit. As the initial transients can become very long, algorithms have been designed to speed up this process [21, 37]. HLC renders targeting algorithms obsolete, as the control-time problem is equivalent to a strange repeller escape (control is achieved, as soon as the orbit lands on the flat top). As a consequence, the convergence onto the selected orbit is exponential [45].

It is also worthwhile emphasising that any control must be expected to have, beyond the effect of the control, a potentially strong effect on the system behaviour. The effects by HLC are fully described by one-dimensional systems. Due to the control, naturally and exclusively, only periodic behaviour is possible. Period doubling cascades emerge that have a super-exponential scaling $\delta ^{-1}(n)\sim 2^{-2^n}$ [45] and therefore are not of the Feigenbaum type. The convergence onto controlled orbits is exponential which renders targeting algorithms obsolete. Controlled orbits are unmodified original orbits only at bifurcation points of the controlled map. For generic one-parameter families of maps, all bifurcation points are regular, and isolated in a compact space. As a consequence, their Lebesgue measure is zero. These properties substantially modify the uncontrolled system behaviour.

6 Natural vs. Control-Induced Cycles

It is a natural general misunderstanding to believe that control methods only apply to inherently unstable systems. Unchanged control methods can similarly be used to control on unstable orbits of inherently stable systems. In either case, the control effort should be minimal. In the noise-free case, we have achieved optimal control if after an initial phase the controller does no longer exercise any noticeable strain. For HLC, this is naturally the case at the bifurcation points of the controlled map. Questions that remain are whether a corresponding statement also holds true for noisy systems, and on which of the orbits we should control.

Economic systems start their evolution in a noisy but stable period-one state, rendering economic predictions as simple as can be. To reduce noise, a limiter can be placed close to, or on top of the periodic point. As the system changes into a period-two, the question is whether to maintain control on the unstable period-one cycle, or whether to move on to the stable period-two. While intuition seems to favour the control of period-two (following a least effort principle, the natural tendency would suggest to follow the ‘natural’ system state), in fact, maintaining the period-one control is preferable, from most economic aspects. Not only that predictions of systems controlled in the latter way are simpler and therefore offer, as a consequence, simpler economic policies. Also most economic indicators (taxes, budgets, etc.) are evaluated over a period of 1 year. Finally, and even most importantly, the period-one x-average will be generally higher than that of the controlled period-two, as well as of any other higher-order cycle. This is a simple consequence of the convexity of the nonlinear map and can easily be proved. To abruptly change a natural higher-order periodic behaviour into a period-one state requires, however, generally a relatively strong initial control action. That this is beneficial nonetheless may appear as counter-intuitive to the public, and needs to be communicated in a well-formulated accompanying economic policy statement.

When the time-scale over which the external parameter μ varies becomes comparable to the cycles wavelength, the optimality of the afore described control may break down, as continued adjustments need to be made in order to follow the changing location of the period-one. In this case, it may be preferential to control on the natural cycle. The most obvious control goal would be in this case to control the system as closely as possible along the underlying noise-free system. In the numerical control results presented below, we have dealt with both mentioned control strategies.

7 Detailed Control Results

The absolute difference between the ‘natural’ underlying solution and the controlled solution, per step, provides a suitable measure to assess the efficacy of a control.

Control in the Regime of Stable Systems

If the underlying system is of periodicity larger than one and the control is on a period-one fixed point, then the control distance becomes particularly large and therefore this measure cannot be used for this case. For our numerical investigations, we restrict ourselves therefore to the control on superstable orbits (by choosing μ = 2 and μ = 1 + 5^1∕2, for the periods one and two, respectively), and apply the control at the cycle maximum. As a measure of efficacy, we calculate the average deviation of the noisy controlled relative to the noise-free system, denoted by dev, as a function of the noise and of the limiter position h. This seems to reflect best the natural tendency of the system to return into the vicinity of the uncontrolled noise-free system once the control is relaxed.

We find that for zero noise, dev(h) is a piecewise first order function (shown in Fig. 15.17 for the period-one orbit), where the nonzero slope, associated with h below the maximum of the function, depends on the periodicity and on the amount of nonlinearity expressed by μ.

Fig. 15.17

Dependence of dev on the control point h (summation over 500 orbit points, period-one orbit). (a) For zero noise, a piecewise linear function with a minimum (= optimal noise-free control point) emerges. (b) In the presence of noise (str = 0.02), the function becomes nonlinear, with a nonzero minimum at the optimal noise-free control point

In the presence of noise, the formerly piecewise linear function becomes nonlinear, with the minimum being situated at the optimal control point of the noise-free system. For noise strengths str < 0.1 considered to cover the realistic cases, the deviation is a function of first order in str (see Fig. 15.17b). The stronger the required corrections, the more the orbit histograms focus around the control point. The controlled orbit, however, deviates ever more from the original system orbit, which leads to a fast increase of dev.

The control on the superstable period-two orbit yields a similar picture. One important difference, though, is that the amount of noise under which control can still be maintained, decreases considerably. Yet, for stable orbits, control can beneficially be applied up to relatively large noise levels (str ∼ 0.08).

Control is lost when due to the effect of noise, interchange of orbit points occurs. This is the reason why in the presence of a substantial amount of noise, only low-order cycles can be controlled. For a period-four orbit, already a noise level of str > 0.01 leads to the loss of control. Interestingly, the function dev(h, str) scales linearly with str (identical curves emerge, if h and dev are replaced by h∕str and dev∕str, respectively). As a rule of thumb, by means of optimal control, the deviation can be reduced by a factor of ∼0.5.

Control in the Regime of Chaotic Systems

If the underlying system is in the chaotic regime, all cycles are unstable, and the control on any of them is, from the point of view represented by the control distance, a-priori equally well justified and natural. Particularly favourable for economics is the fact that control can be established on a period-one orbit with zero control distance in the limit of vanishing noise.

For further investigations we again focus on the fully developed logistic map (μ = 4). To have control on true system orbits, the bifurcation points (cf. Fig. 15.11a) must be chosen as the control points, the location of which can be determined analytically [45]. Without control, chaos prevents the system from staying on a given cycle. Accordingly, the efficacy of the control is measured as the difference between controlled noise-free and controlled noisy systems. In order to obtain a period-one orbit in the noise-free case, the limiter has to be adjusted to h = 0.75. Experiments show that in the presence of noise, the optimal control point moves away from the noise-free optimal control point. This is in contrast to the behaviour in the stable regime, and may be exploited to distinguish between the two cases.

The displacement is a linear function of the noise strength, as is the deviation dev measured at the optimal shifted control point. To provide an unstable noise-free period-two orbit, the controller was adjusted at h = 0.904. Again, the optimal control point’s displacement and the minimal deviation are a function of first order in the noise strength (see Fig. 15.18a, b). The shift of the control point extends over an interval of more than δh = 0.1, and therefore is of a size comparable to the added noise.

Fig. 15.18

Results for the chaotic regime, where an unstable period-two orbit is controlled. (a) First order dependence of the optimal control point displacement δh on the noise strength str. (b) First order dependence of dev at the optimal control point, on the noise strength str

Controlling period-four orbits yields an even stronger shift from the optimal noise-free controller position at h = 0.925. The amount of sustainable noise, however, is further reduced if compared to period-two (by a factor of ∼0.5). Beyond a noise strength of str = 0.04, the orbit escapes control.

8 Conclusions

Control mechanisms of limiter type are common in economics. Quite contrary to the expected and desired effect, it is inherent to this control method that superstable system behaviour is generated, irrespective whether the underlying behaviour periodic or chaotic. A first guess remedy would be the frequent change of the position of the limiter, to compensate for the amplified or newly created cyclic behaviour. This strategy, however, will generate even ever more erratic system behaviour. Our analysis shows that it is more advantageous to keep the limiter fixed, adjusting it only over time scales where the system parameter μ changes noticeably. In this way, reliable cycles of smaller periodicity will emerge. Among these cycles, period-one is generally the optimal one, also seen from most economic perspectives. To recruit this state, a strong initial intervention may be necessary, and the control must be permanent. Otherwise, a strong relaxation onto the suboptimal natural behaviour sets in. In the context of economics, these properties will be used as natural arguments against our proposed control. On the plus side, a very simple control policy can be formulated, which is of primary interest for western democracies.

To maximise system output $\bar x$, the minimal distance to the noise-free dynamics could be chosen as the control target. We demonstrated that when μ varies slowly, this control generally does not lead to the optimum. If superstable orbits are controlled at the highest orbit point of the noise-free behaviour, the location of the optimal control point is independent from the noise strength. In the chaotic regime, in contrast, the optimal control point is displaced, by a function of first order in the noise strength. Controlling at this point reduces the dev-error roughly by one fourth, if compared to the control at the noise-free optimal point.

Detailed investigations show that the observed shift of the optimal control point also depends on the nature of the noise. If purely positive noise is added, the shift vanishes. From the perspective of economics, HLC-induced noise reduction can be regarded as a substantial improvement. Since the period-one orbit has substantial advantages, the control on the latter state is preferential.

Our framework could be of relevance for better understanding and monitoring economic behaviours. It has been found [1] that for either very underdeveloped or developed economies, stable fixed point behaviour is predominant. At an intermediate level, however, complex economics emerge that can induce chaotic dynamics of the entrepreneur’s wealth, W _n [27]. In order to control this case, HLC in the form of a tax on assets with a sufficiently fast progression could be applied, forcing W _n to remain below a maximal value, W _max. With sufficient care, HLC on a period-one could be achieved, and excessive economic variations due to chaotic dynamics could be prevented. Political realisability will often require the use of ‘softer’ limiters (in the sense that W _n > W _max is not strictly prohibited), but the main features of HLC will be valid even in these cases (see our introductory part).

We emphasise that short-term cycles emerge on all levels of economics. It has become, e.g., a common observation, that the demands for certain professionals (in central Europe in particular for teachers) undergo large fluctuations, from 1 year to the next. In 1 year, severe problems are encountered in recruiting a sufficient number, so that the professional requirements have to be lowered, whereas in the next year, there is an excess supply. We propose to interpret this as the signature of an economy that has moved out of period-one behaviour. From the teaching quality as well as from the individual’s biographies point of view, the occurrence of this effect should be prevented or smoothened. Our approach offers a perspective for understanding, studying and, potentially also engineering, such phenomena.

Our final remark refers to a possible interpretation of hard limiter control in economics and its connection with ethics and—potentially— even into the direction of religion. We have found that controlling on a period-one orbit is often the optimal control strategy. Focusing on period-one in terms of GDP entrains to think about what should be done with ‘what is above’ this desired state. The most consistent interpretation probably is, that this is what can be given away, without suffering any loss in the longer term. In real world, such a control would be connected to annihilating or dispose a part of the economic power above the period-one state. Economic power that otherwise could be used, at a higher price to be paid for this later. Put in a nutshell, our investigations can be seen as pointing into the direction that sharing or giving away can be—contradicting principles of human individual selfishness—very beneficial for all. Religions emphasising this point as a religious policy have probably understood this point at an intuitive level; they might even have become successful not least because this attitude leads to more successful economies.