Artificial Spin Ice: Beyond Pyrochlores and Magnetism

Abstract

Artificial spin ices [1,2,3,4] have raised considerable interest for its technological potentials, and as a tailorable medium to investigate collective phenomena in a materials-by-design approach. These metamaterials are made of frustrated arrays of interacting single-domain ferromagnetic nano-islands of about 100 nm size [5]. Figure 15.1 shows the two most representative artificial spin ices, the square [6] and honeycomb [7, 8] arrays; both have been realized experimentally. In this chapter, we review the thermodynamic behaviors and nonequilibrium dynamics of these magnetic nano-arrays from the theoretical point of view. A special focus is the novel emergent phases and phenomena that originate from the magnetic charge degrees of freedom in these metamaterials. Finally, we also discuss recent theoretical proposals of extending ice physics to other artificial systems such as colloidal particles in optical trap arrays and cold atoms in optical lattices.

15.1 Artificial Spin Ice: Basic Energetics and Dynamics

Spin ice materials are essentially frustrated Ising magnets. While the Ising nature of pyrochlore spin-ice compounds such as Dy$_2$Ti$_2$O$_7$ and Ho$_2$Ti$_2$O$_7$ is due to a strong easy-axis spin anisotropy, the effective Ising variables in artificial spin ice result from the large magnetostatic shape anisotropy of the nano-islands. The magnetostatic energy is minimized when the moments align with the long axis of the islands, giving rise to two equilibrium state specified by a Ising variable $\sigma = \pm 1$. The two Ising states of a nano-island are separated by a large energy barrier. Consequently, each Ising configuration $\{\sigma _i\}$ represents a metastable local energy minimum of the array. Transitions between different Ising configurations, on the other hand, are governed by complex magnetization dynamics of individual islands; this process involves the creation and subsequent annihilation of domain walls and other topological defects. A complete description of the magnetic nano-array is given by the magnetization field $\mathbf{m}_i(\mathbf{r}, t)$ of each island or element. In some experimental realizations, the ends of the islands are joined together, giving rise to a connected nano-wire network.

Fig. 15.1

Artificial spin ices as magnetic metamaterials. a square and b honeycomb arrays of single-domain ferromagnetic islands. The centers of the nano-islands form a checkerboard and a kagome lattices for arrays shown in (a) and (b), respectively. The arrows indicate the magnetizations of individual islands. The configuration in a is a generic spin ice state in square array, in which every four-leg vertex has two spins pointing in and two pointing out. A generic kagome ice-I state is shown in b, where every vertex is either in a 2-in-1-out or a 1-in-2-out configurations

Let the magnetization of the i-th nano-island be $\mathbf{m}_i(\mathbf{r})$, the Hamiltonian of the magnetic array is

$$\begin{aligned} \mathscr {H} = \mathscr {A}_\mathrm{ex} \sum _i \int _{\varOmega _i} | \nabla \, \mathbf{m}_i |^2 \, d\mathbf{r} - \frac{\mu _0}{2} \sum _{i, j} \int _{\varOmega _i} \mathbf{m}_i \cdot \mathbf{h}_j \, d\mathbf{r}, \end{aligned}$$

(15.1)

where $\varOmega _i$ is the domain of the ith island, and the demagnetizing field $\mathbf{h}_i(\mathbf{r})$ is related to the magnetization through Maxwell’s equations,

$$\begin{aligned} \nabla \times \mathbf{h}_i = \mathbf{0}, \qquad \nabla \cdot ( \mathbf{h}_i + \mathbf{m}_i) = 0. \end{aligned}$$

(15.2)

The $\mathbf{h}_i$ can be viewed as field generated by magnetic charge density $\rho _i(\mathbf{r}) = -\nabla \cdot \mathbf{m}_i$. The total magnetic field is given by $\mathbf{H} = \sum _i \mathbf{h}_i$, and the total magnetization $\mathbf{M} = \sum _i \mathbf{m}_i$. The first term in (15.1) comes from the microscopic exchange interaction, while the second term is the magnetostatic energy $(\mu _0/2) \int |\mathbf{H}|^2 d\mathbf{r} = -(\mu _0/2) \int \mathbf{M} \cdot \mathbf{H} \, d\mathbf{r}$ in the absence of external current [9]. Here we have neglected magnetocrystalline anisotropy energy, which is a reasonable approximation for most materials used in the nano-arrays.

The dominant energy in (15.1) is the self-coupling term ($i=j$) of the magnetostatic energy. This term favors magnetization pointing along the long axis of the island:

$$\begin{aligned} \mathbf{m}_i(\mathbf{r}) \approx m_0 \, \sigma _i \, \hat{\mathbf{e}}_i, \end{aligned}$$

(15.3)

where $m_0$ is the equilibrium magnetization, $\hat{\mathbf{e}}_i$ is a unit vector pointing along the long axis of the island, and $\sigma _i = \pm 1$ is an Ising variable indicating the two possible orientations. The uniform magnetization described in (15.3) also minimizes the exchange interaction, the first term in (15.1). The magnetic state of the nano-array is then specified by a collection of Ising variables $\{\sigma _i \}$. The effective interactions between these Ising variables is given by the magnetostatic couplings between neighboring islands, the $i \ne j$ terms in (15.1).

Assuming uniform magnetization for each island, the demagnetizing field $\mathbf{h}_i$ can be approximated by a dipolar field, and the interaction energy of the magnetic array becomes:

$$\begin{aligned} \mathscr {H}_\mathrm{dipole} = \frac{\mu _0 m_0^2\,A^2}{8\pi } \sum _{i \ne j} \int \!\! \int d\ell _i \, d\ell _j \frac{ (\hat{\mathbf{e}}_i \cdot \hat{\mathbf{e}}_j) - 3 (\hat{\mathbf{e}}_i \cdot \hat{\mathbf{r}}_{ij}) (\hat{\mathbf{e}}_j \cdot \hat{\mathbf{r}}_{ij} ) }{ |\mathbf{r}_i - \mathbf{r}_j|^3} \sigma _i \, \sigma _j, \end{aligned}$$

(15.4)

where A is the cross section of the island, $\ell _i$ measures the distance along the island, $\mathbf{r}_i = \mathbf{r}(\ell _i)$ is the position of the line element $d\ell _i$, and $\hat{\mathbf{r}}_{ij} = (\mathbf{r}_i - \mathbf{r}_j)/|\mathbf{r}_i - \mathbf{r}_j|$. This Ising model is used to investigate large-scale thermodynamic behaviors of artificial spin ices, to be discussed below.

Magnetic charges as emergent degrees of freedom play an important role in describing the static as well as dynamic properties of spin ice materials [10, 11]. For artificial spin-ice arrays, the magnetostatic energy can also be expressed as the Coulomb interaction of magnetic charges with bulk density $\rho = -\nabla \cdot \mathbf{M}$ and surface density $\rho _s = \mathbf{M} \cdot \hat{\mathbf{n}}$. The magnetostatic energy is minimized when there are no magnetic charges and $\mathbf{H} = 0$. This minimum charge condition leads to the ice rules in artificial spin ice. For a nano-island with uniform magnetization, the surface charges at the two ends of the island are the main source of magnetic charge. A uniformly magnetized island can be approximated by a dumbbell with a pair of magnetic monopoles with charge $\pm q$ located at its two ends [11]. Here $q = \int \rho _s\, dS = m_0 A$. One can then assign a magnetic charge to each vertex as the sum of the monopole charges joining at the vertex, i.e. $Q_\alpha = \sum _{i\in \alpha } q_i$ for vertex $\alpha$. For connected nano-wire network [8], the vertex as junction of the nano-wires has an internal magnetization structure. Unlike isolated islands, most of the charge at these connected junctions come from the bulk charge $\rho = -\nabla \cdot \mathbf{M}$. Its total charge is the volume integral $Q = \int \rho \, dV = -\oint \mathbf{M}\cdot \hat{\mathbf{n}} dA$, which can be converted into surface integrals over the island cross sections; its value again is quantized to multiples of $q = m_0 A$. Examples of dumbbell representations for spin ice are shown in Fig. 15.11.

For a four-legged vertex in a square array, the total charge can be $Q = 0$, $\pm 2 q$, or $\pm 4 q$; see Fig. 15.2a. The minimum charge $Q = 0$ condition leads to the two-in-two-out ice rules. The vertices in a honeycomb lattice, Fig. 15.1b, have three legs and always have a finite magnetic charge $Q = \pm q$ or $\pm 3 q$. The condition of minimum charge gives rise to a different set of two-in-one-out/one-in-two-out pseudo-ice rules.

Fig. 15.2

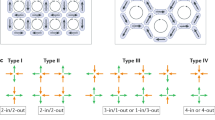
Types of vertices in artificial spin ices. a four-legged vertices have 16 possible moment configurations, which are classified into four symmetry distinct types. The total magnetic charge $Q = 0$ for type-I and II vertices (2-in-2-out), $Q = \pm 2 q$ for type-III (3-in-1-out or 1-in-3-out), and $Q = \pm 4 q$ for type-IV (4-in or 4-out) b the 8 possible three-legged vertices separate into two types of different symmetries. There is always a nonzero charge in a three-legged vertex: $Q = \pm q$ for type-I’ (2-in-1-out or 1-in-2-out), and $Q = \pm 3 q$ for type-II’ (3-in or 3-out). c The four different types of boxes with a height offset h between pairs of parallel moments

The magnetic charge can also be expressed in terms of Ising variables. As both square and honeycomb lattices are bipartite, we define the vector $\hat{\mathbf{e}}_i$ on each link as pointing from sublattice B to A. The magnetic charge of vertex $\alpha$ is then given by $Q_\alpha = \pm q \sum _{i \in \alpha } \sigma _i$, where $+$ (−) sign is used for sublattices A (B). In the dumbbell approximation, the magnetostatic energy becomes

$$\begin{aligned} \mathscr {H}_\mathrm{dumbbell} = \sum _\alpha \frac{Q_\alpha ^2}{2\,C} + \frac{\mu _0}{8\pi } \sum _{\alpha \ne \beta } \frac{Q_\alpha Q_\beta }{|\mathbf{r}_\alpha - \mathbf{r}_\beta |}, \end{aligned}$$

(15.5)

where $C \sim d/\mu _0$ is an effective capacitance for the self-energy of individual vertex, and d is the length scale of a vertex junction. The above Hamiltonian neglects higher-order multipole interactions that are weak and fall off quickly with the distance; these terms are responsible for the long-range ordering of magnetic moments at low temperatures. Note that the dominant $Q_\alpha ^2$ term is equivalent to an antiferromagnetic nearest-neighbor (NN) Ising ice model

$$\begin{aligned} \mathscr {H}_\mathrm{ice} = J \sum _{\langle ij \rangle } \sigma _i \sigma _j, \end{aligned}$$

(15.6)

on the checkerboard and kagome lattices for the two array geometries; here $J = 1/C$ is the effective exchange interaction. Minimization of $\mathscr {H}_\mathrm{ice}$ gives rise to the ice rules, whereas the Coulomb interaction, second term in $\mathscr {H}_\mathrm{dumbbell}$, is the source of novel emergent phenomena associated with magnetic charges to be discussed below.

Fig. 15.3

Magnetization reversal in artificial spin ice. a a domain wall carrying a magnetic charge $-2 q$ is emitted at one end of the link, propagates along the field direction, and gets absorbed by the vertex at the other end. b When the domain wall hits a vertex with like magnetic charge, it creates a high-energy $- 3q$ vertex which quickly emits a new domain wall into an adjacent link. c Micromagnetic simulation using the OOMMF [24] simulator of the reversal of a magnetic island showing a propagating vortex-type head-to-head domain wall, reproduced from [23] by permission of IOP Publishing. CC BY-NC-SA. ©  Deutsche Physikalische Gesellschaft

In terms of the mesoscopic Ising degrees of freedom, the dynamics of artificial spin ice is governed by flipping of the Ising variables $\sigma _i \rightarrow -\sigma _i$. Microscopically, magnetization reversal in a nano-island is a complex process involving the nucleation of domain walls, and their subsequent propagation and annihilation [12, 13]; see Fig. 15.3 for the case of a connected honeycomb array. The process is usually triggered when the total magnetic field at the nano-island, including external and dipolar fields, exceeds a threshold. For connected nano-islands, the magnetization reversal begins when a head-to-head domain wall is emitted at one of the nano-wire vertices. This process conserves the magnetic charge: the emission of a domain wall of charge $\pm 2 q$ converts the charge of the vertex from $\pm q$ to . The Zeeman force $f_Z = \pm 2 q \mu _0 H$ then pushes the domain wall to the opposite end of the island; see Figs. 15.3a, b. For disconnected arrays, the reversal process might start inside the bulk of the island. For example, edge roughness of the island is known to influence the coercive field by creating nucleation sites [14]. In that case, a pair of domain walls enclosing an inverted domain is nucleated and then pulled away by the Zeeman force. However, micromagnetic simulations show that the nucleation of domain walls mostly starts at the ends of disconnected island; the nucleation is assisted by the curling of magnetization at the ends [15].

Although domain walls are mesoscopic one-dimensional objects along a wire [16], microscopically they have complex internal structures. Depending on the width w of the island, the domain wall has a “transverse” or “vortex” structure for small and large w, respectively [17]. In fact, it is shown that domain walls in nanomagnets are composed of elementary topological defects of coplanar spins [18, 19]. These are the ordinary vortices in the bulk, and a novel type of edge defects carrying half vorticity [18]. For connected honeycomb arrays, every $Q =\pm q$ vertex junction contains exactly one such half-vortex. The magnetization dynamics of the nano array can be understood and controlled by the interplay of topological defects bound to domain walls and those innate to the array junctions [20].

A microscopic description of the magnetization process is given by the Landau-Lifshitz-Gilbert (LLG) equation [21, 22]

$$\begin{aligned} \frac{\partial \mathbf{m}_i(\mathbf{r}, t)}{\partial t} = -\gamma \, \mathbf{m}_i \times \left( \frac{\partial \mathscr {H}}{\partial \mathbf{m}_i} + \mathbf{H}_\mathrm{ext} \right) + \frac{\alpha }{m_0} \, \mathbf{m}_i \times \frac{\partial \mathbf{m}_i}{\partial t}, \end{aligned}$$

(15.7)

where $\gamma = g \mu _B / \hbar$ is the gyromagnetic ratio, $\alpha$ is a damping coefficient, $\mathbf{H}_\mathrm{eff}$ is the external magnetic field, and $\partial \mathscr {H} /\partial \mathbf{m}_i$ with $\mathscr {H}$ given by (15.1) is an effective magnetic field originating from the local exchange interaction and the long-range demagnetizing field. Figure 15.3c shows the LLG simulations of magnetization reversal in a honeycomb nanowire [23]. In this case, the reversal is triggered by a vortex-type domain wall.

In micromagnetic simulations of the artificial ice arrays [15], a discretized LLG equation is solved using either a finite-element or a finite-difference scheme [24, 25]. Because of the long-range magnetostatic interaction, such calculation is too costly for large scale simulations and further simplifications are usually required. One simplification is to assume that the magnetization is uniform in individual island [26, 27], i.e. $\mathbf{m}_i(\mathbf{r}) ={\boldsymbol{\mu }}_i / V$, where ${\boldsymbol{\mu }}_i$ is the island magnetization, and V is the volume. In this approach, the magnetostatic energy can be expressed as: $\mathscr {H} = (\mu _0/8\pi ) \sum _{i, j}{\boldsymbol{\mu }}_i \cdot \mathscr {\boldsymbol{N}}_{ij}\cdot {\boldsymbol{\mu }}_j$, where $\mathscr {\boldsymbol{N}}_{ij}$ is the magnetometric tensor and is given by the convolution of the shape-shape correlation function and the dipolar interaction tensor [28]. The effects of island shape and finite size are included in the magnetometric tensor. Approximating the islands as structureless needles, the magnetostatic energy reduces to the dipolar form similar to (15.4). Further simplification is to approximate the shape anisotropy, the $\mathscr {\boldsymbol{N}}_{ii}$ term, by an effective single-spin anisotropy $-D_1 (\boldsymbol{\mu }_i \cdot \hat{\mathbf{e}}_i)^2 + D_2 (\boldsymbol{\mu }_i \cdot \hat{\mathbf{z}})^2$, where $D_{1,2} \sim -\mu _0/4\pi d^3$ originates from magnetostatic energy [29, 30]. However, it is important to note that magnetization reversal in this approach is through the rotation of the Heisenberg-like spin $\boldsymbol{\mu }_i$, which neglects the microscopic details such as domain wall nucleation and propagation. On the other hand, they could be applied to simulating magnetic nano-arrays consisting of circular islands, which have been experimentally realized as artificial XY-magnets [31, 32].

Dynamics based on the Ising Hamiltonian (15.4) is very efficient for large-scale simulations, but is mostly phenomenological. For example, single-spin dynamics based on Metropolis or Glauber type updates is employed in the nonequillibrium studies of pyrochlore spin ice [33]. Connections with microscopic properties, such as transition rates, can be achieved through the kinetic Monte Carlo method [34, 35]. This approach not only introduces a time scale into the Monte Carlo simulations, but also bridges the huge difference between the atomistic and mesoscopic time scales. Kinetic Monte Carlo simulations have been applied to studying the in and out-of equilibrium dynamics of artificial spin ices [36,37,38,39,40]. On the other hand, artificial ice arrays far from equilibrium are governed by pure relaxation dynamics, in which the mesoscopic Ising variables always evolve toward a nearby local minimum in energy landscape [13, 41]. Phenomenological vertex population dynamics are also developed for pyrochlore [33] as well as for artificial spin ices [41].

15.2 Thermodynamic Behaviors

In earlier experimental realizations of artificial spin ice, thermal fluctuations are virtually absent in the nano-arrays: reversing the magnetization of a nano-island requires overcoming an energy barrier of a few million kelvins [6]. Most studies of artificial spin ice treated it as a granular material activated by alternating magnetic field [42, 43]. Such approaches have yielded frozen disordered states with only short-range order. It has been shown that such athermal states can be described by an effective temperature [44, 45]. An indirect attempt of producing thermalized artificial spin ice is to anneal the nano-arrays as they are initially formed [46,47,48,49]. Recent advances in fabrication and control of lithographically created arrays make it possible to realize thermally fluctuating artificial spin ice down to certain temperatures [50,51,52,53]. In light of these recent experimental developments, we discuss the similarities and differences in the thermodynamic behaviors of the square and honeycomb ice arrays.

A full micromagnetic thermodynamic simulation of artificial spin ice can be done using the stochastic LLG formulation [54], sometimes also called the Landau-Lifshitz-Bloch (LLB) equation [55]. In this approach, several random fields are incorporated into the LLG equation (15.7) to represent the effects of thermal fluctuations; the method can even be applied to simulate magnetic arrays that are close to the Curie temperature [56]. The random fields are uncorrelated both spatially and temporally and have standard deviations proportional to $\sqrt{T/V}$, where T is the temperature and V is the island volume. This is consistent with the fact that the blocking temperature of a super-paramagnetic nano-island is proportional to its volume [57]. The LLB method has been used to investigate the growth of a square ice array containing as many as $40\times 40$ islands in [26]. For simplicity, the islands are assumed to be uniformly magnetized with $\mathbf{m}_i = {\boldsymbol{\mu }}_i/V$, as discussed above, and the magnetometric tensors $\mathscr {\boldsymbol{N}}_{ij}$ are computed assuming ellipsoidal shaped islands [26]. Figure 15.4a shows that the dipolar energy of the annealed array is lowered with increasing thickness, and the final state is dominated by type-I vertices. The simulations also find that arrays with slow growth rates show the highest degrees of antiferromagnetic ordering shown in Fig. 15.5a, which is the ground state of coplanar square ice, to be discussed below. These results are consistent with the experimental observations [46]. A similar approach has also been used to study the thermodynamic properties and hysteresis in square ice model [27, 29, 30].

For large scale thermodynamic simulations of artificial spin ice, Monte Carlo method based on the effective Ising Hamiltonian (15.4) is much more efficient, while at the same time giving an accurate description of the low temperature ice and ordered phases. We first discuss Monte Carlo studies on the thermodynamic behaviors of square ice. One important question is whether there exists an ice regime where configurations obeying the ice rules, or the minimum charge conditions, are overwhelmingly present with approximately equal weights. Contrary to the 3D pyrochlore spin ice, this is not the case because the two types of zero charge vertex (I and II) in the square array are inequivalent in symmetry and have different energies. This inequivalence results from the fact that, unlike the case of a tetrahedron, the six bonds between the four coplanar islands in a vertex are not all the same: the interaction $J_{1, \perp }$ between orthogonal pairs is stronger than that $J_{1, \parallel }$ between parallel pairs. However, this can be remedied by introducing a height displacement h between the vertical and horizontal islands [58]; see Fig. 15.2c.

Fig. 15.4

LLB simulations of artificial spin ices. a Dipolar energy of the square array as thickness d increases from 0.1 nm to 5 nm with a growth rate 3.125 $\times 10^{-3}$ nm/ns. The inset shows the population of the four types of vertices vs island thickness. b A snapshot of array magnetizations when $d = 5$ nm [26]. The two grey-shaded areas correspond to the two-fold degenerate antiferromagnetic ground states shown in Fig. 15.5a; they are composed of type-I vertices. The colors of islands on the domain boundaries indicate the dominant magnetization direction: yellow: $+x$, magenta: $-x$ blue: $+y$, and green: $-y$. Figures reprinted from [26] with permission from AIP Publishing

Fig. 15.5

Ordered states of artifical square ice. a Antiferromagnetic order consisting of staggered type-I vertices. b Ferromagnetic order of type-II vertices. c Entropy density S and heat capacity C as functions of temperature obtained from Monte Carlo simulations for square ice arrays [58]. The temperature is measured in units of $J \equiv J_{1, \perp }$. The ideal Ising-ice limit corresponds to $\varepsilon = 1 - \ell / a \rightarrow 0$, which is equivalent to the exactly solvable six-vertex model [60]. For parameter $\ell /a = 0.7$, an intermediate ice regime exists for $T < 0.42 J$. The critical height offset $h_c \approx 0.207 a$. A phase transition into a ordered phase occurs at $T \approx 0.1 J$; the order is of antiferromagnetic (ferromagnetic) type for $h/a = 0.205$ (0.207). Figures reprinted from [58] with permission from the American Physical Society.

The required displacement depends on the geometrical parameters such as length $\ell$ of the island and the lattice constant a. In the so-called point-dipole limit ($\ell / a \rightarrow 0$), the two interactions are equivalent $J_{1,\parallel } = J_{1, \perp }$ when $h_c / a = \sqrt{(3/8)^{2/5}-1/2} \approx 0.419$. Taking into account the finite extension of the islands lowers the required height offset. For $h \le h_c$, we have $J_{1, \perp } > J_{1, \parallel }$ and the ground state is an antiferromagnetic order with staggered arrangement of the two type-I vertices related by time-reversal symmetry, shown in Fig. 15.5a. On the other hand, for large offset $h > h_c$, the type-II vertices have the lowest energy and the ground state is a ferromagnetic ordering of type-II vertices; see Fig. 15.5b. A macroscopic degeneracy can then be realized when the height offset $h = h_c$, as demonstrated by recent experiment [59]. In this special point $h = h_c$, the square array realizes a two-dimensional Coulomb phase with deconfined magnetic monopoles.

Another interesting limit is when $\ell \rightarrow a$. The required height offset $h_c/a \sim \sqrt{2} \varepsilon \rightarrow 0$, where $\varepsilon \equiv (1 - \ell /a)$. Moreover, since interactions beyond $J_1$ vanish identically in this limit [58], the low temperature phase of the array corresponds to an ideal Ising ice, or the symmetric six-vertex model [60, 61]. In this limit, there exists an extensive ground-state degeneracy which manifests itself in the appearance of a entropy-density plateau at $S_\mathrm{ice}/k_B = \frac{3}{4}\ln \frac{4}{3}$ [60] as $T \rightarrow 0$; see Fig. 15.5c. However, it should be noted that in this ideal $\varepsilon \rightarrow 0$ limit the effects of the island internal structure and disorder will start to play a role. Numerical simulations, on the other hand, show that a finite ice phase is possible even for finite $\varepsilon$. As demonstrated in Fig. 15.5c for a square array with $\ell /a = 0.7$, an intermediate ice regime (blue shaded area) is sandwiched between the high-temperature paramagnetic phase and a low-T ordered phase [58]. A generic ice state with disordered spins is shown in Fig. 15.1a. Experimentally, a quasi-ice regime has been observed both in athermal [6] and equilibrated square arrays without height offset [50].

As discussed above, the appearance of an ordered phase at low T is caused by the inequivalence between  type-I and II vertices when $h \ne h_c$. Antiferromagnetic ordering shown in Fig. 15.5a, which is the ground state when $h < h_c$, has been achieved in as-grown arrays [46] as well as the thermalized ones [50]. The selection of the ground state, staggered type-I versus uniform type-II, is completely due to the energetics of vertices, and is not affected by the long-range part of the dipolar interactions. This implies that the nature of the ordering transition can be described by a simplified vertex model, which includes only nearest-neighbor interactions. Indeed, Monte Carlo simulations of a 16-vertex model (with four different types of vertices) [62] agree well with the experimental result [47]. Extensive numerical simulations further show that the ordering into the staggered type-I state is a second-order phase transition [62]. Although this ground state is described by a $Z_2$ Ising order parameter, the ordering transition in square ice seems to belong to a universality class different from that of 2D Ising model [63]. The exact nature of the phase transition remains to be clarified.

Fig. 15.6

Multilayer construction of 3D artificial spin ice. a A three-dimensional network built from the four types of rectangular boxes, or ‘vertices’ shown in Fig. 15.2c. The resultant spin lattice is equivalent to the 3D pyrochlore spin ice. b Schematic diagram showing the arrangement of magnetic nano-islands in the multilayer structure. Figures reprinted from [64] with permission from AIP Publishing

Introduction of the height displacement h also provides an approach to design a 3D magnetic nano-array which is topologically equivalent to the pyrochlore spin ice [64]. The basic frustration unit in this multilayer construction is a rectangular box containing four nano-islands as shown in Fig. 15.2c; these are the analogs of tetrahedra in pyrochlore lattice. Arranging these boxes into a corner-sharing network gives rise to a multilayer structure shown in Fig. 15.6a, which can be viewed as a flattened pyrochlore structure. In each layer, parallel nano-islands form a rectangular lattice with the long and short lattice constants being 2a and a, respectively; the orientation of the islands are aligned with the short axis. The arrays are rotated by 90$^\circ$ from one layer to the next. In addition, the arrays in every other layer are shifted by a along the long axis. Interestingly, the projection of this 3D structure onto the xy plane is exactly the same as a square ice. The approach of building a 3D spin ice by stacking 2D arrays takes advantage of the well developed planar nano-lithography technology. Similar to the square ice array, by properly choosing the interlayer distance h, an extended ice regime at finite temperatures is realized in this 3D structure [64].

We next turn to the thermodynamic phases of honeycomb arrays. As mentioned above, such arrays are realizations of the kagome spin ice, as the centers of the nano-islands form a kagome lattice. The kagome spin ice is first studied in [65] as a frustrated statistical model. It is found that with only nearest-neighbor interactions, kagome ice retains an extensive ground state degeneracy corresponding to an entropy density $S_\mathrm{I}/k_B \approx 0.501$ [65]. In this so-called kagome ice-I manifold, each vertex has either two spins coming in and one going out, or vice versa. The huge degeneracy is lifted upon the introduction of further neighbor couplings [65, 66]. In magnetic honeycomb arrays, the kagome ice rules correspond to the minimum charge condition $Q = \pm q$ at every vertex; a generic disordered ice-I state is shown in Fig. 15.1b. The ice-I phase has been observed experimentally in athermal [7, 8] as well as fully equilibrated kagome ice arrays [50].

Fig. 15.7

Ordered phases of artificial honeycomb array. a An Ising microstate in the ice II phase in which emergent magnetic charge degrees of freedom develop a NaCl-type order, while spins remain disordered. The red and blue dots denote vertices with $\pm q$ charge, respectively. b One of the six-fold degenerate ground states exhibiting the $\sqrt{3}\times \sqrt{3}$ spin order. c Temperature dependence of entropy density S and heat capacity C obtained from Monte Carlo simulations for honeycomb arrays with parameter $\varepsilon = 1 - \ell /a = 0.05$. Figures reprinted from [67] with permission from the American Physical Society

The fact that there are uncompensated magnetic charges at every vertex of the honeycomb array introduces new features that are absent in square ice. The Coulomb interaction (15.5) among these residual charges gives rise to a novel phase in which the residual $\pm q$ charges crystalize into a NaCl-type order [67, 68]; see Fig. 15.7a. This charge-ordered kagome ice, also called the ice-II phase, is closely related to spins in the kagome plane of the pyrochlore spin ice when subjecting to a $\langle 111 \rangle$ magnetic field [69, 70]. While the ice-II phase is ordered in terms of charges, it is still consistent with an exponentially large number of Ising configurations; the degeneracy of the ice-II manifold corresponds to an entropy density $S_\mathrm{II}/k_B \approx 0.108$ [71]. These charge-ordered ice states are exactly degenerate in the dumbbell model (15.5). The degeneracy is lifted by higher-order corrections from the original dipolar interactions (15.4). The ice-II phase is quite robust; charge ordering has been observed experimentally even in non-thermal states generated by alternating field [72, 73]. Incipient crystallization of magnetic charges has been observed in thermalized honeycomb arrays [50].

The above energy hierarchy suggests a sequence of thermodynamic phases demonstrated in Fig. 15.7c. At high temperatures, uncorrelated Ising spins have an entropy density $S/k_B \rightarrow \ln 2 = 0.693$. As the array cools down from the paramagnetic state, it gradually enters the ice-I phase; the entropy curve exhibits a plateau at $S_\mathrm{I}$. At a lower temperature, the magnet undergoes a phase transition into the charge-ordered ice-II phase. Since the order parameter of the staggered NaCl pattern has a discrete $Z_2$ symmetry, the transition belongs to the 2D Ising universality class [68]. The ice-II phase manifests itself in the appearance of a second entropy plateau at $S_\mathrm{II}$. Finally, at an even lower temperature, another phase transition of the 2D Potts universality class [68] completely removes the residual entropy and selects a ground state with $\sqrt{3}\times \sqrt{3}$ spin order shown in Fig. 15.7b. Consistent with the fact that the most favorable arrangement of a single hexagonal ring is for all island magnetizations to point head to tail [37, 43], the selected $\sqrt{3}\times \sqrt{3}$ order maximizes the occurrence of such motif. Thermal ordering of moments into the loop crystal in honeycomb arrays remains an experimental challenge.

15.3 Disorder and Nonequilibrium Dynamics

Experimental realizations of artificial spin ice unavoidably introduce small variations during the array fabrication process, leading to a statistical distribution of island properties. Quenched disorder provides pinning and nucleation sites and strongly affects the dissipative dynamics of the magnetic arrays. It is thus crucial to understand the role of disorder in the nonequilibrium dynamics of artificial spin ice. A full microscopic modeling of disorder based on the LLG equation is computationally too expensive, and is infeasible for large-scale simulations. Models based on the Ising Hamiltonian (15.4) again provide a practical approach to study disorder-induced nonequilibrium phenomena in large lattices. In the relaxation dynamics formulation of artificial ice arrays, mesoscopic Ising degrees of freedom move downhill in the energy landscape until they come to rest at a local energy minimum.

As discussed above, each Ising configuration corresponds to a local minimum of the spin-ice array. Different local minima are connected by flipping one or more Ising spins. Consequently, an important new energy scale for the dynamical process is the energy barrier of magnetization reversal in individual islands. For effective Ising model (15.4), this energy barrier is characterized by a coercive or switching field $H^c_i$. More specifically, an Ising spin $\sigma _i$ is flipped if the total local field, composed of the external field $\mathbf{H}_\mathrm{ext}$ and the dipolar field from all other islands, exceeds its coercive field:

$$\begin{aligned} -\Bigl (\mathbf{H}_\mathrm{ext} + \sum _{j \ne i} \mathbf{h}_j \Bigr ) \cdot \hat{\mathbf{e}}_i > H^c_i. \end{aligned}$$

(15.8)

The energy released during the reversal is completely dissipated into the lattice. We emphasize once again that flipping the Ising spin corresponds microscopically to the nucleation, propagation, and subsequent absorption of domain walls as described in Sect. 15.1. The quenched disorder manifests itself in the random distribution of the coercive fields $H^c_i$. Although disorder is present also in the spin coupling constants, its effect is usually smaller and, to some degree, can be absorbed into the disorder in $H_c$ [74, 78].

When the system is subject to a perturbing external field $H_\mathrm{ext}$, interesting dynamical behaviors occur when $H_\mathrm{ext} \sim {\bar{H}}^c$, where $\bar{H}^c$ is the average switching field. However, the nature of the magnetization dynamics, whether it is mostly single-spin process or multi-spin collective behavior, depends on the relative scales of $\varDelta H^c$ and $E_d$, where $\varDelta H^c$ is a characteristic width of the random distribution and $E_d = \mu _0 m_0^2 V^2 / 4\pi a^3$ is the energy scale of dipolar interactions.

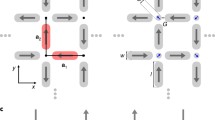
An illuminating example of nonequilibrium dynamics is the rotating-field driven relaxation of square spin ice [41, 74]. In this setup, a strong diagonal field first polarizes the system to the polarized state consisting entirely of one particular type-II vertex. The field is then reduced to a hold value $H_h$ and the sample is rotated in-plane [74]. The relaxation dynamics formulation (15.8) has been applied to study this nonequilibrium process [41, 74]; the results agree well with the experiments. Figure 15.8b, c show the average fractional vertex populations versus the hold field $H_h$ obtained from experiments and simulations, respectively. For $H_h$ smaller than a threshold, the field does not affect the type-II state. Above this threshold, type-I vertices are generated by the field; its population shows a non-monotonic behavior with a maximum at $H_h \approx 520$ Oe experimentally. This non-monotonic behavior can be understood as follows. For small field, chains of reversed moments are generated in a background of polarized type-II vertices. These chains are similar to those observed in the magnetization reversal experiments driven by a dc field [76, 77], to be discussed below. As $H_h$ further increases, small domain of type-I ground states start to form. Near the maximum of about 50 % type-I vertices, the net magnetization approaches zero and all four  type-II vertices have similar populations. Finally, further increasing $H_h$ rapidly suppresses the staggered type-I order. As the interaction is dominated by the Zeeman coupling to the type-II dipoles, most of the spins simply rotate with the field.

Fig. 15.8

Relaxation dynamics driven by rotating field. a Schematic diagram of the experimental setup. b The vertex population vs hold field $H_h$ obtained from experiments [74]. c Numerical simulations of the same process [41, 74]. Open and filled symbols represent data obtained from arrays with open and closed edges, respectively. Figures reprinted from [74] with permission from the American Physical Society

The simulations shown in Fig. 15.8c assume an average ${\bar{H}}_c = 11.25 H_d$ and a rather large standard deviation $\varDelta H_c \approx 1.875 H_d$, where $H_d = \mu _0 m_0 V/4\pi a^3$ is a characteristic dipolar field. The large $\varDelta H_c$ indicates that the system is in the strong disorder regime [78], which also explains the irrelevance of the boundary effects [74]. For athermal artificial arrays driven by magneto-agitation, quenched disorder plays a crucial role by increasing the dynamical pathways in phase space. In this sense, the effects of quenched disorder is similar to thermal fluctuations in equilibrium systems; both provide links between nearly degenerate spin configurations [79]. The effect of disorder on the connectedness of the configurational space can be quantitatively investigated using the network approach [80]. For a given magneto-agitation, the network is defined as a directed graph (or ‘adjacency matrix’) in the configurational space whose dimension is $2^N$ for an array of N islands. A directed link from Ising state A to B is introduced to the network if A can evolve to B under the driving field [81]. Compared with the perfect array, quenched disorder “rewires” the network by significantly increasing the number of links. One important consequence of the increased links is the reversibility of dynamics. This property is related to the concept of strongly connected components in networks [80]. In a directed network, if two configurations A and B are in the same strongly connected component, there exists a path from A to B and vice versa. It is found that the presence of disorder increases both the number and size of such components in the network [79]. The increased links thus can help the system reach lower-energy states through field-driven dynamics. Overall, the network picture provides a framework to understand and control quenched disorder in artificial spin ices.

Quenched disorder also significantly affects the hysteresis curves and magnetization reversal of artificial spin ice [82,83,84,85,86]. Micromagnetic simulations using the LLG equation (15.7) is employed to study demagnetization process of a small-size square array consisting of 144 islands [15]. The LLG simulation clearly identifies that the magnetization reversal is assisted by the proliferation of type-III vertices, or monopole defects to be discussed in the next section. This result is corroborated by real-space observations in both square and honeycomb arrays [15, 76, 77, 84, 85].

Fig. 15.9

Snapshots of spin avalanches during magnetization reversal. The white (green) area denotes the non-inverted (inverted) spins, while the blue area indicate instances of avalanche clusters. The disorder strength is characterized by a dimensionless parameter $r \equiv \varDelta H_c / {\bar{H}}_c$. The three snapshots of the square ice correspond to a weak $r=0.012$, b near critical $r = 0.018$, and c strong disorder $r=0.023$. Similarly for kagome ice, the disorder levels at the three distinct regimes are $r =$ d 0.06, e 0.10, and f 0.12. Figures from [87]

A systematic study of the disorder effects on magnetization reversal of the ice array requires large-scale simulations, which can be achieved, again, using the relaxation dynamics (15.8) for effective Ising models. In these simulations, a strong external field initially polarizes the islands along the diagonal direction in square array, and along one of the island long axis in the honeycomb case. The array is then subject to a reverse field $H_r$ in the opposite direction, with gradually increasing magnitude. Extensive relaxation dynamics simulations on large lattices containing as many as $N \sim 10^6$ spins have been performed for the two representative spin-ice arrays [87]. It is found that both square and kagome spin ices exhibit disorder-induced nonequilibrium phase transitions, with power-law avalanche distributions at the critical disorder level [87, 88]. The phenomena of driven criticality far from equilibrium are observed in many first-order transitions, such as the famous Barkhausen noise [89] in the hysteresis of magnetic materials. The random field Ising model [90] probably is the most studied system in this regard.

In both random field Ising model and artificial spin ices, the reconfiguration of the spin arrangements during magnetization reversal occurs in the form of avalanche events in the vicinity of the critical switching field when $H_r \sim \overline{H}_c$ (the average coercive field). The avalanche dynamics exhibit three different behaviors depending on the level of disorder. The weak disorder regime is dominated by large clusters extending the whole system, while many subsystem size clusters occur in the strong disorder regime; see Fig. 15.9. A critical disorder level separates these two regimes. Interestingly, the square and honeycomb arrays exhibit rather different geometries of the avalanche clusters, as demonstrated in Fig. 15.9: the avalanche clusters mostly propagate along the diagonal direction in the square ice array, whereas the clusters branch out and form fractal-like structures in kagome ice [87].

In square ice array, an avalanche event starts with the flip of a single spin at an island of lowest coercive field. In the monopole picture to be discussed in Sect. 15.4, this single spin flip corresponds to the creation of monopole pairs. The two monopoles carrying opposite charges are then pulled away by the Zeeman force until they are stopped by links of large $H^c$. The two monopoles are connected by a Dirac string [75] running roughly parallel to the diagonal direction. It is worth noting that Dirac strings consisting of type-I vertices are locally stable object since they are ground states of the dipolar interactions. Large-scale simulations find avalanche clusters consisting of inverted domains with edges roughly parallel to the diagonal direction; see Fig. 15.9a–c. This result indicates that a Dirac string (of inverted spins) tends to induce neighboring strings, and the avalanche propagation is driven by the expansion of domain walls.

The avalanche size distribution D(s) at varying level of disorder is shown in Fig. 15.10c, here s is the size of the avalanche cluster. The parameter $r \equiv \varDelta H_c / {\bar{H}}_c$ measures the level of quenched disorder in the array, and a Gaussian distribution of the island switching field $H^c_i$ is assumed in the simulations. The distribution shows two distinct behaviors. For weak disorder, a peak in D(s) at the largest cluster sizes indicates that the avalanches are dominated by large system-wide events, corresponding to the so-called super-critical regime [90]. The resultant magnetization curves $M(H_r)$ shown in Fig. 15.10a are characterized by a pronounced jump in M. For arrays with strong disorder, the large avalanches are cut off at a characteristic size $s_m$ that decreases with increasing r. Close to a critical value of $r_c \approx 0.0145$, the distribution shows a power-law behavior $D(s) \sim s^{-\tau }$, implying avalanches of all sizes occur during the reversal. Interestingly, the numerically obtained exponent $\tau \approx 1.31$ and further scaling analysis [87] are consistent with the scenario of propagating domain walls separating two polarized states [91].

Fig. 15.10

Disorder induced criticality in artificial spin ice. a and b show the normalized magnetization versus applied field at various disorder strengths r for square and kagome ice, respectively. The avalanche size distribution D(s) during magnetization reversal for the two types of ice arrays are shown in c and d. For square ice, the different curves in c correspond to $r =$ 0.011, 0.012, 0.013, 0.014, 0.015, 0.016, 0.022, and 0.030 (from top to bottom). For avalanches in kagome ice, the difference curves in d correspond to $r =$ 0.02, 0.03, 0.05, 0.07, 0.09, 0.1, 0.105, 0.115, and 0.135 (top to bottom). In both cases, the solid curves indicate super-critical regime of avalanches, while the dotted curves belong to the sub-critical regime. The dashed lines indicate the power-law behavior $D(s) \sim s^{-\tau }$ near the critical disorder. Figures from [87].

Avalanche clusters in kagome ice are also triggered by single-spin flip or the creation of monopole pairs [84, 85, 92, 93]. In stark contrast to the square-ice case, the propagation of the clusters is dominated by many branching processes as shown in Fig. 15.9d–f. Such tree-like avalanche clusters are also observed experimentally [93]. Moreover, while the Dirac string in square ice can propagate in both directions along the diagonal, the tree-like cluster in kagome mainly propagates along one direction. The high degree of branching and strong unidirectional growth of the cluster suggest that avalanches in kagome ice belong to the universality class of directed percolation [94]. The avalanche size distribution shown in Fig. 15.10d also shows super- and sub-critical behaviors, similar to the square ice case, at weak and strong disorders, respectively. Interestingly, avalanches in the super-critical regime exhibits an unusual crossover behavior: the exponents of the power-law part $s^{-\tau }$ of D(s) gradually changes from $\tau = 1.5$ at very small $r \lesssim 0.03$ to $\tau = 2$ at the critical disorder $r_c \approx 0.107$. This crossover phenomenon might reflect the reduced dimensionality (from 2D to quasi-2D) of avalanche clusters with increasing r. The exponent $\tau = 2$ agrees very well with the experimental result [93]; it is suggested that the exponent $\tau = 2$ is a result of super-universality for certain classes of time-directed avalanches [95].

Experiments on kagome ice composed of disconnected islands find dimensional reduction phenomenon in magnetization reversal [85, 96]. In this scenario, the propagation of the avalanches is mainly through the (opposite) movements of monopole pairs connected by a Dirac string, similar to some of the square ice clusters. One important consequence of this quasi-1D process is that the avalanche size distribution has a exponential decay $D(s) \sim \exp (-s/s_0)$ [85, 96]. On the other hand, significant branching of avalanche clusters and power-law distribution were observed in connected honeycomb nano-wire networks [93]. Although these two different behaviors could be attributed to the boundary effects of the sample, or the misalignment of the field in the experiments, one intriguing explanation might have something to do with the chiral nature of monopoles in disconnected arrays, as observed in micromagnetic simulations [97]. The spontaneous chiral-symmetry breaking at the $\pm 3q$ vertices might disfavor branching process, and cause the string to grow in one particular direction.

15.4 Elementary Excitations: Monopoles

Magnetic charges in spin ice are not only a useful bookkeeping tool for computing energies, but also true dynamical variables describing low-energy collective phenomena [10, 11]. For example, the ordering of magnetic charges in the kagome ice-II phase discussed in Sect. 15.2 shows that they are emergent degrees of freedom that interact with each other through the Coulomb law. The fact that magnetic charges precisely capture the leading-order interactions in spin ice is best illustrated by the dumbbell picture introduced in Sect. 15.1. Since the lowest-energy vertices in the ice-rule obeying states have minimum charges, excited vertices in this background carry an extra charge and behave as magnetic monopoles. Indeed, these excited vertices are particle-like objects that can be driven by an applied field [10]. These excited vertices or monopoles are also topological defects as they violate the ice rules and must be created and annihilated in pairs. Figure 15.11 shows examples of emergent monopoles in the dumbbell picture for various spin ice lattices. In this Section, we will discuss the monopole excitations in square and honeycomb arrays. In particular, we show that artificial spin ices with mixed lattice coordination numbers contain composite quasi-particles which can be viewed as monopole polarons.

Fig. 15.11

Monopoles in artificial spin ice. a A pair of magnetic monopoles connected by a Dirac string in a square ice array with height offset $h < h_c$. The ground state in this case is a staggered type-I order shown in Fig. 15.5a. These monopoles are called Nambu monopoles [108] because there is a finite tension of the Dirac string that consists of the higher energy type-II vertices. b A pair of $\pm 3 q$ monopoles connected by a tension-less Dirac string in an artificial kagome ice. c Two monopole ‘molecules’ in artificial pentagonal ice. In this lattice, there are both 4-legged and 3-legged vertices. Emergent monopoles (defect vertices) live on the 4-legged vertices and interact with the residual charges on the 3-legged vertices [112]. d Distribution of magnetic charges around a $Q = 2q$ monopole at $x = 0$ for two different temperatures. The extended and oscillatory charge correlation suggest a polaron picture for the composite quasi-particle [112]. Reprinted from [112] with permission from EPL

Associated with monopole excitations is another topological defects called Dirac strings [11]. Since magnetic monopoles in spin ice are not fundamental elementary particles, their charges are not quantized and a Dirac string connecting a pair of monopoles is a visible object [75]. In the ice-rule states, a single-spin flip corresponds to the creation of a monopole pair. When the two monopoles are subsequently separated, a path of inverted spins constitute the visible Dirac string. This process also demonstrate the fractionalization of dipoles into monopoles in spin ice. However, whether the separation of the monopole pair is allowed energetically depends on the tension of the Dirac string. In pyrochlore spin ice, these strings are tensionless and the separated monopoles only interact through a power-law decaying Coulomb potential [11]. In square ice, the inequivalence of the six 2-in-2-out vertices leads to a unique ground state, whose ordering pattern is determined by the height offset h; see Fig. 15.5. But more importantly, the Dirac string acquires a finite tension because of this inequivalence. For example, for coplanar square ice ($h = 0$), the ground state is a staggered arrangement of type-I vertices, and two monopoles are connected by a string of type-II vertices [109, 110]; see Fig. 15.11a. The tension of the Dirac string is $\tau \sim \varepsilon _\mathrm{II} - \varepsilon _\mathrm{I}$. The monopoles in square ice share several features with the monopole particles proposed by Nambu [107]: the Dirac string in both cases are energetic and is oriented [108]. In Nambu’s original theory for hadrons, the monopoles correspond to quarks and the finite string tension is used to describe their confinement [107].

Although magnetic monopoles in square ice with $h \ne h_c$ are not true quasi-particles because of the energetic Dirac strings, it is argued that the string tension might be compensated by its configurational entropy above a critical temperature, and the monopoles become deconfined thermally [111]. Another approach is to modify the string tension through the height offset h [110] as discussed in Sect. 15.2. Detailed numerical calculation shows that the tension diminishes as the offset approaches the critical $h_c$ from both sides and for different string paths. The vanishing string tension also results in a dramatic increase of thermally excited strings at finite temperatures, as observed in Monte Carlo simulations [38].

Magnetic monopoles in kagome ice, on the other hand, are connected by tensionless strings because of the exact degeneracy of the six minimum energy vertices. As discussed in Sect. 15.2, there are uncompensated $\pm q$ charges at every vertex in the ice phases of kagome because of its odd coordination number. In the ice-I phase, monopole excitations refer to the type-II’ vertices carrying $\pm 3q$ charges; an example is shown in Fig. 15.11b. A new type of charge excitations occurs in the ice-II phase of kagome. Recall that in this phase the residual $\pm q$ charges crystallize into a NaCl-type order on the honeycomb lattice, say $+q$ ($-q$) charges in sublattice A (B). A misplaced charge, e.g. a $-q$ vertex in sublattice A, is energy costly and represents elementary defects in the ice-II states. Relative to the background staggered charges in a ice-II state, these defects also carry a relative charge $\pm 2q$, and are sometimes also called monopoles. In magnetization reversal of kagome ice array, both types of monopoles ($\pm 3q$ vertices and charge defects) were observed [84, 85, 116,117,118].

A new collective phenomenon associated with monopoles and magnetic charges is the composite quasi-particles in spin ices with mixed lattice coordinations [112]. This is illustrated in the so-called pentagonal spin ice, shown in Fig. 15.11c. The pentagonal lattice is probably the simplest structure that combines the elementary four- and three-legged vertices shown in Fig. 15.2. In the ice phase of this lattice, there is no charges at the four-legged vertices, whereas uncompensated $\pm q$ charges exist at the 3-legged vertices. Elementary excitations are emergent monopoles carrying $Q = \pm 2 q$ at the $z=4$ sites. These monopoles then attract a cloud of net opposite charges through magnetic Coulomb interaction, forming an entity similar to the electron polaron in crystalline lattice [113]. The unusual charge-charge correlation around such a polaron is demonstrated in Fig. 15.11d obtained from Monte Carlo simulations on the dipolar pentagonal spin-ice [112]. At low temperatures, the strong correlation between the center $\pm 2q$ and the two neighbor charges resembles a H$_2$O molecule. Although the pentagonal ice array has yet to be realized in experiments, similar magnetic charge screening phenomenon has been observed in the shakti lattice [114], to be discussed in Sect. 15.6, and dice lattice [115], both of which have mixed coordination vertices.

15.5 Elementary Excitations: Magnons

In addition to the monopole excitations associated with the mesoscopic Ising degrees of freedom, another elementary excitations in artificial spin ice are magnetic resonances, or spin waves, that correspond to continuous magnetization fluctuations. These two types of excitations also have rather different time scales. Movements of topological defects involve magnetization inversion of individual islands, which needs to overcome an energy barrier and occurs over times on the order of a few nanoseconds. Basically, the system evolves from one local minimum to another; each energy minimum corresponds to a Ising configuration. On the other hand, magnon excitations are small amplitude fluctuations around a given Ising state, or a local minimum. The characteristic frequencies of magnons for typical permalloy materials are on the order of a few GHz or higher.

The finite dimension of nano-islands introduce boundary effects on the spin wave propagation, creating standing-wave modes as well as edge-localized modes [100, 101]. In particular, since the edge modes can extend significantly outside the island and hybridize with similar modes from the neighbors, they play an important role in the collective resonant dynamics that depend on the array geometry. Collective spin wave modes have been extensively studied in 1D chains and 2D arrays [100,101,102], although most of these studies consider rather simple structures such as square or rectangular lattices. Moreover, the magnon resonance also depends on the magnetizations of individual elements for a given array. The engineering of collective spin waves through design of lattice structure, magnetization pattern, the size and geometry of the elements is an intriguing emergent field called magnonics [103,104,105].

In artificial spin ice, the spin wave spectrum is significantly modified by the presence of topological defects [99]. Moreover, different topological excitations, monopole pairs and Dirac strings, display distinct and localized features, both spatially as well as in the frequency domain. These results suggest that artificial spin ice can serve as promising reprogrammable spin-wave waveguides or magnonic crystals. In this section, we will discuss the collective spin wave resonances in the artificial square ice.

Fig. 15.12

Spin-wave spectra of artificial square ice. a Evolution of the spin-wave spectrum with increasing string length and number of monopole pairs compared with the reference state. The shaded labels correspond to the main, distinct signatures of topological defects. The magnetization amplitude $\varDelta m$ of localized resonance mode associated with b monopole pairs G$^+$G$^-$, c Dirac strings, and d doubly charged monopoles G$^{*+}$G$^{*-}$ (all-in/all-out vertices). The splitting of the ferromagnetic resonance peak in the presence of a Dirac string is shown in e. The numbers (1, 2, 3, 6) in the gray-filled circle indicate the corresponding features in the spectra [99]. Figures reprinted from [99] with permission from the American Physical Society.

The calculation of spin wave eigenmodes in nanoscale magnetic particles is an extremely complicated problem when both exchange and magnetostatic contributions are taken into account [106]. Numerically, the magnetization resonant dynamics can be investigated by exciting the artificial ice array with a short magnetic field pulse. The time evolution of the array is simulated using the LLG equation (15.7); information about the eigenmodes can be extracted with the aid of Fourier transform [119]. This approach is applied to study the magnon spectra in an artificial square ice consisting of 112 stadium-shaped nano-islands in [99]. The ferromagnetic state consisting of uniform type-II vertices shown in Fig. 15.5b is used as a reference state. The magnon spectrum of this uniform type-II order is shown in Fig. 15.12a as the gray filled area. The largest peak at $f \sim 8$ GHz (position ) corresponds to the ferromagnetic resonance in which the oscillation is approximately uniform in the interior of the islands. The many smaller peaks at lower frequencies are associated with various kinds of edge modes of the array. For example, the modes at $\sim 2$ GHz and 5 GHz (positions and ) correspond to fundamental and higher-order edge excitations, respectively, at the array boundary.

The various curves in Fig. 15.12a depict the spectrum evolution when monopoles and Dirac strings are inserted into the lattice. First, a new resonance whose amplitude increases almost linearly with the number of monopole pairs appear at frequency $f\sim 2.2$ GHz [99]. Although the frequency of this resonance is close to the edge mode of the reference state, this mode is actually localized around the monopole and antimonopole labeled as G$^+$ and G$^-$, respectively in Fig. 15.12b. The enhanced peak around 5 GHz, roughly at peak of the reference state, is also related to the monopole-antimonopole pairs. Second, the new mode at $f\sim 3.5$ GHz (position ) is attributed to localized modes around the $Q = \pm 4q$ monopole pairs (or type-IV vertices). These doubly charged monopoles are labeled as G$^{*+}$ and G$^{*-}$ in Fig. 15.12d. The pronounced peak at position is also due to these topological defects. In both cases, a similar linear relation between the mode amplitude and the number of doubly-charged monopole pairs is obtained in the numerical simulations [99].

The Dirac strings also leave distinct fingerprints on the magnon spectrum of artificial ice array. A new mode at $f \sim 3$ GHz (position ) corresponds to localized oscillations around the Dirac string connecting the monopole-antimonopole pairs. Since this mode is very localized at the type-I vertices that constitute the Dirac string in a type-II background, as shown in Fig. 15.12c, its amplitude increases linearly with the string length. The dominant ferromagnetic resonance at position is also split and shifted by the Dirac strings. The spatial profile of these two modes, shown in Fig. 15.12e, are obtained by projecting the magnetization along the [11] direction of the string. The peak amplitude of the higher-frequency (8.33 GHz) mode increases with the string length at the expense of the lower-frequency resonance mode at 8.08 GHz.

As the topological defects are mesoscopic objects extending over several islands, their induced resonances are therefore dominated by the non-local magnetostatic energy. However, the spectral features induced by monopoles and strings are quite robust: reducing the lattice constants, hence increasing the magnetostatic interaction, only blue-shifts the peaks while maintaing most of the characteristics of the induced resonances. In summary, micromagnetic LLG simulations show that there is a one-to-one correspondence between the topological defects and the magnon spectrum of the artificial ice array. The fact that these modes are localized around the topological objects implies that contributions from individual defects do not interfere much with each other. Potential applications of artificial ice arrays as dynamical frequency filter or sensor can be envisioned by locally creating and moving monopoles to modify the resonant dynamics.

15.6 Emergent Frustration by Design

Artificial spin ice is one particular class of nano-arrays that belong to a larger family of magnetic metamaterials. One appealing feature of this metamaterial approach is that the frustrated or competing interactions between the constituent nanomagnetic elements can be engineered or designed through, e.g. the lattice geometries. In a narrow sense, spin ices are frustrated magnets in which the spin configuration of elementary units (vertices, triangles, or tetrahedra) follows constraints that are similar to the Bernal-Fowler rules [128] dictating local proton ordering in solid water ice. These systems are exemplified by the square, honeycomb, and pentagonal arrays discussed in previous sections. Broadly speaking, however, the term “artificial spin ice” is used to refer to engineered frustrated Ising-like magnets. The advances in modern nanolithographic fabrication has significantly broaden the scope and applications of such artificial spin systems. Other than the most studied square and honeycomb ices, various array geometries have been proposed. These include the triangular [120, 121], brickwork [122], pentagonal [112] lattices, perpendicular nano-rods arrays [123], three-dimensional structures [64], and quasi-crystals [124]; some of them have also been fabricated.

Fig. 15.13

Emergent frustration in Shakti spin ice. a Building blocks for artificial spin ices. There are four symmetry distinct types of four-leg vertices (type-I, II, III, IV), and three distinct types of 3-leg vertices (I’, II’, and III’). b The magnetic nano-array for Shakti spin ice and a generic ice state. The arrows indicate the island magnetizations. In this ice microstate, every 4-leg vertices are of type-I configuration, half of the 3-leg vertices are in the ground-state type-I’, and the other half are the higher-energy (frustrated) type-II’ state. The frustrated type-II’ vertices are mapped to a defect configuration shown in (c), which is further mapped to a six-vertex configuration in (d).

Instead of building on geometries that have been realized by nature, a systematic method of designing novel frustrated arrays is proposed in [125]. In this approach, frustrated arrays are built from elementary vertices shown in Fig. 15.13a. Other than the conventional four types of 4-legged vertices, the building blocks include three different types of 3-legged vertices with orthogonal islands. The square and brickwork arrays are examples that can be built from these elementary vertices. Because of the orthogonal geometry, the minimum $Q = \pm q$ vertices separate into two types: the lower-energy type-I’ and excited type-II’. Importantly, there is no accidental geometry-induced degeneracy in the lowest energy configurations (for both 3- and 4-legged vertices) other than the time-reversal symmetry. A consequence of this non-degeneracy of lowest-energy vertex is that both the square and brickwork arrays are not frustrated and have a well defined antiferromagnetic-type ground state.

However, it is possible to design lattices with extensive degeneracy based on the building blocks shown in Fig. 15.13a. The frustration in these designed arrays is not due to the many different ways of arranging the degenerate lowest-energy vertices (triangles in kagome or tetrahedra in pyrochlore spin ice). Instead, the frustration comes from the fact that not all vertices can reach their lowest-energy type-I or I’ configurations [125]. In practice, since the energy difference between type-I and II vertices is larger than that between the 3-legged type-I’ and II’, all four-legged vertices are in the lowest-energy type-I configuration. Frustration can be designed such that some of the 3-legged vertices have to be in the higher energy type-II’ state [125].

One representative and intriguing example of this approach is the emergence of a frustrated six-vertex phase in the so-called shakti spin ice [126, 127], shown in Fig. 15.13b. The shakti lattice can be derived from the square lattice by alternatively placing an additional vertical or horizontal island in each square plaquette. To see how the frustration emerges in this array, we first restrict ourself to the vertex model, and neglect dipolar interactions beyond the nearest neighbors. Numerical simulations show that while all four-legged vertices are in the lowest-energy type-I state, only half of the 3-legged vertices can reach the type-I’ state in the ground state [126]. Extensive degeneracy arises from the distribution of the unhappy type-II’ vertices; a generic disordered ground state is shown in Fig. 15.13b. Characterization of this degenerate manifold can be achieved by specifying the location of the unhappy type-II’ vertices, as demonstrated in Fig. 15.13c. This mapping from spins into defects on plaquettes is at least 2-to-1: each spin-ice state and its time-reversal partner are mapped to the same defect configuration. Moreover, when both defects sit at the two ends of the center long island, there is an additional $Z_2$ degrees of freedom associated with the magnetization of the center island; an example of this case is shown by the red dashed line in Fig. 15.13c.

The positions of these type-II’ defects are highly correlated in the degenerate NN ground states. In fact, the local defect configurations satisfy constraints which are exactly equivalent to the Bernal-Fowler ice rules [128]. The mapping is simple: each plaquette can be viewed as a water molecule H$_2$O, with the center of the plaquette being the oxygen and type-II’ defect being the hydrogen atom [126]. In the ground states of the nearest-neighbor shakti array, the ice rules then dictate that each plaquette has exactly two defect vertices [126]; an example is shown in Fig. 15.13c. The shakti spin ice thus provides the first realization of an extensively degenerate planar ice, or six-vertex model. Figure 15.13d shows the mapping of the defect configuration to the six-vertex state. The ice phase of shakti array in which local defect ordering satisfies the Bernal-Fowler rules were also confirmed experimentally [114]. Taking into account the additional $Z_2$ degeneracy when two defects enclose a center long island, the degenerate manifold actually maps to a special 6-vertex model, the F-model, with a larger statistical weight for the symmetric vertices [126]. The notion of frustration by design exemplified by the shakti ice opens avenue to engineer novel collective behaviors in artificial spin ice.

15.7 Other Artificial Ices

The material-by-design approach can be extended beyond magnetic systems, and several artificial systems are shown to exhibit emergent ice physics. Different realizations explore different aspects of the ice or the Coulomb phase that are related to the specific physical features of the system. For example, adding particles into artificial colloidal ice introduces new types of defects that are absent in spin ices. This artificial frustrated system consists of interacting colloidal particles confined in 2D arrays of optical traps [129]; see Fig. 15.14a. Each trap has a double well potential, and the colloidal particle can sit at one of the two minima. When the doping is such that each optical trap has exactly one particle, the double-well trap behaves essentially as an Ising spin. Antiferromagnetic coupling between the Ising variables, which is essential for ice rules, comes from the repulsive interactions between colloidal particles [129]. In square arrays, the vertex where four traps meet corresponds to oxygen atoms in water ice, while the colloidal particles act as protons. The Bernal-Fowler ice rules then correspond to constraints that each vertex has exactly two colloidal particles. Brownian dynamics simulations of colloidal square ice find a finite ice regime at moderate particle repulsion, and an ordered state at strong colloidal-colloidal interactions [129]. Different lattice geometries such as kagome ice can also be realized in a similar setup; a highly degenerate ice ground state is obtained in kagome colloidal ice [130].

The same mechanism, namely repulsive interactions and double-well traps, can be used to realize a novel vortex ice system in nanostructured superconductors [131]. In this setup, non-superconducting islands with the double-hump shape are placed in a superconducting layer. These islands again serve as effective Ising spins when trapping exactly one vortex. The repulsive vortex-vortex interaction then forces ice rules at the junctions of the islands. Vortex ice phases have been observed experimentally in nanostructured MoGe thin films [132]. In both colloidal and vortex ices, the doping level can be easily controlled experimentally. For example increasing or decreasing magnetic field controls the number of vortices. While empty traps are equivalent to vacancy spins, a doubly-occupied trap corresponds to a double-arrow spin, which has no counterpart in spin systems. It is found that adding colloidal particles to the arrays produces dramatically different effects on square and kagome colloidal ices [133]. We note in passing that a similar setup with vortex replaced by magnetic skyrmion has also been proposed recently [134].

Fig. 15.14

Artificial ice systems. a Artificial ices build on repulsive interactions between colloidal particles or superconductor vortices. The dumbbell shaped double-well traps are arranged in a square lattice. Each trap behaves as a giant Ising spin as the particle or vortex can be in one of the two energy minima. b Rydberg cold atom realization of quantum square ice. c Orbital ice states in p-orbital fermonic cold atoms on a diamond lattice. The blue arrays at the diamond-lattice sites indicate the pseudo-vectors $\langle \boldsymbol{\lambda }_i \rangle$, while the red arrows specify the spins on the pyrochlore lattice. Figure reprinted from [143] with permission from the American Physical Society.

Cold atoms in optical lattices provide another platform for engineering artificial ice systems. Thanks to the high-degree of control over the atom dynamics and the advances in creating complex optical lattices, cold-atom systems are used to realize novel phases of matter and simulate complex many-body physics [135]. A recent proposal of realizing quantum square ice in optical lattices [136] is based on the well-established equivalence between hardcore Bose-Hubbard model and the XXZ spin-1/2 Hamiltonian. In this mapping, the presence (absence) of boson corresponds to spin up (down). These bosons are then placed at a checkerboard lattice, shown in Fig. 15.14b. Recall that the Ising degrees of freedom of spin ice, e.g. center of nano-islands in square ice array, form a checkerboard lattice; see Fig. 15.1. The Bose-Hubbard Hamiltonian reads

$$\begin{aligned} \mathscr {H}_\mathrm{HB} = -t \sum _{\langle ij \rangle } (b_i^\dagger b_j^{\;} + \text{ h.c.}) + \sum _{i,j} V_{ij} n_i n_j, \end{aligned}$$

(15.9)

The density-density interaction, second term above, is mapped to the dominant Ising interaction $V_{ij} \sigma _i^z \sigma _j^z$, that is essential for ice physics. However, the interaction potential has to be highly anisotropic and step-like such that $V_{ij}$ is a constant for atoms belonging to a square plaquette and zero otherwise; see (15.6) for the Ising ice model. In particular, this requires the different couplings between nearest neighbors in x and y directions: $V_{\bullet \bullet }^x = V_{\circ \circ }^y = V_{\bullet \circ }^d \ne 0$, while $V_{\bullet \bullet }^y = V_{\circ \circ }^x \approx 0$, where $V_{\bullet \circ }^d$ denotes the coupling between the two sublattices along the diagonal directions; see Fig. 15.14b. Thanks to the advances in Rydberg atom techniques, such complex interactions can be engineered using the laser-excited Rydberg states [136]. For example, the van der Waals forces are strongly anisotropic for Rubidium atoms excited to Rydberg p states [137]. As in the colloidal ice case, doping is another control parameter here and the square ice is realized at half-filling. The Rydberg atom ice offers the opportunity to investigate quantum fluctuations and dynamical emergent gauge field in ice models [136].

While Rydberg quantum ice requires engineering of complex interactions, a novel orbital ice phase occurs naturally in p-band Mott insulator in a diamond lattice [143]. Motivated by experimental advances on higher orbital bands of optical lattices [138,139,140], cold atom systems have emerged as a new playground to investigate novel many-body orbital physics [141]. A characteristic of orbital exchange is the strong coupling between real and orbital spaces, giving rise to novel interactions such as quantum compass and Kitaev models [142]. Here we consider a p-band Hubbard model with spinless fermonic atoms on a diamond lattice. In the Mott insulating phase with two atoms per site, one fill the inert s band while the other occupies one of the three p orbitals. The remaining local degrees of freedom are similar to 3-state Potts variables, and they interact with each other through second-order exchange process. The highly directional p-orbital hopping leads to a new quantum Hamiltonian on the diamond lattice.

To describe the orbital exchange, we first define a pseudo-vector operator ${\boldsymbol{\lambda }} = (\lambda ^x, \lambda ^y, \lambda ^z) = (\lambda ^{(6)}, \lambda ^{(4)}, \lambda ^{(1)})$ acting on the local $p_x$, $p_y$, and $p_z$ basis. Here the components of $\boldsymbol{\lambda }$ are given by the three real-valued off-diagonal Gell-mann matrices; they are the SU(3) analog of the Pauli $\sigma ^x$ matrix. The operators have the following non-zero elements: $\langle p_y | \lambda ^x | p_z \rangle = \langle p_z | \lambda ^y | p_x \rangle = \langle p_x | \lambda ^z | p_y \rangle = 1$. Taking into account only the dominant longitudinal hopping, the effective exchange Hamiltonian is given by [143]

$$\begin{aligned} \mathscr {H}_\mathrm{tetrahedral} = J \sum _{m=0}^3 \sum _{\langle ij \rangle \parallel \hat{\mathbf{n}}_m} \left( \boldsymbol{\lambda }_i \cdot \hat{\mathbf{n}}_m\right) \left( \boldsymbol{\lambda }_j \cdot \hat{\mathbf{n}}_m\right) , \end{aligned}$$

(15.10)

where $m = 0, 1, 2, 3$ corresponds to the four different NN bonds; their orientations are specified by unit vectors $\hat{\mathbf{n}}_0 = [111]$, $\hat{\mathbf{n}}_1 = [1\bar{1}\bar{1}]$, $\hat{\mathbf{n}}_2 = [\bar{1} 1 \bar{1}]$, and $\hat{\mathbf{n}}_3 = [\bar{1} \bar{1} 1]$. Because the anisotropic interactions involve the four $\hat{\mathbf{n}}_m$ of a tetrahedron, this Hamiltonian is called a quantum tetrahedral model [143]. The model is geometrically frustrated in the sense that there is no way to minimize the NN interactions simultaneously. Monte Carlo simulations with variational product states of the form $|\Psi \rangle = \prod _i |\psi _i\rangle$ find extensively degenerate minimum energy states. Remarkably, direct calculation shows that these product states are exact eigenstates of (15.10). Huge degeneracy of the ground states is also obtained in exact diagonalization of small clusters. Moreover, these product ground states are highly correlated; orbitals in the degenerate manifold have to satisfy two constraints. (i) The expectation value of the pseudo-vector only takes on six different values: $\langle \boldsymbol{\lambda }_i \rangle = \pm \hat{\mathbf{x}}$, $\pm \hat{\mathbf{y}}$, and $\pm \hat{\mathbf{z}}$. (ii) Defining an Ising variable on each of the four bonds that attached to site-i: $\sigma _i^m \equiv \sqrt{3} \langle \boldsymbol{\lambda }_i \rangle \cdot \hat{\mathbf{n}}_m = \pm 1$, the NN pairs need to satisfy $\sigma _i^m \sigma _j^m = -1$.

It turns out these two constraints are equivalent to the ice rules [143]: the six different $\langle \boldsymbol{\lambda }_i \rangle$ are mapped to the six distinct 2-in-2-out Ising spins, while constraint (ii) ensures that consistent Ising spins can be assigned on the pyrochlore lattice. Figure 15.14c shows a generic disordered orbital ice state and the mapping to the spin-ice configuration on pyrochlore. The p-band Mott insulator in diamond lattice thus provides an orbital analog of the ice phase. It is worth noting that, unlike most ice models with Ising degrees of freedom defined on a bi-simplex lattice (e.g. kagome or pyrochlore), the fundamental variables in orbital ice are orbital triples on a bipartite diamond lattice. The ice rules are emergent correlations in the ground state of the quantum dynamics.

15.8 Conclusion and Outlook

To summarize, we have reviewed the fundamental theories and physical properties of artificial spin ice, including the basic energetics and dynamics (Sect. 15.1), thermodynamic phases (Sect. 15.2), effects of disorder, nonequilibrium dynamics (Sect. 15.3), and elementary excitations (Sects. 15.4 and 15.5). Contrary to natural spin-ice compounds, the artificial version of spin ice offers the opportunity for researchers to tailor-design the many-body interactions and to directly probe the resultant dynamics “microscopically” in real space. In particular, artificial spin ices provide a new playground for scientists to explore the physics and technological applications of emergent magnetic monopoles. This has inspired the study of a new field dubbed magnetricity, which is the magnetic equivalent of electricity. An intriguing possibility is to use magnetic monopoles as binary mobile memory storages that also serve as the information processing units. Taking advantage of the topological and collective nature of monopole excitations, artificial spin ice opens a new avenue to realize massively parallel computation that goes beyond the conventional von Neumann architecture [145].

While magnetic moments in natural spin-ice compounds are regarded as structureless entities, the Ising “spins” in artificial spin ices are themselves macroscopic ferromagnets that exhibit complex textures and support spin-wave excitations. A unique feature of artificial spin ice is thus the intriguing interplay between its two basic elementary excitations: magnetic monopoles and magnons. As discussed in Sect. 15.5, both the monopoles and the Dirac strings that connect them have unique signatures in the spin-wave excitations of the nanomagnetic arrays. Several recent studies along this line [146,147,148] have further established that artificial spin ices can be viewed as reconfigurable and tunable magnonic crystals that can be used as metamaterials for spin-wave-based applications at the nanoscale. This suggests the fascinating possibility of dynamically controlling the magnon band structure through the motion and configuration of magnetic monopoles.

Another new frontier is the study of electric charges flow through the nano-wires in artificial spin ice. Recent experiments have demonstrated that connected artificial ice arrays exhibit unusual and complex magneto-transport phenomena [98, 149,150,151]. Remarkably, rather large Hall signals are observed in artificial kagome spin ice even in the absence of external magnetic field [150]. Theoretical models based on the anisotropic magneto-resistance effect of permalloy show that significant contribution to the Hall voltage comes from the vertex regions of the connected network [150, 152]. Moreover, an effective circuit model has been developed to understand the complex magneto-transport properties of artificial spin ice [152]. In this picture, the system can be viewed as a resistor network driven by voltage sources that are located at vertices of the spin-ice array. The differential voltages across different terminals of these sources are related to the ice-rules that govern the local magnetization ordering. The circuit model thus underscores the many-body origin of Hall signals in artificial spin ice [152].

Artificial spin ice, originally designed to model the frustrated magnetic interactions in pyrochlore spin-ice compounds, has now become a flourishing field of research with rapid advances in several fronts. A central theme that drives this field is the concept of frustration by design discussed in Sect. 15.6. Thanks to the impressive progress in nano-fabrication and imaging technology, virtually any imaginable lattice geometry can be fabricated and characterized in real space and real time. For example, dedicated geometries have been proposed and realized to explore interesting physics such as magnetic charge screening [114, 115], magnetic charge ice [144, 153], emergent dimensional reduction [154], topological lattice defects [155], and nanoscale spin ratchet [156], to name but a few. The artificial spin array can be used to dynamically imprint complex patterns of magnetic field on other interesting materials, e.g. superconductors, topological matters, and quantum heterostructures, thus opening a new route to create multifunctional metamaterials and devices. Finally, implementation of ice or frustrated systems in other setups as discussed in Sect. 15.7 introduces new dimensions, such as spin vacancy and quantum fluctuations, to the already rich physics of spin ice materials.