Keywords

1 Introduction

Along with the development of computer science and electronic engineering, the advancement of artificial intelligent technologies have been progressing in a great pace in recent years. The most representative intelligent scheme Neural Networks (NNs) have been introduced to many industrial fields, and various of applications in our lives. Owing to the NNs’ excellent features, they are effectively applied in image/speech processing and classification, emotion recognitions and so on. In the applications of NNs, the most classic approach for the learning in them is the Back-Propagation (BP) method, which is a gradient decent algorithm to obtain the weights and biases in NNs. However, owing to the mechanism using cost function in the BP learning, the differential information is necessary in the applications. For most industrial applications, the differential information of the objectives are difficult to be obtained [1].

Meanwhile, the development of evolutionary computation attracts a lot of attentions in recent years, owing to their excellent features in complex optimization problems. They are considered as good solutions to solve the limitations in the learning of NNs. Genetic algorithm (GA), which is constructed according to the evolutionary mechanisms of natural selection, is the most well-regarded algorithm in the evolutionary computation [2]. Since GAs are with fine searching ability, difficult to be trapped in local minima, and can be applied without considering the differential information in the learning procedure, they have been applied in NN for many applications [3]. However, because of the complexity in the encoding manipulations, and the evolution mechanism in GAs, more effective algorithms with simple manipulations and high efficiency are expected.

In previous research, the NN is proposed for the position control of ultrasonic motor (USM). The traditional approach of NN is applied for the position control of USMs [4]. The BP type NN is also constructed for the position control of USM with speed compensation [5]. The proposed method was confirmed effective and easy to be applied in the control of USM. To solve the problem of Jacobian estimation, we introduced the particle swarm optimization (PSO) algorithms for the NN type PID controller in the control of USM [6, 7]. Owing to the excellent features of PSO in optimization both in continuous and discrete problems [8], the swarm intelligence algorithm was introduced to the proposed scheme, and confirmed effective in obtaining high accuracy in position and speed control of USM. However, there are some concerns about the local minimum problem and ability of re-convergence in PSO for the control process. Therefore, in this study, the algorithm of differential evolution (DE) is introduced in an intelligent control application using NN. According to the study from S. Das et al. [9], DE was proofed being with as good convergence characteristics as PSO. Meanwhile, the hybridizations of both the algorithms are excellent comparing with other soft computing tools. In the study of [10], DE was investigated as a global optimization algorithm for feed-forward NN. The good features of DE, such as no learning rate setting requirement and offering high quality solutions were confirmed. Comparing with the traditional GAs, DE algorithms are with superior features such as simpler construction, high efficiency, and excellent convergence features. In the NN scheme, the DE algorithm is applied to update the weight for learning, without considering the differential limitation as in BP algorithms, or the encoding manipulations as in GAs. The proposed DE type NN is applied to an intelligent PID control scheme for USM to confirm the effectiveness. The intelligent automation with the proposed method is expected to contribute in the medical and welfare applications utilizing the excellent features of USMs [11].

The chapter is organized as follows. In Sect. 2, the general introduction about NN, DE, and the proposed DE type NN scheme is given. In Sect. 3, the simulation study of the proposed intelligent scheme using the DE type NN is introduced. Section 4 gives an experimental study of the proposed method on an existent USM servo system. The conclusions are given in Sect. 5.

2 Proposed Intelligent Scheme

2.1 Neural Network

NNs are machine learning methods that imitate the mechanism of the human brain. Owing to the excellent characteristics of them, they have been studied and applied in various kinds of fields as the most representative of artificial intelligence [12]. Figure 1 shows an example of an NN consisting of three layers of neurons. input i is the input signal and the neurons contained the signals consist the first layer. w ij is the coupling weight from the first layer to the second layer (hidden layer), H j is the signal activated according to the sum of the weighted input signals. w ij is the coupling weight from the second layer to the third layer (output layer). O m is the output signal activated according to the sum of the weighted input signals from hidden layer. Theoretically, the weights in general schemes are initialized with random values. However, it is necessary to adjust it to a value suitable for the problem to be dealt with. The BP algorithm is often used for optimization. However, some limitations in traditional methods prevent the BP type NN from wider applications. Therefore, in this study, the DE algorithm is introduced to the learning of NN.

Fig. 1
figure 1

Basic scheme of NN

Full size image

2.2 Differential Evolution

In this study, we use the DE algorithm as an optimization method of the weighting coefficient of the NN. It does not need to be differentiable because it is one of the methods and does not use the gradient of the problem to be optimized. Due to its characteristics, the DE algorithm can be applied even when the problem is discontinuous, or time-varying. The general procedure in DE can be depicted by the flowchart shown in Fig. 2.

Fig. 2
figure 2

Flowchar of DE algorithm

Full size image

2.2.1 Randomly Initialization

Basically, DE algorithm is a global optimization algorithm for obtaining optimal solutions in a D dimensional space. The initialization of the algorithm is usually implemented by random real numbers consisting a vector in the D dimension. The randomly initialized vectors are considered as possible solutions, which can be represented as

$$\displaystyle \begin{aligned} X_{i}=[x_{1}, x_{2}, \ldots, x_{D}] \end{aligned} $$
(1)

If the searching space can be constrained by

$$\displaystyle \begin{aligned} \begin{array}{rcl} X_{i, Min}=[x_{1, Min}, x_{2, Min}, \ldots, x_{D, Min}]& \end{array} \vspace*{-12pt}\end{aligned} $$
(2)
$$\displaystyle \begin{aligned} \begin{array}{rcl} X_{i, Max}=[x_{1, Max}, x_{2, Max}, \ldots, x_{D, Max}]& \end{array} \end{aligned} $$
(3)

Then, the elements in the vector can be randomly initialized by

$$\displaystyle \begin{aligned} x_{i}=x_{i, Min}+rand(0, 1)\cdot(x_{i, Max}-x_{i, Min}) \end{aligned} $$
(4)

where rand(0, 1) is the random number within the range of (0, 1).

2.2.2 Mutation

Following the random initialization, the mutation according to target vector is implemented. The donor vector v i can be generated as linear combination of some vectors in current searching generation selected according to some strategies. There are some strategies introduced in [13]. In this study, we focus on four strategies as follows:

  • DE/rand/1/bin

    $$\displaystyle \begin{aligned} v_{i} = x_{r1}+F\cdot(x_{r2}-x_{r3} ) \end{aligned} $$
    (5)

  • DE/rand/2/bin

    $$\displaystyle \begin{aligned} v_{i} = x_{r1}+F\cdot(x_{r2}-x_{r3})+F\cdot(x_{r4}-x_{r5}) \end{aligned} $$
    (6)

  • DE/current-to/1/bin

    $$\displaystyle \begin{aligned} v_{i} = x_{i}+F\cdot(x_{r2}-x_{r3}) \end{aligned} $$
    (7)

  • DE/best/1/bin

    $$\displaystyle \begin{aligned} v_{i} = x_{best}+F\cdot(x_{r2}-x_{r3}) \end{aligned} $$
    (8)

r1, r2, r3, r4, r5 are the randomly chosen integers with different value from each other and i, within the range of [1, N(number of searching points)].

2.2.3 Crossover

In crossover, the donor vector is applied to be combined with the target vector. There are mainly two kinds of crossover methods (exponential and binomial) applied in DE algorithms. In this study, we employ the binomial crossover, which applies comparison between a random number generated in (0, 1) and a parameter of crossover probability C r to decide the crossover scheme. The trial vector of U i can be generated, and the elements in it can be calculated as

$$\displaystyle \begin{aligned} u_{i, j} = \begin{cases} v_{i, j} \qquad \text{if } rand(0, 1) \leq C_{r}, \quad \text{or} \quad j=j_{rand}\\ x_{i, j} \qquad \text{otherwise}. \end{cases} \end{aligned} $$
(9)

where rand(0, 1) is a real number random number in [0, 1], and j rand is an integer random number in 1, …, D.

2.2.4 Selection

In the selection procedure, the generated target vector is decided to be a survival or not. The decision is made according to the evaluation of objective/evaluation function f(⋅). The procedure can be expressed as

$$\displaystyle \begin{aligned} X_{i} = \begin{cases} U_{i}, \qquad \text{if } f(U_{i}) \leq f(X_{i})\\ X_{i}, \qquad \text{if } f(U_{i}) > f(X_{i}) \end{cases} \end{aligned} $$
(10)

2.3 Proposed DE Type NN Scheme

In this study, the DE algorithm is introduced to update the weights in the learning of NN. The method can be constructed with simple structure, easy to be applied, without considering the differential information.

In the proposed scheme, the vector of DE is designed as the real value of weights in NN. The target vector in DE can be expressed as

$$\displaystyle \begin{aligned} W=[x_{00}, x_{01}, \ldots, x_{ij}, \ldots, x_{jm}] \end{aligned} $$
(11)

The weights in the NNs are updated by the mutation, crossover, and selection procedures in the DE algorithm to obtain the optimal solutions in NN’s learning.

3 Simulation Study

To confirm the effectiveness of the proposed scheme, the simulation study was implemented employing the Rosenbrock function for optimization using NN. The Rosenbrock function is a convex function with two input values, defined as x and y as follows.

$$\displaystyle \begin{aligned} f(x, y)=(1-x)^{2}+100(y-x^{2})^{2} \end{aligned} $$
(12)

The function can be plotted as in Fig. 3. In the study, the NN with the topologic structure shown in Fig. 4 was introduced to find the minimum of the Rosenbrock function. The NN is constructed to find the optimal (x, y) to minimize the Rosenbrock function.

Fig. 3
figure 3

The plot of the Rosenbrock function

Full size image
Fig. 4
figure 4

Structure of DE-NN for simulation

Full size image

The weights in the NN is designed to be updated by the DE introduced in Sect. 2. The weights are initialized by the random real number within the range of (−1.0, 1.0). The mutation strategies were investigated in the simulation to confirm the characteristics in DE. The parameter F which is the scaling factor is set as 0.5. The crossover probability C r is set as 0.8. The number of searching unit in DE is set as 10. To investigate the effectiveness of the proposed scheme comparing with the conventional method, we also implement the NN’s learning using traditional BP algorithm. The weights of NN in BP is updated as follows. The weights between the output layer and the hidden layer can be updated as

$$\displaystyle \begin{aligned} w_{jm} = w_{jm} - \eta \frac{\partial f}{\partial w_{jm}} \end{aligned} $$
(13)

where η is the learning rate in NN, and w jm is the weights between the hidden layer and the output layer. Then, the weights w ij between the input layer and the hidden layer can be updated as

$$\displaystyle \begin{aligned} w_{ij} = w_{ij} - \eta \frac{\partial f}{\partial O_m} \frac{\partial O_m}{\partial H_j} \frac{\partial H_j}{\partial w_{jm}} \end{aligned} $$
(14)

By applying both the methods of DE type NN and BP type NN, the NNs are trained to converge to the optimal values with proper weights. Outputs of the BP and DE type NNs are shown in Fig. 5. The figure shows that the outputs of both NNs converged to the optimal (x,y) to minimize the value of the function in hundreds of iterations. Comparing with the convergence of the BP type NN, the DE type NN showed better convergence characteristics. The errors of the minimum value and the NNs’ outputs are shown in Fig. 6. The variation of the errors shows the same trends as we see in Fig. 5. The variations of weights in the BP and DE type NNs are shown in Fig. 7. The DE type NN with the mutation strategy of DE/best/1/bin. It can be seen that the DE update the NN’s weights in iterations. The weights can converge to certain constant values in short time. The values of weights converged quick in around 100 iterations. Comparing the proposed DE type NN with the traditional BP type NN, the proposed scheme was with an excellent convergence features.

Fig. 5
figure 5

Outputs of the BP and DE type NNs

Full size image
Fig. 6
figure 6

Errors of the BP and DE type NNs

Full size image
Fig. 7
figure 7

Weight convergence of the BP and DE type NNs

Full size image

To confirm the conference characteristics of DE with different mutation strategies, the simulation study was implemented in the optimization of Rosenbrock function using the proposed NN. The DEs with the mutation strategies of DE/best/1/bin, DE/current to/1/bin, DE/rand/1/bin and DE/rand/2/bin were investigated [13]. The variation of the evaluation value was studied as Fig. 8 shows. According to the simulation results, it is clear to see that among the DEs with the strategies, the DE/best/1/bin strategy converged to quite low evaluation value in only a few iterations. The DE/best/1/bin strategy is with great convergence characteristics to approach the optimal. Therefore, the DE/best/1/bin is considered as the best solution for experimental study.

Fig. 8
figure 8

Convergence of DE with different mutation strategies

Full size image

4 Experimental Study

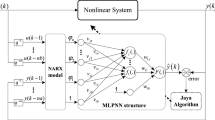
Based on previous research in [7], an intelligent control method using PID control combined with DE type NN is applied as the controller for USM as shown in Fig. 9. The NN scheme we propose is a fixed structure as we see in Fig. 10. In the proposed intelligent scheme, DE type NN is employed for updating the PID gains. The error signal of [e(k), e(k − 1), e(k − 2)] is employed as input. The scheme is designed for tuning PID gains automatically to minimize the error in USM control. The output of the NN unit is the variation of PID gains [ΔK P(k), ΔK I(k), ΔK D(k)]. The output of neurons in hidden-layer is expressed as H j(k), which can be estimated by Eq. 15.

$$\displaystyle \begin{aligned} H_{j}(k)=f_{s}(w_{ij}(k)\cdot I_{i}(k)) \end{aligned} $$
(15)

Then, the output of NN can be estimated as

$$\displaystyle \begin{aligned} \varDelta K_{P, I, D}(k)=f_{s}(w_{jm}(k)\cdot H_{j}(k)) \end{aligned} $$
(16)

where f s(x) is the sigmoid function as shown in Eq. 17.

$$\displaystyle \begin{aligned} f_{s}=\dfrac{1}{1+e^{-x}}-0.5 \end{aligned} $$
(17)

The weights between three layers, expressed by w ij(k) and w jm(k), are updated by BP and DE algorithms. Then, the output of PID controller u(k) can be calculated as

$$\displaystyle \begin{aligned} u(k) &= u(k-1) + (K_{P}(k) + K_{I}(k) + K_{D}(k))e(k)\\ &\quad - (K_{P}(k) + 2K_{D}(k))e(k - 1) + K_{D}(k)e(k - 2) \end{aligned} $$
(18)
Fig. 9
figure 9

Block diagram of the proposed intelligent method using DE type NN

Full size image
Fig. 10
figure 10

The topologic structure of NN controller

Full size image

In our experimental study, the sin wave was applied as the input signal. The response of the proposed method is shown in Fig. 11. There was no visible error in the response of sin wave input. Figure 12 shows the variation of the PID gains updated by the proposed scheme using DE type NN. The gains oscillated in the initial phase in a short period. Then, they converged to certain values quickly. The convergence and accuracy of the proposed method is confirmed according to the experimental results.

Fig. 11
figure 11

Response for sin wave signal input using DE type NN

Full size image
Fig. 12
figure 12

Gain variation by the proposed DE-NN type PID controller

Full size image

5 Conclusions

In this chapter, an intelligent PID control scheme using the DE type NN is proposed. In the proposed scheme, an NN method is employed for optimizing the gains in PID controller for the control of ultrasonic motor. The weights of the NN are designed to be updated by DE algorithm. By employing simulation study, the DE algorithm was confirmed effective in the learning of NN. According to the simulation results, the mutation strategies were investigated. The DE/best/1/bin was the most effectiveness in the optimization process. By the experimental study, the DE type NN was confirmed effectiveness in the PID control of the USM. The proposed method is able to be applied for achieving high control performance in compensating characteristic changes USM. Meanwhile, its application is without any consideration of Jacobian estimation in NN’s leering. By employing the method, USMs are expected more in various applications, such as the meal-assistance robots [14], human support robots, even some humanoid robots [15], especially for the applications in medical and welfare fields in the future.