Keywords

1 Introduction

Power systems tend to be large, complex, and multivariate systems. Therefore, any optimization problem applied to any of the three major components of them, that is, generation, transmission, and distribution (Kothari, 2012), tends to be equally complex and very difficult to solve, suffering also from the dimensionality curse (Song, 2013). Optimization techniques are applied also to several aspects of power systems, such as operation, control, and planning.

Conventional optimization processes, such as linear programming, have been deployed for plain and optimal power flow (Alsac, Bright, Prais, & Stott, 1990; Hyedt & Grady, 1983) or active and reactive power dispatch (Zhu & Irving, 1996). Nonlinear programming techniques have been used again for providing power flow solutions, being more accurate than linear but more time-consuming (Sun, Ashley, Brewer, Hughes, & Tinney, 1984), as well as for the problem of hydrothermal cooperation scheduling (Kothari, 1989). Additionally, there are problems that require integer and/or mixed-integer programming approaches, such as the unit commitment and economic dispatch problems (Chatzivasileiadis, 2018; Defourny & Terlaky, 2015; Dillon, Edwin, Kochs, & Taud, 1978). Dynamic programming has been also deemed necessary, when dealing with transmission planning (Partanen, 1990) or reactive power control (Lu & Hsu, 1995).

Apart from the conventional optimization methods, artificial neural network (ANN) (Dai, He, Fan, Li, & Chen, 1999) and fuzzy logic (Bansal, 2003) are also among the preferred techniques used to solve several power system problems.

On the one hand, notwithstanding the considerable achievements in conventional approaches, the latter still have not be applied to fast and reliable real-time implementations. Thus, significant labor is required to prevent mathematical entrapments, such as ill-conditioning and convergence arduousness. On the other hand, ANN or fuzzy techniques rely heavily on extensive expert domain knowledge. This means that they suffer from the expert user’s knowledge in their design and utilization and moreover the lack of the formal model theory, being vulnerable in that way to the experts’ depth of knowledge in problem definition (Bansal, 2005).

Metaheuristic techniques on the contrary can access deep knowledge via well-established mathematical models. There has been a variety of metaheuristic techniques utilized and in equally diverse variety of problems regarding power systems such as genetic algorithm (GA) in voltage control (Iba, 1994), simulated annealing (SA) for maintenance scheduling (Satoh & Nara, 1991), and tabu search for fault diagnosis/alarm processing (Wen & Chang, 1997).

ODGP is another power system problem that has proved quite a challenge itself (Jordehi, 2016). By strict conditions, ODGP contemplates the best positions, where the DG units should be connected to the distribution network (DN), and what should be their size in terms of rated capacity. Distributed generation includes technologies such as diesel generators (Paliwal, Patidar, & Nema, 2014) and microturbines (Ismail, Moghavvemi, & Mahlia, 2013), called collectively as conventional DG units, since they still use fossil fuels to produce electricity; then, there are also renewable energy sources (RES), such as photovoltaics (PVs) (Palz, 2013), wind turbines (WTs) (World Wind Energy Association, 2014), and hydroelectric power plants (HPPs) (Chen, Chen, & Fath, 2015), that use natural resources, such as solar irradiance, wind, and water kinetic energy, respectively, in order to transform it to electric energy.

2 Literature Review

A few of the benefits that the integration of the DG in the DN offers are the reduction of greenhouse gas emissions, more liberated energy strategies, diversity of energy sources, peak operating cost decrease, network upgrades deferral, reduced power losses, decreased costs in transmission and distribution, and potential service quality augmentation towards the end customer (Georgilakis & Hatziargyriou, 2013). However, all of these, in order to be efficiently applied, require a proper strategic planning. Otherwise, critical consequences could impact the DN, such as loss increase (Atwa & El-Saadany, 2011; Gautam & Mithulananthan, 2007), voltage rise (Schwaegerl, Bollen, Karoui, & Yagmur, 2005; Tu, Yin, & Xu, 2018), reverse power flow (Delfanti, Falabretti, & Merlo, 2013), and reliability reduction (Abdmouleh, Gastli, Ben-Brahim, Haouari, & Al-Emadi, 2017; Esmaili, 2013). Therefore, the siting and sizing of the DGs could greatly affect all of those issues and thus become significantly important to solve.

The ODGP problem is by its nature mixed-integer nonlinear and therefore quite complex to solve. Several approaches have been utilized: empirical methods, such as the “2/3 rule” (Willis, 2000); analytical methods using the exact loss formula (Hung, Mithulananthan, & Bansal, 2010), loss sensitivity factors, or an improved analytical technique (Hung & Mithulananthan, 2011); numerical such as gradient search algorithm (Rau & Wan, 1994), dynamic programming (Khalesi, Rezaei, & Haghifam, 2011), linear programming (Keane & O’Malley, 2005), and exhaustive search method (Singh, Misra, & Singh, 2007); and finally metaheuristics techniques such as GA (Soroudi & Ehsan, 2011), differential evolution (DE) (Arya, Koshti, & Choube, 2012), artificial bee colony (ABC) (Seker & Hocaoglu, 2013), harmony search (Rao, Ravindra, Satish, & Narasimham, 2012), cuckoo search (CS) (Moravej & Akhlaghi, 2013), bacterial foraging optimization algorithm (BFOA) (Mohammadi, Rozbahani, & Montazeri, 2016), grey wolf pack optimization (Sultana, Khairuddin, Mokhtar, Zareen, & Sultana, 2016), ant-lion optimization (Ali, Abd Elazim, & Abdelaziz, 2016), and particle swarm optimization (PSO) (Prakash & Lakshminarayana, 2016).

The empirical methods, as previously stated, rely heavily on the experts’ knowledge depth. Moreover, they are restricted in uniformly distributed loads and radial DNs. As far as the analytical methods are concerned, they are perfectly suited when one DG is contemplated. However, when more than one is considered for installation, the problem becomes perplexed enough to solve via analytical methods. Numerical methods can tackle this issue. However, in order to do so, they either require several assumptions, such as considering the problem as linear, instead of nonlinear, or searching exhaustively all the possible solutions in order to retrieve the optimal one. The former provides a deviation from reality; the latter proves to be rather time-consuming.

As for the metaheuristic techniques, they seem to provide several advantages when contemplating the ODGP: they are not restricted by type or size of the examined DN, load considered, or DG unit number. Moreover, they do not require any assumptions, thus solving the problem in its core. The only disadvantage they present is that being basically random search methods, they require more than one trial and are susceptible to local minima entrapment (Parsopoulos & Vrahatis, 2002). Therefore, the solution that they provide in most cases is near-optimal. Despite of their drawbacks, however, the benefits of using metaheuristics greatly outweigh their demerits.

This chapter focuses mainly on PSO and how it performs when applied to the ODGP problem. A comparison of various PSO versions is presented along with other metaheuristic techniques, in order to further enhance PSO performance. Additionally, the application of PSO in the combined problems of ODGP and NR is described. Finally, the application of PSO in the optimal schedule of EVs is demonstrated.

3 ODGP: Problem Determination

In this section the ODGP problem is determined by defining the objective function and the constraints that are required to be imposed.

3.1 Objective Function

As an objective function, the power losses is examined, that is:

$$ {F}_{\mathrm{loss}}=\min \sum \limits_{k=1}^{l_k}{g}_{m,n}\left[{V}_m^2+{V}_n^2-2{V}_m{V}_n\cos \left({\varphi}_m-{\varphi}_n\right)\right] $$
(17.1)

where:

gm, n:

Conductance between buses m and n, respectively

lk:

Total network line number

Vm, Vn:

Buses m and n voltage magnitudes, respectively

φm, φn:

Buses m and n voltage angles, respectively

3.2 Constraints

The problem is bound to several constraints, such as technical constraints imposed by the DN and power flow constraints:

$$ {P}_{G,m}-{P}_{D,m}-\sum \limits_{n=1}^{l_n}\left|{V}_m\right|\left|{V}_n\right|\left|{Y}_{m,n}\right|\cos \left({\varphi}_{m,n}-{\varphi}_m+{\varphi}_n\right)=0 $$
(17.2)
$$ {Q}_{G,m}-{Q}_{D,m}+\sum \limits_{n=1}^{n_n}\left|{V}_m\right|\left|{V}_n\right|\left|{Y}_{m,n}\right|\sin \left({\varphi}_{m,n}-{\varphi}_m+{\varphi}_n\right)=0 $$
(17.3)

Voltage and line limits:

$$ {V}_m^{\mathrm{min}}\le {V}_m\le {V}_m^{\mathrm{max}} $$
(17.4)
$$ {S}_j\le {S}_j^{\mathrm{max}} $$
(17.5)

where:

PG, m, QG, m:

Bus m active and reactive power generation, respectively

PD, m, QD, m:

Bus m active and reactive power demand, respectively

ln:

Total network node number

Ym, n:

Bus admittance element m,n

φm, n:

Bus admittance element m,n

\( {V}_m^{\mathrm{min}} \), \( {V}_m^{\mathrm{max}} \):

Bus m voltage lower and upper limits, respectively

\( {S}_j^{\mathrm{max}} \):

Line j thermal limit, by terms of apparent power

There are also constraints with respect to the DG units themselves, such as the technical operation limits of the DG units considered for installation:

$$ {S}_{\mathrm{min}}^{DG}\le {S}_i^{DG}\le {S}_{\mathrm{max}}^{DG} $$
(17.6)
$$ {pf}_{\mathrm{min}}^{DG}\le {pf}_i^{DG}\le {pf}_{\mathrm{max}}^{DG} $$
(17.7)

And permitted DG penetration constraint, that is:

$$ \sum \limits_{i=1}^{m_{DG}}{S}_i^{DG}\le \eta \bullet {S}_{\mathrm{Total}}^{\mathrm{Load}} $$
(17.8)

where:

\( {S}_i^{DG}:: \)

DG unit apparent power

\( {pf}_i^{DG} \):

DG unit power factor

\( {S}_{\mathrm{min}}^{DG} \), \( {S}_{\mathrm{max}}^{DG}:: \)

DG unit apparent power lower and upper limits, respectively

\( {pf}_{\mathrm{min}}^{DG} \), \( {pf}_{\mathrm{max}}^{DG} \):

DG unit power factor lower and upper limits, respectively

mDG:

DG unit total number

η:

Desired DG unit penetration level percentage

\( {S}_{\mathrm{Total}}^{\mathrm{Load}} \):

DN total load

4 Penalty Function Formulation

Generally, either deterministic or stochastic techniques have been utilized to solve optimization problems bound by constraints. Deterministic approaches, for example, feasible direction and generalized gradient descent, require strict mathematical properties for the objective function, such as continuity and differentiability. In addition, using analytical techniques to solve the ODGP problem could prove to be complex and time-consuming (Del Valle, Venayagamoorthy, Mohagheghi, Hernandez, & Harley, 2008) or be confined to solutions towards installing only one DG unit. However, these properties are not always present or easily employed. In those cases, evolutionary computation offers a reliable alternative option. Most evolutionary techniques, though, have been primarily designed to address unconstrained problems. Therefore, constrained handling techniques are usually accompanying the implementation of evolutionary techniques in order to detect and avoid any infeasible solutions. The most common practice dictates the use of a penalty function. Despite its disadvantages, if a proper calibration of the penalty parameters is undertaken, it performs rather efficiently (Parsopoulos & Vrahatis, 2007). To that end, constraints are expressed using penalty terms that in turn are incorporated into the objective function. This leads to the formulation of the penalty function. The latter penalizes any infeasible solutions as follows:

$$ P(x)=f(x)+O(x) $$
(17.9)
$$ O(x)=o\left\{{g}^2(x)+{\left[\max \left(0,h(x)\right)\right]}^2\right\} $$
(17.10)

where:

P(x):

Penalty function

f(x):

Objective function

O(x):

Penalty term

o:

Penalty factor

g(x):

Related equality constraints

h(x):

Related inequality constraints

Thus, in the case of the ODGP problem and using, for the sake of argument only, the Floss as the objective as expressed in Eq. (17.1) and the DN technical constraints, that is, the equality constraints as defined in Eqs. (17.2) and (17.3) and inequality constraints as defined in Eqs. (17.4)–(17.8), the updated penalty function is expressed as:

$$ P(x)=\min \left({F}_{\mathrm{loss}}+{O}_P+{O}_Q+{O}_V+{O}_L\right) $$
(17.11)

where OP and OQ refer to the equality constraints:

$$ {O}_P={o}_P\sum \limits_{m=1}^{l_n}\left\{{P}_{G,m}-{P}_{D,m}-\sum \limits_{n=1}^{l_n}\left|{V}_m\right|\left|{V}_n\right|\left|{Y}_{m,n}\right|\cos \left({\varphi}_{m,n}-{\varphi}_m+{\varphi}_n\right)\right\} $$
(17.12)
$$ {O}_Q={o}_Q\sum \limits_{m=1}^{l_n}\left\{{Q}_{G,m}-{Q}_{D,m}+\sum \limits_{n=1}^{l_n}\left|{V}_m\right|\left|{V}_n\right|\left|{Y}_{m,n}\right|\sin \left({\varphi}_{m,n}-{\varphi}_m+{\varphi}_n\right)\right\} $$
(17.13)

and OV and OL to inequality constraints:

$$ {O}_V={o}_V\sum \limits_{m=1}^{l_n}{\left\{\max \left(0,{V}_m^{\mathrm{min}}-{V}_m\right)\right\}}^2+{o}_V\sum \limits_{m=1}^{l_n}{\left\{\max \left(0,{V}_m-{V}_m^{\mathrm{max}}\right)\right\}}^2 $$
(17.14)
$$ {O}_L={o}_L\sum \limits_{j=1}^{l_k}{\left\{\max \left(0,{S}_j-{S}_j^{\mathrm{max}}\right)\right\}}^2. $$
(17.15)

As it can be easily deduced, any other constraints such as Eqs. (17.6), (17.7), or (17.8) can be incorporated in Eq. (17.11) via the same process.

5 PSO Analysis

5.1 General

In this section the PSO algorithm is presented, as addressed and appropriately adjusted, in order to contemplate the ODGP problem.

PSO has been developed by Kennedy and Eberhart (Eberhart & Kennedy, 1995) and was inspired by the movement of fish schools or herds of animals that are trying to find some food source or avoid a potential enemy. Mathematically, the main idea is that, having defined the feasible solution space, a swarm of particles explores it. Their position within the solution space changes with every iteration step, along with their velocity. This change in velocity consists of three terms:

  1. 1.

    The personal or cognitive knowledge of the solution space, as gathered by each individual particle.

  2. 2.

    The social knowledge of the solution space that each particle has gathered after communicating with other particles.

  3. 3.

    Its previous status.

This can be formulated in the following generalized equations:

$$ {v}_h\left(t+1\right)={v}_h(t)+{c}_1{R}_1\left({P}_h(t)-{X}_h(t)\right)+{c}_2{R}_2\left({P}_g(t)-{X}_h(t)\right) $$
(17.16)
$$ {X}_h\left(t+1\right)={X}_h(t)+{v}_h\left(t+1\right) $$
(17.17)

where:

h = 1, …, N:

Particle number

Xh(t):

Current position of particle h

Xh(t + 1):

Next position of particle h

v(t):

Current velocity of particle h

vh(t + 1):

Next velocity of particle h

Ph(t):

Personal best

Pg(t):

Social best

c1, 2:

Weighting factors, i.e., cognitive and social parameters, respectively

R1, 2:

Random variables uniformly distributed within [0,1]

This movement is also depicted in Fig. 17.1.

Fig. 17.1
A diagram of 2 arms labeled V subscript i, t + 1, and V subscript i, t, from the vertex labeled X subscript i, t, which has 2 other arms pointing at circles labeled P subscript g and P subscript i. Another path to the X subscript i, t + 1, aside from V subscript i, t + 1, is established via previous velocity, p best, and g best or l best arms.

PSO velocity diagram. Source: Authors’ own creation

Full size image

6 Velocity Limits

In order to address the swarm explosion issues, velocity thresholds have been imposed separately to each dimension of the particle, i.e.:

$$ {v}_{\max, l}=\frac{b_l-{a}_l}{d} $$
(17.18)

where:

vmax, l:

Maximum velocity threshold for dimension l

bl:

Upper bound of dimension l

al:

Lower bound of dimension l

d:

A denominator factor, most commonly equal to 2

7 Particle Formulation

With respect to the dimensions of each particle, i.e., the solution space as demonstrated in Fig. 17.2, these consist of the bus number where the DG unit should be installed and of the unit size, expressed via its active and reactive rated power.

Fig. 17.2
An equation for X subscript h exhibits 2 segments, namely, D G location and D G active power, under location, active, reactive power of one D G unit, and 1 other segment at the end labeled D G active power.

Solution space formulation of ODGP problem. Source: Authors’ own creation

Full size image

This particle formulation implies that the solution space is directly proportional to the number of DG units considered. The number of DG units is considered equal to the number of buses of the examined DN.

In order to ensure a more rapid convergence, the initially random values of particle dimensions at the beginning of the optimization process are considered within certain limits, such as the maximum number of buses in the examined DN and the operating technical limits of the examined DG units as described in Eqs. (17.5) and (17.6). This does not prevent the algorithm from retrieving the optimal solution. Furthermore it provides a more realistic approach, since it filters infeasible results especially at the first iteration steps.

Additionally, with respect to the algorithm’s termination, two criteria are considered: a maximum number of iteration steps and a minimum convergence deviation between current and previous solution that need both to be met in order for the algorithm to conclude. This way the algorithm is given the opportunity to explore and exploit even more the solution space, thus augmenting its performance.

8 Reducing Perturbation

The first term of the sum in the second leg of Eq. (17.14), i.e., the previous velocity term, is the component that describes the previous status of the particle. As that, it infuses a degree of inertia. However, for the same reason, this term has also been connected to a certain degree of perturbation. As a result, the local minima entrapment risk is reduced, but at the expense of having the particles oscillate on broad ranges around the best positions found (Shi & Eberhart, 1998). Two solutions have been found and applied, that is, the inertia weight and the constriction factor parameters (Eberhart & Shi, 2000), as presented in the following equations:

$$ {v}_h\left(t+1\right)={\omega v}_h(t)+{c}_1{R}_1\left({P}_h(t)-{X}_h(t)\right)+{c}_2{R}_2\left({P}_g(t)-{X}_h(t)\right) $$
(17.19)

where:

$$ \omega (t)={\omega}_{\mathrm{max}}-\left({\omega}_{\mathrm{max}}-{\omega}_{\mathrm{min}}\right)\frac{t}{T_{\mathrm{max}}} $$
(17.20)

where:

ω(t):

Current inertia weight

ωmax:

Maximum inertia weight

ωmin:

Minimum inertia weight

t:

Current iteration

Tmax:

Maximum iteration number

and:

$$ {v}_h\left(t+1\right)=\psi \left[{v}_h(t)+{c}_1{R}_1\left({P}_h(t)-{X}_h(t)\right)+{c}_2{R}_2\left({P}_g(t)-{X}_h(t)\right)\right] $$
(17.21)

where:

ψ:

Constriction factor

Applying these two solutions on a test bus system, i.e., the typical 16-bus system (Civanlar, Grainger, Yin, & Lee, 1988) presented in Fig. 17.3, bears the results depicted in Fig. 17.4. For 1000 iteration steps, it shows that the constriction factor method demonstrates better performance, both in terms of convergence speed and final solution. Therefore, this scheme proves to be more effective when contemplating the ODGP problem.

Fig. 17.3
A diagram exhibits the connections of 16 vertical lines labeled 1 to 16 with text reading, S slash S number sign 1, 1, number sign 2, 2, and number sign 3 3 on the left side. The sixteenth vertical line exhibits a dashed linkage to the seventh vertical line.

Typical 16-bus system. Source: Authors’ own creation

Full size image
Fig. 17.4
A convergence curve graph represents 0 to 0.7 y-axis values versus 1 to 901 x-axis values. The curves P S O w and P S O x decline from around (1, 0.6) to (1001, 0.03) and (1001, 0.01), respectively.

Convergence comparison of inertia weight (PSO w) and constriction factor (PSO χ). Source: Authors’ own creation

Full size image

9 Reducing Local Minima Entrapment

9.1 Local PSO

In cases of multimodal or extremely complex environments, such as the ODGP problem, it has been proven that the swarm fragments because of complete diversity loss (Kennedy, 1999). This indicates that any further exploration of the solution space is no longer possible, and thus the particles are confined to exploit what information they already have and converge there. This hindrance can be attributed to the determination of the Pg(t) term, in the third term of the sum in the second leg of Eq. (17.14). This term refers to the social knowledge gathered by each particle after communicating with other particles. If it is determined as the global best, after creating the global PSO version or GPSO, each particle communicates with all the other particles in the swarm. This provides great convergence capabilities but leads to the aforementioned problem, that is, lower exploration of the solution space and high local minima entrapment risk (Gkaidatzis, Bouhouras, Doukas, Sgouras, & Labridis, 2017).

However, if the social knowledge is diffused by using smaller overlapping groups of particles, this problem is being addressed. These smaller groups are called neighborhoods. There are various schemes under which these neighborhoods can be formed. One simple and effective schema has proven to be the ring topology (Hu & Eberhart, 2002; Mendes, Kennedy, & Neves, 2003), depicted in Fig. 17.5 and described mathematically in Eq. (17.20).

Fig. 17.5
A ring topology model exhibits a cycle of 8 nodes. The 5 nodes at the top are labeled, from left to right, X subscript i minus 2, X subscript i minus 1, X subscript i, X subscript i + 1, and X subscript i + 2, while the 3 nodes below are unlabeled.

Ring topology. Source: Authors’ own creation

Full size image
$$ {v}_h\left(t+1\right)=\psi \left[{v}_h(t)+{c}_1{R}_1\left({P}_h(t)-{X}_h(t)\right)+{c}_2{R}_2\left({P}_l(t)-{X}_h(t)\right)\right] $$
(17.22)

where:

Pl(t):

Local best term

Therefore, instead of using the global best, the local best is used, creating the local PSO version or LPSO.

9.2 uPSO

A comparison between the two, i.e., GPSO and LPSO, leads to the conclusion that the former has the advantage of fast convergence, which explains the reason of its broad use. However, it lacks in solution space exploration. Εrgo the final solution will not be that optimal. The latter, although it provides greater exploration capabilities, lacks in convergence, leading to greater computation times. Therefore, a question is raised whether a PSO version can be developed by combining these two, enhancing their merits while avoiding their drawbacks. This has led to the development of the unified version of PSO, or uPSO, by Vrahatis and Pasropoulos (Parsopoulos & Vrahatis, 2002) which is described in the following equations:

$$ {V}_h^G\left(t+1\right)=\psi \left[{v}_h(t)+{c}_1{R}_1\left({P}_h(t)-{X}_h(t)\right)+{c}_2{R}_2\left({P}_g(t)-{X}_h(t)\right)\right] $$
(17.23)
$$ {V}_h^L\left(t+1\right)=\psi \left[{v}_h(t)+{c}_1{R}_1\left({P}_h(t)-{X}_h(t)\right)+{c}_2{R}_2\left({P}_l(t)-{X}_h(t)\right)\right] $$
(17.24)

with:

$$ {v}_h\left(t+1\right)=\left\{\begin{array}{c}{u}_f{R}_3{V}_h^G\left(t+1\right)+\left(1-{u}_f\right){V}_h^L\left(t+1\right),u\le 0.5\\ {}{u}_f{V}_h^G\left(t+1\right)+\left(1-{u}_f\right){R}_3{V}_h^L\left(t+1\right),u>0.5\end{array}\right. $$
(17.25)

where uf ∈ [0, 1] is the unification factor that basically controls the combination schema of LPSO and GPSO and R3 is an extra random variable uniformly distributed within [0,1] that is applied alternatively on the GPSO and LPSO terms providing even further diversity and thus exploration to the technique. The rest of the parameters of the equation are the same as before.

9.3 Unification Factor Schemes

For the determination of the unification factor value, several processes have been proposed. They are categorized as swarm- and particle-level schemes, depending on the level in which the value assignment takes place. In the swarm level, the same value is provided for all particles. In the particle level, each particle presents its own scheme.

An approach could be an increasing unification factor, thus infusing exploration at the beginning of the process, by giving leverage to LPSO, over GPSO, and gradually shifting the balance towards exploitation, by reversing the initial leverage (Parsopoulos & Vrahatis, 2005, 2007).

A few examples are as follows:

  1. 1.

    Linear: as in the inertia weight case, the unification factor is linearly increased, as described in the following equation:

$$ {u}_f(t)=\frac{t}{T_{\mathrm{max}}} $$
(17.26)
  1. 2.

    Modular: the unification factor increases in repeated pattern, every z iterations, which is selected as a reasonable fraction of the total number of iteration steps:

$$ {u}_f(t)=\frac{t\operatorname{mod}\left(z+1\right)}{z} $$
(17.27)
  1. 3.

    Exponential: as stated, in this scheme the unification factor increases exponentially:

$$ {u}_f(t)=\exp \left(\frac{t\bullet \log (2)}{T_{\mathrm{max}}}\right)-1 $$
(17.28)
  1. 4.

    Sigmoid: the unification factor, in this scheme is increased gradually, i.e.:

    $$ {u}_f(t)=\frac{1}{1+\exp \left[-\lambda \left(t-\frac{T_{\mathrm{max}}}{20}\right)\right]} $$
    (17.29)

A few examples of particle-level schemes are the swarm partitioning (SP) and the self-adaptive (SA).

In the swarm partitioning scheme, the swarm is separated into nonoverlapping groups called partitions. In each partition a unification factor value is assigned, within the range of [0,1], and thus all particles belonging to the same partition share the same unification factor. Since the swarm is already divided into neighborhoods, due to LPSO, in order to avoid having particles with the same unification factor in the same neighborhood or, differently, increase the possibility to have particles with different unification factor values in the neighborhoods, an appropriate assignment scheme should be adopted. An approach would be to assign the first k particles to the partitions 1 to k, respectively, and then repeat the process for the next k particles and so on, thus having particle i in the (1 + (i − 1) mod (k)) partition.

In the self-adaptive scheme, the unification factor is considered as an additional dimension of the solution space and left to be determined by the optimization process itself.

An indicative comparison between the linear, SP, and SA, when applied to the typical test 33-bus system, is demonstrated in Fig. 17.6 (Gkaidatzis, Bouhouras, Doukas, Sgouras, & Labridis, 2016; Gkaidatzis, Bouhouras, Sgouras, Doukas, & Labridis, 2016).

Fig. 17.6
A convergence curve graph represents power losses in megawatts versus number of iterations. Linear, S A, and S P decline from around (1, 0.6) to (76, 0.03), (76, 0.05), and (76, 0.02), respectively.

Convergence of linear, SA, and SP uPSO version. Source: Authors’ own creation

Full size image

SP has been determined as the most promising scheme, providing both better final solutions and better convergence. This uPSO version is further compared to the two basic PSO versions, as shown in Fig. 17.7, when applied again in the typical test 33-bus system (Kashem, Ganapathy, Jasmon, & Buhari, 2000) depicted in Fig. 17.8. It becomes immediately apparent that uPSO indeed presents better performance both in terms of convergence and final solution than either GPSO or LPSO. From Fig. 17.7 additionally, the different exploration/exploitation ratios of the two basic PSO versions become also apparent, since GPSO, though converging fast enough, seems to be locked in a not optimal value, whereas LPSO, though slow at first, it reaches a far lower value which mean a far better solution.

Fig. 17.7
A convergence curve graph represents power losses in megawatts versus number of iterations. L P S O, and U P S O decline from around (1, 0.6) to (1001, 0), and (1001, 0), respectively. G P S O declines from around (1, 0.35) to (1001, 0.03),

Convergence comparison between uPSO, GPSO, and LPSO. Source: Authors’ own creation

Full size image
Fig. 17.8
A diagram exhibits the connections of 18 vertical lines with S, S above the first. Lines 19 to 22 connect to the second, 23 to 25 connect to the third, and 26 to 33 connect to the sixth.

Typical 33-bus system. Source: Authors’ own creation

Full size image

10 Comparison with Other Heuristic Methods

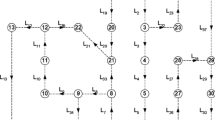
In this section the evaluation of the PSO version as presented will be examined. More specifically, a comparative analysis among the PSO versions and how well they fare against other heuristic techniques such as GA, ABC, CS, and HS is analyzed. To that end, all the techniques have been given an ample time of 1000 iteration steps, i.e., they have been applied 1000 times. The techniques have been tested upon the IEEE-30 bus system (Yokoyama, Bae, Morita, & Sasaki, 1988), presented in Fig. 17.9.

Fig. 17.9
A diagram exhibits the connections of 30 small, horizontal lines. The horizontal line labeled 1 is observed at the top tier, while horizontal lines labeled 20, 24, 25, 26, and 30 are at the bottom, the ninth tier.

IEEE-30 bus system. Source: Authors’ own creation

Full size image

In Table 17.1, results regarding the final solution reached by the various heuristic methods are shown. More specifically, the optimum loss achieved by each method and the respective percentage of loss reduction are shown. Moreover, the DG number for installation are presented and the total DG rated power in MVA, as they have been proposed by the best solution that each of the methods has reached. It is immediately evident that because of the adequate provided time, every method has reached a considerable reduction in losses and the deviations among their reached results are virtually insignificant. However, GA appears to be performing the least efficient than the rest. In Table 17.2 results related to the convergence performance of the various heuristic methods are presented. More specifically, the information provided concern the average trial execution time and the average iteration number required for each method to reach within 10%, 1%, and 0.1% tolerance of the optimal solution proposed. For example, in uPSO, since its optimal solution amounts to 742.10 kW, this means that a 10% tolerance amounts to 816.31 kW loss. Regarding average execution time, requiring an execution time, less than 4 min, HS seems to perform the fastest. Additionally, another metric is introduced, and that is an iteration number required for each method to reach a certain amount of loss reduction. This amount is determined by the average loss reduction reached by the method that performs the least. This seems to be GA, and the amount is therefore set to 35.97%. Despite all methods evidently performing efficiently, it appears that the PSO versions fare rather more efficient than the rest, especially uPSO. With respect to convergence and iteration steps, for instance, they reached their final solution in the least amount of time overall.

Table 17.1 Solution performance comparison of PSO with other heuristic techniques
Full size table
Table 17.2 Scn#1
Full size table

Given that, an argument can be made that, though HS seems more efficient than uPSO, in terms of computation time, the latter can be applied for fewer iterations and ergo overcome this issue. This is further demonstrated in Fig. 17.10, where each method’s average convergence of the 1000 trials is shown, and again in Fig. 17.11, where the same metric is presented, but zooming in particularly within the 10% iteration tolerance of the best performing technique, being uPSO.

Fig. 17.10
An equation for X subscript h exhibits 3 segments under O D G P and 2 segments under N R. The former has location of D G, active power of D G, and reactive power of D G under its umbrella, while the latter houses sectionalizers and tie switches.

Solution space formulation for combined ODGP-NR problem. Source: Authors’ own creation

Full size image
Fig. 17.11
A diagram of the connections of 28 vertical lines with S, S above the first. Dashed linkages are observed as lines 29 to 36 connect to the third, 37 to 40 connect to the fifth, 41, 42, and 62 to 70 connect to the fourth, 43 and 44 connect to the ninth, 45 to 50 and 51 to 57 connect to the tenth, 58 and 59 connect to the twelfth, and 60 and 61 connect to the thirteenth.

Typical 69-bus system with tie switches. Source: Authors’ own creation

Full size image

Furthermore, as demonstrated in Fig. 17.12, the PSO versions, and uPSO in particular, have the least standard deviation convergence along the 1000 iteration sample. This means that during the 1000 trials, they do not deviate much from each other, demonstrating their robustness. This also indicates that even less trials are possible (Gkaidatzis, Doukas, Bouhouras, Sgouras, & Labridis, 2017).

Fig. 17.12
A branching diagram exhibits node 29, nodes 34 and 35, nodes 67 and 68, and node 109 as the final offspring from the multiple branches of node 2, node 30, node 36, and node 69, respectively, under node 1.

EV examined DN. Source: Authors’ own creation

Full size image

11 PSO in Combination to ODGP with NR

In cases of fault occurrences and outages, network reconfiguration (NR) enables the distribution system operator (DSO) to rearrange the DN layout to continue to provide the same services. Over the last decades, this originally reliability-oriented mechanism has been also considered for loss reduction, since it was discovered that a DN layout modification could alter the loading of the DN lines (Bouhouras, Gkaidatzis, & Labridis, 2020).

Techniques for both the ODGP and NR problems have been regarded as efficient towards reducing power losses. The means used however in order to achieve this objective varies, since ODGP aims at the location and size of DG units to be installed, thus affecting the load composition of the DN, whereas NR aims at rearranging the DN layout, thus the topology of the DN (Bouhouras, Gkaidatzis, & Labridis, 2017).

When contemplated individually, the losses are reduced significantly. Therefore, there is high probability that a combination of them will have a considerable impact on the reached optimal solution with respect to the total amount of loss reduction. Let the highest possible loss reduction refer to the ideal 100%. Then, the order at which these problems are considered affects their contribution towards the solution of the overall problem. For example, when considering ODGP, a solution with 100% loss reduction could theoretically be yielded, in the ideal case where DG units are installed in every bus of the DN and generate the same amount of power requested by the load at each bus. In that particular case, to consider solving the NR towards loss reduction is rendered meaningless, since the objective is already achieved. However, if limited available DG units are considered during the ODGP solving process, as it is mostly the case, then further examining the NR could achieve more loss reduction and improve the solution even further.

If the reverse order is contemplated, that is, the NR is examined first and then the ODGP, then it presents great interest to examine the effect this would have on the siting and sizing of the DG, since the ODGP problem will now be solved for a modified DN, that is, with a modified layout, but with the same load composition. Additionally, it would be of great interest to investigate what the results would be, if both problems are solved simultaneously, that is, solving both ODGP and NR at the same time, therefore, formulating the solution space as it presented in Fig. 17.13.

Fig. 17.13
A line graph represents voltage per unit versus time in hours and minutes. Initial without E Vs, regular E Vs schedule, and optimal E Vs schedule exhibit varying fluctuation intensities from around 1 in 16 hours to 1 in 10 hours.

Voltage profile of residence No. 79. Source: Authors’ own creation

Full size image

The aforementioned analysis leads to three scenarios to be considered, with respect to the order of solving ODGP and NR:

  • Scn#1: First NR is solved, then ODGP.

  • Scn#2: First ODGP is solved, then NR.

  • Scn#3: ODGP and NR are solved simultaneously.

The results when using the typical test 69-bus system (Soudi, 2013) are presented in Tables 17.2, 17.3, and 17.4. Scn#1 seems to bear the more advantageous results, due to the switching operations relying on the tie switches already in use. This leads also to less DG capacity required for loss minimization. In Scn#2, as previously analyzed, it seems hardly possible to reach a NR solution, particularly if the ODGP problem is solved rather efficiently towards high loss reduction. Finally, in Scn#3, where both problems are solved simultaneously, the total problem complexity seems to increase exponentially. The main reason behind this is the fact that the particle formulation is extended in order to accommodate both the ODGP and the NR variables, as demonstrated in the following equation:

Table 17.3 Scn#2
Full size table
Table 17.4 Scn#3
Full size table

Sh, l and Th, j , in contrast with xh, l which is an integer and Ph, l and Qh, l that are real variables, are basically binary variables. PSO however has been mainly developed for continuous-valued solution spaces. In order to adjust to these new circumstances for these particular set of variables, the velocity and position equations are updated with the use of the following equations (Engelbrecht, 2007):

$$ {v}_h\left(t+1\right)=\frac{1}{1+{\mathrm{e}}^{-{\upsilon}_{h(t)}}} $$
(17.30)

where:

Sh, l:

Sectionalizer

Th, j:

To tie switch

$$ {x}_h\left(t+1\right)=\left\{\begin{array}{c}1,w<\frac{1}{1+{\mathrm{e}}^{-{v}_h\left(t+1\right)}}\\ {}0,\mathrm{otherwise}\end{array}\right. $$
(17.31)

where w is a randomly distributed variable within [0,1], adding diversity in the process.

Due to this additional complexity, the algorithm seems unable to reach an effective solution. It still requires further examination, to establish if a better solution in this case is overweighed by the increased computational burden (Bouhouras, Andreou, Labridis, & Bakirtzis, 2010; Bouhouras & Labridis, 2012).

12 PSO in Optimal Charging Schedule of EVs

12.1 EV Integration in DN

The ever-growing integration of electric vehicles (EV) in LV networks (Nour, Ramadan, Ali, & Farkas, 2018) is expected to greatly affect the conventional load patterns both of the residential and commercial sectors. Charging the EVs will bear additional burden especially during the night. The EVs’ owners are most commonly expected to connect and charge their EVs the moment they arrive at their homes, which usually occurs at the afternoon or evening. Moreover, they require to depart with the EV fully charged early in the morning of the next day (Antúnez, Franco, Rider, & Romero, 2016), especially during workdays. Thus, any random EV charging not controlled, or monitored, would cause an intense night load peak, leading this way to significant voltage drops and power quality issues. This issue can be tackled by employing optimized coordinated EV charging schedules, setting the time periods within which each individual EV will be charged with the goal to satisfy an objective function, for example, voltage profile improvement (Zheng, Song, Hill, & Meng, 2018), cost minimization (Thomas, Ioakimidis, Klonari, Vallée, & Deblecker, 2016; Wei, Li, & Cai, 2018), energy loss minimization (Zaidi, 2015), or combination of them.

12.2 Problem Formulation

In this case, as an objective function, the voltage improvement is in the epicenter, as described below (Bouhouras et al., 2018, 2019; Bouhouras, Gkaidatzis, & Labridis, 2018):

$$ {F}_{vi}=\min \sum \limits_{\varDelta t=1}^{T_{\mathrm{total}}}\sum \limits_{m=1}^{l_n}\left|1-{V}_m\right| $$
(17.32)

where:

Δt:

The time interval considered, e.g., an hour, half-hour, 15 min, etc.

Ttotal:

The total time period considered

uPSO is utilized to solve this problem and is applied to the DN, depicted in Fig. 17.12.

This DN constitutes a section of a Greek rural-residential DN. In each bus a residence is connected, and in each residence an EV is assigned in turn. For realistic purposes, variation of types of chargers, EV battery capacity, time of arrival, and state of charge at the time of arrival has been considered and is presented in Table 17.5.

Table 17.5 EV parameters
Full size table

The DN technical constraints, as they have been described in the previous sections of this chapter, are taken into account, and the DG technical constraints are replaced by the EV ones, that is, the charger upper and lower operation limits. The penalty function formulation remains also the same with that described in previous sections of this chapter.

For practical purposes though, the EVs are assumed that they arrive no earlier than 20:00 and require to depart with a full battery until 06:00.

In that particular case, the solution space is a combination of binary and real variables, as presented in Eq. (17.31), where for each time step considered, e.g., 1 h, of the total amount of time examined, that is 20:00–06:00, it is to be determined if m EV will charge or not (bi, Δt = k) and with how much power (Pi, Δt = k).

$$ {X}_i=\left[{b}_{i,m,\varDelta t=1}\bullet {P}_{i,m,\varDelta t=1},\dots, {b}_{i,m,\varDelta t=k}\bullet {P}_{i,m,\varDelta t=k},\dots, {b}_{i,m,\varDelta t={T}_{\mathrm{total}}}\bullet {P}_{i,m,\varDelta t={T}_{\mathrm{total}}}\right] $$
(17.33)

This formulation provides the flexibility to examine both continuous and intermittent charging of the EVs, thus offering better EV portfolio management to either the DSO or the EV aggregator, in terms of day-ahead planning. The optimal schedule for the EVs of various residences is presented in Tables 17.6 and 17.7.

Table 17.6 EV charging schedules for residence No. 79
Full size table
Table 17.7 EV charging schedules for residence No. 109
Full size table

In Fig. 17.13 the results of the optimal schedule for residence No. 79 are presented, where the initial voltage profile without any EVs considered (green), a regular EV charging schedule without optimization considered (red), and an optimal EV schedule (blue) are compared. A significant improvement is shown since voltage drop is decreased and formed in a smoother manner, i.e., not so abruptly. The same is evident for residence No. 109, i.e., the furthest residence from the substation, ergo the one with the most voltage drop, as shown in Fig. 17.14.

Fig. 17.14
A line graph represents voltage per unit versus time in hours and minutes. Initial without E Vs, regular E Vs schedule, and optimal E Vs schedule rise respectively from around 0.82, 0.49, and 0.88 in 17 00 to 0.96 in 5 hours.

Voltage profile of residence No. 109. Source: Authors’ Own Creation

Full size image

13 Conclusion and Discussion

In this chapter the applications of PSO in various modern power system problems have been presented, mainly in the solution of ODGP, either alone or in conjunction with NR and optimal EV charging schedules. PSO has been concluded as quite effective to all problems addressed. Moreover, since all of the problems have their own particular requirements, PSO has shown a considerable range and variety of applications, adding to its broad utilization and wide adoption by many different topics, fields, and principles. Provided the dynamic and wide nature of the power system research sector, there is virtually no limitation as to where else PSO can be applied. A few examples might be in the ever-growing microgrid sector (Hossain, Pota, Squartini, & Abdou, 2019), reliability (Yang, Zhang, Ma, Zhou, & Yang, 2019), battery energy storage systems implementation (Yang, Gong, Ma, Wang, & Dong, 2020), and demand-side management and in particular demand response portfolio management (Sood, Ali, & Khan, 2020).