(Quantum) Cryptanalysis of Misty Schemes

Abstract

In this paper, we review the best known cryptanalysis results on the variants of Misty schemes and we provide new (quantum) cryptanalysis results. First, we describe a non-adaptive quantum chosen plaintext attack (QCPA) against 4-round Misty L and Misty LKF schemes, and a QCPA against 3-round Misty R and Misty RKF schemes. We extend the QCPA attack against 3-round Misty RKF schemes to recover the keys of d-round Misty RKF schemes with complexity $\tilde{\mathcal {O}}(2^{(d-3)n/2})$. We then provide a security proof for Misty R schemes with 3 rounds against chosen plaintext attacks using the H coefficients technique. This shows that the best known non-quantum attack against Misty R schemes with 3 rounds is optimal.

1 Introduction

The most studied way to build pseudo-random permutations from random function or random permutation is the d-round Feistel construction. However, there exist other well-known constructions such as the Misty constructions that we analyze in this paper. We study generic attacks on Misty schemes where we assume that the internal permutations $f_1,\dots , f_d$ are randomly chosen. The Misty construction is important from a practical point of view since it has been used as a generic construction to design Kasumi [2] algorithm that has been adopted as the standard blockcipher in the third generation mobile systems.

The plaintext message of a Misty scheme is denoted by [L, R] that stands for Left and Right and the ciphertext message, after applying d rounds, is denoted by [S, T]. Misty L and Misty R schemes are two different variants of Misty schemes. Indeed, the first round of a Misty L scheme takes as input [L, R] and it outputs $[R, R\oplus f_1(L)]$ with $f_1$ a secret permutation from n bits to n bits whereas the first round of a Misty R scheme takes as input [L, R] and it outputs $[R\oplus f_1(L), f_1(L)]$ with $f_1$ a secret permutation from n bits to n bits. We also consider in this paper a particular case of Misty L and Misty R constructions such that each round function $f_i$ is defined by $f_i(x)=F_i(K_i \oplus x)$ with a public function $F_i$ and a round secret key $K_i$. These constructions are named, respectively, d-round Misty LKF scheme and d-round Misty RKF scheme. To simplify the notation, the public functions $F_i$ in each round are all denoted by F. These four variants of Misty schemes are studied in this paper.

Related Work. Cryptanalysis of Misty schemes have been studied by Nachef, Patarin and Treger in [9, 10]. They described Known Plaintext Attack (KPA), Chosen Plaintext Attack (CPA) and Chosen Ciphertext Attack (CCA) against Misty L and Misty R schemes. In particular, they showed that there exists CPA and KPA attacks for $d=5$ with complexity strictly less than $2^{2n}$. They also studied some generic properties of Misty L and Misty R schemes such as the inversion property. They showed that the inverse of a Misty L function is a Misty R function, after composition by a permutation $\mu$ and $\mu ^{-1}$ on the inputs and outputs, where $\mu$ is a permutation on 2n bits such that $\mu ([L,R]) = [R, L\oplus R]$. They then showed that the security of Misty L and Misty R schemes are the same for all attacks where the inputs and outputs have the same possibilities which is the case for example in KPA attack and CCA attack. However, the security of Misty L and Misty R schemes may differ regarding CPA attacks as we will see in this paper for 3 rounds.

Quantum cryptanalysis has received much more attention in the last past years. It is known that Grover’s algorithm [3] could speed up brute force search. Given a n-bit key, Grover’s algorithm allows to recover the key using $\mathcal {O}(2^{n/2})$ quantum steps. It seems that doubling the key-length of one block cipher could achieve the same security against quantum attackers. However, Kuwakado and Morii [6] introduced a new family of quantum attacks using Simon’s algorithm [12] which could find the period of a periodic function in polynomial time in a quantum computer. Indeed, they describe a quantum distinguishing CPA attack on the 3-round Feistel scheme. This work has been then extended by Ito et al. [5] to a quantum CCA distinguisher against the 4-round Feistel cipher.

Luo et al. [8] present quantum attacks on 3-round Misty L and Misty R schemes using Simon’s algorithm. We describe a similar quantum attack on the 3-round Misty R structure. In this paper, we provide additional (quantum) cryptanalysis on variants of Misty L and Misty R schemes as explained in the “Our Contribution” paragraph.

Our Contribution. In this paper, we describe a non-adaptive quantum chosen plaintext attack (QCPA) against 4-round Misty L and Misty LKF schemes, and a non-adaptive quantum chosen plaintext attack (QCPA) against 3-round Misty R and Misty RKF schemes. These attacks enable to distinguish these Misty schemes from random permutations in polynomial time. We extend the quantum distinguishing attack against 3-round Misty RKF schemes to obtain a quantum key recovery attack against d-round Misty RKF schemes with complexity $\tilde{\mathcal {O}}(2^{(d-3)n/2})$. Then, we show that security of Misty L and Misty R schemes with 3 rounds differs regarding CPA attacks. The best known attack against Misty L schemes with 3 rounds has complexity 4 operations with 4 distinct messages. The best known attack against Misty R schemes has complexity $2^{n/2}$ operations with $2^{n/2}$ messages. In this paper, we provide a security proof with the same bound $2^{n/2}$ which shows that the best known cryptanalysis against Misty R schemes is optimal.

Organization. Section 2 describes the four variants of Misty schemes. Section 3 gives an overview of previous works and the new results provided in this paper. In Sect. 4, we present our QCPA against the four variants of Misty schemes and the quantum key recovery attack on Misty RKF schemes. Section 5 provides the security proof of Misty R schemes with 3 rounds against adaptive Chosen Plaintext attack (CPA-2). Finally, we conclude in Sect. 6.

2 Misty Constructions

In this section, we describe the four variants of Misty schemes. The set of all functions from $\{0,1\}^n$ to $\{0,1\}^n$ is denoted by $F_n$ and the set of all permutations from $\{0,1\}^n$ to $\{0,1\}^n$ is denoted by $B_n$. We have $B_n\subset F_n$. We denote by $M^d$ a Misty scheme of d rounds: $f = M^d(f_1,\dots , f_d)$, where $f_1,\dots , f_d$ are permutations from n bits to n bits, and f is a permutation from 2n bits to 2n bits.

2.1 Misty L Scheme

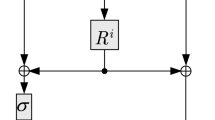
Let $f_1$ be a permutation of $B_n$. Let L, R, S and T be elements in $\{0,1\}^n$. Then by definition we have:

$$ M_L(f_1)([L,R]) = [S, T] \Leftrightarrow S = R \text{ and } T = R \oplus f_1(L) $$

Let $f_1,\dots , f_d$ be d bijections of $B_n$. Then by definition we have:

$$ M^d_L (f_1,\dots , f_d) = M_L(f_d)\circ \dots M_L(f_2) \circ M_L(f_1) $$

The permutation $M^d_L(f_1,\dots , f_d)$ is called a Misty L scheme with d rounds. We describe in detail the equations of Misty L for the first four rounds.

$$ \begin{array}{llll} 1 \text{ round: } &{}{\left\{ \begin{array}{ll} S = R\\ T = R \oplus f_1(L) = X^1\\ \end{array}\right. } &{} 2 \text{ rounds: } &{}{\left\{ \begin{array}{ll} S = X^1\\ T = X^1 \oplus f_2(R) = X^2\\ \end{array}\right. } \\ \\ 3 \text{ rounds: } &{}{\left\{ \begin{array}{ll} S = X^2\\ T = X^2 \oplus f_3(X^1) = X^3\\ \end{array}\right. } &{} 4 \text{ rounds: } &{}{\left\{ \begin{array}{ll} S = X^3\\ T = X^3 \oplus f_4(X^2) = X^4\\ \end{array}\right. } \end{array} $$

The figure of Misty L schemes for the first round is given in Fig. 1.

Fig. 1.

First round of Misty L

Fig. 2.

First round of Misty LKF

Misty LKF Scheme. Let F be a public function of $F_n$ and $K_1$ be a key chosen in $\{0,1\}^n$. Let L, R, S and T be elements in $\{0,1\}^n$. Then, we define:

$$ M_{LKF}(F,K_1)([L,R]) = [S, T] \Leftrightarrow S = R \text{ and } T = R \oplus F(K_1 \oplus L) $$

Let $K_1, \dots , K_d$ be d keys chosen in $\{0,1\}^n$. Then we have:

$$ M^d_{LKF} (F,K_1,\dots , K_d) = M_{LKF}(F,K_d)\circ \dots M_{LKF}(F,K_2) \circ M_{LKF}(F,K_1) $$

In this paper, we call $M^d_{LKF} (F,K_1,\dots , K_d)$ a Misty LKF scheme with d rounds. The equations of the first four rounds of Misty LKF are as follows.

$$ \begin{array}{llll} 1 \text{ round: } &{}{\left\{ \begin{array}{ll} S = R\\ T = R \oplus F(K_1 \oplus L) = A^1\\ \end{array}\right. } &{} 2 \text{ rounds: } &{}{\left\{ \begin{array}{ll} S = A^1\\ T = A^1 \oplus F(K_2 \oplus R) = A^2\\ \end{array}\right. } \\ \\ 3 \text{ rounds: } &{}{\left\{ \begin{array}{ll} S = A^2\\ T = A^2 \oplus F(K_3 \oplus A^1) = A^3\\ \end{array}\right. } &{} 4 \text{ rounds: } &{}{\left\{ \begin{array}{ll} S = A^3\\ T = A^3 \oplus F(K_4 \oplus A^2) = A^4\\ \end{array}\right. } \end{array} $$

The figure of Misty LKF schemes for the first round is given in Fig. 2.

2.2 Misty R Scheme

Let $f_1$ be a permutation of $B_n$. Let L, R, S and T be elements in $\{0,1\}^n$. Then by definition we have:

$$ M_R(f_1)([L,R]) = [S, T] \Leftrightarrow S = R \oplus f_1(L) \text{ and } T = f_1(L) $$

Let $f_1,\dots , f_d$ be d bijections of $B_n$. Then by definition we have:

$$ M^d_R (f_1,\dots , f_d) = M_R(f_d)\circ \dots M_R(f_2) \circ M_R(f_1) $$

The permutation $M^d_R(f_1,\dots , f_d)$ is called a Misty R scheme with d rounds. We describe in detail the equations of Misty R for the first four rounds.

$$ \begin{array}{llll} 1 \text{ round: } &{}{\left\{ \begin{array}{ll} S = R \oplus f_1(L) = Y^1\\ T = f_1(L) \\ \end{array}\right. } &{} 2 \text{ rounds: } &{}{\left\{ \begin{array}{ll} S = f_1(L) \oplus f_2(Y^1) = Y^2\\ T = f_2(Y^1)\\ \end{array}\right. } \\ \\ 3 \text{ rounds: } &{}{\left\{ \begin{array}{ll} S = f_2(Y^1) \oplus f_3(Y^2) = Y^3\\ T = f_3(Y^2)\\ \end{array}\right. } &{} 4 \text{ rounds: } &{}{\left\{ \begin{array}{ll} S = f_3(Y^2) \oplus f_4(Y^3) = Y^4\\ T = f_4(Y^3) \\ \end{array}\right. } \end{array} $$

The figure of Misty R schemes for the first round is given in Fig. 3.

Fig. 3.

First round of Misty R

Misty RKF Scheme. Let F be a public function of $F_n$ and $K_1$ be a key chosen in $\{0,1\}^n$. Let L, R, S and T be elements in $\{0,1\}^n$. Then, we define:

$$ M_{RKF}(F,K_1)([L,R]) = [S, T] \Leftrightarrow S = R \oplus F(K_1 \oplus L) \text{ and } T = F(K_1 \oplus L) $$

Let $K_1, \dots , K_d$ be d keys chosen in $\{0,1\}^n$. Then we have:

$$ M^d_{RKF} (F,K_1,\dots , K_d) = M_{RKF}(F,K_d)\circ \dots M_{RKF}(F,K_2) \circ M_{RKF}(F,K_1) $$

In this paper, we call $M^d_{RKF} (F,K_1,\dots , K_d)$ a Misty RKF scheme with d rounds. The equations of Misty RKF for the first four rounds are as follows:

$$ \begin{array}{ll} 1 \text{ round: } &{} 2 \text{ rounds: }\\ {\left\{ \begin{array}{ll} S = R \oplus F(K_1 \oplus L) = B^1\\ T = F(K_1 \oplus L) \\ \end{array}\right. } &{} {\left\{ \begin{array}{ll} S = F(K_1 \oplus L) \oplus F(K_2 \oplus B^1) = B^2\\ T = F(K_2 \oplus B^1)\\ \end{array}\right. } \\ \\ 3 \text{ rounds: } &{} 4 \text{ rounds: } \\ {\left\{ \begin{array}{ll} S = F(K_2 \oplus B^1) \oplus F(K_3 \oplus B^2) = B^3\\ T = F(K_3 \oplus B^2)\\ \end{array}\right. } &{}{\left\{ \begin{array}{ll} S = F(K_3 \oplus B^2) \oplus F(K_4 \oplus B^3) = B^4\\ T = F(K_4 \oplus B^3) \\ \end{array}\right. } \end{array} $$

The figure of Misty RKF schemes for the first round is given in Fig. 4.

Fig. 4.

First round of Misty RKF

3 Overview of (Quantum) Cryptanalysis on Misty Schemes

In this section, we review the cryptanalysis results of the state of the art on the Misty L and Misty R schemes and we point out the new results provided in this paper.

3.1 Misty L Schemes with Few Rounds

In Fig. 5, we summarize the cryptanalysis results on few rounds of Misty L schemes based on the state of the art distinguishing attacks presented in [9, 10] together with our new contributions.

Fig. 5.

Number of computations to distinguish Misty L schemes (with 1, 2, 3 and 4 rounds) from random permutations

On Misty L schemes with 1 round, we have $S=R$ which gives an attack with one message in all security models. We only have to check whether S is equal to R. For a Misty L scheme, this happens with probability 1 whereas for a random permutation it happens with probability $\frac{1}{2^n}$.

On Misty L schemes with 2 rounds, we have 2 cases depending on the security model. For CPA attack, we can choose 2 messages $[L_1,R_1]$ and $[L_2,R_2]$ such that $L_1 = L_2$. Then, we can check whether $S_1\oplus S_2$ is equal to $R_1\oplus R_2$. For a Misty L scheme, this happens with probability 1 whereas for a random permutation it happens with probability $\frac{1}{2^n}$. This cryptanalysis result is valid for other security models CCA, QCPA and QCCA. For KPA model, the CPA attack can be transformed into a KPA attack using $2^{n/2}$ messages and the birthday paradox bound to find a collision such that $L_i = L_j$.

On Misty L schemes with 3 rounds, there is a CPA attack with 4 messages [9] that can be transformed into a KPA attack with approximately $2^n$ messages and a CCA attack with 3 messages [10]. These two attacks also apply in the quantum model.

On Misty L schemes with 4 rounds, there is a CCA attack with 4 messages [10] that can be transformed into KPA attack or CPA attack. The same attacks in the quantum models hold. However, in this paper we describe a QCPA attack that enables to distinguish a Misty L permutation from a random permutation using only n computations instead of $2^{n/2}$ computations.

Misty LKF with Few Rounds. The KPA, CPA and CCA attacks against Misty L schemes of [9, 10] can be applied on Misty LKF schemes. Therefore, we describe in Sect. 4 the QCPA attack that distinguishes a 4-round Misty LKF scheme from a random permutation using n computations.

3.2 Misty R Schemes with Few Rounds

On Misty R schemes, the results on 1 and 2 rounds are similar to the case of Misty L schemes. On Misty R schemes with 3 rounds and with 4 rounds, the results of the KPA, CCA and QCCA attacks are similar to those of Misty L schemes since a Misty R scheme is the inverse of a Misty L scheme [10].

On Misty R schemes with 3 rounds, the best known attack has a complexity in $2^{n/2}$ computations with $2^{n/2}$ messages [10]. In this paper, we provide the security proof of Misty R schemes with 3 rounds against CPA-2 with the same bound $2^{n/2}$. We describe also a QCPA attack that distinguishes a Misty R scheme from a random permutation by using n computations.

Figure 6 summarizes the cryptanalysis results that are distinguishing attacks on Misty R schemes based on [10] and our new contributions.

Fig. 6.

Number of computations to distinguish Misty R schemes (with 1, 2, 3 and 4 rounds) from random permutations

Misty RKF Schemes. The state of the art distinguishing attacks on Misty R schemes are similar for Misty RKF schemes and are summarized in Fig. 7 together with our new contribution. In this paper, we provide first a QCPA attack that distinguishes a 3-round Misty RKF scheme from a random permutation by using n computations. Then, we describe a QCPA attack that uses this quantum distinguishing attack on 3-round Misty RKF schemes to recover the keys of d-round Misty RKF schemes, for $d>3$, in time $2^{(d-3)n/2}$.

Fig. 7.

Number of computations to distinguish Misty RKF schemes from random permutations and number of computations to recover the keys when explicitly specified

4 Quantum Cryptanalysis on Misty

In this section, we recall the results of the two quantum algorithms that we use in our quantum cryptanalysis. The full details on how the algorithms work can be found in [3, 12]. Then, we describe our QCPA attacks against the four variants of Misty schemes and the key recovery attack against Misty RKF schemes.

4.1 Simon’s and Grover’s Algorithms

Simon’s Problem. Given a Boolean function, $f : \{0,1\}^n \mapsto \{0,1\}^n$, that is observed to be invariant under some n-bit XOR period a, find a.

Simon presents a quantum algorithm [12] that provides exponential speedup and requires only $\mathcal {O}(n)$ quantum queries to find a.

Grover’s Problem. Given a Boolean function $f:\{0,1\}^n \rightarrow \{0,1\}$ and suppose that there exists a unique $x_0 \in \{0,1\}^n$ such that $f(x_0) = 1$. Given an oracle access to f, find $x_0$.

Grover presents a quantum algorithm [3] that requires $\mathcal {O}(2^{n/2})$ quantum queries to find $x_0$.

4.2 Quantum Distinguishing Attack on 4-Round Misty L Schemes

In this section, we describe a quantum chosen plaintext attack that distinguishes a 4-round Misty L scheme from a 2n-bit random permutation in polynomial time. We also apply this attack on Misty LKF schemes to obtain a quantum distinguishing attack on 4-round Misty LKF schemes.

Let $[L_1,R_1], [L_2,R_2], [L_3,R_3], [L_4,R_4]$ be four messages such that $L_1 \ne L_2$, $R_1 \ne R_2$, $L_3 = L_1$, $R_3 = R_2$, $L_4 = L_2$ and $R_1 = R_4$. As it has been shown in [9], for such four messages, we have:

$$ \begin{array}{ccl} X^3_1 \oplus X^3_2 \oplus X^3_3 \oplus X^3_4 &{} = &{} f_3(X^1_1)\oplus f_3(X^1_2)\oplus f_3(X^1_3)\oplus f_3(X^1_4)\\ \end{array} $$

where $X^{3}_i$ is the left half of $M^{4}_L([L_i,R_i])$ as denoted in Sect. 2. Then, we have:

$$ \begin{array}{ccl} X^3_1 \oplus X^3_2 \oplus X^3_3 \oplus X^3_4 &{} = &{} f_3(X^1_1)\oplus f_3(X^1_2)\oplus f_3(X^1_3)\oplus f_3(X^1_4)\\ &{} = &{} f_3(R_1 \oplus f_1(L_1))\oplus f_3(R_2\oplus f_1(L_2))\oplus f_3(R_2\oplus f_1(L_1))\\ &{} &{} \oplus f_3(R_1\oplus f_1(L_2))\\ \end{array} $$

We set $R_1 = x$ and we define the function

$$ g(x)= f_3(x \oplus f_1(L_1)) \oplus f_3(R_2\oplus f_1(L_2))\oplus f_3(R_2\oplus f_1(L_1))\oplus f_3(x\oplus f_1(L_2)) $$

We observe that we have $g(x) = g\left( x\oplus f_1(L_1) \oplus f_1 (L_2)\right)$. Thus, the function g is periodic and the period is $f_1(L_1) \oplus f_1 (L_2)$. Note that, this period works even if $x=R_2$. We can use the Simon’s algorithm on g to get the period $s= f_1(L_1) \oplus f_1 (L_2)$ in polynomial time.

In the case where g is constructed with a 2n-bit random permutation instead of a 4-round Misty L scheme, g is not periodic with overwhelming probability. If we apply Simon’s algorithm on g, the algorithm fails to find a period. Therefore, we can distinguish a 4-round Misty L scheme from a random permutation in polynomial time by using Simon’s algorithm to check if g has a period.

Quantum Distinguishing Attack on 4-Round Misty LKF Schemes. In the same way as for 4-round Misty L schemes, we have a quantum distinguishing attack on 4-round Misty LKF schemes.

Let $[L_1,R_1], [L_2,R_2], [L_3,R_3], [L_4,R_4]$ four messages such that $L_1 \ne L_2$, $R_1 \ne R_2$, $L_3 = L_1$, $R_3 = R_2$, $L_4 = L_2$ and $R_1 = R_4$. We have also for Misty LKF:

$$ \begin{array}{ccl} A^3_1 \oplus A^3_2 \oplus A^3_3 \oplus A^3_4 &{} = &{} F(K_3 \oplus A^1_1) \oplus F(K_3 \oplus A^1_2) \oplus F(K_3 \oplus A^1_3) \oplus F(K_3 \oplus A^1_4) \\ &{} = &{} F(K_3 \oplus R_1 \oplus F(K_1 \oplus L_1)) \oplus F(K_3 \oplus R_2 \oplus F(K_1 \oplus L_2)) \\ &{} &{} \oplus \, F(K_3 \oplus R_2 \oplus F(K_1 \oplus L_1)) \oplus F(K_3 \oplus R_1 \oplus F(K_1 \oplus L_2)) \end{array} $$

where $A^{3}_i$ is the left half of $M^{4}_{LKF}([L_i,R_i])$ as denoted in Sect. 2. We set $R_1 = x$ and we define the function g by

$$ \begin{array}{ccl} g(x) &{} = &{} F(K_3 \oplus x \oplus F(K_1 \oplus L_1)) \oplus F(K_3 \oplus R_2 \oplus F(K_1 \oplus L_2)) \\ &{} &{} \oplus \, F(K_3 \oplus R_2 \oplus F(K_1 \oplus L_1)) \oplus F(K_3 \oplus x \oplus F(K_1 \oplus L_2)) \end{array} $$

We observe that $g(x) = g(x \oplus F(K_1 \oplus L_1) \oplus F(K_1 \oplus L_2))$. Thus, the function g is periodic and the period is $F(K_1 \oplus L_1) \oplus F(K_1 \oplus L_2)$. We can use the Simon’s algorithm on g to get the period $s= F(K_1 \oplus L_1) \oplus F(K_1 \oplus L_2)$ in polynomial time. Thus, we obtain a quantum distinguishing attack on a 4-round Misty LKF scheme by checking with the Simon’s algorithm if g has a period.

4.3 Quantum Distinguishing Attack on 3-Round Misty R Schemes

In this section, we describe a quantum chosen plaintext attack that distinguishes a 3-round Misty R scheme from a 2n-bit random permutation in polynomial time that is already known [8]. We also apply this attack on Misty RKF schemes to obtain a quantum distinguishing attack on 3-round Misty RKF schemes.

We consider the value $S\oplus T = f_2(Y^1) = f_2(R\oplus f_1(L))$ where $[S,T] = M^3_{R}([L,R])$ as described in Sect. 2. Let $[L_1,R], [L_2,R]$ two messages such that $L_1 \ne L_2$. We set $R = x$ and we define the function

$$ \begin{array}{ccl} g(x) &{} = &{} S_1 \oplus T_1 \oplus S_2 \oplus T_2 \\ &{} = &{} f_2(x \oplus f_1(L_1))\oplus f_2(x\oplus f_1(L_2)) \end{array} $$

where $[S_i,T_i] = M^3_{R}([L_i,R])$. We observe that $g(x) = g\left( x\oplus f_1(L_1) \oplus f_1 (L_2)\right)$. Thus, g is a periodic function and the period is $f_1(L_1) \oplus f_1 (L_2)$. We can use the Simon’s algorithm on g to get the period $s= f_1(L_1) \oplus f_1 (L_2)$ in polynomial time.

In the case where we apply Simon’s algorithm on g that is constructed with a 2n-bit random permutation, the algorithm fails to find a period with overwhelming probability. Thus, we can distinguish a 3-round Misty R scheme from a random permutation by checking with the Simon’s algorithm if g has a period.

Quantum Distinguishing Attack on 3-Round Misty RKF Schemes. In the same way as for 3-round Misty R scheme, we have a quantum distinguishing attack on 3-round Misty RKF scheme. We can also consider the value $S \oplus T = F(K_2 \oplus B^1) = F(K_2 \oplus R \oplus F(K_1 \oplus L))$ where $[S,T] = M^3_{RKF}([L,R])$ as described in Sect. 2. Let $[L_1,R], [L_2,R]$ two messages such that $L_1 \ne L_2$. Thus, we set $R = x$ and we define the function g by

$$ \begin{array}{ccl} g(x) &{} = &{} S_1 \oplus T_1 \oplus S_2 \oplus T_2 \\ &{} = &{} F(K_2 \oplus x \oplus F(K_1 \oplus L_1)) \oplus F(K_2 \oplus x \oplus F(K_1 \oplus L_2)) \end{array} $$

where $[S_i,T_i] = M^3_{RKF}([L_i,R])$. We observe that $g(x) = g(x \oplus F(K_1 \oplus L_1) \oplus F(K_1 \oplus L_2))$. The function g is periodic and the period of the function is $F(K_1 \oplus L_1) \oplus F(K_1 \oplus L_2)$. We can use the Simon’s algorithm on g to get the period $s= F(K_1 \oplus L_1) \oplus F(K_1 \oplus L_2)$ in polynomial time.

Thus, we obtain a quantum distinguishing attack on 3-round Misty RKF scheme by using Simon’s algorithm on g to check if g has a period.

4.4 Key Recovery Attack Against Misty RKF Schemes

Based on [1, 4, 7], we combine the quantum distinguishing attack on the 3-round Misty RKF scheme (Sect. 4.3) with the Grover search to obtain a key recovery attack against a d-round Misty RKF scheme. The attack recovers the keys of the d-round Misty RKF scheme $(K_1, \dots , K_d)$. We apply the technique of [4] recalled in Proposition 1.

Proposition 1

(Proposition 3 in [4]). Let $\varPsi : F_m \times F_n \rightarrow F_n$ be a function such that $\varPsi (k,\cdot ): F_n \rightarrow F_n$ is a random function for any fixed $k \in F_m$. Let $\varPhi : F_m \times F_n \rightarrow F_n$ be a function such that $\varPhi (k,\cdot ): F_n \rightarrow F_n$ is a random function for any fixed $k \in F_m \setminus \{k_0\}$ and $\varPhi (k_0,x) = \varPsi (k_0, x \oplus k_1)$. Then, given a quantum oracle access to $\varPhi (\cdot ,\cdot )$ and $\varPsi (\cdot ,\cdot )$, we can recover $(k_0,k_1)$ with a constant probability and $\mathcal {O}((m+n^2)2^{m/2})$ queries, using $\mathcal {O}(m+n^2)$ qubits.

For our attack, the key $k_0$ in Proposition 1 corresponds to the keys of the last $(d-3)$-round of a d-round Misty RKF scheme $K_4,...,K_d$ and $k_1$ corresponds to the period s recovered in the quantum distinguishing attack on the 3-round Misty RKF scheme described in Sect. 4.3. The idea is to search for the correct key $k_0 = (K_4,...,K_d)$ with the Grover search and check if $\varPhi (\cdot ,\cdot ) \oplus \varPsi (\cdot ,\cdot )$ is periodic or not for the candidate key $k = (K'_4,...,K'_d)$ by running the Simon’s algorithm in parallel.

The attack is the following. Assume that we have a quantum encryption oracle of a d-round Misty RKF scheme $\mathcal {O}: \{0,1\}^{2n} \rightarrow \{0,1\}^{2n}$. For $k = (K'_4,...,K'_d) \in \{0,1\}^{(d-3)n}$, let $D_k : \{0,1\}^{2n} \rightarrow \{0,1\}^{2n}$ denotes the partial decryption of the last $(d-3)$-round of Misty RKF with the key candidate k. Let $W:\{0,1\}^{(d-3)n} \times \{0,1\}^{n} \times \{0,1\}^{n} \rightarrow \{0,1\}^{n}$ be the function that is the sum of the right part and the left part obtained after the 3-round of the Misty RKF scheme. W is defined by

$$ W(k,L,R):= \text {the sum of the left and right halves of } D_k \circ \mathcal {O}(L,R) $$

We implement a quantum circuit of W using the quantum encryption oracle $\mathcal {O}$. In the case where $k = k_0$, then $W(k_0,L,R) = F(K_2 \oplus R \oplus F(K_1 \oplus L))$.

Then, we choose two different n-bits string $\alpha ,\beta$ and define $\varPsi :\{0,1\}^{(d-3)n} \times \{0,1\}^{n} \rightarrow \{0,1\}^{n}$ and $\varPhi : \{0,1\}^{(d-3)n} \times \{0,1\}^{n} \rightarrow \{0,1\}^{n}$ by $\varPsi (k,x) := W(k,\alpha ,x) \text { and } \varPhi (k,x):= W(k,\beta ,x).$ The function $\varPsi (k,\cdot )$ is an almost random function for each k and $\varPhi (k,\cdot )$ is also an almost random function for each $k \ne k_0$. In the case where $k = k_0$, we have $\varPhi (k_0,x) = \varPsi (k_0,x \oplus k_1)$ where $k_1 = F(K_1 \oplus \alpha ) \oplus F(K_1 \oplus \beta )$. Indeed, we have:

$$\begin{aligned} \begin{aligned} \varPsi (k_0,x \oplus k_1)&= W(k,\alpha ,x \oplus k_1) \\&= F(K_2 \oplus x \oplus F(K_1 \oplus \alpha ) \oplus F(K_1 \oplus \beta ) \oplus F(K_1 \oplus \alpha ))\\&= F(K_2 \oplus x \oplus F(K_1 \oplus \beta )) = W(k,\beta ,x) = \varPhi (k_0,x) \end{aligned} \end{aligned}$$

Thus, we can apply Proposition 1 and recover the keys $K_4,\dots ,K_{d}$. Then, we can recover $K_1$. To this end, we construct a quantum circuit that calculates the first 3 rounds of the Misty RKF scheme. Then, we compute the period $s = F(K_1 \oplus \alpha ) \oplus F(K_1 \oplus \beta )$ with the quantum distinguishing attack on the 3-round Misty RKF scheme with two arbitrary messages $[\alpha ,x],[\beta ,x]$ such that $x, \alpha , \beta \in \{0,1\}^{n}$ and $\alpha \ne \beta$. Thus, we can recover $K_1$ by using the Grover search. Finally, we can easily recover $K_2$ and $K_3$ using the Grover search and the recovered key $K_1$.

Attack Complexity. By Proposition 1, we can recover $(K_4, \dots , K_{d})$ in time $\mathcal {O}(2^{(d-3)n/2})$¹. Since the last keys $K_1, K_2$ and $K_3$ are recovered by using the Grover search in time $\mathcal {O}(2^{n/2})$, the complexity of the key recovery attack against a Misty RKF scheme is $\tilde{\mathcal {O}}(2^{(d-3)n/2})$.

5 Security Proof on Misty R Scheme with 3 Rounds

The best known CPA-1 attack against a Misty R scheme with 3 rounds is in $\mathcal {O}(2^{n/2})$ messages and computations [10]. In this section, we prove the security of the 3-round Misty R scheme against adaptive Chosen Plaintext CPA-2 attacks when the number of queries q is significantly smaller than $2^{n/2}$. Since this proof and the best known attack have the same bound $2^{n/2}$, the cryptanalysis of the 3-round Misty R scheme is optimal. For this proof, we use the result on H coefficients technique provided in [11].

5.1 H Coefficient Technique

Let N be a positive integer. Let $I_N$ be the set $\{0,1\}^N$ and $F_N$ be the set of all applications from $I_N$ to $I_N$. Let $B_N$ be the set of permutations from $I_N$ to $I_N$. Let K denotes a set of k-uples of functions $(f_1,\dots , f_k)$ of $F_N$. We define G as an application of $K\rightarrow F_N$.

Definition 1

(H coefficient). Let q be a positive integer. Let $(a_1,\dots ,a_q)$ with $a_i\in I_N$ for $i=1,\dots ,q$ be a sequence of pairwise distinct elements of $I_N$ . Let $(b_1,\dots ,b_q)$ with $b_i\in I_N$ for $i=1,\dots ,q$. The H coefficient denoted by H(a, b) or simply by H is the number of $(f_1,\dots , f_k)\in K$ such that:

$$ \forall i, 1\le i\le q, G(f_1,\dots , f_k)(a_i) = b_i $$

5.2 Application to Misty R Scheme with 3 Rounds

Theorem 1

(Adaptive Chosen Plaintext attack with q queries) [11]. Let $\varepsilon$ and $\beta$ be positive real numbers. Let E be a subset of $I_N^q$ such that $|E|\ge (1-\beta )2^{Nq}$. If for all $(a_1,\dots ,a_q)$ with $a_i\in I_N$ for $i=1,\dots ,q$ such that $a_i\ne a_j$ when $i\ne j$ and for all $\beta \in E$ we have:

$$ H \ge \frac{|k|}{2^{Nq}}(1-\varepsilon ) $$

Then, the advantage $Adv^\mathtt{CPA-2}$ to distinguish $G(f_1,\dots ,f_k)$ with $(f_1,\dots ,f_k)\in _R K$ from a random function $f\in _R F_N$ fulfills:

$$ Adv^\mathtt{CPA-2}\le \beta + \varepsilon . $$

Theorem 2

(CPA-2 security on 3 rounds Misty R). The advantage of an attacker in an adaptive chosen plaintext attack against the construction Misty R with 3 rounds is upper bounded by:

$$ Adv^\mathtt{CPA-2}\le \frac{3}{2}\frac{q(q-1)}{2}\frac{1}{2^n} $$

Proof

On Misty R schemes with 3 rounds, the set of keys K is equal to $B_N^3$ with $N=2n$.

The transformation $M_R$ sends $[L_i,R_i]$ to $[U_i,T_i]$ such that:

$$ {\left\{ \begin{array}{ll} U_i = T_i\oplus S_i = f_2(R_i\oplus f_1(L_i))&{} \\ T_i = f_3(f_1(L_i)\oplus U_i) &{} \\ \end{array}\right. } $$

We are looking to $H=\{(f_1,f_2,f_3)\in B_n^3$ such that $\forall i, 1\le i \le q, M_R[L_i,R_i] = [U_i,T_i] \}$.

Let E be the set defined as follows: $E = \{[U_i,T_i], 1\le i \le q, U_i\ne U_j$ when $i\ne j\}$. We have:

$$ |E|\ge 2^{Nq}\left( 1 - \frac{q(q-1)}{2\cdot 2^ n}\right) $$

and we deduce that we have $\beta = \frac{q(q-1)}{2\cdot 2^n}$.

We select $f_1$ such that the values $R_i\oplus f_1(L_i)$ are pairwise distinct and the values $U_i\oplus f_1(L_i)$ are pairwise distinct with $[U_i,T_i]\in E$.

• $R_i\oplus f_1(L_i) = R_j\oplus f_1(L_j)$ implies that $L_i\ne L_j$ or $R_i\ne R_j$ since $i\ne j$. Then we have to remove at most $\frac{q(q-1)}{2\cdot 2^n}|B_n|$ permutations $f_1$.

• $f_1(L_i)\oplus U_i = f_1(L_j)\oplus U_j$ implies $L_i\ne L_j$ since we have $U_i\ne U_j$. Then we have to remove at most $\frac{q(q-1)}{2\cdot 2^n}|B_n|$ permutations $f_1$.

Now, the function $f_1$ is chosen and both $f_2$ and $f_3$ are fixed in q points pairwise distinct. Then we have:

$$ H\ge \frac{[B_n|^3}{2^{2nq}} \left( 1 - \frac{q(q-1)}{2^n}\right) = \frac{|K|}{2^{Nq}}\left( 1 - \frac{q(q-1)}{2^n}\right) $$

Then, by applying Theorem 1, we have $\varepsilon = \frac{q(q-1)}{2^n}$, $\beta = \frac{q(q-1)}{2\cdot 2^n}$ and

$$ Adv^\mathtt{CPA-2}\le \left( \frac{3}{2}\right) \frac{q(q-1)}{2}\frac{1}{2^n} $$

This concludes the proof.

6 Conclusion

In this paper, we provide a quantum cryptanalysis of four variants of Misty schemes. Indeed, we describe QCPA attacks that enable to distinguish 4-round Misty L and Misty LKF schemes, and 3-round Misty R and Misty RKF schemes, from random permutations in complexity $\mathcal {O}(n)$ instead of $\mathcal {O}(2^{n/2})$. Note that the QCPA attack on 3-round Misty R schemes is already known in [8]. Moreover, we extend the quantum distinguishing attack on 3-round Misty RKF schemes to obtain a key recovery attack against Misty RKF schemes which recovers the keys of d-round Misty RKF schemes in time $\mathcal {O}(2^{(d-3)n/2})$. Then, we provide the security proof of 3-round Misty R schemes against CPA-2 attack with a complexity in $\mathcal {O}(2^{n/2})$. Since the best known attack against the 3-round Misty R schemes has the same bound, this shows that the state of the art attack is then optimal.