Slip Effect on an Unsteady Ferromagnetic Fluid Flow Toward Stagnation Point Over a Stretching Sheet

Abstract

In this paper the heat transfer characteristics of ferromagnetic fluid flow towards stagnation point has been investigated numerically. In this study we deal with the slip boundary condition in the presence of electromagnetic field over a stretching sheet considering the Brownian motion impacts on ferrofluid viscosity. The mathematical model is presented in the form of partial differential equations. The governing equations determine the flow conditions, and these equations are reduced by similarity transformations. Finite difference method is implemented to acquire the solution of the problem. The effect of various physical parameters on the flow is also investigated. Graphs are plotted to examine the influence of pertinent flow parameters involved, such as velocity profile, temperature profile. The important physical quantities of skin friction coefficient and the local Nusselt number are also studied. It is observed that increasing value of ferromagnetic interaction parameter enhances the velocity field and reverse observation holds for temperature field.

1 Introduction

A ferrofluid is a liquid that becomes strongly magnetized in the presence of a magnetic field. These fluids are liquids such as kerosene, heptane, or water. Mechanics of ferrofluid motions is influenced by strong forces of magnetization. Ferrohydrodynamics usually deals the nonconducting liquids with magnetic properties. Ferrofluids are used to image magnetic domain structures on the surface of ferromagnetic materials. Many researchers analyze heat transfer through boundary layers over a stretching surface. This field has received a significant attention due to its useful engineering applications such as solar collectors, designing building, and thermal insulation and cooling of electronic components. Pioneer works have been done by Crane et al. [14] on the boundary layer flow of an electrically conducting viscous incompressible fluid over a stretching sheet. Elbashbeshy et al. [16] analyzed the laminar flow and heat transfer over an unsteady stretching surface when the surface temperature is constant. In the presence of variable surface temperature, Chakrabarti et al. [11] studied the magnetohydrodynamic MHD flow with uniform suction over a stretching sheet at different temperatures. Grubka et al. [21] studied the heat transfer analysis over a stretching surface in the presence of heat flux. Ellahi et al. [18] studied the influence of temperature-dependent viscosity on MHD flow of non-Newtonian fluid. The fact that velocity of pseudoplastic fluids decreases with decrease in Hartmann number was found by Khan et al. [32]. Hayat et al. [23] investigated the heat transfer effect of Eyring–Powell fluid considering exponentially stretching sheet. Narayana et al. [42] studied the influence of unsteadiness parameter on the flow of thin film over an unsteady stretching sheet. Abdel-Wahed and Emam [3] studied the MHD flow of nanofluid over a moving surface in a nanofluid under thermal radiation and convective boundary layer conditions. Abdelwahed et al. [2] and [4] inspected the variation of the thermal conductivity and viscosity on the MHD flow. Heat transfer in a Newtonian fluid in the presence of thermal conductivity was analyzed by Chiam et al. [13]. Khan and Pop et al. [30] studied the behavior of laminar flow of nanofluid over a stretching surface and investigated the influence of Brownian motion and thermophoresis parameters have inclination to the fluid temperature. Raju et al. [44] analyzed the heat and mass transfer on MHD flow over a permeable stretching sheet. Similar type of study of unsteady flow through a stretching sheet was performed by Mustafa et al. [41]. Aziz et al. [7] investigated the problem of mixed convective fluid flow along a stretching sheet with variable viscosity. Dutta et al. [15] determined the temperature distribution of heat flux over a stretching surface. Khan M. et al. [34] studied the Brownian motion and thermophoresis effect on heat and mass transfer. Hayat et al. [22] studied the boundary layer flow at stagnation point through a porous medium in the presence of thermal radiation over a stretching vertical plate. Ishak et al. [27] presented the concept of unsteadiness in mixed convection boundary layer flow and heat transfer through vertical stretching surface. Ibrahim and Bhandari et al. [25] analyzed the heat transfer on a permeable stretching surface due to a nanofluid with the influence of magnetic field and slip boundary conditions. Andersson et al. [5] examined impact of magnetic field on the flow of viscoelastic fluid over the stretching surface. Elbashbeshy et al. [17] obtained an analytical solution for the boundary layer flow over a moving plate. Khan M. et al. [33] studied the two-dimensional incompressible Casson nanofluid in the presence of magnetic field. Bachok et al. [9] inspected the flow of a nanofluid at stagnation point over a stretching or shrinking sheet. Effects of heat transfer in the presence of magnetic field on ferrofluid flow was reported by Sheikholeslami et al. [46]. Chen et al. [12] studied the effect of continuous surface on heat transform in laminar flow. Viscoelastic fluid characteristics were investigated in the presence of temperature viscosity by Faraz et al. [20]. Abbas et al. [1] investigated the flow of a viscous fluid at stagnation point over an unsteady surface. Stagnation point flow of Maxwell nanofluid was investigated by Khan et al. [35]. Mukhopadhyay and Battacharyya et al. [40] studied the influence of Maxwell fluid in the heat transfer across a stretching sheet. Bachok et al. [8] studied the two-dimensional stagnation point flow of a nanofluid over a stretching or shrinking sheet. Partha et al. [43] tackled the heat transfer over an exponential stretching vertical sheet with dissipation effect. Khan et al. [31] discussed the heat transform reactions of nanofluid with the effect of viscous dissipation and thermal radiation along a stretching sheet under the action of thermophoresis with the help of finite difference scheme. Maxwell fluid is one of the examples of non-Newtonian fluid. Mukhopadhyay and Bhattacharyya et al. [39] determined the influence of Maxwell parameters on the unsteady flow of Maxwell fluid with chemical reaction. Heat transfer analysis on boundary layer flow with specific entropy generation was studied by Ellahi et al. [19]. Khan M. et al. [36] developed a Cattaneo–Christov model by using Fourier’s and Fick’s laws and solved by numerical method. Bovand et al. [10] investigated the two-dimensional MHD flow in the porous medium in different laminar flows. The study showed that the steady flow depends on magnetic fields. The heat transfer and fluid flow investigation of different kinds of base fluids on a stretching sheet was performed by Makarem et al. [38]. Numerical investigation of heat transfer enhancement by utilizing the properties of nanofluids was conducted by Sheri and Thuma et al. [47]. Numerical solution of Maxwell fluid with the condition of viscous dissipation was obtained by Khan M. et al. [37]. Unsteady magnetohydrodynamics mixed convection flow in a rotating medium with double diffusion was studied by Jian and Ismail et al. [29]. Computation and physical aspects of MHD Prandtl–Eyring fluid flow analysis over a stretching sheet were investigated by Hussain and Malik et al. [24]. Jafer et al. [28] studied the effects of external magnetic field, viscous dissipation, and Joule heating on MHD flow and heat transfer over a stretching or shrinking sheet. Analysis of modified Fourier law in the flow of ferromagnetic, Powell-Eyring fluid considering two equal magnetic dipoles was performed by Ijaz and Zubair et al. [26]. The characteristic of dust particles in a ferromagnetic fluid with thermal convection in a porous medium was analyzed by Sharma et al. [45].

Most of the studies depict that properties of ferromagnetic fluid such as higher thermal conductivity and strong influence of magnetic field are useful in the analysis of numerous fluid problems. The ferromagnetic fluids have the properties of both liquid and magnetized solid particles. Ferromagnetic fluids flow toward magnetic field if the external magnetic field is applied, and the flow resistance increases using ferrofluids under an applied magnetic field for enhancement of heat transfer, and hence ferrofluids are more useful compared with conventional nanofluids.

2 Mathematical Formulation

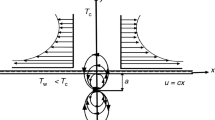
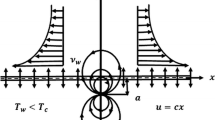
In this study we consider a two-dimensional unsteady ferromagnetic fluid flow over a stretching sheet in the presence of magnetic field with the dipole effects. Existence of magnetic field develops the higher intensity of the ferrofluid particles. Heat produced by the internal friction of the fluid, which is caused by the increase in temperature, affects the viscosity of the fluid, and so the viscosity of the fluid cannot be taken as constant. The rise of temperature leads to a local increase in the transport phenomenon by reducing the viscosity across the momentum boundary layer and so the heat transfer rate at the wall is also affected significantly. The study also characterized the phenomena of stagnation point. Coordinate X is taken along the stretching surface where the sheet is placed at y = 0. The velocity of the sheet u _w = c _p x, where c _p > 0 is stretching rate presented in Fig. 1. Y  is normal to the stretching surface where the fluid flow is restricted by y > 0. Flow takes place by the two equal and opposite forces in the direction of X-axis. A magnetic dipole is placed in the center with distance “a” from the surface. The temperature of the surface is T _w and Curie temperature is taken as T _c, and the temperature of ferrofluid from the surface of the sheet is T _∞ = T _c; when the ferrofluid reaches the curie temperature,

Fig. 1

Geometry of the flow

magnetization ends at this point. The obtained boundary layer equations that govern the flow and heat transfer of ferrofluid are written as

$$\displaystyle \begin{aligned} \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} \end{aligned} $$

(1)

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \frac{1}{\mu_e}\left(u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)& =&\displaystyle \frac{M}{\widehat{p}}\frac{\partial M}{\partial x}-\frac{1}{\widehat{p}}\frac{\partial H}{\partial x}+\frac{\mu}{\widehat{p}\mu_e}+\left(\frac{\partial^2u}{\partial x^2}+\frac{\partial ^2u }{\partial y^2}\right)\\ & &\displaystyle +\frac{g}{\widehat{p}\mu_e}g(T_c-T_f) \end{array} \end{aligned} $$

(2)

$$\displaystyle \begin{aligned} \frac{1}{\mu}\left(u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}\right)=\frac{M}{\widehat{p}}\frac{\partial M}{\partial y}-\frac{1}{\widehat{p}}\frac{\partial H}{\partial y}+\frac{\mu}{\widehat{p}\mu_e}\left(\frac{\partial^2v}{\partial x^2}+\frac{\partial ^2v }{\partial y^2}\right)+\frac{g\beta}{\widehat{p}\mu_e}g(T_c-T_f)\end{aligned} $$

(3)

$$\displaystyle \begin{aligned} & \frac{c_p}{\mu_e}\left(u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}\right)\frac{\partial M}{\partial x}+\frac{T}{\widehat{p}}\left(u\frac{\partial H}{\partial x}+v\frac{\partial H}{\partial y}\right)\frac{\partial M}{\partial T}= \frac{1}{\widehat{p}}\frac{\partial ^2T}{\partial y^2} + \frac{2\mu}{\widehat{p}\mu_e}\left[\left(\frac{\partial u}{\partial x}\right)^2 \right.\\ &\quad \left.+\left(\frac{\partial u}{\partial y}\right)^2+\left(\frac{\partial v}{\partial x}\right)^2+\left(\frac{\partial v}{\partial y}\right)^2+\frac{\partial v}{\partial x}\frac{\partial u}{\partial y}\right] \end{aligned} $$

(4)

In the above set of equations (u, v) are velocity components along x- and y-axis, respectively. T _f is the fluid temperature, μ represents the dynamic viscosity, $\widehat {p}$ signifies the fluid density, μ _e denotes the magnetic permeability, c _p signifies the specific heat, H represents the magnetic field, and M denotes the magnetization. The terms $\mu _eM\frac {\partial H}{\partial x}$ and $\mu _eM\frac {\partial H}{\partial y}$ given in Eqs. (2) and (3) represent the magnetic force and magnetic gradient corresponding to x- and y-coordinates, respectively. The corresponding boundary conditions expressed as

$$\displaystyle \begin{aligned} u=u_w+S\frac{\partial u}{\partial y} , v= -v_w,T_f=T_w+d_1 at y=0 \end{aligned} $$

(5)

$$\displaystyle \begin{aligned} u=0,T_f=T_c+d_2x,P+\frac{1}{2}\widehat{p}(u^2+v^2)=C at y \Rightarrow\infty \end{aligned} $$

(6)

where u _w and v _w are surface velocity along x- and y-direction, S represents the velocity slip factor, C is positive constant, and d ₁ and d ₂ are dimensionless constants.

3 Mathematical Analysis

$$\displaystyle \begin{aligned} \zeta=\frac{\lambda}{2\pi}\left(\frac{x}{x^2+(y+d)^2}\right) \end{aligned} $$

(7)

where λ represents the magnetic field strength. We know that body force is directly proportionate to gradient of the magnitude, and the magnitude H of the magnetic strength is represented as

$$\displaystyle \begin{aligned} H=\sqrt{\left(\frac{\partial \zeta}{\partial x}\right)^2+\left(\frac{\partial \zeta}{\partial y}\right)^2} \end{aligned} $$

(8)

Components of magnetic field H are

$$\displaystyle \begin{aligned} \frac{\partial H}{\partial x}= - \frac{\lambda}{2\pi}\left(\frac{2x}{(y+d)^4}\right) \end{aligned} $$

(9)

$$\displaystyle \begin{aligned} \frac{\partial H}{\partial x}= \frac{\lambda}{2\pi}\left(\frac{-2}{(y+d)^3}+\frac{4x^2}{(y+d)^5}\right) \end{aligned} $$

(10)

Magnetization M leads to the expression of temperature given by Anderson et al. [6]

$$\displaystyle \begin{aligned} M=K^c(T_c-T_f). \end{aligned} $$

(11)

4 Solution Procedure

It is pertinent to introduce the dimensionless variables and transformation considered by [6]

$$\displaystyle \begin{aligned} \psi(\tau,\eta)=\frac{\mu}{\widehat{p}}\tau f(\eta) \end{aligned} $$

(12)

$$\displaystyle \begin{aligned} \alpha(\tau,\eta)=\frac{T_c-T_f}{T_c-T_w}=\theta(\eta)+\tau^2\Phi(\eta) \end{aligned} $$

(13)

where ψ(τ, η) and α(τ, η) are dimensionless steam function and temperature, respectively, and dimensionless coordinates τ and η are as follows:

$$\displaystyle \begin{aligned} \tau = \sqrt{\frac{c\widehat{p}}{\mu}}x ,\eta = \sqrt{\frac{c\widehat{p}}{\mu}}y \end{aligned} $$

(14)

$$\displaystyle \begin{aligned} u=\frac{\partial \psi}{\partial y}=cx \cdot f'(\eta) \end{aligned} $$

(15)

$$\displaystyle \begin{aligned} v=-\frac{\partial \psi}{\partial x}= - (cv)^{\frac{1}{2}}\cdot f(\eta) \end{aligned} $$

(16)

Substituting Eqs. (12)–(16) into Eqs. (2)–(4) and comparing coefficients up to n ², we get the reduced nonlinear ordinary differential equations:

$$\displaystyle \begin{aligned} f'''+ff''-f^{\prime 2} +\frac{2\beta \theta}{(\eta+\delta_1)^4}N[2ff''''-(f^{\prime\prime})^2]=0 \end{aligned} $$

(17)

$$\displaystyle \begin{aligned} \theta''+Pr(f\theta'-2f'\theta)+\frac{2N\beta(\theta-w)f}{(\eta+\delta_1)^3}-4N(f')^2+2(w^2-1)=0 \end{aligned} $$

(18)

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} & &\displaystyle \phi''+\frac{2N\beta f\theta_2}{(\eta+\delta_1)^3}- Pr(4f'\phi'-f\phi)-N\beta(\theta-w)\left[\frac{4f}{(\eta+\delta_1)^5}+\frac{2f'}{(\eta+\delta_1)^4}\right]\\ & &\displaystyle \quad -N(f'')^2=0 \end{array} \end{aligned} $$

(19)

Also boundary conditions (5) and (6) are converted as

$$\displaystyle \begin{aligned} f=S,f'=1,\theta = 1+\alpha f''(0) ,\phi =0 , \text{ at }\, \eta = 0 \end{aligned} $$

(20)

$$\displaystyle \begin{aligned} f' \rightarrow 0 ,\theta \rightarrow 0,\phi \rightarrow 0 \, \text{ at }\, \eta \rightarrow \infty \end{aligned} $$

(21)

In the above system of nonlinear equations, β (ferromagnetic interaction parameter), N (viscoelastic parameter), Pr (Prandtl number), w (dimensionless curie temperature ratio), λ (dimensionless distance), and γ (viscous dissipation) are defined as

$$\displaystyle \begin{aligned} \begin{array}{rcl} \beta = \frac{\lambda\widehat{p}K^c}{2\pi\mu_e^2}\mu_e(T_c-T_w), N =\frac{c\mu^2}{\widehat{p}(T_c-T_w)}, \mathrm{Pr}=\frac{\mu c_p}{k} , \end{array} \end{aligned} $$

$$\displaystyle \begin{aligned} \begin{array}{rcl} w=\frac{T_c}{T_c-T_w}, \lambda=\sqrt{\frac{k\widehat{p}d^2}{\mu}}, \gamma=\frac{c\mu^2}{\widehat{p}k(T_c-T_w)} \end{array} \end{aligned} $$

The skin friction coefficient and Nusselt number are defined as

$$\displaystyle \begin{aligned} C_{f_x} =-\frac{2\tau_w}{\rho(cx)^2} \end{aligned} $$

(22)

(23)

where

$$\displaystyle \begin{aligned}C_fRe_x^{\frac{1}{2}} = -2(1-N*)f''(0)\end{aligned}$$

$$\displaystyle \begin{aligned}Nu_x = -[(\theta'(0)+\xi^2\phi'(0)]Re_x^{\frac{1}{2}}\end{aligned}$$

We first transformed differential equations (12)–(16) together with boundary conditions into a system of set of first-order ODE, which must be solved numerically by finite difference method. The step size is taken as ∇η = 0.01. We choose η(max) = 15 with simulation error chosen as 10⁵ in order to assure asymptotic convergence criteria. Trial values of f‴(0), f″(0), θ′(0), and Φ′(0) were adjusted iteratively in order to satisfy the far-field boundary condition.

5 Results and Discussion

The Influence of Ferromagnetic Interaction Parameter (β)

The fixed values of these physical parameters are taken as Pr = 7, N = 0.01, 𝜖 = 2.0, andδ ₁ = 0. Figures 2 and 3 are plotted to examine the influence of ferromagnetic parameter β on velocity profile f(η) and temperature profile θ(η), respectively. As we increase the value of ferromagnetic parameter β, viscosity of the ferrofluid rises up and as a result velocity profile shows the decreasing behavior. This behavior occurs due to microsized particles in ferrofluid. It is observed that temperature profile increases significantly as β (ferromagnetic interaction parameter) increases. This phenomenon happened due to the interaction between ferrofluid particles. Thus velocity profile f′(η) reduces due to contact of ferrofluid particles and magnetic field, but the reverse condition is observed in temperature profile θ(η).

Fig. 2

Impact of β on f′(η)

Fig. 3

Impact of β on θ(η)

The Influence of Viscoelastic Parameter (N)

Figure 4 shows the impact of viscoelastic parameter (N) on velocity profile, as the increasing value of N enhances the velocity profile gradually. From this graph, it is confirmed that rising the values of viscoelastic parameter N restricts the fluid motion near the stretching sheet, while it assists the fluid motion far away from the stretching sheet. Increasing values of N permit the fluid to flow at a faster rate, because there is a decrease in the heat transfer. So by enlarging the values of N, the dimensionless stream function and velocity increase. Figure 5 illustrates the effect of viscoelastic parameter N on temperature profile θ(η) against η and thickness of temperature profile decreases with increase in viscoelastic parameter.

Fig. 4

Impact of N on f′(η)

Fig. 5

Impact of N on θ(η)

Analysis of Skin Friction Coefficient and Local Nusselt Number (Effect of Ratio 𝜖)

Figure 6 designated the impact of 𝜖 on skin friction coefficient. The enhancement in the value 𝜖 reduces the skin friction coefficient. For upper values of 𝜖, the velocity of ferrofluid controls the velocity of plate, and due to this, skin friction coefficient decreases. We can observe in Fig. 7 that the local Nusselt number reduces with the increasing value of β.

Fig. 6

Impact of ε on Skin friction coefficient

Fig. 7

Impact of ε on Local Nusselt number

Effect of Velocity Slip Parameter

Figure 8 shows that skin friction coefficient increases with variation of β; however, the reverse is true for slip parameter α. Skin friction coefficient decreases with the increase in slip parameter. The maximum surface sheer stress occurs in no slip condition (α = 0). The local Nusselt number presented in Fig. 9 decreases for both slip parameter α and ferromagnetic field β with the increasing value of slip parameter.

Fig. 8

Impact of α on Skin friction coefficient

Fig. 9

Impact of α on Local Nusselt number

6 Concluding Remarks

The two-dimensional ferrofluid problem towards stagnation point with slip boundary condition has been studied in this paper. Using similarity transformations, the governing equations were converted into nonlinear ordinary differential equations and the equations were solved numerically. The major findings of this study are as follows:

• 1. Velocity profilef′(η) decreases with the effect of ferromagnetic interaction parameter β. Thus temperature profile increases with the increase in β.

• 2. Velocity profile increases with the increase in viscoelastic parameter N. Temperature profile decreases with the increase in N.

• 3. The skin friction coefficient reduces with the increase in ratio (𝜖). Similar impact of ferromagnetic parameter β is observed on local Nusselt number.

• 4. The skin friction coefficient and local Nusselt number both decrease with the increase in slip parameter α.